旋转设备的润滑与密封问题是制约设备性能的关键因素[1-2],高速工况下的轴承润滑多采用喷射润滑、油气润滑和油雾润滑等微量高效润滑形式[3-4].喷射润滑通过轴承使小油滴与空气充分均匀混合形成油气两相润滑介质[5-6].油气润滑是一种滑油消耗量是纯油润滑百分之一的环状流微量润滑[7-8].油雾润滑以压缩空气为载体,利用油雾发生器形成微米级的雾化油滴[9-10].相应的油气两相密封处于高转速、变压差、变载荷、油气两相混合介质、操作条件多变等复杂工况[11-12],对密封的追随动态性能要求非常高.良好的追随动态特性可防止因密封系统受到干扰时产生端面接触或间隙过大,从而避免密封环剧烈磨损或密封泄漏量过大,保证密封运转的稳定性.近年来,密封的追随动态特性因其重要性已受到国内外众多学者的关注和重视,邓国强等[13]对国内外近年来螺旋槽干气密封动态特性的研究现状进行了总结综述,提到了步进法、直接数值频率响应法、摄动法等多种理论研究方法. Faria[14]基于Galerkin加权残差法编写了用于分析干气密封动态特性的有限元程序,在恒膜厚下分析了扰动频率对密封动态刚度和阻尼的影响.宋鹏云等[15]采用维里方程修正实际气体效应的气体润滑雷诺方程,基于摄动法和有限差分法分析了实际气体效应对T形槽干气密封的气膜动态刚度和阻尼等动态特性的影响.徐恒杰等[16]考虑实际气体效应和阻塞流效应,分析了干气密封操作参数对气膜动态刚度及阻尼的影响规律. Green等[17]提出了一种直接数值模拟解决方案,用于分析非接触式气体润滑密封在密封间隙呈收敛锥度时的动态特性,结果表明存在两种不稳定模式. Miller等[18]同时利用有限单元法和有限体积法,求解了气体润滑方程和补偿环运动方程来研究密封的动态特性,给出了对静环未对准和动环跳动的瞬态响应的示例.李双喜等[19]基于高阶函数的有限元方法,分析了高速螺旋槽端面密封的轴向微扰特性,求得了密封动态刚度和阻尼,并分析了压缩因数和扰动频率因数对动态系数的影响. Ruan[20-21]基于气体润滑螺旋槽密封的动态刚度和阻尼系数,在三个自由度上分析了补偿环在非补偿环扰动下的追随响应特性,给出了螺旋槽气体密封在瞬态运行时具有代表性的动态跟踪运动和关键密封特性.张树强等[22-23]基于摄动法求解了表征动静压混合式气体密封动态特性的气膜刚度和阻尼系数,研究了密封在受到三个方向简谐激励作用下的动态特性,并得到了阻封气压力对动态特性的影响.陈源等[24-25]在同时考虑轴向和角向气膜扰动的共同作用下,建立了挠性安装静环运动方程,分析了膜厚的扰动行为,提出以最大端面膜厚扰动量峰值和受干扰后的稳定时间作为表征密封追随动态特性的参数,分别研究了三种典型结构干气密封的追随动态特性.
前人对密封补偿环响应运动和追随动态特性的研究主要针对气相润滑密封,且多数没有同时考虑力变形和热变形对密封追随动态特性的影响,但其研究方法和研究成果对油气两相润滑动压密封追随特性的研究具有指导和借鉴意义.本文在前人研究基础上,采用流固热耦合研究方法,对比分析油气两相润滑和纯气相润滑的密封补偿环响应运动,揭示转速、压差、油气比、弹簧刚度以及O形圈阻尼对密封追随动态特性的影响规律.
1 结构原理 1.1 结构形式如图 1所示为油气两相动压密封的示意图,润滑油由图中喷油嘴喷出,经轴承与空气充分混合成油气两相介质.油气两相流体在轴承腔内的流动形式为油膜、油滴与空气共存,其中液相占密封腔空间体积的2%~20%,油滴颗粒直径大小为3~7μm[26].密封端面外侧为油气两相介质,内侧为空气.动环随轴旋转,动环与旋转轴之间的压紧力由传动轴套提供,石墨静环作为补偿环,波形弹簧为补偿元件,O形圈为辅助密封,保证密封形成封闭空间.
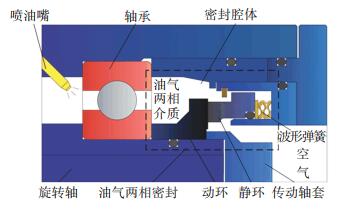
|
图 1 油气两相密封示意图 Fig. 1 Diagram of oil-gas mixed-phase seal |
油气两相动压密封的主要作用是防止润滑油从轴承腔内部泄漏至空气中,因此在动环端面的内侧上开设微米级的动压螺旋槽.当密封运转时,动环随着旋转轴旋转,油气两相流体在压差流的作用下进入密封端面.由于螺旋槽的存在,油气两相流体产生动态效应并提供开启力,以克服静环受到的由介质压力和波形弹簧的弹力组合成的闭合力,在密封端面间形成一个微米级的流体膜,维持密封端面处于非接触的状态.同时油气两相介质在密封环端面间提供润滑作用,防止动静环端面产生磨损.当受到干扰时,静环随动环追随运动,良好的追随动态特性能够有效避免密封环间隙过大、剧烈磨损或密封泄漏量过大,保证密封运转的稳定性.动环密封端面结构如图 2所示.
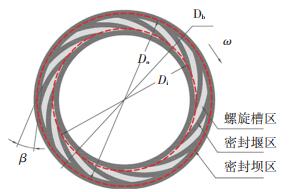
|
Db—密封坝直径;Do—端面外径;Di—端面内径;β—螺旋角;ω—旋转方向 图 2 动环的端面结构 Fig. 2 End face structure of the rotary ring |
油气两相介质侧的压力高于空气侧,部分流体会随着压差流的作用泄漏至低压侧,即密封环的内侧.同时,存在于密封环内侧的螺旋槽将部分泄漏至低压侧的流体重新泵回密封端面,从而保证了润滑油的低泄漏.位于低压侧的部分空气同样也会被螺旋槽泵吸至密封端面,在动静环端面低压侧形成一圈气膜,在理想状态下,可实现润滑油的零泄漏.
1.3 密封参数| 表 1 结构参数 Tab. 1 Parameters of the structure |
| 表 2 分析参数设置 Tab. 2 Parameters of the analysis |
假设密封腔中油滴与空气均匀混合,油滴彼此间的相互作用忽略不计,且油滴颗粒互相之间不产生碰撞、破碎或聚合.密封在高速运转下的端面间油滴与空气以相同的速度进行运动,端面间的端面间的油气两相介质流场可分解为单个单元分析.油滴在密封腔气体中所占的体积率(即油气比)为c,密封端面间流体膜的膜厚为h,设油滴在混合介质中的位置为σh(0≤σ≤1-c),u1、u2为密封静环和动环的转速,由于静环的转速为0,因此有u1=0.沿x轴流场中单个流体流动单元的力平衡方程为
| $ p{\rm{d}}z + (\tau + \frac{{\partial \tau }}{{\partial z}}{\rm{d}}z){\rm{d}}x = (p + \frac{{\partial p}}{{\partial x}}{\rm{d}}x){\rm{d}}z + \tau {\rm{d}}x. $ | (1) |
式中:
| $ \mu \frac{{{\partial ^2}u}}{{\partial {z^2}}} = \frac{{\partial p}}{{\partial x}}. $ | (2) |
其中边界条件为
| $ \begin{array}{*{20}{c}} {u = {u_1} = 0(z = 0),u = {u_2}(z = h),}\\ {\frac{{\partial u}}{{\partial z}}|{{\left. {z = \sigma h = \frac{{\partial u}}{{\partial z}}} \right|}_{z = (\sigma + c)h}}.} \end{array} $ |
式(2)在经过积分之后,可得速度u为
| $ u = \left\{ \begin{array}{l} {u_1} + \frac{{{u_2}}}{{(1 - c)h}} - \frac{1}{{2\mu }}\frac{{\partial p}}{{\partial x}}[(1 - c)hz - {z^2}],\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le z \le \sigma h;\\ {u_1} + \frac{{{u_2}}}{{(1 - c)h}} - \frac{{{z^2}}}{{2\mu }}\frac{{\partial p}}{{\partial x}}[(1 - c)\sigma - {\sigma ^2}],\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma h \le z \le (c + \sigma )h;\\ {u_2} + \frac{{{u_2}}}{{(1 - c)h}}(z - h) - \frac{1}{{2\mu }}\frac{{\partial p}}{{\partial x}}[(1 - c)h(z -\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} h) + {(z - h)^2}],\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (c + \sigma )h \le z \le h. \end{array} \right. $ | (3) |
利用速度u可得到流量表达式:
| $ \begin{array}{*{20}{l}} {{q_{\rm{x}}} = \int\limits_0^h {u{\rm{d}}z} = {u_2}(1 - c - \sigma )h + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{u_2}h}}{{2(1 - c)}}[ - {{(1 - c)}^2} + 2\sigma ] - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{h^3}}}{{12\mu }}\frac{{\partial p}}{{\partial x}}[{{(1 - c)}^3} - 6\alpha \beta (1 - c - \sigma )].} \end{array} $ | (4) |
油滴与空气均匀混合,由此得到在流通截面上油气两相流体的平均流量为
| $ \overline {{q_x}} = \frac{{\int_0^{(1 - c)h} {{q_x}} {\rm{d}}z}}{{\int_0^{(1 - c)h} {\rm{d}} z}} = \frac{{{u_2}h}}{2} - \frac{{{h^3}}}{{12\mu }}\frac{{\partial p}}{{\partial x}}{(1 - c)^3}. $ | (5) |
其中,取油气两相流体的等效粘度为μm,则平均流量有如下表达式:
| $ \overline {{q_x}} = \frac{{{u_2}h}}{2} - \frac{{{h^3}}}{{12{\mu _{\rm{m}}}}}\frac{{\partial p}}{{\partial x}}. $ | (6) |
由式(5)和式(6)可得
| $ {\mu _{\rm{m}}} = \frac{\mu }{{{{(1 - c)}^3}}}. $ | (7) |
气体的粘度会因为温度和压力的变化而变化,但本文在常温下分析,因此不考虑温度对气体粘度的影响,且通常情况下,压力对其影响很小,可以忽略.因此,在油气比不变的情况下,粘度为常数.油气两相流体的等效密度为
| $ {\rho _{\rm{m}}} = {\rho _{{\rm{liq}}}}c + {\rho _{{\rm{gas}}}}(1 - c). $ | (8) |
由油气两相流体物理模型可知,端面间流体符合理想气体的状态方程:
| $ p = {\rho _{\rm{m}}}{R_{\rm{m}}}T. $ | (9) |
式中:Rm为等效气体常数.等效气体常数和等效分子质量的表达式分别如下所示:
| $ {R_{\rm{m}}} = \frac{{8.314}}{{{M_{\rm{m}}}}}, $ | (10) |
| $ {M_{\rm{m}}} = {M_{{\rm{gas}}}} \times (1 - c) + {M_{{\rm{liq}}}} \times c. $ | (11) |
压力控制方程(Reynolds方程)是可以描述油气两相动压密封的密封端面间流体膜压力分布的基本方程,因此,油气两相流体的二维极坐标压力控制方程经修正后的表达式为
| $ \frac{\partial }{{{r^2}\partial \theta }}(\frac{{{\rho _{\rm{m}}}{h^3}}}{{{\mu _{\rm{m}}}}}\frac{{\partial p}}{{\partial \theta }}) + \frac{\partial }{{r\partial r}}(\frac{{r{\rho _{\rm{m}}}{h^3}}}{{{\mu _{\rm{m}}}}}\frac{{\partial p}}{{\partial r}}) = 6\omega \frac{{\partial ({\rho _{\rm{m}}}h)}}{{\partial \theta }}. $ | (12) |
在油气两相动压密封系统中,可将补偿环(静环)视为具有刚度和阻尼特性的支撑系统,如图 3所示. 图 4为油气两相动压密封动态特性分析的动力学模型,密封转轴中心线与z轴重合,坐标系的原点o假定为静环的稳态位置h0(即动平衡位置).密封系统受到微小扰动时,静环在稳态位置上沿z轴向、绕x轴和绕y轴存在轴向振动和角向摆动,这三个方向的运动分别见图 4中Δz、Δα和Δβ.补偿环的响应运动可以利用油气两相介质流体膜的刚度和阻尼来表征,通过求解流体膜的刚度系数和阻尼系数,可分析密封的追随动态特性.
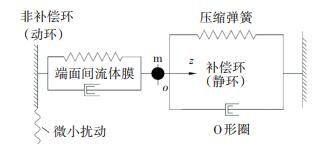
|
图 3 追随动态特性分析模型示意图 Fig. 3 Analysis model of dynamic tracking characteristics |
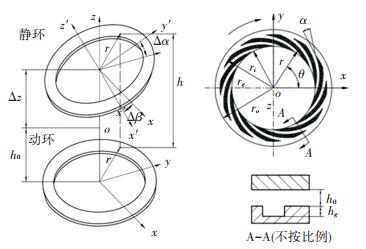
|
图 4 油气两相动压密封动力学模型 Fig. 4 Dynamics model of oil-gas two-phase hydrodynamic seals |
将图 4中补偿环的微扰运动定义为简谐运动:
| $ \left\{ {\begin{array}{*{20}{l}} {z(t) = |\Delta z|{{\rm{e}}^{{\rm{i}}vt}},}\\ {\alpha (t) = |\Delta \alpha |{{\rm{e}}^{{\rm{i}}vt}},}\\ {\beta (t) = |\Delta \beta |{{\rm{e}}^{{\rm{i}}vt}}.} \end{array}} \right. $ | (13) |
式中:t代表时间;i为虚数单位;v为补偿环受到微扰的频率.对式(13)求导得
| $ \left\{ {\begin{array}{*{20}{l}} {\dot z(t) = {\rm{i}}v|\Delta z|{{\rm{e}}^{{\rm{i}}vt}} = {\rm{i}}vz(t),}\\ {\dot \alpha (t) = {\rm{i}}v|\Delta \alpha |{{\rm{e}}^{{\rm{i}}vt}} = {\rm{i}}v\alpha (t),}\\ {\dot \beta (t) = {\rm{i}}v|\Delta \beta |{{\rm{e}}^{{\rm{i}}vt}} = {\rm{i}}v\beta (t).} \end{array}} \right. $ | (14) |
端面间油气两相介质流体膜的压力扰动由补偿环的微扰运动引起,对上式中的变量进行泰勒级数展开,可得端面间流体膜的瞬态压力表达式为
| $ \begin{array}{l} p = {\left. {{p_0} + {p^\prime } = {p_0} + \frac{{\partial p}}{{\partial z}}} \right|_0}{\left. {z(t) + \frac{{\partial p}}{{\partial \alpha }}} \right|_0}{\left. {\alpha (t) + \frac{{\partial p}}{{\partial \beta }}} \right|_0}\beta (t) + \\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial p}}{{\partial \dot z}}} \right|_0}{\left. {\dot z(t) + \frac{{\partial p}}{{\partial \dot \alpha }}} \right|_0}{\left. {\dot \alpha (t) + \frac{{\partial p}}{{\partial \dot \beta }}} \right|_0}\dot \beta (t). \end{array} $ | (15) |
式中:p0为端面间油气两相介质流体膜的稳态压力分布,与此相对应的工作膜厚(平衡膜厚)为h0;p′为流体膜微扰压力.分别定义微扰压力的实部和虚部为
| $ \left\{ {\begin{array}{*{20}{l}} {{p_{z{\rm{r}}}} = {{\left. {\frac{{\partial p}}{{\partial z}}} \right|}_0}}\\ {{p_{z{\rm{i}}}} = {{\left. {v\frac{{\partial p}}{{\partial \dot z}}} \right|}_0}} \end{array}} \right.;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {{p_{\alpha {\rm{r}}}} = {{\left. {\frac{{\partial p}}{{\partial \alpha }}} \right|}_0}}\\ {{p_{\alpha {\rm{i}}}} = {{\left. {v\frac{{\partial p}}{{\partial \dot \alpha }}} \right|}_0}} \end{array}} \right.;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {{{\left. {{p_{\beta {\rm{r}}}} = \frac{{\partial p}}{{\partial \beta }}} \right|}_0}}\\ {{{\left. {{p_{\beta {\rm{i}}}} = v\frac{{\partial p}}{{\partial \dot \beta }}} \right|}_0}} \end{array}} \right.. $ | (16) |
式中:i、r分别代表流体膜微扰压力的虚部和实部.
补偿环受到微扰时产生微扰压力p′,由此引起的油气两相介质流体膜对补偿环的沿z轴的轴向力Fz、绕x轴的角向偏转力矩Mx与绕y轴的角向偏转力矩My的增量,其表达式如下:
| $ \left( {\begin{array}{*{20}{c}} {\Delta {F_z}}\\ {\Delta {M_x}}\\ {\Delta {M_y}} \end{array}} \right) = \int\limits_0^{2{\pi ^r}} {\int\limits_{{r_i}}^o {\left( {\begin{array}{*{20}{c}} 1\\ {r{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }\\ { - r{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta } \end{array}} \right){p^\prime }r{\rm{d}}r{\rm{d}}\theta } } . $ | (17) |
式中:ro、ri分别为密封环的外半径和内半径.结合式(15)、式(16)和式(17)可得
| $ \begin{array}{l} \left( {\begin{array}{*{20}{c}} {\Delta {F_z}}\\ {\Delta {M_x}}\\ {\Delta {M_y}} \end{array}} \right) = \int\limits_0^{2{\pi ^r}} {\int\limits_{{r_i}}^o {\left[ {\begin{array}{*{20}{c}} {{p_{z{\rm{r}}}}}&{{p_{\alpha {\rm{r}}}}}&{{p_{\beta {\rm{r}}}}}\\ {r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{z{\rm{r}}}}}&{r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{\alpha {\rm{r}}}}}&{r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{\beta {\rm{r}}}}}\\ { - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{z{\rm{r}}}}}&{ - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{\alpha {\rm{r}}}}}&{ - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{\beta {\rm{r}}}}} \end{array}} \right]r{\rm{d}}r{\rm{d}}\theta } } \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{l}} {z(t)}\\ {\alpha (t)}\\ {\beta (t)} \end{array}} \right] + \frac{1}{v}\int\limits_0^{2{\pi ^r}} {\int\limits_{{r_i}}^o {\left[ {\begin{array}{*{20}{c}} {{p_{z{\rm{i}}}}}&{{p_{\alpha {\rm{i}}}}}&{{p_{\beta {\rm{i}}}}}\\ {r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{z{\rm{i}}}}}&{r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{\alpha {\rm{i}}}}}&{r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{\beta {\rm{i}}}}}\\ { - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{z{\rm{i}}}}}&{ - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{\alpha {\rm{i}}}}}&{ - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{\beta {\rm{i}}}}} \end{array}} \right]} } \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r{\rm{d}}r{\rm{d}}\theta \left[ {\begin{array}{*{20}{c}} {\dot z(t)}\\ {\dot \alpha (t)}\\ {\dot \beta (t)} \end{array}} \right]. \end{array} $ | (18) |
因此油气两相介质流体膜对补偿环的轴向力Fz和角向偏转力矩Mx、My的增量表达式可用刚度和阻尼的形式表达为
| $ \begin{array}{l} \left( {\begin{array}{*{20}{c}} {\Delta {F_z}}\\ {\Delta {M_x}}\\ {\Delta {M_y}} \end{array}} \right) = - \left[ {\begin{array}{*{20}{l}} {{k_{zz}}}&{{k_{zx}}}&{{k_{zy}}}\\ {{k_{xz}}}&{{k_{xx}}}&{{k_{xy}}}\\ {{k_{yz}}}&{{k_{yx}}}&{{k_{yy}}} \end{array}} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {z(t)}\\ {\alpha (t)}\\ {\beta (t)} \end{array}} \right] - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{c_{zz}}}&{{c_{zx}}}&{{c_{zy}}}\\ {{c_{xz}}}&{{c_{xx}}}&{{c_{xy}}}\\ {{c_{yz}}}&{{c_{yx}}}&{{c_{yy}}} \end{array}} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {\dot z(t)}\\ {\dot \alpha (t)}\\ {\dot \beta (t)} \end{array}} \right]. \end{array} $ | (19) |
式中:kij,cij(i, j=z, x, y)代表油气两相介质流体膜的动态性能参数,其中负号表示流体膜阻止补偿环的运动.
由式(6)和式(7)可得油气两相介质流体膜的动态性能参数可由微扰压力实部和虚部表示为
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{l}} {{k_{zz}}}&{{k_{zx}}}&{{k_{zy}}}\\ {{k_{xz}}}&{{k_{xx}}}&{{k_{xy}}}\\ {{k_{yz}}}&{{k_{yx}}}&{{k_{yy}}} \end{array}} \right] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \int\limits_0^{2{\pi ^r}} {\int\limits_{{r_i}}^o {\left[ {\begin{array}{*{20}{c}} {{p_{z{\rm{r}}}}}&{{p_{\alpha {\rm{r}}}}}&{{p_{\beta {\rm{r}}}}}\\ {r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{z{\rm{r}}}}}&{r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{\alpha {\rm{r}}}}}&{r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{\beta {\rm{r}}}}}\\ { - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{z{\rm{r}}}}}&{ - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{\alpha {\rm{r}}}}}&{ - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{\beta {\rm{r}}}}} \end{array}} \right]r{\rm{d}}r{\rm{d}}\theta ,} } \\ {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{c_{zz}}}&{{c_{zx}}}&{{c_{zy}}}\\ {{c_{xz}}}&{{c_{xx}}}&{{c_{xy}}}\\ {{c_{yz}}}&{{c_{yx}}}&{{c_{yy}}} \end{array}} \right] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{1}{v}\int\limits_0^{2{\pi ^r}} {\int\limits_{{r_i}}^o {\left[ {\begin{array}{*{20}{c}} {{p_{z{\rm{i}}}}}&{{p_{\alpha {\rm{i}}}}}&{{p_{\beta {\rm{i}}}}}\\ {r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{z{\rm{i}}}}}&{r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{\alpha {\rm{i}}}}}&{r{\rm{sin}}{\kern 1pt} {\kern 1pt} \theta {p_{\beta {\rm{i}}}}}\\ { - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{z{\rm{i}}}}}&{ - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{\alpha {\rm{i}}}}}&{ - r{\rm{cos}}{\kern 1pt} {\kern 1pt} \theta {p_{\beta {\rm{i}}}}} \end{array}} \right]} } r{\rm{d}}r{\rm{d}}\theta . \end{array} $ | (20) |
式(8)即为流体膜9个动态刚度系数和9个动态阻尼系数的表达式.
2.3 流固热耦合分析模型密封端面间的油气两相介质流体膜部分为密封环的变形提供流体膜压力,密封环的变形则会影响到流体膜的膜厚进而改变油气两相介质流体膜压力,密封环变形和油气两相介质流体膜压力互相之间的影响是一个耦合的过程.密封环受到热应力的影响产生热变形,同样会影响到油气两相介质流体膜压力,这使得密封环变形和油气两相介质流体膜压力之间互相影响,最终形成一个新的动态稳定状态,各分析模块之间的影响关系如图 5所示.
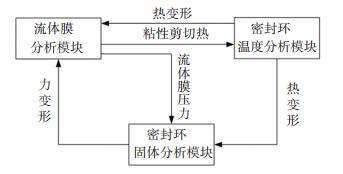
|
图 5 流固热耦合分析模块之间的影响关系 Fig. 5 Relationship between flow-solid-thermal coupling analysis modules |
在MATLAB中建立密封环与油气两相介质流体膜的有限元耦合模型,油气两相介质流体膜的分布同周期性螺旋槽一样,具有周期性,选取流体膜的单个周期作为分析区域建立有限元模型,如图 6所示.选取单个周期可以对流体膜有限元模型进行较为精细的网格划分,保证了网格精细度和计算准确度.
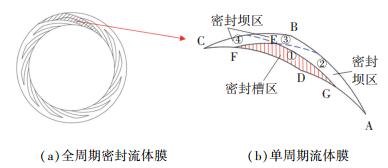
|
图 6 流体膜数学模型单元 Fig. 6 The element of fluid film mathematical model |
在MATLAB编程中,膜厚变量的值可以通过给不同区域的网格赋值来实现,因此不考虑膜厚方向的建模,而是采用平面4节点等参元建立2D的流体膜有限元模型.在螺旋槽的边界线上,即槽区和坝区、槽区和堰区的交界线上,由于微米级螺旋槽的存在,流体膜的厚度存在着突变,因此需要将网格的边界线设成与槽区边界线重合.因此对流体膜有限元模型进行了四个部分的划分,如图(b)所示,分为①、②、③、④四个区域,确保螺旋槽的边界线DGEF及其交点与网格结点重合.
对于网格精密程度要求很高的模型,在编制网格结点顺序的时候,需要注意到网格结点的一致性和规律性,网格的具体划分如表 3所示.考虑到流体膜模型周向网格数量小于径向网格数量的特点,为了得到具有最小带宽的总刚矩阵,对流体膜模型在编制网格单元及结点时,采用先周向后轴向的顺序进行.经网格无关性验证,流体膜单周期的有限元模型划分后包含312个单元,351个结点.
| 表 3 流体膜有限元模型网格划分 Tab. 3 Meshing of fluid film finite element model |
与流体膜取一个周期建模相同,在对密封的动环和静环建模时,同样取一个周期.考虑密封环的轴向变形对端面间流体膜厚度的影响,密封端面上的网格划分需要与流体膜的网格划分一致,保证螺旋槽的边界线和角点都落在网格结点上.密封环模型在轴向上每层的网格划分与流体膜模型的网格划分方法相同. 图 7为密封环结构示意图.

|
图 7 密封环结构示意图 Fig. 7 Schematic diagram of three-dimensional model of seal rings |
在密封环模型网格划分中,网格单元的编号顺序为周向—径向—轴向.每层网格按照逆时针的方向,从内而外地对每个结点编号.每个结点与其坐标值相对应,所有的结点和其储存的结点坐标值形成结点信息数组.另外,由于密封环固体模型存在着阶梯型结构,因此在为网格结点编号时,为了得到最小带宽的总刚矩阵,将固体模型沿着突变处分为若干块,先后为每一个结点以轴向—周向—径向的顺序进行编号.具体的密封环网格单元及结点的编号顺序如图 8所示. x、y、z分别代表径向、周向和轴向.经过网格无关性验证,划分出动环的网格单元总计2 040个,结点总计2 626个,静环的网格单元总计1 740个,结点2 262个.
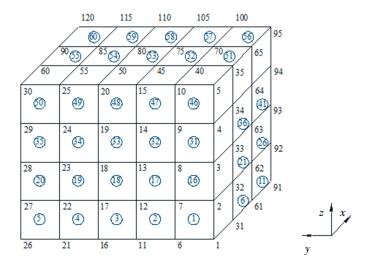
|
图 8 密封环网格单元及结点编号顺序示意图 Fig. 8 Numbering sequence diagram of seal rings grid unit and node |
考虑密封系统内的密封环受到的力载荷和热载荷,计算在流固热耦合作用下油气两相动压密封动态特性参数.补偿环在轴向、角向上的运动是互相解耦的,补偿环在三个方向上的运动方程[27-28]为
| $ m\ddot z + ({c_{zz}} + {c_s})\dot z + ({k_{zz}} + {k_s})z = {c_{zz}}{\dot z_r} + {k_{zz}}{z_r}, $ | (21) |
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{I_x}}&0\\ 0&{{I_y}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\ddot \alpha }\\ \beta \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{c_{xx}} + {c_{sx}}}&{{c_{xy}}}\\ {{c_{yx}}}&{{c_{yy}} + {c_{sy}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot \alpha }\\ {\dot \beta } \end{array}} \right] + \\ \left[ {\begin{array}{*{20}{c}} {{k_{xx}} + {k_{sx}}}&{{k_{xy}}}\\ {{k_{yx}}}&{{k_{yy}} + {k_{sy}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} \alpha \\ \beta \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {{c_{xx}}}&{{c_{xy}}}\\ {{c_{yx}}}&{{c_{yy}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot \alpha }_r}}\\ {{{\dot \beta }_r}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{k_{xx}}}&{{k_{xy}}}\\ {{k_{yx}}}&{{k_{yy}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\alpha _r}}\\ {{\beta _r}} \end{array}} \right]. \end{array} $ | (22) |
式中:z为密封环补偿环轴向响应;α和β分别为密封补偿环绕x轴和y轴的角向响应;zr为密封非补偿环的轴向激励;αr和βr分别为密封非补偿环绕x轴和y轴的角向激励;m为非补偿环质量;Ix,Iy为非补偿环转动惯量,可由式(23)计算得到;ks、ksx和ksy分别为弹簧刚度和角向刚度;cs、csx和csy分别为辅助O形圈的阻尼和角向阻尼,可由式(24)计算得到[29].
| $ {I_x} = {I_y} = \int {{r^2}} {\rm{d}}m. $ | (23) |
| $ \left\{ {\begin{array}{*{20}{l}} {{k_{sx}} = {k_{sy}} = 1/2{k_s}r_s^2,}\\ {{c_{sx}} = {c_{sy}} = 1/2{c_s}r_s^2.} \end{array}} \right. $ | (24) |
式中:rs为O形圈的径向位置.
非补偿环的激励引入形式为
| $ {z_r} = {A_{rz}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (vt),{\alpha _r} = {A_{rx}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (vt),{\beta _r} = {A_{ry}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (vt). $ | (25) |
式中:Arz、Arx和Ary分别为轴向激励和角向激励的赋值;υ为扰动频率(旋转轴角速度),υ=ω.
给定的运动方程的初始条件设为:
| $ z(0) = {h_0},\dot z(0) = \dot \alpha (0) = \beta (0) = \dot \beta (0) = 0,\alpha (0) = {A_{rx}}. $ | (26) |
式(1)经拉普拉斯变换后,可得密封补偿环轴向运动的表达式为
| $ Z(s) = \frac{{({c_{zz}}s + {k_{zz}}){Z_r}(s)}}{{[m{s^2} + ({c_{zz}} + {c_s})s + ({k_{zz}} + {k_s})]}}. $ | (27) |
式中:Z(s)和Zr(s)分别为z和zr的拉普拉斯变换;s为拉普拉斯变换中的复变量.
由流体膜动态性能参数的特点,有:kxx=kyy、kxy=-kyx、cxx=cyy和cxy=-cyx,经拉普拉斯变换后得到补偿环运动表达式(22)可变为
| $ \left\{ {\begin{array}{*{20}{l}} {A(s)}\\ {B(s)} \end{array}} \right\} = {D^{ - 1}}\left\{ {\begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {{c_{xx}}s + {k_{xx}}}&{{c_{xy}}s + {k_{xy}}}\\ { - {c_{xy}}s - {k_{xy}}}&{{c_{xx}}s + {k_{xx}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{A_r}(s)}\\ {{B_r}(s)} \end{array}} \right\} - \left[ {\begin{array}{*{20}{c}} {{c_{xx}}}&{{c_{xy}}}\\ { - {c_{xy}}}&{{c_{xx}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\alpha _r}(0)}\\ {{\beta _r}(0)} \end{array}} \right\}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \left[ {\begin{array}{*{20}{c}} {{I_x}s + {c_{xx}} + {c_{sx}}}&{{c_{xy}}}\\ { - {c_{xy}}}&{{I_y}s + {c_{xx}} + {c_{sy}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {\alpha (0)}\\ {\beta (0)} \end{array}} \right\}} \end{array}} \right\}. $ | (28) |
式中:A(s)、B(s)、Ar(s)和Br(s)分别是α、β、αr和βr的拉普拉斯变换;D的表达式为
| $ D = \left[ {\begin{array}{*{20}{c}} {{I_x}{s^2} + ({c_{xx}} + {c_{sx}})s + {k_{xx}} + {k_{sx}}}&{{c_{xy}}s + {k_{xy}}}\\ { - {c_{xy}}s - {k_{xy}}}&{{I_y}{s^2} + ({c_{xx}} + {c_{sy}})s + {k_{xx}} + {k_{sy}}} \end{array}} \right]. $ | (29) |
式(28)和式(29)再进行一次拉普拉斯反变换,然后将初始条件式(27)代入,可以求得油气两相动压密封补偿环的响应运动,进而可分析密封的追随动态特性.在密封补偿环的追随响应运动中,密封流体膜厚有以下表达式:
| $ \begin{array}{*{20}{l}} {h(r,\theta ,t) = {h_o}(r,\theta ) + [z(t) - {z_r}(t)] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [\alpha (t) - {\alpha _r}(t)]r{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta - [\beta (t) - {\beta _r}(t)]r{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta .} \end{array} $ | (30) |
图 9为端面间流体膜在一个振动周期内4个时刻的厚度(忽略槽深)分布的云图,选取的4个时刻分别为t=(n+0.25)T、t=(n+0.5)T、t=(n+0.75) T以及t=nT,n为自然数,T=2π/ω.其中流体膜的厚度变化率定义为∣h-h0∣/h0.由图 9可知油气两相动压密封流体膜的厚度变化率最大为22.3%,膜厚值大小的波动相对较为平缓,且不会发生间隙过大或端面接触的现象.因此,油气两相动压密封在非补偿环的扰动下仍能实现良好的追随响应,可以保证密封始终运行在工作膜厚附近,不会因为受扰引起泄漏率过大或端面磨损而失效.
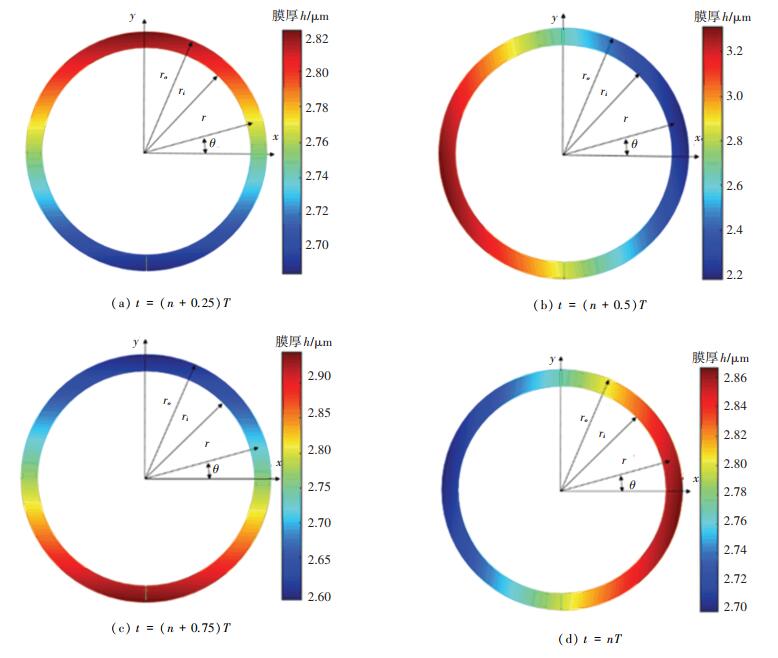
|
图 9 密封流体膜厚度周期变化云图 Fig. 9 Response movement of the seal compensation ring |
为了验证数值计算方法的有效性,采用文献[30]的密封分析参数,使用本文研究方法,计算得出无量纲流体膜动态性能参数随无量纲扰动频率的变化规律,并与文献[30]的计算结果进行对比,其中文献[30]的密封端面结构为外侧开设螺旋槽,结果如图 10所示.由图 10可知,本文和文献[30]的计算结果有极好的一致性,最大误差为7.14%,在误差允许范围内,算例验证了本文数值计算方法的正确性.
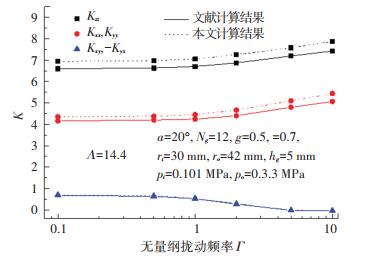
|
图 10 数值计算有效性验证 Fig. 10 Validation of numerical calculation |
油气两相动压密封追随动态特性的好坏以静环(补偿环)的响应运动来表征,即在忽略相位差的前提下,静环响应运动的幅值越接近动环扰动运动的幅值,密封的追随动态特性越好,反之则越差.对于油气两相动压密封的追随动态特性而言,操作参数、弹簧刚度以及O形圈阻尼都会对其有影响.下面将基于流固热耦合研究不同转速、压差、油气比、弹簧刚度以及O形圈阻尼对密封追随动态特性的影响,并对比分析了不同密封介质(油气两相、纯气相)对密封追随动态特性的影响规律.
3.1 转速图 11为密封转速对油气两相动压密封静环响应运动(振幅Az、Ax和Ay)的影响规律.静环的轴向和角向响应振幅均随着转速的增大而增大,并越来越接近动环扰动运动的振幅.其中耦合前的两相密封和纯气相密封的轴向和角向响应振幅随着转速的增大而线性增大,纯气相密封的响应振幅整体小于两相密封的响应振幅,因此在同样的结构参数和操作参数下,两相密封的追随动态特性优于纯气相密封的追随动态特性,这是由于充分混合后的两相流体粘度和密度增加,导致两相流体膜刚度比纯气相流体膜刚度更大,两相流体膜稳定性更好.对比流固热耦合前后的结果可以发现,耦合后两相密封的响应振幅变化趋势随转速增大呈减速递增特性,这是因为转速的增加有助于提高两相流体的均匀混合程度、流体膜刚度和密封端面开启力,进而提高密封的抗干扰能力,而且其响应振幅减速递增特性更符合实际情况.因此在一定的转速范围内,转速的升高有利于提高密封的追随动态特性.
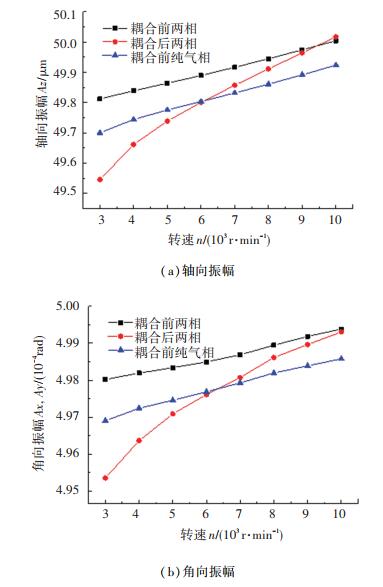
|
图 11 密封转速对静环响应振幅的影响 Fig. 11 Effect of speed on response amplitude of static ring |
分析压差对油气两相动压密封静环响应运动(振幅Az、Ax和Ay)的影响,结果如图 12所示.随着压差的增大,静环的响应振幅都表现出近线性减小,原因在于内侧开槽的端面结构导致其密封端面开启力随压力增大程度较小,而密封端面闭合力则会大幅增大,进而压制密封静环的响应振幅,因此在一定范围内压差的增大不利于密封静环的追随响应运动.在压差较小时,耦合前后的两相密封以及纯气相密封的响应振幅相差不大,但随着压差的逐渐增大,这是由于高压导致两相流体膜的密度和粘度增大,进而提高两相流体膜的刚度和稳定性,3种情况下的密封追随动态特性区别渐渐变得明显,耦合后两相密封的响应振幅随压力增大更敏感.
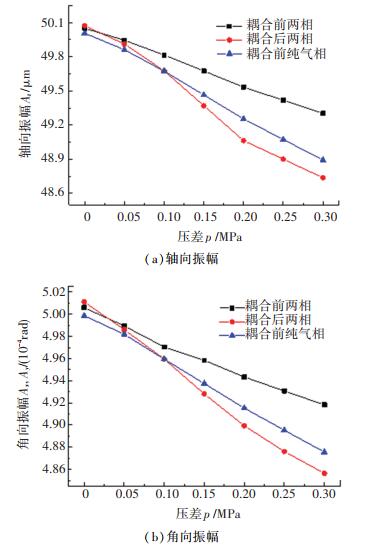
|
图 12 压差对静环响应振幅的影响 Fig. 12 Effect of pressure difference on response amplitude of static ring |
图 13为油气比对油气两相动压密封静环响应运动(振幅Az、Ax和Ay)的影响规律.整体上随着油气比的增大,静环的响应振幅减速增大.对于轴向振幅而言,当油气比为0.15~0.20时静环的轴向响应振幅最为接近动环扰动运动的轴向振幅,此时密封的追随动态特性最佳.对于角向振幅而言,油气比的增大让静环的角向振幅接近动环扰动运动的角向振幅,因此油气比的提高会提升密封角向追随动态特性.另外图 13中油气比为0时即代表此时密封为纯气相密封,由此可知密封的追随动态特性随着密封介质中油气比的增大而有所提升.油气比的增大导致静环的响应振幅增大的原因在于两相流体膜的密度和粘度随油气增大而增大,从而导致密封端面开启力和流体膜刚度增大,进而提高密封的抗干扰能力和静环响应追随能力.
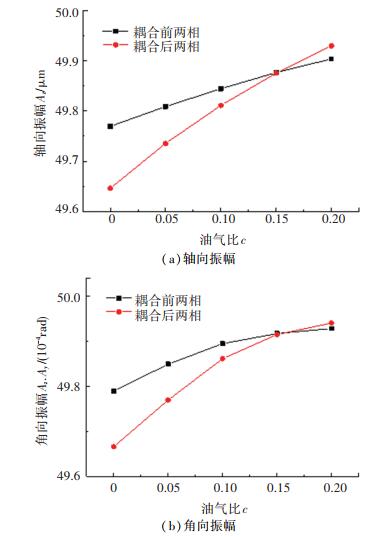
|
图 13 油气比对静环响应振幅的影响 Fig. 13 Effect of oil to gas ratio on response amplitude of static ring |
图 14为密封静环响应运动(振幅Az、Ax和Ay)在不同弹簧刚度下的变化规律.随着弹簧刚度的增大,油气两相密封的追随动态特性略优于纯气相密封.弹簧刚度小于1×105时,静环响应振幅变化很小,此范围内的密封追随动态特性对弹簧刚度不敏感.当弹簧刚度大于1×105时,油气两相动压密封静环的各向响应振幅急剧减小,此时密封的追随动态特性受到很大影响.这是由于弹簧刚度起增大弹簧力和密封端面闭合力的作用,当弹簧刚度较小时,弹簧力较小,相对于压力对密封端面流体膜受力来说,弹簧力所占比例较小,不是影响流体膜刚度的决定性因素,所以响应振幅对小弹簧刚度不敏感;当弹簧刚度增大到一定程度时,弹簧力对密封端面流体膜受力的影响逐渐与压力同一程度,甚至超过压力对密封端面流体膜受力的影响,此时弹簧力是影响流体膜刚度的决定性因素,所以响应振幅对大弹簧刚度较敏感,因此为了密封具有良好的追随动态特性,密封的弹簧刚度不宜过大.
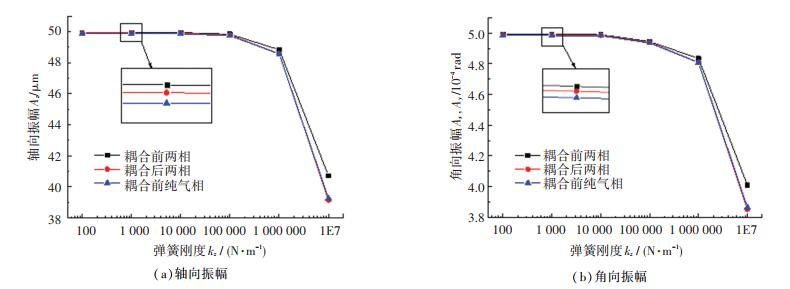
|
图 14 静环响应振幅在不同弹簧刚度下的变化 Fig. 14 Variation of response amplitude of static ring at different spring stiffness |
图 15为密封静环响应运动(振幅Az、Ax和Ay)在不同密封圈阻尼下的变化规律.随着O形圈阻尼的增大,油气两相密封的追随动态特性略优于纯气相密封.在O形圈阻尼小于1×104时,静环的响应振幅变化很小,即此范围内的密封圈阻尼对密封追随动态特性影响很小.当O形圈阻尼大于1×104时,油气两相动压密封静环的轴向及角向上的响应振幅急剧减小,密封在此时的追随动态特性受到很大影响.原因在于O形圈阻尼起阻碍静环补偿响应运动的作用,O形圈阻尼较小时,O形圈对静环的摩擦力较小,压力和弹簧力的综合作用能轻易克服摩擦力对静环补偿作用的影响,而且对于密封端面间流体膜受力来说,摩擦力所占比例较小,不是影响流体膜刚度的决定性因素,所以响应振幅对小O形圈阻尼不敏感;当O形圈阻尼增大到一定程度时,压力和弹簧力的综合作用逐渐克服不了O形圈摩擦力对静环的补偿作用,甚至逐渐超过压力和弹簧力对密封端面流体膜受力的影响,此时O形圈摩擦力成为密封端面流体膜受力的关键影响因素,所以响应振幅对大O形圈阻尼较敏感,因此为了确保密封具有良好的追随动态特性,密封的密封圈阻尼不宜过大.
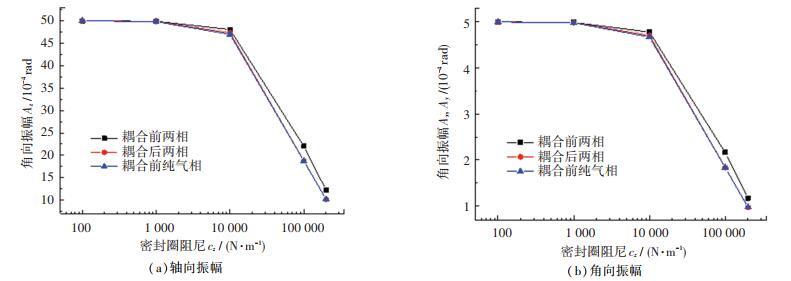
|
图 15 静环响应振幅在不同密封圈阻尼下的变化 Fig. 15 Variation of response amplitude of static ring at different O-shaped ring damping |
1) 得到了基于流固热耦合的油气两相动压密封的追随动态特性求解方法.
2) 油气两相密封的追随动态特性优于纯气相密封的追随动态特性.
3) 提高转速和油气比有利于提高密封的追随动态特性,压差的增大不利于密封静环的追随响应运动.
4) 弹簧刚度和O形圈阻尼增大前期,静环响应振幅变化不敏感,两者对密封追随动态特性影响很小;增大后期,静环响应振幅急剧降低,两者对密封追随动态特性影响较大;弹簧刚度和O形圈阻尼不宜过大.
| [1] |
束坤.高速轻载航空轴承打滑监测技术研究[D].哈尔滨: 哈尔滨工业大学, 2015 SHU K.Research on monitoring technologies of high-speed and light-load aero-bearings' skidding[D]. Harbin: Harbin University of Technology, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10213-1015982461.htm |
| [2] |
王跃飞, 孙启国, 吕洪波. 滚动轴承油气润滑及喷油润滑温度场对比研究[J]. 润滑与密封, 2014, 39(2): 66. WANG Y F, SUN Q G, LU H B. Comparing study on temperature field of rolling bearing under oil-air lubrication and spray lubrication[J]. Lubrication Engineering, 2014, 39(2): 66. DOI:10.3969/j.issn.0254-0150.2014.02.013 |
| [3] |
孙道永, 陆继, 刘焜. 轴向受载的高速滚动轴承动态特性分析[J]. 中国科技论文, 2014, 9(8): 920. SUN D Y, LU J, LIU T. Dynamic characteristics of high-speed rolling bearing under axial load[J]. China Science Paper, 2014, 9(8): 920. DOI:10.3969/j.issn.2095-2783.2014.08.015 |
| [4] |
PINEL S I, SINGER H R, ZARETSKY E V. Comparison between oil-mist and oil-jet lubrication of high-speed, small-bore, angular-contact ball bearings[J]. Tribology Transactions, 2001, 44(3): 327. DOI:10.1080/10402000108982465 |
| [5] |
郭凯, 苑士华, 邵子桐. 喷射润滑高速轴承内部油气两相流动研究[J]. 北京理工大学学报, 2012, 32(10): 1022. GUO K, YUAN S H, SHAO Z T. Study on oil-air two-phase flow inside the high-speed bearings cavity with jet lubricated[J]. Journal of Beijing University of Technology, 2012, 32(10): 1022. DOI:10.15918/j.tbit1001-0645.2012.10.017 |
| [6] |
COE H H, ZARETSKY E V. Predicted and experimental performance of jet-lubricated 120-millimeter-bore ball bearings perating to 2.5 million DN NASA, TP-1196[R]. Washington, DC: NASA, 1978
|
| [7] |
姚静, 孔祥东, 孟赵一, 等. 油气润滑气液两相环状流流动特性分析[J]. 润滑与密封, 2012, 37(5): 65. YAO J, KONG X D, MENG ZY, et al. Research on flow characteristics of air-oil two phase annular flow for oil-air lubrication[J]. Lubrication Engineering, 2012, 37(5): 65. DOI:10.3969/j.issn.0254-0150.2012.05.015 |
| [8] |
ESTRADE J P, CARENTZ H, LAVERGNE G. Experimental investigation of dynamic binary collision of ethanol droplets-a model for droplet coalescence and bouncing[J]. International Journal of Heat and Fluid Flow, 1999, 20(5): 486. DOI:10.1016/S0142-727X(99)00036-3 |
| [9] |
PATHAK M, DASS A K DEWAN A. An investigation of turbulent rectangular jet discharged into a narrow channel weak crossflow[J]. Journal of Hydrodynamics, 2008, 20(1): 154. DOI:10.1016/S1001-6058(08)60041-4 |
| [10] |
XU S L, FAN J Y, WANG D Z. PDA measurements of two-phase flow structure and particle dispersion for a particle-laden jet in crossflow[J]. Journal of Hydrodynamics, 2010(1): 9. DOI:10.1016/S1001-6058(09)60022-6 |
| [11] |
陈国定, 陈薄, 刘亚军, 等. 航空发动机轴承腔含油滴油气两相介质的流动模拟[J]. 西北工业大学学报, 2011, 29(1): 62. Chen GD, CHEN B, LIU Y J, et al. Exploring through numerical simulation lubrication flow inside an aeroengine bearing chamber with film/droplet/air interactions taken into consideration[J]. Journal of Northwest Polytechnic University, 2011, 29(1): 62. DOI:10.3969/j.issn.1000-2758.2011.01.012 |
| [12] |
吴昊天, 陈国定. 轴承腔油气两相泡状流动的数值研究[J]. 机械工程学报, 2008, 44(9): 70. WU H T, CHEN G D. Numerical research of two/phase oil-gas bubble flow in bearing chamber[J]. Journal of Mechanical Engineering, 2008, 44(9): 70. DOI:10.3321/j.issn:0577-6686.2008.09.012 |
| [13] |
邓强国, 宋鹏云, 许恒杰, 等. 干气密封动力学研究新进展[J]. 润滑与密封, 2018, 43(6): 118. DOI:10.3969/j.issn.0254-0150.2018.06.022 |
| [14] |
FARIA M T C. An efficient finite element procedure for analysis of high-speed spiral groove gas face seals[J]. Journal of Tribology, 2001, 123(1): 205. |
| [15] |
宋鹏云, 胡晓鹏, 许恒杰. 实际气体对T槽干气密封动态特性的影响[J]. 化工学报, 2014, 65(4): 1344. DOI:10.3969/j.issn.0438-1157.2014.04.026 |
| [16] |
许恒杰, 宋鹏云, 毛文元, 等. 考虑氢气实际气体效应和阻塞流效应的螺旋槽干气密封动态特性分析[J]. 化工学报, 2017, 68(12): 4675. |
| [17] |
GREEN I, BARNSBY R M. A simultaneous numerical solution for the lubrication and dynamic stability of noncontacting gas face seals[J]. Journal of Tribology, 2001, 123(2): 388. DOI:10.1115/1.1308020 |
| [18] |
MILLER B A, GREEN I. Numerical formulation for the dynamic analysis of spiral-grooved gas face seals[J]. Journal of Tribology, 2001, 123(2): 395. |
| [19] |
李双喜, 蔡纪宁, 陈罕, 等. 高速螺旋槽气体密封轴向微扰的有限元分析[J]. 北京化工大学学报, 2003, 30(1): 52. LI S X, CAI J N, CHEN H, et al. A finite element procedure for axial perturbation of high-speed spiral groove gas-face seals[J]. Journal of Beijing University of Chemical Technology, 2003, 30(1): 52. DOI:10.13543/j.cnki.bhxbzr.2003.01.014 |
| [20] |
RUAN B. A semi-analytical solution to the dynamic tracking of non-contacting gas face seals[J]. Journal of Tribology, 2002, 124(1): 196. DOI:10.1115/1.1398292 |
| [21] |
RUAN B. Numerical modeling of dynamic sealing behaviors of spiral groove gas face seals[J]. Journal of Tribology, 2002, 124(1): 186. |
| [22] |
张树强, 李双喜, 蔡纪宁, 等. 动静压混合式气体密封追随性及主动调控振动特性数值分析[J]. 航空学报, 2012, 33(7): 1336. ZHANG S Q, LI S X, CAI J N, et al. Numerical analysis for tracking property and active regulation vibration characteristics dynamic-hydrostatic hybrid gas seals[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1336. |
| [23] |
张树强, 王良, 陈杰, 等. 弹簧和密封圈刚度和阻尼对气体端面密封追随性的影响研究[J]. 振动与冲击, 2018, 37(3): 54. ZHANG S Q, WANG L, CHEN J, et al. Effects of stiffness and damping of spring and secondary seal on tracking property gas face seals[J]. Journal of Vibration and Shock, 2018, 37(3): 54. DOI:10.13465/j.cnki.jvs.2018.03.009 |
| [24] |
陈源, 彭旭东, 李纪云, 等. 螺旋槽结构参数对干气密封动态特性的影响研究[J]. 摩擦学学报, 2016, 36(4): 397. CHEN Y, PENG X D, LI J Y, et al. The influence of structure parameters of spiral groove on dynamic characteristics of dry gas seal[J]. Tribology, 2016, 36(4): 397. DOI:10.16078/j.tribology.2016.04.001 |
| [25] |
陈源, 彭旭东, 江锦波, 等. 密封环挠性安装形式对干气密封动态追随性的影响[J]. 摩擦学学报, 2017, 37(2): 139. CHEN Y, PENG X D, JIANG J B, et al. The influence of flexible mounted ways of seal rings on dynamic tracking of dry gas seal[J]. Tribology, 2017, 37(2): 139. |
| [26] |
LI S Z, GUO G D. Content-based audio classification and retrieval using SVM learning[C]//Proceedings of ICME(IEEE International Conference on Multimedia and Expo). Tokyo: IEEE Computer Society 2001 Contents, 2001: 749
|
| [27] |
张义民, 李鹤. 机械振动学基础[M]. 北京: 高等教育出版社, 2010. ZHANG Y M, LI H. Fundamentals of mechanical vibration[M]. Beijing: Higher Education Press, 2010. |
| [28] |
刘延柱, 陈文良, 陈立群. 振动力学(第二版)[M]. 北京: 高等教育出版社, 2011. LIU Y Z, CHEN W L, CHEN L Q. Vibration mechanics (Second Edition)[M]. Beijing: Higher Education Press, 2011. |
| [29] |
GREEN I, ETSION I. Stability threshold and steady-state response of noncontacing coned-face seals[J]. ASLE Trans, 1985, 28(4): 449. |
| [30] |
RUAN B. A semi-analytical solution to the dynamic tracking of non-contacting gas face seals[J]. Journal of Tribology, 2002, 124(1): 196. DOI:10.1115/1.1398292 |
 2020, Vol. 52
2020, Vol. 52


