2. 江西长江化工有限责任公司, 江西 九江 332006
2. Jiangxi Changjiang Chemical Co., Ltd, Jiujiang 332006, Jiangxi, China
纤维增强聚合物基复合材料因具有比强度高、比刚度高和可设计性好等优点而被广泛地应用于先进轻质结构中,如航空航天飞行器、火箭发动机壳体、火箭武器定向器等[1-3].这些结构的设计服役寿命通常是几年甚至十几年,因此在结构设计时需要考虑材料的长期力学性能.大多数聚合物在载荷和环境因素作用下表现出时间相关的粘弹性响应,使得粘弹性成为聚合物基复合材料长期力学性能的重要组成部分.
国内外学者基于力学元件组合模型和时间-温度等效原理对聚合物及其复合材料的线性粘弹性开展了大量研究工作[4-7].然而,研究表明:聚合物基复合材料的线性粘弹性存在应力阈值,即当应力超过一定值或在高温、高湿度环境下会表现出明显的非线性特征[8].因此,研究人员提出很多理论模型来描述材料的非线性粘弹性响应,主要包括多重积分理论和单积分理论.多重积分理论,如G-R理论[9],尽管能够准确地描述材料的非线性粘弹性,但是需要通过一系列复杂的试验来获得繁多的材料参数,很难应用到实际工程问题. Bernstein等[10]在G-R理论的基础上提出了预测应力松弛行为的非线性粘弹性本构方程(BKZ模型).王礼立等[11]通过对多种材料进行试验研究,提出了一种适用于中低应变率(10-4~103)的非线性唯象本构模型(ZWT模型).该模型与其他非线性粘弹性模型有本质区别,其非线性体现在非线弹性响应,而模型中的粘弹性部分则是线性的. Schapery[12]基于不可逆热动力学理论,提出了一种含折算时间的非线性粘弹性本构关系.该模型表征的材料的非线性粘弹性响应由4个与应力、温度和吸湿量有关的参数来控制. Schapery模型较为简单,并且可通过选择不同的线性粘弹性模型,如幂率模型[13]和广义Kelvin模型[14],来获得多种不同形式的非线性本构模型,在聚合物以及聚合物基复合材料中得到了广泛应用.应用Schapery模型的关键是通过一系列不同应力水平的短期(0.5~8 Hrs)蠕变-回复试验获得非线性参数随应力的变化规律,通常采用数值拟合法[8]和基于等效性原理的图形移位法[15]辨识非线性参数,存在效率低、人为主观因素对结果影响较大的缺点.
复合材料的粘弹性主要受聚合物基体控制,通常认为连续纤维增强聚合物基复合材料在纤维方向上不具有粘弹性,而在横向和面内剪切方向上具有明显的粘弹性[16].因此,本文针对玻纤/环氧复合材料,分别在横向和面内剪切方向上开展不同应力水平的短期(1 Hrs)拉伸蠕变-回复试验,根据试验得到的典型蠕变-回复应变曲线提出一种基于解析法的非线性参数辨识方法,获得非线性参数随应力的变化规律,研究玻纤/环氧复合材料的非线性粘弹性响应.
1 理论模型 1.1 Schapery非线性本构关系等温条件下单轴载荷作用时,Schapery单积分型非线性粘弹性本构关系为
| $ \varepsilon = {\text{ }}{g_0}{D_0}\sigma \left( t \right) + {g_1}\int_0^t {\Delta D\left( {\psi - {\psi ^\tau }} \right)} \frac{\partial }{{\partial \tau }}\left[ {{g_2}\sigma \left( \tau \right)} \right]{\text{d}}\tau , $ | (1) |
式中: ψ和ψ′称为折算时间
| $ \psi = \psi (t) = \int_0^t {\frac{{{\text{d}}\zeta }}{{{a_\sigma }}}, } $ | (2) |
| $ {\psi ^\tau } = \psi (\tau ) = \int_0^\tau {\frac{{{\text{d}}\zeta }}{{{a_\sigma }}}, } $ | (3) |
D0为初始柔量,与时间无关,表征材料的瞬时弹性响应;非线性参数g0,g1,g2和aσ均与应力有关,且受环境温度和材料吸湿量影响[17].当g0=g1=g2=aσ=1时,式(1)退化为线性粘弹性本构. ΔD(ψ)为时间相关的瞬态线性蠕变柔量,表征材料的蠕变响应,通常采用幂率模型来表示:
| $ \Delta D\left( \psi \right) = D{\psi ^n}, $ | (4) |
式中D、n与环境温度和材料吸湿量有关,与应力水平无关.
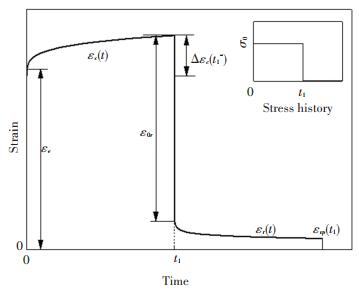
1.2 非线性参数辨识方法对于蠕变-回复试验,施加图 1所示的应力历史,得到的典型非线性蠕变-回复应变时间曲线如图 1所示.可以看出,聚合物基复合材料在经过一段时间的回复过程后,会存在一定的残余粘塑性应变.因此,将粘塑性应变分量引入Schapery非线性本构关系,得到
|
图 1 蠕变-回复试验应变时间曲线 Fig. 1 Typical strain-time curve for creep-recovery test |
| $ \begin{gathered} \varepsilon (t) = {\text{ }}{g_0}{D_0}\sigma \left( t \right) + {g_1}\int_0^t {\Delta D\left( {\psi - } \right.} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi ^\tau }\frac{\partial }{{\partial \tau }}\left[ {{g_2}\sigma \left( \tau \right)} \right]{\text{d}}\tau + {\varepsilon _{vp}}\left( t \right), \hfill \\ \end{gathered} $ | (5) |
将式(4)由幂律模型表示的瞬时蠕变柔量代入式(5)中,得到材料的蠕变、回复应变分别为
| $ \begin{gathered} {\varepsilon _c}\left( t \right) = \left[ {{g_0}{D_0} + {g_1}{g_2}D{{\left( {\frac{t}{{{a_\sigma }}}} \right)}^n}} \right]{\sigma _0} + {\varepsilon _{vp}}\left( t \right), \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 < t < {t_1}; \hfill \\ \end{gathered} $ | (6) |
| $ \begin{gathered} {\varepsilon _c}\left( t \right) = \frac{{\Delta {\varepsilon _1}}}{{{g_1}}}\left[ {{{\left( {1 - {a_\sigma }\lambda } \right)}^n} + {{\left( {{a_\sigma }\lambda } \right)}^n}} \right]{\sigma _0} + {\varepsilon _{vp}}\left( t \right), \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} t > {t_1}. \hfill \\ \end{gathered} $ | (7) |
式中λ=(t-t1)/t称为无量纲时间,Δε1=g1g2D(t/aσ)nσ0为蠕变应变.
1.2.1 非线性参数g0和g1非线性参数g0表示不同应力水平下初始弹性柔量偏离线性响应的程度,可通过将不同应力水平的初始弹性柔量与最低应力水平对应的初始弹性柔量对比获得.
非线性参数g1反映了粘弹性响应在应力和环境因素影响下的非线性程度,可采用解析法获取不同应力水平下的参数值.由式(6)可知,在卸载前的瞬间,即t=t1-时,总应变响应为
| $ {\varepsilon _c}\left( {t_1^ - } \right) = \left[ {{g_0}{D_0} + {g_1}{g_2}D{{\left( {\frac{{t_1^ - }}{{{a_\sigma }}}} \right)}^n}} \right]{\sigma _0} + {\varepsilon _{vp}}\left( {t_1^ - } \right). $ | (8) |
定义粘性应变响应Δεc(t1-),包括粘弹性应变分量和粘塑性应变分量:
| $ \Delta {\varepsilon _c}\left( {t_1^ - } \right) = {g_1}{g_2}D{\left( {\frac{{t_1^ - }}{{{a_\sigma }}}} \right)^n}{\sigma _0} + {\varepsilon _{vp}}\left( {t_1^ - } \right), $ | (9) |
对于卸载后的瞬间,即t=t1+时,由式(7)得到回复应变为
| $ {\varepsilon _r}\left( {t_1^ + } \right) = {g_2}D{\left( {\frac{{t_1^ + }}{{{a_\sigma }}}} \right)^n}{\sigma _0} + {\varepsilon _{vp}}\left( {t_1^ + } \right), $ | (10) |
结合式(9)和式(10)可以得到卸载瞬间的应变变化量为
| $ {\varepsilon _{0r}} = {\varepsilon _c}\left( {t_1^ - } \right) - {g_2}D{\left( {\frac{{t_1^ + }}{{{a_\sigma }}}} \right)^n}{\sigma _0} - {\varepsilon _{vp}}\left( {t_1^ + } \right). $ | (11) |
由此得到加载与卸载瞬间的应变差值为
| $ \Delta {\varepsilon _0} = {\varepsilon _{0r}} - {\varepsilon _e} = {g_2}\left( {{g_1} - 1} \right)D{\left( {\frac{{{t_1}}}{{{a_\sigma }}}} \right)^n}{\sigma _0}, $ | (12) |
求解式(12)得到非线性参数g1的解析解如下:
| $ {g_1} = \frac{{\Delta {\varepsilon _c}\left( {t_1^ - } \right) - {\varepsilon _{vp}}}}{{\Delta {\varepsilon _c}\left( {t_1^ - } \right) - \Delta {\varepsilon _0} - {\varepsilon _{vp}}}}, $ | (13) |
式中
对于线性蠕变-回复响应,g1=1,则εvp=0,即线性情况下不存在残余粘塑性应变,这与试验观察到的现象一致.
1.2.2 非线性参数aσ和g2非线性参数aσ表示时间移位因子,反映了高应力水平对复合材料蠕变行为的加速效应.式(7)中Δε1和εvp(t1)可以直接从蠕变-回复应变曲线上获得,因此若已知时间指数n的值,则非线性参数aσ可利用式(5)对由试验得到的回复应变数据做单一参数拟合得到.
非线性参数g2反映了加载速率对粘弹性响应的影响程度.在已知非线性参数g1,aσ和n的前提下,可以得到非线性参数g2的解析解.
由式(12)得到
| $ \Delta {\varepsilon _{0\left( {nl} \right)}} = \frac{{{g_2}\left( {{g_1} - 1} \right)}}{{a_\sigma ^n}}Dt_1^n{\sigma _{0\left( {nl} \right)}}, $ | (14) |
线性情况下蠕变应变可由幂律模型表示,即Δεc(l)=Dt1nσ0(l),由此得到非线性参数g2的解析解为
| $ {g_2} = \frac{{\Delta {\varepsilon _{0\left( {nl} \right)}}}}{{\Delta {\varepsilon _{c\left( l \right)}}}}\frac{{a_\sigma ^n}}{{\left( {{g_1} - 1} \right)}}\frac{{{\sigma _{0\left( l \right)}}}}{{{\sigma _{0\left( {nl} \right)}}}}. $ | (15) |
式中:Δε0(nl)表示非线性情况下加载与卸载瞬的瞬时应变差值;Δεc(l)表示线性情况下保载t1时长后的蠕变应变量;σ0(nl)和σ0(l)分别表示非线性与线性情况下施加的应力值,本文选择最低应力水平作为σ0(l).
2 试验材料与方法 2.1 试验材料及成型工艺由于目前没有可依据的蠕变试验标准,参照复合材料基本力学性能测试标准GB/T3354-2014[18]和GB/T3355-2014[19]制备复合材料蠕变试样.试样原材料为G20000型单向玻璃纤维预浸料,名义厚度为0.17 mm,单位面积质量为200 g/m2,纤维体积含量约为67%,由威海光威复材有限公司提供.试样采用模压成型工艺制备,铺层方式为[90]16和[±45]4S,厚度约为2 mm.固化工艺:120 ℃,2 MPa条件下保温2 h,保压冷却至室温后脱模.
2.2 试验方法蠕变试验前,先进行准静态拉伸试验测试单向板的基本力学性能,为合理选择蠕变试验的应力水平提供依据.蠕变试验中加载的应力水平应在极限强度的10%~80%之间,若应力水平过高,试样容易出现蠕变断裂,应力水平过低,则短期内不会出现明显的蠕变变形[20].准静态试验采用2 mm/min的加载速度,测试得到单向板基本力学性能参数如表 1所示,表中数据为5个试样的平均值.
| 表 1 单向板弹性性能 Tab. 1 Elastic properties of GFRP unidirectional plates |
在室温环境下,采用1 h蠕变/1 h回复的方式开展拉伸蠕变-回复试验,其中,横向上共包括7个应力水平,分别为横向拉伸强度的35%、41%、47%、53%、60%、66%和72%;面内剪切方向上共包括8个应力水平,分别为剪切强度的19%、25%、31%、37%、43%、49%、56%和62%.由于受到试验机力传感器的限制,加载时采用最大允许加载速度250 N/s来加载,所有试样均在15 s之内完成加载,与蠕变-回复时间相比,加载时间足够短,可以近似认为是瞬时加载.准静态试验与蠕变-回复试验均在三思纵横UTM5105-G型电子万能材料试验机上进行.利用汉中精测BF120-3AA型电阻应变计、江苏联能YE3818C型动态应变仪、YE29003A型桥盒和美国NI9215型数据采集器测量记录试样的应变值.为排除试样吸湿对复合材料粘弹性的影响,在粘贴应变片之前利用南京沃环WH101-2A(S)型电热鼓风干燥箱将试样烘干72 h至恒重,烘干温度为50 ℃.此外,试验过程中接入温度补偿片,排除环境温度变化造成的应变测试误差.
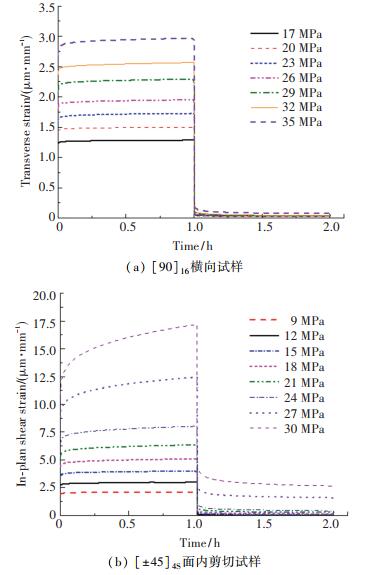
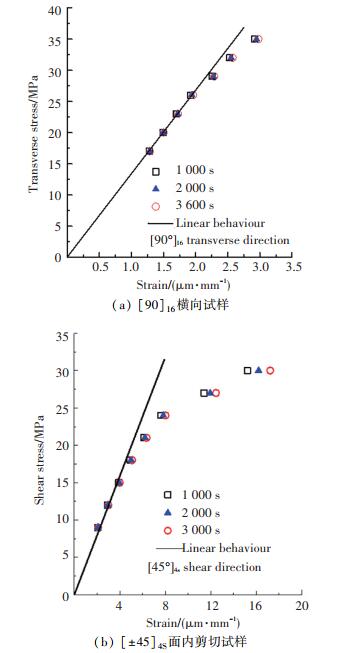
3 结果分析 3.1 蠕变-回复应变时间曲线试验得到不同应力水平的蠕变-回复应变时间曲线如图 2所示.可以看出,玻璃纤维增强环氧树脂复合材料在基体性能主导的材料方向上表现出明显的粘弹性行为,并且随着应力水平的升高,呈现出一定的非线性.此外,观察试验结束时刻的应变值,可以发现在低应力水平下,残余粘塑性应变非常接近零线,而随着应力的增大,残余粘塑性应变明显增大,这在一定程度上说明了提出的参数辨识方法的合理性.不同时间点试样的等时应变曲线如图 3所示.可以看出,当施加的横向拉伸应力超过26 MPa,面内剪切应力超过15 MPa时,试样的应变偏离线性行为,表现出明显的非线性粘弹性.
|
图 2 GFRP在不同应力水平下的蠕变-回复应变曲线 Fig. 2 The 1 h creep and 1 h recovery strain curves of GFRP corresponding to different stress levels |
|
图 3 不同时间点的等时应力-应变曲线 Fig. 3 Isochronous stress strain curves at different time periods |
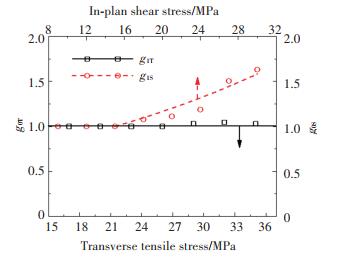
根据不同应力水平加载结束时刻的应力应变计算得到初始弹性柔量,并分别与低应力水平对应的初始弹性柔量对比,得到非线性参数g0随应力的变化规律如图 4所示.横向上,参数g0T基本不随应力发生变化,说明玻纤/环氧树脂复合材料的横向弹性柔量与应力无关;面内剪切方向上,当施加的剪应力大于15 MPa时,参数g0S随应力呈指数增加.根据初始弹性柔量计算得到横向弹性模量为13.7 GPa,面内剪切模量为4.42 GPa,与表 1中通过准静态拉伸试验得到的弹性模量有一定区别,这主要是由于加载方式和加载速度不同引起的,说明聚合物基复合材料为率相关材料.
|
图 4 非线性参数g0随应力的变化规律 Fig. 4 Nonlinear parameter g0 as a function of applied stress |
根据式(13)计算得到不同应力水平下非线性参数g1如图 5所示.可以看出,两个材料方向上,当应力大于非线性应力阈值时,非线性参数g1T和g1S均随应力线性增加,表明随着应力的增加,复合材料的非线性粘弹性程度逐渐增加.

|
图 5 非线性参数g1随应力的变化规律 Fig. 5 Nonlinear parameter g1 as a function of applied stress |
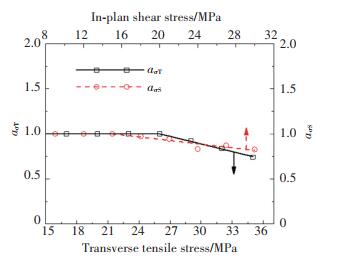
在获得非线性参数aσ之前,首先需要获取幂率模型的时间指数n的值.研究表明,在恒温恒湿度环境中,时间指数n与应力水平无关.并且,n与蠕变的时间尺度有关,而与回复的时间尺度无关[8].因此,首先利用式(7)对线性粘弹性范围内(此时,g0=g1=g2=aσ=1)的回复应变曲线进行拟合,得到横向上时间指数n的平均值为0.080,面内剪切方向上时间指数n的平均值为0.044.在此基础上,采用Levenberg Marquardt迭代算法,利用式(7)拟合非线性回复应变曲线,得到aσ随应力的变化规律如图 6所示.可以看出,在非线性范围内,两个材料方向上的非线性参数aσ均小于1,并且随应力线性降低,这说明高应力水平下短时间的粘弹性响应与低应力水平下长时间的粘弹性响应相对应,即高应力水平对玻纤/环氧复合材料的粘弹性起到了加速作用.
|
图 6 非线性参数aσ随应力的变化规律 Fig. 6 Nonlinear parameter aσ as a function of applied stress |
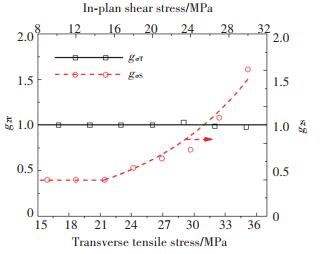
由于参数g1,aσ和n已知,利用式(15)采用解析法直接求得参数g2,如图 7所示.横向上,非线性参数g2T基本不随应力发生变化,g2S在非线性范围内则随应力呈指数增加.需要特别注意的是,按照本文提出的参数辨识方法,非线性参数aσ和g2的准确性主要依赖于g1,因此要在原始试验数据中准确判断各关键节点,如蠕变起点、终止点和回复起点等.
|
图 7 非线性参数g2随应力的变化规律 Fig. 7 Nonlinear parameter g2 as a function of applied stress |
1) 通过在Schapery非线性本构关系中引入残余粘塑性应变分量,提出一种基于解析法的非线性参数辨识方法,只需要依据原始试验数据确定蠕变起点、终点和回复起点的应变值,便能快速获取非线性参数随应力的变化规律.
2) 当施加的横向拉伸应力大于26 MPa(横向拉伸强度的53%),面内剪切应力大于15 MPa(剪切强度的31%)时,玻纤/环氧复合材料表现出明显的非线性粘弹性响应.
3) 在横向上,非线性参数g0T和g2T与应力无关,g1T随应力线性增加,而aσT则随应力线性降低.
4) 在面内剪切方向上,非线性参数g0S和g2S随应力呈指数增加,g1S随应力线性增加,而aσS则随应力线性降低.
| [1] |
YU C G, SUN T S, XIAO G Y. Study on creep performance of launch canister under long-term storage[J]. Transactions of the Canadian Society for Mechanical Engineering, 2019, 43: 199. DOI:10.1139/tcsme-2018-0028 |
| [2] |
顾善群, 刘燕峰, 李军, 等. 碳纤维/环氧树脂复合材料高速冲击性能[J]. 材料工程, 2019, 47(8): 110. GU Shanqun, LIU Yanfeng, LI Jun, et al. High speed impact properties of carbon fiber/epoxy resin composites[J]. Journal of Material Engineering, 2019, 47(8): 110. |
| [3] |
SÁ M F, GOMES A M, CORREIA J R, et al. Creep behavior of pultruded GFRP element-part 1:Literature review and experimental study[J]. Composite Structures, 2011, 93(10): 2450. DOI:10.1016/j.compstruct.2011.04.013 |
| [4] |
张小玉, 黄乾钰, 陈建中, 等. 聚合物基复合材料单向板黏弹性模型[J]. 华中科技大学学报(自然科学版), 2015, 43(1): 30. ZHANG Xiaoyu, HUANG Qianyu, CHEN Jianzhong, et al. The viscoelastic model of PMC unidirectional plates[J]. J. Huazhong Univ. of Sci. & Tech.(Natural Science Edition), 2015, 43(1): 30. |
| [5] |
任超, 陈建钧, 潘红良. 纤维增强复合材料黏弹性行为的预测模型[J]. 复合材料学报, 2012, 29(1): 162. REN Chao, CHEN Jianjun, PAN Hongliang. Prediction model for visco-elastic behavior of fiber reinforced composites[J]. Acta Materiae Compositae Sinica, 2012, 29(1): 162. |
| [6] |
ARAO Y, KOYANAGI J, TAKEDA S I, et al. Simple method for obtaining viscoelastic parameters of polymeric materials by incorporating physical-aging effects[J]. Mechanics of Time-Dependent Materials, 2012, 16(2): 169. |
| [7] |
NAKADA M, MIYANO Y, CAI H, et al. Prediction of long-term viscoelastic behavior of amorphous resin based on the time-temperature superposition principle[J]. Mechanics of Time-Dependent Materials, 2011, 15(3): 309. DOI:10.1007/s11043-011-9139-8 |
| [8] |
TUTTLE M E, BRINSON H F. Prediction of the long-term creep compliance of general composite laminates[J]. Experimental Mechanics, 1986, 26(1): 89. |
| [9] |
GREEN A E, RIVLIN R S, SPENCER A J M. The mechanics of nonlinear materials with memory[J]. Arch for Rational Mechanics and Analysis, 1959, 3(1): 82. DOI:10.1007/BF00284166 |
| [10] |
BERNSTEIN B, KEARSLEY E A, ZAPAS L J. A study of stress relaxation with finite strain[J]. Transaction of the Society of Rheology, 1963, 7(1): 391. DOI:10.1122/1.548963 |
| [11] |
王礼立, 施绍裘, 陈江瑛, 等. ZWT非线性热粘弹性本构关系的研究与应用[J]. 宁波大学学报(理工版), 2000, 13(增刊): 141. WANG Lili, SHI Shaoqiu, CHEN Jiangying, et al. Research and application of ZWT nonlinear thermoviscoelastic constitutive relation[J]. Journal of Ningbo University, 2000, 13(Sup): 141. |
| [12] |
SCHAPERY R A. On the characterization of a nonlinear fiber-reinforced plastic[J]. Polymer Engineering and Science, 1969, 9(4): 295. DOI:10.1002/pen.760090410 |
| [13] |
RAFIEE R, MAZHARI B. Modeling creep in polymeric composites: developing a general integrated procedure[J]. International Journal of Mechanical Sciences, 2015, 99: 112. DOI:10.1016/j.ijmecsci.2015.05.011 |
| [14] |
GUEDES R M. Nonlinear viscoelastic analysis of thick-walled cylindrical composites pipes[J]. Journal of Mechanical Sciences, 2010, 52(8): 1064. DOI:10.1016/j.ijmecsci.2010.04.003 |
| [15] |
TOUGUI A, GAMBY D, LAGARDE A, et al. Nonlinear photoviscoelasticity: theory and measurement[J]. Experimental Mechanics, 1983, 23(3): 314. |
| [16] |
BEHZADPOOR H, MASOUMI S, SALEHI M. Micromechanical analysis of nonlinear viscoelastic unidirectional fiber-reinforced composites[J]. Applied Mechanics & Materials, 2012, 110-116: 1166. DOI:10.4028/www.scientific.net/AMM.110-116.1166 |
| [17] |
MOHAN R, ADAMS D F. Nonlinear creep-recovery response of a polymer matrix and its composites[J]. Experimental Mechanics, 1985, 25(3): 262. DOI:10.1007/BF02325096 |
| [18] |
中国国家标准化管理委员会.定向纤维增强聚合物基复合材料拉伸性能试验方法: GB/T 3354-2014[S].北京: 中国标准出版社, 2014
|
| [19] |
Test method for tensile properties of orientation fiber reinforced polymermatrix composite materials: GB/T 3354-2014[S]. Beijing: Standardization Administration of the People's Republic of China, 2014
|
| [20] |
中国国家标准化管理委员会.聚合物基复合材料纵横剪切试验方法: GB/T 3355-2014[S].北京: 中国标准出版社, 2014
|
| [25] |
Test method for in-plan shear response of polymermatrix composite materials: GB/T 3355-2014[S]. Beijing: Standardization Administration of the People's Republic of China, 2014
|
| [26] |
JIS K 7078-1996. Testing methods for tensile creep of carbon fiber reinforced plastics[S]. Tokyo: Japanese Standards Association, 1996
|
 2020, Vol. 52
2020, Vol. 52


