2. 北京理工大学 先进加工技术国防重点实验室, 北京 100081
2. Key Laboratory of Fundamental Science for Advanced Machining, Beijing Institute of Technology, Beijing 100081, China
精密孔类零件是工业生产中应用最广泛的零部件之一,广泛应用于航空、航天、汽车、军工、船舶、石油、冶金等精密制造行业.轴线直线度误差是孔类零件的一项重要指标,影响零部件的工作性能、装配精度与使用寿命,必须严格控制精密孔类零部件的轴线直线度误差.随着精密制造行业对孔类零件的轴线直线度误差的控制要求越来越高,对误差评定方法的精度也提出越来越严格的要求.
轴线直线度误差属于空间直线度误差.对于空间直线度误差评定,国家标准提出3种基本方法[1]:两端点连线法、最小二乘法和最小区域法.其中最小区域法符合空间直线度误差的定义,但是对于“最小区域”的求解,国家标准却没有给出具体的方法.近年来,国内外的研究重点聚焦于通过确定最小区域来求解空间直线度误差.
为拟合空间直线,胡仲勋[2]与王炳杰[3]提出了三维最小二乘法,从本质上克服了最小二乘法的理论缺陷,实现真正的三维拟合,有效提高了求解精度;Ding等运用切比雪夫理论[4]与半定规划理论[5]拟合空间直线,实现对空间直线度误差评定;Samuel等[6]通过构建测点集的外凸包确定了包容区域;Dhanish等[7]与Endrias等[8]对参考点组合迭代计算,得到最小区域的控制点组合.利用投影可将空间问题简化为平面问题,降低求解难度.黄富贵等[9]将任意方向上直线度误差的评定问题转化为给定平面内直线度误差与圆度误差的评定问题;Cheraghi等[10]将空间直线度问题转化为平面求解最小外接圆问题;为了提升投影法的评定精度,罗钧等[11]根据投影面重合点数目的不同提出了不同的包容圆求解方法;张新宝等[12]针对两点在包容圆上的分布情况,旋转圆柱体轴线得到了更精确的空间直线度误差评定值.近年来,智能优化算法在形位精度误差评定中的应用日益广泛.粒子群算法[13-14]、遗传算法[15]、蜂群算法[16]等智能算法相继被运用到空间直线度误差评定中,这些算法的结果通常受到目标函数形式与初始参数选择的影响.
传统投影法是将测点向垂直于最小二乘中线的中垂面投影,将空间问题转化为圆度评定问题[11].不同于传统投影法,本文将测点向空间坐标系o-xyz的垂直面(yoz面或xoz面)投影,考虑到直接投影会遗漏控制点的问题,提出一种旋转投影法评定轴线直线度误差.通过对测量点进行齐次坐标变换与旋转投影,将空间直线度评定转化为平面直线度问题,从而实现快速准确的误差评定.
1 测量点的旋转投影 1.1 轴线直线度误差模型图 1为轴线直线度误差模型示意图,图中实际直线指被测实际直线,测点指被测实际直线上的采样点,理想直线由测点拟合得到.轴线直线度误差属于空间直线度误差,指被测直线相对于其理想直线在任意方向上存在的变动量.国家标准规定,空间直线度误差值等于包络所有误差测点的最小圆柱面的直径[1].理想直线L由最小原则确定,设直线L的方向向量为(l, m, n),通过点(a, b, c),该直线的方程可以表示为
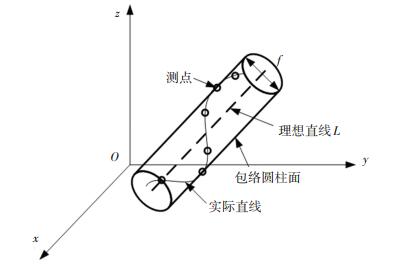
|
图 1 轴线直线度误差模型 Fig. 1 Model of axis straightness error |
| $ \frac{{x - a}}{l} = \frac{{y - b}}{m} = \frac{{z - c}}{n} $ | (1) |
其中直线参数l, m, n, a, b, c为需要确定与优化的变量.测点与理想直线的距离表示为
| $ {r_i} = \frac{{\left\| {\begin{array}{*{20}{c}} i&j&k\\ {{x_i} - a}&{{y_i} - b}&{{z_i} - c}\\ l&m&n \end{array}} \right\|}}{{\sqrt {{l^2} + {m^2} + {n^2}} }}. $ | (2) |
ri的最大值即为包容所有测点圆柱面的圆柱半径,该半径的2倍即为所求空间直线度误差.包容所有测点的圆柱面的数量很多,其中具有最小直径的圆柱面即为最小区域.求解最小区域的过程是一个复杂的非线性优化过程[9].
通过投影的方式可以将空间误差评定问题转化为平面误差评定问题,简化求解难度.在平面上求解包络所有测点的最小区域的值,即为空间直线度误差值,位于包容区域边界上的测点称为控制点.但是,投影过程必然会丢失一些测点之间的空间几何关系,如何减少误差,获得更为精确的最小区域是投影法面临的难点之一.
1.2 齐次坐标变换为便于后续误差评定,将测点由坐标系o-xyz向坐标系o′-x′y′z′转化,使最小二乘中线经过坐标系o′-x′y′z′的原点,并与z′轴重合.设测点最小二乘中线的方向向量(l, m, n),通过点(a, b, c),则齐次坐标变换公式为
| $ [{x^\prime },{y^\prime },{z^\prime },1] = [x,y,z,1] \cdot {\mathit{\boldsymbol{R}}_t} \cdot {\mathit{\boldsymbol{R}}_x} \cdot {\mathit{\boldsymbol{R}}_y}, $ | (3) |
其中
| $ {\mathit{\boldsymbol{R}}_t} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ { - a}&{ - b}&{ - c}&1 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{R}}_x} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha }&{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha }&0\\ 0&{ - {\rm{sin}}{\kern 1pt} {\kern 1pt} \alpha }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha }&0\\ 0&0&0&1 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{R}}_y} = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta }&0&{{\rm{sin}}{\kern 1pt} {\kern 1pt} \beta }&0\\ 0&1&0&0\\ { - {\rm{sin}}{\kern 1pt} {\kern 1pt} \beta }&0&{{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta }&0\\ 0&0&0&1 \end{array}} \right]. $ |
α与β为最小二乘中线与坐标平面的夹角,其中
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha = \frac{n}{{\sqrt {{n^2} + {m^2}} }},{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha = \frac{m}{{\sqrt {{n^2} + {m^2}} }},}\\ {{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta = \frac{{\sqrt {{n^2} + {m^2}} }}{{\sqrt {{l^2} + {m^2} + {n^2}} }},{\rm{sin}}{\kern 1pt} {\kern 1pt} \beta = \frac{l}{{\sqrt {{l^2} + {m^2} + {n^2}} }}.} \end{array} $ |
齐次坐标变换的示意图如图 2所示.
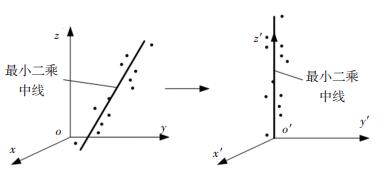
|
图 2 齐次坐标变换 Fig. 2 Homogeneous coordinate transformation |
齐次坐标变换后测点的分布如图 3所示.
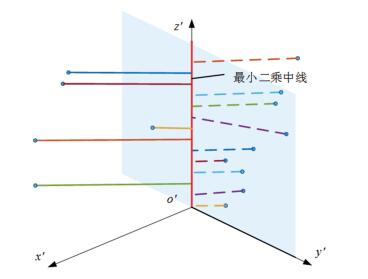
|
图 3 坐标变换后测点分布 Fig. 3 Measuring point distribution after coordinate transformation |
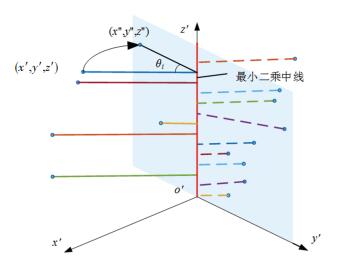
如图 4所示,若直接将测点向y′o′z′平面投影,当测点与其最小二乘中线上垂足的连线和y′o′z′平面的角趋近90°时,无论测点与中线距离长短,投影点始终会在z′轴附近,这类测点的距离关系无法在投影点中体现,称为投影抑制点.
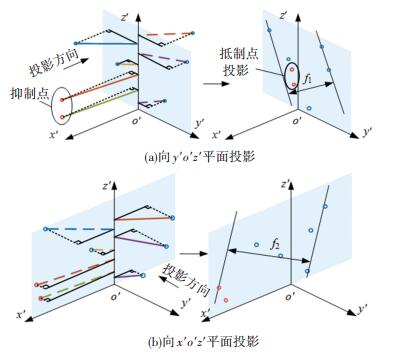
|
图 4 直接投影法误差分析 Fig. 4 Error analysis of direct projection method |
在y′o′z′投影面上,抑制点的投影点被其他测点的投影点包围.评定最小包容区域时,抑制点不会成为控制点.若抑制点集中某测点与中线的距离大于其他测点,该测点应成为控制点,但是直接投影法无法求解.因此,直接将测点向y′o′z′平面投影会遗漏控制点组合,影响评定结果的精度.
为全面反映测点的分布情况,需要同时将测点向x′o′z′平面投影,最后拟合两个平面的评定结果,从而得到空间直线度误差值.直接投影法需要两次投影,增加了计算量并且拟合过程引入的评定误差会影响评定精度[2].
旋转投影法将测点绕最小二乘中线旋转投影到y′o′z′平面上,仅需一次投影就能得到包容所有测点的最小区域,如图 5所示.
|
图 5 旋转投影 Fig. 5 Rotating projection |
图 5中,θi为测点i与其在最小二乘中线上垂足的连线与y′o′z′平面的夹角,采用旋转投影法,将各测点绕z′轴旋转角度θi,使各个测点落在y′o′z′平面上,转换后的坐标表示为
| $ \begin{array}{*{20}{l}} {[{x^{\prime \prime }},{y^{\prime \prime }},{z^{\prime \prime }},1] = [{x^\prime },{y^\prime },{z^\prime },1] \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}({\theta _i})}&{{\rm{sin}}({\theta _i})}&0&0\\ { - {\rm{sin}}({\theta _i})}&{{\rm{cos}}({\theta _i})}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right].} \end{array} $ | (4) |
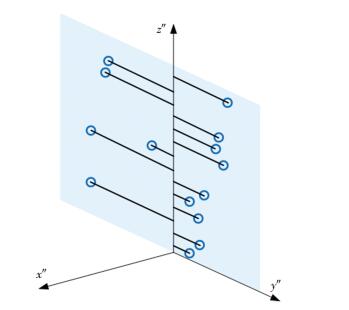
旋转投影后各测点的分布如图 6所示.通过旋转投影,各测点与最小二乘中线的距离关系被保留下来并转换到y′o′z′平面,轴线直线度误差评定问题转化为平面直线度评定问题,包容平面测点的两平行直线的距离即为轴线直线度误差值.
|
图 6 旋转投影后坐标分布 Fig. 6 Coordinates distribution after rotating projection |
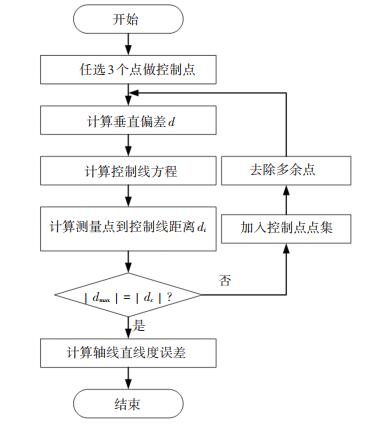
为便于后续误差评定,z′轴与y′轴分别作为平面坐标系的X轴与Y轴,组成平面坐标系XOY,在XOY平面进行误差评定,评定流程图如图 7所示.
|
图 7 评定流程图 Fig. 7 Flow chart of evaluation |
在测量点中任选3个点作为控制点,其坐标分别为(X1, Y1),(X2, Y2),(X3, Y3),求解控制点确定的控制线的直线方程,如图 8所示.

|
图 8 控制点与控制线 Fig. 8 Control point and control line |
按式(5)计算控制点与控制线的垂直偏差d.
| $ d = \frac{{{\lambda _1}{Y_1} + {\lambda _2}{Y_2} + {\lambda _3}{Y_3}}}{{ - (|{\lambda _1}| + |{\lambda _2}| + |{\lambda _3}|)}}, $ | (5) |
其中,λ1=X3-X2,λ2=X1-X3,λ3=X2-X1.
按式(6)计算控制线对应点的纵坐标
| $ \begin{array}{*{20}{l}} {{Y_1}{\rm{'}} = {Y_1} + ( {\rm{sign}} ({\lambda _1}))d,}\\ {{Y_2}{\rm{'}} = {Y_2} + ( {\rm{sign}} ({\lambda _2}))d,}\\ {{Y_3}{\rm{'}} = {Y_3} + ( {\rm{sign}} ({\lambda _3}))d.} \end{array} $ | (6) |
得到控制线经过的三点坐标为(X1, Y1′),(X2, Y2′),(X3, Y3′),按式(7)计算控制线的斜率k与截距b.
| $ \begin{array}{*{20}{l}} {k = ({Y_1}{\rm{'}} - {Y_2}{\rm{'}})/({X_1} - {X_2}),}\\ {b = {Y_1}{\rm{'}} - k{X_1}.} \end{array} $ | (7) |
计算各测量点到控制线的距离di.
| $ {d_i} = \frac{{k{X_i} - {Y_i} + b}}{{\sqrt {1 + {k^2}} }}. $ | (8) |
di的正负号反映测量点与控制线的位置关系.符号为正表示测量点在控制线上侧,符号为负表示测量点在控制线下侧.
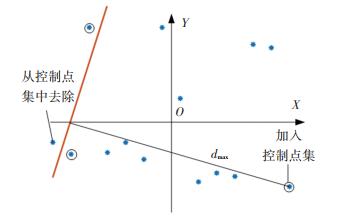
式(8)计算得到的结果中,距离绝对值的最大值记为|dmax|,对应的点坐标为(Xdmax, Ydmax);控制点到控制线距离的绝对值记为|dc|.若|dmax|>|dc|,则|dmax|对应的测量点加入控制点点集,并从原控制点中去除多余的点,如图 9所示.
|
图 9 控制点加入与去除 Fig. 9 Control point addition and removal |
被去除的点序号按式(9)~(10)来计算.
| $ \left\{ {\begin{array}{*{20}{l}} {{c_1} + {c_2} + {c_3} + 1 = 0,}\\ {{c_1}{X_1} + {c_1}{X_1} + {c_1}{X_1} + {X_{d{\rm{max}}}} = 0,} \end{array}} \right. $ | (9) |
令c3=1,计算三点的距离比例系数q1,q2,q3.
| $ {q_1} = \frac{{{c_1}}}{{{\lambda _1}}},\quad {q_2} = \frac{{{c_2}}}{{{\lambda _2}}},\quad {q_3} = \frac{{{c_3}}}{{{\lambda _3}}}. $ | (10) |
若sign(d)·dmax>0,则距离比例系数最小的点被去除,相反,去除距离比例系数最大的点.去除多余点后,根据3个新控制点的坐标,重复上述步骤,直至|dmax|=|dc|.由控制线方程的计算过程可知,每次迭代的控制点都满足最小区域的“高低高”或“低高低”准则,因此当|dmax|=|dc|时,可以认为该控制线确定的区域即为包容平面测点的最小区域,此时轴线直线度误差f=2|dmax|,如图 10所示.
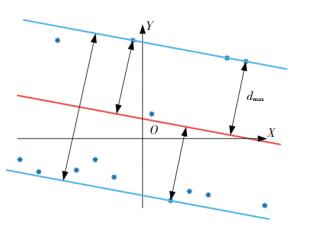
|
图 10 直线度误差评定结果 Fig. 10 Evaluation result of straightness error |
为验证旋转投影法的有效性与准确性,根据上述原理编写误差评定程序.采用软件为Matlab 2017b,电脑操作系统为win10,处理器为Intel i5-7400 CPU@3.00 Hz,安装内存为8.00 GB,系统类型为64位.采用文献[11]的空间测量点数据,便于与不同评定算法进行比较.
测点数据经过坐标变换与旋转投影后,在XOY平面的坐标如表 1所示.
| 表 1 空间坐标转换后测量点的投影坐标 Tab. 1 Projection coordinates of measuring points after transformation of space coordinates |
每次循环计算的控制点序号如表 2所示.
| 表 2 每次循环的控制点序号 Tab. 2 Control point number for each cycle |
由表 2中的数据可知,每经历一次循环,距离最大值对应的测量点都加入到控制点点集,多余点按第3节所述计算方法被去除. 5次循环后,确定最小区域控制点.此时各测点与控制线的距离di如表 3所示.
| 表 3 测点与控制线的距离 Tab. 3 Distance between measuring points and control line |
由表 3的数据可知,第7、9、12、13点与控制线距离值最大,为4.625 μm,其中,7、9、13点为计算得到的控制点.由表中数据可知,这3点符合“低高低”的最小区域准则,因此可以证明该方法的评定结果是有效的,直线度误差评定结果为9.25 μm.
除去控制点点集,第12点同样具有最大距离. GB/T 11336-2004规定,包容空间测点的最小圆柱区域有3个点在圆柱面上,4个点在圆柱面上和5个点在圆柱面这3种类型,文献[11]数据即属于4个点在包容圆柱面上的类型.
为验证旋转投影法的准确性,将评定结果与其他方法的评定结果进行比较,结果如表 4所示.
| 表 4 不同算法直线度误差评定结果 Tab. 4 Evaluation results of straightness error by different methods |
当用最小包容区域准则评定直线度误差时,在满足最小区域的前提下,评定结果越小越接近实际最小包容区域[12].由表 4的数据可知,在包容所有测点的前提下,本文方法的评定值最小.结果表明:相比其他方法,旋转投影法可以得到更为精确的直线度误差值.
为更加全面分析旋转投影法,参考不同文献来源,将旋转投影法与相对应文献内的算法进行扩展对比分析,结果如表 5所示.
| 表 5 不同数据来源评定结果 Tab. 5 Evaluation results from different data sources |
由表 5数据可知,在处理不同的数据时,旋转投影法的评定结果均能保持较好的精度,计算时间在0.1 s以内,综合前文所述,本方法能够应用在孔类零件轴线直线度误差评定等工程领域.
4 结论为精确计算轴线直线度误差值,满足精密制造业对孔类零件轴线直线度误差的控制要求,本文提出一种旋转投影的误差评定方法.通过齐次坐标变换与旋转投影,测量点围绕最小二乘中线做旋转投影转换到同一平面,保留了测点之间的距离关系,避免了直接投影遗漏控制点组合的问题,在平面上实现对轴线直线度误差的评定.本方法无需复杂的非线性优化求解过程,计算量小.计算结果表明,在符合最小区域要求的前提下,本文方法的评定结果优于其他算法,能够用于精密制造行业孔类零件的直线度误差数据评定.此外,本方法更可拓展用于轴类等回转体零件误差评定,具有较高理论与实际应用价值.
| [1] |
GB/T 11336-2004.直线度误差检测[S]. 2004 GB/T 11336-2004. Measurement of departures from straightness[S]. 2004 |
| [2] |
胡仲勋, 杨旭静, 金湘中. 评定空间直线度误差的3DLSA算法研究[J]. 中国机械工程, 2010, 21(3): 325. HU Zhongxun, YANG Xujing, JIN Xiangzhong. Research on 3DLSA for evaluating spatial straightness errors[J]. China Mechanical Engineering, 2010, 21(3): 325. |
| [3] |
王炳杰, 赵军鹏, 王春洁. 基于三维最小二乘方法的空间直线度误差评定[J]. 北京航空航天大学学报, 2014, 40(10): 1477. WANG Bingjie, ZHAO Junpeng, WANG Chunjie. Spatial straightness error evaluation based on three-dimensional least squares method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(10): 1477. |
| [4] |
DING Ye, ZHU Limin, DING Han. Semi-definite programming for Chebyshev fitting of spatial straight line with applications to cutter location planning and tolerance evaluation[J]. Precision Engineering, 2007, 31(4): 364. DOI:10.1016/j.precisioneng.2007.04.001 |
| [5] |
DING Ye, ZHU Limin, DING Han. A unified approach for circularity and spatial straightness evaluation using semi-definite programming[J]. International Journal of Machine Tools and Manufacture, 2007, 47(10): 1646. DOI:10.1016/j.ijmachtools.2006.12.001 |
| [6] |
SAMUEL G L, SHUNMUGAM M S. Evaluation of straightness and flatness error using computational geometric techniques[J]. Computer-Aided Design, 1999, 31(13): 829-843. DOI:10.1016/S0010-4485(99)00071-8 |
| [7] |
DHANISH P B, MATHEW J. A fast and simple algorithm for evaluation of minimum zone straightness error from coordinate data[J]. International Journal of Advanced Manufacturing Technology, 2007, 32(1-2): 92. DOI:10.1007/s00170-005-0317-1 |
| [8] |
ENDRIASD H, FENG Hisyung, MA Ji, et al. A combinatorial optimization approach for evaluating minimum-zone spatial straightness errors[J]. Measurement, 2012, 45(5): 1170. DOI:10.1016/j.measurement.2012.01.020 |
| [9] |
黄富贵, 崔长彩. 任意方向上直线度误差的评定新方法[J]. 机械工程学报, 2008, 44(7): 221. HUANG Fugui, CUI Changcai. New method for evaluating arbitrary spatial straightness error[J]. Journal of Mechanical Engineering, 2008, 44(7): 221. DOI:10.3321/j.issn:0577-6686.2008.07.037 |
| [10] |
CHERAGHI S H, JIANG Guohua, AHMAD J S. Evaluating the geometric characteristics of cylindrical features[J]. Precision Engineering, 2003, 27(2): 195. |
| [11] |
罗钧, 麻锦侠, 刘学明, 等. 三维坐标点集的空间直线度高精度快速评定[J]. 上海交通大学学报, 2016, 50(5): 730. LUO Jun, MA Jinxia, LIU Xueming, et al. High-precision and fast evaluation of spatial straightness error of 3D coordinate point set[J]. Journal of Shanghai Jiaotong University, 2016, 50(5): 730. DOI:10.3969/j.issn.1674-8115.2016.05.023 |
| [12] |
张新宝, 谢江平. 空间直线度误差评定的逼近最小包容圆柱法[J]. 华中科技大学学报(自然科学版), 2011, 39(12): 6. ZHANG Xinbao, XIE Jiangping. Evaluating spatial straightness error by approaching minimum enclosure cylinder[J]. Journal of Huazhong University of Science and Technology (Natural Science), 2011, 39(12): 6. |
| [13] |
CUI Changcai, LI Tukun, BLUNT L A, et al. The assessment of straightness and flatness errors using particle swarm optimization[J]. Procedia CIRP, 2013, 10: 271. DOI:10.1016/j.procir.2013.08.041 |
| [14] |
PATHAK V K, SINGH A K. Form error evaluation of noncontact scan data using constriction factor particle swarm optimization[J]. Journal of Advanced Manufacturing Systems, 2017, 16(3): 205. DOI:10.1142/S0219686717500135 |
| [15] |
WEN Xiulan, SONG Aiguo. An improved genetic algorithm for planar and spatial straightness error evaluation[J]. International Journal of Machine Tools and Manufacture, 2003, 43(11): 1157. DOI:10.1016/S0890-6955(03)00105-6 |
| [16] |
LUO Jun, WANG Qian. A method for axis straightness error evaluation based on improved artificial bee colony algorithm[J]. The International Journal of Advanced Manufacturing Technology, 2014, 71(5-8): 1501. DOI:10.1007/s00170-013-5567-8 |
 2020, Vol. 52
2020, Vol. 52


