两栖机器人是一种既可以在陆地、滩涂上行走, 又可以在水中浮游的特种机器人, 驱动装置为机器人提供动力,是两栖机器人的心脏,其性能直接决定了两栖机器人的越障性、机动性、稳定性等运动性能.其构型与功能的创新设计已经成为近年来的研究热点[1-3].
目前两栖机器人从驱动方式上分为叠加型驱动[4-6]和复合型驱动[7-12].叠加型驱动方式是指在现有的水下或陆地机器人的本体上添加一套独立的用于在另一种环境下行进的驱动装置,例如:日本香川大学Guo等人将喷水推进器叠加到多关节腿足端[4]、瑞士Rinspeed公司将螺旋桨叠加到车形机器人底部[6].复合型驱动方式是指对现有单一环境下的驱动器进行结构上的改造,使其可以通过结构上的变换来适应水下和陆地这两种不同的环境.例如:中科院沈阳自动化研究所的唐元贵等将车轮与螺旋桨复合[6]、北京理工大学的Xie等将划水板与车轮复合[7]、澳大利亚科廷大学的Lei等和中科院王明辉等将履带与桨板复合[8-9].然而目前采用这两种方式的机器人都只对单一环境具有适应性,对两栖环境适应性较差,并且叠加型驱动方式所需驱动器数量太多,复合型驱动需要进行结构变化才能穿越两栖环境.所以,亟需研发一种可以同时对水下和陆地环境都具有较好的适应性,且无需进行结构变换的复合型两栖机器人驱动装置.
受到垂直起降飞行器的启发[10],本文选用轮与轴流泵进行复合,设计了一种基于喷水推进的轮泵复合式两栖驱动装置,并建立了相应的推力与转矩预估模型.该装置使两栖机器人的机动性和环境适应性都较强,并且具有无缝运动模式切换能力和所需驱动器数量少的优点.
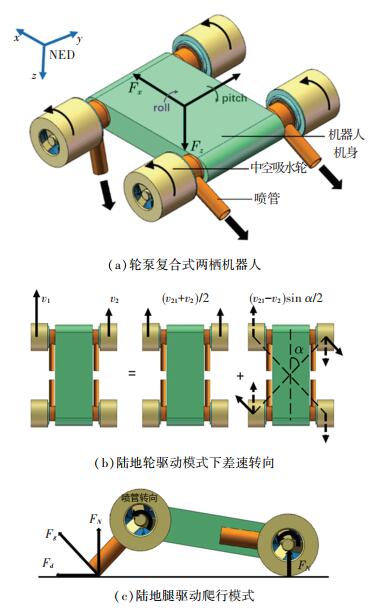
1 轮泵复合式两栖推进方案对于水下驱动,喷水推进方式相对于其他驱动方式更稳定,更容易控制且效率高、噪音低;在陆地上轮式驱动机动性更强,因此选用轮驱动与喷水驱动进行复合.由于轮泵复合型两栖推进器的吸水口和喷水口处于相互垂直的方向,在垂直于推进器推力方向上还存在因推进器吸水而产生微弱的拉力,因此该推进装置需要对称安装机器人本体的两侧.如图 1所示,采用复合两栖推进装置的机器人具有水下游动、陆地轮驱动以及陆地爬行3种运动模式.
|
图 1 轮泵复合式两栖机器人运动示意图 Fig. 1 Motion sketch of wheel-pump compound amphibious robot |
图 2所示为轮泵复合式两栖驱动装置,在驱动轮内部安装叶片,无刷电机带动中空轮转动.沉浸在液体中的叶片对液体产生推挤作用,液体被吸入和压出.压出后的液体经过导叶流入工作管路叶轮的机械能被传递给液体使液体的压力升高和流速增加,从而使液体从喷管中喷出产生反推力.现有的轮桨复合式两栖机器人需要通过调整轮子的方向来调节螺旋桨的方向,而本文设计的轮泵复合式两栖驱动装置使用空心轴的无刷电机驱动中空轮并在轮侧安装有可以360°转动的喷管,因此喷管可以提供一个平面二元矢量推力.叶片设计成轴流式叶片,转动时可以为水流提供一个前向压力能和旋转动能,在叶片和喷管之间有一段锥形截面收缩管路,用于将水流的压力势能转化为前向动能,管路内部的导流叶片也可将水流的旋转动能转变为前向动能.喷管由喷管转动电机驱动,推进器整体通过喷管轴连接到机器人躯体上.

|
图 2 轮泵复合式两栖驱动装置示意图 Fig. 2 Diagram of wheel-pump compound amphibious driving device |
推进器获得推力是水产生动量变化所致,所以可以通过水的动量变化率来计算推力[11].
根据动量定理,喷水推进器的推力可以表示为[12]
| $ T = \rho Q\left( {{v_{\text{o}}} - {v_{\text{h}}}} \right). $ | (1) |
式中:T为喷水推进器产生的推力;ρ为流经流道的水流量;vo为喷出水流流速度;vh为机器人在喷管轴线方向的分速度.
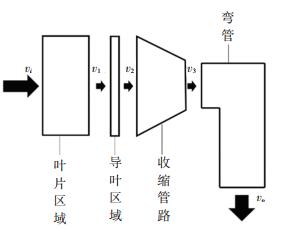
由式(1)可知,求解出喷管喷口喷出水流的平均速度即可求出轮泵复合式两栖推进装置的推力,但复合式推进装置内部为一个复杂的流动系统,很难直接求解出其喷口速度.这里对其进行简化将推进装置内部流动区域分为如图 3所示的叶片区域、导叶区域、收缩管道区域、弯管区域.水流在内部的流动的过程如图 3所示,水流被吸入叶片区域内会被叶片加速至v1,经过导叶的转化后前向速度变为v2;在收缩管路中,压力能转变为动能速度进一步增加至v3;最后,在弯管区域动能由于流体撞击壁面会产生一定的损失并以速度vo从喷口喷出.
|
图 3 复合式推进器内部的流动系统图 Fig. 3 Flow system diagram in composite propulsor |
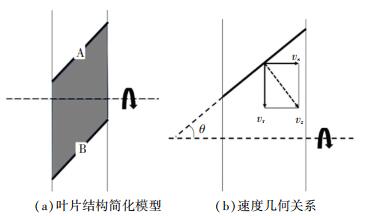
两个相邻扇叶以及其中流体结构的结构关系可以简化为如图 4(a)所示,图中A、B为吸水轮中两个相邻的扇叶.假设吸水轮两相邻叶片之间流体的体积为V(即阴影部分),不考虑叶片的翼形等因素,将叶片看作无厚度薄片,并把两叶片之间的水体看作是瞬时固体.这样就可以认为吸水轮每旋转一圈,两个相邻扇叶之间流体会全部被叶片挤出叶片区域,若叶轮中叶片数量为m,则叶轮每旋转一圈其排出的流体体积为mV.
|
图 4 叶片简化模型 Fig. 4 Simplified blade model |
假设中空叶轮的转速为n,则从叶片区域排出水流在叶轮轴向上的平均速度为
| $ {v_1} = n\frac{{mV}}{{{A_1}}}, $ | (2) |
式中A1为叶轮区域的有效面积.
水流受到轴流式叶片加速后同时具有前向动能和旋转动能,其前向速度和旋转速度的几何关系如图 4(b)所示,它们之间的关系可以表达为vr=vs/tanθ,其中vs=v1, vr为旋转速度,θ为叶片倾角.
在水流经过导叶时,水流的轴向速度保持不变.但是由于导叶的导向作用,有一部分旋转速度被转化为轴向速度,另外一部分转化为内能.导叶设计为45°的转化效率大约为50%左右[11],那么叶轮单位时间内从导叶部分流出的水流速度为
| $ {v_2} = {v_1} + 0.5{v_{\text{r}}} $ | (3) |
在不考虑损失时,由连续性方程可知,在变截面管道中速度与截面之间存在如下关系式:
| $ {v_2}{A_2} = {v_3}{A_3}, $ | (4) |
式中:v2, A2为收缩管路入口截面的速度和面积且A2=A1; v3, A3为收缩管路出口截面速度和面积.
由式(4)可以得到v3=v2A2/A3,在忽略弯管损失时v3=vo.因此,联立式(2)~(4)可以得到喷口喷出水流的速度可以表达为
| $ {v_{无损}} = {v_{\text{o}}} = \frac{{{v_2}{A_2}}}{{{A_3}}}. $ | (5) |
令航速,且流量表示为vh=0,且流量表示为Q=voA3,联立式(2)~(5),将式(5)中得到的vo代入式(1),可以得到在静水中不考虑损失的推力表达式为
| $ {T_{理想}} = \rho \frac{{{n^2}{m^2}{V^2}{{\left( {1 + \frac{1}{{2\tan \theta }}} \right)}^2}}}{{{A_3}}}. $ | (6) |
即使是不考虑流体粘度的影响(即假设内部流道光滑无摩擦的情况下),流体在流经锥形断面收缩管和弯管时仍旧会有能量的损失.流体在管路中流动主要取决于速度、密度、管长、管径、管壁粗糙度、压力变化、加速度、粘度和弹性体积模量这9个物理量,在水流的流动过程中,压力变化与流体密度和水流速度的平方成正比.由于喷管的长度很小,可以忽略Froude数对压力降低的影响.另外,考虑到水流在进入喷嘴之前的流速远低于水的声速,还可以忽略马赫数的影响.所以,可以认为水流在圆管中流动时,压力变化主要由Reynolds数和管道参数决定,即有
| $ \frac{1}{2}\rho {v^2}_{无损} = \frac{1}{2}\rho {v^2}_{有损} + {p^*}. $ | (7) |
若流体在管路中的流阻系数为ζ,则压力损耗可以表示为p*=ζv2/2,由于目前从理论上无法导出ζ的表达式,所以通常根据实验来给出的经验值.
令ζ1、ζ2、ζ3和p1*、p2*、p3*分别为直管、弯管、收缩管道的流阻系数和压力损失.由于之前已经假设推进器内部流道壁面光滑无摩擦, 所以可以忽略水流在直管中的阻力损失系数ζ1=0即p1*=0.
在弯管中,管壁迫使水流的流速方向发生改变,水流受到向心力的作用,易产生脱流现象,形成旋涡而造成压力损失[13].当弯管为标准的肘管时,流阻系数ξ2=0.9, 则水流在经过弯管时的压力损失为
在流道发生断面收缩时,流阻系数主要取决于发生变化前后流道横截面积之比,截面积变化越大,流阻系数越大.实验结果显示[13],当水流从大容器流入锐缘进口的管道时,流阻系数为ξ3=0.5.因此,在水流在收缩截面中的压力损失为
由式(7)得
| $ \frac{1}{2}\rho {v^2}_{无损} = \frac{1}{2}\rho {v^2}_{有损} + p_1^* + p_2^* + p_3^*. $ | (8) |
因此考虑管路中压力损失情况下,将求解出的v有损代入(1)式,并与(6)式对比,可以得考虑局部损失的情况下推进器的在静水中的推力为
| $ {T_{有损}} = {T_{理想}} - 2{A_3}p_{{\text{all}}}^* $ | (9) |
式中pall*=p1*+p2*+p3*.
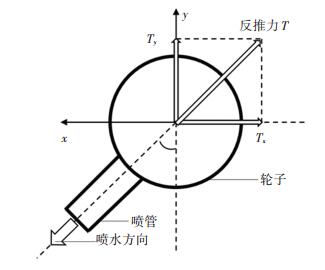
复合式两栖推进器可以提供一个平面推力,对于机器人本体这个推力可以分解为使机器人前进后退的水平推力和上浮下潜的竖直推力,建立如图 5所示坐标系,可以得到两栖驱动器的分解推力表达式为
|
图 5 推进器推力分解示意图 Fig. 5 Diagram of propeller thrust decomposition |
| $ \left[ {\begin{array}{*{20}{c}} {{T_x}} \\ {{T_y}} \end{array}} \right] = {T_{理想}}\left[ {\begin{array}{*{20}{c}} {\sin \alpha } \\ {\cos \alpha } \end{array}} \right] - 2{A_3}p_{{\text{all}}}^*\left[ {\begin{array}{*{20}{c}} {\sin \alpha } \\ {\cos \alpha } \end{array}} \right]. $ | (10) |
根据能量守恒原理,单位时间内水流从叶轮区域流出所具有的动能全部来源于叶轮转动的机械能,单位时间内叶轮转动所做的功为
| $ W = {E_e} = \frac{1}{2}m{v^2} = n\frac{1}{2}{A_1}v_z^3. $ | (11) |
式中:Ec为水流获得的动能,n为电机的转速,vz为水流从叶轮流出的合速度vz=v1+v1/tanθ.
由旋转力矩做功公W=Mφ=2πMn计算可以得到理想状态下轮驱动电机的扭矩为
| $ {M_{理想}} = \frac{W}{{2\pi n}} = \frac{{\rho {A_1}v_z^3}}{{4\pi }}. $ | (12) |
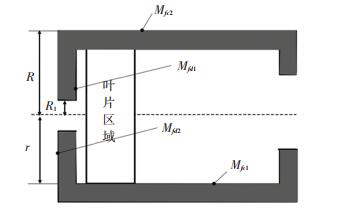
由于轮子内外表面的面积较大,因此其在水中旋转产生的扭矩不可忽略.叶轮旋转时表面扭矩分布简化为如图 6所示.轮子的壁厚较小,所以在这里忽略壁厚的影响并认为内外表面具有相同的表面积,即默认内外表面扭矩相等.
|
图 6 表面扭矩简化 Fig. 6 Simplification of surface torque |
圆柱形转子底面和侧面在水中转动的阻力矩为[14]
| $ {M_{fd1}} = {M_{fd2}} = {\rm{ \mathsf{ π} }}\rho {\omega ^2}\int_{R1}^R {{r^4}} \frac{{{c_1}}}{{\left( {\lg \frac{{\rho {r^2}\omega }}{\mu }} \right)}}dr, $ | (13) |
| $ {M_{fc1}} = {M_{fc2}} = H{R^4}\frac{{{c_1}{\rm{ \mathsf{ π} }}\rho {\omega ^2}}}{{{{\left( {\lg \frac{{\rho {R^2}\omega }}{\mu }} \right)}^{c2}}}}. $ | (14) |
式中:R为圆柱面半径,R1为中心圆孔半径,c1, c2为粘滞系数取决于材料特性,μ为水的动力粘度.
由式(12)~(14)得轮驱动电机在真实情况下的总的扭矩为
M真实=M理想+Mfd+Mfc.
3 推进器内部流动及推力仿真经过理论计算可以得到复合两栖推进器的推进性能,还需要对其进行软件仿真以验证理论计算的正确性.
将整个装置固定在仿真水域中,其入口速度设置为0,环境压力设置为一个大气压,环境温度设置为300 K.在水下环境中叶片转速过高会引起叶片的空化效应,因此将吸水轮转速数值设定较低,大小为0~2 800 r/min.
1) 设定吸水轮的转速在一定的范围内变化,保持喷管方向不变,并测出水流对整个装置的反推力即可获得推进器的推力数据.
2) 保持吸水轮转速不变,使喷管转动360°并测量装置受到的前进推力和抬升推力变化曲线即可得到推进器的二维矢量推进数据.
在此分别对理想情况下和考虑收缩管与弯管损失情况下的装置进行仿真分析.
仿真模型的尺寸参数:叶片区域宽度为12 mm,叶片倾角为60°,叶片数目为3个.截面收缩管的长度Lz=50 mm,小截面直径D1=20 mm,大截面直径D2=86 mm;弯管半径R=30 mm;喷管长度LP=100 mm,直径Do=20 mm.
为保证精度采用商用CFD软件对轮泵复合推进装置进行网格划分和瞬态分析.采用滑移动网格并在叶片区域进行网格加密,仿真模型的网格数量分别为15.675万个和19.982万个.
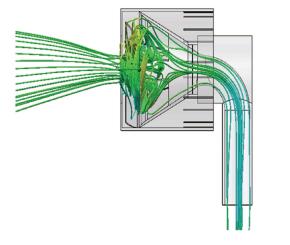
从图 7所示的速度流线中可以看出,在吸水轮旋转时,吸水孔对水流有抽吸的作用,并且使水流同时具有了旋转速度和前向速度,水流经过导流叶片后旋转速度被转化为前向速度,并从喷口喷出.说明2.1节中的结构设计是可行的.
|
图 7 两栖推进器内部流线图 Fig. 7 Thrust decomposition diagram of propeller |
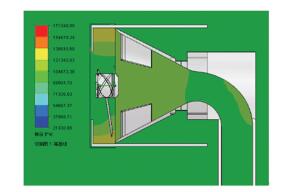
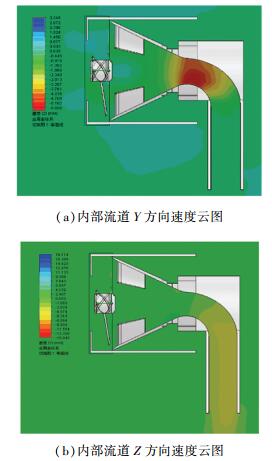
从如图 8和图 9所示的推进器内部流道的压力分布云图和速度分布云图中可以看出,水流从叶片区域流入锥形截面收缩管中后,流体的压力升高,在叶轮转速为2 800 r/min时最大压力为1.3 MPa, 此时叶轮转动的机械能转化为水流的压力势能;当水流流出锥形管小截面之后压力降低至外界环境的压力,速度急剧增加,此时水流的压力势能被转换为水流的动能,这与2.1中理论分析的结论是一致的.
|
图 8 推进器内部流道压力云图 Fig. 8 Pressure nephogram of inner channel of propeller |
|
图 9 推进器内部流道速度云图 Fig. 9 Velocity nephogram of inner channel of propeller |
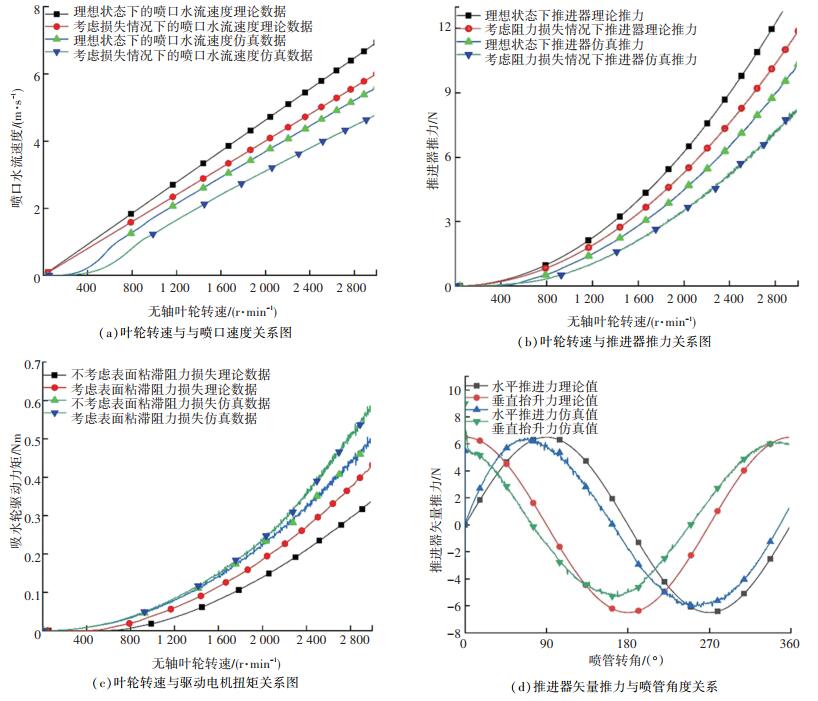
从图 10(a)中可以看出,喷口喷出的速度与吸水轮转速成正比关系.仿真条件下,转速达到200 r/min左右时喷口水流才具有明显的喷出速度,这是因为在转速较低时,多数流体处于被搅动的状态而不是被加速状态,叶片为水流提供的动能不足以抵消外界的压力.在速度高于400 r/min后喷口喷水速度与吸水轮转速为近似线性关系,在速度达到2 800 r/min时真实情况下的喷出速度达到5.5 m/s.
|
图 10 理论与仿真数据对比图 Fig. 10 Comparison between theory and simulation data |
如图 10(b),推力大小与吸水轮转速为二次函数关系,这与理论推导的结果是一致的.转速低于400 r/min时几乎没有推力,随着转速的增加推力逐渐上升,在转速为2 800 r/min时极限理论推力为9 N左右,仿真结果为6.9 N.
在设定表面粗糙度为0.01 μm的条件下,轮驱动电机的扭力与吸水轮转速也是二次函数的关系,仿真结果有幅度约为0.005 N·m的波动,如图 10(c)所示.从曲线中可以看出粘滞阻力带来的影响随着转速的增加而增加,在转速达到2 800 r/min时粘滞阻力引起的扭矩约为0.1 N·m.
喷管以360 degree/s的转动速度转动时,从图 10(d)可以看出仿真结果中推力的变化趋势与理论结果趋于一致,仿真曲线略有超前.在喷管分别为90°和270°时推进器获得最大的前进和后退推力.在喷管转角分别为0°和180°时推进器获得最大抬升和下潜推力.
4 推进器推进性能实验为了获得两栖推进装置的推进能力,并进一步验证结构设计与理论分析的正确性,因此在与软件仿真相同的条件下,进行实验验证,实验装置的结构和原理如图 11所示.

|
图 11 实验装置结构与原理图 Fig. 11 Structure and schematic diagram of experimental device |
通过3d打印技术制作了两栖推进器实验样机,其空间尺寸为150 mm×100 mm×90 mm,自重约为2.5 N.
该实验装置主要由两栖推进器本体,水池,力传感器以及数据采集设备组成,其中两栖推进装置的轮驱动电机为420 KV的有感无刷电机,使用Arduino开发板加无刷有感电调对电机进行控制,通过改变PWM信号实现电机的转速控制并能够实时反馈转速数据.轮驱动电机用伺服舵机代替,可以驱动喷管在0~180°的范围定角度转动,同样使用Arduino开发板通过调节PWM信号来调整喷管转角.传感器为2维力传感器, 可以同时获取两栖推进装置的前进力和抬升力.使用直流电源为无刷电机供电,可以读取其电压、电流大小来确定无刷电机的功率P,从而利用公式T=9 550 P/n计算出无刷电机的实际扭矩.
按照实验原理图进行实验验证,将直流电源电压锁定为10 V,在此条件下电机的理论最大转速为4 200 r/min可以满足设定的3 000 r/min的使用要求.首先,舵机为停止状态,控制电调的PWM信号占空比从第5 s开始匀速增加,同时检测有感电调反馈的转速信号,当转速达到3 000 r/min时停止增加占空比,并停留20 s.在此过程中,记录直流电源显示屏上电流的数值,并计算出电机的扭矩.
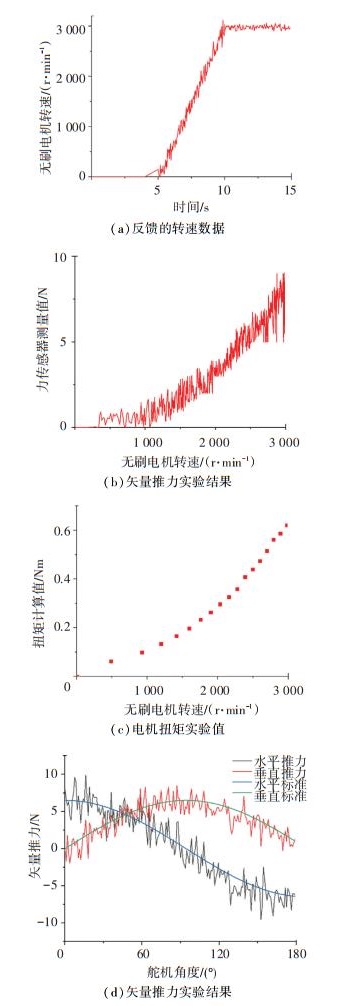
反馈的转速数据如图 12(a), 将推力与转速整合之后可以得到图 12(b),从图中可以看出推力与转速之间的关系接近理论结果.但是实际推力会有约±0.3 N的波动,在2 800 r/min的额定转速下,推力约为6.5 N.转速进一步升高时,推力出现了下降的趋势,说明叶轮在转速约为3 000 r/min时出现了空化现象.
|
图 12 推进器性能的实验结果 Fig. 12 Experimental results of propeller performance |
计算机无法直接采集到供电电流的变化,只能通过人工记录直流电源显示屏的电流读数.这里每调节一次转速记录一个点,共记录20个点,并且转速越大记录越密集.转速数据与计算得到的扭矩数据之间的关系如图 12(c)所示.可以看出扭矩与转速的关系接近于仿真结果,但实验数据要比仿真数据大0.1 N·m左右,这是一些附加因素产生阻力矩导致的.
控制舵机转动使喷管转到一水平位置,使用Arduino控制板控制输出至电调的PWM信号的占空比以保证无刷电机的转速保持在2 800 r/min,调整输出至舵机的PWM信号使其占空比从,即喷管从以0°转到180°的位置,以喷管角度为横轴,推力为纵轴可以得到图 12(d).矢量推力结果与理想的曲线基本拟合,但有约为±0.5 N的波动.
图 12中的结果与理论和仿真中的结果基本一致,但是实验结果的波动明显要比仿真结果更大,并且转速越大波动越大.
5 结论1) 根据两栖类机器人的发展需求,将可旋转喷管引入喷水推进器并且与轮进行复合,设计了一种轮泵复合式的矢量喷水两栖驱动装置.在陆地上具有轮驱动的高机动同时具有一定的越障能力,水下具有喷水推进的稳定性并可以提供矢量推力,是一种可以无缝切换多种运动模式的多功能驱动装置.
2) 所提的基于动量定理和压力损耗理论的推力估算方法和基于能量守恒和阻力矩损耗的扭矩估算法能够快速地实现对非标长水设备的推力和扭矩的快速预估,并且误差值处于可接受的范围.
3) 通过水下实验,证明了该两栖推进装置在水下可以提供有效的推力,验证了结构设计和理论方法的有效性与正确性.
| [1] |
MO Jixue, MIAO Zhihuai, LI Bing, et al. Design analysis and performance verification of a water jet thruster for amphibious jumping robot[J]. Proceedings of the Institution of Mechanical Engineers, 2019, 233(15): 1. |
| [2] |
ZHONG Bin, ZHOU Youcheng, LI Xiaoxiang, et al. Locomotion performance of the amphibious robot on various terrains and underwater with flexible flipper legs[J]. Journal of Bionic Engineering, 2016, 13(4): 525. DOI:10.1016/S1672-6529(16)60325-6 |
| [3] |
何彦霖, 董明利, 孙广开, 等. 复合式驱动小型两栖机器人水下运动控制研究[J]. 仪器仪表学报, 2019, 40(1): 219. HE Yanlin, DONG Mingli, SUN Guangkai, et al. Research on underwater motion control of small amphibious robot with compound drive[J]. Chinese Journal of Scientific Instrument, 2019, 40(1): 219. |
| [4] |
LI Maoxun, GUO Shuxiang, HIRATA H, et al. A roller-skating/walking mode-based amphibious robot[J]. Robotics and Computer Integrated Manufacturing, 2017, 44: 17. DOI:10.1016/j.rcim.2016.06.005 |
| [5] |
FREJEK M, NOKLEBY S. Design of a small-scale autonomous amphibious vehicle[C]//2008 Canadian Conference on Electrical and Computer Engineering-CCECE. Niagara Falls: IEEE, 2008: 781
|
| [6] |
唐元贵, 张艾群, 俞建成, 等. 两栖机器人轮桨腿驱动机构多目标优化设计[J]. 机器人, 2009, 31(3): 276. TANG Yuangui, ZHANG Aiqun, YU Jiancheng, et al. Multi objective optimization design of wheel oar leg driving mechanism of amphibious robot[J]. Robot, 2009, 31(3): 276. DOI:10.3321/j.issn:1002-0446.2009.03.014 |
| [7] |
XIE Xiaolin, GAO Feng, HUANG Chuan, et al. Design and development of a new transformable wheel used in amphibious all-terrain vehicles (A-ATV)[J]. Journal of Terramechanics, 2017, 69: 45. DOI:10.1016/j.jterra.2016.11.001 |
| [8] |
CUI L, CHEONG P, ADAMS R, et al. AmBot: a bio-inspired amphibious robot for monitoring the swan-canning estuary system[J]. Journal of Mechanical Design, 2014, 136(11): 115001. DOI:10.1115/1.4028094 |
| [9] |
王明辉, 马书根, 李斌, 等. 非叠加型可变形两栖机器人水下推进方法[J]. 机械工程学报, 2015, 51(3): 1. WANG Minghui, MA Shugen, LI Bin, et al. Underwater propulsion method of non superimposed deformable amphibious robot[J]. Journal of Mechanical Engineering, 2015, 51(3): 1. |
| [10] |
陈钻钻. F-35系列战斗机将面向国际市场[N].科技日报, 2015-08-04(012) CHEN Zuanzuan. F-35 series fighter will face the international market[N]. Science and Technology Daily, 2015-08-04 (012 |
| [11] |
曹玉良, 王永生, 靳栓宝. 喷水推进轴流泵三元水力设计[J]. 交通运输工程学报, 2015, 15(2): 42. CAO Yuliang, WANG Yongsheng, JIN Shuanbao. Three dimensional hydraulic design of jet driven axial flow pump[J]. Journal of Traffic and Transportation Engineering, 2015, 15(2): 42. DOI:10.3969/j.issn.1671-1637.2015.02.007 |
| [12] |
张帅, 肖晶晶. 水下矢量推进器研究综述[J]. 舰船科学技术, 2019, 41(7): 1. ZHANG Shuai, XIAO Jingjing. Review of underwater vector propulsion devices[J]. Ship Science and Technology, 2019, 41(7): 1. DOI:10.3404/j.issn.1672-7649.2019.07.001 |
| [13] |
李海军, 何远航, 段卓平. 超高压水射流形成过程中的压力损失研究[J]. 高压物理学报, 2004, 18(2): 139. LI Haijun, HE Yuanhang, DUAN Zhuoping, et al. Study on pressure loss in the formation of ultrahigh pressure water jet[J]. Chinese Journal of High Pressure Physics, 2004, 18(2): 139. DOI:10.3969/j.issn.1000-5773.2004.02.008 |
| [14] |
高善群.液体中圆柱转子旋转运动的阻力研究[D].洛阳: 河南科技大学, 2013 GAO Shanqun. Study on the resistance of rotating motion of a cylindrical rotor in liquid[D]. Luoyang: Henan University of Science and Technology, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10464-1014013323.htm |
 2020, Vol. 52
2020, Vol. 52


