随着现代计算机技术和数值分析的发展,计算流体力学(简称CFD)已取得了长足的进步,涌现出了可用于先进飞行器设计的各类CFD计算软件[1-5].这类软件大多选用网格单元进行计算区域的离散,因此,这类方法可统称为“网格方法”,通常在流场数值模拟前都要求先对计算区域进行网格生成.由于网格拓扑的约束,要对包含飞机全机等复杂几何外形的计算区域生成合适的整体网格并非易事,尤其要求刻画出多体小间隙等几何细节时.因此,如何局部或完全摆脱网格的约束问题,成为人们开始关注和研究的热点[6-8],出现了一类意在完全打破网格拓扑限制的算法,无网格算法.这类算法对于处置和刻画复杂几何外形细节将更具灵活性,其理由主要有:计算区域是用无网格点云点布点离散的,具有灵活性和兼容性,既可按要求直接布点,也可利用已有的结构或非结构网格的网格点;无网格点上的空间导数近似仅依赖于当地点云点上的信息,而点云点无须连成网格.许多学者正是受这些重要特征的驱动,开始对其研究,各具特色的无网格算法相继涌现[9-14].就作者熟悉的空气动力学领域而言,最引人注目的是早期Batina[6]的工作.他采用中心差分格式,发展了显式无网格算法,成功地求解了带有激波的可压缩绕流.之后,Morinishi[11]采用虚拟中点(点云中心点与卫星点之间)迎风处理策略和加权最小二乘空间导数逼近,成功地发展了隐式无网格算法.近年来,成功应用无网格算法的算例[15-18]已不难在文献中找到,借助于现代图形处理器(GPU)等并行加速技术,算法的收敛速度也进一步得到了强化[19-22].但同时可以注意到,上述无网格算法大多是基于可压缩流发展的,不能直接拓展到模拟几乎不可压的低马赫数流.
本文致力于发展出一种带预处理的隐式无网格算法,既能模拟可压跨音速流,又能模拟几乎不可压的低马赫数流.众所周知,在低马赫数下,特征型欧拉方程的3个不同特征值代表的波速存在巨大差异,会导致原控制方程产生系统病态,即所谓的“刚性”问题[23].而这反过来也会导致迭代计算收敛困难,数值模拟解往往偏离实际物理解.为此,本文先沿用网格算法中著名的Weiss-Smith型预处理矩阵[24],对无网格半离散型欧拉方程进行矩阵预处理,以期缩减方程特征值在低马赫数条件下的差异,改善上述所谓的“刚性”问题;接着给出了无网格点上受预处理影响的人工耗散项及远场边界条件等实施细节,并通过无网格点排序与点云分割,实现了LU-SGS算法[25]的时间推进求解,形成了预处理隐式无网格算法.最后,先选用典型翼型算例进行了数值模拟,并与文献或实验结果进行了验证比较;接着给出了机翼及翼身组合体等三维跨音速和低马赫数绕流算例.算例表明所发展的隐式算法如预期比相应的显式算法收敛更快,已从单纯模拟可压缩流动拓展到模拟几乎不可压的低马赫数流.
1 控制方程在直角坐标系(x, y, z)上,与时间t相关的三维欧拉方程的守恒形式为[26]
| $ \frac{{\partial \mathit{\boldsymbol{W}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial y}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial z}} = 0. $ | (1) |
其中W为守恒矢变量,E,F和G为矢通量,可分别写为
| $ {\mathit{\boldsymbol{W}} = {{[\rho ,\rho u,\rho v,\rho w,\rho E]}^{\rm{T}}},} $ | (2) |
| $ {\mathit{\boldsymbol{E}} = {{[\rho u,\rho {u^2} + p,\rho uv,\rho uw,\rho uH]}^{\rm{T}}},} $ | (3) |
| $ {\mathit{\boldsymbol{F}} = {{[\rho v,\rho vu,\rho {v^2} + p,\rho vw,\rho vH]}^{\rm{T}}},} $ | (4) |
| $ {\mathit{\boldsymbol{G}} = {{[\rho w,\rho wu,\rho wv,\rho {w^2} + p,\rho vH]}^{\rm{T}}}.} $ | (5) |
式中:ρ,p,E和H分别代表了密度、压强、单位质量的总能和总焓;u,v和w为速度分量.完全气体满足状态方程,有如下关系式成立:
| $ {\rho E = \frac{p}{{(\gamma - 1)}} + \frac{1}{2}\rho ({u^2} + {v^2} + {w^2}),} $ | (6) |
| $ {\rho H = \rho E + p.} $ | (7) |
其中,γ为流体的比热比,对于空气而言,γ=1.4.通过求解上述方程组寻求满足∂W/t=0的定常解.
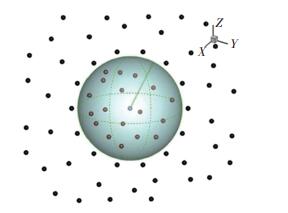
2 无网格空间导数近似采用无网格算法,计算域先需布点离散.布点离散后,即可形成由每一点临近点构成的当地点云结构[6, 8].记C(i)为第i点的点云,其构成参见图 1.图中,点云的中心点即为i点,点云的其余点被称作卫星点.
|
图 1 三维点云C(i)示意图 Fig. 1 Three-dimensional cloud of points for C(i) |
无网格空间导数近似是在计算域离散点上进行的.基于图 1所示的点云结构,任一可微函数f的空间导数可近似为[8, 27]
| $ \left\{ \begin{array}{*{35}{l}} {{\left. \frac{\partial f}{\partial x} \right|}_{i}}=\sum\limits_{\begin{smallmatrix} k\in C(i) \\ k\ne i \end{smallmatrix}}{{{\alpha }_{ik}}}{{f}_{ik}}, \\ {{\left. \frac{\partial f}{\partial y} \right|}_{i}}=\sum\limits_{\begin{smallmatrix} k\in C(i) \\ k\ne i \end{smallmatrix}}{{{\beta }_{ik}}}{{f}_{ik}}, \\ {{\left. \frac{\partial f}{\partial z} \right|}_{i}}=\sum\limits_{\begin{smallmatrix} k\in C(i) \\ k\ne i \end{smallmatrix}}{{{\gamma }_{ik}}}{{f}_{ik}}. \\ \end{array} \right. $ | (8) |
其中fik为第k个卫星点与中心点i连线中点处的近似值.显然,系数αik,βik和γik满足
| $ \sum\limits_{\begin{smallmatrix} k\in C(i) \\ k\ne i \end{smallmatrix}}{{{\alpha }_{ik}}}=0,\sum\limits_{\begin{smallmatrix} k\in C(i) \\ k\ne i \end{smallmatrix}}{{{\beta }_{ik}}}=0,\sum\limits_{\begin{smallmatrix} k\in C(i) \\ k\ne i \end{smallmatrix}}{{{\gamma }_{ik}}}=0. $ | (9) |
上述空间导数近似式中的系数,可用加权的最小二乘曲面逼近来求得[8, 19].
3 预处理隐式无网格算法 3.1 通量计算应用(8)式,欧拉方程的通量可近似写为
| $ \begin{array}{*{20}{l}} {{{\left( {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial y}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial z}}} \right)}_i} = \sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {({\alpha _{ik}}{\mathit{\boldsymbol{E}}_{ik}} + {\beta _{ik}}{\mathit{\boldsymbol{F}}_{ik}} + {\gamma _{ik}}{\mathit{\boldsymbol{G}}_{ik}})} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {{\mathit{\boldsymbol{L}}_{ik}}} .} \end{array} $ | (10) |
其中i和k连线中点上的数值通量Lik具体可写为
| $ {\mathit{\boldsymbol{L}}_{ik}} = \left[ {\begin{array}{*{20}{c}} {{\rho _{ik}}{U_{ik}}}\\ {{\rho _{ik}}{u_{ik}}{U_{ik}} + {\alpha _{ik}}{p_{ik}}}\\ {{\rho _{ik}}{v_{ik}}{U_{ik}} + {\beta _{ik}}{p_{ik}}}\\ {{\rho _{ik}}{w_{ik}}{U_{ik}} + {\gamma _{ik}}{p_{ik}}}\\ {{\rho _{ik}}{H_{ik}}{U_{ik}}} \end{array}} \right]. $ | (11) |
这里Uik与逆变速度定义类似,可定义为
| $ {U_{ik}} = {\alpha _{ik}}{u_{ik}} + {\beta _{ik}}{v_{ik}} + {\gamma _{ik}}{w_{ik}}. $ | (12) |
假定中心点i和卫星点k连线的中点处存在一个虚拟的交界面,那么交界面上的通量Lik可以通过选择合适的格式,从i点和k点处的守恒变量计算确定.采用中心格式,交界面处的守恒变量可简单地写为
| $ {\mathit{\boldsymbol{W}}_{ik}} = \frac{1}{2}({\mathit{\boldsymbol{W}}_i} + {\mathit{\boldsymbol{W}}_k}). $ | (13) |
显然,交界面上Lik可由Wik计算得到.
必须指出,上述中差计算形成的格式与网格算法中采用的中心差分格式类似,迭代计算会出现不稳定.一般在激波这样的强间断附近会产生解的非物理振荡,这种振荡也可能因所谓的奇偶失联而发生在任何无网格点上.因此,本文沿用Jameson[28]在网格算法中的做法,在离散的方程中添加人工耗散项Disi以保证算法稳定.基于无网格点云结构,人工耗散项可写为
| $ \begin{array}{l} {\rm{Di}}{{\rm{s}}_i} = \sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {{\lambda _{ik}}} \varepsilon _k^{(2)}({\mathit{\boldsymbol{W}}_k} - {\mathit{\boldsymbol{W}}_i}) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}}^{k \ne i} {{\lambda _{ik}}} \varepsilon _k^{(4)}({\nabla ^2}{\mathit{\boldsymbol{W}}_k} - {\nabla ^2}{\mathit{\boldsymbol{W}}_i}), \end{array} $ | (14) |
其中ε(2)和ε(4)为可调系数,λik则为雅克比矩阵Aik=∂Lik/∂Wik的谱半径,其形式为
| $ {\lambda _{ik}} = |{U_{ik}}| + {c_{ik}}\sqrt {\alpha _{ik}^2 + \beta _{ik}^2 + \gamma _{ik}^2} , $ | (15) |
这里
应用(10)式,添加上人工耗散项后,得到方程(1)的半离散形式,具体可简写为
| $ {\left. {\frac{{\partial \mathit{\boldsymbol{W}}}}{{\partial t}}} \right|_i} = - \sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {{\mathit{\boldsymbol{L}}_{ik}}} + {\rm{Di}}{{\rm{s}}_i} $ | (16) |
可以注意到,上述交界面上欧拉方程的3个不同的特征值为
| $ {U_{ik}},{U_{ik}} \pm {c_{ik}}\sqrt {\alpha _{ik}^2 + \beta _{ik}^2 + \gamma _{ik}^2} . $ | (17) |
在低马赫数下,如前述,这3个特征值代表的波速会存在巨大差异,雅克比矩阵Aik的条件数过大,会导致迭代计算收敛困难.为此,本文考虑对方程(16)进行矩阵预处理以减小矩阵条件数.从网格算法中可知,适用于低马赫数流动的预处理矩阵[24, 29-32]可有多种选择,其中较为著名的是Weiss-Smith型预处理矩阵[24].对守恒型方程,该矩阵具体可写为
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = \\ \left[ {\begin{array}{*{20}{c}} {\varphi \theta + 1}&{ - u\theta }&{ - v\theta }&{ - u\theta }&\theta \\ {\varphi u\theta }&{ - {u^2}\theta + 1}&{ - vu\theta }&{ - wu\theta }&{u\theta }\\ {\varphi v\theta }&{ - u\theta }&{ - {v^2}\theta + 1}&{ - wv\theta }&{v\theta }\\ {\varphi u\theta }&{ - uw\theta }&{ - vu\theta }&{ - {w^2}\theta + 1}&{w\theta }\\ {\varphi H\theta }&{ - uH\theta }&{ - vH\theta }&{ - wH\theta }&{\varphi \theta + \frac{1}{\sigma }} \end{array}} \right]. \end{array} $ | (18) |
其中:
| $ {\varphi = \frac{1}{2}({u^2} + {v^2} + {w^2}),} $ | (19) |
| $ {\theta = \frac{{\gamma - 1}}{{{c^2}}}\left( {\frac{1}{\sigma } - 1} \right),} $ | (20) |
| $ {\sigma = {\rm{min}}[{\rm{max}}(M{a^2},Ma_\infty ^2),1].} $ | (21) |
这里的Ma和Ma∞分别代表了当地和来流马赫数.应用(18)式进行矩阵预处理,方程(16)可改写为
| $ {\left. {\frac{{\partial \mathit{\boldsymbol{W}}}}{{\partial t}}} \right|_i} = - \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_i^{ - 1}\sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {{\mathit{\boldsymbol{L}}_{ik}}} + {\rm{Dis'}}{ _i}, $ | (22) |
其中,Dis′i为预处理以后的人工耗散项.必须指出,预处理以后的雅克比矩阵Bik=Γi-1∂Lik/Wik,其谱半径为
| $ \begin{array}{*{20}{l}} {\lambda {{\rm{'}}_{ik}} = \frac{1}{2}(1 + \sigma )|{U_{ik}}| + }\\ {\frac{1}{2}\sqrt {{{(1 - \sigma )}^2}U_{ik}^2 + 4\sigma c_{ik}^2(\alpha _{ik}^2 + \beta _{ik}^2 + \gamma _{ik}^2)} ,} \end{array} $ | (23) |
因此,预处理以后人工耗散项可改写为
| $ \begin{array}{l} {\rm{ Dis'}}{{\rm{ }}_i} = \sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {\lambda {{\rm{'}}_{ik}}} \varepsilon _k^{(2)}({\mathit{\boldsymbol{W}}_k} - {\mathit{\boldsymbol{W}}_i}) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {\lambda {{\rm{'}}_{ik}}} \varepsilon _k^{(4)}({\nabla ^2}{\mathit{\boldsymbol{W}}_k} - {\nabla ^2}{\mathit{\boldsymbol{W}}_i}). \end{array} $ | (24) |
本文将采用LU-SGS隐式算法,对预处理以后的半离散方程(22)进行时间离散求解.
3.3 时间离散依据Jameson和Yoon的做法[25],对预处理以后的数值通量引入如下线性化处理:
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_i^{ - 1}\mathit{\boldsymbol{L}}_{ik}^{n + 1} \approx \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_i^{ - 1}\mathit{\boldsymbol{L}}_{ik}^n + \mathit{\boldsymbol{B}}_{ik}^ + ({\mathit{\boldsymbol{W}}_i})\mathit{\varDelta}{\mathit{\boldsymbol{W}}_i} + \mathit{\boldsymbol{B}}_{ik}^ - ({W_k})\mathit{\varDelta}{\mathit{\boldsymbol{W}}_k}. $ | (25) |
这里通量雅克比矩阵Bik按文献[25]中的分裂方式定义为
| $ \mathit{\boldsymbol{B}}_{ik}^ \pm = \frac{1}{2}({\mathit{\boldsymbol{B}}_{ik}} \pm \lambda {{\rm{'}}_{ik}}I), $ | (26) |
其中I为单位矩阵.那么方程(22)的时间后差隐式格式可以写为
| $ \begin{array}{l} \left( {\frac{1}{{\mathit{\varDelta}{t_i}}}\mathit{\boldsymbol{I}} + \sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {\mathit{\boldsymbol{B}}_{ik}^ + } ({\mathit{\boldsymbol{W}}_i})} \right)\mathit{\varDelta}{\mathit{\boldsymbol{W}}_i} + \sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {\mathit{\boldsymbol{B}}_{ik}^ - } ({\mathit{\boldsymbol{W}}_k})\mathit{\varDelta}{\mathit{\boldsymbol{W}}_k} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \mathit{\boldsymbol{R}}(\mathit{\boldsymbol{W}}_i^n). \end{array} $ | (27) |
其中Δti为点云中心点i的时间步长,R为空间导数用点云近似的残值,ΔW定义为
| $ {\varDelta}\mathit{\boldsymbol{ \boldsymbol W}} = {\mathit{\boldsymbol{W}}^{n + 1}} - {\mathit{\boldsymbol{W}}^{n + 1}} $ | (28) |
因为系数αik,βik和γik具有式(9)的特性,雅克比矩阵Bik也应该具有如下特性:
| $ \sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {{\mathit{\boldsymbol{B}}_{ik}}} ({\mathit{\boldsymbol{W}}_i}) = \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_i^{ - 1}\sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {{\mathit{\boldsymbol{A}}_{ik}}} ({\mathit{\boldsymbol{W}}_i}) = 0, $ | (29) |
因而,隐式格式(27)可退化为
| $ \begin{array}{l} \left( {\frac{1}{{\mathit{\varDelta}{t_i}}} + \frac{1}{2}\sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {\lambda {{\rm{'}}_{ik}}} } \right)\mathit{\boldsymbol{I }}{\varDelta}{\mathit{\boldsymbol{W}}_i} + \sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {\mathit{\boldsymbol{B}}_{ik}^ - } ({\mathit{\boldsymbol{W}}_k})\mathit{\varDelta}{\mathit{\boldsymbol{W}}_k} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \mathit{\boldsymbol{R}}(\mathit{\boldsymbol{W}}_i^n). \end{array} $ | (30) |
式(30)用LU-SGS算法[25]求解,格式可分为如下两步:
| $ {\varDelta}\mathit{\boldsymbol{ \boldsymbol W}}_i^* = \mathit{\boldsymbol{D}}_i^{ - 1}[ - \mathit{\boldsymbol{R}}{\rm{'}}(\mathit{\boldsymbol{W}}_i^n) - \sum\limits_{k{\kern 1pt} \in {\kern 1pt} L(i)} {\mathit{\boldsymbol{B}}_{ik}^ - } ({\mathit{\boldsymbol{W}}_k}){\varDelta}\mathit{\boldsymbol{ \boldsymbol W}}_k^*], $ | (31) |
| $ \Delta {\mathit{\boldsymbol{W}}_i} = \Delta \mathit{\boldsymbol{W}}_i^* - \mathit{\boldsymbol{D}}_i^{ - 1}\sum\limits_{k{\kern 1pt} \in {\kern 1pt} U(i)} {\mathit{\boldsymbol{B}}_{ik}^ - } ({\mathit{\boldsymbol{W}}_k})\mathit{\varDelta}{\mathit{\boldsymbol{W}}_k}. $ | (32) |
其中,L(i)和U(i)为点云C(i)卫星点的LU分割. Di定义为
| $ {\mathit{\boldsymbol{D}}_i} = \left( {\frac{1}{{\mathit{\varDelta}{t_i}}} + \frac{1}{2}\sum\limits_{\begin{array}{*{20}{c}} {k \in C(i)}\\ {k \ne i} \end{array}} {\lambda {{\rm{'}}_{ik}}} } \right)\mathit{\boldsymbol{I}}. $ | (33) |
实际计算中,沿用Sharov和Nakahashi[33]的做法,涉及的矩阵运算Aik(Wk)Δ(Wk)由通量的增量ΔLik(Wk)来简化计算,减少工作量.
必须指出的是,L(i)和U(i)如果分割不当会导致算法退化为运算较慢的Jacobi迭代[33].为避免该问题,文献[33]依据网格间的连接关系先进行网格分层编号,再进行LU分割.层号比当前网格层号小的相邻网格单元被归入L(i),反之归入U(i).对于无网格算法,点云点间不存在网格拓扑这样的刚性连接关系,为此,本文利用卫星点与中心点的虚拟连接关系来构造类似的分层结构.作者曾提出一种多层点云的重排算法,优化了GPU的内存访问模式,实现了GPU并行无网格算法的进一步加速[22].本文沿用这一方法对无网格点进行类似的分层编号重排.分层后,对点云C(i)的卫星点进行LU分割.将层号比中心点i层号小的卫星点分割纳入L(i),反之则纳入U(i).本文将这一分割做法用于了后续的算例运算.
3.4 边界条件对于物面边界条件,无粘条件下满足的无穿透边界条件[6]在预处理前后都一样.而远场基于特征分析的无反射边界条件,预处理后由于特征值的改变,必须作相应的修正. Turkel[34]早期给出了精确的基于特征分析的预处理远场边界条件,之后又对其进行了简化,用于处理几乎不可压流动.本文沿用Turkel的简化处理[32],预处理远场边界条件是结合无网格布点离散灵活的特点实施的.为此,本文把远场边界面处理成临近内点的镜面,每一离镜面最近的内点对应一个虚拟的镜像点,纳入该点的点云中.那么,虚拟点上的物理量可直接根据Turkel的方法确定.
以远场边界入流为例,虚拟点处的原始变量可取为
| $ {\rho _g} = {\rho _\infty },{u_g} = {u_\infty },{v_g} = {v_\infty },{w_g} = {w_\infty },{p_g} = {p_i}. $ | (34) |
这里的下标g为虚拟点,而下标i为内部流场点,下标∞代表了自由流.注意,这里g是i的镜像点.
需要指出的是,位于远场边界外引入的镜像虚拟点是在计算域布点离散过程中生成的.这样做,相当于远场边界条件位于虚拟点和对应内部点的中点处,而所有位于计算域内与远场边界条件相关的临近边界点都可以按照内部点的方式处理.可以看出,这样处理的远场边界条件实施更为简单方便.
4 算例与分析本文用上述预处理隐式无网格算法,先对NACA 0012对称翼型和AGARD三段翼型进行了低马赫数绕流的数值模拟,通过与文献或实验结果的对比分析,验证所提算法的计算效率和准确性,展示隐式无网格算法的快速收敛特性;接着给出了机翼及翼身组合体等跨音速和低马赫数两类绕流的算例,展示算法通过预处理对这两类流动模拟的兼容能力.
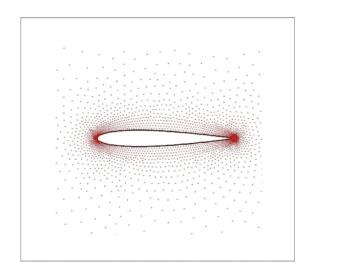
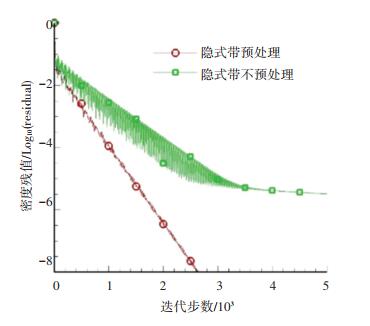
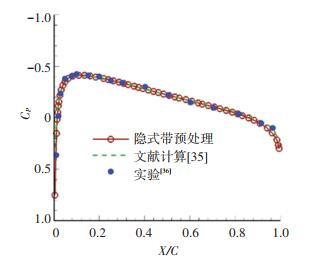
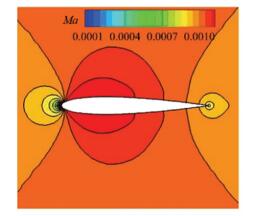
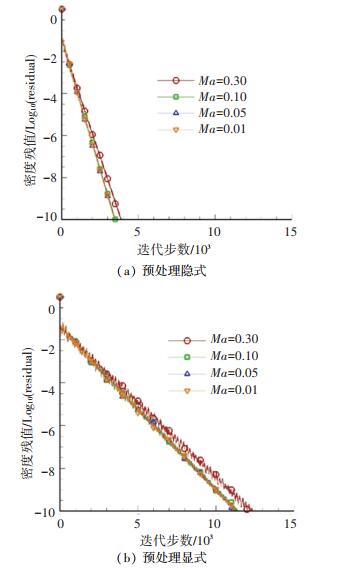
4.1 NACA 0012翼型低马赫数绕流本文选用NACA 0012翼型几乎不可压的低马赫数绕流对发展的算法进行了考核计算验证.如图 2所示,计算域用3343个无网格点进行离散.先用马赫数Ma=0.001,攻角为0°的绕流模拟展示了预处理对收敛历程的影响(见图 3).图中可看出,发展的预处理隐式算法,在如此小的马赫数下仍能快速收敛,图中同时给出了不加预处理的收敛困难的情形供比较.对应的翼型表面压强系数分布(见图 4)取得了与文献[35]和实验[36]一致的结果.图中横坐标X/C代表离前缘的相对距离,C为对应翼型的弦长,纵坐标Cp则为压强系数. 图 5则给出了对应的马赫数等值线和云图.图中反映的流场对称性与零攻角对称翼型绕流的物理特性吻合.接着,通过不同马赫数的数值模拟展示了马赫数对算法收敛历程的影响.从图 6中可看出,模拟的4个来流马赫数(0.3,0.1,0.05,0.01)都能很好收敛.图中同时给出了显式预处理算法[23]的收敛历程供比较.必须指出,在几乎不可压的低马赫数下,很有必要使算法具有良好收敛特性.这一点从捕捉的流场解可以看出. 图 7给出了隐式无网格算法带与不带预处理计算获得的流场密度等值线(Ma=0.05)比较.图中可看出,预处理后流场解更加合理,表现为等值线更加光滑.
|
图 2 NACA 0012翼型周围点分布 Fig. 2 Points around NACA 0012 airfoil |
|
图 3 预处理对收敛历程的影响 Fig. 3 Effects of preconditioning on convergence histories |
|
图 4 型表面压强系数分布(Ma=0.001) Fig. 4 Pressure coefficient distribution(Ma=0.001) |
|
图 5 马赫数等值线及云图(Ma=0.001) Fig. 5 Mach number contours (Ma=0.001) |
|
图 6 马赫数对收敛历程的影响 Fig. 6 Effects of Mach numbers on convergence histories |

|
图 7 隐式无网格算法密度等值线比较(Ma=0.05) Fig. 7 Density contours of implicit gridless methods(Ma=0.05) |
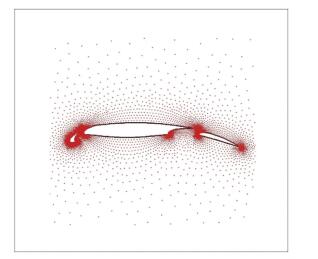
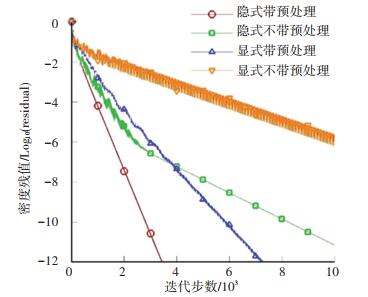
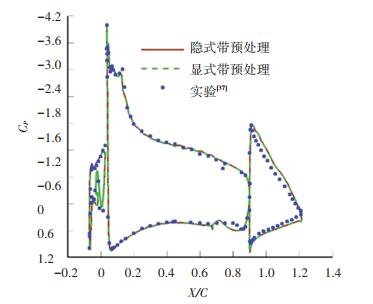
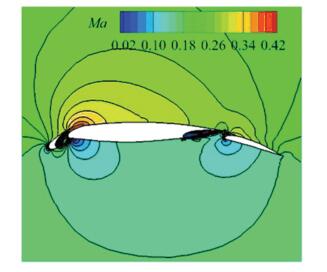
这里给出外形更为复杂的AGARD三段翼型[37]几乎不可压的低马赫数绕流的计算结果.几何外形可从图 8中看出.计算域用5865个无网格点进行离散.来流马赫数按实验条件[37]取为0.197,迎角取为4.01°.如图 9收敛历程所示,发展的隐式预处理无网格算法再次呈现出快速收敛特性,图中同时给出了隐式不带预处理、显式带与不带预处理无网格算法的收敛历程供比较.对应的翼面压强系数分布(见图 10)与实验[37]吻合的较好,这一点可从主翼上捕捉的激波位置和强度看出. 图 11则给出了对应的马赫数等值线和云图,展示出了多段翼型的流动特征.
|
图 8 多段翼型周围点分布 Fig. 8 Points around multi-element airfoil |
|
图 9 不同无网格算法收敛历程比较 Fig. 9 Convergence histories of different methods |
|
图 10 表面压强系数分布 Fig. 10 Pressure coefficient distribution |
|
图 11 马赫数等值线和云图 Fig. 11 Mach number contours |
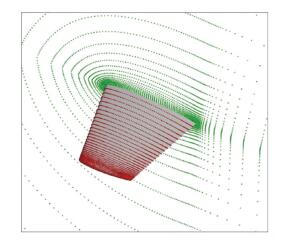
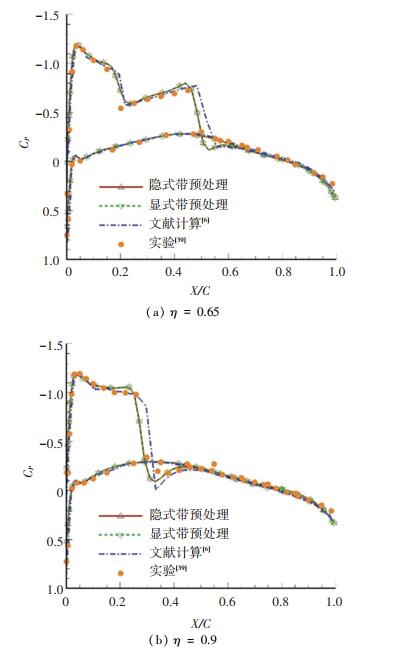
M6机翼[6, 38]经常被用来考核发展的算法.本文先进行了绕M6机翼跨音速流动的数值模拟.计算采用了54320个无网格点(见图 12),来流马赫数为0.84,攻角为3.06°.典型机翼翼剖面的压强系数分布见图 13.图中η代表机翼翼剖面展向相对位置,翼尖η为1,翼根η为0.计算结果与文献[6]和实验[39]进行了比较.如预期,带预处理的隐式无网格算法仍能用于该跨音速绕流计算,表现为计算结果与不带预处理的结果十分吻合.
|
图 12 M6机翼周围点分布 Fig. 12 Points around ONERA M6 wing |
|
图 13 机翼表面压强系数分布(Ma=0.84) Fig. 13 Pressure coefficient distribution(Ma=0.84) |
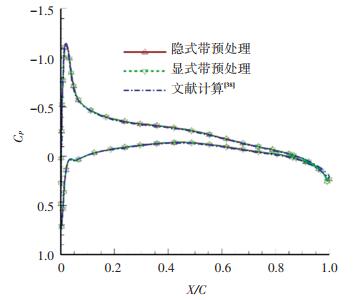
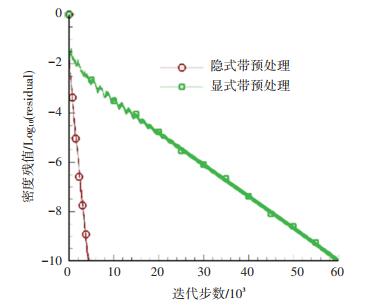
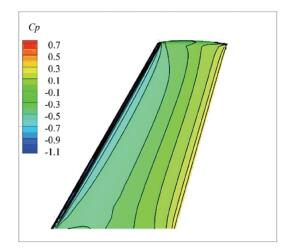
接着,沿用文献[38]的做法,进行了几乎不可压马赫数绕流(Ma=0.01)的考核运算. 图 14给出了计算获得的η=0.8处的翼剖面压强系数分布,从图中可以看出,发展的预处理隐式无网格算法与预处理显式算法一样,计算结果都与文献[38]结果十分吻合.比较而言,隐式预处理无网格算法较显式收敛特性更优(见图 15). 图 16则给出了对应的上翼面压强系数等值线云图,可以看出捕捉的等值线光滑有序,一定程度上反映出M6机翼上翼面几乎不可压的低速流动特征.
|
图 14 机翼表面压强系数分布(Ma=0.01,η=0.8) Fig. 14 Pressure coefficient distribution (Ma=0.01, η=0.8) |
|
图 15 收敛历程(Ma=0.01) Fig. 15 Convergence histories(Ma=0.01) |
|
图 16 机翼上表面压强系数等值线及云图(Ma=0.01) Fig. 16 Pressure coefficient contours on the upper surface of the wing (Ma=0.01) |
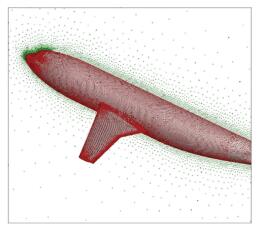
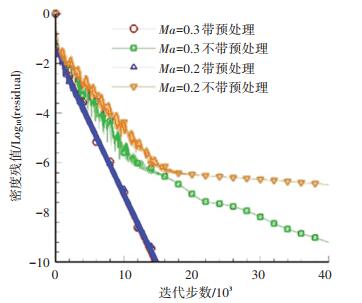
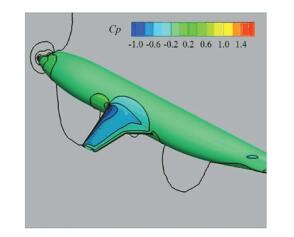
面向实际应用,这里给出DLR-F4组合体低马赫数绕流的演示算例.众所周知,马赫数0.3在工程中常作为判断一个流动是可压与不可压的参考马赫数.必须指出,按照可压和不可压的这一区分标准,对于来流马赫数为0.3的翼身组合体绕流,其流场存在驻点附近等局部低马赫数区和机翼上翼面等局部高马赫数区,一定程度上可理解为可压和不可压并存的混合流场.不难看出,随着来流马赫数的降低,流场中局部低马赫数的不可压区在整个流场中的占比将逐渐增大,这会一定程度上影响到迭代格式的收敛特性.本文选用这一特别的来流马赫数对发展的算法进行了收敛历程测试.计算采用了75060个无网格点(见图 17). 图 18则给出了对应的收敛历程,图中可以看出,加预处理可以明显改善低马赫数来流的收敛特性,一定程度上有助于提高解的捕捉精度(参见表面压强系数等值线云图 19). 图 18中同时给出了来流马赫数0.2的收敛历程供比较,也可以看出,随着来流马赫数的减小,流场中低马赫数的不可压区占比扩大,如预期,加预处理的必要性更加显现,表现为加与不加预处理,收敛差异更大.
|
图 17 DLR-F4翼身组合体周围点分布 Fig. 17 Points around DLR-F4 |
|
图 18 收敛历程 Fig. 18 Convergence histories |
|
图 19 组合体表面压强系数等值线云图 Fig. 19 Pressure coefficient contours |
本文通过无网格点重排与点云分割,成功地结合LU-SGS算法,发展出一种基于Weiss-Smith预处理矩阵的预处理隐式无网格算法,用于求解三维欧拉方程.借助于无网格布点,远场边界虚拟镜像点的引入,简化了预处理远场边界的实施.发展的算法通过了二维和三维多个算例的计算考核.算例表明,相较于显式预处理算法,发展的预处理隐式算法收敛特性更优;算法的数值模拟能力已从单纯模拟可压缩跨音速等流动拓展到模拟几乎不可压的低马赫数流.此外,算法整体是基于无网格技术发展的,计算域只需布点离散,有助于灵活处理三维复杂气动外形.当然,实际工程绕流问题大多需考虑粘性的影响,这就要求发展的算法从求解欧拉方程拓展到求解Navier-Stokes方程,会涉及反映粘性绕流特征的异性点云结构的构造、合适湍流模型的嵌入、基于点云结构的粘性预处理谱半径的确定等问题,将是未来研究的重点.
| [1] |
JASAK H. OpenFOAM: open source CFD in research and industry[J]. International Journal of Architecture and Ocean Engineering, 2009, 1(2): 89. DOI:10.3744/JNAOE.2009.1.2.089 |
| [2] |
SCANLON T J, ROOHI E, WHITE C, et al. An open source, parallel DSMC code for rarefied gas flows in arbitrary geometries[J]. Computers & Fluids, 2010, 39(10): 2078. |
| [3] |
FAN Jizhuang, ZHANG Wei, ZHU Yanhe, et al. CFD-based self-propulsion simulation for frog swimming[J]. Journal of Mechanics in Medicine and Biology, 2014, 14(6): 1. DOI:10.1142/S0219519414400119 |
| [4] |
YANG Xiawei, ZHU Jingchuan, LI Wenya. CFD-supported optimization of flow distribution in quench tank for heat treatment of A357 alloy large complicated components[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(10): 3399. DOI:10.1016/S1003-6326(15)63975-9 |
| [5] |
BHUSARE V H, DHIMAN M K, KALAGA D V, et al. CFD simulations of a bubble column with and without internals by using OpenFOAM[J]. Chemical Engineering Journal, 2017, 317(1): 157. |
| [6] |
BATINA J T. Agridless Euler/Navier-Stokes solution algorithm for complex-aircraft applications[C]//31st Aerospace Sciences Meeting. Reno: AIAA, 1993: 1 DOI: 10.2514/6.1993-333
|
| [7] |
NGUYEN V P, RABCZUK T, BORDAS S, et al. Meshless methods:a review and computer implementation aspects[J]. Mathematics and Computers in Simulation, 2008, 79(3): 763. DOI:10.1016/j.matcom.2008.01.003 |
| [8] |
KATZ A, JAMESON A. A comparison of various meshless schemes within a unified algorithm[C]//47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando: AIAA, 2008: 1. DOI: 10.2514/6.2009-596
|
| [9] |
ONATE E, IDELSOHN S, ZIENKIEWICZ O C, et al. A stabilized finite point method for analysis of fluid mechanics problems[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(4): 315. DOI:10.1016/S0045-7825(96)01088-2 |
| [10] |
LISZKA T J, DUARTE C A M, TWORZYDLO W W. Hp-meshless cloud method[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(1): 263. |
| [11] |
MORINISHI K. Gridless type solver-generalized finite difference method[C]//Notes on Numerical Fluid Mechanics. Berlin: Springer, 2001: 43
|
| [12] |
DESHPANDE S M, ANANDHANARAYANAN K, PRAVEEN C, et al. Theory and application of 3-D LSKUM based on entropy variables[J]. International Journal for Numerical Methods in Fluids, 2002, 40(1): 47. DOI:10.1002/fld.266 |
| [13] |
SRIDAR D, BALAKRISHNAN N. An upwind finite difference scheme for meshless solvers[J]. Journal of Computational Physics, 2003, 189(1): 1. DOI:10.1016/S0021-9991(03)00197-9 |
| [14] |
KOH E P C, TSAI H M, LIU F. Euler solution using cartesian grid with least squares technique[C]//41st Aerospace Sciences Meeting and Exhibit. Reno: AIAA, 2003: 1. DOI: 10.2514/6.2003-1120
|
| [15] |
SINGH M K, RAMESH V, BALAKRISHNAN N. Implicit scheme for meshless compressible Euler solver[J]. Engineering Applications of Computational Fluid Mechanics, 2015, 9(1): 382. DOI:10.1080/19942060.2015.1048621 |
| [16] |
DUAN Zhaowen, WANG Z J, VU B. Recent progresses on a meshless Euler solver for compressible flows[C]//22nd AIAA Computational Fluid Dynamics Conference. Dallas: AIAA, 2015: 14
|
| [17] |
ZHANG Aman, SUN Pengnan, MING Furen, et al. Smoothed particle hydrodynamics and its applications in fluid-structure interactions[J]. Journal of Hydrodynamics, 2017, 29(2): 187. DOI:10.1016/S1001-6058(16)60730-8 |
| [18] |
LIN Ji, REUTSKIY S Y, LU Jun. A novel meshless method for fully nonlinear advection-diffusion-reaction problems to model transfer in anisotropic media[J]. Applied Mathematics and Computation, 2018, 339(1): 459. DOI:10.1016/j.amc.2018.07.045 |
| [19] |
MA Zhihua, WANG Hong, PU Saihu. GPU computing of compressible flow problems by a meshless method with space-filling curves[J]. Journal of Computational Physics, 2014, 263(1): 113. |
| [20] |
ZHANG Jiale, CHEN Hongquan, CAO Cheng. A graphics processing unit-accelerated meshless method for two-dimensional compressible flows[J]. Engineering Applications of Computational Fluid Mechanics, 2017, 11(1): 526. DOI:10.1080/19942060.2017.1317027 |
| [21] |
ZHANG Jiale, MA Zhihua, CHEN Hongquan, et al. A GPU-accelerated implicit meshless method for compressible flows[J]. Journal of Computational Physics, 2018, 360: 39. DOI:10.1016/j.jcp.2018.01.037 |
| [22] |
CAO Cheng, CHEN Hongquan, ZHANG Jiale, et al. A multi-layered point reordering study of GPU-based meshless method for compressible flow simulations[J]. Journal of Computational Science, 2019, 33(1): 45. DOI:10.1016/j.jocs.2019.04.001 |
| [23] |
CAO Cheng, CHEN Hongquan. A preconditioned gridless method for solving Euler equations at low Mach numbers[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2015, 32(4): 399. DOI:10.16356/j.1005-1120.2015.04.399 |
| [24] |
WEISS J M, SMITH W A. Preconditioning applied to variable and constant density flows[J]. AIAA Journal, 1995, 33(11): 2050. DOI:10.2514/3.12946 |
| [25] |
YOON S, JAMESON A. Lower-upper symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations[J]. AIAA Journal, 1988, 26(2): 1025. DOI:10.2514/3.10007 |
| [26] |
DAVIS R L, DANNENHOFFER J F Ⅲ. Three-dimensional adaptive grid-embedding Euler technique[J]. AIAA Journal, 1994, 32(6): 1167. DOI:10.2514/3.12116 |
| [27] |
CHEN Hongquan, SHU Chang. An efficient implicit mesh-free method to solve two-dimensional compressible Euler equations[J]. International Journal of Modern Physics C, 2005, 16(3): 439. DOI:10.1142/S0129183105007327 |
| [28] |
JAMESON A, MAVRIPLIS D. Finite volume solution of the two-dimensional Euler equations on a regular triangular mesh[J]. AIAA Journal, 1986, 24(4): 611. DOI:10.2514/3.9315 |
| [29] |
TURKEL E. Preconditioned methods for solving the incompressible and low speed compressible equations[J]. Journal of Computational Physics, 1987, 72(2): 277. DOI:10.1016/0021-9991(87)90084-2 |
| [30] |
TURKEL E. Review of preconditioning methods for fluid dynamics[J]. Applied Numerical Mathematics, 1992, 12(1): 257. DOI:10.1016/0168-9274(93)90122-8 |
| [31] |
CHOI Y H, MERKLE C L. Theapplication of preconditioning in viscous flows[J]. Journal of Computational Physics, 1993, 105(2): 207. DOI:10.1006/jcph.1993.1069 |
| [32] |
TURKEL E, RADESPIEL R, KROLL N. Assessment of preconditioning methods for multidimensional aerodynamics[J]. Computers & Fluids, 1997, 26(6): 613. DOI:10.1016/s0045-7930(97)00013-3 |
| [33] |
SHAROV D, NAKAHASHI K. Reordering of 3-D hybrid unstructured grids for vectorized LU-SGS Navier-Stokes computations[C]//13th Computational Fluid Dynamics Conference. Snowmass Village: AIAA, 1997: 131. DOI: 10.2514/6.1997-2102
|
| [34] |
TURKEL E, FITERMAN A, VAN LEER B. Preconditioning and thelimit to the incompressible flow equations: NASA-CR-191500[R]. Hampton: NASA, 1993
|
| [35] |
刘晨, 王江峰, 伍贻兆. 低马赫数流动中的预处理Euler方程的收敛特性[J]. 航空学报, 2009, 30(5): 842. LIU Chen, WANG Jiangfeng, WU Yizhao. Convergence characteristics of preconditioned Euler equations at low Mach numbers[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(5): 842. DOI:10.3321/j.issn:1000-6893.2009.05.012 |
| [36] |
ABBOTT I H, VON DOENHOFF A E. Theory of wing sections[M]. New York: Dover Publications, 1959: 311.
|
| [37] |
RUMSEY C L, GATSKIT B, YING S X, et al. Prediction of high-lift flows using turbulent closure models[J]. AIAA Journal, 1998, 36(5): 1. DOI:10.2514/2.435 |
| [38] |
XIE Futian, SONG Wenping, HAN Zhonghua. Numerical study of high-resolution scheme based on preconditioning method[J]. Journal of Aircraft, 2008, 46(2): 520. DOI:10.2514/1.37976 |
| [39] |
SCHMITT V, CHARPIN F. Pressure distribution on the ONERA M6 wing at transonic Mach numbers: AGARD-AR-138[R]. London: NATO Advisory Group for Aerospace Research and Development, 1979
|
 2020, Vol. 52
2020, Vol. 52


