2. 吉林大学 汽车仿真与控制国家重点实验室, 长春 130025;
3. 吉林省立新汽车配件有限公司, 长春 130012
2. State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130025, China;
3. Jilin Lixin Auto Parts Co. LTD, Changchun 130012, China
汽车轻量化已经成为汽车行业的研究热点[1],在综合性能满足驾驶安全要求前提下,车轮轻量化效果是其他零件的1.5倍,直接影响到汽车的平稳性、操纵性和灵活性等[2].车轮轻量化设计有两种常用方法,一是基于疲劳累积损伤理论,通过优化结构设计获得更好的可靠性;二是使用高性能轻量化材料[3]. Yeh-Liang Hsu等利用顺序神经网络逼近法,分别研究车轮在径向及弯曲疲劳约束下的结构优化及轻量化问题[4];Weiwei Song基于汽车驾驶历史的车轮载荷运动学模型对铝合金轮轴进行失效分析[5];Akbulut H考虑车轮材料弹塑性影响,通过有限元仿真获得最佳轮辋厚度[6];Federico基于局部应力梯度的材料疲劳修正法提出铝制车轮的轻量化[7];闫胜昝等以固体力学数学模拟为基础,利用参数相关法、多目标驱动法等完成轻质合金轮辋的优化设计[8].
在车轮疲劳试验的仿真分析及疲劳寿命预测计算方面,Kocabicak U采用有限元法对车轮在弯曲疲劳试验下进行寿命预测[9];Zhan-GuangZheng利用雨流算法对车轮进行多轴疲劳寿命预测[10];Ballo F等利用原材料S-N曲线,仿真分析得到车轮弯曲疲劳寿命预测曲线[11];Mehmet Firat等对车轮在非比例循环载荷下进行径向疲劳的数值分析[12];Dong Shang等提出考虑冲压残余应力下的钢制车轮轴向疲劳寿命分析方法[13];王登峰等分析了镁铝组装车轮在径向和弯曲疲劳试验下的受力及强度,对车轮进行了多目标拓扑优化[14];Denghong Xiao等主要研究以车轮柔度、特征频率为优化目标的钢轮多目标拓扑优化的编程算法[15];Xiaofei Wan等突破传统车轮的研究方法,提出双轴疲劳试验方法,对车轮疲劳寿命进行预测分析[16].
现阶段学者对车轮结构优化和轻量化的研究,多局限于单一的合金材料.随着高强度钢的普及以及车轮设计水平的提高,利用钢轮良好的成型性能、疲劳特性、安全性能以及特有的可焊接性能,能够达到与铝合金相当的重量,将不同种类的钢材良好地结合形成组合车轮结构,从而在改善车轮性能的同时降低成本.东北大学国家重点轧制自动化实验室就曾提出利用新材料钢研制新型钢制轮毂可获得更长的寿命及更好的使用性能[17-18].而研究中常用的弯曲疲劳试验及径向疲劳试验方法,与实际工况下车轮承受的载荷有很大差异,直接影响了对车轮可靠性和真实疲劳寿命判断的准确性.
因此,本文以某型号的异种钢材组装式车轮为研究对象,在LBM公司[19]的应力分析试验装置的基础上,采用一种多变循环载荷疲劳试验仿真分析及优化方法.应用有限元分析软件对车轮组件包括加载轴法兰盘及螺栓在内的整体结构进行有限元建模与分析,基于Kriging理论[20],对车轮进行多目标优化设计,最佳优化模型经有限元仿真分析及弯曲疲劳台架试验验证,实现车轮的轻量化设计.本文的主要研究路线如图 1所示.

|
图 1 本文研究路线 Fig. 1 Research route |
以11.25-20型号车轮为研究对象见图 2,轮辋外形及尺寸初步设计遵循《SAEJ1992-2001车轮/轮辋-军用车-试验方法和性能要求》,根据以往车轮破坏处的经验统计,车轮的轮辋体焊缝处与轮缘处为疲劳失效的多发位置,考虑到车轮部件的工作环境及失效形式,本文车轮采用异种材料内外轮辋组合式结构.
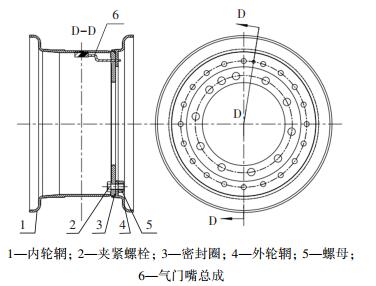
|
图 2 车轮结构设计 Fig. 2 Wheel structure design |
王登峰团队[14]在国内做过关于乘用车铝合金材料铸造内轮辋,镁合金铸造外轮辋的组装式车轮设计研究,开启了异种材料组装车轮的研究方向.由于合金材料不具有良好的热稳定性、耐磨性、耐冲击性以及其高昂的生产成本,使其暂时无法适用于商用车大载荷复杂工况的车轮研究中,车轮产品中主要还是以钢材为主导.随着轻量化要求的提出,车轮用钢高强化是汽车用钢的发展趋势.从车轮用钢的服役状况来看,高的强度、良好的疲劳性能、高的表面质量以及卓越的焊接性能是其所必备的综合性能,故本文车轮内轮辋1采用热轧高强钢材料和外轮辋2为低碳钢,两部分靠螺栓连接,其材料属性见表 1.
| 表 1 材料性能参数 Tab. 1 Material performance parameters |
该设计充分发挥了高强钢优良轻度重量比性能,自重较轻,断面惯性矩大,受力性能好,承载力较高,整体刚度性大,加工工艺简单,在易发生破坏部位有着良好的性能优势,同时,与铝合金相比,具有造价低廉,对环境损耗小等优良特性.此种分体式组装车轮,两种不同材料部分采用螺栓组合,降低了焊接工艺难度,同时两部分分开制造,提高了车轮的制造工艺和生产效率;在轮辋受损后可分别对内、外轮辋体进行更换,能够有效改善其维修经济性.
1.2 加载原理车轮疲劳寿命测试试验方法如图 3所示.车轮行驶过程中,轮胎与地面接触,受到地面挤压,产生沿接触面法线方向的径向载荷Fv和转弯时准静态转矩产生的轴向力FL,此装置可模拟多种工况下的车轮载荷,本文主要针对轮毂结构进行分析,将轮胎作用于车轮上的载荷进行等效作用于轮辋.
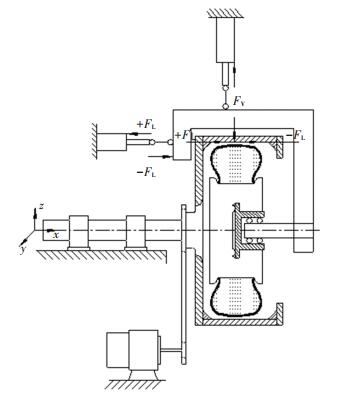
|
图 3 车轮疲劳寿命测试试验方法 Fig. 3 Basic principle of loading |
车轮的应力分布状态取决于某一工作状况下瞬时载荷,除受制造、装配等影响外,还与车辆自重及路面状况有关.因本文分析的车轮的轮辐为圆盘式结构,所以车轮在制动和启动加速产生的纵向力及力矩可忽略不计.
本文在多变循环载荷分析中主要分为理想光滑路面直行、粗糙颠簸路面直行和转弯3种特定的行驶工况,轮辋受到螺栓预紧力T、轮胎充气压力Pt、垂直径向载荷Fr和轴端力Fl.
1.2.1 螺栓预紧力及胎压载荷分析螺栓预紧力使车轮安装区域受到初始压缩力,其大小直接关系车轮安装区域的失效.
预紧力计算公式为
| $ T = \frac{{F \cdot {D_{{\rm{Bolt}}}}}}{2}\tan \left( {\lambda + {\rho _{\rm{v}}}} \right). $ | (1) |
式中: T为拧紧力矩,F为预载荷,DBolt为螺栓中径,λ为螺纹升角,ρv为当量摩擦角.
1.2.2 理想路面、粗糙或颠簸路面直行载荷分析车轮在理想光滑路面上直行,只受到车辆自身重力的静载荷,车轮受到作用于轮胎表面的径向垂直载荷,其产生应力进一步通过轮胎与轮辋体的接触传递到胎圈座.胎圈座应力近似认为关于波形中心线呈最大偏转角为θ0的对称余弦分布,如图 4所示.
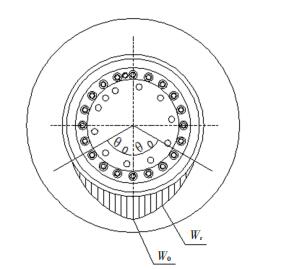
|
图 4 车轮径向加载示意图 Fig. 4 Schematic diagram of wheel radial loading |
对车轮施加垂直径向载荷
| $ {F_{\rm{r}}} = {F_{\rm{v}}} \cdot K, $ | (2) |
当单个径向施加载荷与压力加载范围2θ0的中线夹角为θ时,车轮等效径向分布力Wr与等效最大径向分布力W0之间的关系为
| $ {W_{\rm{r}}} = {W_0}\cos \left( {\frac{{\rm{ \mathsf{ π} }}}{2}\frac{\theta }{{{\theta _0}}}} \right), $ | (3) |
对公式进行积分有
| $ F = B\int_{ - {\theta _{}}}^{{\theta _0}} {{W_{\rm{r}}}{r_{\rm{B}}}{\rm{d}}\theta = \frac{{{F_{\rm{r}}}}}{2}} , $ | (4) |
| $ F = 4B{r_{\rm{B}}}{\theta _0}\frac{{{W_0}}}{{\rm{ \mathsf{ π} }}}, $ | (5) |
即:
其中,Fr为垂直径向载荷,Fv为由车辆或车轮制造商规定的额定负载值,K为强化试验系数,B为胎圈座的宽度,rB为胎圈座半径.
车轮在粗糙或颠簸路面上行驶,同样受到车重的静载,同时会受到摩擦及一定的竖直方向的冲击载荷,不同路面其值的大小不同,其叠加作用通过实际路况信息数据采集或模拟生成载荷谱进行添加.
1.2.3 转弯行驶载荷分析当车辆在转弯过程中,轮胎和地面之间会产生相互作用力,可分解为径向载荷和轴向载荷2个分量,导致车轮上产生转矩.因本文研究内容不考虑到轮胎模型的建立,所以将转矩等效换算到加载轴的轴端施加,于是有转矩计算公式:
| $ M = {F_{\rm{r}}} \cdot d + {F_{\rm{L}}} \cdot R = \left( {\mu R + d} \right){F_{\rm{v}}}S $ | (6) |
式中: Fr为轮胎承受径向载荷,FL为轮胎承受轴向载荷,M为转矩,μ为轮胎和路面间设定的摩擦系数, R为最大轮胎的静态负载半径, d为车轮的偏距,S为强化系数.
可转换为加载轴的轴端加载力为
| $ {F_1} = M/L $ | (7) |
式中,Fl为加载轴轴端力,L为加载轴长度.
1.3 有限元模型建立及边界条件设定为了简化计算,模型中忽略影响不大的气门孔、倒角和密封槽等,只考虑内、外轮辋和轮辐板结构及安装螺栓作为研究对象进行分析,同时车轮通过法兰与长度L=1 m的加载轴连接.利用Solidworks建立简化物理模型,导入到ANSYS Workbench环境下,对整个模型采用四面体网格多区划分,将螺栓与轮辐发生接触的位置细化网格以提高计算精度,有限元模型共包含了782 025个节点,442 468个单元.
轮辐与轴盘相连接的螺栓孔内表面六自由度全约束,释放绕轴转动的旋转自由度,加载轴与车轮的3个平移自由度和除绕车轮中心轴线转动外的其他2个旋转自由度受到约束.
2 多变循环加载疲劳性能分析 2.1 应力分析本文将理想路面、粗糙或颠簸路面直行、转弯行驶3种工况下的载荷在有限元软件中分别独立施加,研究分析不同种载荷下车轮的应力、应变规律.由于此种无内胎式车轮为非圆周对称结构,故载荷的施加方向对车轮不同位置的疲劳寿命影响不同.所以,为找到车轮受载后最薄弱位置,同时又便于计算,将在圆周方向划分出等间夹角为15°的24个加载方向,进行仿真分析.根据仿真结果分析, 发现转弯行驶工况下,轮辋受载荷影响最大,内、外轮辋最大等效应力云图如图 5、图 6所示,等效应变云图如图 7所示,总体位移云图如图 8所示.
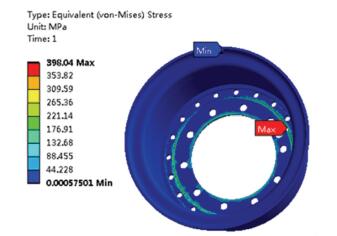
|
图 5 内轮辋等效应力云图 Fig. 5 Internal rim equivalent stress |
|
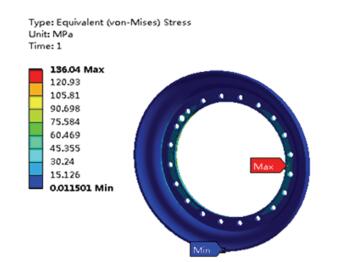
图 6 外轮辋等效应力云图 Fig. 6 External rim equivalent stress |

|
图 7 车轮等效应变云图 Fig. 7 Wheel equivalent elastic strain |

|
图 8 车轮位移云图 Fig. 8 Wheel total deformation |
由图 5、图 6可知,在转弯工况下,等效力施加于定位孔同角度位置处时,车轮产生最大等效应力.内轮辋产生最大应力为398.04 MPa,发生在轮辐板安装孔处;外轮辋的最大应力为136.04 MPa,发生在安装凸台与轮辋的焊接处;由图 7可知,车轮的最大应变为5.8e-4,出现在凸台根部焊接处;内轮辋轮缘底部产生最大位移0.14 mm.内、外轮辋体的应力,应变值均小于表 1中给出的材料许用值,车轮节点的最大偏移量小于许用值0.8 mm,该设计满足强度、刚度要求.
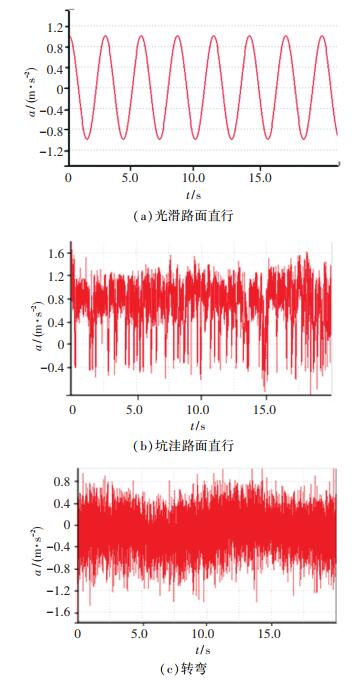
2.2 疲劳寿命分析车轮在行驶过程中多为低载高周疲劳损伤导致失效,且车轮应力发生频率的总体分布是由光滑平坦路面直行、粗糙颠簸路面直行和转弯等多种情况产生的应力频率循环作用形成的混合分布,如图 9所示为利用Fatigue Tool模拟车轮的行驶状况生成载荷谱,横坐标为仿真加载时间,纵坐标为幅值.
|
图 9 不同行驶工况下加载应力谱 Fig. 9 Loading stress spectrum of the simulated vehicle under different travle conditions |
车轮不同位置上的应变要根据材料性能的疲劳准则转换成应力,本文采用名义应力法(S-N疲劳曲线法)描述零件最大应力与疲劳寿命之间的关系,对零件进行疲劳寿命预估.
S-N曲线表现的是材料从疲劳试验中获得的单轴应力状态,有数学表达式:
| $ N{S^m} = C $ | (8) |
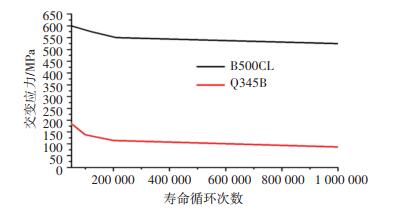
式中:m和C为材料常数,S为应力.高强钢和低碳钢材料的S-N曲线如图 10所示.
|
图 10 高强钢和低碳钢材料的S-N曲线 Fig. 10 S-N curves of high-strength steel and low-carbon steel materials |
根据Palmgren-Miner线性疲劳损伤累积理论可知,在不同交变应力载荷下部件的疲劳损伤和疲劳寿命可以分步计算后叠加求和,有
| $ D = \sum\limits_{i = 1}^k {\frac{{{n_i}}}{{{N_i}}}} = a\left( {a \le 1} \right). $ | (9) |
式中: D为疲劳损伤,ni为第i级载荷循环次数,Ni为疲劳寿命,k为应力水平级数.
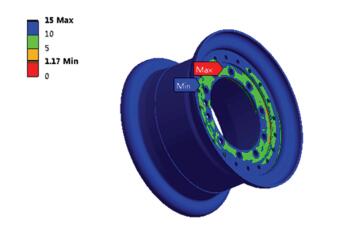
基于上述方法,在Fatigue Tool中进行车轮多变循环载荷下的分工况加载疲劳寿命计算.在转弯工况下分别得到车轮的疲劳寿命及易出现疲劳损伤的位置,如图 11所示.
|
图 11 疲劳安全系数云图 |
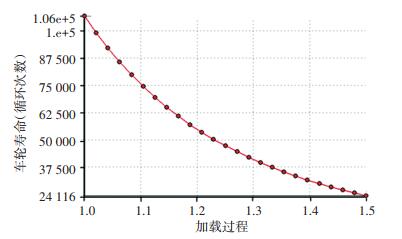
疲劳危险点出现在外轮缘与小轮辐板连接位置及两轮辐板接触处;根据中国汽车行驶工况统计数据分析[21],行驶工况下低、中、高速行驶时间占比分别为19%、54.9%、26.1%,转弯操作在低速工况下进行,中高速下直行,对仿真数据按照2种工况比例加和计算得到图 12所示车轮多变载荷下疲劳敏感曲线,在1.2倍载荷下,车轮疲劳循环次数大于规定的循环次数60 000次.根据车轮应力及疲劳寿命分析结果可知,车轮结构满足材料许用应力及产品设计要求,可对车轮进行多目标优化设计.
|
图 12 疲劳敏感寿命曲线 Fig. 12 Fatigue life curve |
根据疲劳寿命分析结果显示,车轮的主要破坏工况是在转弯行驶工况下,为使车轮的质量和性能达到最优,在保证与给定轮胎配对尺寸不变的情况下,对车轮在该种工况下,以车轮的结构尺寸为设计变量进行多目标优化设计.对车轮建立参数化模型,将车轮中除去与轮胎配合尺寸外的8个可更改的主要结构参数定义为设计变量,取值范围如表 2所示.其中,受到车轮结构限制,变量x5和x7关联,变量x6和x8关联,其数值大小同步变化.
| 表 2 车轮设计变量参数及取值范围 Tab. 2 Wheel design variables and ranges of values |
车轮的优化问题涉及多个变量,函数关系复杂,为了在一定保真度内提高优化效率,利用Kriging近似模型替代物理模型,为各设计变量件提供相对平滑的函数关系,根据拉丁超方优化设计,对有限元模型进行均匀随机采样,选取150个样本点,拟合各性能指标的Kriging近似模型, 如式:
| $ y(x){\rm{ = }}\sum\limits_{j = 1}^p {{B_j}{f_j}(x){\rm{ }} + {\rm{ }}Z(x)} . $ | (10) |
式中:fj(x)为已知回归函数的基函数;βj为基函数的系数;p为基函数的个数.
假定随机函数Z(x), x∈D为一组观测值,{z(xi)}, i=1, 2, ..., n,定义一个随机函数
| $ z'(x) = z(x) - {\mu _m}(x), x \in D, $ | (11) |
式中,μm(x)为另一组观测集合M(x)的数学期望,设其为常数.
| $ E[z({x_0}){\rm{ }} - z^*({x_0})] = 0, $ | (12) |
| $ {\rm{Var}}\left[ {z\left( {{x_0}} \right) - {z^*}\left( {{x_0}} \right)} \right] = \min . $ | (13) |
式中,x0为区域D中一点;λi(i=1, 2, ..., n)为待定加权系数.即当无偏估计和估计方差最小时,计算完成,获得最优解.
由于Kriging近似模型具有对初始值有极大依赖性,易过早收敛等特点,因此,要在Kriging近似模型作为目标函数前进行精确度检验.
采用R2检验精度,表达式:
| $ {R^2} = \frac{{\sum\limits_{i = 1}^n {{{\left( {{{\hat y}_i} - \bar y} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} }}. $ | (14) |
式中:n为样本的个数;
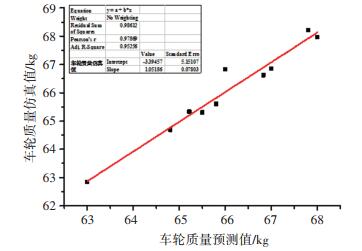
R2的值越接近100%,Kriging近似模型的拟合精度越高.另外选取10个样本点,通过Hammersley设计验证代理模型的准确性,各性能指标的确定系数R2均大于95%,满足代理模型拟合精度要求.零件质量性能指标的代理模型精度测试结果如图 13所示.
|
图 13 质量指标的代理模型精度 Fig. 13 Surrogate model accuracy of quality index |
综合考虑车轮的各项性能指标,该车轮要达到的优化目标为:1)质量最小;2)疲劳寿命最大;3)安全系数最大.建立优化问题模型如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \min \left( {m\left( x \right)} \right)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \max \left( {{N_b}\left( x \right), {s_N}\left( x \right)} \right), }\\ {{\rm{s}}{\rm{.t}}.\left\{ \begin{array}{l} {\sigma _{bn}}\left( x \right) \le {\sigma _{n0}}, \\ {\sigma _{bw}}\left( x \right) \le {\sigma _{w0}}, \\ {D_b} \le {D_{b0}}, \\ {N_b}\left( x \right) \ge {N_{b0}}, \\ {f_1} \ge {f_{10}}, \\ {x_i} \in \left[ {{x_{{\rm{L}}i}}, {x_{{\rm{U}}i}}} \right], 1 \le i \le 8 \end{array} \right.} \end{array}} \right. $ | (15) |
式中:x为设计变量,m(x)为多目标优化中轮辋质量,Nb(x)为车轮弯曲载荷下疲劳寿命,s(x)为车轮弯曲载荷下安全系数;σbn、σbw为内、外轮辋在弯曲载荷工况下最大Von Mises应力;σn0、σw0为内、外轮辋材料的屈服应力;Db、Db0为车轮弯曲载荷下节点的最大位移值、许用位移值;Nb、Nb0为车轮弯曲载荷下疲劳寿命值、许用值,Nb0=6×105循环;f1、f10为车轮的一阶模态频率和许用频率;xL、xU为设计变量取值的下限和上限.
将Soildworks建立的车轮参数化模型与ANSYS DesignXplorer多目标优化模块进行关联,在ANSYS/DS中设置设计变量和优化目标,选用NSGA-Ⅱ算法基于近似模型对车轮进行多目标优化分析,优化流程如图 14所示.

|
图 14 车轮多目标优化分析模型 Fig. 14 Multi-objective optimization and analysis model of wheel |
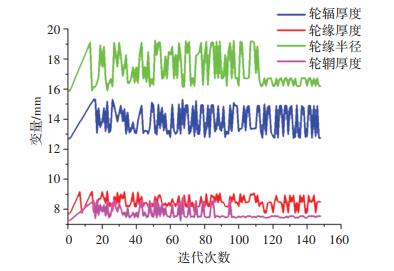
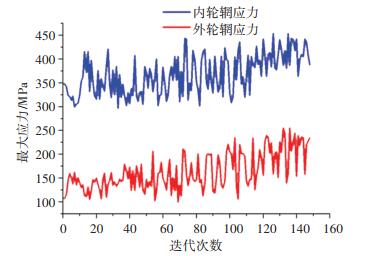
迭代150次后,根据收敛准则,Pareto Percentage与Stability Percentage均保持在设定允许变化范围1内,认为迭代收敛.在得到优化后的所有参数值,查看迭代图形,横坐标代表迭代次数,纵坐标为对应的值.部分设计变量迭代如图 15所示,应力迭代如图 16所示,对比两图趋势,可知,车轮上轮辐厚度和轮辋厚度对应力值的影响呈负相关,厚度越大则车轮上受到的应力值越小.
|
图 15 设计变量迭代 Fig. 15 Design variable iteration |
|
图 16 应力迭代 Fig. 16 Stress iteration |
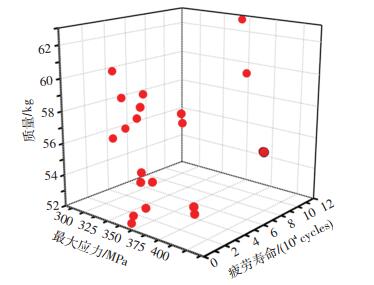
如图 17所示,选取车轮质量、车轮最大应力和转弯工况下疲劳寿命这3个目标在迭代次数内所筛选的20组Pareto前沿数据制成Tradeoff权衡图,由散点图可知,3个目标之间存在矛盾关系,并非同步变化的,要达到最优解,需平衡三者之间的关系.按照使用要求,优先考虑轮辋的质量较小和疲劳寿命周期较大,在解集中选取一个妥协解作为最终优化结果,用其他2种工况检验优化车轮的性能,车轮的优化后结果及优化前后的性能对比如表 3、表 4所示.
|
图 17 Tradeoff权衡 Fig. 17 Tradeoff chart |
| 表 3 优化前后设计变量取值 Tab. 3 Values of design variables before and after optimization |
| 表 4 优化前后性能功能对比 Tab. 4 Comparison of performance and performance before and after optimization |
由表 4可知,通过对Kriging近似模型进行迭代优化,使车轮的质量比传统经验设计降低了9.73%,多变循环载荷下疲劳寿命降低了3.53%,安全系数依然符合要求,各项性能指标均满足设计要求.
4 试验验证大量的试验证明,疲劳损坏是轮辋主要的失效形式,且弯曲疲劳破坏程度远大于径向疲劳破坏[22].所以,依据SAE J1992-2001标准相关规定,对制造出的5个优化后车轮结构做弯曲疲劳试验分析.
本次试验在中汽协车轮质量监督检验中心完成,采用CFT-05弯曲疲劳试验机,将试件牢固的夹紧到试验夹具上,轮缘下部与压边圈接触,用螺栓将压边圈固定住,电机转速设定为1 072 r/min, 施加与仿真条件相同的载荷,如图 18所示.

|
图 18 弯曲疲劳试验 Fig. 18 Bending fatigue test |
当产生应力导致的可见疲劳裂纹或原有裂纹扩展,该试件试验终止,试验后车轮形变如图 19所示,其出现裂纹的位置与仿真分析车轮最大应力处位置一致,出现在外轮缘与小轮辐板连接位置及两轮辐板接触处.

|
图 19 明显可见裂纹 Fig. 19 Clearly visible crack |
在未考虑焊接热影响区的情况下,从结构分析和疲劳分析的结果来看,在螺栓预紧力610 N·m,转矩29 072 N·m的载荷状态下,内外轮辋连接处应力较大,相对危险.安装孔位置及轮缘焊接处应力集中现象明显,容易出现疲劳失效,且能够满足设计寿命60 000的要求.
通过试验验证,在螺栓预紧力610 N·m转矩29 072 N·m的载荷状态下,轮辋实际破坏位置为轮缘焊接处,轮辋最低寿命60 407次循环,满足设计要求Nb≥6×104.
弯曲疲劳试验目的是检验车轮受到连续变化载荷时车轮的刚性,仿真与试验结果表明,本组装式车轮的刚性和抗冲击性能优良.
5 结论1) 以匹配16.00-R25轮胎的无内胎车轮为研究对象,首次采用内、外轮辋不同型号钢材通过螺栓连接的组装式车轮形式,对车轮进行了更贴近于使用工况的多变循环加载仿真分析.得到组装式车轮在3种工况下产生的应力、强度、疲劳寿命与安全系数等性能参数,研究了各性能参数与车轮结构之间的关系.
2) 综合考虑了车轮行驶中的路面信息和车轮内部应力的传递路径,建立了车轮的参数化模型,运用了Kriging模型理论和拉丁超方设计方法,对车轮进行了多目标优化设计.得到了满足各方面性能要求的轻量化车轮.结果表明:单个轮辋在经过优化后质量减少6.1 kg,在满足各方面性能的要求的同时,相对于同类型单一钢材制造的轮辋更加轻便、耐用,相较于同等要求的镁铝合金车轮大大降低了制造成本和简化了加工工艺.
3) 通过对车轮的理论载荷分析、参数化模型建立和疲劳试验性能仿真分析,实现了一套基于车轮多变循环载荷下疲劳性能的结构设计及优化流程,为之后重型车辆钢制车轮的多目标优化和轻量化设计提供了理论依据和技术指导.
| [1] |
蒋荣超, 王登峰, 秦民, 等. 基于疲劳寿命的轿车后悬架扭转梁轻量化设计[J]. 吉林大学学报(工学版), 2016, 46(1): 35. JIANG Rongchao, WANG Dengfeng, QIN Min, et al. Lightweight design of torsional girder of car rear suspension based on fatigue life[J]. Journal of Jilin University (Engineering Edition), 2016, 46(1): 35. |
| [2] |
李珩, 单颖春, 路洪洲, 等.钢制车轮疲劳仿真分析及含铌高强钢替代设计[C]//中国汽车工程学会年会论文集.北京: 中国汽车工程学会, 2014 LI Heng, SHAN Yingchun, LU Hongzhou, et al. Fatigue simulation analysis of steel wheels and alternative design of niobium-containing high strength steel[C]//Proceedings of the 2014 Annual Meeting of China Automotive Engineering Society. Beijing: China Society of Automotive Engineering, 2014 |
| [3] |
ZHANG Y, LAI X, ZHU P, et al. Lightweight design of automobile component using high strength steel based on dent resistance[J]. Materials & Design, 2006, 27(1): 64. |
| [4] |
HSU Y L, HSU M S. Weight reduction of aluminum disc wheels under fatigue constraints using a sequential neural network approximation method[J]. Computers in Industry, 2001, 46(2): 167. |
| [5] |
SONG W, WOODS J L, DAVIS R T, et al. Failure analysis and simulation evaluation of an Al 6061 alloy wheel hub[J]. Journal of Failure Analysis and Prevention, 2015, 15(4): 521. DOI:10.1007/s11668-015-9969-9 |
| [6] |
AKBULUT H. On optimization of a car rim using finite element method[J]. Finite Elements in Analysis & Design, 2003, 39(5): 433. DOI:10.1016/S0168-874X(02)00091-4 |
| [7] |
BALLO F, MASTINU G, GOBBI M. Lightweight design of a racing motorcycle wheel[C]// SAE World Congress & Exhibition. Detroit: SAE, 2016
|
| [8] |
闫胜昝.铝合金车轮结构设计有限元分析与实验研究[D].杭州: 浙江大学, 2008 YAN Shengzan. Finite element analysis and experimental study of aluminum alloy wheel structure design[D]. Hangzhou: Zhejiang University, 2008 http://d.wanfangdata.com.cn/thesis/Y1405180 |
| [9] |
KOCABICAK U, FIRAT M. Numerical analysis of wheel cornering fatigue tests[J]. Engineering Failure Analysis, 2001, 8(4): 339. DOI:10.1016/S1350-6307(00)00031-5 |
| [10] |
ZHENG Z G, SUN T, XU X Y, et al. Numerical simulation of steel wheel dynamic cornering fatigue test[J]. Engineering Failure Analysis, 2014, 39: 124. DOI:10.1016/j.engfailanal.2014.01.021 |
| [11] |
BALLO F, FRIZZI R, MASTINU G, et al. Lightweight design and construction of aluminum wheels[C]// SAE World Congress & Exhibition. Detroit: SAE, 2016
|
| [12] |
FIRAT M, KOZAN R, OZSOY M, et al. Numerical modeling and simulation of wheel radial fatigue tests[J]. Engineering Failure Analysis, 2009, 16(5): 1533. DOI:10.1016/j.engfailanal.2008.10.005 |
| [13] |
SHANG D, LIU X, SHAN Y, et al. Research on the stamping residual stress of steel wheel disc and its effect on the fatigue life of wheel[J]. International Journal of Fatigue, 2016, 93: 173. DOI:10.1016/j.ijfatigue.2016.08.020 |
| [14] |
王登峰, 张帅, 陈辉, 等. 基于疲劳试验的车轮拓扑优化和多目标优化[J]. 汽车工程, 2017(12): 1351. WANG Dengfeng, ZHANG Shuai, CHEN Hui, et al. Novel steel wheel design based on multi-objective topology optimization[J]. Journal of Mechanical Science & Technology, 2017(12): 1351. |
| [15] |
XIAO D, ZHANG H, LIU X, et al. Novel steel wheel design based on multi-objective topology optimization[J]. Journal of Mechanical Science & Technology, 2014, 28(3): 1007. |
| [16] |
WAN X, SHAN Y, LIU X, et al. Simulation of biaxial wheel test and fatigue life estimation considering the influence of tire and wheel camber[J]. Advances in Engineering Software, 2016, 92(C): 57. |
| [17] |
路洪洲, 李军, 王杰功, 等.乘用车轻量化钢制车轮的发展[C]//中国汽车工程学会年会论文集.北京: 中国汽车工程学会, 2014 LU Hongzhou, LI Jun, WANG Jiegong, et al. Development of lightweight steel wheels for passenger vehicles[C]//Proceedings of the 2014 Annual Meeting of China Automotive Engineering Society. Beijing: China Society of Automotive Engineering, 2014 http://d.wanfangdata.com.cn/conference/8862046 |
| [18] |
WANG Ning, LI Yi, DU Linxiu, et al. Fatigue property of low cost and high strength wheel steel for commercial vehicle[J]. Journal of Iron and Steel Research, International, 2009, 16(4): 44. DOI:10.1016/S1006-706X(09)60059-5 |
| [19] |
GRUBISIC V, FISCHER G. Procedure for optimal lightweight design and durability testing of wheels[J]. International Journal of Vehicle Design, 1984, 5(6): 659. |
| [20] |
ECHARD B, GAYTON N, LEMAIRE M. AK-MCS: an active learning reliability method combining Kriging and Monte Carlo Simulation[J]. Structural Safety, 2011, 33(2): 145. |
| [21] |
中国国家标准化管理委员会. GB/T 38146.2-2019[S].北京: 中国标准出版社, 2019
|
| [22] |
TOPAC M M, ERCAN S, KURALAY N S. Fatigue life prediction of a heavy vehicle steel wheel under radial loads by using finite element analysis[J]. Engineering Failure Analysis, 2012, 20: 67. DOI:10.1016/j.engfailanal.2011.10.007 |
 2020, Vol. 52
2020, Vol. 52


