2. 海军工程大学 舰船动力工程军队重点实验室, 武汉 430033
2. Military Key Laboratory for Naval Ship Power Engineering, Naval University of Engineering, Wuhan 430033, China
现代燃气轮机涡轮进口温度不断提升,高温燃气在涡轮动叶叶顶间隙产生的泄漏流在降低涡轮效率的同时,更是加剧了叶顶的热负荷[1-2],使得叶顶表面极易超温,高温区冷却不及时会导致烧蚀,直接影响燃气轮机的安全运行.
涡轮凹槽叶顶是控制间隙泄漏流动,改善叶顶换热的典型方式之一[3-4]. Metzger等[5]最先通过实验的方法给出了机匣壁面静止时凹槽叶顶内部的换热情况;Ma等[6]采用实验的方法研究了涡轮叶栅叶顶几何结构对气动性能的影响,给出了凹槽状叶顶降低气动泄漏损失的机理;Kang等[7]研究了凹槽几何参数对顶部间隙泄漏流动结构与内壁面传热特性的影响,给出了凹槽结构参数对降低叶顶的平均换热系数的作用机理,后来Maral等[8]进一步研究了间隙高度不均匀时凹槽深度和肋条宽度对叶顶气热特性的影响;国内学者杜昆等[9]考虑到叶顶的非定常流动传热特性,针对GE-E3高压动静叶干涉现象,数值研究了对凹槽内流动特性的影响.
然而由于高温流体通过较窄的凹槽顶部间隙时,会对凹槽底部形成射流冲击,导致凹槽肋条和底部局部区域出现较高的热负荷[10].为降低这部分热负荷,可以通过在凹槽叶顶布置气膜冷却孔,使得冷却气体能有效阻隔高温流体对壁面的直接接触[11].周治华等[12]考虑到间隙泄漏流对凹槽底面的流动冲击特性,重点分析了吹风比、冷却孔位置及喷射角度对内壁面换热Nu数的影响. Wang等[13]通过研究跨音速流动中顶部冷却射流与泄漏热流的相互作用,在此基础上分析了考虑冷却射流时凹槽结构的设计原则. Ma等[14]发现在凹槽底部近前缘区域的冷却气体与泄漏流会产生强烈的相互作用. Zhou等[15]研究了叶顶冷却孔位置对换热特性的影响,发现换热效果在叶顶分离泡区域内冷气喷射效果要优于泄漏流再附位置.
对泄漏流与顶部冷却射流相互作用的流动与传热特性分析是为了在降低叶片温度的同时,减小由于温度分布不均而产生的热应力,有效延长叶片的使用寿命[16-18].因此对叶顶的传热研究应当在耦合顶部流动特性的同时,进一步考虑固体材料物性,研究流固耦合条件下冷却射流的流动与传热特性.本文通过流固耦合的计算方法,研究了气膜冷却孔近压力面布置时,产生的顶部冷却射流与间隙泄漏流的相互作用,分析了吹风比、冷却孔进、出气角及固体导热系数对凹槽内流动与固体壁面传热的影响,为凹槽状叶顶冷却优化设计提供参考依据.
1 计算模型及验证 1.1 计算模型Metzger等[5]对未考虑气膜冷却的凹槽间隙进行了传热实验,并对不同湍流模型下的Nu系数进行了数值计算.本文基于Metzger等[5]未考虑气膜冷却的凹槽实验模型,以带气膜冷却的叶顶凹槽为研究对象.
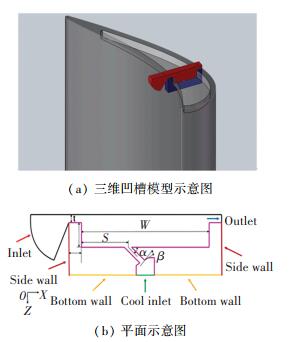
计算模型包括流体域和固体域,如图 1(a)所示,流体域采用带圆弧进口的凹槽间隙模型,模拟涡轮叶片的叶顶间隙流域(红色部分),叶顶凹槽固体区域(蓝色部分)为固体域.平面示意图如图 1(b)所示,间隙高度t=0.5 mm,肋条宽度w=1 mm,底部宽度W=10 mm,凹槽高度H=1.5 mm,垂直于纸面的深度为2 mm.
|
图 1 计算模型示意图 Fig. 1 Schematic diagram of computational model |
如图 1(b)所示,气膜冷却孔位于凹槽底部S/W=0.1处,孔型采用应用最为广泛的圆型孔,将冷却孔中心轴线与凹槽底面的夹角定义为倾斜角α,冷却孔长度L=2 mm,冷却孔半径R=0.254 mm.将冷却孔和冷却腔接触平面的法向方向与冷却孔中心线的夹角定义为进气角β,同时定义顺时针方向为正方向,逆时针方向为负方向.
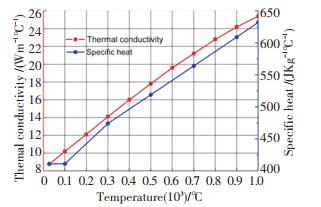
1.2 边界条件及网格划分流体域计算模型中将主流与Y轴垂直的两个面设为周期性对称面.主流进口方向设置为垂直于弧面,冷气进口方向为Z轴负方向.流体域与固体域相交界面设置为流固传热交界面,固体域左右壁面(Side wall)设置为换热系数1 000 W/(m2·K),外部参考温度(700 K)的外部换热壁面,固体域底面(Bottom wall)设置为换热系数1 200 W/(m2·K),外部参考温度(550 K)的内部换热壁面.机匣壁面设置沿X轴负方向的速度而叶顶保持静止来模拟动叶的相对转动,同时机匣壁面设为固定壁面温度.固体材料为某标准高温合金(以下简称Normal),密度为8 326 kg/m3,其导热系数以及比热都是和温度相关的函数,通过拟合多项式给定如图 2所示,表 1为计算边界条件.其中冷却进口速度由吹风比确定,ρm和vm分别为泄漏流密度和泄漏流速度,ρc为冷却气体密度,实际计算中采取了多次试算的方法来选取不同工况下冷却进口速度的取值.
|
图 2 Normal材料的导热系数和比热曲线图 Fig. 2 Thermal conductivity and specific heat graph with Normal material |
| 表 1 凹槽状叶顶计算边界条件 Tab. 1 Boundary condition of computational in grooved tip |
计算网格采用ANSYS中的Mesh模块进行网格划分,流体域网格和固体域网格分别如图 3(a)、图 3(b)所示,流体域对孔出口区域及壁面网格进行加密,保证第一层网格的y+ < 1,从而满足湍流模型的要求,固体域对孔出口处网格进行加密.

|
图 3 网格划分 Fig. 3 Schematic diagram of mesh |
数值计算验证采用与文献[5]中实验相同的模型和边界条件,其中t/W=0.1,w/W=0.2,进口雷诺数为15 000,网格总数约为429万.与实验模型一样,数值计算验证模型没有考虑气膜冷却孔以及机匣运动产生的端壁运动效应的影响.
1.3 湍流模型的验证数值计算采用商用软件ANSYS-CFX,选取前期研究者指出的对叶顶传热预测准确度较高的k-ω,SST湍流模型以及带有转捩的SST γ-θ湍流模型.本文基于Metzger等[5]未考虑气膜冷却的凹槽间隙传热实验结果,对不同湍流模型下的Nu系数进行了数值计算.
为了和实验设置相同,数值计算时采用了实验研究的几何结构和边界条件,其中肋条宽度为9.5 mm,t/W=0.1,H-W=0.2,雷诺数取值为1.5×104.
数值计算和实验数据对比结果如图 4所示,可以看出,数值计算结果与实验结果符合程度最好的是SST γ-θ湍流模型.其中k-ω模型在凹槽肋条区域的计算值误差较大,SST模型计算值整体偏高,因此本文计算均采用SST γ-θ湍流模型.

|
图 4 数值计算和实验数据对比 Fig. 4 Comparison of numerical and experimental data |
定义努塞尔系数为
| $ Nu = \frac{{qt}}{{\kappa \left( {{T_W} - {T_i}} \right)}}. $ |
式中:q为热流量,t为间隙高度,K为气体导热率,TW和Ti分别为等壁面温度和主流温度.
定义展向平均努塞尔系数为
| $ Nu = \frac{1}{{\Delta y}}\int {Nu\left( {x, y} \right)} {\rm{d}}y, $ |
式中y表示垂直于主流的侧向方向.
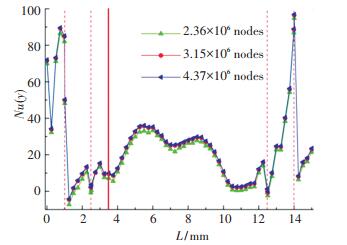
1.4 网格无关性验证由于本文的计算模型与数值验证的模型存在几何尺寸出入,为了排除网格数量对计算结果的影响,对带有冷却气膜孔(S/W=0.1,α=90°)的流固耦合模型进行了网格无关性验证,验证结果如图 5所示.其中,L为凹槽壁面沿流向长度,图中红色实线表示冷却孔中心所在位置,红色虚线区域表示肋条侧壁面区域.当带气膜孔模型的网格数大于315万(其中流体域219万,固体域96万)时,计算结果基本不随网格数变化.
|
图 5 网格无关性 Fig. 5 Grid independence of Nu(y) |
图 6给出了α=90°以及β=0°时3种不同吹风比下凹槽间隙的流动传热特性. 图 6(a),6(c),6(e)分别为吹风比M=0.5,M=1,M=1.5时中截面马赫数分布云图、凹槽壁面Nu分布云图以及间隙泄漏流和冷却气流掺混处中截面的局部二维流线图. 图 6(b),6(d),6(f)分别为吹风比M=0.5,M=1,M=1.5时凹槽壁面Nu分布云图以及等涡量面(λ=0.0012)的湍动能(TKE)分布云图,其中等涡量面模型选择Lambda 2-criterion[19].

|
图 6 吹风比对凹槽间隙流动传热的影响 Fig. 6 Effects of blowing ratio on clearance flow and heat transfer in squealer tip |
当M=0.5时,如图 6(a)、(b)所示,冷却气流受到间隙泄漏流的阻挠下压,部分冷却气体产生逆向回流冲击凹槽底部气孔前缘(孔左侧)区域后沿着肋条侧壁面上升在A点处与泄漏流掺混形成高湍动能区域.机匣的相对运动在中部区域产生一个较大的逆时针涡,泄漏流与其相互作用后冲击凹槽底部在B点处形成明显的高换热区域,随后逐渐抬升,并再次与逆时针涡作用,在C点处形成二次附着区域,造成局部的传热恶化.
当M=1.0时,如图 6(c)、(d)所示,部分冷却气体受到泄漏流阻挡,被吹向第一条肋侧壁面,在第一条肋角区形成复杂的涡流,并在近肋条顶部区域造成扰动和掺混,使得第一条肋顶部区域换热强度升高.泄漏流受到冷却气流的冲击略有抬升,而后在逆时针涡的作用下冲击凹槽底面在E点处形成高换热区域.
当M=1.5时,如图 6(e)、(f)所示,冷却气体直接冲击泄漏流在F点处产生强烈的掺混,同时冷却气体产生明显的侧向流动冲击肋条侧壁面,使得肋条侧壁面近顶部区域出现较大的负Nu,并将泄漏流压向两侧,使得肋条顶部两侧区域出现明显的高换热区域.冷却气流的冲击使得一部分泄漏流在F点处压向两侧,最终在凹槽底部形成两长条状的换热区,另一部分泄漏流在G点处受涡流作用上抬冲击机匣壁面,随后压向两侧与中部的冷却气流一起贴着靠近机匣区域流向间隙出口.
随着吹风比的增加,由于冷却气流冲击作用的增强,间隙入口处的泄漏流速度降低,同时冷却流量的增加使得间隙出口处速度有所升高.吹风比的增加使得泄漏流冲击凹槽底面的传热恶化区域后移,高吹风比时(M=1.5)泄漏流完全被压向两侧形成更加靠近间隙出口的长条状换热区.
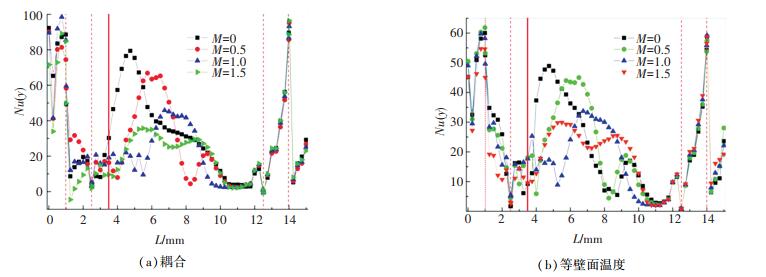
图 7(a)、7(b)分别给出了耦合和等壁面温度下凹槽壁面沿流向的展向平均努赛尔系数分布.如图 7(a)所示,随着吹风比的增加,凹槽底部壁面Nu峰值减小,分布更加均匀,说明冷却气体覆盖范围更广.大吹风比对第一条肋侧壁面有较好的冷却效果,冷却气体对近第二条肋区域几乎没有影响.如图 7(b)所示,等壁面温度条件下,各吹风比下展向平均努赛尔系数分布趋势与耦合计算结果基本一致,但在第一条肋侧壁面位置,M=1.0和M=1.5工况出现了相反的规律.主要是因为耦合计算下由于考虑了固体材料的导热,在冷却气体的冲击下迅速带走壁面温度,局部出现了负Nu区域, 即壁面温度低于气体温度,气体向壁面传热,冷却气流的冲击越强,效果越明显.
|
图 7 吹风比对展向平均Nu(y)分布的影响 Fig. 7 Effects of blowing ratio on distribution of Nu(y) |
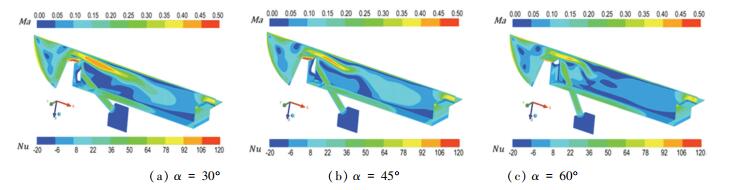
图 8给出了M=1.5及β=0°时冷却孔不同倾斜角对凹槽间隙流动与传热的影响.由图 8可见,当气膜孔存在倾斜角时,冷却气流直接冲击凹槽第一条肋侧壁面,在冲击位置处形成局部的负Nu区域,随后冷却气体沿着壁面上升与间隙泄漏流混合.随着倾斜角的增大,冷却气流的冲击位置逐渐上移,肋条顶部传热恶化得到有效改善,同时倾斜角的增大使得冷却气流对间隙泄漏流的冲击增强,间隙入口处泄漏流的流向速度降低.
|
图 8 倾斜角对凹槽间隙流动传热的影响 Fig. 8 Effects of hole angles on clearance flow and heat transfer in squealer tip |
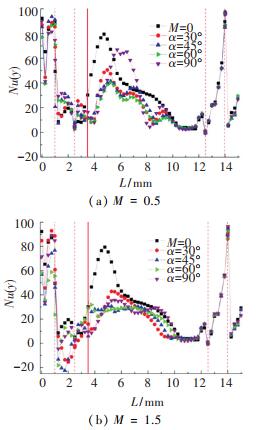
小吹风比(M=0.5)和大吹风比(M=1.5)时冷却孔不同倾斜角对凹槽壁面沿流向的展向平均努赛尔系数分布的影响如图 9所示.在低吹风比工况时,冷却孔倾斜角对第一条肋顶部和侧壁面的Nu分布影响较小,没有出现局部的负Nu区域,同时孔后区域Nu分布的波动性要大于高吹风比工况.主要是由于低吹风比工况下冷却气流的速度较小,没有对凹槽侧壁面形成明显的冲击,同时对孔后区域的覆盖性较差,在泄漏流的冲击下增加了局部区域的扰动.在高吹风比工况时,α=60°对肋条顶部冷却效果较好,α=45°时肋条侧壁面局部Nu最低,负Nu值区域最大,对肋条侧壁面局部冷却效果较好,总体上α=45°与α=60°的冷却效果要优于其他倾斜角.
|
图 9 不同倾斜角展向平均Nu(y)对比 Fig. 9 Comparison on distribution of Nu(y) between different hole angles at M=0.5 and M=1.5 |
图 10给出了M=1.5及α=45°时不同进气角冷却孔中截面的马赫数云图和流线图,进气角对凹槽间隙流动传热的影响实质上是改变了冷却气体在孔道中的分布,产生“喷射效应”,从而改变孔处口出冷却气流的位置和角度.

|
图 10 中心截面上气膜孔内速度云图和流线图 Fig. 10 Velocity contours and streamlines on center section of film cooling hole region |
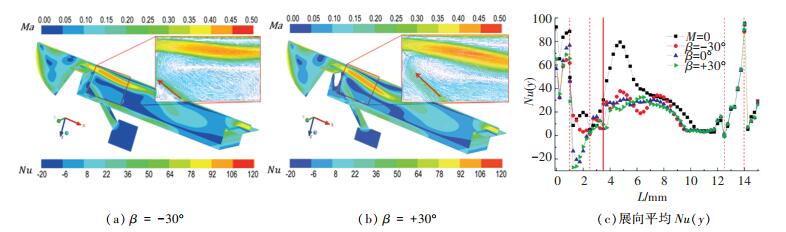
从图 10(b)中可以看出当β=0°时,冷气进入气膜孔后流线分布比较均匀,流线方向基本与孔道轴线一致.当β≠0°时,冷气气流进入气膜孔后与孔轴线方向形成一定的夹角从而在孔道内形成分离,形成了明显的高速区和低速区.当β>0°时,高速区在气膜孔的上半部分如图 10(c)所示;而当β < 0°时,高速区在气膜孔的下半部分如图 10(a)所示.孔道入口区域内高低速区的分离形成,改变了冷却气体在孔道内的分布,产生“喷射效应”.
图 11给出了不同进气角对凹槽间隙流动传热的影响,如图 11(a)所示,当β < 0°时,箭头指示的冷却气体高速流体更靠近壁面,使得泄漏流回流流体在靠近壁面处形成了冲击,导致第一条肋侧壁面Nu数有所增大.如图 11(c)所示,当β>0°时,箭头指示的冷却气体高速流体有效阻挡了泄漏流回流冲击壁面,有效降低了侧壁面Nu数.如图 11(c)所示,当存在“喷射效应”时,冷却气流有效改善了凹槽第一条肋顶部区域的换热,整体上当β=+30°时凹槽壁面的流动传热更低.
|
图 11 近气角对凹槽间隙流动传热的影响 Fig. 11 Effects of inlet angles on clearance flow and heat transfer in squealer tip |
气体与固体间的对流传热特性受到固体材料物性参数的影响,其中导热系数是传热计算中一个重要的参数,因此为了研究导热系数对耦合传热性能的影响,本文对比了M=1.5工况时3种不同导热系数材料中截面处的无量纲温度分布,如图 12所示,高导热系数材料铝Al的材料导热系数为237 (W/m·K),低导热系数材料选用Lu等[20]使用的材料,其导热系数为0.331 5(W/m·K).

|
图 12 不同材料固体中截面无量纲温度分布云图 Fig. 12 Dimensionless temperature contours on center section of solid with different material |
无量纲温度定义为
| $ {T_\theta } = \frac{{T - {T_c}}}{{{T_i} - {T_c}}}. $ |
式中Ti与Tc分别表示为主流温度和冷却气体温度.
由图 12可见,文献[20]中的低导热系数材料(接近绝热工况)中截面的无量纲温度呈现明显的层状温度梯度分布,气流的对流换热占主导作用,其流固交界面处的无量纲温度分布趋势与图 9(b)中α=45°曲线的Nu分布趋势相互对应.高导热系数材料AL中截面的无量纲温度分布趋于一致(约为0.684)固体的导热占主导作用,气流对流换热的强弱几乎没有影响.
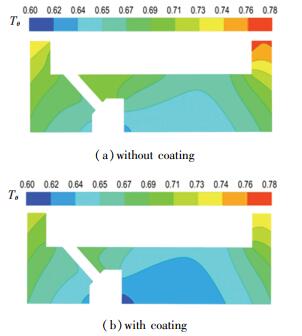
图 13进一步对比了同一基体材料(Normal)是否带有某型涂层(覆盖一定厚度的低导热系数材料)对无量纲温度分布的影响,带有涂层材料的无量纲温度分布与不带涂层基本一致,但整体数值降低.
|
图 13 固体中截面带涂层与不带涂层无量纲温度分布云图 Fig. 13 Dimensionless temperature contours with and without coating on center section of solid |
图 14给出了上述不同导热系数材料凹槽壁面沿流向的展向努塞尔系数分布.低导热系数材料有效降低了凹槽肋条顶部及凹槽底部孔后区域的Nu,同时也一定程度上阻碍了冷却气体向第一条肋侧壁面传热,整体上低导热系数材料降低了气流对固体壁面的对流换热,使得壁面的对流换热更加均匀.高导热系数材料Al与合金材料Normal相比,Nu分布基本一致,同时从图 12(a)和图 12(b)中看出其无量纲温度分布及数值差异也不明显.合金材料Normal的导热系数由图 2可得在14.5(W/m·K)左右,远远小于Al的237(W/m·K),因此在一定条件下,导热系数超过某一数值时,其对固体温度分布和壁面对流换热的影响基本不变.

|
图 14 不同导热系数展向Nu(y)对比 Fig. 14 Comparison on distribution of Nu(y) between different thermal conductivity |
本文针对涡轮凹槽叶顶顶部喷气冷却,考虑固体材料物性,耦合凹槽叶顶流动与传热特性,采用流固耦合计算方法,分析研究了吹风比、冷却孔倾斜角、进气角以及固体导热系数对叶顶凹槽内泄漏流与冷却气流相互作用的流动与传热特性,得到如下结论:
1) 凹槽壁面Nu数分布受吹风比影响较大,吹风比增大能有效改善凹槽压力面肋侧壁面及凹槽底部的换热,使Nu数分布更加均匀.
2) 相比于非耦合计算,耦合计算考虑了固体导热作用,对于冷却气流冲击区域局部出现了负Nu数,即壁面温度低于气体温度,气体向壁面传热,冷却气流的冲击越强,效果越明显.
3)在高吹风比(M=1.5)工况下,气膜孔倾斜角能有效降低冷气冲击位置附近的Nu数,出现局部范围的负Nu数区域;倾斜角增加,能有效改善压力面肋顶部的换热,降低泄漏流的速度.
4) 孔道进气角产生的“喷射效应”改变了冷却气流高速区的出口相对位置,当进气角β < 0°时,冷气阻隔高温流体的能力减弱,壁面Nu有所升高;反之当进气角β>0°时,冷却气体能有效阻隔高温流体,壁面Nu降低.
5) 低导热系数材料固体内部温度分布对流换热占主导作用,高导热系数材料固体内部温度分布导热占主导作用;低导热系数材料降低了气流对固体壁面的对流换热,使得壁面的对流换热更加均匀.
| [1] |
BUNKER R S. Axial turbine blade tips: function, design and durability[J]. AIAA Journal of Propulsion and Power, 2006, 22(2): 271. DOI:10.2514/1.11818 |
| [2] |
YANG H, ACHARY S, EKKAD S V. Numerical simulation of flow and heat transfer past a turbine blade with a squealer-tip[C]//Proceedings of ASME Turbo Expo 2002. Amsterdam: ASME, 2002: 295
|
| [3] |
AZAD J S, HAN J C, TENG S, et al. Heat transfer and pressure distributions on a gas turbine blade tip[J]. ASME Journal of Turbomachinery, 2000, 122(4): 717. DOI:10.1115/1.1308567 |
| [4] |
KWAK J S, HAN J C. Heat transfer coefficients of a turbine blade-tip and near-tip regions[J]. Journal of Thermophysics Heat Transfer, 2003, 17: 297. DOI:10.2514/2.6776 |
| [5] |
METZGER D E, BUNKER R S, CHYU M K. Cavity heat transfer on a transverse grooved wall in a narrow flow channel[J]. Journal of Heat Transfer, 1989, 111(1): 73. DOI:10.1115/1.3250661 |
| [6] |
MA H, WANG L. Experimental study of effects of tip geometry on the flow field in a turbine cascade passage[J]. Journal of Thermal Science, 2015, 24(1): 1. DOI:10.1007/s11630-015-0748-4 |
| [7] |
KANG D B, LEE S W. Effect of squealer rim height on heat/mass transfer on the floor of cavity squealer tip in a high turbine blade cascade[J]. International Journal of Heat and Mass Transfer, 2016, 99: 283. DOI:10.1016/j.ijheatmasstransfer.2016.03.121 |
| [8] |
MARAL H, SENEL C B, KAVURMACIOGLU L. A parametric and computational aerothermal investigation of squealer tip geometry in an axial turbine: a parametric approach suitable for future advanced tip carving optimizations[J]. ASME Paper 49705, 2016, GT2016-58107. DOI:10.1115/GT2016-58107 |
| [9] |
杜昆, 李军. 涡轮叶片凹槽状叶顶非定常流动传热特性的数值研究[J]. 推进技术, 2017, 38(3): 551. DU KUN, LI Jun. Numerical investigations on unsteady leakage flow and heat transfer characteristics of turbine blade with squealer tip[J]. Journal of Propulsion Technology, 2017, 38(3): 551. |
| [10] |
HAN J C, DUTTA S, EKKAD S. Gas turbine heat transfer and cooling technology[M]. second edition.[S.L.]: Taylor and Francis Group, 2013
|
| [11] |
BUNKER R S. A review of turbine blade tip heat transfer[C] // Turbine 2000 Symposium on Heat Transfer in Gas Turbine System. Cesme Turkey: [s.n.], 2000
|
| [12] |
周治华, 陈绍文, 李伟航, 等. 叶顶凹槽间隙气膜冷却的传热数值研究[J]. 推进技术, 2018, 39(3): 575. ZHOU Zhihua, CHEN Shaowen, LEE Weihang, et al. Heat transfer numerical research on film cooling of tip groove clearance[J]. Journal of Propulsion Technology, 2018, 39(3): 575. |
| [13] |
WANG Z, ZHANG Q, LIU Y, et al. Impact of cooling injection on the transonic over-tip leakage flow and squealer aerothermal design optimization[J]. Journal of Engineering for Gas Turbine and Power, 2015, 137(6): 062603. DOI:10.1115/1.4029120 |
| [14] |
MA H, ZHANG Q, HE L, et al. Cooling injection effect on a tran- sonic squealer tip: part 2: analysis of aerothermal interaction physics[C] // ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition. Seoul: ASME, 2016
|
| [15] |
ZHOU C, HODSON H, LOCK G. Thermal performance of cooled tips in a high pressure turbine cascade[J]. Journal of Propulsion and Power, 2012, 28(5): 900. DOI:10.2514/1.B34299 |
| [16] |
JIANG Y T, ZHENG Q, DONG P, et al. Conjugate heat transfer analysis of leading edge and downstream mist-air film cooling on turbine vane[J]. International Journal of Heat and Mass Transfer, 2015, 90: 613. DOI:10.1016/j.ijheatmasstransfer.2015.07.005 |
| [17] |
JUNG E Y, CHUNG H, CHO S M, et al. Conjugate heat transfer on full-coverage film cooling with array jet impingements with various Biot numbers[J]. Experimental Thermal and Fluid Science, 2017, 83: 1. DOI:10.1016/j.expthermflusci.2016.12.008 |
| [18] |
ZHU W, WANG J W, YANG L, et al. Modeling and simulation of the temperature and stress field in a 3D turbine blade coated with thrmal barrier coating[J]. Surface and Coating Technology, 2017, 315: 443. DOI:10.1016/j.surfcoat.2017.03.012 |
| [19] |
JEONG J, HUSSAIN F. On the identification of a vortex[J]. Fluid Mesh, 1995, 285: 69. |
| [20] |
LU X C, JIANG P X, SUGISHIA H, et al. Conjugate heat transfer analysis of film cooling flows[J]. Journal of Thermal Sciecce, 2006, 15(1): 85. DOI:10.1007/s11630-006-0085-8 |
 2020, Vol. 52
2020, Vol. 52


