2. 北京航空航天大学 交通科学与工程学院,北京 100191
2. School of Transportation Science and Engineering, Beihang University, Beijing 100191, China
基于开口薄壁结构轻盈美观、强度较高的优点,该类结构广泛应用于城市轨道交通工程、桥梁工程及航空航天等领域中.忽略剪切变形影响的传统扭转计算理论在计算短跨开口构件或者非弹性扭转性能时总存在较大的偏差,因此剪切变形的影响在分析开口薄壁构件扭转性能时应引起足够的重视.
1910年,文献[1]首先致力于研究开口薄壁构件的约束扭转性能,并以工字钢为例进行了计算分析.文献[2-3]在前人研究成果的基础上,采用一套新的主扇性坐标系,推导了约束扭转的变形、作用力表达公式,同时利用扭矩的平衡微分方程,获得了开口薄壁结构复合扭转的弹性解,建立最经典的开口薄壁结构扭转理论,又称为Vlasov理论.随后,文献[4]对Vlasov理论进行了系统总结、拓展和完善.基于Vlasov理论,文献[5-6]发展了新的扭转理论并应用于复合材料开口截面扭转性能研究,文献[7]探究开口薄壁构件的弯扭复合受力,文献[8-9]探究曲线开口梁的扭转性能等.
Vlasov理论在推导过程中采用了中面无剪切变形的假定,其计算结果与试验结果不可避免地存在偏差.文献[10-11]表明,在开口薄壁短梁或者闭口截面薄壁梁的约束扭转中,翘曲扭矩的剪切作用的影响不能忽略.同时,文献[12-14]提出中面剪切变形对钢筋混凝土U形薄壁梁的扭转性能的影响不能忽略,尤其是混凝土开裂后的非线性扭转阶段.近年来,探究剪切变形对开口薄壁结构的扭转性能的影响已成为一大研究热点.文献[15]假定中面的剪应力沿截面长度方向的变化率为定值,通过推导获得了考虑剪切作用的开口薄壁梁扭转的近似解.文献[16]从能量的角度,利用余能驻值原理建立了考虑剪切效应的翘曲弯矩的微分方程和相容条件,针对预设的不同应力场,可得该应力场下解析解.利用翘曲扭转与梁的二次弯曲理论的相似性,文献[17-18]将考虑剪切作用的翘曲扭转类比于梁的二次弯曲理论,直接建立刚度矩阵,但是该过程缺乏严谨的理论推导.
目前,考虑中面剪切变形的扭转计算理论研究仍处于起步阶段,尚没有系统成熟的理论来解决该问题.本文以Vlasov扭转理论为基础,通过设定截面中线的剪应变γzs(γzs≠0),推导了考虑剪切作用的平衡微分方程,并利用初参数法,获得了变形及作用力关于初始参量的表达式.此外,针对U形薄壁梁的算例,将本文扭转理论的计算值与经典的Vlasov理论进行了对比.
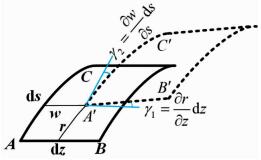
1 考虑剪切变形的开口构件扭转计算公式的推导 1.1 中面剪切变形的引入图 1给出了微元dsdz剪切变形前(实线)、后(虚线)的示意图.z为开口构件的纵向坐标轴,s为开口构件横向截面的曲线坐标轴,两者所对应的坐标分别为w和r.微元的剪切变形大小为
|
图 1 微元的剪切变形 Fig. 1 Shear deformation of an infinitesimal element |
| $ {\gamma _{zs}} = \frac{{\partial r}}{{\partial z}} + \frac{{\partial w}}{{\partial s}}. $ | (1) |
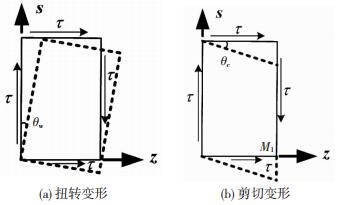
Vlasov理论做出两个基本假设:1)刚周边;2)中面无剪切变形,即γzs=0.显然,Vlasov理论只考虑了单元整体扭转所引起的转角,见图 2(a),而忽略了图 2(b)中剪切变形所引起的另一部分扭转角.
|
图 2 两类扭转角的成因 Fig. 2 Causes of two kinds of torsional rotation |
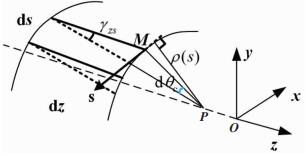
本文摒弃中面无剪切变形假定,即认为开口构件截面中线的剪切变形作用γzs≠0.假设截面中线剪切变形γzs所引起的扭转角表示为θc.图 3可知,γzs与θc之间的关系为
|
图 3 中面剪应变形所引起的扭转角 Fig. 3 Torsional rotation caused by shear deformation in middle surface |
| $ {\gamma _{zs}} = \rho (s)\frac{{{\rm{d}}{\theta _{\rm{c}}}(z)}}{{{\rm{d}}z}}, $ | (2) |
式中ρ(s)为扭转中心P到点M处切线的距离.
在纯扭矩作用下,绕扭转中心P点的总扭转角θ(z)所对应的沿s方向的切线位移r(s, z)可表达为
| $ r(s, z) = \rho (s)\theta (z). $ | (3) |
将式(2)、(3)代入式(1)可得曲线位移w的偏分:
| $ \frac{{\partial w}}{{\partial s}} = - \rho (s)[\frac{{\partial \theta (z)}}{{\partial z}} - \frac{{{\rm{d}}{\theta _{\rm{c}}}(z)}}{{{\rm{d}}z}}], $ | (4) |
假设构件的弹性模量为E,则沿构件纵向的翘曲正应力表达式为
| $ {\sigma _{\rm{M}}} = E[w_0^\prime - \theta _{\rm{w}}^{\prime \prime }(z)\Omega (s)]. $ | (5) |
式中θw″(z)=θ″(z)-θc″(z)为总扭转角除去剪切变形引起的扭转角外剩余扭转角的二阶导数,Ω(s)=∫s ρ(s)ds为扇性坐标.
扇性坐标转换为主扇性坐标,式(5)转换为
| $ {\sigma _{\rm{M}}} = - E\theta _{\rm{w}}^{\prime \prime }(z)\omega (s), $ | (6) |
式中ω(s)为截面的主扇性面积坐标.
由微元dsdz在z轴方向的应力平衡条件
| $ \frac{{\partial ({\sigma _{\rm{M}}}t)}}{{\partial z}} + \frac{{\partial ({\tau _{\rm{M}}}t)}}{{\partial s}} = 0, $ | (7) |
式中τM为翘曲剪应力,t为截面厚度.
将式(6)代入式(7)可得翘曲剪应力τM的表达式为
| $ {\tau _{\rm{M}}} = E\theta _{\rm{w}}^{\prime \prime \prime }(z){S_\omega }(s)/t, $ | (8) |
式中Sω=∫AωdA为主扇性面积静矩.
1.3 翘曲扭矩及翘曲弯矩由翘曲扭矩的定义可知
| $ {T_{\rm{M}}} = \int_A {{\tau _{\rm{M}}}} t{\rm{d}}\omega , $ | (9) |
将式(8)代入式(9)可得翘曲扭矩的另一表达方式为
| $ {T_{\rm{M}}} = - E{I_\omega }\theta _{\rm{w}}^{\prime \prime \prime }, $ | (10) |
式中Iω=∫Aω2dA为主扇性惯性矩.
联立式(8)和式(10)建立TM与τM的关系式为
| $ {\tau _{\rm{M}}} = - \frac{{{T_{\rm{M}}}}}{{{I_\omega }t}}{S_\omega }(s). $ | (11) |
同理,翘曲弯矩的计算公式为
| $ {B_{\rm{M}}} = - E{I_\omega }\theta _{\rm{w}}^{\prime \prime }(z). $ | (12) |
翘曲弯矩与翘曲正应力的关系为
| $ {\sigma _{\rm{M}}} = \frac{{{B_{\rm{M}}}}}{{{I_\omega }}}\omega (s). $ | (13) |
本文涉及3个扭转角,即总扭转角θ、剪切变形引起的扭转角θc以及整体扭转引起的扭转角θw,三者存在关系:
| $ {\theta ^\prime } = \theta _{\rm{w}}^\prime + \theta _{\rm{c}}^\prime . $ | (14) |
采用虚功原理,由外虚功等于内虚功可知
| $ {\theta _{\rm{c}}}(z) = \int_V {[ - \frac{{{S_\omega }(s)}}{{{I_\omega }t}}][ - \frac{{{T_{\rm{M}}}{S_\omega }(s)}}{{G{I_\omega }t}}]{\rm{d}}V} . $ | (15) |
式(15)等号两边同时对z求导得
| $ \theta _{\rm{c}}^\prime (z) = \frac{{{T_{\rm{M}}}}}{{G{K_{\rm{s}}}}}, $ | (16) |
式中
将式(10)代入式(16)建立θc与θw的关系式:
| $ \theta _{\rm{c}}^\prime = - \frac{{E{I_\omega }}}{{G{K_{\rm{s}}}}}\theta _{\rm{w}}^{\prime \prime \prime }. $ | (17) |
将式(17)代入式(14)可建立θ与θw的关系式:
| $ {\theta ^\prime } = \theta _{\rm{w}}^\prime - \frac{{E{I_\omega }}}{{G{K_{\rm{s}}}}}\theta _{\rm{w}}^{\prime \prime \prime }. $ | (18) |
引入式(16),扭转角协调方程式(14)可转化为
| $ {\theta ^{\prime \prime }}(z) = \frac{{T_{\rm{M}}^\prime }}{{G{K_{\rm{s}}}}} - \frac{{{B_{\rm{M}}}}}{{E{I_\omega }}}. $ | (19) |
由外扭矩T由翘曲扭矩TM和自由扭矩Tc共同抵抗可知
| $ T = {T_{\rm{M}}} + {T_{\rm{c}}}. $ | (20) |
等号两边同时对z求导,式(20)转换为
| $ T_{\rm{M}}^\prime = {T^\prime } - T_{\rm{c}}^\prime . $ | (21) |
由圣维南原理可知自由扭矩的计算公式为
| $ {T_{\rm{c}}} = (GK){\theta ^\prime }, $ | (22) |
式中GK为自由扭转刚度.
联立式(21)、(22)和式(19)建立关系式:
| $ (1 + \frac{K}{{{K_{\rm{s}}}}}){\theta ^{\prime \prime }} + \frac{{{B_{\rm{M}}}}}{{E{I_\omega }}} - \frac{{{T^\prime }(z)}}{{G{K_{\rm{s}}}}} = 0, $ | (23) |
式中:T′(z)为作用外荷载的一阶导数,对于集中扭矩作用T′(z)=0,对于均布扭矩q作用,T′(z)=-q.
等号两边同时对z求导,且考虑到TM=BM′,式(23)可进一步转化为
| $ (1 + \frac{K}{{{K_{\rm{s}}}}}){\theta ^{\prime \prime }} + \frac{{{T_{\rm{M}}}}}{{E{I_\omega }}} = 0. $ | (24) |
对式(24)再次求导,同时引入式(21)、(22),可得通过θ表达的平衡微分方程式:
| $ {\theta ^{\prime \prime \prime \prime }} - \chi _\omega ^2{\theta ^{\prime \prime }} = - \frac{\kappa }{{E{I_\omega }}}T(z), $ | (25) |
式中:χω2为自由扭转刚度与翘曲扭转刚度的比值,
为方便扭矩平衡微分方程的求解,式(25)可转换为以θw为变量的平衡微分方程:
| $ \theta _{\rm{w}}^{\prime \prime \prime \prime } - \chi _\omega ^2\theta _{\rm{w}}^{\prime \prime } = - \frac{\kappa }{{E{I_\omega }}}{T^\prime }(z). $ | (26) |
四阶平衡微分方程(26)采用初参数法求解.方程的解包括两部分:通解和特解.本文就通解的计算过程详述如下:
通解所对应的齐次方程为
| $ \theta _{\rm{w}}^{\prime \prime \prime \prime } - \chi _\omega ^2\theta _{\rm{w}}^{\prime \prime } = 0. $ | (27) |
方程(27)的解可采用双曲函数表示为
| $ {\theta _{\rm{w}}} = {C_1} + {C_2}z + {C_3}{\rm{sinh}}({\chi _\omega }z) + {C_4}{\rm{cosh}}({\chi _\omega }z), $ | (28) |
式中C1、C2、C3、C4为常系数.
联立式(10)、(12)、(18)、(20)和式(28),可得转角及各作用力:
| $ \left\{ {\begin{array}{*{20}{l}} {\theta = {C_2}z + {C_3}\kappa {\rm{sinh}}({\chi _\omega }z) + {C_4}\kappa {\rm{cosh}}({\chi _\omega }z) + {C_5}, }\\ {{\theta _{\rm{w}}} = {C_1} + {C_2}z + {C_3}{\rm{sinh}}({\chi _\omega }z) + {C_4}{\rm{cosh}}({\chi _\omega }z), }\\ {\theta _{\rm{w}}^\prime = {C_2} + {C_3}{\chi _\omega }{\rm{cosh}}({\chi _\omega }z) + {C_4}{\chi _\omega }{\rm{sinh}}({\chi _\omega }z), }\\ {{B_{\rm{M}}} = - {C_3}\kappa GK{\rm{sinh}}({\chi _\omega }z) - {C_4}\kappa GK{\rm{cosh}}({\chi _\omega }z), }\\ {T = {C_2}GK.} \end{array}} \right. $ | (29) |
该构件的初始参数,即边界约束截面处的初始力学状态参数θ0、θw0、θw0′、BM0和T0可通过构件的边界条件获得,不同边界条件所对应的参数值见表 1.将初始参数代入式(29),常系数可由式(30)算得.
| 表 1 不同边界条件所对应的初始参数 Tab. 1 Initial parameters corresponding to different boundary conditions |
| $ \left\{ {\begin{array}{*{20}{l}} {{C_1} = {\theta _{{\rm{w0}}}} + \frac{1}{{\kappa GK}}{B_{{\rm{M0}}}}, }\\ {{C_2} = \frac{1}{{GK}}{T_0}, }\\ {{C_3} = \frac{1}{{{\chi _\omega }}}\theta _{{\rm{w0}}}^\prime - \frac{1}{{{\chi _\omega }GK}}{T_0}, }\\ {{C_4} = - \frac{1}{{\kappa GK}}{B_{{\rm{M0}}}}, }\\ {{C_5} = {\theta _0} + \frac{1}{{GK}}{B_{{\rm{M0}}}}.} \end{array}} \right. $ | (30) |
将式(30)代入式(29)可知,四阶平衡微分方程的通解为:
| $ \left[ {\begin{array}{*{20}{l}} \theta \\ {{\theta _{\rm{w}}}}\\ {\theta _{\rm{w}}^\prime }\\ {{B_{\rm{M}}}}\\ T \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&{\frac{\kappa }{{{\chi _\omega }}}{\rm{sinh}}({\chi _\omega }z)}&{1 - {\rm{cosh}}({\chi _\omega }z)}&{[z - \frac{\kappa }{{{\chi _\omega }}}{\rm{sinh}}({\chi _\omega }z)]}\\ 0&1&{\frac{{{\rm{sinh}}({\chi _\omega }z)}}{{{\chi _\omega }}}}&{\frac{{1 - {\rm{cosh}}({\chi _\omega }z)}}{\kappa }}&{[z - \frac{{{\rm{sinh}}({\chi _\omega }z)}}{{{\chi _\omega }}}]}\\ 0&0&{{\rm{cosh}}({\chi _\omega }z)}&{ - \frac{{{\chi _\omega }{\rm{sinh}}({\chi _\omega }z)}}{\kappa }}&{[1 - {\rm{cosh}}({\chi _\omega }z)]}\\ 0&0&{ - {\chi _\omega }E{I_\omega }{\rm{sinh}}({\chi _\omega }z)}&{GK{\rm{cosh}}({\chi _\omega }z)}&{\frac{{\kappa GK}}{{{\chi _\omega }}}{\rm{sinh}}({\chi _\omega }z)}\\ 0&0&0&0&{GK} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\theta _0}}\\ {{\theta _{{\rm{w0}}}}}\\ {\theta _{{\rm{w0}}}^\prime }\\ {\frac{{{B_{{\rm{M0}}}}}}{{GK}}}\\ {\frac{{{T_0}}}{{GK}}} \end{array}} \right]. $ | (31) |
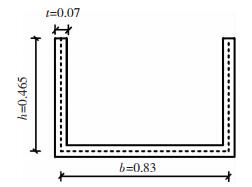
针对文献[12, 14]中U型试验梁进行算例分析.该U型梁边界条件为两端固结,跨中截面承受集中扭矩T=10 kN·m,截面几何尺寸见图 4,混凝土的弹性模量为3.607×104 MPa.梁跨度分别取为:1)l1=6.65 m;2)l2=3.325 m.分别采用本文计算方法,Vlasov理论和有限元分析计算.其中,有限元分析采用ABAQUS软件建模,混凝土采用C3D8R实体单元,单元长度0.01 m.限制端部截面的6个自由度以模拟完全固支的边界条件.梁跨中施加大小相等方向相反的集中力以模拟跨中扭矩的作用.有限元模型见图 5.
|
图 4 U型梁截面尺寸(m) Fig. 4 Dimensions of U-shaped beam (m) |

|
图 5 U型梁的有限元模型 Fig. 5 Finite element simulation model of U-shaped beam |
将本文计算方法、Vlasov理论及有限元模拟3种方法的计算结果汇总,从U型梁的扭转角及内力两个方面进行对比分析.
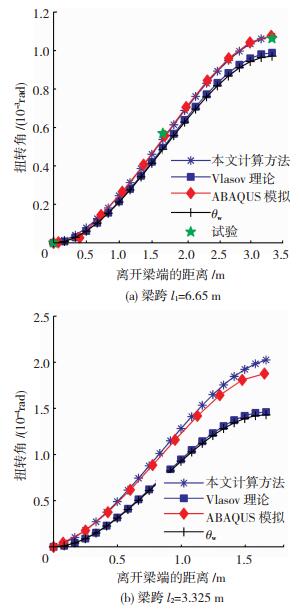
4.1 剪切变形对扭转角的影响图 6给为不同跨度(6.65 m和3.325 m)的U型梁沿梁长方向(Z向)各截面的扭转角变化曲线,包括本文计算方法、Vlasov理论、有限元模拟和试验结果得到的曲线.由图 6(a)可知,6.65 m跨U型梁不同截面扭转角的试验值和有限元模拟结果拟合良好.由表 2可知,3个不同截面的扭转角的有限元模拟结果与试验结果的误差分别为0%、1.75%和1.32%,平均误差为1.02%,说明有限元模拟结果可以可靠有效的预测U型梁的扭转性能,因此,有限元软件多参数分析结果具有科学性和可靠性.
|
图 6 集中扭矩作用下沿梁长方向扭转角变化曲线 Fig. 6 Curves of torsional rotation along longitudinal direction of U-shaped beams under concentrated torsion |
| 表 2 不同截面扭转角的试验结果与有限元模拟结果 Tab. 2 Experimental and simulation results of torsional rotation in different sections |
将本文计算方法及Vlasov理论所得到的跨中截面扭转角汇总于表 3.由图 6(a)可知,对于跨度较大(l/h=14.3)的U型梁扭转角,本文计算方法的计算结果与ABAQUS模拟结果吻合良好,最大扭转角的相对误差为0.185%;Vlasov理论的计算结果比试验值略小,但是误差仍然在可接受的范围内(相对误差为7.056%),且Vlasov理论的计算结果与θw基本一致.以上现象说明:1)对于跨度较大的U型梁,本文计算方法、Vlasov理论的计算结果与试验结果差别不大; 2)中面剪切变形所引起的扭转角θc很小(θc/θ=1.04/10.75=9.67%),可忽略其影响,可用θw近似估计总扭转角θ,两种计算理论都可适用.
| 表 3 跨中截面扭转角计算结果对比 Tab. 3 Comparison of torsional rotation in mid-span section calculated by different methods |
由图 6(b)可知,对于跨度较小(l/h=7.15)的U型梁扭转角,本文计算方法计算结果与ABAQUS模拟结果吻合良好,最大扭转角相对误差为7.889%,而此时Vlasov理论计算结果与ABAQUS模拟结果偏差很大,最大扭转角相对误差达到27.85%.同样的,Vlasov理论计算结果与θw基本一致.以上现象说明,当U型梁跨度减小时,中面剪切变形所引起的扭转角占总扭转角的比例不断增大(θc/θ=0.594/2.03=29.26%),此时如果忽略该影响,而采用Vlasov理论计算只考虑扭转角的部分值θw,极大低估了扭转角数值,使构件的使用及承载功能存在巨大的安全隐患.本文计算方法在θw基础上,考虑剪切变形影响所引起的另一部分扭转角θc,能够很好的预测短跨U型梁的扭转性能.
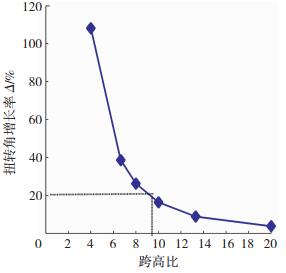
为更直观表现剪切变形对不同跨度U型梁扭转变形性能的影响,对跨度分别为2、3.325、4、5、6.65和10 m(所对应的跨高比l/h分别为4、6.65、8、10、13.3和20)的U型梁分别进行计算分析.Vlasov扭转理论计算所得跨中截面扭转角为θVlasov,利用本文计算方法得到的跨中截面扭转角为θshear,定义参数Δ为跨中截面扭转角的增长率,表达为
|
图 7 跨中截面扭转角增长率随跨高比的变化曲线 Fig. 7 Variation of increasing rate of torsional rotation in mid-span section with span-height ratio |
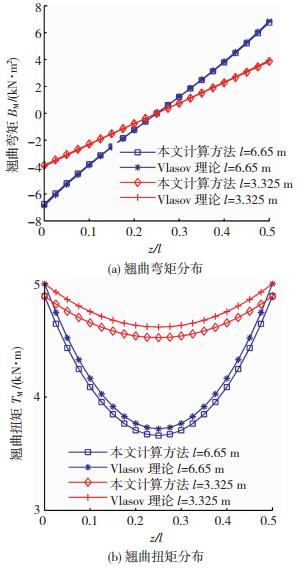
分别采用本文计算方法和Vlasov理论对本例中U型梁的内力作用(翘曲弯矩和翘曲扭矩作用)进行了计算和对比分析,计算结果见图 8.同时,特征截面,即跨中截面和l/4截面的翘曲弯矩、翘曲扭矩和自由扭矩的计算值汇总于表 4.
|
图 8 两种理论对翘曲弯矩和翘曲扭矩的计算曲线 Fig. 8 Calculated results of warping moment and warping torsion by two methods |
| 表 4 跨中及l/4截面翘曲弯矩及翘曲扭矩的计算值对比 Tab. 4 Comparison between calculated results of warping moment and warping torsion in mid-span and l/4 sections by two methods |
由图 8(a)可知,不论是U型长梁(l=6.65 m)还是U型短梁(l=3.325 m),两种理论的计算结果曲线几乎完全重合;表 4给出的两种理论对跨度为6.65、3.325和2 m的U型梁的翘曲弯矩的计算值差异率分别为-1.83%、-2.08%和-2.08%.以上现象说明,不管是长跨还是短跨的U型梁,剪切变形对翘曲弯矩值的计算影响较小,本文提出的计算方法和Vlasov理论都可应用于翘曲弯矩的计算.
同样地,本文计算方法和Vlasov理论应用于长跨和短跨U型梁所获得的翘曲扭矩的计算曲线(见图 8(b))基本一致,且两种理论对翘曲扭矩的计算值的最大差异率为2.18%,平均差异率为2.04%.说明剪切变形对翘曲扭矩的计算影响很小,可忽略不计,因此,本文提出的计算方法和Vlasov理论都可应用于翘曲扭矩的计算.
5 结论本文考虑了中面剪切变形的影响,推导并提出适用于开口薄壁弹性构件的扭转性能计算方法,并针对一根U型薄壁梁的扭转试验,将本文计算方法的结果、Vlasov理论计算结果、试验及有限元模拟结果进行对比分析,得到如下结论:
1) 本文提出的考虑剪切变形影响的扭转计算方法,与试验及有限元模拟结果吻合良好,不仅适用于大跨高比的开口薄壁构件的扭转计算(误差为1.115%),还适用于小跨高比的开口薄壁结构的扭转分析(误差为7.889%).
2) Vlasov理论未考虑中面剪切变形的影响,当用于计算大跨高比的开口薄壁构件(本文算例要求l/h > 10)的扭转性能时准确度尚可;但当应用于跨高比较小的构件(本文算例中U型梁l/h < 6)时,严重低估截面的扭转角,无法准确计算构件的扭转效应.
3) 剪切变形能够影响开口构件的扭转变形性能,影响程度的大小取决于构件的跨高比、边界条件;考虑剪切变形对开口构件的翘曲弯矩和翘曲扭矩分布影响较小,翘曲弯矩和翘曲扭矩计算值的平均差异率分别为1.997%和2.044%;但是,对自由扭矩分布影响较大,随跨高比不断减小(l/h=13.3~4),自由扭矩计算值差异率从4.61%增大到71.53%.
4) 本文计算方法克服了Vlasov经典理论中中面无剪切变形假定的局限,能更准确地预测小跨高比U型梁的扭转变形,更好地满足工程设计需求.
| [1] |
TIMOSHENKO S P. Theory of bending, torsion and buckling of thin-walled members of open cross section[J]. Journal of the Franklin Institute, 1945, 239(4): 249. DOI:10.1016/0016-0032(45)90161-X |
| [2] |
VLASOV V. Thin-walled elastic beams[M]. Moscow: National Technical Information Service, 1984: 1.
|
| [3] |
包世华, 周坚. 薄壁杆件结构力学[M]. 北京: 中国建筑工业出版社, 1991: 38. BAO Shihua, ZHOU Jian. Structural mechanics of thin-walled bars[M]. Beijing: China Architecture & Building Press, 1991: 38. |
| [4] |
KOLLBRUNNER C F, BASLER K. Torsion in structures: an engineering approach[M]. Berlin: Springer Science & Business Media, 2013: 158.
|
| [5] |
SAPOUNTZAKIS E, MOKOS V. 3-D beam element of variable composite cross section including warping effect[J]. Acta Mechanica, 2004, 171(3): 151. DOI:10.1007/s00707-004-0148-4 |
| [6] |
陈卓异, 李传习, 黄侨, 等. 波形钢腹板组合槽形梁抗扭性能试验研究[J]. 工程力学, 2017, 34(3): 113. CHEN Zhuoyi, LI Chuanxi, HUANG Qiao, et al. Experimental study on tortional property of composite trough girder with corrugated steel webs[J]. Engineering Mechanics, 2017, 34(3): 113. DOI:10.6052/j.issn.1000-4750.2015.08.0706 |
| [7] |
BACK S Y, WILL K M. A shear-flexible element with warping for thin-walled open beams[J]. International Journal for Numerical Methods in Engineering, 1998, 43(7): 1173. DOI:10.1002/(SICI)1097-0207(19981215)43:7<1173::AID-NME340>3.0.CO;2-4 |
| [8] |
FU C C, HSU Y T. The development of an improved curvilinear thin-walled Vlasov element[J]. Computers & Structures, 1995, 54(1): 147. DOI:10.1016/0045-7949(94)P4141-Y |
| [9] |
甘亚南, 荀勇, 周广春. 考虑自平衡条件槽形曲梁的静力学特性分析[J]. 工程力学, 2013, 30(10): 28. GAN Yanan, XUN Yong, ZHOU Guangchun. Analysis of static characteristics of thin-walled cured U-shaped beams considering self-equilibrium[J]. Engineering Mechanics, 2013, 30(10): 28. |
| [10] |
LAUDIERO F, SAVOIA M. Shear strain effects in flexure and torsion of thin-walled beams with open or closed cross-section[J]. Thin-Walled Structures, 1990, 10(2): 87. DOI:10.1016/0263-8231(90)90058-7 |
| [11] |
WANG Zhaoqiang, ZHAO Juncheng, ZHANG Daxu, et al. Restrained torsion of open thin-walled beams including shear deformation effects[J]. Journal of Zhejiang University SCIENCE A, 2012, 13(4): 260. DOI:10.1631/jzus.A1100149 |
| [12] |
CHEN Shenggang, DIAO Bo, GUO Quanquan, et al. Experiments and calculation of U-shaped thin-walled RC members under pure torsion[J]. Engineering Structures, 2016, 106: 1. DOI:10.1016/j.engstruct.2015.10.019 |
| [13] |
CHEN Shenggang, YE Yinghua, GUO Quanquan, et al. Nonlinear model to predict the torsional response of U-shaped thin-walled RC members[J]. Structural Engineering and Mechanics, 2016, 60(6): 1039. DOI:10.12989/sem.2016.60.6.1039 |
| [14] |
陈圣刚, 许见超, 郭全全, 等. 混凝土U形薄壁梁纯扭及弯扭承载力计算[J]. 建筑结构学报, 2017, 38(2): 99. CHEN Shenggang, XU Jianchao, GUO Quanquan, et al. Ultimate bearing capacity of U-shaped thin-walled RC beams under pure torsion and bending-torsion interaction[J]. Jornal of Building Structures, 2017, 38(2): 99. |
| [15] |
PAVAZZA R. Torsion of thin-walled beams of open cross-section with influence of shear[J]. International Journal of Mechanical Sciences, 2005, 47(7): 1099. DOI:10.1016/j.ijmecsci.2005.02.007 |
| [16] |
ERKMEN R E, MOHAREB M. Torsion analysis of thin-walled beams including shear deformation effects[J]. Thin-Walled Structures, 2006, 44(10): 1096. DOI:10.1016/j.tws.2006.10.012 |
| [17] |
AMINBAGHAI M, MURIN J, HRABOVSKY J, et al. Torsional warping eigenmodes including the effect of the secondary torsion moment on the deformations[J]. Engineering Structures, 2016, 106: 299. DOI:10.1016/j.engstruct.2015.10.022 |
| [18] |
MUR N J, KUTIŠ V. An effective finite element for torsion of constant cross-sections including warping with secondary torsion moment deformation effect[J]. Engineering Structures, 2008, 30(10): 2716. DOI:10.1016/j.engstruct.2008.03.004 |
 2020, Vol. 52
2020, Vol. 52


