悬索桥是当今大跨度桥梁中跨越能力最大的桥型,其加劲梁可以采用钢箱梁和钢桁架梁.钢桁架梁具有整体刚度大、抗风性能好、空间高度大、方便布置双层交通等优点,是悬索桥中常用的加劲梁形式,例如,在主跨1 991 m的日本明石海峡大桥、主跨1 377 m的香港青马大桥、主跨1 280 m的美国金门大桥均能看到钢桁架加劲梁的身影.钢桁架加劲梁的等效是工程中经常遇到的问题.一方面,大跨度悬索桥桁架加劲梁中杆件众多,上下桥面混凝土或加劲钢板的铺层常作为受力结构,U型肋、I型肋等细节众多,采用有限元模拟存在大量的单元节点,计算量巨大,计算结果冗杂(如全桥模态中出现大量加劲梁局部振型),不利于设计优化的进行.单主梁或双主梁鱼骨模型在悬索桥分析中形式简洁、高效,被广泛使用,桁架加劲梁简化为单主梁则需要等效.另一方面,悬索桥全桥气弹模型试验抗风性能研究中加劲梁的刚度和质量采用芯梁来模拟,芯梁可为等截面钢材或铝材制成,可视为经典的欧拉梁,芯梁截面尺寸依据等效计算的截面抗弯刚度和抗扭刚度参数.
悬索桥中,全桥的竖向刚度主要由主缆提供,加劲梁起着支撑桥面系, 传递车辆及人行荷载的作用,对于竖向刚度的贡献较小.悬索桥施工中首先架设主缆,加劲梁逐节拼装,这样的施工过程也决定了悬索桥的加劲梁承受较小的弯矩,即使为构件较多的桁架梁,加劲梁变形时也可近似假设满足平截面假定,采用等截面欧拉梁对其进行模拟是合理的.
钢桁架加劲梁等效为欧拉梁中刚度等效分为抗弯刚度和抗扭刚度,抗弯刚度分竖弯方向和侧弯方向,不过两方向抗弯刚度计算方法相同.基于悬臂梁的静力位移相等原则被广泛使用[1-3],此处称为悬臂静力法.悬臂静力法选取部分长度桁架加劲梁建模,一端施加固结约束,另一端则是自由的,且施加集中荷载(计算抗弯刚度加集中力,抗扭刚度加集中扭矩),通过有限元程序计算等到位移响应.对比悬臂梁在自由端集中荷载作用下位移响应计算公式,反算出等效梁抗弯惯性矩和扭转惯性矩.悬臂静力法形式简单,边界条件施加方便,被多数桁架梁等效建模所采用.但是,其计算方法上存在以下不足:1)在计算扭转刚度时,需要施加一个扭矩,不太方便于有限元计算;2)扭转作用下扭转角的计算需要确定合理的扭心,这需要细心选择[4];3)在悬臂端加载点附近存在较大的局部变形,在许多算例中均采用加补偿段和多点挠度拟合的方式来消除局部变形的影响[4];4)计算结果只有等效刚度参数,没有等效梁的质量参数,无法直接用于悬索桥的动力响应分析,质量参数还需通过其他途径获得.
除了悬臂静力法,文献[5-6]提出基于能量相等原则的等效方法,推导了板桁结合型加劲梁主桁架腹杆和下平联的连续化等效板厚计算公式,根据板桁结合型加劲梁的弯曲与扭转受力特点分别构造了相应的连续化等效截面, 该方法计算较为复杂.
桁架加劲梁质量等效包括等效质量和等效质量惯性矩.等效质量通过求和自重作用下的支座反力便可计算得到,求解比较简单.等效质量惯性矩若按质量惯性矩定义直接对截面杆件和板进行积分计算过程繁琐,且不同截面质心位置存在变化,增加了计算难度,在文献[7-8]中给出一种基于均匀附加扭转质量惯性矩前后结构扭转频率的变化计算钢桁梁扭转质量惯性矩的方法,并基于有限元离散后的代数控制方程给出了理论解释,该方法简单有效.
针对静力悬臂法中的不足之处,本文首先给出欧拉梁在悬臂和两端固结两种约束条件下,基于连续偏微分控制方程得到的自振频率计算公式;然后,利用该公式直接得到等效抗弯、抗扭参数计算表达式,并对文献[7-8]中等效质量惯性矩计算方法给出更直接的理论解释,同时利用该方法计算等效质量惯性矩; 然后,针对某桁架加劲梁悬索桥,对比了本文方法与悬臂静力法的计算结果; 最后将本方法应用于不同长度的桁架加劲梁等效,分析了在原理上采用欧拉梁等效桁架加劲梁存在的问题.
1 等截面欧拉梁基频桁架加劲梁精细化建模中施加等效的等截面梁的铰接边界条件比较困难,而固结和自由边界则比较容易,因此本文对两端固结以及悬臂式等截面欧拉梁动力特性进行理论分析.等截面梁欧拉梁与相应等效桁架加劲梁如图 1所示,在具有同样的动力特性情况下,等截面梁具有以下参数:面积A(此处只用于计算质量,不考虑轴向刚度),截面竖向抗弯惯性矩Izz, 截面侧向抗弯惯性矩Iw, 截面抗扭惯性矩It,截面扭转质量惯性矩Ix,密度ρ,长度L.

|
图 1 等截面梁欧拉梁与相应等效桁架加劲梁示意图 Fig. 1 Schematic diagram of uniform section Euler beam and corresponding equivalent truss girder |
忽略梁的轴向变形,无限自由度欧拉梁竖向自由振动时控制方程[8]为
| $ \rho A\frac{{{\partial ^2}w(x,t)}}{{\partial {t^2}}} + EI\frac{{{\partial ^4}w(x,t)}}{{\partial {x^4}}} = 0. $ | (1) |
式中:E为材料弹性模量,ρ为材料密度.
模态分析中考虑w为简谐振动,可以利用分离变量法分解为只与时间有关项和只与坐标有关项的乘积,即
| $ w(x,t) = \phi (x)Y(t). $ | (2) |
式中:ϕ(x)为振型,Y(t)可假设为简谐振动Y(t)=sin ωt,其中ω即为自振圆频率.
将式(2)代入式(1),可以得到
| $ {\phi ^{\prime \prime \prime }}(x) - \frac{{{\omega ^2}\rho A}}{{EI}}\phi (x) = 0. $ | (3) |
ϕ(x)的通解为
| $ \phi (x) = {A_1}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ax + {A_2}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ax + {A_3}{\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ax + {A_4}{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ax, $ | (4) |
其中$a^{4}=\frac{\omega^{2} \rho A}{E I}$.
梁两端固结时,即
| $ \begin{array}{l} \phi (0) = 0,{\phi ^\prime }(0) = 0,\phi (L) = 0,{\phi ^\prime }(L) = 0,\\ \left[ {\begin{array}{*{20}{c}} 1&0&1&0\\ 0&a&0&a\\ {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} aL}&{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} aL}&{{\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} aL}&{{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} aL}\\ { - a{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} aL}&{a{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} aL}&{a{\rm{sinh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} aL}&{a{\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} aL} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{A_1}}\\ {{A_2}}\\ {{A_3}}\\ {{A_4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 0 \end{array}} \right]. \end{array} $ | (5) |
为了使得关于Ai(i=1, 2, 3, 4)的方程存在非0解,系数矩阵的行列式为0,即得
| $ 2{a^2}(1 - {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} aL \cdot {\rm{cosh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} aL) = 0. $ | (6) |
对此特征值问题,求解非线性方程根可以得到a1L=4.730 1,由此得到单一截面梁的两端固结弯曲基频为
| $ {f_{\rm{b}}} = \frac{\omega }{{2\pi }} = 3.561\sqrt {\frac{{EI}}{{\rho A{L^4}}}} . $ | (7) |
对于悬臂梁,一端固结、一端自由的方式,边界条件为ϕ(0)=0,ϕ′(0)=0,ϕ"'(L)=0,ϕ″″(L)=0,具体频率和振型推导过程在文献[8]中有详细介绍,此处只呈现结果:
| $ {f_{\rm{b}}} = \frac{\omega }{{2\pi }} = 0.559{\kern 1pt} {\kern 1pt} {\kern 1pt} 5\sqrt {\frac{{EI}}{{\rho A{L^4}}}} . $ | (8) |
式(7)、(8)分别适用于竖弯和侧弯频率等效,其中竖弯时I=Izz, 侧弯时I=Iyy.
1.2 扭转振型基频无限自由度梁扭转位移θ振动控制方程[9]为
| $ {I_x}\frac{{{\partial ^2}\theta (x,t)}}{{\partial {t^2}}} = G{I_{\rm{t}}}\frac{{{\partial ^2}\theta (x,t)}}{{\partial {x^2}}}. $ | (9) |
式中:G为剪切模量,各项同性材料中取G=$\frac{E}{2(1+\nu)}$;ν为泊松比;It为抗扭惯性矩;Ix为扭转质量惯性矩,圆形截面等简单截面可取为ρ(Iyy+Izz),桁架加劲梁中需采用另外方法计算.
同样假设自由振动时θ可以利用分离变量法分解为只与时间有关项和只与坐标有关项的乘积,即
| $ \theta (x,t) = \phi (x)Y(t). $ | (10) |
式中:ϕ(x)为振型;Y(t)假设为简谐振动Y(t)=sin ωt,其中ω为自振圆频率.
将式(10)代入式(9)可得
| $ {\phi ^{\prime \prime }}(x) + \frac{{{I_x}{\omega ^2}}}{{G{I_{\rm{t}}}}}\phi (x) = 0. $ | (11) |
ϕ(x)的通解为
| $ \phi (x) = {A_1}{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta x + {A_2}{\rm{sin}}{\kern 1pt} {\kern 1pt} \beta x. $ | (12) |
式中β2=$\frac{\omega^{2} I_{x}}{G I_{\mathrm{t}}}$.两端固结情况对应φ(0)=0, φ(L)=0, 即
| $ \left[ {\begin{array}{*{20}{c}} 1&0\\ {{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta L}&{{\rm{sin}}{\kern 1pt} {\kern 1pt} \beta L} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{A_1}}\\ {{A_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} 0\\ 0 \end{array}} \right]. $ | (13) |
要使得A1, A2存在非0解,即sin βL=0.易得β1L=π, 由此得到单一截面梁两端固结扭转基频为
| $ {f_{\rm{t}}} = 0.5\sqrt {\frac{{G{I_{\rm{t}}}}}{{{I_x}{L^2}}}} . $ | (14) |
对于悬臂梁,一端固结一端自由的方式,边界条件为扭转边界为ϕ(0)=0, ϕ′(L)=0, 即
| $ \left[ {\begin{array}{*{20}{c}} 1&0\\ { - {\rm{sin}}{\kern 1pt} {\kern 1pt} \beta L}&{{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta L} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{A_1}}\\ {{A_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} 0\\ 0 \end{array}} \right]. $ | (15) |
得到cos βL=0,则有β1L=$\frac{\pi}{2}$.由此特征值可得一端固结一端自由梁扭转频率为
| $ {f_{\rm{t}}} = 0.25\sqrt {\frac{{G{I_{\rm{t}}}}}{{{I_x}{L^2}}}} . $ | (16) |
扭转和弯曲基频与扭转和弯曲刚度及质量的关系见表 1.
| 表 1 等截面欧拉梁动力特性公式汇总 Tab. 1 Formulas for dynamic characteristics of uniform section Euler beam |
从表 1可以看出,扭转频率对两端固结或悬臂情况均有ft反比于$\sqrt{I_{x}}$, 设系数为k, 若给扭转质量惯性矩一个增量ΔI时,有
| $ \left\{ {\begin{array}{*{20}{l}} {{f_{{\rm{t1}}}} = k\sqrt {\frac{1}{{{I_x}}}} ,}\\ {{f_{{\rm{t2}}}} = k\sqrt {\frac{1}{{{I_x} + \Delta I}}} .} \end{array}} \right. $ | (17) |
由式(17)可得
| $ {I_x} = \Delta I\frac{{f_{t2}^2}}{{f_{t1}^2 - f_{t2}^2}}, $ | (18) |
此结果与文献[8]结果相一致.
2 等效计算方法根据上述推导的单截面欧拉梁频率和刚度表达,提出等效计算方法如下.桁架加劲梁每延米质量通过计算自重下支座反力或者设计给定,作为输入参数m和密度ρ一起给定,用于计算等效欧拉梁的截面积.在桁架加劲梁等效为等截面欧拉梁计算中,首先,选取某长度桁架精细化模型进行动力特性分析,动力特性分析分两次,第二次相比于第一次,给桁架加劲梁增加扭转质量惯性矩一个增量ΔI.通过动力特性分析,可得到以下4个参数:fbv,原桁架加劲梁精细化模型一阶竖弯频率;fbl,原桁架加劲梁精细化模型一阶侧弯频率;ft1,原桁架加劲梁精细化模型一阶扭转频率;ft2,增加扭转质量惯性矩之后桁架加劲梁精细化模型一阶扭转频率.其中,精细化桁架加劲梁可选择两端固结或者悬臂式约束方式.等效等截面欧拉梁方法以这4个参数作为输入,代入表 2对应公式即可得到等效质量和刚度参数.
| 表 2 桁架加劲梁等效等截面欧拉梁截面计算公式 Tab. 2 Formulas for equivalent uniform section Euler beam of truss girder |
表 1结果为本文等效方法的基础,尤以其中两端固结梁结果较少见于文献,为验证理论分析得到的单截面欧拉梁频率和截面特性的公式关系,采用有限元手段和理论公式,给以相同的截面特性输入,对比两者结果.本文选取L=20 m,E=1.0×108 Pa, ρ=1.0×103 kg/m3两端固结不同截面(宽为3 m,高从0.1 m变化到2.9 m的矩形截面)的梁段,有限元模拟采用通用有限元软件ANSYS中beam4单元进行计算,截面特性和有限元计算得到的基频结果列于表 3,有限元与理论公式计算得到频率结果对比如图 2所示,从图 2可以看出式(7)和式(14)与ANSYS计算结果符合很好.
| 表 3 不同截面两端固结梁有限元截面输入参数和对应竖向及扭转频率计算结果 Tab. 3 Calculation results of input section parameters for finite element method of two-end fixed beam with different sections and corresponding vertical and rotational frequencies |

|
图 2 不同截面参数有限元和理论计算频率结果对比 Fig. 2 Comparison of frequency results between finite element method and analytical method with different cross sections |
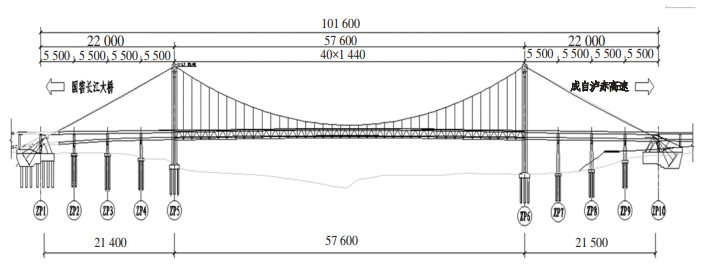
桁架加劲梁等效欧拉梁的主要工作量在于建立一段(无需整跨)精细化的加劲梁有限元模型,计算得到各模态的自振频率,以及添加附加扭转质量惯性矩后的扭转振动基频.本算例中等效对象为某主跨576 m悬索桥的板桁加劲梁,全桥立面图如图 3所示.该加劲梁为正交异性钢桥面与钢桁梁结合的板桁结合形式,全宽30.1 m,双片主桁为华伦式,并带有斜杆, 节间长度14.4 m.加劲梁断面如图 4所示.以此加劲梁节间桁架形式进行扩展,采用通用有限元软件ANSYS进行建模,上下桥面采用SHELL63单元,并准确模拟出U型肋与I型肋,桁架杆件采用BEAM188单元模拟,分别建立长度为144、288、432、576 m跨径的板桁结合梁精细化有限元模型.以288 m跨径为例,有限元模型如图 5所示.
|
图 3 某板桁结合梁主跨576 m悬索桥立面图(cm) Fig. 3 Elevation of a plate-truss girder suspension bridge with main span of 576 m (cm) |

|
图 4 板桁结合梁横断面(mm) Fig. 4 Cross section of the plate-truss girder (mm) |

|
图 5 精细化板桁结合梁288 m跨径有限元模型 Fig. 5 Finite element model for delicate plate-truss girder with span of 288 m |
针对这4种跨径精细化板桁结合梁,共计算20个工况:1)4种跨径在悬臂式边界条件下计算动力特性工况4个;2)4种跨径在悬臂式边界条件,同时在桁架的节点上施加共5.0×105 kg·m2/m的附加扭转质量惯性矩,计算动力特性工况4个;3)4种跨径在悬臂式边界条件下,在自由端施加共105 N的集中竖向荷载,计算静力响应工况4个;4)4种跨径在悬臂式边界条件下,在自由端施加共105 N的集中侧向荷载,计算静力响应工况4个;5)4种跨径在两端固结边界条件下,计算动力特性工况4个.
其中工况组1)和工况组2)分别对应的4组工况可用于求解等效扭转惯性矩,等效质量直接通过模型参数得到,计算结果见表 4.在获取等效质量和等效惯性矩之后,由工况组1)和工况组5)中的8个工况,根据表 2中对应公式可以计算得到等效竖弯、侧弯抗弯惯性矩及抗扭惯性矩,计算结果见表 5、6.以288 m跨径为例,其两端固结和悬臂式边界下一阶竖弯、侧弯、扭转振型如图 6、7所示.
| 表 4 质量及质量惯性矩等效结果 Tab. 4 Results of equivalent mass and mass moment of inertia |
| 表 5 不同长度板桁结合梁精细化模型悬臂式动力特性及等效结果汇总 Tab. 5 Dynamic characteristics and results of equivalent beam for delicate cantilever plate-truss girder of different lengths |
| 表 6 不同长度板桁结合梁精细化模型两端固结动力特性及等效结果汇总 Tab. 6 Dynamic characteristics and results of equivalent beam for delicate two-end fixed plate-truss girder of different lengths |

|
图 6 288 m跨径悬臂式约束条件振型 Fig. 6 Mode shapes of cantilever truss girder with span of 288 m |

|
图 7 288 m跨径两端固结约束条件振型 Fig. 7 Mode shapes of two-end fixed truss girder with span of 288 m |
另外,针对工况组3)和工况组4)中的8个工况,本文采用悬臂静力法计算其等效竖弯和侧弯抗弯刚度.悬臂静力法[3]利用了悬臂梁在端部集中荷载P作用下的挠度曲线:
| $ d(x) = \frac{{P{x^2}(3L - x)}}{{6EI}}. $ | (19) |
具体实施步骤:1)在精细化建模的桁架加劲梁有限元模型中,施加端部力P;2)获取多个断面x处的竖向或侧向挠度d(x);3)根据x, d(x)拟合得到式(19)中的I值.
其计算结果见表 7,该表结果可与本文基于动力特性等效抗弯刚度进行对比. 图 8给出288 m跨径施加竖向集中荷载工况中,拟合Izz参数得到的拟合位移曲线与有限元计算不同截面处挠度对比示意图,可以看出该工况下等效效果较好.
| 表 7 悬臂静力法计算结果汇总 Tab. 7 Calculation results of static cantilever method |

|
图 8 288 m悬臂桁架加劲梁有限元静力计算挠度值及式(19)的拟合挠度曲线 Fig. 8 Deflection results of finite element method and fitting curve of Eq. (19) for cantilever truss girder with span of 288 m |
等效竖向及侧向抗弯刚度结果悬臂静力法与本文中基于悬臂式边界动力特性方法(此处称为悬臂动力法)结果对比见表 8,从表中可见悬臂动力法和悬臂静力法可提供相同精度的等效抗弯惯性矩的计算结果,而且计算更加方便.
| 表 8 悬臂静力法与悬臂动力法等效抗弯刚度对比 Tab. 8 Comparison of equivalent bending stiffness between static and dynamic cantilever methods |
从表 5、6计算结果可以看出随着跨径L的增加,Iyy和Izz都呈现单调上升并趋向“稳定”的现象.另外在同样的跨径下两端固结与悬臂式边界下Iyy和Izz计算公式不同且达到“稳定”的速度不同,后者能更快达到稳定状态.相比Iyy和Izz,It的计算结果则要稳定得多.另从式(7)、(8)可以看出等截面欧拉梁理论弯曲的频率反比于长度平方,而表 5、6可以看出精细化桁架加劲梁有限元模拟结果中竖弯和侧弯频率并不遵从反比于长度平方的关系.
本文认为这是因为桁架加劲梁中存在着剪切效应,纯弯曲的欧拉梁无法捕捉剪切效应,从而导致了上述现象.这是欧拉梁此处等效在本质上的缺陷.下面针对剪切效应在静力位移反算抗弯刚度方法中的影响进行定性分析.
悬臂梁中,当在自由端施加一个集中荷载P,如果只考虑弯曲的影响,自由端部的挠度为
| $ {d_{{\rm{ bend }}}} = \frac{{P{L^3}}}{{3EI}}. $ | (20) |
而如果只考虑剪切作用,在自由端部的挠度为
| $ {d_{{\rm{ shear }}}} = \frac{{\kappa PL}}{{GA}}. $ | (21) |
其中κ为剪应力沿截面分布不均匀而引起的与截面形状有关的系数[10].可得悬臂梁在集中力作用下弯和剪对自由端竖向挠度的贡献比值为
| $ {r_{{\rm{ cantilever }}}} = \frac{{{d_{{\rm{ shear }}}}}}{{{d_{{\rm{ bend }}}}}} = \frac{{3\kappa EI}}{{GA}} \cdot \frac{1}{{{L^2}}}. $ | (22) |
从式(22)中可以看出,随着L增大,剪的作用在自由端竖向挠度占比变小,采用位移反算抗弯刚度就会出现达到“稳定状态”的现象.
同样,可以分析两端固结梁在跨中作用一个集中力P时的跨中挠度响应.当只考虑弯的效应时,跨中挠度响应为
| $ {d_{{\rm{ bend }}}} = \frac{{P{L^3}}}{{192EI}}; $ | (23) |
当只考虑剪效应时,跨中挠度响应为
| $ {d_{{\rm{ shear }}}} = \frac{{\kappa PL}}{{4GA}}. $ | (24) |
由此可得两端固结梁在集中力作用下,弯和剪对跨中挠度的贡献比为
| $ {r_{{\rm{ twoFixed }}}} = \frac{{{d_{{\rm{ shear }}}}}}{{{d_{{\rm{ bend }}}}}} = \frac{{48\kappa EI}}{{GA}}\frac{1}{{{L^2}}}. $ | (25) |
对比式(22)、(25)可以看出在不同的约束条件下,弯与剪对挠度的贡献程度占比是不一样的.换言之,如果用两端固结梁跨中挠度反算等效抗弯刚度比用悬臂梁自由端挠度反算等效抗弯刚度,需要更长的桁架梁段才能达到稳定.
5 结论1) 提出了一种基于结构动力特性的桁架梁等效成等截面欧拉梁的等效质量惯性矩、等效抗弯惯性矩、等效抗扭惯性矩计算方法,介绍了两端固结和悬臂式边界桁架梁动力特性反算等效欧拉梁两类公式.
2) 该计算方法具有的优势:在计算等效抗弯刚度上,悬臂动力方法具有与基于悬臂静力位移等效刚度方法等同的计算精度,但计算上更方便;能同时提供等效质量,质量惯性矩等静力方法无法提供的信息.
3) 仿真分析结果表明:将桁架梁等效为等截面欧拉梁的理论可对现有基于悬臂动力法计算等效惯性矩方法给出简单明了的新解释;等效抗弯惯性矩与选择的桁架梁长度和边界约束条件有关,在悬索桥中的桁架加劲梁比较满足欧拉梁的纯弯曲假设情况,应选择较长和悬臂式的的精细化桁架加劲梁来进行等效,因为同样的约束条件下,桁架加劲梁越长,剪切效应越小,而当长度一定时,悬臂桁架加劲梁中的剪切效应较两端固结桁架加劲梁小.
| [1] |
胡峰强, 陈艾荣. 桁架悬索桥全桥气弹模型设计方法研究[J]. 公路, 2009(4): 124. HU Fengqiang, CHEN Airong. A study on design method of full bridge aeroelastic model of suspension bridge with truss[J]. Highway, 2009(4): 124. |
| [2] |
吴新元, 马如进, 陈艾荣, 等. 加劲桁架悬索桥的主梁挠曲扭转刚度分析[J]. 上海公路, 2005(4): 27. WU Xinyuan, MA Rujin, CHEN Airong, et al. Bending and torsional stiffness analysis on main girder of suspension bridge with stiffend truss[J]. Shanghai Highways, 2005(4): 27. DOI:10.3969/j.issn.1007-0109.2005.04.008 |
| [3] |
李春光, 陈政清, 张志田. 大跨度桁式加劲梁悬索桥气弹模型等效设计[J]. 振动与冲击, 2009, 28(9): 171. LI Chunguang, CHEN Zhengqing, ZHANG Zhitian. Equivalent design of aeroelastic model for a long-span suspension bridge with truss stiffening girder[J]. Journal of Vibration and Shock, 2009, 28(9): 171. DOI:10.3969/j.issn.1000-3835.2009.09.037 |
| [4] |
滕小竹.大跨度钢桁梁悬索桥关键问题研究[D].上海: 同济大学, 2008 TENG Xiaozhu. Study of key questions on long-span steel truss suspension bridge[D]. Shanghai: Tongji University, 2008 |
| [5] |
周绪红, 秦凤江, 狄谨, 等. 基于能量原理的板桁结合型加劲梁连续化分析方法[J]. 中国公路学报, 2014, 27(6): 34. ZHOU Xuhong, QIN Fengjiang, DI Jin, et al. Continuous analysis method for deck-truss composite stiffening girder based on energy principle[J]. China Journal of Highway and Transport, 2014, 27(6): 34. |
| [6] |
秦凤江.板桁结合型加劲梁受力机理与计算理论研究[D].西安: 长安大学, 2015 QIN Fengjiang. The research for the stress mechanism and the calculating theory of deck-truss composite stiffening girder[D]. Xi'an: Chang'an University, 2015 |
| [7] |
于永帅.钢桁架悬索桥抖振响应及其影响参数分析[D].长沙: 湖南大学, 2011 YU Yongshuai. Parametric analysis of buffeting response of steel truss suspension bridge[D]. Changsha: Hunan University, 2011 |
| [8] |
华旭刚, 杨坤, 温青, 等. 悬索桥钢桁梁断面质量惯性矩简化计算方法[J]. 湖南大学学报(自然科学版), 2017, 44(3): 1. HUA Xugang, YANG Kun, WEN Qing, et al. A simplified method for calculating mass moment of inertia of stiffening truss in suspension bridges[J]. Journal of Hunan University (Natural Sciences), 2017, 44(3): 1. DOI:10.16339/j.cnki.hdxbzkb.2017.03.001 |
| [9] |
克拉夫RW. 结构动力学[M]. 北京: 高等教育出版社, 1981. CLOUGH R W. Structural dynamics[M]. Beijing: Higher Education Press, 1981. |
| [10] |
朱慈勉, 张伟平. 结构力学(上册)[M]. 北京: 高等教育出版社, 2004. ZHU Cimian, ZHANG Weiping. Structural mechanics (volume one)[M]. Beijing: Higher Education Press, 2004. |
 2020, Vol. 52
2020, Vol. 52


