在城市信号自组织控制系统中,对于路口独立完成信号配时的自组织控制模型,各路口的配时方案都趋向于实现通行能力的最大化,从而造成相邻路口间通行效率冲突的问题.相邻路口间路网结构越复杂,效率冲突问题越明显.因此,需要对各路口的自组织控制规则参数进行动态整定,降低各路口通行效率的冲突.参数整定是指通过在控制规则设计取值的基础上,对其数值进行小幅度的调整,在保证各路口合理的通行能力下,使得各路口流量传递更加平稳,但未必是过程中的最优解.
文献[1]将城市交通信号控制划分为协调式控制与驱动式控制两种形式.协调式控制是将所有路口周期统一处理;驱动式控制则是在每个周期内对预先排序的交通流逐一进行绿相时长处理.文献[2-4]证明了当协调控制对于一个足够小的交通网络可以找到一组优化方案,该信号优化问题就变成了一个基于网络维度的NP类问题,因此控制子区域不能随意扩大.文献[5]证明了任意分布的驱动式信号控制方式都会演化成自组织行为,但是规则的设定很容易导致系统严重偏向于高流量运动的连续性,会忽略部分交通流需求.文献[6]利用线性整数规划(MILP)方法实现动态的调节协调控制中的预设参数,从而达到加速动态分配频率以及缩短冗长周期的目的.文献[7-8]利用一种理想化的CTM模型[9]为驱动控制中容易被忽略的交通流需求添加了一种周期约束,限制了高流量运动的优先权限,使得全局优化得到了提升,但是没有为路口间流量传递进行匹配.文献[10]尝试利用自组织控制中局部范围内相位差的二次扩展实现协调控制与驱动控制的结合,从而保证高流量连续通过路口的带宽,形成局部范围内的协调,但是由于模型的有限性,局部范围划分的依据以及计算初值条件未明确列举.综上所述,为解决各路口间通行效率冲突的问题,需要实现路口间交通流动态传递的表达,以添加对应交通需求的状态约束,从而确定各路口对应规则参数的整定范围.
本文利用流体力学来解析交通流的变化过程,利用参数有效表征不同交通状态的特征,并以此为自组织控制规则的设计空间.当各自路口计算信号方案时,通过流量分配的方式,确定各自路口所需求的放行流量,利用混合整数非线性规划计算最小区域各参数的优化,并按照优化的参数进行绿相计算,完成规则参数的整定过程.
1 路口元胞自组织控制规则的设计空间 1.1 城市交通信号自组织单元对比于经典的自组织控制模型[11],元胞自动机是一种可实现快捷运算的控制模型[12],可有效连接任意路口与其相邻路口形成一个控制单元,并通过设定的状态参数建立控制规则.元胞自动机模型的不足在于其状态参数在时空上均离散,对交通流的连续变化缺乏描述.因此本文采用元胞自动机为基础控制模型,并通过补充交通流的微观表达以完善控制规则.
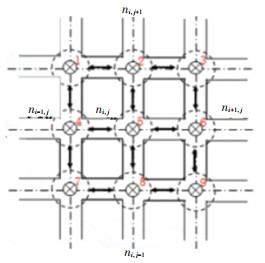
为了使可独立完成信号配时的路口(定义为本地路口)在一个控制单元内进行信号协调,建立以本地路口与其相邻的4个路口为最小区域的自组织单元,设定每个路口均为3车道,其空间结构如图 1所示.
|
图 1 最小区域的自组织单元 Fig. 1 Self-organizing unit of smallest area |
图 1中,以ni, j为本地路口,与其相邻的4个路口ni-1, j, ni+1, j, ni, j-1, ni, j+1组成了一个最小区域的自组织单元,使本地路口可以从各个驶入驶出方向获得对应的交通信息,以进行配时的计算. 图 1中的双向箭头代表交通信息仅在相邻路口之间进行传递交互.
在该最小区域的自组织单元中,基于信号切换规则实现信号控制,该控制规则源于流体动力学中N-S方程,在一维x方向上(东西直行方向)对N-S方程进行数学重构后控制规则基础表达式[12]为
| $ \frac{{{\rm{d}}u}}{{{\rm{d}}t}} = - \frac{1}{\rho }\nabla p + \mu \frac{{{\partial ^2}v}}{{\partial {x^2}}}. $ | (1) |
式中:
式(1)中,流体密度ρ对应交通量可以替代为道路上车辆数,通过检测数据获得,流量梯度为路口上下游流量差值.粘滞系数指流体的运动粘性系数,对应到城市交通中,由于无法直接实现该参数计算,其值与车流的密度、道路形态以及驶出路口距离有关[12].
在东西直行方向上利用差分方程对式(1)进行推导,可得到关于任意路口n的t+1时刻下的状态自组织控制规则为
| $ \begin{array}{*{20}{l}} {l(t)_{n,k}^{t + 1} = (1 - 2{\lambda _1} - {\lambda _2})l(t)_{n,k}^t + ({\lambda _1} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _2})l(t)_{n - 1,k}^t + ({\lambda _1} + {\lambda _2})l(t)_{n + 1,k}^t + \frac{{{\lambda _2}}}{2}.} \end{array} $ | (2) |
式中:
在y方向(南北方向直行)上利用差分方程对式(1)进行推导的过程与式(2)相同.信号相位k的相对拥挤强度l(t)到达预设阈值l(t)threshold时,会向路口提出信号切换请求.路口会根据l(t)具体数值大小决定绿相时长.
1.2 自组织控制规则设计空间自组织控制规则设计空间为控制规则相关参数,通过参数的修改提升规则的动态适应性.需要整定的规则相关参数如下:
1) 拥挤强度特征阈值l(t)threshold.拥挤强度特征阈值是用于判断信号是否切换的最高优先条件,每条道路都有自己的拥挤强度特征阈值,受道路长度、车道数、允许最大行驶速度等参数影响,由道路上实际检测到的车速与流量决定其数值,为无量纲参数. l(t)threshold基础值为0.7,由于自组织微观特征中单车道的拥挤相的临界值为0.75,而多车道间车辆的相互运动可以降低该值[13],因此选择3车道的基础值为0.7,具体数值根据路网结构可调整设计.
2) 流量分配影响系数α1、α2、α3.影响系数按顺序依次代表左转、直行、右转,表示本地路口可放行到下游路口中的流量比例关系,是式(2)中各分项权重系数计算来源的依据.影响系数通过流量分配原则计算,以当前路口内车道实时流量状态为标准,联合其上下游车道实时流量状态完成分配.影响系数αn表达为
| $ {\alpha _n} = \frac{{{M_{{n_{i,j}}}}Q_{{n_{i,j}}}^{{\rm{ out }}}(t)}}{{\sum\limits_{i \in {\alpha _n}}^{{M_i}} {{M_i}} Q_{{n_{i,j}}}^{{\rm{in}}}(t)}}. $ | (3) |
式中:Q(t)为表示时刻t的流量,in、out表示对应下标路口东西直行方向上的驶入驶出方向,M为对应路口内道路数,Mi为对应路口内道路序号.式(3)决定路口的通行能力大小,若未达到下游交叉口当前所允许的最大车辆数,则释放车辆数至本地路口特征拥挤强度降低至临界流量压力(l(t)=0.35);若已达到下游交叉口当前所允许的最大车辆数,则释放所允许放行的车辆数;若需要调配主次干道影响因素,则依据实际历史数据进行修正.
3) 绿相时长tg.由于自组织控制属于变周期控制,且各信号相序的绿相时长也是时变的,其长度为迭代时间步长的整数倍.在基础自组织模型中,绿相时长为国标最小绿时与迭代次数对应时间之和,无法及时提供给相邻路口信号切换信息,所以会导致路口间效率冲突.利用参数整定,以当前道路的拥挤强度特征阈值为基础,直接生成当前信号的绿相时长,才能准确建立流量的传递过程.
2 城市路网元胞传输CTM模型将城市道路元胞化以观察车流的动态变化过程是一种有效的手段,常见的CTM、TSM模型[14]都有效地验证了这种方法的可行性,本文选择采用CTM模型来表达车道内的微观传递.
以一维连续交通流LWR模型为代表的传输模型,可以有效表达每个元胞内流量与密度间的变化关系.该方法未考虑在元胞连接处的流量传递关系以及相邻元胞传输的影响作用,这主要是由早期研究中网格与车速的划分形式决定的.在自组织控制中,以一定的车道长度作为元胞长度,可以解决因状态离散而导致车道上实际车辆分布情况无法确定的问题.利用元胞对车辆行驶进行定位,通过每个时间步逐一对元胞状态进行扫描,可实现每个元胞队列的速度-密度表达,由于元胞长度确定,因此可预测每个元胞队列在下一时间步的运行状态.综合所有元胞的运行状态即可构建该信号相位的队列预测模型[15],从而确定基础放行流量.元胞长度是模型中重要的参数,不宜过长或过短,主要体现为两个因素:1)元胞传输模型遵循先进先出的运行方式,若长度过长,则难以捕捉车辆运行顺序,从而建立的预测队列准确性无法保证;若元胞长度过短,则运行队列在单位时间步长内驶过的元胞个数难以确定,会使得元胞间传递产生的计算误差会进一步放大. 2)元胞长度决定了迭代步数,因为整定过程是在信号相位开始前计算完成,车道内元胞的个数即为迭代的基础步数.若长度过长,迭代次数减少,则迭代结果的准确性难以保证;若长度过短,迭代次数增加,则使整个计算时间上升.
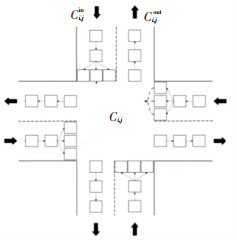
因此,在城市交通道路长度一般不超过1 000 m的实际情况下,鉴于整个控制系统采用的时间步长为15 s,选取元胞长度为50 m,使其能在一个时间步长内完成迭代计算.将本地路口的网格划分定义为图 2所示CTM模型. 图 2中,Ci, j为该路口内所有元胞,T为离散时间步,Ci为属于Ci, j的第i个元胞,Ci, jin为驶入路口Ci, j的边界位置元胞,Ci, jout为驶出路口Ci, j的边界位置元胞,CL为元胞长度.通过对元胞模型描述微观传递过程,并借助元胞间流量传递添加必要状态约束.
|
图 2 本地路口元胞化模型 Fig. 2 Cellization model of local intersection |
定义P(i)、S(i)为元胞i连接元胞集合,其中P(i)为驶入元胞i的集合,其中S(i)为元胞i驶出的集合,用集合的方式表示是由于车道数变化,可能存在一对多或者多对一的情况. xit表示时刻t下元胞i的车辆占据数,yijt表示任意元胞j∈S(i)在时刻t下元胞j与元胞i之间的车辆占据数,qint(i)、qoutt(i)表示时刻t流入、流出该元胞i的车辆数,git表示时刻t下元胞i对应的路口的信号需放行流量.
本文建立模型的求解目标函数为各自路口通行量的最大化,目标函数的离散状态表示为每个路口驶入、驶出元胞在时刻t下某个子集内所有元胞的车辆占有数:
| $ F(x) = {\rm{max}}\sum\limits_{\forall t \in T} {\sum\limits_{\forall i \in C_{i,j}^{{\rm{in}}}} {x_i^t} } . $ | (4) |
以车辆数作为元胞的初始变量状态,将其离散为
| $ \begin{array}{*{20}{l}} {x_i^{t + \Delta t} = x_i^t + q_{{\rm{ in }}}^t(i - 1) - {q_{{\rm{ in }}}}(i) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} q_{{\rm{ in }}}^t(C_{i,j}^{{\rm{ in }}} - q_{{\rm{ in }}}^t(C_{i,j}^{{\rm{ out }}}).} \end{array} $ | (5) |
为了确保交通流中各车辆准确的占据在元胞内,令d为时刻t下驶出的交通需求状态,对式(5)添加元胞间传递约束:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\delta _{i - b}} + {\delta _{i - {\rm{IN}}}})\sum\limits_{l \in P(i)} {y_{i - l}^t} - ({\delta _{i - {\rm{OUT}}}} + {\delta _{i - b}})\sum\limits_{j \in S(i)} {y_{ij}^t} + \\ d_i^t({\delta _{i - {\rm{OUT}}}}) = ({\delta _{i - b}} + {\delta _{i - {\rm{IN}}}} + {\delta _{i - {\rm{OUT}}}})(x_i^{t + 1} - x_i^t),\\ \forall t \in T,\forall i \in {C_{i,j}},\forall b \notin \{ C_{i,j}^{{\rm{in}}},C_{i,j}^{{\rm{out}}}\} ,{\delta _{m - n}} = 1(m = \\ n),{\delta _{m - n}} = 0(m \ne n). \end{array} $ | (6) |
时刻t下元胞i内已存在的车辆数,表达为
| $ \sum\limits_{j \in S(i)} {y_{ij}^t} \le x_i^t,\;\:\forall t \in T,\;\:\forall i \in {C_{i,j}}. $ | (7) |
定义Mj为元胞j所能容纳的最大车辆数,为了保证在相邻两个元胞内行驶的车辆都可以准确的被两个元胞空间容纳,需要添加约束条件:
| $ \sum\limits_{j \in P(i)} {y_{ij}^t} \le {M_j} - x_i^t,\;\:\forall t \in T,\forall j \in {C_{i,j}}. $ | (8) |
在任意时刻t下,从元胞Ci, jout在路口Ci, j驶出的各方向到对应下游的车辆不应多于对应总车辆与转弯系数(即流量分配系数)α的乘积,以保证放行流量大小,需要添加约束条件:
| $ y_{ij}^t \le r_{ij}^t\sum\limits_{k \in S(i)} {\alpha _{ik}^t} . $ | (9) |
定义饱和状态下对应的信号状态, 即饱和状态下需要放行的车辆数,这部分车辆数需停靠在驶出位置,放行数量的约束条件为
| $ f_i^t = g_i^t{F_i},{F_i} = l{(t)_{{\rm{ threshold }}}},\sum\limits_{j \in S(i)} {y_{ij}^t} \le f_i^t. $ | (10) |
城市元胞路网自组织控制系统的规则切换不同于常用的干线协调或带宽匹配的设计方式,由于本地路口被赋予了调整周期与各绿相时长的决策能力,因此本地路口结合最小区域内各路口当前交通状态自行设计所需求的通行流量,并利用整数线性规划联合修正下一信号绿相放行时间的长短与开启时刻,通过参数的整定从而形成演化状态的更迭.
3.1 排队长度预测在城市元胞路网自组织控制模型中,以每个道路的拥挤状态进行信号决策,拥挤状态由队列长度决定,但是整个过程中缺乏微观表达,因此以上下游压力差来表征队列的形成与消散[16-19].为实现微观交通流变化表达,建立元胞模型下的队列预测方法,实现对元胞间传递过程的表达,同时也实现路口间交通流连续传递的描述.在流体力学的表达中,车辆数与流量及时间的变化表达为
| $ \frac{{{\rm{d}}{N_{{c_{i,j}}}}}}{{{\rm{d}}t}} = Q_{{C_{i,j}}}^{{\rm{in}}}(t) - Q_{{C_{i,j}}}^{{\rm{out}}}(t), $ | (11) |
式中N(t)为时刻t下的道路上的车辆数.
因此车辆需要驶出该道路的基本的通行时间T(t)与车辆数的关系可表达为
| $ {N_{{C_{i,j}}}}(t) = \int\limits_t^{t + {T_{{c_{i,j}}}}(t)} {Q_{{C_{i,j}}}^{{\rm{ out }}}} ({t^\prime }){\rm{d}}{t^\prime }. $ | (12) |
式(11)、(12)适用于自由相下的交通状态,在自由相中,车辆较少,车辆较快,一般不需要对队列进行预测.
随着交通拥堵程度不断上升,元胞内形成队列,需要对交通流运行的状态进行描述,设决策开始前已有队列L1(t), 可新生成队列为L2(t), 结算总队列为L(t).首先计算各元胞内每个时间步长内驶入、驶出的车辆数,结算当前时间步长内剩余的队列长度,作为下个时间步长内队列长度的初值,从而形成连续的迭代过程.车道上元胞i当前的运行状态方程为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} N_i^{{\rm{ out }}}(t) = \\ \left\{ \begin{array}{l} {v_{{\rm{ out }}}} \times \Delta t,{v_{{\rm{ out }}}} \times \Delta t < {L_{1i}}(t);\\ {L_{1i}}(t),{v_{{\rm{ out }}}} \times \Delta t \ge {L_i}(t),{T_i}(t) > \Delta t;\\ {L_{1i}}(t) + {L_{2i}}(t),{v_{{\rm{ out }}}} \times \Delta t \ge {L_i}(t),{T_i}(t) < \Delta t; \end{array} \right. \end{array} $ | (13) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} N_i^{{\rm{in}}}(t) = \\ \left\{ {\begin{array}{*{20}{l}} {N_{i - 1}^{{\rm{ out }}}(t),}\\ {{N_{i{\rm{MAX}}}} - {L_{1i}}(t - \Delta t),N_{i - 1}^{{\rm{ put }}}(t) > {N_{i{\rm{MAX}}}} - {L_{1i}}(t - \Delta t);} \end{array}} \right. \end{array} $ | (14) |
| $ {{T_i}(t) = ({C_L} - x_{{\rm{ first }}}^p)/{v_{{\rm{ first }}}};} $ | (15) |
| $ {{L_{2i}}(t) = ({N_i}(t) - {L_{1i}}(t)) \times \frac{{{T_i}(t) - \Delta t}}{{{T_i}(t)}};} $ | (16) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {L_i}(t) = \\ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{L_{1i}}(t) - {v_{{\rm{ out }}}} \times \Delta t,{v_{{\rm{ out }}}} \times \Delta t < {L_{1i}}(t);}\\ {0,{v_{{\rm{ out }}}} \times \Delta t \ge {L_i}(t),{T_i}(t) > \Delta t;} \end{array}\\ \begin{array}{*{20}{c}} {({N_i}(t) - {L_{1i}}(t)) \times (1 - \frac{{{T_i}(t) - \Delta t}}{{{T_i}(t)}}),}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {v_{{\rm{ out }}}} \times \Delta t \ge {L_i}(t),{T_i}(t) < \Delta t;} \end{array} \end{array} \right. \end{array} $ | (17) |
| $ {N_i}(t + \Delta t) = {N_i}(t) - N_i^{{\rm{out}}}(t) + N_i^{{\rm{in}}}(t). $ | (18) |
式中:xfirstp为元胞内正在运行队列的头车位置,vfirst为该头车速度,因为遵循先进先出的原则,队列平均速度由头车决定,in、out代表元胞i的流入、流出方向,NiMAX代表最大车辆容量数,v为平均速度.
由式(13)计算当前时间步内元胞驶出车辆,由式(14)计算当前时间步内元胞驶入车辆,由式(15)~(17)结算当前时间步剩余队列长度,从而建立每个元胞的输入输出关系,依据自组织模型自行迭代计算决策开始前车道内各元胞依次传递至路口的队列,该队列即为最终的预测队列,定义元胞长度为CL.假设最终有r个元胞被完全占据,则最终预测队列长度为
| $ {L_{{C_{i,j}}}}(t) = r \times {C_L} + {L_{{\rm{ out }} - r}}(t). $ | (19) |
由于CTM自身的离散性,虽然通过添加元胞间传递方式的过程描述,依然不是完整的连续流体方程.利用流体力学的连续表达,对可连续任意点的动态密度函数ρ(x, t),按元胞长度CL与元胞间队列重新稳定的时间ts来检验稳定性, 稳定时间指在新的时间步长开始后, 在元胞内完成新老队列融合或新队列车速稳定的时间.由于离散后传递方式为一阶线性过程,其线性一阶的泰勒展开式为
| $ \begin{array}{*{20}{c}} {\rho (x + {C_L},t - {t_{\rm{s}}}) = \rho (x,t) + \frac{1}{2}({C_L}\frac{\partial }{{\partial x}} - }\\ {{t_{\rm{s}}}\frac{\partial }{{\partial y}}{)^2}\rho (x + \varepsilon {C_L},y - \varepsilon {t_{\rm{s}}}).} \end{array} $ | (20) |
将式(16)代入式(13),用密度-速度模型改写流量形式,使得目标函数Q(ρ)≥0,即
| $ \gamma \rho \{ (x,t)v(\rho )[q(\rho ){t_{\rm{s}}} + {C_L}{\varepsilon ^\prime }]\} \ge 0. $ | (21) |
式中:γ为无量纲系数,与流量传递的大小有关; ε′取值为(0, ε).
因此线性稳定的基本条件为
| $ q(\rho ) \ge - \frac{{{\varepsilon ^\prime }{C_L}}}{{{t_{\rm{s}}}}}. $ | (22) |
式(22)中,各参数本身均为正值,由于q(s)为正值,因此该传递满足稳定条件,可收敛.随着各级相变的产生, 系统趋向动态不稳定.当CL越大, 系统可获得的稳定域越大;当ts越大,系统可获得的稳定域越小.把路口视作整个元胞,将元胞间流量传递表征为路口间流量传递时,因自组织控制中追求本地路口通行的最大效率,导致在本地路口的队列稳定的时间会变大,系统会变得愈发不稳定,这也说明了解决该问题的意义.
3.3 规则整定城市元胞自组织模型按照路网拓扑结构对参数赋值,并以这部分赋值作为系统的初值条件[20].当本地路口有任意信号相位的l(t)达到预设值,自组织系统通过差分方程形成上下游压力状态差,计算本地路口放行流量需求,并以此需求为基础分配一个基础绿灯时长tg,并计算该绿灯的开启时刻tgp,从而保证相邻路口间相位差不会偏差过大,避免ts过大使系统稳定性下降.依据该需求相位与其相邻路口的实时交通状态,建立该信号相位的放行目标函数.通过拥挤强度的预测叠加与释放对比,重新分配该范围内各子系统间输入输出匹配的规则参数,并返回给本地路口,完成规则参数的整定过程.其整个优化过程是一个混合整数非线性规划问题(MINLP).以式(4)所表示的最大通行能力为目标,令G(tg)最大,计算过程为
| $ \left\{ {\begin{array}{*{20}{l}} {G({t_{\rm{g}}}) = \sum\limits_{i = n - 1}^{n + 1} {{\alpha _{{C_{i,j}}}}} {l_{{C_{i,j}}}}{{(t)}_{{\rm{ threshold }}}} \times {P_{{C_{i,j}}}},}\\ {{P_{{C_{i,j}}}} = F[(t_{{C_{i,j}}}^{{\rm{gp}}} - t_{{C_{i + 1,j}}}^{{\rm{gp}}}),(t_{{C_{i,j}}}^{{\rm{gp}}} + t_{{C_{i - 1,j}}}^{{\rm{gp}}}){L_{{C_{i,j}}}}(t)].} \end{array}} \right. $ | (23) |
利用混合整数线性规划对目标区域进行求解的过程:1)选定联合路口的个数,当前为最小区域5个路口; 2)将各路口的约束条件联合代入; 3)将原有的信号切换条件代入式(2)~(10)、(13)~(19)、(23),进行规则参数整定; 4)对需求切相的相位分配绿相时间,最终整定的参数值应满足式(4), F(x)达到最大值.
完成整定后,本地路口对应的各绿灯时长与开启时刻也随之确定,保证相邻路口间可以更准确地建立交通流的传递过程,使本地路口与其相邻路口都能实现相对良好的通行效率.虽然该方法限制了部分自组织演化的能力,但也因此避免了自组织偏向特定流量的演化状况,起到了有效的优化效果.
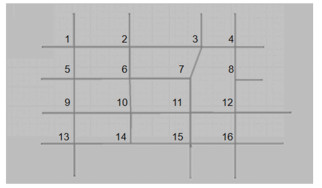
4 仿真验证为验证元胞路网下自组织规则整定方法对提高系统控制稳定性与通行效率的影响,通过对比未整定与整定后的自组织控制效果进行分析.设计如图 3所示仿真模型,该验证模型采用了VISSIM中16路口的路网模型,通过二次开发改写内置参数,选取路口9、10、11从东向西行驶的检测数据为观察数据,选取路口10为本地路口,其中路口12到路口11道路长度为400 m,路口11到路口10、路口10到路口9道路长度均为600 m;信号相序为东西直行+南北右转、东西左转、南北直行+东西右转、南北左转,相序不可变.每个路口每个方向均为3车道,依次为左转、直行、右转,设定车辆在道路中段不可再次进行换道行为.车道内每个元胞长度为50 m,以内置检测器为节点,分别安装于道路进入口及每个元胞的入口处.混车率取98%,最大速度为60 km/h,最小速度为10 km/h.最大周期为180 s,最小周期为90 s.输入流量从600 puc/h到1 800 pcu/h分路口输入.仿真总时长取3 600 s.取每一时间步(time step)为15 s,由于仿真软件初始流量只能产生在边界,路网内部流量不稳定,因此从路网内流量相对平均稳定后开始记录数据,记录为第1个时间步长,共160个记录时间步长,取每个时间步内平均预测队列长度为评价目标,仿真结果如图 4~6所示.
|
图 3 路网示意图 Fig. 3 Road network diagram |

|
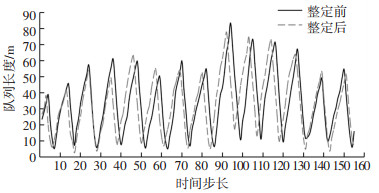
图 4 路口11整定前后控制对比 Fig. 4 Comparison of tuning control and untuning control at intersection 11 |
|
图 5 路口10整定前后控制对比 Fig. 5 Comparison of tuning control and untuning control at intersection 10 |
|
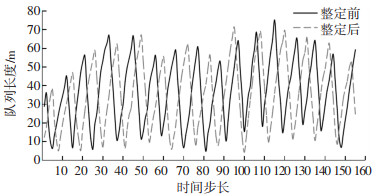
图 6 路口9整定前后控制对比 Fig. 6 Comparison of tuning control and untuning control at intersection 9 |
由于对时间步长内的预测排队长度平均化,因此在系统相对运行稳定的状态下,图中数据在几个时间步长之间变化斜率值相差不大,而本文所研究的重点在于相邻路口间的协调通行能力,主要观察对象为相邻路口的相位差,选择平均排队长度来评价实验结果.由图 4~6数据可知,由于选取路口10为本地路口,路口9、11为路口10的关联相邻路口,因此路口10对应数据整体在时域上的各周期位移最小;路口9对应数据整体在时域上波动较大主要是由于边界输入压力大于路口11,因此为缓解该部分流量压力,导致路口9频繁调整信号周期,从而影响其相邻路口的通行效率.经过整定后,路口11的最大队列长度为整定前的90.3%,平均队列长度为整定前的92.3%;路口10的最大队列长度为整定前的93.3%,平均队列长度为整定前的94.7%;路口9的最大队列长度为整定前的93.7%,平均队列长度为整定前的95.1%.在东西直行信号相位下,经过整定后,路口11跟路口10的平均相位差由6.3个时间步长减少至3.8个时间步长;路口10跟路口9的平均相位差由8.7个时间步长减少至4.1个时间步长,因此路口间可以保持一定的绿相带宽以提高通行效率,在仿真过程中由于不存在各类延误及车辆启动时间,所以该提升效果在仿真数据中显示不明显.综上所述,自组织控制规则在整定前,有明显的因相邻路口间各自最优通行效率冲突所带来的通行效率问题;经过整定后的自组织规则,能够保持相邻路口间必要的绿相带宽,并能保证预设的最大通行目标不受干扰,因此可以有效提升各路口的通行效率.实验数据也证明了该自组织控制整定方法的有效性.
5 结论1) 通过对路口的元胞化,建立了满足自组织控制需求的最小区域自组织单元的多车道控制模型,设计了规则参数空间,以实现最小区域内实时交通需求的分配.
2) 通过对道路内元胞化,结合细胞传输模型,实现了交通流微观传递的表达,并利用流体力学将元胞间的传递关系给予了连续状态的表达,通过元胞间不断的传递迭代,建立了用于决策的排队长度预测模型,其计算过程简便快捷.
3) 结合最小区域自组织单元内各路口的实时交通状态,针对各路口自组织规则中的流量分配系数、绿灯时长需求、相邻路口相位差以及特征拥挤强度等规则参数,以通行能力最大化为目标函数,对上述规则参数进行必要的整定.仿真结果证明,该规则参数的整定方法不仅解决了城市自组织控制单元中路口间效率冲突的问题,而且有效提高了区域内各路口的通行效率,并相较于未整定的城市自组织控制模型,路口间相位差也更为合理.下一步需要提升最小区域的规模以避免实际路网中道路尺寸比例差过大所带来的通行能力问题,以及为了提高不同交通状态下的通行能力,如何选取合适的各交通参数.
| [1] |
KOONCE P, RODEGERDTS L, LEE K, et al. Traffic signal timing manual[M]. 2nd ed. Washington DC: Federal Highway Administration, 2008: 13.
|
| [2] |
ADACHER L, GEMMA A, OLIVA G. Decentralized spatial decomposition for traffic signal synchronization[J]. Transportation Research Procedia, 2014, 3: 992. DOI:10.1016/j.trpro.2014.10.079 |
| [3] |
HAJBABAIE A, BENEKOHAL R. Does traffic metering improve network performance efficiency?[C]//Proceedings of 14th International IEEE Conference on Intelligent Transportation Systems (ITSC). Washington DC: IEEE, 2011: 1114
|
| [4] |
WVNSCH G. Coordination of traffic signals in networks and related graph theoretical problems on spanning trees[D]. Berlin: Technischen Universit at Berlin, 2008: 5
|
| [5] |
LÄMMER S, HELBING D. Self-control of traffic lights and vehicle flows in urban road networks[J]. Journal of Statistical Mechanics: Theory and Experiment, 2008, 4: 5. DOI:10.1088/1742-5468/2008/04/P04019 |
| [6] |
BEARD C, ZILIASKOPOULOS A. System optimal signal optimization formulation[J]. Transportation Research Record: Journal of the Transportation Research Board, 2006, 1978(1): 102. DOI:10.1177/0361198106197800114 |
| [7] |
GERSHENSON C. Self-organizing traffic lights[J]. Complex Systems, 2005, 16(1): 29. |
| [8] |
GERSHENSON C, ROSENBLUETH A. Adaptive self-organization vs static optimization: a qualitative comparison in traffic light coordination[J]. Kybernetes, 2012, 41(3/4): 386. DOI:10.1108/03684921211229479 |
| [9] |
DAGANZO C. The cell transmission model: a simple dynamic representation of highway traffic[J]. Transportation Research Part B: Methodological, 1994, 28(4): 269. DOI:10.1016/0191-2615(94)90002-7 |
| [10] |
CESME B, FURTH P G. Self-organizing traffic signals using secondary extension and dynamic coordination[J]. Transportation Research Part C: Emerging Technologies, 2014, 48: 3. |
| [11] |
莫祥伦.城市道路交通流自组织运行机理及控制研究[D].长春: 吉林大学, 2014 MO Xianglun. Study onoperation mechanism and control of self organization traffic flow in urban road net[D]. Changchun: Jilin University, 2014 |
| [12] |
魏俊华.城市交通信号自组织控制方法的研究[D].上海: 上海交通大学, 2005 WEI Junhua. Research on self-organized control method of urban traffic signals[D]. Shanghai: Shanghai Jiao Tong University, 2005 |
| [13] |
TAKASHI N. Self-organization in 2D traffic flow model with jam-avoiding drive[J]. Physical Society, 1995, 65(4): 1421. |
| [14] |
ZHAO S Z, LIANG S D, LIU H S. CTM based real-time queue length estimation at signalized intersections[J]. Mathematical Problems in Engineering, 2015, 2015: 5. DOI:10.1155/2015/328712 |
| [15] |
HAJBABAIE A, BENEKOHAL R. A program for simultaneous network signal timing optimization and traffic assignment[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(5): 2573. DOI:10.1109/TITS.2015.2413360 |
| [16] |
CHOW A H F, SHA R. Performance analysis of centralized and distributed systems for urban traffic control[J]. Transportation Research Record: Journal of the Transportation Research Board, 2015, 2557(1): 66. DOI:10.3141/2557-07 |
| [17] |
CLEMPNER J B, POZNYAK A S. Modeling the multi-traffic signal control synchronization: a Markov chains game theory approach[J]. Engineering Applications of Artificial Intelligence, 2015, 43: 147. DOI:10.1016/j.engappai.2015.04.009 |
| [18] |
王安麟, 孙晓龙, 钟馥声. 一种基于通行优先度规则的城市交通信号自组织控制方法[J]. 重庆交通大学学报(自然科学版), 2018, 37(2): 96. WANG Anlin, SUN Xiaolong, ZHONG Fusheng. Self-organizing control method for urban traffic signal based on the pass-priority rules[J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2018, 37(2): 96. DOI:10.3969/j.issn.1674-0696.2018.02.15 |
| [19] |
STRÖMBOM D, DUSSUTOUR A. Self-organized traffic via priority rules in leaf-cutting ants[J]. PLoS Computational Biology, 2018, 14(10): 1. DOI:10.1371/journal.pcbi.1006523 |
| [20] |
钟馥声, 王安麟, 姜涛, 等. 城市交通信号自组织控制规则的邻域重构[J]. 哈尔滨工业大学学报, 2020, 52(3): 74. ZHONG Fusheng, WANG Anlin, JIANG Tao, et al. Neighborhood reconstruction of urban traffic signal self-organizing control rules[J]. Journal of Harbin Institute of Technology, 2020, 52(3): 74. DOI:10.11918/201906054 |
 2020, Vol. 52
2020, Vol. 52


