高速公路改扩建、养护施工区因持续时间短,事故资料少,交通冲突作为一种非事故统计技术对于高速公路施工区的交通安全评价具有很好的适用性[1-2].现有交通冲突研究方法主要分为集计方法和非集计方法.集计方法[3-4]多采用统计模型建立特定时空内的交通冲突模型,并对冲突频率与道路条件、交通条件因素进行回归寻找出两者之间的关系,其不足在于难以评估微观的道路环境下的交通冲突状况.非集计方法[5-6]是以单个交通冲突为研究对象的方法,非集计方法的研究多为通过车辆运动学建立交通冲突的物理模型,大部分非集计交通冲突研究只对冲突两车进行研究分析,未考虑冲突两车的相邻车辆对于冲突两车的影响,考虑相互作用车辆较少.
本文以单个交通冲突为研究对象,同时参考车联网技术[7-8],考虑冲突主体两车之外的车辆对交通冲突主体的影响,使用机器学习通过大量数据训练构造交通冲突贝叶斯网络模型,研究交通冲突与速度、加速度等12个交通微观信息之间的相互关系,基于机器学习的贝叶斯网络与其他建模方法相比,可以更为直观地表达出微观数据与交通冲突之间的关系.同时对交通冲突模型在交通领域对车联网下无人驾驶干预冲突技术提出了展望.
1 数据采集与分析 1.1 数据采集为了构建交通冲突贝叶斯网络模型,在2019年1月10日至1月25日,选取了济青高速公路改扩建施工区多个区段合流区,通过雷达采集交通冲突数据.高速公路改扩建合流路段是在施工区对两车道进行合流变为单车道的路段,有两种类型:一种是匝道合流路段;另一种是车辆变换车道同时合流的路段.合流路段道路状况变化较大,交通情景复杂,具有重要的研究价值,本次实验所选的施工区合流路段,设计车速为100 km/h,施工时限速为80 km/h.两种合流路段采集现场如图 1所示,为了考虑施工区道路技术条件难以量化因素,选择多个不同区段进行数据采集,以提升训练得到的贝叶斯网络对于不同交通场景的适应性.

|
图 1 两种类型的合流路段 Fig. 1 Two types of confluence sections |
本次数据采集时间包含早高峰8:00—9:00时,晚高峰16:00—17:00时以及平峰10:00—11:00时、15:00—16:00时,采集地点为济南-青岛高速公路K130+800、K176+800、K259+500、K277+300、K283+500、K287+700六个标段,共采集了25 h的数据,经过整理,保留数据完整的35 418帧的数据.
本次实验使用SmartRader SR600G型路段跟踪雷达,覆盖长度为200 m,将雷达架设在高速公路上方高架桥或道路侧向较高点,可以对道路车辆行驶数据进行精确的采集,相比传统的数据采集方式,雷达可在夜间光线较差时工作,采集的数据连续性更好,在模型中的表达能力更强.每秒采集10帧数据,以帧为单位获得的数据,数据量更大,数据更为精确,位置误差小于0.3 m,速度误差小于0.3 m/s.
1.2 数据描述及分析本文以B车和C车之间的交通冲突为研究主体,A、D车为整条道路上除C车外与B车相距最近的车辆,A、B、C、D车可以在相同的车道也可以在不同的车道,车辆位置由前到后分别为A、B、C、D.研究加入A、D车的车辆信息以综合考虑研究冲突主体的两车B、C受道路上的相邻车辆A、D的影响.后续部分将4车分别描述为:相邻车辆A、冲突车辆B、冲突车辆C、相邻车辆D,单个冲突微观研究范围如图 2所示.
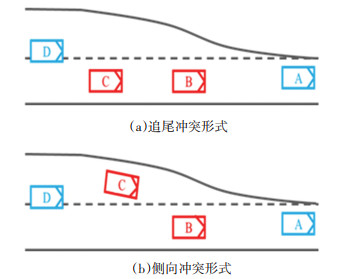
|
图 2 单个冲突微观研究范围 Fig. 2 Microscopic research scope of individual conflicts |
本次实验视频识别得到的数据为某一帧的车辆信息,此处选取TDTC(time difference to collision)作为实验的冲突指标. TDTC定义为在某个时刻,假定车辆的速度和方向保持不变,两辆车通过当前轨迹的交叉点(冲突点)的时间差[9]. TDTC作为一种新的冲突指标能同时对异车道冲突、同车道冲突进行识别,也可对冲突的前期预测分析,很好地弥补了TTC(time to collision)和PET(post encroachment time)的不足[10].因为高速公路施工区的车辆行为比正常路段更为复杂,TDTC的特点使得其作为高速公路施工区的冲突指标具有很好的适应性.以t时刻,冲突车辆B、冲突车辆C两车为冲突主体简单描述TDTC的概念,如图 3所示.
| $ {\rm{TDTC}} = {T_{\rm{C}}} - {T_{\rm{B}}} = \frac{{{s_{\rm{C}}}}}{{{V_{\rm{C}}}}} - \frac{{{s_{\rm{B}}}}}{{{V_{\rm{B}}}}}, $ | (1) |

|
图 3 TDTC概念描述 Fig. 3 Schematic diagram of TDTC concept |
式中:TC为C车到达冲突点M的所需时间, s;VC为C车在t时刻的瞬时速度,m/s2;sC为C车t时刻距冲突点M的距离, m;TB为B车到达冲突点M的所需时间, s;VB为B车t时刻的瞬时速度,m/s2;sB为B车t时刻到达冲突点M的距离, m.
当B、C两车无交点M时两车无冲突.在训练集中,目标变量为B、C车之间的交通冲突,通过TDTC指标进行判断,本文参考国内外相关研究,同时考虑高速公路施工区这一特殊交通场景,选取TDTC为3 s为严重冲突的阈值,通常在TDTC远大于3 s时,将交通冲突划归潜在冲突,因为本次贝叶斯网络建模受限于数据量,需要通过控制变量的离散类型以提高模型的精确度,同时考虑到交通事故与严重冲突的相关性远大于一般冲突,此次只将交通冲突分为严重冲突、一般冲突、无冲突3种类型.
1.3 变量选择及数据离散借鉴学者对前后两车辆在特定断面上的交通冲突微观分析技术,考虑前后左右4个近邻车辆在较大区域时空上的连续相互作用,选择与交通冲突(目标变量)可能具有相关性的12个微观交通数据作为构建贝叶斯网络的变量.下面分别对这些变量进行介绍.
ΔVx为B、C车纵向速度差,即C车纵向车速减去B车纵向车速(可为负);ΔVy为B、C车横向速度差,即C车横向车速减去B车横向车速(可为负);ΔVAB为A、B车速度差,即B车速度减去A车速度(可为负);ΔVCD为C、D车速度差,即D车速度减去C车速度(可为负);aB为B车加速度,即B车的加速度;aC为C车加速度,即C车的加速度;LAB为A、B车辆距离,即A车与B车之间的距离;YBC为B、C车横向间距,即B车与C车之间的横向距离;XBC为B、C车纵向间距,即B车与C车之间的纵向距离;LCD为C、D车辆距离,即C车与D车之间的距离;ω为车辆类型;θ为合流路段类型;φ为冲突类别.
为了提高训练数据的表达能力,加强贝叶斯网络模型的稳定性,首先需要对数据进行离散处理.通过查阅交通冲突领域的相关文献[11-13],同时考虑高速公路施工区这一特殊交通场景,分析各个变量与B、C车交通冲突的关系,确定了离散的具体阈值见表 1.
| 表 1 数据离散描述 Tab. 1 Data discrete description |
贝叶斯网络是概率论与图论的结合体,由两部分组成,一部分为一个有向无环图, 由代表变量的节点及连接这些节点有向边构成;另一部分为给定数据的条件概率表,它决定了变量之间的关系强度.对于一个有n个节点(x1, x2, …, xn)的联合概率分布的表示形式为
| $ P\left( {{x_1}, {x_2}, \ldots , {x_n}} \right) = \mathop \Pi \limits_{i = 1}^n P\left( {{x_i}{\rm{|parent}}\left( {{x_i}} \right)} \right), $ | (2) |
式中:P(xi|parent(xi))为与节点i相关的局部条件概率分布,parent(xi)为标记节点i的父节点(如果节点i没有父节点,parent(xi)可以为空)[14].
2.2 贝叶斯网络建模贝叶斯网络建模包括结构学习和参数学习两个步骤.
2.2.1 结构学习贝叶斯网络结构学习即确定贝叶斯网络的有向无环图(DAG).考虑到此次试验的变量个数较多,模型复杂,为了提高贝叶斯网络模型的精度,将融合先验知识对贝叶斯网络进行结构学习[15-16].最终基于先验知识确定的变量相互关系为
| $ \left[ {\left( {\Delta {V_x}, \varphi } \right);\left( {\Delta {V_y}, \varphi } \right);\left( {{a_{\rm{B}}}, \varphi } \right);\left( {{a_{\rm{C}}}, \varphi } \right)} \right] \in {\delta _{\rm{e}}}, $ | (3) |
| $ \left[ \begin{array}{l} \left( {\omega , \varphi } \right);\left( {{X_{{\rm{BC}}}}, \varphi } \right);\left( {{Y_{{\rm{BC}}}}, \varphi } \right);\left( {{a_{\rm{B}}}, \Delta {V_x}} \right);\\ \left( {{a_{\rm{C}}}, \Delta {V_x}} \right);\left( {\Delta {V_{{\rm{AB}}}}, {L_{{\rm{AB}}}}} \right);\left( {\Delta {V_{{\rm{CD}}}}, {L_{{\rm{CD}}}}} \right) \end{array} \right] \in {\delta _{\rm{a}}}, $ | (4) |
式中δe,δa的解释如下:(x, y)∈δe表示在搜索学习的过程中x→y这个结构始终存在于网络结构中;(x, y) ∈δa表示在搜索学习的过程中,始终存在x→y或者y→x.
采用MATLAB软件,融合先验知识学习得到的贝叶斯网络结果,如图 4所示.
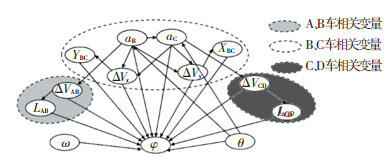
|
图 4 贝叶斯网络结构学习结果 Fig. 4 Bayesian network structure learning results |
在确定了贝叶斯网络的结构后,需要对贝叶斯网络进行参数学习,参数学习实质上是在已知网络结构的条件下,来获得每个节点的条件概率表(CPT).本次采集的数据集为完善数据集,无缺失数据,采用最大似然估计的方法进行参数学习.
下面以C车加速度ac变量为例,比较实际计算的条件概率与参数学习的结果,简单描述参数学习过程,见表 2.
| 表 2 C车加速度的参数学习 Tab. 2 Parameter learning for acceleration of vehicle C |
由表 2可以看出,无缺失数据的状况下,对贝叶斯网络C车加速度进行的参数学习与实际计算结果一致,参数估计无误差.
2.3 可靠性验证考虑到采集的数据来自于6个路段,为了验证训练得到的贝叶斯网络对于不同交通场景的适应性,本文引进K-Fold交叉验证的方式对机器学习得到的贝叶斯网络进行验证[17].该验证方式可以对模型的泛化能力进行评价,即检验训练得到的贝叶斯网络对于各种不同交通场景的适用性.本文中K值取10,对贝叶斯网络进行交叉验证.
利用交叉验证的方法对贝叶斯网络进行验证,验证结果表明无冲突识别精度为97.84%,一般冲突识别精度为78.16%,严重冲突识别精度为71.69%,总体精度为88.82%.
交叉验证结果表明该贝叶斯网络识别的交通冲突类型可靠性较高,也说明了该网络模型对于不同交通场景均具有较高的适用性.
3 基于模型的交通冲突影响因素分析目前贝叶斯网络的推理方法种类很多,本文采用联合树算法进行推理,因为其应用较广,研究较成熟[18].
3.1 单变量对交通冲突的影响分析以车辆类型对交通冲突的影响为例,说明单变量对交通冲突影响分析,不同车辆类型的高速公路施工区交通冲突类型的概率分布,如图 5所示.
由图 5可知,当B、C两车都为小车时,交通冲突和严重交通冲突发生的概率均较低;当B、C两车为一辆小车与一辆大车时,交通冲突发生的概率和严重冲突发生概率有所增加;当B、C两车都为大车时,交通冲突的概率较两车都为小车时增加,但严重冲突低于一辆大车与一辆小车的情景.考虑到大车在高速行驶速度通常较快且因惯性较大,减速较慢,在高速公路合流区易提升交通冲突发生的概率.当B、C车均为大车时,因为道路环境复杂,且都为大车,通常会提前减速谨慎通过,故交通冲突发生概率较B、C车为一辆大车一辆小车时稍低.在高速公路改扩建施工区的合流路段,大车对于交通冲突发生概率的影响较大.
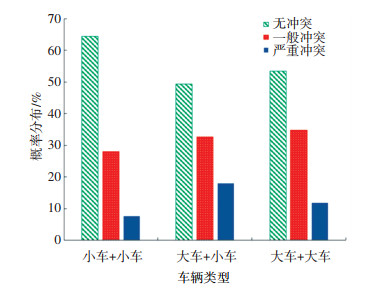
|
图 5 车辆类型对冲突类型的影响 Fig. 5 Influence of vehicle types on conflict types |
类似地,基于学习得到的贝叶斯网络可以分析各变量对高速公路施工区交通冲突的影响.
3.2 多变量对交通冲突的影响分析 3.2.1 综合考虑B、C车横向间距、纵向速度差对交通冲突的影响以B、C车横向间距、纵向速度差对交通冲突的影响为例,说明多变量对交通冲突影响分析,不同B、C车横向间距、纵向速度差的高速公路施工区交通冲突类型的概率分布,如图 6所示.
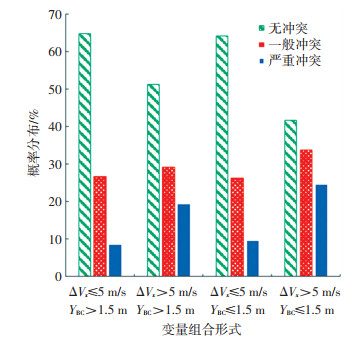
|
图 6 B、C车横向间距、纵向速度差对交通冲突的影响 Fig. 6 Influence of horizontal spacing and longitudinal speed difference of vehicles B and C on traffic conflicts |
由图 6可知,当ΔVx>5 m/s, YBC≤1.5 m时,B、C处于同车道且后车速度比前车快,发生冲突的概率较高,且易发生严重冲突;当ΔVx>5 m/s, YBC>1.5 m时,B、C两车发生严重冲突的概率为19.38%,一般冲突的概率为29.35%.此时,车辆间距大于1.5 m时,在高速公路施工区合流路段处于车道二转一状态,当此时后车速度较前车速度快时,后车处于加速超车抢道行为,总结得到,车辆的超车抢道行为在一定程度上会提升与相邻车辆发生冲突的概率.
3.2.2 对比分析A车与D车对B、C车交通冲突的影响基于训练得到的贝叶斯网络,对比分析A车与D车对B、C车交通冲突的影响,如图 7所示.
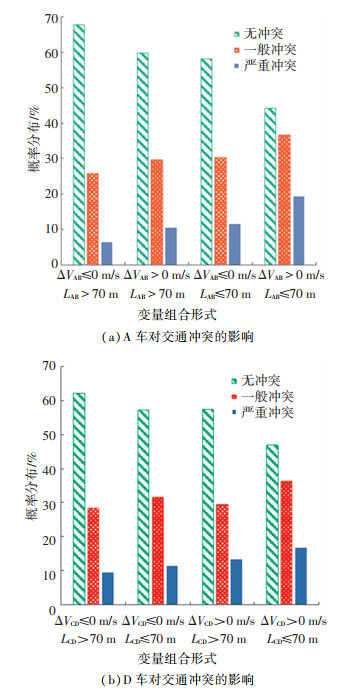
|
图 7 A车与D车对B、C车交通冲突的影响 Fig. 7 Influence of vehicles A and D on traffic conflicts of vehicles B and C |
由图 7分析可知,A、D车的行驶状态均会对B、C车发生交通冲突的概率产生影响,特别是当A、D两车距离交通冲突主体B、C车较近时,会提升交通冲突发生的概率.比较A、D车辆对交通冲突的影响,发现A车对于B、C车冲突的影响较D车更大.结果表明,驾驶员在驾驶车辆时,由于视觉关注点的原因,驾驶的注意重心相较于后方车辆D车会更多地倾向于前方车辆A,因此A车对B、C车冲突的影响大于D车,同时,在合流路段,匝道车辆加速驶入主道时,受前车影响很大,A车若处于减速状态,会引起B车跟随减速,提升B车与C车之间发生交通冲突的概率,在施工区应在符合施工规范条件下,减少合流区长度,优化合流区道路线形,使前车能尽快加速驶离合流区.
3.2.3 对比分析不同类型合流路段与车辆类型对交通冲突的影响由图 8分析可知,匝道合流路段交通冲突发生的概率高于转幅合流路段,特别是当B、C车为一辆小车和一辆大车时,交通冲突发生的概率较高.由于高速公路施工区的匝道合流路段匝道两旁的交通标牌、防撞桶等设施较多,可能会干扰匝道驾驶员合入主道时的行车视距,因此易提高交通冲突发生的概率.
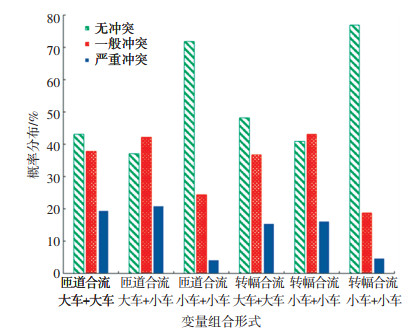
|
图 8 不同类型合流路段与车辆类型对交通冲突的影响 Fig. 8 Influence of different types of confluence sections and vehicle types on traffic conflicts |
类似,可以基于高速公路施工区交通冲突贝叶斯网络对其他单变量及多变量对交通冲突的影响进行分析.
4 基于交通冲突预测的驾驶策略评估可以基于表 2的离散类型输入已知的预测变量来对交通冲突进行预测,下面以采集的数据分布集中的1个例子来对交通冲突的预测过程进行描述,示例输入信息见表 3.
| 表 3 示例变量信息 Tab. 3 Variable information of the example |
基于贝叶斯网络的预测作用,可以为车辆的冲突规避措施提供指导,以本例中的C车为例,输入表4各变量信息,可以得到该时刻B、C车不发生冲突的概率为38.75%,一般冲突的概率为34.82%,严重冲突的概率为26.43%.本文利用贝叶斯网络的预测功能,计算C车后续的行为对交通冲突的影响,并以此来指导C车采取最合适的交通冲突规避措施,以策略I为例说明过程,步骤为:1)减速至C车加速度-2 m/s2 < ac≤0 m/s2;2)保持该加速度直至B、C车速度差ΔVx < 5 m/s;3)保持该行驶状态至B、C车纵向距离XBC>70 m.该策略链下B、C车交通冲突变化情况如图 9所示.
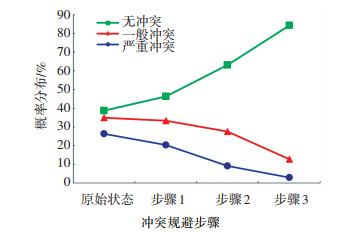
|
图 9 策略I对交通冲突状况的改变 Fig. 9 Effect of strategy I on traffic conflict situations |
通过图 9可以看出,当C车辆完成步骤1)时,发生严重冲突的概率由26.43%降低到20.34%,一般冲突概率由34.82%降低到33.27%;完成步骤2)时,严重冲突概率又降低到9.25%,一般冲突概率降低到27.59%;当完成步骤3)时,严重冲突的概率降低至3.03%,一般冲突的概率降至12.83%,策略链I的3个步骤会逐步减低交通冲突发生的概率及严重性.
类似地,该种交通冲突预测功能的应用可以为车辆避免冲突发生的驾驶行为作出指导,通过将车辆的后续采取的驾驶策略输入模型,输出交通类型概率分布,通过得到的概率分布对驾驶策略进行评估,对车辆进行驾驶指导,可以有效规避冲突,改善安全性.
参考贝叶斯网络建模的思想,可以基于搜索评分的算法对当前驾驶状态下所有后续可行驾驶策略进行搜索,后续通过交通冲突模型对各驾驶策略进行评估,选取评分最高的驾驶策略指导无人驾驶车辆后续驾驶,为无人驾驶对于车辆行驶的干预策略优化提供了一种思路.
5 结论1) 大型车的参与会提高交通冲突发生的概率以及冲突的严重性;车辆在高速公路施工区合流路段的超车抢道行为会提高交通冲突的概率;与冲突两车的相邻车辆会对交通冲突情况产生影响,因为驾驶员视觉的原因,冲突主体的前车对交通冲突影响更大;匝道合流路段发生交通冲突的概率和严重性较转幅路段更高.基于得到的结论可针对性的采取措施来降低交通冲突概率,提升交通安全水平,如分流大车;在特定路段采取管制措施禁止超车,设置车距确认设施;在符合规范的条件下减少合流区长度,优化道路线形等.
2) 在交通冲突建模过程中,融合交通冲突领域的先验知识,提前确定交通冲突模型的部分结构,再基于数据学习得到最终的模型,可以在提高建模效率的同时,提高模型的精确度.
3) 基于交通冲突模型,可以对车辆后续的驾驶策略进行评估或优化,指导车辆驾驶,为无人驾驶对车辆驾驶行为的干预提供了一种新思路.
4) 本研究主要考虑高速公路改扩建施工区合流路段的车辆因素,未引入道路参数与交通流数据(如主道匝道交通流量比、大车比等),道路参数及交通流的影响在一定程度上已经体现在采集到的微观车辆信息内,同时基于交叉验证的结果,可以看出该不足之处对交通冲突模型的结果影响较小.其次,受限于数据量,对预测变量的离散分类不够细化,下一步将采集更多的数据,细化变量的离散类型,更精确的对交通冲突进行研究.
| [1] |
JOHNSSON C, LAURESHYN A, De CEUNYNCK T. In search of surrogate safety indicators for vulnerable road users: a review of surrogate safety indicators[J]. Transport Reviews, 2018, 38(6): 765. DOI:10.1080/01441647.2018.1442888 |
| [2] |
MAHMUD S M S, FERREIRA L, HOQUE M S, et al. Application of proximal surrogate indicators for safety evaluation: a review of recent developments and research needs[J]. IATSS Research, 2017, 41(4): 153. DOI:10.1016/j.iatssr.2017.02.001 |
| [3] |
UZONDU C, JAMSON S, LAI F. Exploratory study involving observation of traffic behaviour and conflicts in Nigeria using the Traffic Conflict Technique[J]. Safety Science, 2018, 110: 273. DOI:10.1016/j.ssci.2018.08.029 |
| [4] |
ESSA M, SAYED T. Traffic conflict models to evaluate the safety of signalized intersections at the cycle level[J]. Transportation Research Part C: Emerging Technologies, 2018, 89: 289. DOI:10.1016/j.trc.2018.02.014 |
| [5] |
DAVIS G A, HOURDOS J, XIONG H, et al. Outline for a causal model of traffic conflicts and crashes[J]. Accident Analysis & Prevention, 2011, 43(6): 1907. DOI:10.1016/j.aap.2011.05.001 |
| [6] |
STYLIANOU K, DIMITRIOU L, ABDEL-ATY M A. Development of a spatio-temporal hybrid conflict severity indicator on urban network[R]. Washington DC: Transportation Research Board 97th Annual Meeting, 2018
|
| [7] |
KONG L, KHAN M K, WU F, et al. Millimeter-wave wireless communications for IoT-cloud supported autonomous vehicles: overview, design, and challenges[J]. IEEE Communications Magazine, 2017, 55(1): 62. DOI:10.1109/MCOM.2017.1600422CM |
| [8] |
LOSCRI V, RUGGERI G, VEGNI A, et al. Social structure analysis in Internet of Vehicles[C]// Proceedings of CoWPER Workshop, IEEE International Conference on Sensing, Communication and Networking. Hong Kong: IEEE, 2018: 1
|
| [9] |
朱顺应, 蒋若曦, 王红, 等. 机动车交通冲突技术研究综述[J]. 中国公路学报, 2020, 33(2): 15. ZHU Shunying, JIANG Ruoxi, WANG Hong, et al. Review of research on traffic conflict techniques[J]. China Journal of Highway and Transport, 2020, 33(2): 15. DOI:10.19721/j.cnki.1001-7372.2020.02.002 |
| [10] |
GETTMAN D, HEAD L. Surrogate safety measures from traffic simulation models[J]. Transportation Research Record: Journal of the Transportation Research Board, 2003, 1840(1): 104. DOI:10.3141/1840-12 |
| [11] |
JIA H F, JUAN Z C. Development of a car-following model based on desired spacing[J]. China Journal of Highway and Transport, 2000, 13(4): 86. |
| [12] |
ZHENG L, SAYED T, ESSA M. Validating the bivariate extreme value modeling approach for road safety estimation with different traffic conflict indicators[J]. Accident Analysis & Prevention, 2019, 123: 314. DOI:10.1016/j.aap.2018.12.007 |
| [13] |
LAURESHYN A, SVENSSON A, HYDÉN C. Evaluation of traffic safety, based on micro-level behavioural data: theoretical framework and first implementation[J]. Accident Analysis & Prevention, 2010, 42(6): 1637. DOI:10.1016/j.aap.2010.03.021 |
| [14] |
JENSEN F V, NIELSEN T D. Bayesian networks and decision graphs[M]. New York: Springer-Verlag, 2001.
|
| [15] |
De CAMPOS L M, CASTELLANO J G. Bayesian network learning algorithms using structural restrictions[J]. International Journal of Approximate Reasoning, 2007, 45(2): 233. DOI:10.1016/j.ijar.2006.06.009 |
| [16] |
HECKERMAN D, GEIGER D, CHICKERING D M. Learning Bayesian networks: the combination of knowledge and statistical data[J]. Machine Learning, 1995, 20(3): 197. |
| [17] |
KOHAVI R. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]// Proceedings of International Joint Conference on Artificial Intelligence. Montreal: IJCAI Inc., 1995: 1137
|
| [18] |
LARRANAGA P, KARSHENAS H, BIELZA C, et al. A review on evolutionary algorithms in Bayesian network learning and inference tasks[J]. Information Sciences, 2013, 233: 109. DOI:10.1016/j.ins.2012.12.051 |
 2020, Vol. 52
2020, Vol. 52


