2. 武汉理工大学 土木工程与建筑学院, 武汉 430070
2. School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan 430070, China
混凝土建筑物的大部分构件在服役年限内大都会出现不同程度的损伤,这直接影响了建筑的承载能力和变形能力.在最近几十年里,纤维增强复合材料(简称FRP)已被证明其能够有效提高混凝土结构的承载能力、变形能力和抗震性能[1-3].然而,目前关于FRP加固混凝土结构,尤其是加固混凝土柱的研究主要侧重于加固未损伤混凝土[4-7],而大部分混凝土构件在修复加固的过程中都是持载荷的或者有一定的损伤程度的.现有的试验结果表明,FRP约束已损伤混凝土柱和FRP约束未损伤混凝土柱的力学性能是不同的[8-11]. FRP修复损伤混凝土柱的机理是FRP环向约束抑制了混凝土柱的环向膨胀变形,从而提高了混凝土柱的强度和延性.因此,确定FRP约束损伤混凝土柱的环向应变-轴向应变关系是研究FRP修复损伤混凝土柱机理的基础.目前已有大量关于FRP约束混凝土环向应变-轴向应变关系模型[12-15],但只适应于FRP约束未损伤混凝土或者带载混凝土(混凝土承受荷载未超过其承载能力),尚未有FRP约束预损伤混凝土的环向应变-轴向应变关系模型.文献[12]通过大量试验数据与理论分析,推导出了FRP约束未损伤混凝土的环向应变-轴向应变关系模型.文献[15]基于建立的数据库,验证了文献[12]提出模型的准确性,也提出了FRP约束混凝土环向应变-轴向应变的关系模型.文献[16]在文献[12]模型的基础上引入极限膨胀比因子得到FRP约束损伤程度较小混凝土的环向应变-轴向应变关系模型.
鉴于现有FRP约束混凝土柱环向应变-轴向应变关系模型的局限性,本文首先建立数据库,对现有FRP约束混凝土的环向应变-轴向应变关系模型进行评估;然后基于Jiang等模型[12],提出了FRP约束损伤混凝土的环向应变-轴向应变关系模型,该模型考虑了混凝土的截面形状与抗压强度、混凝土的损伤类型与损伤程度、FRP约束层数等参数;最后通过数据库验证了新提出模型的准确性.
1 数据库建立本文从文献[8-9, 11-12, 16-22]中收集了264条试验曲线.收集到的试件截面形状包括圆形、正方形和长方形截面,其中正方形边长在100~200 mm之间,长方形截面尺寸为200 mm×400 mm,方形倒角半径在15~45 mm之间.进行预加载或者预损伤试验的FRP材料包括碳纤维增强复合材料(CFRP)、玄武岩纤维增强复合材料(BFRP)和玻璃纤维增强复合材料(GFRP),其中CFRP弹性模量Efrp在105~273 GPa之间,BFRP弹性模量Efrp为87 GPa,GFRP弹性模量Efrp为22 GPa. FRP厚度tfrp在0.111~2.54 mm之间.混凝土有普通混凝土和高强度混凝土两种,混凝土强度fco在16.47~70.2 MPa之间.相应的轴向应变峰值εco也在0.1%~0.33%之间,具体参数见表 1.
| 表 1 数据库参数 Tab. 1 Parameters of database |
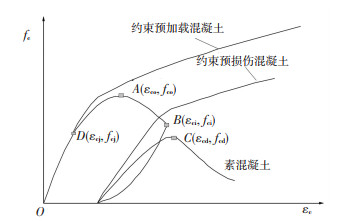
现有关于FRP约束损伤混凝土分为两种类型:(Ⅰ)FRP约束预损伤混凝土[8, 11],是采用加载设备对混凝土试件加载至预定数值,然后卸载至零,再进行FRP的包裹;(Ⅱ)FRP约束预加载混凝土[16, 20-21],是采用加载设备对混凝土试件加载至预先设定值,然后保持荷载不变,再进行FRP的包裹. FRP约束两种损伤类型的典型应力-应变关系曲线如图 1所示.
|
图 1 应力-应变关系曲线 Fig. 1 Stress-strain curves |
混凝土损伤程度被用来计算不同混凝土损伤类型的损伤.文献[11]提出了损伤类型(Ⅰ)中混凝土的损伤程度δ1计算公式为
| $ {\delta _1} = \frac{{{f_{{\rm{co}}}} - {f_{{\rm{cd}}}}}}{{{f_{{\rm{co}}}}}}, $ | (1) |
本文同样采用式(1)计算混凝土的损伤程度δ1.当εci≤εco时,fcd/fco=1-0.028 5m;当εci>εco时,fcd/fco=0.64(2-m)2-2.72(2-m)+3.1.其中:fcd为混凝土的残余强度;fci为卸载时混凝土承受的应力,fci在应力-应变关系曲线上升段卸载为正值,在应力-应变关系曲线下降段卸载为负值;εci为卸载时的混凝土轴向应变;fco为混凝土的强度;m为混凝土柱的卸载水平,m=fci/fco, 以百分数表示.
对于混凝土损伤类型(Ⅱ),文献[16]认为影响环向应变-轴向应变的关系的参数包括带载应力水平p、FRP约束应力fl和混凝土强度fco,所以本文拟建立混凝土损伤类型(Ⅱ)的损伤函数φ的计算公式为
| $ {\varphi = {a_1}\frac{{{p^{{a_2}}}}}{{{{({f_\text{l}}/{f_{{\rm{co}}}})}^{{a_3}}}}},} $ | (2) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} p = \frac{{{f_{{\rm{cj}}}}}}{{{f_{{\rm{co}}}}}},\\ {f_\text{l}} = \frac{{2{E_{{\rm{frp}}}}{t_{{\rm{frp}}}}{\varepsilon _{\rm{f}}}}}{b}. \end{array} $ |
式中:a1,a2,a3为待确定的常数;b为圆形截面的直径,或者正方形截面的边长,或者长方形截面的短边长度;fcj为带载包裹FRP时混凝土承受的应力;p为带载水平,以百分数表示;εf为FRP的极限应变.
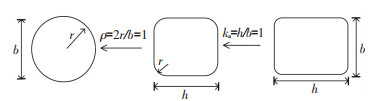
2.2 不同混凝土截面形状的转换关系为了方便计算FRP约束不同截面混凝土柱的力学性能,文献[23]基于FRP约束不同截面的混凝土的试验数据,提出用倒角半径比例系数ρ来转换正方形和圆形截面之间的几何关系,文献[24]用长宽比系数ka进一步扩展了正方形和长方形截面之间的几何关系. 3种截面形状的转换关系:当ρ=0、ka=1时,混凝土截面为正方形;当ρ=1、ka=1,混凝土截面为圆形;当ka≠1时,混凝土截面为长方形.不同截面形状的转换如图 2所示.本文也采用倒角半径比例系数ρ和长宽比系数ka表述这3种不同截面的转化关系.
|
图 2 不同截面转换 Fig. 2 Conversion of different cross sections |
为了评估现有环向应变-轴向应变关系模型是否适用于FRP约束损伤混凝土柱.本文选取了几个典型模型进行评估.
3.1.1 Jiang等模型文献[12]通过对48个FRP约束混凝土圆柱进行分析,得到了FRP约束未损伤混凝土圆柱的环向应变-轴向应变关系模型.计算公式为
| $ \begin{array}{*{20}{l}} {\frac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{co}}}}}} = 0.85\left( {1 + 8\frac{{{\sigma _\text{l}}}}{{{f_{{\rm{co}}}}}}} \right)\left\{ {{{\left[ {1 + 0.75\left( {\frac{{ - {\varepsilon _\text{l}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)} \right]}^{0.7}} - } \right.}\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left[ { - 7\left( {\frac{{ - {\varepsilon _\text{l}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)} \right]} \right\}.} \end{array} $ | (3) |
式中:εc为FRP约束混凝土柱轴向应变,εl为FRP约束混凝土柱环向应变,σl为FRP的应变为εl时对应的环向约束应力.
3.1.2 Lim等模型文献[15]基于2 038个试验数据,提出了FRP约束未损伤混凝土圆柱的环向应变-轴向应变关系模型,计算公式为
| $ {\varepsilon _{\rm{c}}} = \frac{{{\varepsilon _\text{l}}}}{{{v_{\rm{i}}}{{\left[ {1 + {{\left( {\frac{{{\varepsilon _\text{l}}}}{{{v_{\rm{i}}}{\varepsilon _{{\rm{co}}}}}}} \right)}^n}} \right]}^{\frac{1}{n}}}}} + 0.04\varepsilon _\text{l}^{0.7}\left[ {1 + 21{{\left( {\frac{{{\sigma _\text{l}}}}{{{f_{{\rm{co}}}}}}} \right)}^{0.8}}} \right]. $ | (4) |
式中:vi为混凝土的初始泊松比,n为控制曲线过渡段的形状参数.
3.1.3 何政等模型文献[16]通过对29个混凝土圆柱进行预加载试验,提出了预加载作用下FRP约束混凝土圆柱的环向应变-轴向应变的发展趋势.该模型在Jiang等模型基础上,考虑了带载应力水平,引入极限膨胀比影响因子,得到
| $ \begin{array}{*{20}{l}} {\frac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{co}}}}}} = 0.85\left\{ {{{\left[ {1 + 0.75\left( {\frac{{ - {\varepsilon _\text{l}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)} \right]}^{0.7}} - } \right.}\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left[ { - 7\left( {\frac{{ - {\varepsilon _\text{l}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)} \right]} \right\}\left( {1 + 8\frac{{{\sigma _\text{l}}}}{{{f_{{\rm{co}}}}}}} \right)\frac{1}{\xi }.} \end{array} $ | (5) |
式中ξ为带载约束混凝土极限膨胀比的影响因子.
3.2 现有模型评价基于表 1中的试验数据,对以上3个典型模型的准确性进行评估,评估结果见图 3.其中,图 3(a)为FRP约束未损伤混凝土,图 3(b)~3(f)为FRP约束预损伤混凝土曲线,图 3(g)~3(h)为FRP约束预加载混凝土曲线.

|
图 3 模型评价 Fig. 3 Evaluation of lateral strain-axial strain models |
图 3(c)、3(d)、3(f)中的试件编号依次为混凝土强度、包裹FRP层数和卸载水平.例如30-1L--90,代表C30的混凝土强度,包裹层数为1层,卸载水平m=-90%的混凝土试件. 图 3中其他图表的试件编号采用参考文献中的编号.
从图 3(a)可以看出,Jiang等模型和Lim等模型均可以准确计算FRP约束未损伤混凝土柱的环向应变-轴向应变关系;随着损伤程度δ1的逐渐增大,现有模型的计算值与试验值的偏离水平也逐渐增大,如图 3(b)~3(f)所示.由图 3(g)~3(h)可知,现有的模型不能准确计算FRP约束预加载混凝土柱的环向应变-轴向应变关系,其原因在于Jiang等模型和Lim等模型均是基于FRP约束未损伤混凝土试验数据提出的,随着混凝土损伤程度的增大,混凝土内部已经产生了裂缝,虽然包裹了FRP,损伤混凝土在轴向荷载作用下的环向变形与未损伤混凝土的环向变形仍然不同.文献[21]认为Jiang等模型可以用于FRP约束预加载圆形和矩形混凝土柱的环向应变-轴向应变关系.从图 3(g)、3(h)可以看出Jiang等模型在预测FRP约束预加载正方形混凝土柱的环向应变-轴向应变关系时,存在一定误差.此外,从图 3(b)、3(e)、3(h)可以看出,混凝土柱的截面类型对环向应变-轴向应变的关系影响也非常显著.此外,混凝土方柱作为建筑结构中一种常见的截面形式也需要进行分析.因此,需要建立一个考虑混凝土截面形状、混凝土损伤程度和损伤类型的模型,以便更加准确地预测FRP约束损伤混凝土柱的环向应变-轴向应变关系.
4 新模型的建立 4.1 模型推导现有文献[15, 21]和本文评估结果均表明Jiang等模型能够准确地预测FRP约束未损伤混凝土环向应变-轴向应变关系,但是该模型预测FRP约束损伤混凝土的环向应变-轴向应变关系存在误差.因此本文在Jiang等模型基础上,考虑截面形状系数(ρ,ka)、混凝土损伤φ,建立能够适用于FRP约束不同截面损伤混凝土的环向应变-轴向应变的关系模型,计算公式为
| $ \begin{array}{l} \frac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{co}}}}}} = 0.85\left[ {1 + 8\frac{{{\sigma _\text{l}}}}{{{f_{{\rm{co}}}}}} + d{\varphi ^e}{{\left( {\frac{{2r}}{b}} \right)}^f}{{\left( {\frac{h}{b}} \right)}^g}} \right] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {{{\left[ {1 + 0.75\left( {\frac{{ - {\varepsilon _\text{l}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)} \right]}^{0.7}} - \left[ {{\rm{exp}} - 7\left( {\frac{{ - {\varepsilon _\text{l}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)} \right]} \right\}. \end{array} $ | (6) |
式中:r为倒角半径,d、e、f、g为待确定的系数,φ为与混凝土损伤有关的函数.
对于损伤类型(Ⅰ)的混凝土试件,损伤函数φ为δ1.根据表 1中的FRP约束预损伤方柱与圆柱的数据,对式(6)进行非线性回归分析得到d、e、f、g的值分别为0.053、0.10、-1.072、-9.703,然后根据FRP约束预加载方柱与圆柱的数据,对式(2)非线性回归分析得到a1、a2、a3分别为0.11、0.21、1.99,所以式(2)可写为
| $ \varphi = 0.11\frac{{{p^{0.21}}}}{{{{({f_\text{l}}/{f_{{\rm{co}}}})}^{1.99}}}}. $ | (7) |
将两种不同损伤类型的损伤函数进行汇总,得
| $ \varphi = \left\{ {\begin{array}{*{20}{c}} {{\delta _1},}&{适用混凝土损伤类型(\text{I});}\\ {0.11\frac{{{p^{0.21}}}}{{{{({f_\text{l}}/{f_{{\rm{co}}}})}^{1.99}}}},}&{适用混凝土损伤类型(\text{II}).} \end{array}} \right. $ | (8) |
将式(8)和系数d、e、f、g的值代入式(6),即可得到FRP约束不同截面损伤混凝土的环向应变-轴向应变的关系表达式为
| $ \begin{array}{l} \frac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _{{\rm{co}}}}}} = 0.85\left[ {1 + 8\frac{{{\sigma _\text{l}}}}{{{f_{{\rm{co}}}}}} + 0.053{\varphi ^{0.10}}{{\left( {\frac{{2r}}{b}} \right)}^{ - 1.072}}{{\left( {\frac{h}{b}} \right)}^{ - 9.703}}} \right] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {{{\left[ {1 + 0.75\left( {\frac{{ - {\varepsilon _\text{l}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)} \right]}^{0.7}} - {\rm{exp}}\left[ { - 7\left( {\frac{{ - {\varepsilon _\text{l}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)} \right]} \right\}. \end{array} $ | (9) |
式中:σl为FRP约束不同截面混凝土柱的约束应力,σl=2Efrpεltfrp/b,其中Efrp为FRP的弹性模量, tfrp为加固混凝土的FRP厚度,其数值为单层FRP厚度与FRP层数的乘积.
当φ≠0,2r/b=1,h/b=1时,式(9)适用于FRP约束圆形损伤混凝土柱;当φ≠0,2r/b≠1,h/b=1时,式(9)适用于FRP约束正方形损伤混凝土柱;当φ≠0,2r/b≠1,h/b≠1时,式(9)适用于FRP约束长方形损伤混凝土柱;当参数φ=0时,表示混凝土没有损伤,此时式(9)转化为Jiang等模型.因此,式(9)是合理的,能够计算FRP约束不同截面、不同损伤类型混凝土柱的环向应变-轴向应变关系曲线.
4.2 模型评价 4.2.1 模型应于FRP约束损伤混凝土柱根据表 1中收集的数据对新提出的模型,即式(9)进行评价,评价结果如图 3所示. 图 3中评估系数ω用来量化不同模型的准确性:
| $ \omega = \frac{{\sum\nolimits_1^{{n_1}} {\left| {{\rm{Exp}}{{\rm{e}}_i} - {\rm{The}}{{\rm{o}}_i}} \right|} }}{{\sum\nolimits_1^{{n_1}} {\left| {{\rm{Exp}}{{\rm{e}}_i}} \right|} }}. $ | (10) |
式中Theoi、Expei和n1分别为第i个点的理论值、试验值和试验值的数量.
在图 3中的试验曲线上等间距取20点,计算系数ω值.当ω接近0时,说明理论值接近实验值.其中ω1、ω2、ω3和ω4分别用来表示式(9)、Jiang等模型、Lim等模型和何政等模型与试验值的相关性.
由图 3(a)、3(c)、3(f)可知,系数ω1均比ω2、ω3、ω4小. 图 3(d)中,系数ω1也相对较小.说明式(9)能够比Jiang等模型和Lim等模型更准确地预测FRP约束不同卸载水平混凝土圆柱的环向应变-轴向应变关系曲线.由图 3(b)、3(e)可知,式(9)也可准确预测FRP约束预损伤混凝土方柱的环向应变-轴向应变关系.由图 3(g)、3(h)可知,系数ω1均比相应的ω2、ω3、ω4小,说明式(9)比Jiang等模型,Lim等模型和何政等模型可以更准确地描述FRP约束预加载混凝土柱的环向应变-轴向应变关系.综上所述,相比现有的其他模型,本文新模型可以准确预测FRP约束不同损伤类型、不同损伤程度和不同截面类型的混凝土柱的环向应变-轴向应变关系,其原因是本文模型同时考虑了混凝土的损伤程度和截面类型.
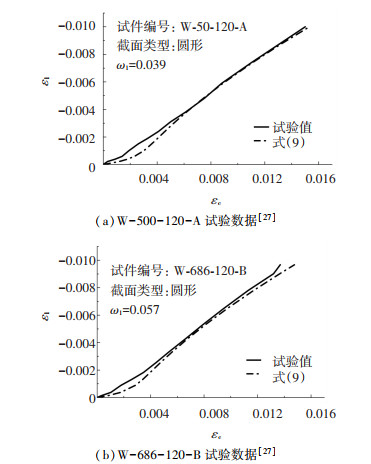
4.2.2 模型应于FRP约束高温损伤混凝土柱现有文献[25-27]表明:混凝土柱的高温损伤也是一种混凝土损伤类型,高温作用对混凝土应力-应变关系曲线的形状基本没有影响,只是改变了峰值应变、峰值应力及弹性模量.该结果与预加载、预损伤对混凝土的影响效果相同.文献[26]在FRP约束未损伤混凝土抗压强度模型基础上引入与本文相同的混凝土残余强度fcd,提出了FRP约束高温损伤混凝土柱抗压强度模型,这从另一角度说明高温损伤混凝土和预损伤、预加载损伤混凝土的损伤效果相同.因此,可以用FRP约束高温损伤混凝土柱的环向应变-轴向应变关系试验曲线,验证本文提出的模型,即式(9)的准确性.式(9)与FRP约束高温损伤混凝土柱的数据[27]对比结果如图 4所示.
|
图 4 模型预测高温损伤混凝柱 Fig. 4 Model prediction of high temperature damage concrete columns |
由图 4可知,式(9)的预测结果与试验值较吻合,系数ω1为0.039和0.057,这进一步验证了式(9)的准确性.因此,式(9)不仅可以用于预测FRP约束损伤混凝土柱的环向应变-轴向应变关系,也可以用于预测FRP约束高温损伤混凝土柱的环向应变-轴向应变关系.
5 结论1) 现有的FRP约束未损伤混凝土柱的环向应变-轴向应变关系模型不适用于FRP约束损伤混凝土.随着混凝土损伤程度的增加,现有模型的计算值与试验值的偏差增加.
2) 在Jiang等模型的基础上,基于FRP约束两种损伤类型、3种混凝土截面的264条环向应变-轴向应变关系,对FRP约束不同截面、不同损伤类型混凝土的环向应变-轴向应变关系模型进行推导,建立了FRP约束不同损伤混凝土柱的环向应变-轴向应变关系新模型,该模型既可以同时适用于FRP约束预损伤圆形、正方形、长方形截面混凝土柱,也可以计算FRP约束预加载混凝土圆柱与正方形柱.通过比较发现,该模型的预测曲线与试验曲线吻合度较高.
3) 现有文献中关于FRP约束损伤混凝土应力-应变关系试验曲线均具有强化特征,所以新模型只适用于具有应变强化特征的FRP约束损伤混凝土环向应变-轴向应变关系.
4) 在建立的数据库中,FRP约束长方形损伤混凝土柱的试验曲线较少,为进一步提高预测FRP约束长方形损伤混凝土环向应变-轴向应变关系的准确性,还需要进行大量的试验.
| [1] |
CAO Y G, JIANG C, WU Y F. Cross-sectional unification on the stress-strain model of concrete subjected to high passive confinement by fiber-reinforced polymer[J]. Polymers, 2016, 8(5): 186. DOI:10.3390/polym8050186 |
| [2] |
CAO Y G, WU Y F, LI X Q. Unified model for evaluating ultimate strain of FRP confined concrete based on energy method[J]. Construction and Building Materials, 2016, 103: 23. DOI:10.1016/j.conbuildmat.2015.11.042 |
| [3] |
ZHOU Y, LI M, SUI L, et al. Effect of sulfate attack on the stress-strain relationship of FRP-confined concrete[J]. Construction & Building Materials, 2016, 110: 235. DOI:10.1016/j.conbuildmat.2015.12.038 |
| [4] |
WU Y F, CAO Y. Energy balance method for modeling ultimate strain of confined concrete[J]. ACI Structural Journal, 2017, 114(2): 373. DOI:10.14359/51689429 |
| [5] |
WU Y F, CAO Y G. Effect of load path on behavior of FRP-confined concrete[J]. Journal of Composites for Construction, 2017, 21(4): 04017014. DOI:10.1061/(ASCE)CC.1943-5614.0000799 |
| [6] |
WU Y F, JIANG C. Quantification of bond-slip relationship for externally bonded FRP-to-concrete joints[J]. Journal of Composites for Construction, 2013, 17(5): 673. DOI:10.1061/(ASCE)CC.1943-5614.0000375 |
| [7] |
WU Y F, WEI Y. General stress-strain model for steel-and FRP-confined concrete[J]. Journal of Composites for Construction, 2015, 19(4): 04014069. DOI:10.1061/(ASCE)CC.1943-5614.0000511 |
| [8] |
LI P D, SUI L, XING F, et al. Stress-strain relation of FRP-confined predamaged concrete prisms with square sections of different corner radii subjected to monotonic axial compression[J]. Journal of Composites for Construction, 2019, 23(2): 04019001. DOI:10.1061/(ASCE)CC.1943-5614.0000921 |
| [9] |
MA G, LI H, DUAN Z. Repair effects and acoustic emission technique-based fracture evaluation for predamaged concrete columns confined with fiber-reinforced polymers[J]. Journal of Composites for Construction, 2012, 16(6): 626. DOI:10.1061/(ASCE)CC.1943-5614.0000309 |
| [10] |
MA G, LI H, YAN L, et al. Testing and analysis of basalt FRP-confined damaged concrete cylinders under axial compression loading[J]. Construction and Building Materials, 2018, 169: 762. DOI:10.1016/j.conbuildmat.2018.02.172 |
| [11] |
WU Y F, YUN Y, WEI Y, et al. Effect of predamage on the stress-strain relationship of confined concrete under monotonic loading[J]. Journal of Structural Engineering, 2014, 140(12): 04014093. DOI:10.1061/(ASCE)ST.1943-541X.0001015 |
| [12] |
JIANG T, TENG J. Analysis-oriented stress-strain models for FRP-confined concrete[J]. Engineering Structures, 2007, 29(11): 2968. DOI:10.1016/j.engstruct.2007.01.010 |
| [13] |
OZBAKKALOGLU T, LIM J C, VINCENT T. FRP-confined concrete in circular sections: review and assessment of stress-strain models[J]. Engineering Structures, 2013, 49: 1068. DOI:10.1016/j.engstruct.2012.06.010 |
| [14] |
KWAN A K H, DONG C X, HO J C M. Axial and lateral stress-strain model for FRP confined concrete[J]. Engineering Structures, 2015, 99: 285. DOI:10.1016/j.engstruct.2015.04.046 |
| [15] |
LIM J C, OZBAKKALOGLU T. Lateral strain-to-axial strain relationship of confined concrete[J]. Journal of Structural Engineering, 2014, 141(5): 04014141. DOI:10.1061/(ASCE)ST.1943-541X.0001094 |
| [16] |
何政, 金建平, 宋继广. 带载状态下CFRP约束混凝土圆柱膨胀比试验研究[J]. 工程力学, 2009, 26(9): 145. HE Zheng, JIN Jianping, SONG Jiguang. Experimental study on CFRP confined cylindrical expansion ratio under load[J]. Engineering Mechanics, 2009, 26(9): 145. |
| [17] |
XIAO Y, WU H. Compressive behavior of concrete confined by carbon fiber composite jackets[J]. Journal of Materials in Civil Engineering, 2000, 12(2): 139. DOI:10.1061/(ASCE)0899-1561(2000)12:2(139) |
| [18] |
DALGIC K D, ISPIR M, BINBIR E, et al. Effects of pre-damage on axial behavior of CFRP jacketed non-circular members[C]//Proceedings of the Conference on Civil Engineering Infrastructure based on Polymer Composites. Krakow, Poland: CECOM, 2012
|
| [19] |
DALGIC K D, ISPIR M, ILKI A. Cyclic and monotonic compression behavior of CFRP-jacketed damaged noncircular concrete prisms[J]. Journal of Composites for Construction, 2016, 20(1): 04015040. DOI:10.1061/(ASCE)CC.1943-5614.0000603 |
| [20] |
PAN Y, GUO R, LI H, et al. Analysis-oriented stress-strain model for FRP-confined concrete with preload[J]. Composite Structures, 2017, 166: 57. DOI:10.1016/j.engstruct.2017.01.007 |
| [21] |
PAN Y, GUO R, LI H, et al. Study on stress-strain relation of concrete confined by CFRP under preload[J]. Engineering Structures, 2017, 143: 52. DOI:10.1016/j.engstruct.2017.04.004 |
| [22] |
GUO Y, XIE J, XIE Z, et al. Experimental study on compressive behavior of damaged normal- and high-strength concrete confined with CFRP laminates[J]. Construction & Building Materials, 2016, 107: 411. DOI:10.1016/j.conbuildmat.2016.01.010 |
| [23] |
WU Y F, WANG L M. Unified strength model for square and circular concrete columns confined by external jacket[J]. Journal of Structural Engineering, 2009, 135(3): 253. DOI:10.1061/(ASCE)0733-9445(2009)135:3(253) |
| [24] |
WU Y F, WEI Y Y. Effect of cross-sectional aspect ratio on the strength of CFRP-confined rectangular concrete columns[J]. Engineering Structures, 2010, 32(1): 32. DOI:10.1016/j.engstruct.2009.08.012 |
| [25] |
吴波, 马忠诚, 欧进萍. 高温后混凝土在重复荷载作用下的应力-应变关系[J]. 地震工程与工程振动, 1997, 17(3): 36. WU Bo, MA Zhongcheng, OU Jinping. Stress-strain relations for concrete under cyclic loading after high temperature up to 800 ℃[J]. Earthquake Engineering & Engineering Vibration, 1997, 17(3): 36. |
| [26] |
欧阳利军, 许峰, 高皖扬, 等. 玄武岩纤维布约束高温损伤混凝土方柱轴压力学性能试验[J]. 复合材料学报, 2019, 36(2): 469. OUYANG Lijun, XU Feng, GAO Wanyang, et al. Axial compressive behavior of post-heated square concrete columns wrapped by BFRP sheets: an experimental investigation[J]. AMCS, 2019, 36(2): 469. DOI:10.13801/j.cnki.fhclxb.20180611.001 |
| [27] |
BISBY L A, CHEN J F, LI S Q, et al. Strengthening fire-damaged concrete by confinement with fibre-reinforced polymer wraps[J]. Engineering Structures, 2011, 33(12): 3381. DOI:10.1016/j.engstruct.2011.07.002 |
 2020, Vol. 52
2020, Vol. 52


