故障预测与健康管理(prognostic and health management, PHM)技术是利用大量状态监测数据和信息,借助各种故障模型和人工智能算法,监测、诊断、预测和管理设备健康状态的技术,实现从事后维修到视情维修的转变,实现设备的自主保障[1].随着国家城市轨道交通建设的发展,轨道车辆的检修也开始引入PHM[2].地铁塞拉门作为直接关系乘客安全的核心部件,是轨道交通系统设备中的重要子系统,一旦发生故障,会影响列车正常运行,耽误乘客出行,甚至危及乘客安全,发展地铁塞拉门PHM势在必行[3].目前针对地图塞拉门的PHM研究相对较少,也缺乏经过实践检验的塞拉门PHM模型.虽然可以将其他设备的PHM模型框架移植到地铁塞拉门PHM应用中,但仍需记录具有较高精度的原始波形数据,以便后续改进和完善PHM模型[4].对塞拉门PHM建模而言,最有用的数据是开关门过程中的电机电流数据,在目前实际设备中采用分布式采集和集中存储的条件下,无法提供使用原始数据直接进行高精度实时传输和保存所需的网络传输带宽以及海量数据存储空间.为了解决数据细节精度和数据存储空间之间的矛盾,有必要实现一种高压缩比和高细节还原度的数据压缩算法.
为保存海量过程数据可使用无损压缩和有损压缩两种方法,无损压缩实现了数据完美重构,但压缩后的体积约为原体积的50%,不利于数据的长期保存[5].有损压缩则在保证原始信号主要特征不丢失的前提下,大大提高了数据的压缩比.海量过程数据压缩在电力系统、地质勘探和心电图等行业中普遍并广泛应用了基于小波的有损数据压缩方法[6-8],其中一维小波需要存储空间小,算法成熟且应用简单,广泛应用于实时压缩存储场合[9-11].原始信号经过一维小波变换后,只对小波分解系数进行压缩存储,从而大大较少了需要保存的数据量.
在电力系统录波、地质勘探和心电图数据记录等实时应用中,广泛采用一维小波变换进行数据压缩[12-14].由于塞拉门无刷电机具有三相电流数据,与电力系统的三相实时录波相似,因此可借鉴电力系统行业中的一维小波变换进行压缩.地铁塞拉门采集到的电机电流采样数据幅值变化较大,数据冗余度不高,不同于电力系统中较低的畸变率,塞拉门电机电流采样数据中含有较多的高频成分,直接使用一维小波压缩,在波形细节还原度要求较高情况下压缩效果还有待提升,需对一维小波压缩方法进行适应性调整.
针对以上问题,本文提出了一种基于自适应阈值的一维小波压缩算法,该方法通过对采集到的原始电机电流数据进行分段预处理,根据各段幅值特点设定对应的阈值,将部分小波系数置零,仅处理剩下的系数,从而实现对海量原始过程数据的压缩.相较于传统全局固定阈值的小波变换压缩方法,基于分段自适应阈值小波变换的压缩方法在保证压缩率的前提下尽可能多地保留原始数据细节部分,具有更好的压缩效果,为后期地铁塞拉门PHM发展积累了大量的过程数据.
1 有损数据压缩方法 1.1 FFT压缩方法快速傅里叶变换(fast Fourier transform,FFT)是离散傅里叶变换的快速算法,该算法通过对数据进行FFT计算,在某个给定的错误容限下,把小于相应阈值的FFT系数置零,减少需要传输的系数,从而实现原始数据的压缩操作[15].
1.2 小波变换压缩方法小波变换是一种对信号的时间-频率的变尺度分析方法,与傅里叶分析相比,小波变换在时频两域都具有表征信号局部特征的能力[16],有利于对信号的局部特征进行分析.经过小波变换后,原始信号可由近似系数和细节系数进行表示,在保证重构信号误差的前提下大大减少了数据的存储空间,实现了数据的有损压缩,简要的压缩过程可分为以下3个步骤:1)根据选用的小波基和分解层数对原始信号进行小波分解,得到近似系数和细节系数;2)根据实际压缩需要(压缩比、误差比等性能指标),对各分解层系数进行处理,去除冗余的系数,得到新的小波系数;3)对新小波系数逆变换,重构信号.
1.3 常用压缩方法在数据压缩中,常使用的方法是FFT和小波变换相结合.电力系统中,记录的数据近似呈稳态周期性变化,信号以基波分量为主,高次谐波只占据很少的部分.针对此特点,文献[15]对数据默认进行FFT压缩,以重构信号与原始信号的误差作为压缩是否成功的依据,若误差大于阈值,则进行小波变换压缩,否则对下一通道数据进行压缩,通过两种压缩方法的结合,在满足误差精度的前提下大大提高了系统压缩率.
2 地铁塞拉门数据压缩方案 2.1 地铁塞拉门数据特点针对文献[15]的方法,本文对一次正常开关门过程中的电机电流霍尔传感器电压采集数据进行FFT分析,如图 1所示.高次谐波占据很大比重,数据能量没有集中在基波处,因此FFT压缩法不适用于塞拉门电机电流过程数据压缩,本文拟采用小波变换进行数据压缩.

|
图 1 塞拉门测试数据FFT分析结果 Fig. 1 FFT analysis results of plug door test data |
对原始采样数据进行数理统计,其中最大值为1.375 6 V,最小值为-0.722 2 V,平均值为0.013 5 V,标准差为1.167 6.从结果可以看出,原始信号的幅值变化较大,最大最小值间差值较大,同时数据在开关门启动阶段波动很大,这与心电图信号和地震录波信号特点相似.在心电图信号和地震录波应用中,对原始信号直接全部使用小波变换处理,通过压缩重构将幅值低的部分置零,只保留高幅值部分数据达到数据压缩目标[17-18].由于地铁塞拉门PHM应用还处于初步阶段,为了后续研究不遗漏主要信息,采集到的原始数据的高幅值和低幅值数据的细节部分都应尽量保留,直接使用小波变换对全局数据进行处理是不可取的,为此,应寻求其他可行方法压缩数据.
2.2 数据压缩新方案根据录波数据的上述特点,本文提出了一种基于小波变换的分段自适应阈值压缩算法,录波数据的压缩流程如图 2所示.通过预先设定的阈值及相关限制条件,将数据进行自动分段处理,在每一段数据中根据预先设定的压缩比对阈值进行修正,进行小波变换,将分解出来的系数进行保存,对比计算压缩率,若满足预设则表明本组数据已经压缩完毕,可以开始下一组数据的压缩流程,否则对阈值系数继续修正,直到达到预期的压缩比,完成数据压缩.

|
图 2 数据压缩流程图 Fig. 2 Flow chart of data compression |
小波变换不同于傅里叶变换,其基函数不具有唯一性,导致选取不同的小波基产生的结果不尽相同.小波的性质主要包括正交性、正则性、对称性、消失矩和紧支性等,选择小波基时应综合考虑这些性质,几种常用的小波基性质见表 1[19].
| 表 1 常见小波基性质对比 Tab. 1 Comparison of base properties of common wavelets |
由表 1可以看出,db系列小波具有良好的紧支集特性,较高的消失矩,一定的光滑性和近似对称,属于双正交小波,较为适合分析具有较大差距幅值的塞拉门电机信号,因此本文选用db3小波作为数据压缩的小波基.
3.2 分解层数的选择不同的信号,不同的压缩比下都存在一个压缩效果最好或接近最好的分解层数.分解层数对于压缩效果的影响很大,通常分解层数过多,经过后期对每一层小波空间的系数进行阈值处理会造成信号信息的丢失严重,重构的信号与原始信号相比误差较大,同时也会导致运算量增大,降低系统处理效率.分解层数过少,压缩效果不太理想,一般选用的小波分解层数在3~5层之间[20-21],通过对比试验,选用最合适的分解层数,在满足误差精度要求的前提下尽可能地提高数据压缩率,本文选用的是4层小波分解.
3.3 小波阈值的选取及阈值处理方法小波压缩中,阈值的选取是数据压缩的核心问题,目前阈值的选取方法有很多,本文参考文献[9]中的通用阈值法,该方法具有自适应强、计算量小的特点.
令信号f(t)在尺度1~m(1<m<j)上的阈值计算如下:
| $ {t_j} = \gamma \sigma \sqrt {2{\rm{log}}\;n} . $ | (1) |
式中:n为小波分解得到的小波系数的个数总和; j为尺度; σ为噪声强度; γ为比例常数,通常默认为1.
噪声的小波变换系数随尺度的增大而减小,信号的小波变换系数随尺度的增大而增大[10].因此在最小尺度空间,采用噪声的小波变换系数得出的噪声强度更占优势,其计算公式为
| $\sigma = \sqrt {\frac{1}{n}\sum\limits_{i = 0}^{n - 1} {{{({d_i} - \bar d)}^2}.} } $ | (2) |
式中:di为经过i次小波变换得到的最小尺度空间的小波系数;d为均值;n为该尺度小波系数个数.
使用式(1)对采集到的数据进行压缩试验发现,γ取1不利于提高数据压缩率.为此,本文针对不同区间段,不同的工况选取不同的优化后的γ值,实现数据的自适应压缩,在满足试验允许的重构误差的前提下尽可能地提高压缩比.
目前,阈值处理主要有两种方法,分别为硬阈值法和软阈值法[22].硬阈值法在解决均方误差问题上计算更简单,数据处理后系数中0的比例会大幅增加,便于提高压缩率,因此,在大数据压缩中,常使用硬阈值方法,其表达式为
| $ {u_{j, k}} = \left\{ \begin{array}{l} {u_{j, k}}, \;\;\;|{u_{j, k}}| \ge {t_j};\\ 0, \;\;\;\;\;\;\;|{u_{j, k}}| < {t_j}. \end{array} \right. $ | (3) |
式中uj, k为尺度j上的各点小波系数.
3.4 自适应分段由于小波压缩时的阈值根据数据的幅值进行设定,而原始数据幅值变化大,若采用不分段处理,全局阈值只有一个,压缩时若阈值较小,则重构精度高,但压缩率低,反之若提高了压缩率则无法保证足够的精度[23].
在保证过程数据具有较高压缩率的前提下,尽可能多地保留高幅值和低幅值的数据,使数据重构误差保持在允许范围内.现对原始数据进行分段处理,设原始信号为,其中一段数据为f(i),当这段数据的最大与最小值之差没有超过预设阈值m时,该部分数据视为一个数据段.分段过程中,若|f(i)max-f(i)min|≤m, 则
| $ {f_n}\left( i \right) = f\left( i \right). $ | (4) |
其中:fn(i)为分段后的单段数据,n为分段后的段数编号;m为预设定好分段阈值;i∈[i1, i2],i1~i2为原始数据中的一段连续数据.
3.5 压缩算法评估参数为衡量重构信号精度,本文选取了5个评估参数对压缩算法进行评估[24]:
1) 压缩率(compression ratio, CR)为
| $ {\rm{CR}} = \frac{{{N_{{\rm{save}}}}}}{{{N_0}}} \times 100\% . $ | (5) |
式中:N0为原始信号的大小,Nsave为压缩后保留的小波系数的大小.
2) 误差百分比(percentage error, PR)为
| $ {\rm{P}}{{\rm{R}}_i} = \frac{{\left| {{N_{{\rm{iop}}}}\left( i \right) - {N_{{\rm{out}}}}\left( i \right)} \right|}}{{{N_{{\rm{out}}}}\left( i \right)}} \times 100\% . $ | (6) |
式中:Niop为原始信号,Nout为压缩重构后信号,n为信号总个数,且1≤i≤n.
3) 最大误差百分比(maximum error, MAXE)为
| $ {\rm{MAXE}} = {\rm{max}}({\rm{P}}{{\rm{R}}_i}). $ | (7) |
4) 平均误差百分比(mean error, MEAE)为
| $ {\rm{MEAE}} = {\rm{mean}}({\rm{P}}{{\rm{R}}_i}). $ | (8) |
5) 失真率(distortion ratio, DR)为
| $ {\rm{DR}} = \frac{{\sqrt {\sum\limits_{i = 1}^n {{{({N_{{\rm{iop}}}}\left( i \right) - {N_{{\rm{out}}}}\left( i \right))}^2}} } }}{{\sqrt {\sum\limits_{i = 1}^n {{N_{{\rm{out}}}}{{\left( i \right)}^2}} } }}. $ | (9) |
本文使用的塞拉门电机电流采样数据来自于江苏省无锡市地铁2号线查桥车辆段段内实测数据.规定单次完整开关门过程中的霍尔传感器电压采样数据为一组试验数据,采集过程中,在开关门前后各延时1 s进行信号采集,一组数据塞拉门电机单相电流霍尔传感器电压采集数据波形如图 3所示.本次试验共取10组数据进行数据压缩试验.

|
图 3 原始信号波形 Fig. 3 Waveform of original signal |
采用db3小波作为小波基,分解层数取4,使用硬阈值法对原始信号进行压缩试验,当采用相近数据压缩率时(2.5%左右),使用自适应分段法将数据分为14段,分段后的各段的阈值放大系数i1~i14分别为:66.521、12.814、21.053、33.815、41.328、28.485、5.961、63.120、26.026、53.352、55.323、62.985、62.825、68.128.使用文献[15]中的不分段全局阈值小波压缩算法和FFT压缩算法作对比试验,i0为不分段小波压缩时的阈值放大系数,其值为54.525.
原始数据经过多种压缩算法压缩后,不同压缩算法处理得到的重构波形和百分比误差结果如图 4~6所示,各项参数对比结果汇总见表 2.
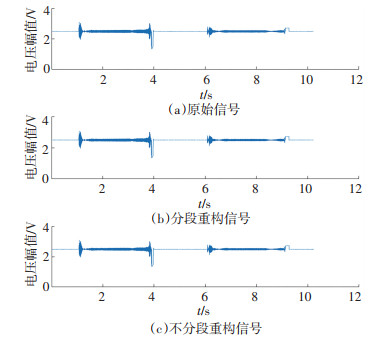
|
图 4 原始信号和重构信号 Fig. 4 Original signal and reconstructed signal |

|
图 5 原始信号和重构信号百分比误差 Fig. 5 Percentage error of original signal and reconstructed signal |

|
图 6 原始信号和重构信号局部放大图 Fig. 6 Partial enlarged detail of original signal and reconstructed signal |
| 表 2 不同算法处理后参数对比 Tab. 2 Comparison of parameters processed by different algorithms |
从图 4~6和表 2可以看出,FFT压缩算法各项误差均是最大的,该算法不适用于地铁塞拉门开关门过程中的电机电流采样数据压缩.同时在压缩率(约2.5%)、百分比误差和整体失真率(约0.3%)相近的前提下,采用分段自适应阈值压缩的重构信号在波形幅值较小的区域,数据细节得到了更好的保留,相对于传统不分段方法,本文方案在幅值较小的区域可以保留更多的时频域细节信息,系统的局部失真率更小.
对剩余多组数据进行分段自适应阈值小波压缩试验,结果汇总见表 3,从表 3可以看出,基于分段自适应阈值小波压缩的方法效果稳定.
| 表 3 各组数据压缩后各参数汇总 Tab. 3 Parameters of each data group after compression |
综上所述,分段自适应阈值小波压缩法在塞拉门电机电流信号采样数据实时压缩传输领域具有良好的使用效果,在保证较大压缩率的同时保留了更多原始信号的局部细节,有利于后期对重构信号的分析研究.
5 结论1) 针对传统小波压缩算法在地铁塞拉门PHM过程数据实时压缩传输中的不足,提出了一种基于分段自适应阈值的小波变换压缩算法.
2) 改进的压缩算法通过对原始数据进行自动分段、自动调整各段阈值放大系数,更有效地去除了数据的冗余性,兼顾了高、低幅值数据处理效果,在保证重构信号精度的前提下实现了原始数据的大压缩比有损压缩与重构.
3) 改进的压缩算法在现场进行推广应用,可以有效解决海量数据的存储问题,为后期地铁车辆塞拉门PHM应用提供丰富和可靠的数据来源.
| [1] |
年夫顺. 关于故障预测与健康管理技术的几点认识[J]. 仪器仪表学报, 2018, 39(8): 1. NIAN Fushun. Viewpoints about the prognostic and health management[J]. Chinese Journal of Scientific Instrument, 2018, 39(8): 1. |
| [2] |
李雪昆. 故障预测与健康管理技术在地铁列车上的应用[J]. 城市轨道交通研究, 2018, 21(2): 105. LI Xuekun. Application of fault prediction and health management technology in metro train[J]. Urban Mass Transit, 2018, 21(2): 105. |
| [3] |
高伟民, 茅飞. 地铁车门PHM系统应用[J]. 城市轨道交通, 2019(5): 33. GAO Weiming, MAO Fei. Application of PHM system in plug door[J]. China Metros, 2019(5): 33. |
| [4] |
王玘, 何正友, 林圣, 等. 高铁牵引供电系统PHM与主动维护研究[J]. 西南交通大学学报, 2015, 50(5): 942. WANG Qi, HE Zhengyou, LIN Sheng, et al. PHM and active maintenance for high-speed railway traction power supply system[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 942. |
| [5] |
刘箭言, 郭哲, 刘娜, 等. 基于DFT的油井数据有损压缩算法[J]. 北京理工大学学报, 2015, 35(3): 299. LIU Jianyan, GUO Zhe, LIU Na, et al. A lossy compression algorithm based on DFT for working parameters of oil well[J]. Journal of Beijing Institute of Technology, 2015, 35(3): 299. |
| [6] |
陈祖斌, 王丽芝, 宋杨, 等. 基于压缩感知的小波域地震数据实时压缩与高精度重构[J]. 石油地球物理勘探, 2018, 53(4): 674. CHEN Zubin, WANG Lizhi, SONG Yang, et al. Seismic data real-time compression and high-precision reconstruction in the wavelet domain based on the compressed sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 674. |
| [7] |
刘毅, 宋余庆, 刘哲, 等. 一种面向体域网的ECG信号小波阈值去噪法[J]. 计算机科学, 2014, 41(11): 175. LIU Yi, SONG Yuqing, LIU Zhe, et al. Wavelet threshold de-noising method oriented to body area networks[J]. Computer Science, 2014, 41(11): 175. |
| [8] |
鄢海舟, 胥布工, 李海滨, 等. 小波去噪与压缩在电厂设备中的应用[J]. 电测与仪表, 2017, 54(11): 110. YAN Haizhou, XU Bugong, LI Haibin, et al. Application of wavelet denoising and compression in the equipment of power plant[J]. Electrical Measurement & Instrumentation, 2017, 54(11): 110. |
| [9] |
李清泉, 秦冰阳, 司雯, 等. 混合粒子群优化小波自适应阈值估计算法及用于局部放电去噪[J]. 高电压技术, 2017, 43(5): 1485. LI Qingquan, QIN Bingyang, SI Wen, et al. Estimation algorithm for adaptive threshold of hybrid particle swarm optimization wavelet and its application in partial discharge signals de-noising[J]. High Voltage Engineering, 2017, 43(5): 1485. |
| [10] |
杨博雄, 柳林, 秦前清. 基于形态小波的地震数据压缩方法研究[J]. 武汉大学学报(信息科学版), 2011, 36(7): 785. YANG Boxiong, LIU Lin, QIN Qianqing. Research of seismic data compression method based on morphological wavelet[J]. Geomatics and Information Science of Wuhan University, 2011, 36(7): 785. |
| [11] |
李雪梅, 王学伟, 温丽丽, 等. 整数算法小波变换实时数据压缩与重构算法[J]. 电测与仪表, 2013, 50(8): 20. LI Xuemei, WANG Xuewei, WEN Lili, et al. Real-time data compression & reconstruction algorithm based on integer arithmetic wavelet transform[J]. Electrical Measurement & Instrumentation, 2013, 50(8): 20. |
| [12] |
赵艳粉, 杨洪耕. 二维离散小波变换在电能质量检测数据压缩中的应用[J]. 电力系统自动化, 2006(15): 51. ZHAO Yanfen, YANG Honggeng. Data compression method using 2-dimensional discrete wavelet transform for power quality detection[J]. Automation of Electric Power Systems, 2006(15): 51. |
| [13] |
AGARWAL S, REGENTOVA E E, KACHROO P. Multidimensional compression of ITS data using wavelet-based compression techniques[J]. Transactions on Intelligent Transportation Systems, 2017, 18(7): 1907. |
| [14] |
BENZID R, MARIR F, BOUGUECHAL N. Electrocardiogram compression method based on the adaptive wavelet coefficients quantization combined to a modified two-role encoder[J]. Signal Processing Letters, 2007, 14(6): 373. |
| [15] |
黄纯, 杨帅雄, 梁勇超, 等. 电力系统故障录波数据实用压缩方法[J]. 电力自动化设备, 2014, 34(6): 162. HUANG Chun, YANG Shuaixiong, LIANG Yongchao, et al. Practical data compression method for power system fault records[J]. Electric Power Automation Equipment, 2014, 34(6): 162. |
| [16] |
CAGNAZZO M, PARRILLI S, POGGI G, et al. Improved class-based coding of multispectral images with shape-adaptive wavelet transform[J]. Geoscience and Remote Sensing Letters, 2007, 4(4): 566. |
| [17] |
蒋国华, 潘健勇, 董齐芬, 等. 基于嵌入式零树小波的心电信号压缩算法及实现[J]. 传感技术学报, 2012, 25(7): 880. JIANG Guohua, PAN Jianyong, DONG Qifen, et al. Embedded zero-tree wavelet based ECG signal compression algorithm and its implementation[J]. Chinese Journal of Sensors and Actuators, 2012, 25(7): 880. |
| [18] |
吴继伟, 孔祥茜, 岳继光. 地震数据的小波变换压缩方法[J]. 电子技术应用, 2006(1): 34. WU Jiwei, KONG Xiangxi, YUE Jiguang. Wavelet transform compression method for seismic data[J]. Application of Electronic Technique, 2006(1): 34. |
| [19] |
张明, 龚建峰, 何顺帆. 基于谐波滤波器组的电能质量扰动数据压缩方法[J]. 电力系统自动化, 2016, 40(15): 93. ZHANG Ming, GONG Jianfeng, HE Shunfan. Data compression method for power quality disturbance based on harmonic filter bank[J]. Automation of Electric Power Systems, 2016, 40(15): 93. |
| [20] |
贾毅婷, 张东来, 张斌. 基于小波尺度相关性的暂态数据降噪压缩方法[J]. 电力系统自动化, 2013, 37(5): 68. JIA Yiting, ZHANG Donglai, ZHANG Bin. Power quality disturbance data denoising and compression using signal's scale-dependencies of wavelet coefficients[J]. Automation of Electric Power Systems, 2013, 37(5): 68. |
| [21] |
刘志刚, 钱清泉. 基于多小波的电力系统故障暂态数据压缩算法[J]. 中国电机工程学报, 2003, 239(10): 22. LIU Zhigang, QIAN Qingquan. Compression of fault transient data in electric power system based on multiwavelet[J]. Proceedings of the CSEE, 2003, 239(10): 22. |
| [22] |
杨丹, 秦梦芝, 徐彬, 等. 基于EMD的心电信号压缩算法[J]. 东北大学学报(自然科学版), 2014, 35(7): 926. YANG Dan, QIN Mengzhi, XU Bin, et al. ECG compression algorithm based on empirical mode decomposition[J]. Journal of Northeastern University (Natural Science), 2014, 35(7): 926. |
| [23] |
鲁晓帆, 刘志刚, 吴峰. 多核系统的小波包并行算法及其在电力系统数据压缩中的应用[J]. 电力自动化设备, 2013, 33(5): 130. LU Xiaofan, LIU Zhigang, WU Feng. Parallel wavelet packet algorithm based on multi-core system and its application in power data compression[J]. Electric Power Automation Equipment, 2013, 33(5): 130. |
| [24] |
何正友, 钱清泉. 电力系统暂态信号分析中小波基的选择原则[J]. 电力系统自动化, 2003, 27(10): 45. HE Zhengyou, QIAN Qingquan. An electric power system fault transient data compression method based on optimal wavelet[J]. Proceedings of the CSEE, 2003, 27(10): 45. |
 2020, Vol. 52
2020, Vol. 52


