2. 武汉科技大学 城市学院,武汉 430083
2. City College, Wuhan University of Science and Technology, Wuhan 430083, China
随着服役时间的增加,船壳的防腐涂层不可避免地会遭到破损,裸露的钢质船体与铜合金螺旋桨在海水中形成电偶腐蚀,腐蚀电流流过具有导电性的海水会在船体附近产生腐蚀电场[1].学者们研究了海床电导率、海水电导率、温度、流速、深度等海洋环境因素及潜艇自身潜水状态对舰船腐蚀电场的影响[2-3],建立了舰船腐蚀电场等效电偶极子模型,并分析了水平和垂直电偶极子在多层介质中产生的电磁场[4-6].由于舰船腐蚀电场对船体周围的电磁环境产生一定的影响,尤其是给船上电磁通信带来了很大的干扰,因此,必须对其进行抑制或者消除.基于舰船消磁思想,通过在船体上安装电场补偿装置,使补偿电流与腐蚀电流在海水中产生的电场方向相反,从而实现降低海水中腐蚀电场的目的[7].补偿阳极位置是电场补偿装置的重要参数之一,其对腐蚀电场防护效果具有显著的影响,如何选择合适的补偿阳极位置是电场补偿装置列装前亟需解决的问题,目前,这方面的研究鲜见报道.
边界元法广泛地运用于石油钻井平台、海底管道、舰船等各种海洋结构件的腐蚀及阴极保护系统优化问题的仿真[8-10].边界元法是基于加权余量法,将边值问题转化为边界积分方程问题,再利用有限元离散技术构造线性方程组的一种方法[11],早在20世纪80年代,就有人开始将边界元法应用于海洋工程结构的腐蚀防腐问题的研究[12-13].
本文采用三维边界元法建立潜艇腐蚀静电场模型,并将实验所测得的非线性极化曲线作为模型的边界条件,研究补偿阳极位置对腐蚀电场防护效果的影响,得到了阳极位置对电场防护效果的影响规律,结合舰船等效电偶极子模型理论合理地解释了电场防护的原理.
1 边界元法的基本理论对于三维腐蚀电场问题,腐蚀介质与电极表面的电位分布符合拉普拉斯方程与下述边界条件[8, 12]为
| $ {\nabla ^2}u = \frac{{{\partial ^2}u}}{{{\partial ^2}x}} + \frac{{{\partial ^2}u}}{{{\partial ^2}y}} + \frac{{{\partial ^2}u}}{{{\partial ^2}z}} = 0, $ | (1) |
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{\rm{恒电位边界}}:u = {u_0},}\\ {{\rm{恒电流边界}}:q = \frac{{\partial u}}{{\partial n}} = {q_0},} \end{array}\\ \begin{array}{*{20}{l}} {{\rm{阳极极化边界}}:q = \frac{{{i_{\rm{a}}}}}{\sigma } = \frac{1}{\sigma }{f_{\rm{a}}}({u_{\rm{a}}}),}\\ {{\rm{阴极极化边界}}:q = \frac{{{i_{\rm{c}}}}}{\sigma } = \frac{1}{\sigma }{f_{\rm{c}}}({u_{\rm{c}}}).} \end{array} \end{array} \right. $ | (2) |
式中:u为海水介质及电极表面的电位;n为边界外法线;q为电位的法向导数(场强);u0、q0分别为S1和S2边界上的u、q恒定值;σ为海水电导率;ia、ic分别表示阳极电流密度和阴极电流密度;fa(ua)、fc(uc)分别表示阳极极化方程和阴极极化方程.
式(1)的等价边界积分方程为
| $ {c_i}{u_i} + \int\limits_S u (\xi )\frac{{\partial {u^*}(i,\xi )}}{{\partial n(\xi )}}{\rm{d}}S = \int\limits_S q (\xi ){u^*}(i,\xi ){\rm{d}}S. $ | (3) |
式中:ui为Ω域内任一场点i处的电位;ci为常数,当场点i位于光滑边界面上时,ci=1/2,当场点i位于Ω域内时,ci=1,当场点i位于Ω域外时,ci=0;u(ξ)、q(ξ)分别表示边界上任一点ξ的电位和电位法向导数;u*(i, ξ)为三维静态电磁场问题的基本解,其表达式为
| $ {u^*}(i,\xi ) = \frac{1}{{4\pi r}}. $ | (4) |
其中r为i、ξ间的距离.
利用有限元离散技术将边界进行剖分并根据边界积分方程(3)构造线性方程组,即可求得求解域内的电位,得到海水域中电位分布后,再由极化方程(5)求得电流密度分布,最后由方程(6)求解电场分布.
| $ {\left\{ {\begin{array}{*{20}{l}} {{i_c}}&{ = f({u_c}),}\\ {{i_a}}&{ = f({u_a}).} \end{array}} \right.} $ | (5) |
| $ {E = \frac{i}{\sigma }.} $ | (6) |
利用Solidworks 2016建立潜艇空间直角坐标系下的几何模型.考虑到舰船停靠码头时,船体左右舷两侧容易被码头磨损导致涂层脱落,故设定两处破损(总破损率为2%)对称分布于潜艇左右舷两侧.本文不考虑潜艇的外加电流阴极保护系统(将ICCP视为关闭状态),而仅考虑一对电场补偿阳极对称分布于潜艇左右舷两侧.采用COMSOL Multiphysics仿真软件中电流分布(边界元)接口建立潜艇腐蚀静电场边界元模型,结合实际情况,将螺旋桨和涂层破损处视为裸露金属浸泡于海水中,而将船体及舵视为有机涂层完好包覆.整个模型的求解域及边界条件设定如下:1)无限空区域为均匀海水介质,电导率σ=4 S/m;2)将碳钢的非线性极化曲线设置为破损处的边界条件;3)将铜合金的非线性极化曲线设置为螺旋桨的边界条件;4)补偿阳极为恒电流边界,其余默认为绝缘边界.对潜艇表面进行网格剖分,剖分结果如图 1所示,边界节点总数为45 973个,边界三角形单元总数为91 942个,最后采用BiCGStab迭代求解器对模型进行求解.
|
图 1 潜艇三维模型网格剖分示意图 Fig. 1 Meshing diagram of submarine by COMSOL |
模拟了补偿阳极在6个不同位置的腐蚀电场分布情况,补偿阳极中心点坐标分别为:A(1 m, 0°),B(5 m, 0°),C1(10. 8 m, 0°),C2(10.8 m, 45°),C3(10.8 m, 90°)和D(16.6 m, 0°),第一个坐标为纵向坐标,即相应点在所建三维坐标系下的X轴坐标,第二个坐标为周向坐标,即相应点到X轴的垂线与XOY平面的夹角.其中,A、B、C1、D均为0°,研究阳极位置纵向变化对电场防护效果的影响,而C1、C2、C3的X轴坐标相同,研究阳极位置周向变化对电场防护效果的影响.
2.2 动电位极化曲线测试模型中船壳及舵均采用高强低合金921A钢,螺旋桨采用耐腐蚀性较好的B10铜合金,采用三电极体系在CS310电化学工作站上测试上述两种船用材料的动电位极化曲线,实验介质为电导率σ=4 S/m的NaCl溶液.其中,工作电极采用环氧树脂封装的921A低合金钢和B10铜合金,试样尺寸为ϕ1.1 cm×1 cm,故金属暴露面积为1.0 cm2,用SiC湿砂纸逐级打磨至1 000目,丙酮脱脂,并依次用乙醇和蒸馏水冲洗,然后置于干燥箱中烘干;参比电极为Ag/AgCl电极;辅助电极为面积S=2 cm2的铂片电极.工作电极先在溶液中浸泡一段时间,等到开路电位基本稳定后开始测试,扫描电位为-1.1~0 V,扫描速率为1.0 mV/s.
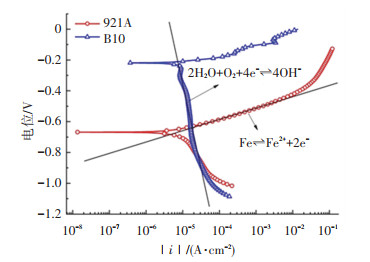
3 结果与讨论 3.1 极化曲线分析921A钢和B10铜合金的极化曲线如图 2所示,由图可知,921A和B10的开路电位分别为-0.68、-0.28 V(参比电极为Ag/AgCl).由于吸氧腐蚀的氧还原反应速度由氧扩散步骤控制,因此,铜合金的阴极极化电流密度在一定电位范围内几乎保持不变,即极限电流密度;而钢具有较高的析氢过电位,阴极极化过程中氧还原的同时发生析氢反应,故钢的阴极极化过程中没有出现极限电流密度.以钢为材料的船体破损处和以铜合金为材料的螺旋桨,在海水中形成破损处—海水—螺旋桨—大轴—破损处的回路,从而构成电偶腐蚀,其中,破损处阳极极化发生金属本身的氧化,如式(7)所示,而螺旋桨阴极极化发生氧还原反应,如式(8)所示.
| $ {{\rm{Fe}} \to {\rm{F}}{{\rm{e}}^{2 + }} + {\rm{2}}{{\rm{e}}^ - },} $ | (7) |
| $ {{\rm{2}}{{\rm{H}}_{\rm{2}}}{\rm{O}} + {{\rm{O}}_2} + {\rm{4}}{{\rm{e}}^ - } \to {\rm{4O}}{{\rm{H}}^ - }.} $ | (8) |
|
图 2 921A钢和B10铜合金的实测极化曲线 Fig. 2 Polarization curves of 921A steel and B10 copper alloy |
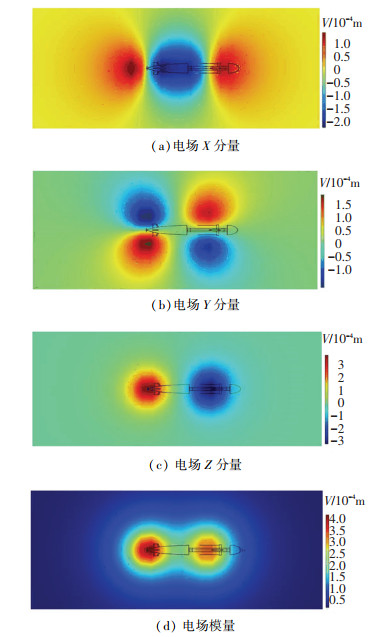
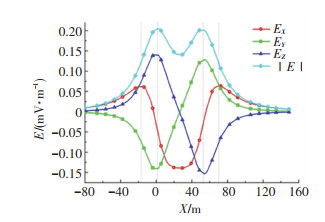
图 3为没有补偿电流时Z=-16 m平面上的电场三分量及电场模值分布,X分量、Z分量和模量均对称分布于XOZ平面两侧,而Y分量关于XOZ平面反对称分布.为了更直观地分析舰船水下腐蚀电场的分布,选择以点(-80,16,-16)和点(160,16,-16)为端点的路径作为观测对象. 图 4为无电流补偿时,电场三分量及电场模量的线分布,EX在X=-16 m和X=68 m附近有正峰值,而在X=25 m附近有负峰值;EY在X=0 m(螺旋桨)附近有负峰值而在X=52.5 m(破损区域中点)附近有正峰值;EZ分布与EY相反;|E|呈现双峰分布,两个峰值分别分布在螺旋桨和破损区域中点附近.以上电场峰值均在10-4 V/m数量级.
|
图 3 无电流补偿时Z =-16 m平面上的腐蚀电场分布 Fig. 3 Corrosion electric field distribution on plane Z=-16 m without compensation current |
|
图 4 无电流补偿时指定路径上的电场线分布 Fig. 4 Electric field distribution on specified path without compensation current |
本文设定补偿阳极的输出总电流为6 A,通过改变补偿阳极位置研究其对舰船腐蚀电场防护效果的影响,图 5为补偿阳极在B位置时Z=-16 m平面上的电场三分量及电场模量分布.由于补偿阳极布置在靠近螺旋桨的位置,外加补偿电流后舰艉处的电场增大,而涂层破损处的电场减小.与无电流补偿时的电场分布相比,外加补偿电流后的电场X分量分布发生较大的变化,舰舯部的负峰值区域明显减小,而电场Y分量、Z分量和模量没有明显变化,均在舰艉和涂层破损处出现电场峰值.
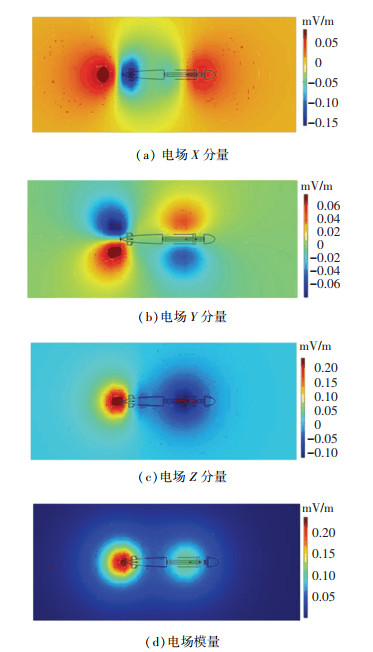
|
图 5 补偿阳极在B位置时Z =-16 m平面上的腐蚀电场分布 Fig. 5 Corrosion electric field distribution on plane Z=-16 m with compensation anode at position B |
图 6为研究路径上电场三分量及电场模量随补偿阳极位置变化的分布,表 1给出了补偿阳极在不同位置时电场最大绝对值和相应的电场防护效果.电场防护效果定义为
| $ \Delta |E| = \frac{{|E{|_0} - |E{|_{{\rm{cur}}}}}}{{|E{|_0}}} \times 100\% . $ | (9) |
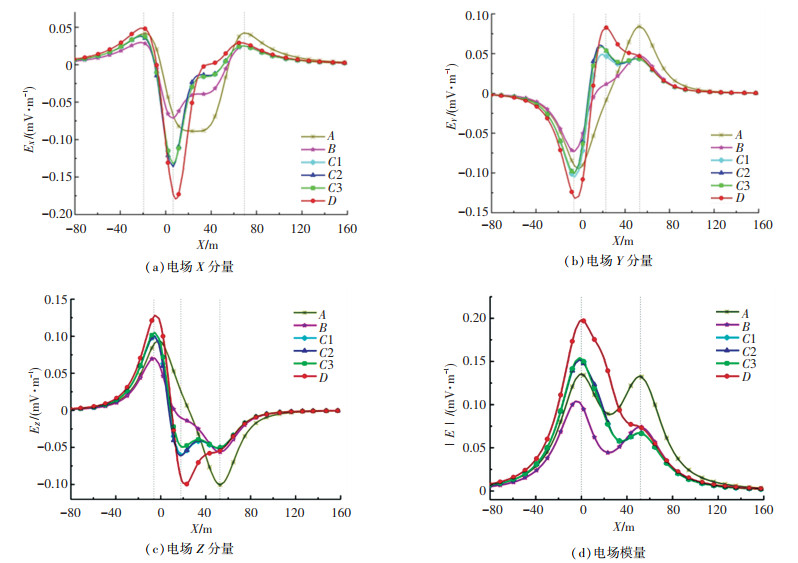
|
图 6 指定路径上电场线分布随补偿阳极位置的变化 Fig. 6 Variation of electric field distribution along specified paths with positions of compensation anode |
| 表 1 补偿阳极在不同位置时电场最大绝对值和相应的电场防护效果 Tab. 1 Maximum absolute value of electric field and corresponding damping effect for compensation anode at different positions |
式中:Δ|E|表示电场防护效果,|E| 0表示无电流补偿时的电场最大绝对值,|E| cur表示外加电流补偿时的电场最大绝对值.
当补偿阳极在C1、C2和C3位置时,电场线分布曲线几乎重合,说明阳极位置周向变化对舰船腐蚀电场的影响很小,而阳极位置纵向变化(A/B/C1/D)对电场分布有显著的影响.当补偿阳极位置改变时,EX分布由对称曲线变为非对称曲线,电场正峰值位置保持不变而负峰值移动至螺旋桨附近,EY负峰值位置保持不变而正峰值由破损处向舰艉移动,EZ与EY反对称分布,随着阳极位置由舰艉向舰艏移动,电场模量曲线由双峰逐渐变为单峰,破损处的峰值消失.由表 1可知,随着阳极位置由舰艉向舰艏移动时,电场补偿效果先增大后减小,当补偿阳极位于B位置时,腐蚀电场防护效果最好,EX、EY、EZ及电场模量的防护效果分别为48.92%、47.86%、54.55%和49.27%,当补偿阳极位于D位置时,电场补偿装置几乎没有防护效果.
根据舰船的电偶极子建模理论[14-16]:将发生阳极反应的破损处视为电偶极子的正电荷,而将发生阴极反应的螺旋桨视为电偶极子的负电荷,将船体产生的腐蚀电场等效为相应电偶极子产生的电场,决定电偶极子所产生电场大小的电偶极矩
| $ \overrightarrow {{P_e}} = I \cdot {\rm{d}}\vec l. $ | (10) |
式中:I为正电荷流向负电荷的电流大小,
由于外加补偿电流,船体正电荷由破损处转移至更靠近负电荷的补偿阳极处,相当于减小式(10)中的
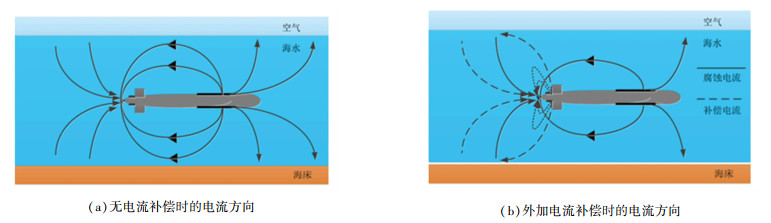
|
图 7 电场防护原理示意图 Fig. 7 Schematic diagram of electric field damping principle |
1) 补偿阳极周向位置对电场防护效果影响较小,而纵向位置对电场防护效果有明显的影响.
2) 基于静电场防护原理,补偿阳极越靠近螺旋桨,腐蚀电场的防护效果越好,但是当补偿阳极与螺旋桨的距离太小时,由于补偿电流对螺旋桨起到了阴极保护的作用反而降低了电场防护效果.
3) 当阳极与螺旋桨纵向距离为5 m时,腐蚀静电场能减少50%左右,当阳极与螺旋桨纵向距离大于16.6 m时,补偿电流基本没有防护效果.
| [1] |
王向军, 嵇斗. 舰船电场防护原理[M]. 武汉: 海军工程大学出版社, 2016: 123. WANG Xiangjun, JI Dou. Electric field elimination principle of ship[M]. Wuhan: Naval University of Engineering Press, 2016: 123. |
| [2] |
SCHAEFER D, DOOSE J, PICHLMAIER M. Conversion of UEP signatures between different environmental conditions using shaft currents[J]. IEEE Journal of Oceanic Engineering, 2016, 41(1): 105. DOI:10.1109/JOE.2015.2401991 |
| [3] |
KIM Y S, LEE S K, CHUNG H J. Influence of a simulated deep sea condition on the cathodic protection and electric field of an underwater vehicle[J]. Ocean Engineering, 2018, 148: 223. DOI:10.1016/j.oceaneng.2017.11.027 |
| [4] |
陈聪.舰船电磁场的模型研究和深度换算[D].武汉: 海军工程大学, 2008 CHEN Cong. Research on the modeling and the extrapolation of electromagnetic field of a ship[D]. Wuhan: Naval University of Engineering, 2008 |
| [5] |
陈聪, 龚沈光, 李定国. 基于混合模型的舰船腐蚀相关静态电、磁场[J]. 哈尔滨工业大学学报, 2010, 42(3): 495. CHEN Cong, GONG Shenguang, LI Dingguo. Corrosion related static electric and magnetic field of ships based on mixed modeling[J]. Journal of Harbin Institute of Technology, 2010, 42(3): 495. |
| [6] |
毛伟.浅海环境下运动舰船轴频电磁场建模方法及传播规律研究[D].武汉: 海军工程大学, 2009 MAO Wei. Research on modeling method of the moving ship SREM field and its propagation in shallow sea[D]. Wuhan: Naval University of Engineering, 2009 |
| [7] |
HOLMES J J. Application of models in the design of underwater electromagnetic signature reduction systems[J]. Naval Engineers Journal, 2007, 119(4): 19. DOI:10.1111/j.1559-3584.2007.00083 |
| [8] |
XING Shaohua, LI Yan, SONG Haiqing, et al. Optimization the quantity, locations and output currents of anodes to improve cathodic protection effect of semi-submersible crane vessel[J]. Ocean Engineering, 2016, 113: 144. DOI:10.1016/j.oceaneng.2015.12.047 |
| [9] |
KIM Y S, KIM J, CHOI D, et al. Optimizing the sacrificial anode cathodic protection of the rail canal structure in seawater using the boundary element method[J]. Engineering Analysis with Boundary Elements, 2017, 77: 36. DOI:10.1016/j.enganabound.2017.01.003 |
| [10] |
LAN Zhigang, WANG Xiutong, HOU Baorong, et al. Simulation of sacrificial anode protection for steel platform using boundary element method[J]. Engineering Analysis with Boundary Elements, 2012, 36(5): 903. DOI:10.1016/jenganabound.2011.07.018 |
| [11] |
倪光正, 杨仕友, 钱秀英, 等. 工程电磁场数值计算[M]. 北京: 机械工业出版社, 2006: 87. NI Guangzheng, YANG Shiyou, QIAN Xiuying, et al. Numerical calculation of engineering electromagnetic field[M]. Beijing: Machinery Industry Press, 2006: 87. |
| [12] |
许立坤, 马力, 邢少华, 等. 海洋工程阴极保护技术发展评述[J]. 中国材料进展, 2014, 33(2): 106. XU Likun, MA Li, XING Shaohua, et al. Review on cathodic protection for marine structures[J]. Chinese Material Progress, 2014, 33(2): 106. DOI:10.7502/j.issn.1674-3962.2014.02.06 |
| [13] |
邢少华, 李焰, 马力, 等. 深海工程装备阴极保护技术进展[J]. 装备环境工程, 2015, 12(2): 49. XING Shaohua, LI Yan, MA Li, et al. Research progress in cathodic protection technology for marine infrastructures in deep sea environment[J]. Equipment Environment Engineering, 2015, 12(2): 49. DOI:10.7643/issn.1672-9242.2015.02.011 |
| [14] |
BAKLEZOS A T, NIKOLOPOULOS C D, CAPSALIS C N. An equivalent dipole method with novel measurement positioning for modeling electric emissions in space missions[J]. Electromagnetics, 2017, 23(6): 1. DOI:10.1080/02726343.2017.1376902 |
| [15] |
CHEN Zhiyi, ZHOU Suihua. SLF electromagnetic fields in stratified media[J]. Applied Mechanics and Materials, 2012, 263-266: 35. DOI:10.4028/www.scientific.net/AMM.263-266.35 |
| [16] |
张立琛, 王英民, 陶林伟. 舰船腐蚀相关轴频电磁场场源建模[J]. 哈尔滨工程大学学报, 2017, 38(10): 1525. ZHANG Lichen, WANG Yingmin, TAO Linwei. Modeling of ship corrosion related shaft-rate electromagnetic field[J]. Journal of Harbin Engineering University, 2017, 38(10): 1525. DOI:10.11990/jheu.201605099 |
 2020, Vol. 52
2020, Vol. 52


