实际工业对象大部分为多变量系统，各通道相互耦合，实际被控对象的模型参数通常处于波动状态.设计解耦器, 消除系统中各回路间的耦合关系, 然后对每组通道逐一进行控制，是多变量系统控制的常用方法.解耦器是通过被控对象的传递函数矩阵设计出来的，当对象传递函数阶数和输入输出变量维数加大时，常规的对角矩阵法、相对增益法、特征曲线法等设计出的解耦器复杂程度大增，当被控对象的数学模型不准确时，系统的解耦性能将受到影响^[1].逆系统解耦方法利用反馈思想极大地简化了解耦器设计的复杂程度, 结构形式简单, 然而系统内外扰动及模型误差会影响系统的跟踪特性和鲁棒性^[2].运用神经网络^[3-4]、模糊方法^[5-6]、支持向量机^[7-8]等方法进行解耦优化，成为了解耦控制的一个研究热点.然而，神经网络解耦控制虽然实现了动态解耦，但需利用大量实际数据进行学习，且网络权值的调整方法存在局限性.模糊控制需要制定复杂的控制规则，支持向量机核函数参数需要适时调整，这些都给解耦优化的实际应用造成了困难.

文献[9]提出的自抗扰控制技术(active disturbance rejection control, ADRC)以积分器串联型作为反馈系统的标准型，采用扩张状态观测器(ESO)对异于标准型的总和扰动进行实时估计，并主动补偿，从而把充满扰动、不确定性和非线性的被控对象转化为标准型进行控制.文献[10]将多输入多输出系统中各个子系统之间的耦合也归结到总扰动中，然后对每一个通道用扩张状态观测器各自独立地进行在线跟踪及补偿，从而实现分散式解耦控制.与常规分散控制算法相比，自抗扰控制具有更强的解耦和抗干扰能力，因而引起了诸多学者的兴趣，并被广泛应用于工业系统的控制中.将逆解耦与ADRC相结合，文献[1]设计了精馏塔过程自抗扰控制器，文献[11]设计了四水箱的液位控制器；针对六极混合磁轴承三自由度之间的耦合性和非线性特点，文献[12]采用线性/非线性自抗扰切换控制方法进行了解耦控制；针对制冷系统非线性、强耦合、大时滞等特点，文献[13]设计了一种改进的自抗扰解耦控制器；针对级联H桥静止无功发生器，文献[14]基于自抗扰控制设计了多变量解耦控制系统；文献[15]通过引入虚拟控制量，实现了强制循环蒸发系统液位与出料密度的ADRC解耦控制；将预测控制ADRC相结合，文献[16]设计了既具信息预估又具扰动补偿的预测自抗扰控制器，并应用于制水行业待滤水浊度过程控制；针对热连轧活套系统多变量、非线性和强耦合特点，文献[17]设计了热连轧电动活套系统的高度和张力自抗扰控制器；针对气体流量装置实验管路流量、压力耦合系统，文献[18]对气体流量装置进行了自抗扰解耦控制.

这种分散式自抗扰解耦控制把各回路间的耦合作用看作扰动进行补偿，在一定程度上降低了回路间的相互影响, 但是当回路间有较强耦合时, 这种方法的解耦效果有限，而且，在对各个回路进行ADRC控制时，需要根据实验结果整定各个回路的控制参数，导致参数整定工作量非常大，所整定的参数也会互相影响，一个参数调到最优后，另一个参数对应的性能又恶化了，最终所得到的只是各个参数折中的结果，整体控制性能大打折扣.针对以上不足，本文提出了一种m个输入m个输出(MIMO)系统的自解耦控制方法(self-decoupling control，SDC).该法利用线性扩张状态观测器(LESO)对系统中的耦合部分、非线性部分及扰动部分进行估计并补偿，通过设计合适的控制律实现系统各环节的自解耦，将3m个LESO的增益转化为由系统硬件决定的常量，将2m个待整定的反馈控制量增益转化为系统误差微分方程的Hurwitz稳定矩阵的特征值配置，实现了MIMO系统控制的单参数调整，并应用Lyapunov方法对SDC法的稳定性进行了严格的数学证明.

1 问题描述

考虑如下一类m输入m输出系统，其控制量增益b_ij是状态变量和时间的函数b_ij($\boldsymbol{x}, \dot{\boldsymbol{x}}, t$):

$ \left\{ {\begin{array}{*{20}{l}} {{{\ddot x}_1} = {f_1}({x_1},{{\dot x}_1}, \cdots ,{x_m},{{\dot x}_m}) + {b_{11}}{u_1} + \cdots + {b_{1m}}{u_m},}\\ {{{\ddot x}_2} = {f_2}({x_1},{{\dot x}_1}, \cdots ,{x_m},{{\dot x}_m}) + {b_{21}}{u_1} + \cdots + {b_{2m}}{u_m},}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots }\\ {{{\ddot x}_m} = {f_m}({x_1},{{\dot x}_1}, \cdots ,{x_m},{{\dot x}_m}) + {b_{m1}}{u_1} + \cdots + {b_{mm}}{u_m},}\\ {{y_1} = {x_1},{y_2} = {x_2}, \cdots ,{y_m} = {x_m}.} \end{array}} \right. $

(1)

假定耦合矩阵

$ \mathit{\boldsymbol{B}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{\dot x}},t) = \left[ {\begin{array}{*{20}{c}} {{b_{11}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{\dot x}},t)}& \cdots &{{b_{1m}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{\dot x}},t)}\\ \vdots & \vdots & \vdots \\ {{b_{m1}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{\dot x}},t)}& \cdots &{{b_{mm}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{\dot x}},t)} \end{array}} \right] $

可逆，并且x =[x₁, x₂, …, x_m]^T，f =[f₁, f₂, …, f_m]^T，u =[u₁, u₂, …, u_m]^T，同时引入虚拟控制量U = B ($\boldsymbol{x}, \dot{\boldsymbol{x}}, t$) u，方程(1)变为

$ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\ddot x}} = \mathit{\boldsymbol{f}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{\dot x}},t) + \mathit{\boldsymbol{U}},}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{x}}.} \end{array}} \right. $

(2)

则系统第i个通道的输入输出关系为

$ \left\{ {\begin{array}{*{20}{l}} {{{\ddot x}_i} = {f_i}({x_1},{{\dot x}_1}, \cdots ,{x_m},{{\dot x}_m},t) + {U_i},}\\ {{y_i} = {x_i}.} \end{array}} \right. $

(3)

这样每个通道的虚拟控制量U_i与输出y_i形成了一种单输入单输出关系，实现了各通道间的解耦，利用虚拟控制量U_i，设计m个自抗扰控制器就能对各通道进行控制.但这也意味着耦合矩阵B ($\boldsymbol{x}, \dot{\boldsymbol{x}}, t$)必须可逆，而且要设计m个自抗扰控制器.在工程实践中，B ($\boldsymbol{x}, \dot{\boldsymbol{x}}, t$)不一定可逆，对m个控制器的参数进行整定也很不容易，这就使这种传统的自抗扰解耦控制方法不仅应用受限，而且控制系统设计复杂，参数调整工作量也很大.

2 MIMO系统的自解耦控制器设计

方程(1)所述的MIMO系统可表示为

$ \begin{array}{*{20}{c}} {{{\ddot y}_i} = {f_i}({x_1},{{\dot x}_1}, \cdots ,{x_m},{{\dot x}_m}) + {b_{i1}}{u_1} + \cdots + {b_{im}}{u_m},}\\ {(i = 1,2,3, \cdots ,m).} \end{array} $

(4)

将方程(4)进一步表示为

$ {\ddot y_i} = {R_i} + {b_i}{u_i}. $

(5)

式中R_i为状态量y_i的总和扰动，包括耦合项、外扰等，$R_{i}=f_{i}\left(x_{1}, \dot{x}_{1}, \cdots, x_{m}, \dot{x}_{m}\right)+b_{i 1} u_{1}+\cdots+\left(b_{i 1}-\right.$ $\left.b_{i}\right) u_{i}+\cdots+b_{i m} u_{m}$，b_i为b_ii的估计值，b_i≈b_ii.

设总和扰动$\left\{\begin{array}{l}\left|R_{i}\right| \leqslant \delta_{i}, \\ \left|\dot{R}_{i}\right| \leqslant \bar{\delta}_{i}.\end{array}\right.$其中δ_i, $\bar{\delta}_{i}$是正实数.令$x_{i 1}=y_{i}, x_{i 2}=\dot{y}_{i}, x_{i 3}=R_{i}, r_{i}=\dot{R}_{i}$则方程(5)可扩张为

$ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot X}}}_i} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{X}}_i} + {b_i}{u_i}\mathit{\boldsymbol{B}} + {r_i}\mathit{\boldsymbol{D}},}\\ {{y_i} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{X}}_i}.} \end{array}} \right. $

(6)

式中：

$ \begin{array}{l} \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{l}} 0&1&0\\ 0&0&1\\ 0&0&0 \end{array}} \right],\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{l}} 0\\ 1\\ 0 \end{array}} \right],\mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{l}} 0\\ 0\\ 1 \end{array}} \right],\mathit{\boldsymbol{C}} = {\left[ {\begin{array}{*{20}{l}} 1\\ 0\\ 0 \end{array}} \right]^{\rm{T}}},\\ {\mathit{\boldsymbol{X}}_i} = \left[ {\begin{array}{*{20}{c}} {{x_{i1}}}\\ {{x_{i2}}}\\ {{x_{i3}}} \end{array}} \right]. \end{array} $

根据方程(6)设计线性扩张状态观测器(LESO)：

$ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot Z}}}_i} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{Z}}_i} + {b_i}{u_i}\mathit{\boldsymbol{B}} + \mathit{\boldsymbol{L}}({y_i} - {{\hat y}_i}),}\\ {{{\hat y}_i} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{Z}}_i}.} \end{array}} \right. $

(7)

式中：$\boldsymbol{Z}_{i}=\left[\begin{array}{ll}z_{i 1}, & z_{i 2}, & z_{i 3}\end{array}\right]^{\mathrm{T}}$为向量X_i的状态估计，$\hat{y}_{i}$为y_i的状态估计，L =[β₀₁, β₀₂, β₀₃]^T为观测增益向量.

将y_i环的反馈控制量设计为

$ {u_i} = {k_{i1}} \cdot ({v_i} - {z_{i1}}) + {k_{i2}} \cdot ({\dot v_i} - {z_{i2}}) - {z_{i3}}/{b_i}. $

(8)

式中:v_i为y_i的目标值，k_i1、k_i2为反馈控制量增益.

将方程(8)代入方程(5)，可得

$ \begin{array}{*{20}{l}} {{{\ddot y}_i} = {R_i} + {b_i}({k_{i1}} \cdot ({v_i} - {z_{i1}}) + {k_{i2}} \cdot ({{\dot v}_i} - {z_{i2}}) - {z_{i3}}/{b_i}) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {b_i}[{k_{i1}} \cdot ({v_i} - {z_{i1}}) + {k_{i2}} \cdot ({{\dot v}_i} - {z_{i2}})] + {R_i} - {z_{i3}}.} \end{array} $

(9)

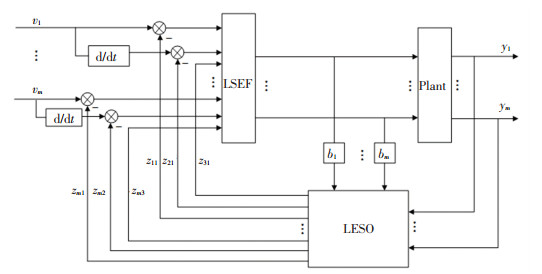
当扩张状态观测器的误差e_i3=R_i1-z_i3足够小时，根据方程(9)的积分特性可知，系统的输出量y_i将不受未知扰动(包括外部扰动、耦合项、非线性项等)的影响，达到了自解耦的目的，因此这类MIMO系统可以采用控制框图来进行控制，如图 1所示.在这种控制方式下，每一个输出量y_i不再使用虚拟控制量，而是使用实际控制量进行控制，物理意义更加明确，而且不要求系统具有可逆的耦合矩阵，拓宽了控制系统的使用范围.

3 MIMO系统自解耦控制参数分析

从自解耦控制器的设计过程可以看出，MIMO系统自解耦控制的待定参数包括线性扩张状态观测器的观测增益向量、各通路的反馈控制量增益及控制量放大系数的估计值b_i，对于m输入m输出系统，待确定的b_i为m个，观测向量增益为3m个，控制量增益为2m个，如果根据实验或仿真结果来进行调整，将导致参数整定工作量非常大，技术要求高，而且所整定的参数互相影响，一个参数调到最优后，另一个参数对应的性能又恶化了，最终所得到的只是各个参数折中的结果，整体控制性能大打折扣，因此有必要从MIMO系统自解耦控制的要求出发，尽可能减少待整定参数.考虑到b_i为m个控制量放大系数b_ii的估计值，在控制中可采用实际的b_ii.

文献[19]根据线性扩张状态观测器(LESO)带宽构造了LESO的观测增益向量：

$ \mathit{\boldsymbol{L}} = {\left[ {\begin{array}{*{20}{l}} {{\beta _{01}}}&{{\beta _{02}}}&{{\beta _{03}}} \end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{l}} {3{\omega _0}}&{3\omega _0^2}&{\omega _0^3} \end{array}} \right]^{\rm{T}}}. $

(10)

其中ω₀为LESO的带宽，ω₀越大，线性扩张状态观测器的稳态误差越小，收敛速度也越快.带宽受到数值计算迭代步长的制约，大带宽需要小迭代步长，否则会因为迭代步长过大而产生较大的相位滞后，引起超调或者系统不稳定.在实际控制系统中迭代步长由系统硬件决定，探讨迭代步长与扩张状态观测器带宽之间的关系，可以将MIMO系统各环节的扰动用统一的线性扩张状态观测器进行集中观测补偿.

由于扩张状态观测器的增益系数与迭代步长联系紧密，文献[9]运用Fibonacci数列，根据迭代步长构建了三阶线性扩张状态观测器的参数序列：

$ \left\{ {\begin{array}{*{20}{l}} {{{\bar \beta }_{01}} = \frac{1}{h},}\\ {{{\bar \beta }_{02}} = \frac{1}{{3{h^2}}},}\\ {{{\bar \beta }_{03}} = \frac{2}{{{8^2}{h^3}}}.} \end{array}} \right. $

(11)

其中:h为迭代步长，由系统硬件决定; β₀₁、β₀₂、β₀₃分别为三阶线性扩张状态观测器的参数.

对比方程(10)、(11)表示的参数序列关系，将带宽和步长的迭代关系设计为

$ {\omega _0} = k\frac{1}{h}. $

(12)

其中k为待定系数.

为使方程(10)表示的参数序列与方程(11)表示的参数序列尽可能接近，将方程(10)、(11)作方差运算，并以方差最小化为目标，即

$ {\rm{min}}[{({\beta _{01}} - {\bar \beta _{01}})^2} + {({\beta _{02}} - {\bar \beta _{02}})^2} + {({\beta _{03}} - {\bar \beta _{03}})^2}]. $

(13)

将方程(10)~(12)代入方程(13)，可得

$ {\rm{min}}\left[ {\frac{1}{{{h^2}}}{{(1 - 3k)}^2} + \frac{1}{{{h^4}}}{{\left( {\frac{1}{3} - 3{k^2}} \right)}^2} + \frac{1}{{{h^6}}}{{\left( {\frac{1}{{32}} - {k^3}} \right)}^2}} \right]. $

(14)

解得

$ {\omega _0} = \frac{1}{{3h}}. $

(15)

据此, 将线性扩张状态观测器的观测增益向量设计为${\boldsymbol{L}}=\left[\frac{1}{h}, \frac{1}{3 h^{2}}, \frac{1}{27 h^{3}}\right]^{\mathrm{T}}$.

假定MIMO系统的目标值为$\left(x_{1}, \dot{x}_{1}, x_{2}, \dot{x}_{2}, \cdots, \right.$$\left.x_{m}, \dot{x}_{m}\right)=\left(v_{1}, \dot{v}_{1}, v_{2}, \dot{v}_{2}, \cdots, v_{m}, \dot{v}_{m}\right)$，其误差可定义为

$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi _1} = {x_1} - {v_1},{\psi _2} = {{\dot x}_1} - {{\dot v}_1},{\psi _3} = {x_2} - {v_2},{\psi _4} = {{\dot x}_2} - \\ {{\dot v}_2}, \ldots ,{\psi _{2m - 1}} = {x_m} - {v_m},{\psi _{2m}} = {{\dot x}_m} - {{\dot v}_m}. \end{array} $

(16)

令$\boldsymbol{\psi}(t)=\left[\begin{array}{lllll}\psi_{1} & \psi_{2} & \cdots & \psi_{2 m-1} & \psi_{2 m}\end{array}\right]^{\mathrm{T}}$，针对ψ (t)对时间t求导，并综合方程(8)、(9)，得整个控制系统的误差方程为

$ \mathit{\boldsymbol{\dot \psi }}(t) = {\mathit{\boldsymbol{A}}_\psi }\mathit{\boldsymbol{\psi }}(t) + \sum\limits_{i = 1}^{2m} {{\mathit{\boldsymbol{A}}_{ei}}} {\mathit{\boldsymbol{e}}_i}(t). $

(17)

其中:

$ \begin{array}{l} {A_\psi } = \left[ {\begin{array}{*{20}{c}} 0&1& \cdots &0&0\\ { - {b_1}{k_{11}}}&{ - {b_1}{k_{12}}}& \cdots &0&0\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0&0& \cdots &0&1\\ 0&0& \cdots &{ - {b_m}{k_{m1}}}&{ - {b_m}{k_{m2}}} \end{array}} \right],\\ {\mathit{\boldsymbol{A}}_{ei}} = \left[ {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ \vdots & \vdots & \vdots \\ 0&0&0\\ {{b_i}{k_{i1}}}&{{b_i}{k_{i2}}}&1\\ \vdots & \vdots & \vdots \\ 0&0&0\\ 0&0&0 \end{array}} \right],{\mathit{\boldsymbol{e}}_i}(t) = \left[ {\begin{array}{*{20}{c}} {{e_{i1}}}\\ {{e_{i2}}}\\ {{e_{i3}}} \end{array}} \right]. \end{array} $

为扩张状态观测器的观测误差向量，且e_i1=$x_{i 1}-z_{i 1}, e_{i 2}=x_{i 2}-z_{i 2}, e_{i 3}=x_{i 3}-z_{i 3}$.

为使A_ψ是Hurwitz稳定矩阵，将A_ψ的特征值λ都配置在点$(-\bar{\omega}, 0)$上，其中$\bar{\omega}$ >0，即

$ |\lambda \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{A}}_\psi }| = {(\lambda + \bar \omega )^{2m}}. $

(18)

式中I为3阶单位矩阵.

求解方程(18)，可得

$ \left\{ {\begin{array}{*{20}{l}} {{k_{i1}} = \frac{{{{\bar \omega }^2}}}{{{b_i}}},}\\ {{k_{i2}} = \frac{{2\bar \omega }}{{{b_i}}}.} \end{array}} \right. $

(19)

则SDC的线性控制量(LSEF)为

$ {u_i} = \frac{{{{\bar \omega }^2}}}{{{b_i}}} \cdot ({v_i} - {z_{i1}}) + \frac{{2\bar \omega }}{{{b_i}}} \cdot ({\dot v_i} - {z_{i2}}) - \frac{{{z_{i3}}}}{{{b_i}}}. $

(20)

对于输入输出数目均为m的MIMO系统，方程(20)中的控制量始终只有一个可调参数$\bar{\omega}$，调整$\bar{\omega}$，各环节的控制量增益会随之变化，并自动生成各环节的反馈控制量，因此，在SDC中，不需要对每个输出环都设计反馈控制量，通过调整参数$\bar{\omega}$，各环节的控制量会自动调整，使其控制性能达到最优，SDC大大简化了这类MIMO系统的控制过程，也使繁琐复杂的控制量增益调整变得简单容易.

4 MIMO系统自解耦控制器稳定性证明

定理1  在持续变化的扰动R_i作用下，扩张状态观测器(7)的观测值存在有界稳态误差；当扰动R_i保持不变或停止作用时，扩张状态观测器(7)的观测误差(e_i1, e_i2, e_i3)迅速收敛于(0, 0, 0).

证明  将式(6)减去式(7)，得LESO误差的微分方程:

$ {\mathit{\boldsymbol{\dot e}}_i} = \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{e}}_i} + {\mathit{\boldsymbol{R}}_i}\mathit{\boldsymbol{F}}. $

(21)

其中：$\boldsymbol{E}=\boldsymbol{A}-\boldsymbol{L} \boldsymbol{C}=\left[\begin{array}{ccc}-3 \omega_{0} & 1 & 0 \\ -3 \omega_{0}^{2} & 0 & 1 \\ -\omega_{0}^{3} & 0 & 0\end{array}\right], \boldsymbol{F}=\left[\begin{array}{l}0 \\ 0 \\ 1\end{array}\right]$.

将线性扩张状态观测器的Lyapunov函数设计为

$ {V_1} = {\mathit{\boldsymbol{e}}_i}^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{e}}_i}. $

(22)

其中P为假定存在的对称正定矩阵，

$ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{l}} {{k_{11}}}&{{k_{12}}}&{{k_{13}}}\\ {{k_{12}}}&{{k_{22}}}&{{k_{12}}}\\ {{k_{13}}}&{{k_{12}}}&{{k_{33}}} \end{array}} \right]. $

对V₁(t)求导，并将方程(21)代入，得

$ {\dot V_1}(t) = {\mathit{\boldsymbol{e}}_i}^{\rm{T}}({\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{PE}}){\mathit{\boldsymbol{e}}_i} + 2{\mathit{\boldsymbol{r}}_i}{\mathit{\boldsymbol{e}}_i}^{\rm{T}}\mathit{\boldsymbol{PF}}. $

(23)

其相应的Lyapunov方程取为

$ {\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{PE}} = - \mathit{\boldsymbol{I}}. $

(24)

将P、E代入方程(24)，可得

$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{c}} { - 3{\omega _0}}&1&0\\ { - 3\omega _0^2}&0&1\\ { - \omega _0^3}&0&0 \end{array}} \right]^{\rm{T}}} \cdot \left[ {\begin{array}{*{20}{l}} {{k_{11}}}&{{k_{12}}}&{{k_{13}}}\\ {{k_{12}}}&{{k_{22}}}&{{k_{12}}}\\ {{k_{13}}}&{{k_{12}}}&{{k_{33}}} \end{array}} \right] + \\ \left[ {\begin{array}{*{20}{l}} {{k_{11}}}&{{k_{12}}}&{{k_{13}}}\\ {{k_{12}}}&{{k_{22}}}&{{k_{12}}}\\ {{k_{13}}}&{{k_{12}}}&{{k_{33}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} { - 3{\omega _0}}&1&0\\ { - 3\omega _0^2}&0&1\\ { - \omega _0^3}&0&0 \end{array}} \right] = - \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right]. \end{array} $

(25)

求解方程(25), 可得

$ \left\{ {\begin{array}{*{20}{l}} {{k_{11}} = \frac{3}{{16{\omega _0}}} + \frac{3}{4}{\omega _0} + \frac{1}{{16}}\omega _0^3,}\\ {{k_{12}} = - \frac{1}{2},}\\ {{k_{13}} = - (\frac{3}{{4{\omega _0}}} + \frac{3}{{16}}{\omega _0} + \frac{1}{{16\omega _0^3}}),}\\ {{k_{22}} = \frac{3}{{4{\omega _0}}} + \frac{3}{{16}}{\omega _0} + \frac{1}{{16\omega _0^3}},}\\ {{k_{33}} = \frac{{33}}{{16{\omega _0}}} + \frac{7}{{4\omega _0^3}} + \frac{3}{{16\omega _0^3}}.} \end{array}} \right. $

(26)

将方程(26)代入P中，可得:当ω₀>0时，$\left|k_{11}\right|>0, \quad\left|\begin{array}{ll}k_{11} & k_{12} \\ k_{12} & k_{22}\end{array}\right|>0, \left[\begin{array}{lll}k_{11} & k_{12} & k_{13} \\ k_{12} & k_{22} & k_{12} \\ k_{13} & k_{12} & k_{33}\end{array}\right]>0$，因此矩阵P正定，即式(22)中所假设的正定矩阵P存在.

将方程(26)代入方程(23)，可得

$ {\dot V_1}(t) = - e_{i1}^2 - e_{i2}^2 - e_{i3}^2 + 2{r_i}{\mathit{\boldsymbol{e}}_i}^{\rm{T}}\mathit{\boldsymbol{PF}}. $

(27)

定义集合Γ₁包含所有的满足${\dot V_1}$(t)=0的点，则在集合Γ₁中，Lyapunov函数V₁(t)为常数.则当扰动R_i保持不变或停止作用时，即当r_i=0时，

$ {\dot V_1}(t) = - e_{i1}^2 - e_{i2}^2 - e_{i3}^2 = 0. $

(28)

由方程(28)，易得

$ ({e_{i1}},{e_{i2}},{e_{i3}}) = (0,0,0). $

(29)

即扩张状态观测器(7)的观测误差会迅速收敛于点(0, 0, 0).

当扰动R_i为持续变化的扰动时，即r_i≠0时，系统的观测值会出现一定误差.由式(7)、(17)可得稳态误差范围为

$ \left\{ {\begin{array}{*{20}{l}} {{e_{i1}}(t) \le {\delta _i}/\omega _0^3,}\\ {{e_{i2}}(t) \le 3{\delta _i}/\omega _0^2,}\\ {{e_{i3}}(t) \le 3{\delta _i}/{\omega _0}.} \end{array}} \right. $

(30)

由方程(29)、(30)的结论可知，定理1得证.

定理2  在持续变化的扰动R_i作用下，MIMO系统(1)在SDC的线性控制律(20)的作用下整个控制系统的误差在零点附近大范围稳定，存在有界稳态误差；当扰动R_i保持不变或停止作用时，整个控制系统的误差会迅速收敛于零点.

证明  将式(17)进一步表示为

$ \mathit{\boldsymbol{\dot \psi }}(t) = {\mathit{\boldsymbol{A}}_\psi }\mathit{\boldsymbol{\psi }}(t) + g(t), $

(31)

其中$\mathit{\boldsymbol{g}}(t) = \sum\limits_{i = 1}^{2m} {{\mathit{\boldsymbol{A}}_{ei}}} {\mathit{\boldsymbol{e}}_i}(t)$.

矩阵A_ψ是Hurwitz稳定矩阵，因此可将A_ψ作为式(29)的Lyapunov方程：

$ {{V_2} = {\mathit{\boldsymbol{\psi }}^{\rm{T}}}{\mathit{\boldsymbol{A}}_\psi }\mathit{\boldsymbol{\psi }}.} $

(32)

则

$ {{{\dot V}_2}(t) = - \bar \omega \sum\limits_{i = 1}^{2m} {\psi _i^2} + 2{\mathit{\boldsymbol{\psi }}^{\rm{T}}}{\mathit{\boldsymbol{A}}_\psi }\mathit{\boldsymbol{\dot g}}(t).} $

(33)

定义集合Γ₂包含所有的满足${\dot V_2}$(t)=0的点，在集合Γ₂中，Lyapunov函数V₂为常数.当扰动R_i保持不变或停止作用时，由定理1可知，此时$\mathit{\boldsymbol{\dot g}}$ (t)=0，由式(33)可知：

$ {{{\dot V}_2}(t) = - \bar \omega \sum\limits_{i = 1}^{2m} {\psi _i^2} = 0.} $

(34)

由式(34)易得

$ {\psi _{2i - 1}} = 0,{\psi _{2i}} = 0. $

(35)

当扰动R_i为持续变化的扰动时，则系统存在稳态误差.当系统稳定时，系统误差微分方程(17)的左边全为零，则根据式(30)，可得

$ {g_{2i}}(t) \le \left| {{b_i}{k_{i1}}\frac{{{\delta _i}}}{{\omega _0^3}} + {b_i}{k_{i2}}\frac{{3{\delta _i}}}{{\omega _0^2}} + \frac{{3{\delta _i}}}{{{\omega _0}}}} \right|. $

(36)

将方程(36)代入方程(31)，可得系统的稳态误差范围为

$ \left\{ {\begin{array}{*{20}{l}} {{\psi _{2i - 1}} \le \left| {\frac{{{b_i}{k_{i1}}\frac{{{\delta _i}}}{{\omega _0^3}} + {b_i}{k_{i2}}\frac{{3{\delta _i}}}{{\omega _0^2}} + \frac{{3{\delta _i}}}{{{\omega _0}}}}}{{{b_i}{k_{i2}}}}} \right|,}\\ {{\psi _{2i}} = 0.} \end{array}} \right. $

(37)

由式(35)和(37)的结论可知，定理2得证.

5 MIMO系统自解耦控制的应用分析 5.1 算例一热连轧活套系统的自解耦控制

热轧机电动活套系统控制的优劣直接影响成品带钢的宽度、厚度和板形精度，辊缝移动、负荷扰动、被控对象变化会使张力出现较大波动，使得活套控制比较复杂.参见文献[17]，可知热连轧活套系统模型为

$ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{\tilde Ax}} + \mathit{\boldsymbol{\tilde Bu}},}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\tilde Cx}}.} \end{array}} \right. $

(38)

式中：

$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{x}} = \left[ {\begin{array}{*{20}{l}} {{x_1}}\\ {{x_2}}\\ {{x_3}}\\ {{x_4}}\\ {{x_5}} \end{array}} \right],\\ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0\\ j&0&{\frac{6}{J}}&{ - \frac{6}{J}\frac{{\partial {M_T}}}{{\partial \sigma }}}&0\\ 0&0&{ - \frac{1}{{{T_{{\rm{ACR}}}}}}}&0&0\\ 0&{\frac{E}{L}\frac{{\partial {\Delta _d}}}{{\partial \theta }}}&0&\ell &{ - \frac{E}{L}(1 + f)}\\ 0&0&0&0&{ - \frac{1}{{{T_{{\rm{ASR}}}}}}} \end{array}} \right],\\ \mathit{\boldsymbol{B}} = {\left[ {\begin{array}{*{20}{c}} 0&0\\ 0&0\\ {\frac{1}{{{T_{{\rm{ACR}}}}}}}&0\\ 0&0\\ 0&{\frac{1}{{{T_{{\rm{ASR}}}}}}} \end{array}} \right]^{\rm{T}}},\mathit{\boldsymbol{C}} = {\left[ {\begin{array}{*{20}{l}} 1&0\\ 0&0\\ 0&0\\ 0&1\\ 0&0 \end{array}} \right]^{\rm{T}}}\;\:,\mathit{\boldsymbol{u}} = \left[ {\begin{array}{*{20}{l}} {{u_1}}\\ {{u_2}} \end{array}} \right],\\ \mathit{\boldsymbol{y}} = \left[ {\begin{array}{*{20}{l}} {{y_1}}\\ {{y_2}} \end{array}} \right]. \end{array} $

其中

$ \begin{array}{*{20}{c}} {j = - \frac{6}{J}\left( {\frac{{\partial {M_G}}}{{\partial \theta }} + \frac{{\partial {M_S}}}{{\partial \theta }} + \frac{{\partial {M_T}}}{{\partial \theta }}} \right),}\\ {\ell = - \frac{E}{L}\left( {{v_{n + 1}}\frac{{\partial \beta }}{{\partial \sigma }} + {v_n}\frac{{\partial f}}{{\partial \sigma }}} \right).} \end{array} $

采用本文提出的自解耦控制方法，根据方程(20)设计高度回路和张力回路的反馈控制律为

$ \left\{ {\begin{array}{*{20}{l}} {{u_1} = 0.01{{\bar \omega }^2} \cdot ({v_i} - {z_{i1}}) + 0.02\bar \omega \cdot ({{\dot v}_i} - {z_{i2}}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.01 \cdot {z_{i3}},}\\ {{u_2} = 0.04{{\bar \omega }^2} \cdot ({v_i} - {z_{i1}}) + 0.08\bar \omega \cdot ({{\dot v}_i} - {z_{i2}}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.04 \cdot {z_{i3}}.} \end{array}} \right. $

(39)

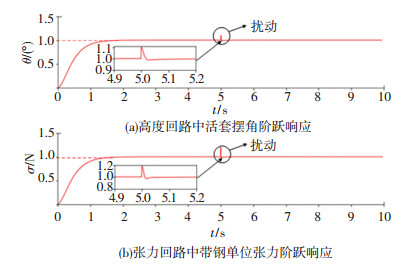
仿真实验迭代步长取h=0.001 s，经过充分整定后，ω选为4.与文献[17]一样，将热连轧电动活套系统的高度回路和张力回路分别施加单位阶跃信号，系统稳定后分别给高度回路和张力回路施加相同的阶跃扰动.应用SDC法对活套系统进行控制，所得实验结果见图 2和表 1，相比文献[17]中的自抗扰控制方法(需整定的参数为6个)，SDC法的各项控制性能都有一定的改善，且在受扰动之后，可快速恢复到稳定状态，且摆角和张力的恢复时间比文献[17]中的结果更短.

5.2 算例二气体流量装置的自解耦控制分析

气体流量和压力对气体流量装置的计量性能影响很大，参见文献[18]，可得气体流量装置的双输入双输出模型：

$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{l}} {{Q_m}(s)}\\ {p(s)} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\frac{{48.252}}{{0.36{s^2} + 0.916{\kern 1pt} {\kern 1pt} {\kern 1pt} 3s + 1}}}&{\frac{{55.913}}{{0.348{\kern 1pt} {\kern 1pt} {\kern 1pt} 9{s^2} + 0.905s + 1}}}\\ {\frac{{54.55}}{{0.894{s^2} + 0.428{\kern 1pt} {\kern 1pt} {\kern 1pt} 5 + 1}}}&{\frac{{ - 70.429}}{{0.084{s^2} + 0.905s + 1}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{I_1}(s)}\\ {{I_2}(s)} \end{array}} \right]. \end{array} $

(40)

其中：I₁、I₂分别为调节阀1、调节阀2的给定电流值，mA；Q_m为管路的流量，kg/h；p为管路的压力, kPa.

将式(40)改成式(4)的形式：

$ \left\{ {\begin{array}{*{20}{l}} {{{\ddot y}_1} = {f_1}({Q_m},{{\dot Q}_m},p,\dot p) + ({b_{11}} - {b_1}){I_1} + {b_{12}}{I_2} + {b_1}{I_1},}\\ {{{\ddot y}_2} = {f_2}({Q_m},{{\dot Q}_m},p,\dot p) + {b_{21}}{I_1} + ({b_{22}} - {b_2}){I_2} + {b_2}{I_2},}\\ {{y_1} = {Q_m},{y_2} = p.} \end{array}} \right. $

(41)

采用本文提出的SDC法，根据式(20)设计气体流量装置的反馈控制量式(42)，b₁、b₂分别采用控制量u₁、u₂增益的实际值.

$ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{I_1} = \frac{{{{\bar \omega }^2}}}{{134.8}} \cdot ({v_1} - {z_{11}}) + \frac{{2\bar \omega }}{{134.8}} \cdot ({{\dot v}_1} - {z_{12}}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{z_{13}}}}{{134.8}},} \end{array}\\ \begin{array}{*{20}{l}} {{I_2} = - \frac{{{{\bar \omega }^2}}}{{838.4}} \cdot ({v_2} - {z_{21}}) - \frac{{2\bar \omega }}{{838.4}} \cdot ({{\dot v}_2} - {z_{22}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{z_{23}}}}{{838.4}}.} \end{array} \end{array} \right. $

(42)

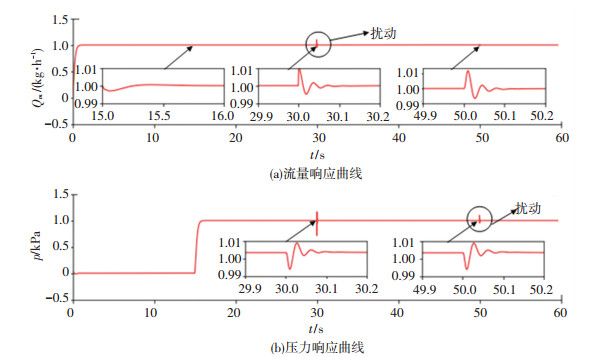
和文献[18]一样，在t=0时，给流量控制回路加入幅值为1的阶跃信号，在t=15 s时，给压力控制回路加入幅值为1的阶跃信号，在30 s和50 s时分别对流量和压力施加与文献[18]相同的阶跃扰动.迭代步长取h=0.001 s，经过充分整定后，ω取8，应用SDC法对气流装置进行控制，所得实验结果见图 3及表 2，相比文献[18]中的ADRC方法(需整定的参数为6个)，采用SDC法，在15 s时在压力控制回路加入的阶跃信号对流量的影响更小，最大变化量仅0.002 kg/h，而采用ADRC法流量的最大变化量是0.05 kg/h，说明SDC法的解耦能力优于ADRC法，各项控制性能指标也大幅占优(见表 2)，且在扰动作用下，由SDC法控制的流量和压力恢复稳定的时间均小于0.1 s，远小于ADRC法.

6 结论

1) 利用统一的线性扩张状态观测器(LESO)对系统中的耦合部分、非线性部分及扰动部分进行估计并补偿，通过设计合适的控制律实现了系统各环节的自解耦，整个SDC控制系统结构简单、紧凑，并用Lyapunov方法证明了其稳定性.

2) 采用由系统硬件决定的迭代步长确定3m个LESO的增益，通过Hurwitz稳定矩阵特征值配置将2m个待整定的反馈控制量增益转化为一个待整定参数，极大地减少了MIMO系统待整定的参数和调参难度.

3) 在SDC控制方式下不再使用虚拟控制量，使用实际控制量对每一个输出量进行控制，物理意义明确，而且不要求系统具有可逆的耦合矩阵，拓宽了控制系统的使用范围.

4) 算例说明SDC不仅最大限度地减少了MIMO系统的待整定参数，而且获得了比传统自抗扰解耦控制法更好的控制效果.