2. 西南交通大学 土木工程学院, 成都 610031;
3. 中交第一公路勘察设计研究院有限公司, 西安 710075;
4. 太原理工大学 建筑与土木工程学院, 太原 030024
2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China;
3. CCCC First Highway Consultants Co., Ltd., Xi'an 710075, China;
4. College of Architecture and Civil Engineering, Taiyuan University of Technology, Taiyuan 030024, China
钢结构已广泛应用于交通基础设施工程中,由于设计、施工、运营管理不当,或因超载、锈蚀、疲劳等原因,钢结构会造成一定的损伤.传统的加固方法是将钢板焊接、螺栓连接或粘接到原结构损伤部位,以改善结构的受力,但会产生新的问题,如焊接残余应力和削弱原截面等.粘贴CFRP加固钢结构技术具有高强高效、施工快捷、可操作性、可设计性、不改变结构自重及尺寸等优点,因而适用于多种结构类型和复杂部位的加固.已有研究表明粘贴CFRP加固技术能有效提高钢结构的抗弯承载力、整体刚度、抗疲劳能力和耐久性等[1].
CFRP与钢界面的主要破坏模式之一为界面剥离[2],因此界面的极限承载力和粘结滑移本构关系是国内外学者研究的重点.加固用胶黏剂根据应力-应变关系的不同,可将其分为线性胶和非线性胶.文献[3-6]均建议采用双线性模型表征线性胶的界面粘结滑移本构关系,但模型中各参数表达式不同,其中峰值滑移量差别最大,文献[3, 5]认为峰值滑移量与胶黏剂抗拉强度、剪切模量和胶层厚度有关,而文献[4]则认为其只与胶层厚度有关.文献[7]研究认为可采用三线性模型表征非线性胶的界面粘结滑移本构关系,文献[8]采用三维数字图像技术也得到了相同的结论.文献[9]研究了胶黏剂(线性低强、线性高强、非线性低强、非线性高强)性能对界面粘结性能的影响.文献[10]开展了胶黏剂养护龄期对界面粘结性能的影响.
上述研究是在界面没有任何作用历史情况下进行的.实际上加固结构服役期间是持续受到荷载作用的.胶黏剂作为高分子聚合物,在荷载作用下具有蠕变变形[11],引起的界面蠕变损伤将影响界面的粘结性能.文献[12]给出了持续荷载作用下CFRP-混凝土界面的粘结滑移本构模型.而目前CFRP-钢界面还缺乏相关研究,因此,本文开展了27个CFRP-钢双剪试件的长期加载试验,研究了不同荷载作用历史对界面粘结性能的影响,通过试验数据分析,给出了界面粘结滑移本构关系及极限承载力计算公式.
1 试验 1.1 试验材料及试件设计试验采用钢板为热轧Q235B,厚度为6 mm. CFRP布为东丽UT70-30型,厚度为0.167 mm.采用Araldite XH 180作为胶黏剂,Araldite胶的环氧树脂与固化剂质量比为4:1.试验用材料基本力学参数见表 1. 表 1中CFRP布和胶黏剂力学性能符合JTG/T J22—2008[13]中的有关规定.
| 表 1 材料力学性能 Tab. 1 Mechanical properties of materials |
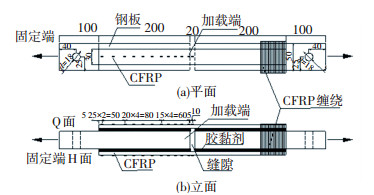
试件采用双面搭接剪切试件,由两片宽度30 mm的单层CFRP布粘贴在两块50 mm宽的钢板上,如图 1所示.每块钢板长度为300 mm.文献[6, 14]试验表明,CFRP-钢有效粘结长度不超过200 mm,为充分观察CFRP剥离扩展全过程,取CFRP粘贴长度取200 mm.另外,在一侧钢板上用宽度为50 mm的CFRP布缠绕锚固,保证界面剥离发生在另一侧.为增加试验数据,在每个试件每一面粘贴12个应变片,共计24个应变片,如图 1所示.为方便试验结果表达,将测试面分别定义为Q面和H面,应变片编号从加载端到固定端依次定义为Q0#~Q11#及H0#~H11#.其中编号Q0#和H0#两个应变片位于两块钢板空隙处的CFRP布上.
|
图 1 CFRP-钢板双剪试件及应变片布置(mm) Fig. 1 CFRP-steel plate double-lap specimen and layout of strain gauges (mm) |
将钢板及CFRP布按图 1所示的尺寸加工成型.采用电砂轮对钢板表面进行打磨,保证钢板表面具有同样的粗糙度,用砂纸磨掉钢板表面毛刺,并用丙酮擦拭,钢板处理完成后需要在12 h内进行涂胶粘贴CFRP布,加工完成后的试件在实验室条件下养护7 d.
试验共制作27个CFRP-钢双剪试件,其中3个试件进行拉伸破坏试验以确定界面的极限粘结强度,A组3个试件的极限承载力分别为27.4、28.8、31.6 kN,平均值Pu为29.3 kN,标准差为2.1. CFRP宽度bc=30 mm,CFRP粘结长度lc=200 mm,平均极限剪切强度τu=Pu/(2bclc)=2.44 MPa.其他24个试件进行持续拉伸试验.持续施加的界面名义剪应力τ0和持续时间见表 2. B组、C组、D组、E组界面名义剪应力τ0分别为0.22τu、0.44τu、0.60τu和0.73τu.
| 表 2 试件分组 Tab. 2 Arrangement of specimens |
长期加载采用自制的加载装置.待试件规定的加载时间后进行卸载.卸载后的试件采用WDW-100微控电子万能试验机进行拉伸试验,按位移控制加载,加载速率为0.3 mm/min.采用TST3826F-L静态电阻应变仪进行应变采集.试验加载装置如图 2所示.

|
图 2 试验装置 Fig. 2 Test setup |
CFRP-钢界面剥离破坏的模式有6种[15]:Ⅰ型,钢/胶界面失效;Ⅱ型,胶层内聚破坏;Ⅲ型,CFRP/胶界面失效;Ⅳ型,CFRP层离;Ⅴ型,CFRP断裂;Ⅵ型,钢板屈服.双剪试件钢板厚为6 mm、CFRP的弹性模量为237 GPa,避免了发生Ⅴ型和Ⅵ型破坏.胶黏剂能渗透到CFRP布,并与碳纤维丝形成较好地粘结,故Ⅲ型和Ⅳ型不易发生.
试验能观察到的破坏模式有Ⅰ型、Ⅱ型及两者伴随发生,如图 3所示.所有试件破坏形态中更多的是钢/胶界面失效与胶层内聚破坏伴随发生.

|
图 3 CFRP/钢界面破坏模式 Fig. 3 Failure modes of CFRP-steel interface |
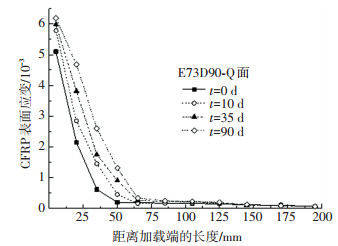
选取E73D90试件Q面CFRP表面应变分布来说明持续荷载对CFRP应变的影响,如图 4所示.总体上CFRP应变呈非线性减小,在加载端端部附近应变数值较大,距加载端越远应变越小.同一测点在不同持载时间的应变数值不同,其应变随着持载时间的增加而增大.
|
图 4 CFRP应变分布随时间变化 Fig. 4 Strain distribution of CFRP varying with time |
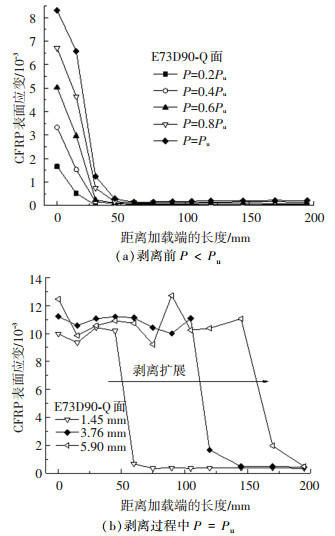
图 5为E73D90试件Q面CFRP应变分布图,图中0 mm处应变由缝隙处Q0#应变值代替,其他应变值为Q1#~Q11#.当拉伸荷载P小于极限承载力Pu时,界面未发生剥离,CFRP应变如图 5(a)所示.由图可知,界面剥离前仅在加载端50 mm以内CFRP应变较大,随着距离加载端越远应变值越小,说明只有一部分CFRP参与了受力.另外,随着P/Pu比值的增大,加载端附近CFRP应变值逐渐增加.当P小于等于Pu时,CFRP应变只在加载端一定长度范围内存在,说明CFRP实际参与工作的长度是一定的,这一长度就是有效粘结长度Le, 各组试件的Le见表 3.
|
图 5 CFRP应变分布 Fig. 5 Strain distribution of CFRP |
当拉伸荷载P达到极限承载力Pu时,界面开始出现剥离,已经剥离的CFRP布其应变达到最大值且基本保持不变,该不变的应变长度即为CFRP剥离长度.此后,虽然两块钢板之间的相对位移不断增大,但CFRP应变分布形状基本不变,极限荷载基本不变.随着剥离不断向固定端发展,直到剩余的CFRP粘贴长度小于有效粘结长度,界面整体剥离.
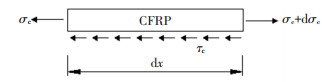
3 CFRP-钢界面粘结性能 3.1 界面剪应力如图 6所示,由静力平衡可得
| $ {\sigma _{\rm{c}}}{b_{\rm{c}}}{t_{\rm{c}}} + {\tau _{\rm{c}}}{b_{\rm{c}}}{\rm{d}}x = ({\sigma _{\rm{c}}} + {\rm{d}}{\sigma _{\rm{c}}}){b_{\rm{c}}}{t_{\rm{c}}}. $ | (1) |
|
图 6 CFRP受力图 Fig. 6 Force diagram of CFRP |
式中:σc为CFRP微段上的拉应力,τc为CFRP微段上界面剪应力,tc为CFRP的厚度,bc为CFRP的宽度.
将σc=Ecεc代入式(1)中,并进行整理, 得
| $ {\tau _{\rm{c}}} = {E_{\rm{c}}}{t_{\rm{c}}}\frac{{{\rm{d}}{\varepsilon _{\rm{c}}}}}{{{\rm{d}}x}}. $ | (2) |
式中:Ec为CFRP弹性模量,εc为CFRP的拉伸应变.
当应变测点布置较多时,界面剪应力可由差分原理简化求得,即
| $ {\tau _{i\backsim i + 1}} = \left| {\frac{{{E_{\rm{c}}}{t_{\rm{c}}}({\varepsilon _{{\rm{c}},i + 1}} - {\varepsilon _{{\rm{c}},i}})}}{{{L_{i + 1}} - {L_i}}}} \right|. $ | (3) |
式中:τi~i+1为CFRP应变测点i和i+1中点的剪应力,εc, i+1为CFRP应变测点i+1处的应变值,Li+1为CFRP应变测点i+1到端部的距离.
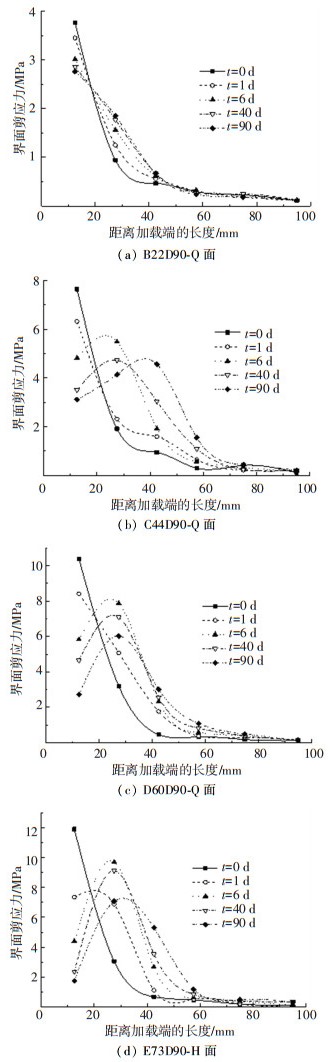
在持续加载阶段,CFRP-钢界面剪应力随加载时间变化如图 7所示,由于超过CFRP的有效粘结长度后界面剪应力非常小,因此图中只给出了100 mm以内的界面剪应力.观察图 7可知,随着加载时间增加,界面剪应力发生了应力重分布现象,峰值剪应力逐渐降低,原因是界面胶黏剂具有黏弹性特性,在荷载作用下会发生蠕变变形[16],胶层蠕变导致应力重分布,从而端部界面应力集中情况得到缓解.试件在持续加载90 d后,B组、C组、D组和E组试件在12.5 mm处界面剪应力分别减小了26.6%、59.2%、73.8%、85.4%,而其他各点剪应力均有不同程度的增加,27.5 mm处剪应力增加最多.这是因为持续施加的荷载大小不变,所以不同时刻剪应力曲线与坐标轴所围成的面积应保持不变.
|
图 7 界面剪应力随时间变化 Fig. 7 Interfacial shear stress varying with time |
CFRP应变测点i的局部滑移量si可由积分求得, 即
| $ {s_i} = \int {{\varepsilon _{\rm{c}}}} {\rm{d}}x. $ | (4) |
改写成数值积分形式:
| $ {s_i} = \sum\limits_{j = 0}^{i - 1} {\frac{{({\varepsilon _{{\rm{c}},j + 1}} + {\varepsilon _{{\rm{c}},j}})}}{2}} ({L_{j + 1}} - {L_j}). $ | (5) |
则测点i和i+1中点的滑移量为
| $ s(x) = \frac{{{s_i} + {s_{i + 1}}}}{2}. $ | (6) |
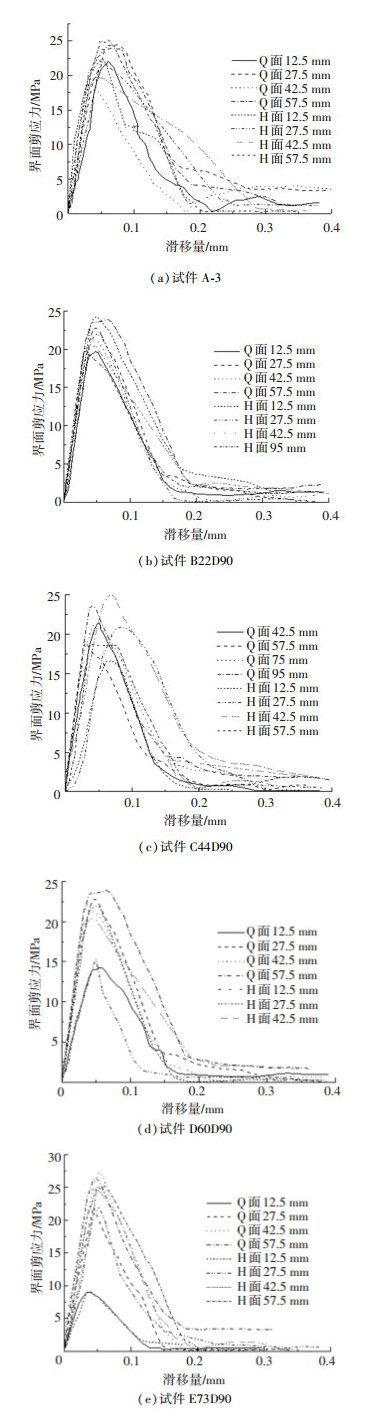
根据上述公式,即可计算相邻两个应变片中点的剪应力τ和滑移量s. 图 8中给出了典型试件Q面和H面的粘结滑移曲线.图例中12.5 mm表示该点离加载端长度为12.5 mm.
|
图 8 界面粘结滑移曲线 Fig. 8 Interfacial bond-slip curves |
由图 8可知,各试件粘结滑移曲线虽有一定差别,但总体上曲线由上升段和下降段组成,并具有较高的一致性.将界面剪应力增量与滑移量增量定义为的界面粘结刚度,该值的大小直接反映了直线上升段的斜率.粘结滑移曲线大致由4个阶段组成:1)上升段,滑移量较小而界面粘结刚度较大,界面呈弹性变形;2)软化段,当滑移量达到一定数值后,粘结刚度呈现逐渐减小趋势,即剪应力增大速率降低;3)下降段,一旦界面剪应力超过最大值,界面随即发生剥离并逐渐扩展,随着滑移量增加而剪应力降低;4)下降段末期,剪应力由两种材料之间的摩擦力和机械咬合力承担.
对比图 8中各图的粘结滑移曲线特征点可知,试件A-3和B22D90的各点峰值滑移量s0和峰值剪应力τmax较为接近,试件C44D90的H面12.5 mm处的峰值滑移量s0和峰值剪应力τmax较其他各点的数值小,其中τmax表现的最为突出,这种现象在试件D60D90和E73D90中更为明显.
根据试验结果整理的各试件峰值滑移量s0和峰值剪应力τmax见表 3. 表 3中Q1-2表示Q面1#和2#测点之间即离加载端12.5 mm处的平均值,H1-2表示H面1#和2#测点之间的平均值.分析表中数据:当持续施加的界面名义剪应力τ0为0.22τu(B组)时,峰值滑移量s0和峰值剪应力τmax没有明显变化;而当界面名义剪应力τ0≥0.44τu(C组、D组、E组)时,荷载持续作用的时间越长,s0和τmax均越小,且τ0越大,对应的s0和τmax均越小.这是因为加固用的环氧树脂胶黏剂为黏弹性材料,在持续的界面剪应力τ0作用下,界面会造成蠕变损伤,当界面剪应力水平较低(如:τ0/τu=0.22)时,界面蠕变损伤不大,其对s0和τmax几乎没有影响;当界面剪应力水平较高(如:τ0/τu≥0.44)时,界面蠕变损伤对粘结滑移曲线影响显著,且当剪应力越大持续时间越长,界面损伤越多,导致粘结滑移曲线s0和τmax越小.另外,由图 7可知,界面剪应力仅在加载端部分范围内存在,故该区域界面蠕变损伤严重,其粘结滑移曲线的s0和τmax低于其他位置,而加载端以外各点的s0和τmax未受到影响,这一点可从图 8(c)~8(e)得到证明.
| 表 3 试验结果 Tab. 3 Test results |
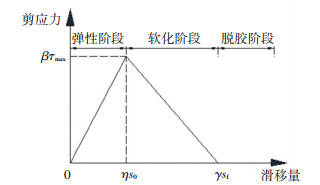
根据3.2节分析,采用双线性模型表征界面的粘结滑移本构关系,如图 9所示.模型中引入3个系数β、η和γ,分别考虑界面蠕变损伤对粘结滑移本构关系中峰值剪应力τmax、峰值滑移量s0和最大滑移量sf的影响,3个系数均与界面应力水平κ(κ=τ0/τu)及时间t有关. 图 9中考虑损伤的双线性模型可写成:
| $ \tau = \left\{ {\begin{array}{*{20}{l}} {\beta {\tau _{{\rm{max}}}}\frac{s}{{\eta {s_0}}},s \le \eta {s_0};}\\ {\beta {\tau _{{\rm{max}}}}\frac{{\gamma {s_{\rm{f}}} - s}}{{\gamma {s_{\rm{f}}} - \eta {s_0}}},\eta {s_0} < s \le \gamma {s_{\rm{f}}};}\\ {0,s > \gamma {s_{\rm{f}}}.} \end{array}} \right. $ | (7) |
|
图 9 考虑损伤的双线性粘结滑移本构 Fig. 9 Bilinear bond-slip constitutive relation considering damage |
根据3.2节分析以及试验结果,对于C组、D组、E组试件加载端以外区域以及A组、B组试件均不考虑界面发生蠕变损伤,参照已有研究成果以及本文试验数据,可得符合本试验得粘结滑移曲线特征参数.
1) 峰值滑移量s0.参考文献[5]的研究成果并结合试验数据,峰值滑移量s0可采用下式计算:
| $ {s_0} = 0.162{({t_{\rm{a}}}/{G_{\rm{a}}})^{0.65}}{f_{{\rm{t,a}}}}. $ | (8) |
式中:ft, a为胶黏剂的抗拉强度,MPa;Ga为胶黏剂的剪切强度,MPa;ta为胶黏剂胶层厚度mm.
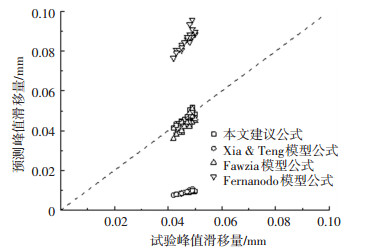
图 10为s0的计算结果与试验对比.由图 10可知,式(8)计算出的s0与本文试验结果的吻合程度要优于与其他学者的计算结果,相关系数R2= 0.790.
|
图 10 峰值滑移量的预测结果和试验结果 Fig. 10 Prediction and test results of peak slip |
2) 峰值剪应力τmax.文献[3-5]通过研究一致认为τmax只与胶黏剂的抗拉强度ft, a有关,而与其他因素无关.根据试验结果,峰值剪应力τmax可采用下式计算:
| $ {\tau _{{\rm{max}}}} = 0.485{f_{{\rm{t,a}}}}. $ | (9) |
表 1中胶黏剂的ft, a =47 MPa,由式(9)计算的τmax =22.80 MPa,这与表 3中的试验结果吻合较好.
3) 最大滑移量sf.采用文献[5]建议的sf计算公式:
| $ {s_{\rm{f}}} = 2{G_{\rm{f}}}/{\tau _{{\rm{max}}}}. $ | (10) |
式中Gf为CFRP-钢界面断裂能,即界面粘结-滑移曲线所包围的面积.
Gf采用文献[3]建议的计算公式.根据本次试验结果得到Gf的表达式为
| $ {G_{\rm{f}}} = 17{\left( {\frac{{{f_{{\rm{t,a}}}}}}{{{G_{\rm{a}}}}}} \right)^{0.56}}t_{\rm{a}}^{0.27}. $ | (11) |
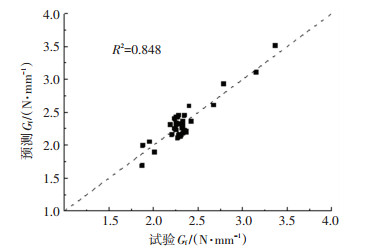
由式(11)计算的Gf和试验计算的Gf,如图 11所示.由图 11可知式(11)Gf的计算结果与试验结果符合较好.
|
图 11 界面断裂能的预测结果和试验结果 Fig. 11 Prediction and test results of interfacial fracture energy |
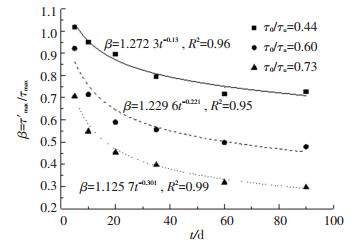
当界面剪应力水平τ0/τu≥0.44时,根据3.2节分析以及试验结果,C组、D组、E组试件在加载端附近区域(距离加载端12.5 mm处)应考虑胶黏剂蠕变引起的界面损伤对粘结滑移曲线的影响. 3个系数β、η、γ都是界面应力水平κ及时间t的函数.以系数β为例,界面损伤区峰值剪应力τ′max=βτmax,其中τmax为界面非损伤区峰值剪应力,则系数β=τ′max/τmax,根据试验结果回归分析可得到β与持载时间t的关系式,如图 12所示(图中峰值剪应力为Q1-2和H1-2的平均值).
|
图 12 参数β与时间t关系 Fig. 12 Relation between parameters β and t |
参考图 12中各回归方程的形式,可将β统一写成如下形式:
| $ \beta = {\tau ^\prime }_{\max }/{\tau _{\max }} = {f_\beta }(\kappa ){t^{{g_\beta }(\kappa )}}, $ | (12) |
式中参数fβ(κ)和gβ(κ)均为与剪应力水平κ有关的系数.通过回归分析可得到参数fβ(κ)和gβ(κ)的表达式,分别为
| $ {{f_\beta }(\kappa ) = - 1.36{\kappa ^2} + 1.14\kappa + 1.03,} $ | (13) |
| $ {{g_\beta }(\kappa ) = - 0.57\kappa + 0.125.} $ | (14) |
采用与系数β一样的推导方法,可得到系数η、γ分别为
| $ \left\{ {\begin{array}{*{20}{l}} {\eta = {f_\eta }(\kappa ){t^{{g_\eta }(\kappa )}},}\\ {{f_\eta }(\kappa ) = ( - 3.06{\kappa ^2} + 3.83\kappa + 0.88) \times {{10}^{ - 3}},}\\ {{g_\eta }(\kappa ) = 0.5{\kappa ^2} - 0.69\kappa + 0.17;} \end{array}} \right. $ | (15) |
| $ \left\{ {\begin{array}{*{20}{l}} {\gamma = {f_\gamma }(\kappa ){t^{{g_\gamma }(\kappa )}},}\\ {{f_\gamma }(\kappa ) = - 0.012{\kappa ^2} + 0.015\kappa + 0.004,}\\ {{g_\gamma }(\kappa ) = 0.48{\kappa ^2} - 0.53\kappa + 0.26.} \end{array}} \right. $ | (16) |
在求得系数β、η、γ后,通过式(7)可得到考虑界面损伤的双线性粘结滑移本构模型,分为以下两种情况考虑:
1) 当界面没有荷载作用历史或者虽有持续荷载作用,但界面剪应力水平κ≤0.22,此时不考虑荷载作用历史对界面的损伤影响,令β = η = γ = 1,根据式(8)~(10)分别计算s0、τmax、sf.
2) 当界面上有持续荷载作用且0.44≤κ≤0.73时,应考虑界面损伤对粘结滑移本构的影响,利用式(12)、(15)、(16)分别计算系数β、η、γ后,并代入式(7)中得到不同剪应力水平κ及不同加载时间t的界面粘结滑移本构关系.
值得注意的是,当0.22 < κ < 0.44或κ>0.73时,本文试验未涉及,因此界面蠕变损伤对粘结滑移本构关系的影响还需要进一步研究.
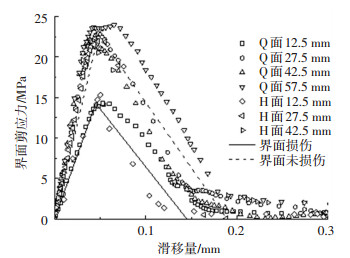
为验证粘结滑移本构模型的预测准确性,以试件E60D90为例,将式(7)计算得到的粘结滑移曲线与试验结果对比,如图 13所示.由图 13可看出,在上升段两者较为接近,下降段两者差距较大,这是由于界面损伤退化不均匀所致.
|
图 13 本构模型与试验数据对比 Fig. 13 Comparison between constitutive model and test results |
CFRP-钢界面极限承载力Pu试验结果见表 3. 表 3中极限承载力Pu试验值的平均值为28.3 kN,标准差为2.3 kN.界面极限承载力采用文献[17]对CFRP-混凝土界面剥离提出的计算公式,该公式已广泛应用于CFRP-钢界面承载力计算[3, 5-6, 9, 14],即
| $ {P_{{\rm{pre}}}} = {b_{\rm{c}}}\sqrt {2{G_{\rm{f}}}{E_{\rm{c}}}{t_{\rm{c}}}} , $ | (17) |
式中: Gf为界面断裂能,Ec为CFRP弹性模量.
由式(17)计算的界面极限承载力Ppre见表 3,计算结果Ppre与试验结果Pu比值的平均值为0.91,标准差为0.08,可见两者符合较好.
由表 3中可知,当CFRP粘贴长度大于有效粘结长度时,荷载作用历史对界面极限承载力Pu影响不显著.式(17)中Gf是粘结滑移曲线所包围的面积,当κ≤0.22时,粘结滑移曲线中s0和τmax几乎不变,蠕变损伤未引起Gf变化;当0.44≤κ≤0.73时,蠕变损伤仅造成加载端附近的s0和τmax减小,其他位置未受蠕变损伤影响,界面剥离时刻Gf由CFRP末端局部粘结滑移曲线性质决定,因此,界面局部损伤不会对最终界面Pu造成影响.这一结论与文献[12]中胶黏剂层蠕变损伤未导致CFRP-混凝土界面极限承载力受损相一致. 表 3中各试件极限承载力Pu不同, 主要是试件制作或加载过程中可能存在的偏心以及试验测量误差引起的.应该指出,当CFRP粘结长度小于有效粘结长度时,界面损伤对极限承载力的影响需要开展进一步的研究工作.
4 结论1) 当CFRP-钢双剪试件有持续荷载作用时,CFRP应变在加载端端部最大,随着距加载端越远CFRP应变越小,且其随着加载时间的增加而增大.
2) 持续荷载作用下胶黏剂发生蠕变变形导致界面剪应力发生应力重分布,剪应力峰值随加载时间逐渐降低. B组、C组、D组、E组试件加载90 d后,在12.5 mm处界面剪应力分别减小了26.6%、59.2%、73.8%、85.4%,缓解了端部界面剪应力集中现象.
3) 当持续施加的界面剪应力水平κ较低(κ≤0.22)时,界面没有蠕变损伤或蠕变损伤很小,对峰值滑移量s0和峰值剪应力τmax没有明显影响;当界面剪应力水平κ较高(0.44≤κ≤0.73)时,加载端12.5 mm内界面蠕变损伤对粘结滑移曲线影响显著,且当κ越高加载时间t越长,界面损伤越大,s0和τmax越小,在此范围以外,界面损伤对粘结性能基本没有影响.
4) 当CFRP粘贴长度大于有效粘结长度时,界面极限承载力不受界面蠕变损伤影响.
| [1] |
郑云, 叶列平, 岳清瑞. FRP加固钢结构的研究进展[J]. 工业建筑, 2005, 35(8): 20. ZHENG Yun, YE Lieping, YUE Qingrui. Progress in research on steel structures strengthened with FRP[J]. Industrial Construction, 2005, 35(8): 20. DOI:10.3321/j.issn:1000-8993.2005.08.005 |
| [2] |
李春良, 李凯, 张立辉, 等. CFRP端部被锚固后加固钢结构的界面粘结行为[J]. 哈尔滨工业大学学报, 2016, 48(9): 113. LI Chunliang, LI Kai, ZHANG Lihui, et al. Interfacial bond behavior of CFRP reinforced steel structures with end anchorage[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 113. DOI:10.11918/j.issn.0367-6234.2016.09.020 |
| [3] |
XIA S, TENG J. Behaviour of FRP-to-steel bonded joints[C]// Proceedings of the International Symposium on Bond Behaviour of FRP in Structures (BBFS 2005). Hong Kong: International Institute for FRP in Construction, 2005: 419
|
| [4] |
FAWZIA S, ZHAO X L, AL-MAHAIDI R. Bond-slip models for double strap joints strengthened by CFRP[J]. Composite Structures, 2010, 92(9): 2137. DOI:10.1016/j.compstruct.2009.09.042 |
| [5] |
FERNANDO N D. Bond behaviour and debonding failures in CFRP-strengthened steel members[D]. Hong Kong: The Hong Kong Polytechnic University, 2010
|
| [6] |
LI C, LU K, HE J, et al. Effects of mechanical properties of adhesive and CFRP on the bond behavior in CFRP-strengthened steel structures[J]. Composite Structures, 2019, 211: 163. DOI:10.1016/j.compstruct.2018.12.020 |
| [7] |
FERNANDO D, YU T, TENG J G. Behavior of CFRP laminates bonded to a steel substrate using a ductile adhesive[J]. Journal of Composites for Construction, 2014, 18(2): 04013040. DOI:10.1061/(ASCE)CC.1943-5614.0000439 |
| [8] |
WANG H T, WU G, DAI Y T, et al. Experimental study on bond behavior between CFRP plates and steel substrates using digital image correlation[J]. Journal of Composites for Construction, 2016, 20(6): 04016054. DOI:10.1061/(ASCE)CC.1943-5614.0000701 |
| [9] |
何俊.胶粘剂性能对CFRP-钢界面粘结破坏行为的影响研究[D].哈尔滨: 哈尔滨工业大学, 2017 HE Jun. Research on the effects of adhesive properties on the failure behaviours of CFRP-to-steel interface[D]. Harbin: Harbin Institute of Technology, 2017 |
| [10] |
薛耀, 张龙, 曹双寅, 等. 低龄期下CFRP-钢界面黏结性能试验研究[J]. 东南大学学报(自然科学版), 2015, 45(2): 360. XUE Yao, ZHANG Long, CAO Shuangyin, et al. Experimental study on bonding behavior of CFRP-to-steel interface under early curing age[J]. Journal of Southeast University (Natural Science Edition), 2015, 45(2): 360. DOI:10.3969/j.issn.1001-0505.2015.02.028 |
| [11] |
HOUHOU N, BENZARTI K, QUIERTANT M, et al. Analysis of the nonlinear creep behavior of concrete/FRP-bonded assemblies[J]. Journal of Adhesion Science and Technology, 2014, 28(14/15): 1345. DOI:10.1080/01694243.2012.697387 |
| [12] |
马明, 徐佰顺, 张方, 等. 持续荷载下CFRP-混凝土界面黏结性能试验与分析[J]. 哈尔滨工业大学学报, 2018, 50(3): 128. MA Ming, XU Baishun, ZHANG Fang, et al. Experiment and performance analysis on bonding behavior of CFRP-concrete interface under sustained load[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 128. DOI:10.11918/j.issn.0367-6234.201703086 |
| [13] |
公路桥梁加固设计规范: JTG/T J22—2008[S].北京: 人民交通出版社, 2008 Specifications forstrengthening design of highway bridges: JTG/T J22—2008[S]. Beijing: China Communications Press, 2008 |
| [14] |
YU T, FERNANDO D, TENG J G, et al. Experimental study on CFRP-to-steel bonded interfaces[J]. Composites Part B: Engineering, 2012, 43(5): 2279. DOI:10.1016/j.compositesb.2012.01.024 |
| [15] |
ZHAO X L, ZHANG L. State-of-the-art review on FRP strengthened steel structures[J]. Engineering Structures, 2007, 29(8): 1808. DOI:10.1016/j.engstruct.2006.10.006 |
| [16] |
徐佰顺, 钱永久, 唐继舜, 等. 基于黏弹性本构的CFRP-钢界面应力参数敏感性分析[J]. 公路交通科技, 2017, 34(11): 57. XU Baishun, QIAN Yongjiu, TANG Jishun, et al. Analysis on CFRP-to-steel interfacial stress parameter sensitivity based on viscoelastic constitution[J]. Journal of Highway and Transportation Research and Development, 2017, 34(11): 57. |
| [17] |
YUAN H, TENG J G, SERACINO R, et al. Full-range behavior of FRP-to-concrete bonded joints[J]. Engineering Structures, 2004, 26(5): 553. DOI:10.1016/j.engstruct.2003.11.006 |
 2020, Vol. 52
2020, Vol. 52


