2. 河北建筑工程学院 土木工程学院,河北 张家口 075000;
3. 山西大学 土木工程系,太原 030013;
4. 河北建筑工程学院 建筑与艺术学院,河北 张家口 075000;
5. 石家庄铁道大学 土木学院,石家庄 050043
2. School of Civil Engineering, Hebei University of Architecture, Zhangjiakou 075000, Hebei, China;
3. Department of Civil Engineering, Shanxi University, Taiyuan 030013, China;
4. School of Architecture and Art, Hebei University of Architecture, Zhangjiakou 075000, Hebei, China;
5. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
围岩类型对隧道及地下工程的整体稳定性和施工工艺影响较大,而深埋于地下的岩体往往会形成各种裂隙、断层、节理等弱化结构面,承受较大的地应力,内部积聚的能量较大[1-3];在工程实际过程中,为了克服不同施工开挖速率,有可能造成的岩爆、坍塌等工程灾害,对弱化结构面往往会采取注浆加固措施.因此,研究不同速率对注浆体力学特性的影响,对合理评估注浆效果,选择施工方案和风险评估有着极其重要的意义[4-7].国内外专家针对不同加载速率对岩石力学特性影响方面展开了大量工作,其中, 文献[8]借助单轴压缩试验,研究了不同加载速率下红砂岩变形局部化演化特征与岩石、泊松比变化及能量积累和释放特征的对应关系;文献[9-12]基于岩体单轴试验,研究了不同应变速率的应变速率效应、弹性参数变化、岩体破裂特性以及破环程度的影响;文献[13]借助单轴压缩试验研究了能量演化在含黏结面不完整岩石受载过程中的规律;文献[14]采用4种不同的加载速率对红砂岩试件进行了单轴循环加、卸载试验,得到了弹性能和耗散能随应力的演化及分配规律;文献[15]研究了岩石损伤破坏过程中能量耗散过程与剪胀变形间的关系;文献[16]通过均质岩石试件单轴压缩实验,分析了破坏特征,损伤演化过程中的能量耗散与传递规律.
虽然前人关于岩石加载速率效应方面作了很多研究工作,而针对裂隙注浆体力学性能、加载过程中能量变化及分配规律、最终破坏形态等三者之间关系的研究相对较少,本文基于这3个方面,借助单轴压缩试验、高清摄像技术和数字散斑等方法展开研究,探求其中的关系,为注浆加固工程的定性和定量研究提供新的思路.
1 试验设计 1.1 试验材料试验样品选自山东临沂莒南红砂岩,主要成分是黏土质、硅质、陆源粉砂.其中,黏土质含量(质量分数)为50%~55%;硅质含量为35%~40%;陆源粉砂含量约为10%.
PG-SI无收缩自密实高强灌浆料主要组份:1)胶凝材料:高强水泥、微硅粉;2)膨胀组分:石膏;3)早强组分:硫酸钠、氯化锂早强剂;4)减水组分:聚羧酸高效减水剂;5)增稠保水组分:低粘度的纤维素醚;6)骨料:河砂.
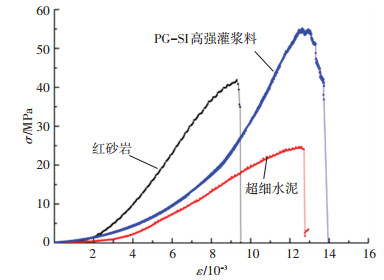
为确保试验的科学性和准确性,缩短养护时间、提高强度上升速度、减少注浆后浆体部分的收缩变形,进一步研究高强注浆体变应变速率下力学性能,配置的PG-SI高强灌浆料材料配比:m(水):m(减水剂):m(PG-SI灌浆料)=100:5:20,试验所用红砂岩、注浆材料及称量设备见图 1.通过对红砂岩、P.O 42.5和PG-SI无收缩自密实高强灌浆料试样进行单轴抗压强度试验得出,三者的单轴抗压强度值分别为46.85、24.66、54.93 MPa. 图 2为3种材料强度对比图.

|
图 1 注浆试样与主要仪器 Fig. 1 Grouting sample and main instruments |
|
图 2 岩体及注浆材料强度对比 Fig. 2 Comparison of strength between rock mass and grouting material |
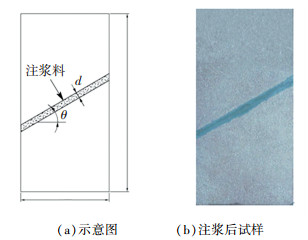
为了确保切割、打磨后试样的尺寸准确与规范,在对原始红砂岩岩样初次切割时,各方向多预留2 mm,即借助割石机、磨石机将红砂岩制作成规格为32 mm×62 mm×122 mm长方体初步试样.以倾角θ和宽度d的线条试样制作为例,借助工具尺和画线笔,在试样表面的长度和宽度方向确定其中轴线和尺寸中心点并进行标记;通过三角函数关系得到倾角θ裂纹斜向长度中线,以此中线为基准,上下各偏移d/2,即得到倾角θ和宽度d的试样线条,然后沿着所得的两条斜线进行切割、植入对应厚度d的橡胶垫,并绑扎胶带;而后对预留宽度d的红砂岩裂隙岩体进行注浆注浆、养护,具体试样见图 3.
|
图 3 试验试样 Fig. 3 Schematic diagram of sample |
为实现变应变速率对注浆体力学性质的研究,共设计6种应变速率试验工况,分别为10-5、5×10-5、10-4、5×10-4、10-3、5×10-3 s-1;单轴压缩试验加载时,采用YAW-2000微机控制电液伺服压力试验机,试验加载前在试样上下端面涂抹凡士林,以消除端部效应;加载时,需计算出各应变速率所对应的位移加载速率,以实现位移控制加载,直至试样破坏,同时借助动静态应变测试分析系统采集试验加载过程中试样的轴向应变;为方便观察和试样裂纹变化过程,记录最后破坏形态,整个试验过程利用高清摄像机全过程摄像.主要试验设备及仪器见图 4.

|
图 4 主要试验设备及仪器 Fig. 4 Main test equipment and instruments |
基于单轴抗压强度试验,对6种加载速率工况下试样的应变变化规律、峰值应变、峰值强度以及弹性模量等力学指标展开研究,分析变应变速率对其力学特性的影响.
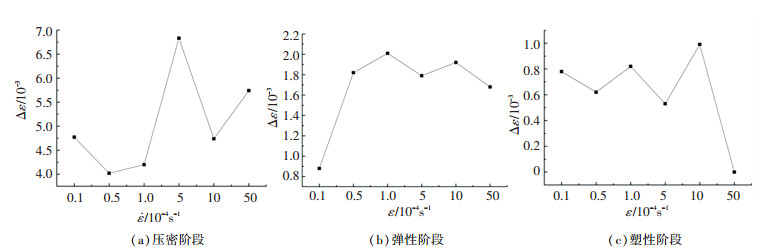
2.1 应变变化规律根据试样应力-应变变化特性,可将其分为压密阶段、弹性阶段和塑性阶段3个阶段. 图 5为不同加载速率下3个阶段应变变化曲线.加载速率对各个阶段的应变增量变化规律有所影响,具体规律如下.
|
图 5 不同应变速率对应的应变增量 Fig. 5 Relation between strain increment and strain rate |
1) 压密阶段.应变速率对该阶段应变量Δε1的影响分为两个阶段:a)应变速率为10-5~10-4s-1阶段,Δε1总体呈逐渐减小趋势,变化幅度相对较小,变化幅度分别为15.66%、12.32%;b)应变速率为5×10-4~5×10-3s-1阶段,Δε1较应变速率为10-5~10-4s-1阶段,整体增长,增幅分别为61.90%、12.62%、36.90%,其最小值为0.004 8(增幅为12.62%).
2) 弹性阶段.应变速率对该阶段应变量Δε1的影响可分为两个阶段:a)应变速率从10-5s-1增大到10-4s-1时,Δε1逐渐增大,增幅分别为103.40%、11.39%;b)当应变速率从5×10-4s-1增大到5×10-3s-1时,Δε1增幅仅为6.8%,降幅为14.14%,变化幅度相对较小,Δε2总体呈逐渐减小趋势.
3) 塑性阶段.应变速率对该阶段应变量Δε3的影响可分为两个阶段:a)应变速率为10-5~10-4 s-1阶段,Δε3总体上保持相对稳定;b)应变速率为5×10-4~5×10-3s-1阶段,随应变速率增大,Δε3先急剧增大至最大值0.001,增幅达为92.60%,随后减小至0,降幅为100%.
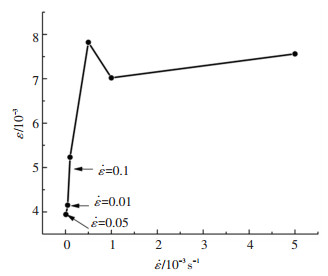
2.2 峰值应变分析注浆体峰值应变与应变速率的关系(图 6)可知:应变速率在10-5~5×10-5 s-1之间时的峰值应变较小;当应变速率从5×10-5 s-1增大到5×10-4 s-1时,峰值应变急剧上升,增幅为42.55%;当应变速率从5×10-4 s-1增大到5×10-3s-1时,峰值应变先减小,降幅为16.78%,随后保持稳定.
|
图 6 峰值应变随应变速率变化关系 Fig. 6 Variation of peak strain with strain rate |
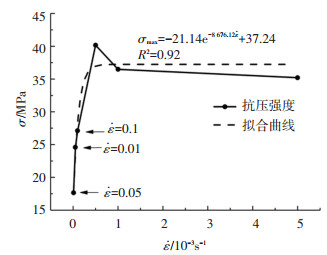
分析注浆体峰值强度与应变速率的关系(图 7)可得出:注浆体峰值强度随着应变速率增大而增大,二者呈指数函数关系:
|
图 7 峰值强度随应变速率变化关系 Fig. 7 Variation of peak strength with strain rate |
应变速率对注浆体峰值强度的影响可分为敏感和滞缓应变两阶段,其中敏感阶段的峰值强度变化幅度较大,而滞缓阶段变化较小,具体变化规律:1)敏感应变率阶段.位于低频应变率区域(10-5~5×10-4 s-1)的峰值强度由17.64 MPa增至40.16 MPa,增幅为127.62%. 2)滞缓应变率阶段.位于高频应变率区域(10-3~5×10-3 s-1)的峰值强度由36.48 MPa降至35.21 MPa,降幅仅为3.49%.
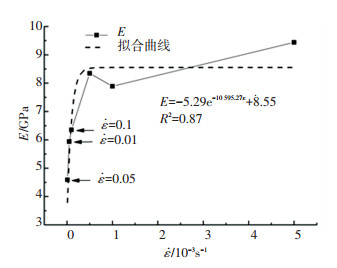
2.4 弹性模量分析注浆体弹性模量与应变速率关系曲线图 8可知, 注浆体的弹性模量整体随着应变速率增大而增大,且弹性模量与应变速率呈现指数函数关系:
| $ E=-5.29 \mathrm{e}^{-10595.27 \dot{\varepsilon}}+8.55, R^{2}=0.87. $ |
|
图 8 弹性模量随应变速率变化关系 Fig. 8 Variation of elastic modulus with strain rate |
应变速率对注浆体弹性模量影响可分为两个阶段:1)敏感应变率阶段.位于低频应变率在10-5~5×10-4 s-1之间时,试样的弹性模量由3.605 GPa增至8.348 GPa,增幅为131.57%. 2)滞缓应变率阶段.位于高频应变率在10-3~5×10-3 s-1之间时,试样的弹性模量7.89 GPa升高至9.44 GPa,升高幅度仅为19.63%.整体而言,敏感阶段试样的弹性模量受加载速率影响明显.
3 变应变速率作用下注浆体能量演化及分配规律研究针对注浆体试样在不同加载速率过程中的破坏特征,结合能量原理,分析单轴抗压强度试验过程能量分配规律,从另一个角度研究加载速率对力学性质的影响.
3.1 能量原理根据热力学第一定律,注浆体试样单轴压缩破坏过程中,能量转化遵守能量守恒定律.假设任意单位体积岩体单元在外力作用下产生变形,该物理过程与外界没有能量交换,认为外力所做的功全部被试样吸收并转化为弹性能和耗散能.
理想加固体结构的弹性能是可逆的,即在卸载过程中,试样内部弹性能以机械能的形式释放出去.而对于内部存在各种缺陷的岩体,在能量输入时,总会造成部分粒子间的价键断裂,引起结构的不可逆损伤.当岩体内部存储的弹性能达到一定程度,将会发生破坏或失稳,并转化为其他形式的能量.因此,对于试样破坏失稳前,均伴随着弹性能的大量存储,当达到一定程度后会发生破坏而释放部分能量,发生能量转化.
基于上述,外力所做功产生的能量U=Ue+Ud.其中, U表示外力做功产生的能量, Ud表示耗散能, Ue表示弹性能.
注浆体的耗散能量可分为3类:峰值强度前、轴向破裂部分、剪切破坏部分,即Ud=U1d+U2d+U3d.其中, U1d表示峰值强度前耗散能, U2d表示轴向破裂部分耗散能, U3d表示剪切破坏部分耗散能.
弹性能包括峰值强度前、轴向破裂部分、剪切破坏等3个部分,即Ue=U1e+U2e+U3e.其中, U1e表示峰值强度前弹性能, U2e表示轴向破裂部分弹性能, U3e表示剪切破坏部分弹性能.
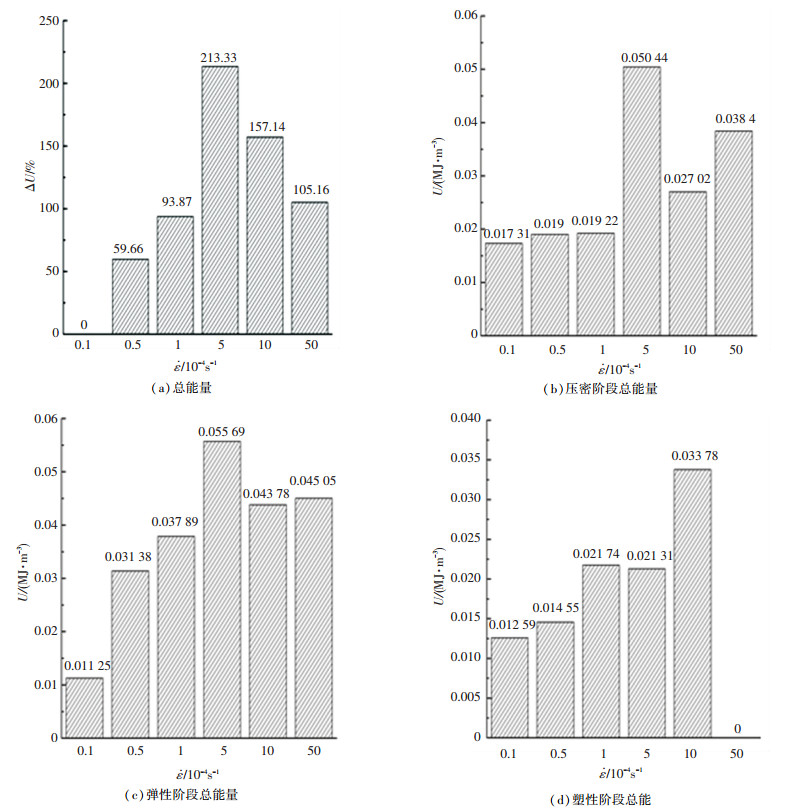
3.2 能量演化规律 3.2.1 裂隙注浆体总能量规律依据能量基本原理:随着应变速率的增大,注浆体的总能量也随之增大;滞缓应变率阶段总能量比敏感应变率阶段的大.
依据试样应力-应变曲线特征的压密、弹性、塑性阶段,进一步得出试样总能量的演化规律(见图 9):1)总体来讲,滞缓应变率阶段的各阶段比敏感应变率对应阶段总能量大. 2)压密阶段.滞缓应变率阶段总能量约为敏感应变率阶段的1.41~2.91倍. 3)弹性阶段.敏感应变率阶段随应变速率的增大,总能量增大,增幅分别为64.15%、20.75%、46.98%;而滞缓应变率阶段随应变速率增大变化不明显. 4)塑性阶段.滞缓应变率阶段随应变速率增大变化不明显,但总能量波动较大,由0.021 31 MJ·m-3陡增至0.033 78 MJ·m-3,而后骤降至0 MJ·m-3;压密阶段总能量变化幅度是最大的,塑性阶段次之,弹性阶段最小.
|
图 9 应变速率与各阶段能量变化规律 Fig. 9 Variation of energy with strain rate in each stage |
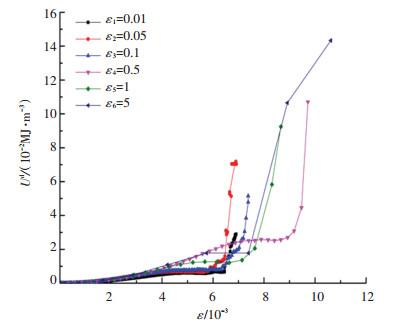
由图 10可得出耗散能密度随着应变速率的变化规律:应变为0~4×10-3时,敏感应变率阶段与滞缓应变率阶段的耗散能相差无几;应变>4×10-3时,敏感应变率阶段与滞缓应变率阶段的耗散能差异较大,其中,敏感应变率阶段的耗散能密度保持不变,滞缓应变率阶段较敏感应变率阶段明显增大.
|
图 10 耗散能密度随应变变化规律 Fig. 10 Variation of dissipated energy density with strain |
由图 11、12分析得出积聚能密度随着应变变化规律:应变为0~3×10-3时,敏感应变率阶段与滞缓应变率阶段的积聚能密度相差无几;应变>3×10-3时,随着应变速率的增大,注浆体的积聚能密度先增大而后急剧降低,之后出现再增大的变化特点,转折点处的应变速率为5×10-4;敏感应变率阶段积聚能密度随着应变速率的增大而增大,滞缓应变率积聚能密度随着应变速率的增大显现先增大后降低趋势.
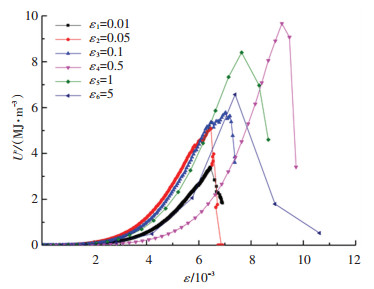
|
图 11 积聚能密度随应变变化规律 Fig. 11 Variation of accumulated energy with strain |
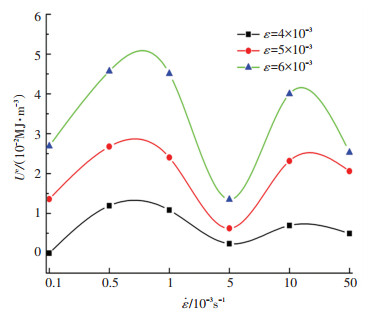
|
图 12 不同应变下积聚能密度随应变速率变化曲线 Fig. 12 Variation of accumulated energy density with strain rate under different strain |
随着加载速率的增大,注浆体压密阶段的耗散能均大于弹性和塑性阶段的耗散能.敏感应变率阶段,注浆体压密阶段积聚能变化很小,而弹性阶段积聚能明显增大;滞缓应变率阶段,注浆体压密阶段积聚能相对变化平缓,弹性阶段积聚能与压密阶段耗散能呈相同变化规律(图 13).
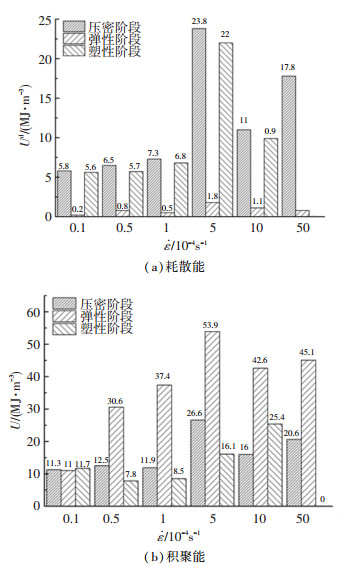
|
图 13 应变速率与能量分配关系直方图 Fig. 13 Histogram of strain rate and energy distribution |
由图 14可得:1)压密阶段.敏感应变率阶段,62%~66%能量为积聚能,34%~38%为耗散能,积聚能与耗散能之比(积散比)约为1.86~1.63;滞缓应变率阶段,53%~59%能量为积聚能,41%~47%为耗散能,积散比约为1.44~1.13. 2)弹性阶段.无论是敏感应变率阶段还是滞缓应变率阶段,积聚能所占比例均大于98%. 3)塑性阶段.敏感应变率阶段,不同应变速率裂隙注浆体的能量分配差异较大;总而言之,随着应变速率增大,试样的耗散能占比逐渐增大,且应变速率为10-4 s-1时积散比低于1(以耗散能为主);滞缓应变率阶段,应变速率为5×10-4~10-3 s-1时,积散比均为3,基本相同;应变速率为5×10-3 s-1时无明显塑性区,故无能量分配.
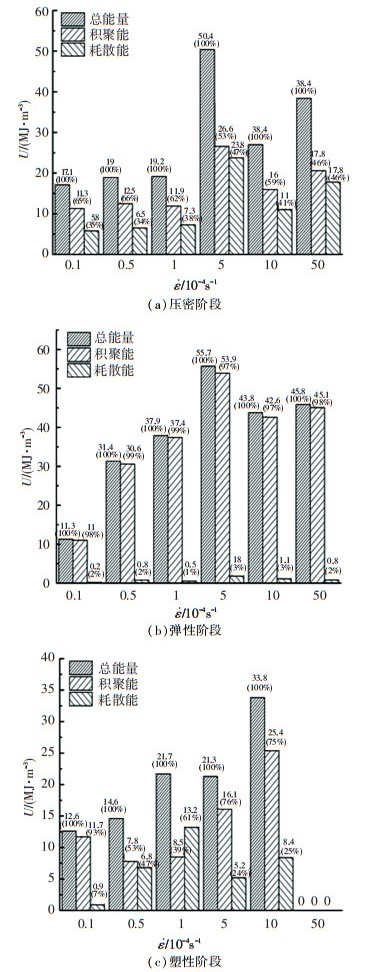
|
图 14 各阶段注浆体能量分配规律直方图 Fig. 14 Histogram of energy distribution law of grouting in each stage |
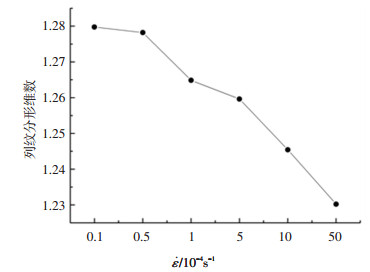
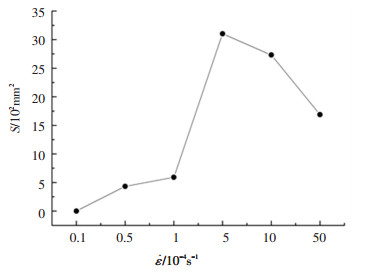
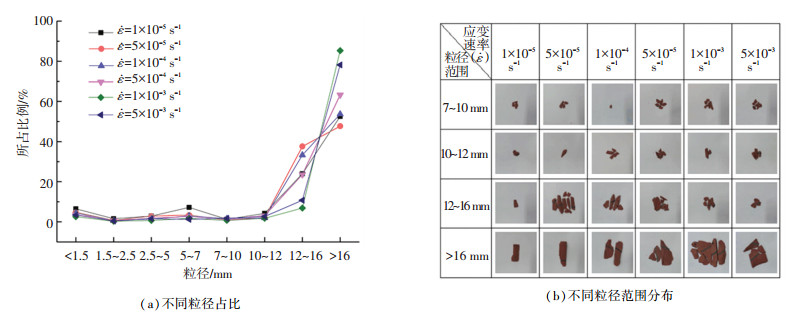
依据分形理论,汇总得到裂纹分形维数、试样脱落面积和破碎块粒径与应变速率的关系(图 15~17),对比分析得出以下规律:1)随着应变速率增大,注浆体的裂纹分形维数随之降低,脱落面积与力学特性变化规律相吻合,碎块可较好反映其力学特征或能量演化特征. 2)随着应变速率的增大,碎块以大块为主(大粒径的比重逐渐增加),主要表现在粒径>12 mm的破碎出现差异,敏感应变率阶段破碎颗粒粒径在12~16 mm之间的数量较滞缓应变率阶段的多,破碎颗粒粒径>16 mm的规律与之相反.此规律吻合随着应变速率增大,滞缓应变率阶段较敏感应变率阶段塑性阶段耗散能密度明显增大.说明耗散能密度影响着裂隙注浆岩体破坏脱落面积以及粒径分布,耗散能密度越大,碎块以大块为主(粒径大的比率逐渐增加),故其破碎块体较敏感应变率阶段也较大.
|
图 15 裂纹分形维数随应变速率变化 Fig. 15 Variation of crack fractal dimension with strain rate |
|
图 16 破坏脱落面积随应变速率变化 Fig. 16 Variation of failure area with strain rate |
|
图 17 破坏粒径分布特征 Fig. 17 Distribution characteristics of failure particle size |
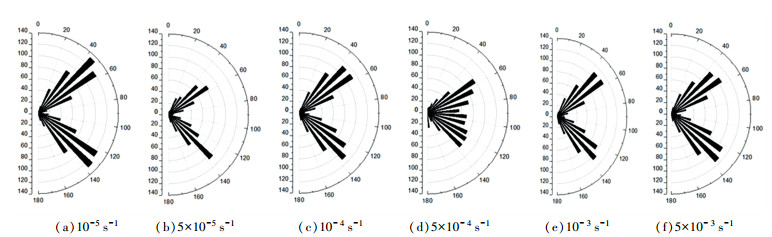
基于PFC离散元数值计算方法,注浆体在应变速率分别为10-5、5×10-5、10-4、5×10-4、10-3、5×10-3 s-1时的剪切裂纹和张拉裂纹的倾角以及分布, 如图 18、19所示.
|
图 18 不同应变速率下剪切裂纹分布特征 Fig. 18 Distribution characteristics of shear crack at different strain rates |
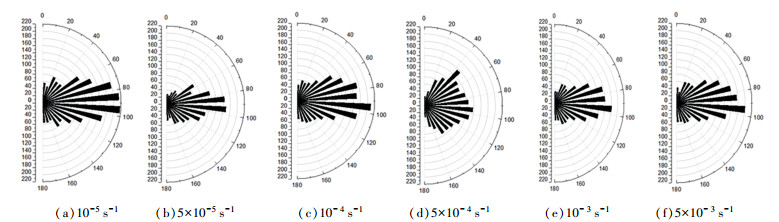
|
图 19 不同应变速率下张拉裂纹分布特征 Fig. 19 Distribution characteristics of tension crack at different strain rates |
通过分析变化规律可得出:随着应变速率的增大,注浆体的剪切裂纹总是先减少后增多,最后保持相对稳定;拉张裂纹和剪切裂纹呈现相似的变化规律.本节以剪切裂纹为例阐述其机理:1)敏感应变率阶段,应变速率为10-5 s-1时,剪切裂纹数最多,且裂纹倾角主要集中在40°~60°和120°~140°之间(近似平行和垂直于裂纹);应变速率为5×10-5 s-1时,剪切裂纹数明显降低,裂纹倾角主要集中在50°~60°和130°~140°之间,但集中程度明显较10-5 s-1应变速率时低很多;应变速率为10-4 s-1时,剪切裂纹数明显增多,裂纹倾角依然集中在40°~ 60°和120°~140°之间,且集中程度明显较5×10-5 s-1应变速率时降低. 2)滞缓应变速率阶段时,应变速率为5×10-4 s-1时,裂纹倾角均匀分布在50°~130°之间,无明显集中规律;应变速率为10-3 s-1时,较5×10-4 s-1时裂纹数变化很小,但裂纹倾角出现集中规律,主要集中于40°~60°和120°~140°之间,但集中程度将敏感应变率阶段小很多;应变速率为5×10-3 s-1时与应变速率为10-3 s-1时的规律相似.
5 变应变速率对注浆体力学特性影响的机理分析随着应变速率增大,注浆体的总能量也随之增大;压密阶段总能量变化幅度最大,塑性阶段次之,弹性阶段最小.压密阶段是影响不同应变速率注浆体力学特性的主要阶段;注浆体的分形维数、破坏特征及裂纹倾角分布与力学特性表现出较好的相关性.
综合分析可得:1)敏感应变率阶段而言,注浆体压密阶段耗散能作用于试样颗粒的滑移密实,而受裂隙倾角影响,颗粒滑移主要集中在与裂隙倾角相同方向或垂直方向,此阶段产生裂纹较多,倾角主要集中在40°~60°和120°~140°之间(近似平行或垂直裂隙方向),且程度较大,该部分耗散的能量相对较少,积散比为1.86~1.63. 2)滞缓应变率阶段而言,压密阶段耗散能仍主要作用于试样颗粒滑移密实,但颗粒滑移方向性逐渐降低,致使裂纹产生相对较少,倾角程度也相应的降低,该部分耗散能量相对较多,积散比为1.44~1.13,尤其以应变速率为5×10-4 s-1时,裂纹数最少,无集中分布现象,积散比达到最小值1.13.耗散能密度决定着裂隙注浆岩体破坏脱落面积以及粒径分布,耗散能密度越大,碎块越以大块为主(大粒径的比重逐渐增加),滞缓应变率阶段破碎块体较敏感应变率阶段大.
6 结论1) 随应变速率增加,注浆体峰值强度、弹性模量均随之而增大,且峰值强度随应变速率呈指数函数变化.
2) 注浆体对应变速率响应分为两个阶段:敏感应变率阶段,位于低频应变率为10-5~5×10-4s-1之间,峰值强度变化率为127.62%,弹性模量变化率为131.57%;滞缓应变率阶段,位于高频应变率为5×10-4~5×10-3 s-1之间,峰值强度变化率仅为12%,弹性模量变化率仅为22%.
3) 随着应变速率增大,裂隙注浆体的总能量也随之增大;滞缓应变率阶段较敏感应变率阶段的总能量大,两个应变速率阶段的压密阶段总能量变化幅度最大,塑性阶段次之,弹性阶段最小.
4) 压密阶段:敏感应变率阶段,62%~66%能量为积聚能,34%~38%为耗散能,积散比为1.86~1.63;滞缓应变率阶段,53%~59%能量为积聚能,41%~47%为耗散能,积散比为1.44~1.13.
5) 敏感应变率阶段裂隙注浆岩体产生裂纹角度,且倾角主要集中在40°~60°和120°~140°之间(近似平行或垂直裂隙方向),集中程度较大,故而其强度较低.
6) 耗散能密度决定着裂隙注浆岩体破坏脱落面积以及粒径分布,耗散能密度越大,碎块越以大块为主(大粒径的比率逐渐增加),滞缓应变率阶段破碎块体较敏感应变率阶段较大.
| [1] |
谢和平, 鞠杨, 黎立云. 基于能量耗散与释放原理的岩石强度与整体破坏准则[J]. 岩石力学与工程学报, 2005, 24(17): 3003. XIE Heping, JU Yang, LI Liyun. Criteria for strength and structural failure of rocks based on energy dissipation and release principles[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3003. DOI:10.3321/j.issn:1000-6915.2005.17.001 |
| [2] |
谢和平, 彭瑞东, 鞠杨, 等. 岩石破坏的能量分析初探[J]. 岩石力学与工程学报, 2005, 24(15): 2603. XIE Heping, PENG Ruidong, JU Yang, et al. On energy analysis of rock failure[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(15): 2603. DOI:10.3321/j.issn:1000-6915.2005.15.001 |
| [3] |
赵忠虎, 谢和平. 岩石变形破坏过程中的能量传递和耗散研究[J]. 四川大学学报, 2008, 40(2): 26. ZHAO Zhonghu, XIE Heping. Energy transfer and energy dissipation in rock deformation and fracture[J]. Journal of Sichuan University, 2008, 40(2): 26. |
| [4] |
周辉, 杨艳霜, 肖海斌, 等. 硬脆性大理岩单轴抗拉强度特性的加载速率效应研究—试验特征与机制[J]. 岩石力学与工程学报, 2013, 32(9): 1868. ZHOU Hui, YANG Yanshuang, XIAO Haibin, et al. Research on loading rate effect of tensile strength of hard brittle marble—test characteristics and mechanism[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(9): 1868. DOI:10.3969/j.issn.1000-6915.2013.09.019 |
| [5] |
黄达, 黄润秋, 张永兴. 粗晶大理岩单轴压缩力学特性的静态加载速率效应及能量机制试验研究[J]. 岩石力学与工程学报, 2012, 31(2): 245. HUANG Da, HUANG Runqiu, ZHANG Yongxing. Experimental investigations on static loading rate effects on mechanical properties and energy mechanism of coarse crystal grain marble under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 245. DOI:10.3969/j.issn.1000-6915.2012.02.003 |
| [6] |
孟庆彬, 韩立军, 浦海, 等. 应变速率和尺寸效应对岩石能量积聚与耗散影响的试验[J]. 煤炭学报, 2015, 40(10): 2386. MENG Qingbin, HAN Lijun, PU Hai, et al. Experimental on the effect of strain rate and size on the energy accumulation and dissipation of rock[J]. Journal of China Coal Society, 2015, 40(10): 2386. DOI:10.13225/j.cnki.jccs.2014.1771 |
| [7] |
MOUTHEREAU F, FILLON C, MA K F. Distribution of strain rates in the Taiwan orogenic wedge[J]. Earth and Planetary Science Letters, 2009, 284(3/4): 361. DOI:10.1016/j.epsl.2009.05.005 |
| [8] |
宋义敏, 邢同振, 邓琳琳, 等. 不同加载速率下岩石变形场演化试验研究[J]. 岩土力学, 2017, 38(10): 2773. SONG Yimin, XING Tongzhen, DENG Linlin, et al. Experimental study of evolution characteristics of rock deformation field at different loading rates[J]. Rock and Soil Mechanics, 2017, 38(10): 2773. DOI:10.16285/j.rsm.2017.10.001 |
| [9] |
MAHMUTOǦLLU Y. The effects of strain rate and saturation on a micro-cracked marble[J]. Engineering Geology, 2006, 82(3): 137. DOI:10.1016/j.enggeo.2005.09.001 |
| [10] |
FUENKAJORN K, SRIAPAI T, SAMSRI P. Effects of loading rate on strength and deformability of Maha Sarakham salt[J]. Engineering Geology, 2012, 135-136. DOI:10.1016/j.enggeo.2012.02.012 |
| [11] |
LIANG W G, ZHAO Y S, XU S G, et al. Effect of strain rate on the mechanical properties of salt rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(1): 161. DOI:10.1016/j.ijrmms.2010.06.012 |
| [12] |
苏承东, 李怀珍, 张盛, 等. 应变速率对大理岩力学特性影响的试验研究[J]. 岩石力学与工程学报, 2013, 32(5): 943. SU Chengdong, LI Huaizhen, ZHANG Sheng, et al. Experimental investigation on effect of strain rate on mechanical characteristics of marble[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(5): 943. DOI:10.3969/j.issn.1000-6915.2013.05.012 |
| [13] |
苏晓波, 纪洪广, 裴峰, 等. 单轴压缩荷载下含黏结面花岗岩能量演化研究[J]. 哈尔滨工业大学学报, 2018, 50(8): 161. SU Xiaobo, JI Hongguang, PEI Feng, et al. Study on energy evolution law of defective granite specimen under uniaxial compressive loading and unloading[J]. Journal of Harbin Institute of Technology, 2018, 50(8): 161. DOI:10.11918/j.issn.0367-6234.201710130 |
| [14] |
张志镇, 高峰. 单轴压缩下红砂岩能量演化试验研究[J]. 岩石力学与工程学报, 2012, 31(5): 953. ZHANG Zhizhen, GAO Feng. Experimental research on energy evolution of red sandstone and stone samples under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(5): 953. DOI:10.3969/j.issn.1000-6915.2012.05.012 |
| [15] |
张振杰, 朱杰兵, 汪斌, 等. 基于能量耗散机制的片麻状花岗岩损伤与剪胀演化规律[J]. 岩石力学与工程学报, 2018, 38(增刊1): 3441. ZHANG Zhenjie, ZHU Jiebing, WANG Bin, et al. The damage and shear dilation property evolution based on energy dissipation mechanism of gneissic granite[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 38(S1): 3441. DOI:10.13722/j.cnki.jrme.2017.1200 |
| [16] |
张东明, 白鑫, 尹光志, 等. 含层理岩石单轴损伤破坏声发射参数及能量耗散规律[J]. 煤炭学报, 2018, 43(3): 646. ZHANG Dongming, BAI Xin, YIN Guangzhi, et al. Analysis of acoustic emission parameters and energy dissipation characteristics and damage evolution of bedding rock failure process under uniaxial compression[J]. Journal of China Coal Society, 2018, 43(3): 646. |
 2020, Vol. 52
2020, Vol. 52


