由于轮毂电机驱动电动汽车(in-wheel motor electric vehicle, IWM-EV)具有环境友好和能源节约的优点,已成为追逐的研究热点和未来发展方向[1-2].由于引入轮毂电机非簧载质量过大导致车辆垂向振动负效应问题的产生,路面和电机耦合作用产生不平衡电磁力,使得轮毂电机驱动电动汽车较内燃机和单电机集中驱动的汽车相比,出现车辆平顺性与安全性下降问题.目前,国内外学者对轮毂电机驱动电动汽车平顺性问题开展了一些研究.文献[3]指出轮毂电机电动车非簧载质量过大,对车辆平顺性产生负效应.文献[4]提出可以通过将轮毂电机作为动力吸振器质量元件悬置于车轮,以改善轮毂电机与车轮直接相连对车辆产生的冲击.文献[5]给出簧下质量对车辆垂向负效应的具体分析,并将轮毂电机悬置于轮内进行模型仿真.文献[6]提出轮内悬置结构,并以非簧载质量的垂向振动量为目标函数,对构型主要参数进行优化分析.文献[7]指出开关磁阻电机激励对电动车辆垂向性能的影响主要在低车速范围.文献[8]提出一种新型内置悬置电动轮结构,分析了路面和电磁双重激励下电动车辆垂向振动性能.以上研究虽然对轮毂电机驱动电动汽车垂向性能降低问题有所论述,并提出相应的解决措施,但没有考虑到在双重激励下电机悬置作为质量元件部分的优化方案或给予原理解释.
针对上述问题,本文对比了传统集中电机和常规轮毂电机驱动电动汽车垂向性能,然后分析加入动态吸振器方案的可行性,在此基础上,提出两种轮毂电机作为悬置的动态吸振器的质量元件的构型方案,建立两种方案的1/4电动轮车辆振动模型,在定转子位移不超过轮辋内部限制的前提下,分析在路面激励和电机垂向激励共同作用下两种方案的平顺性能,并综合选出较优方案,最后利用基于Pareto解的精英策略非支配排序遗传NSGA-Ⅱ算法对优选的悬置方案中动态吸振器参数进行多目标优化设计.
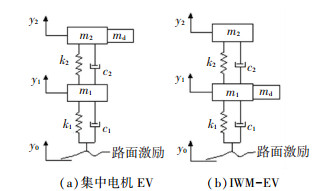
1 IWM-EV动力学模型 1.1 1/4车辆动力学模型轮毂电机驱动电动汽车采用了轮毂电机作为新的驱动系统并将其集中在各个驱动轮内,底盘结构明显改变,电机的电磁振动将直接作用于悬架,进而传递至车身,从而加剧车身振动和噪声,对车辆平顺性和安全性均产生不利影响.传统集中电机驱动电动汽车(electric vehicle, EV)和常规轮毂电机驱动电动汽车区别在于电机安置方式不同导致簧载质量与非簧载质量比值差异,具体模型如图 1所示.
|
图 1 1/4车辆垂向振动分析模型 Fig. 1 Vertical vibration analysis model of quarter vehicle |
图 1中两种模型的振动微分方程分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{m_1}{{\ddot y}_1} + {k_1}({y_1} - {y_0}) + {c_1}({{\dot y}_1} - {{\dot y}_0}) + }\\ {{k_2}({y_1} - {y_2}) + {c_2}({{\dot y}_1} - {{\dot y}_2}) = 0,}\\ {({m_2} + {m_{\rm{d}}}){{\ddot y}_2} + {k_2}({y_2} - {y_1}) + {c_2}({{\dot y}_2} - {{\dot y}_1}) = 0.} \end{array}} \right. $ | (1) |
| $ \left\{ \begin{array}{l} ({m_1} + {m_{\rm{d}}}){{\ddot y}_1} + {k_1}({y_1} - {y_0}) + {c_1}({{\dot y}_1} - {{\dot y}_0}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_2}({y_1} - {y_2}) + {c_2}({{\dot y}_1} - {{\dot y}_2}) = 0,\\ {m_2}{{\ddot y}_2} + {k_2}({y_2} - {y_1}) + {c_2}({{\dot y}_2} - {{\dot y}_1}) = 0. \end{array} \right. $ | (2) |
式中:m1为非簧载质量;m2为簧载质量;md为电机质量;y0为路面激励;yi表示相应质量块的位移,i=1、2;k1、c1分别表示轮胎刚度、阻尼;k2、c2分别表示悬架刚度、阻尼.
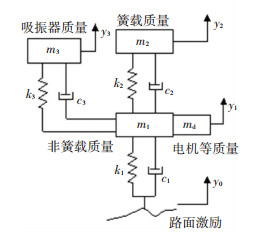
1.2 内置动态吸振器模型为减缓轮毂电机驱动电动汽车由于轮毂电机的引入使得非簧载质量过大带来的轮毂电机驱动电动汽车的轮胎波动量增大等车辆垂向振动负效应问题,对于内置轮毂电机车轮部分加置动态吸振器(dynamic vibration absorber, DVA),模型如图 2所示.动态吸振器中的质量元件通过橡胶衬套与车轮部分相连,用于吸收车轮部分质量振动.
|
图 2 内置动态吸振器IWM-EV动力学模型 Fig. 2 Dynamic model of IWM-EV with dynamic vibration absorber |
图 2模型的振动微分方程为
| $ \left\{ \begin{array}{l} ({m_1} + {m_d}){{\ddot y}_1} + {k_1}({y_1} - {y_0}) + {c_1}({{\dot y}_1} - {{\dot y}_0}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_2}({y_1} - {y_2}) + {c_2}({{\dot y}_1} - {{\dot y}_2}) + {k_3}({y_1} - {y_3}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_3}({{\dot y}_1} - {{\dot y}_3}) = 0,\\ {m_2}{{\ddot y}_2} + {k_2}({y_2} - {y_1}) + {c_2}({{\dot y}_2} - {{\dot y}_1}) = 0,\\ {m_3}{{\ddot y}_3} + {k_3}({y_3} - {y_1}) + {c_3}({{\dot y}_3} - {{\dot y}_1}) = 0. \end{array} \right. $ | (3) |
式中:m3、k3、c3、y3分别为动态吸振器的质量、刚度、阻尼和位移,其他参数如前所述.具体参数取值[9]:m1=45 kg,m2=420 kg,md=30 kg,m3=30 kg,k1=360 kN/m,k2=80 kN/m,k3=40 kN/m,c1= 1 kN/(m·s-1),c2=5 kN/(m·s-1),c3=1 kN/(m·s-1).
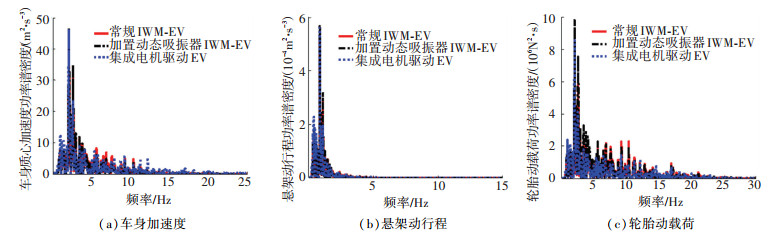
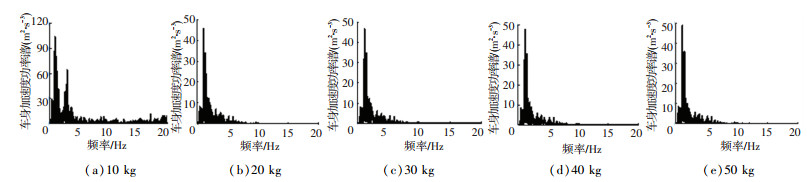
1.3 3种电动汽车1/4模型分析比较选取B级路面,车速为60 km/h时以上3种车辆模型进行平顺性仿真,并选取车身垂向加速度、悬架动行程、轮胎动载荷为评价指标,应用MATLAB搭建模型,其垂向性能对比结果如图 3所示. 图 3表明,常规轮毂电机驱动汽车的平顺性指标响应值均高于集成电机驱动电动车,而加置动态吸振器后的轮毂电机驱动电动车在5 Hz频率附近及更高频率区域处的平顺性较常规轮毂电机驱动电动汽车有显著的改善,减缓了车轮共振频率和人体敏感区域的垂向振动.在仿真中,电机部分质量和吸振器质量元件都为30 kg,现分别将质量元件取值为10、20、30、40、50 kg进行对比分析悬置质量对平顺性的影响,加置动态吸振器的轮毂电机驱动电动汽车垂向性能指标功率谱密度如图 4~6所示.
|
图 3 功率谱密度对比 Fig. 3 Comparison of power spectral density |
|
图 4 B级路面下不同质量车身加速度功率谱密度 Fig. 4 Power spectral density of vehicle body acceleration with different mass on grade B road |
|
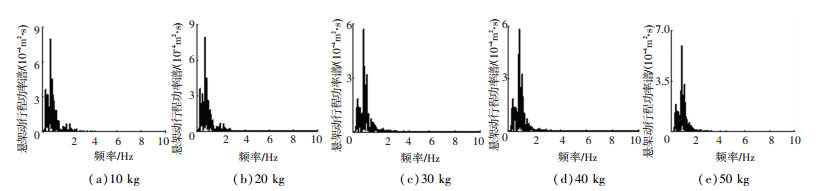
图 5 B级路面下不同质量悬架动行程功率谱密度 Fig. 5 Power spectral density of suspension working space with different mass on grade B road |
|
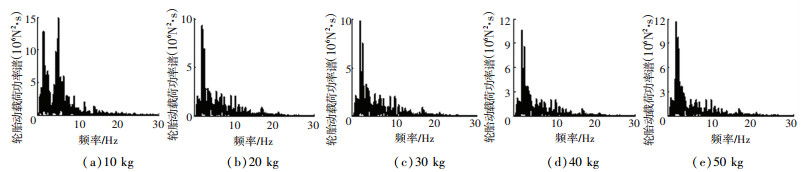
图 6 B级路面下不同质量轮胎动载荷功率谱密度 Fig. 6 Power spectral density of tyre dynamic load with different mass on grade B road |
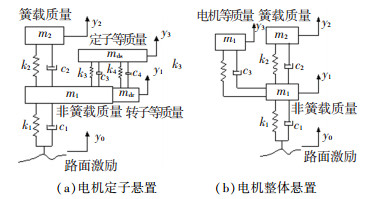
由图 4~6可知,动态吸振器中的质量元件存在使轮毂电机驱动电动汽车垂向振动性能改善较大的有效值区域,当动态吸振器中的质量元件取[10 kg, 30 kg]时,可显著改善电动汽车的车身加速度和轮胎动载荷,提高车辆平顺性.电机转化为动态吸振器后能改善轮毂电机驱动电动汽车因非簧载质量过大而带来垂向振动负效应,也能有效减小非簧载质量.根据质量元件合适的取值区间,考虑将轮毂电机中定子部分悬置或将轮毂电机整体悬置作为动态吸振器中的质量元件,两种方案见图 7.
|
图 7 两种1/4 IWM-EV车辆模型 Fig. 7 Two IWM-EV quarter vehicle models |
根据图 4~6中各响应值功率谱密度可计算得到不同质量下的均方根值,质量从10 kg依次递增10 kg至50 kg所对应的车身加速度均方根值依次为2.364、1.411、1.389、1.396、1.385 m/s2,悬架动行程均方根值依次为3.914、3.912、3.895、3.890、3.850 mm,轮胎动载荷均方根值依次为837.136、808.112、812.785、817.455、823.899 N.
两种轮毂电机悬置方案的振动微分方程分别为
| $ \left\{ \begin{array}{l} ({m_1} + {m_{{\rm{dr}}}}){{\ddot y}_1} + {k_1}({y_1} - {y_0}) + {c_1}({{\dot y}_1} - {{\dot y}_0}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_2}({y_1} - {y_2}) + {c_2}({{\dot y}_1} - {{\dot y}_2}) + {k_3}({y_1} - {y_3}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_3}({{\dot y}_1} - {{\dot y}_3}) + {k_4}({y_1} - {y_3}) + {c_4}({{\dot y}_1} - {{\dot y}_4}) = 0,\\ {m_2}{{\ddot y}_2} + {k_2}({y_2} - {y_1}) + {c_2}({{\dot y}_2} - {{\dot y}_1}) = 0,\\ {m_{{\rm{ds}}}}{{\ddot y}_3} + {k_3}({y_3} - {y_1}) + {c_3}({{\dot y}_3} - {{\dot y}_1}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_4}({y_3} - {y_1}) + {c_4}({{\dot y}_3} - {{\dot y}_1}) = 0; \end{array} \right. $ | (4) |
| $ \left\{ \begin{array}{l} {m_1}{{\ddot y}_1} + {k_1}({y_1} - {y_0}) + {c_1}({{\dot y}_1} - {{\dot y}_0}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_2}({y_1} - {y_2}) + {c_2}({{\dot y}_1} - {{\dot y}_2}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_3}({y_1} - {y_3}) + {c_3}({{\dot y}_1} - {{\dot y}_3}) = 0,\\ {m_2}{{\ddot y}_2} + {k_2}({y_2} - {y_1}) + {c_2}({{\dot y}_2} - {{\dot y}_1}) = 0,\\ {m_{\rm{d}}}{{\ddot y}_3} + {k_3}({y_3} - {y_1}) + {c_3}({{\dot y}_3} - {{\dot y}_1}) = 0. \end{array} \right. $ | (5) |
对于路面激励,其功率谱密度Gq(f)[10]表示为
| $ {{G_q}(f) = \frac{1}{u}{G_q}(n),} $ | (6) |
| $ {{G_q}(n) = {G_q}({n_0})\frac{{{n_0}^2}}{{{n^2} + {n_q}^2}}.} $ | (7) |
式中:f为路面激励时间频率,f=un,其中u为车速,n为空间频率;n0为参考空间频率;nq为下截止空间频率;Gq(n0)为路面不平度系数.
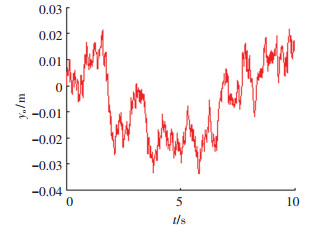
将一阶滤波器作为系统特性建立滤波白噪声,系统输入为理想白噪声,系统输出为路面激励如图 8所示,则基于滤波白噪声对应式(7)的路面激励为
| $ \dot q(t) = - 2\pi {n_q}uq(t) + 2\pi {n_0}\sqrt {{G_q}({n_0})u} \omega (t). $ | (8) |
|
图 8 B级路面激励 Fig. 8 Grade B road excitation |
式中q为路面激励,ω(t)为零均值和单位功率谱密度的理想白噪声.
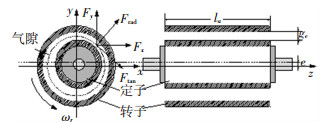
2.2 轮毂电机垂向激励 2.2.1 轮毂电机气隙长度模型轮毂电机气隙模型如图 9所示,对于表面贴式永磁同步电机(permanent magnet synchronous motor, PMSM)来说,电机均匀/不均匀气隙长度为时间t的函数,可表示[11]为
| $ {g_e}(\theta ,t) = {g_0}[1 - \varepsilon {\rm{cos}}({\omega _r}t - \gamma )]. $ | (9) |
|
图 9 表面贴式永磁同步电机气隙模型 Fig. 9 Air gap model of surface mounted permanent magnet synchronous motor |
式中:ge为偏心转子气隙;g0为转子不偏心时平均气隙长度;ε为相对偏心率,ε=e/g0, e为定转子相对位移量;ωr为转子转速;γ为转子角位置.
2.2.2 气隙磁通密度计算瞬态气隙磁场的磁通密度包含空载气隙磁场磁通密度和绕组产生电枢反应磁场的磁通密度两部分[12-13],径向电磁力可以通过气隙磁密和真空磁导率进行求解,此时总的负载磁通密度为
| $ {{B_L}(\alpha ,r,t) = [{B_m}({\theta _m},r) + {B_a}(\alpha ,r,t)] \cdot \tilde \lambda (\alpha ,r),} $ | (10) |
| $ {{\theta _m} = \alpha - {\omega _r}t,} $ | (11) |
| $ {\tilde \lambda (\alpha ,r) = \sum\limits_{n = 0}^\infty {{{\tilde \varLambda }_n}} (r){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} n{Q_s}\alpha .} $ | (12) |
式中:α为A相绕组轴线对应的定子角位置,θm为磁极轴线对应的转子角位置,
根据计算得到的气隙磁密,依据Maxwell应力张量理论[14],极坐标下气隙磁场的径向力密度和切向力密度分别为
| $ {{f_{{\rm{rad}}}} = - \frac{1}{{2{\mu _0}}}[{B_{{\rm{ }}L{\rm{rad }}}}{{(s,t)}^2} - {B_{{\rm{ }}L{\rm{tan }}}}{{(s,t)}^2}],} $ | (13) |
| $ {{f_{{\rm{ tan }}}} = - \frac{1}{{{\mu _0}}}{B_{{\rm{ }}L{\rm{rad }}}}(s,t){B_{{\rm{ }}L{\rm{tan }}}}(s,t).} $ | (14) |
式中:μ0为真空磁导率,BLrad(s, t)、BLtan(s, t)分别为气隙偏心下的径向和切向磁通密度.
根据图 9,将式(13)、(14)转换至Cartesian坐标系,有
| $ {f_y} = {f_{{\rm{rad}}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta - {f_{{\rm{tan}}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta , $ |
对上式积分,可得径向电磁力为
| $ \begin{array}{l} {F_y} = {l_a}\int\limits_0^{2\pi } {{f_y} \cdot r{\rm{d}}\theta } = - \frac{{r \cdot {l_a}}}{{2{\mu _0}}} \cdot \int\limits_0^{2\pi } {\{ [{B_{L{\rm{rad}}}}{{(s,t)}^2}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{B_{{\rm{ }}L{\rm{tan }}}}{{(s,t)}^2}]{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta - [2{B_{L{\rm{rad}}}}(s,t){B_{{\rm{ }}L{\rm{tan }}}}(s,t)] \cdot }\\ {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \} {\rm{d}}\theta ,} \end{array} \end{array} $ | (15) |
式中:la为永磁同步电机轴向气隙长度,r为积分半径.
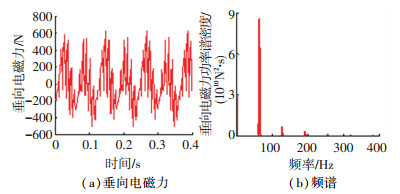
在均匀气隙下电磁力密度呈周期分布排列在圆周方向,当受到路面激励后,轮胎跳动、轴承磨损及偏移等都将导致气隙呈偏心分布,进而引起气隙磁场畸变产生异常气隙电磁力波并作用于定、转子振动,且进一步影响轮毂电机临界转速,加大气隙不均匀程度.利用MATLAB建立轮毂电机电动轮汽车模型并进行求解,可得到偏心气隙情况下的垂向电磁力. B级路面下车速为60 km/h工况下电机垂向电磁激励功率谱密度及频谱如图 10所示.
|
图 10 偏心情况下电机垂向激励 Fig. 10 Vertical excitation of motor under eccentricity |
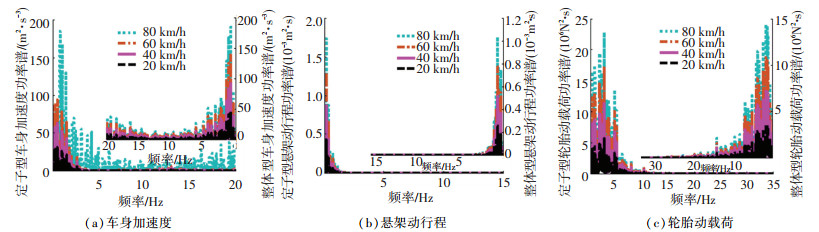
针对已建立的定子悬置轮毂电机电动汽车和电机整体悬置电动汽车的非线性模型,取B级路面,车速以20 km/h的增量从20 km/h并变化到80 km/h,考虑电机转子相对定子绕组偏心,电机相对偏心率ε取30%,进行傅里叶变换得到不同车速下各性能指标的功率谱密度如图 11所示.由图 11可以看出,路面和电机产生的耦合激励作用下,两种电机悬置方案的垂向振动性能指标与车速呈递增关系,且在低车速范围内增幅比在高速范围内增幅大,随后增速递减.电机自身的设计使得速度低时输出大,导致低速范围内电机垂向激励大,且此时汽车受路面激励较小,因此在低速范围内增幅较为突出,随车速增大后,车辆平顺性逐渐变差,与常规轮毂电机驱动电动汽车一致.此外,经过增幅百分比计算可知,低速对整体悬置方案中悬架影响最大为46.67%,其次是电机整体悬置方案的轮胎动载荷和定子悬置方案中悬架动行程的波动.故加入电机激励后低速范围内对两种悬置方案的电动轮汽车的悬架均带来了较大影响.
|
图 11 车速对两种悬置方案影响 Fig. 11 Influence of vehicle speed on two suspended configuration schemes |
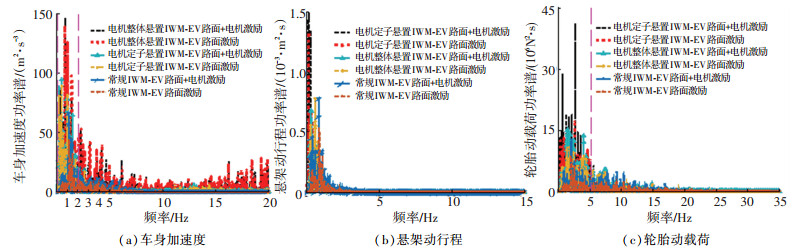
选取常规轮毂电机驱动电动汽车以及两种悬置车型进行电机垂向激振力对车辆垂向振动性能的影响研究,分别进行B级路面激励和“路面+电机”双重激励的仿真,选取车速为60 km/h,各振动响应量指标见图 12和表 1,图 12(a)和12(c)中虚线左侧部分为加入电机激励后恶化较为严重的频率范围.
|
图 12 双重激励下3种IWM-EV比较 Fig. 12 Comparison of three IWM-EVs under dual excitations |
| 表 1 B级路面激励下IWM-EV车辆垂向响应有效值 Tab. 1 Effective values of IWM-EVs vertical response under grade B road excitation |
由图 12和表 1的各性能指标的统计值可知:电机垂向激励对定子悬置轮毂电机驱动电动汽车平顺性的影响最大,其他依次为整体悬置轮毂电机驱动电动汽车和常规轮毂电机驱动电动车;而对各响应量有效值比较后得出,受路面激励后的轮毂电机产生的不平衡电磁激励对轮胎动载荷的影响最大,对悬架动行程的影响度最小.在双重激励下,整体悬置轮毂电机驱动电动汽车的综合垂向性能优于定子悬置型,其3个响应量的恶化程度从大到小依次为轮胎动载荷40.91%,车身加速度8.06%,悬架动行程2.57%.
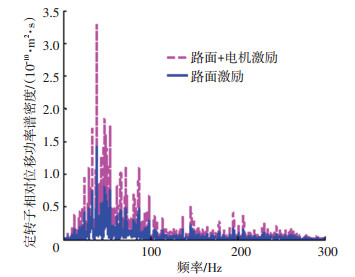
3.2.2 定转子相对位移定子悬置方案中,由于轮毂电机定子、转子之间由橡胶衬套连接,故存在定转子相对位移较大的问题,导致电机偏心问题加剧,图 13为双重激励下车速60 km/h的B级路面谱下定子悬置方案的定转子相对位移的频域仿真计算结果.
|
图 13 定转子相对位移功率谱密度 Fig. 13 Power spectral density of relative displacement of stator and rotor |
由图 13可以明显地看到加入电机垂向激励后定转子之间的位移增大,可知电机垂向激励对定转子相对位移的负面影响显著,定转子相对位移的最大值和均方根值分别增大73.5%和50.21%,但未超出该定子悬置轮毂电机驱动电动汽车的安全允许范围.可见,电机垂向激励不仅能恶化轴承的工作受载荷量,并且影响定转子相对位移进而加剧偏心,在50 Hz频率附近易引发系统共振,导致更大规模的电机振动与噪声的产生,甚至可能会造成电机定转子碰撞或电机与车体碰撞的危险工况.
4 模型优化及验证 4.1 动力吸振器参数对车辆平顺性影响规律综合悬置元件质量、车速、电机激励、定转子位移等影响计算结果,两种悬置方案中电机整体悬置轮毂电机驱动电动汽车为优选方案,其垂向振动性能和各响应值要优于电机定子悬置为动态吸振器质量元件的选型.故本节的模型优化建立在轮毂电机整体悬置方案基础上,抑制其垂向振动负效应,提高该选型车辆平顺性能.由于悬置电机作为动态吸振器的质量元件而引入复合材料的橡胶衬套,其刚度和阻尼对车辆垂向运动特性的影响,故有必要对动力吸振器参数进行分析,便于对进一步的优化设计提供理论依据.
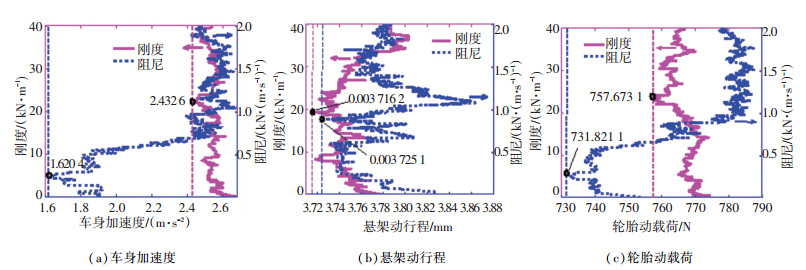
图 14为B级路面下,车速u为60 km/h,橡胶衬套阻尼c3取1 kN/(m·s-1),橡胶衬套刚度k3从50 N/m递增至40 kN/m,以及橡胶衬套刚度k3为40 kN/m,橡胶衬套阻尼c3从50 N/(m·s-1)逐渐加至2 kN/(m·s-1),各性能指标的均方根值变化规律.
|
图 14 橡胶衬套参数灵敏度 Fig. 14 Sensitivity of rubber bushing parameters |
由图 14可以看出,对于车身加速度这一指标,在达到最小值后其基本与刚度呈线性增长,而随着阻尼的增大反而有所递减;在悬架动行程方面浮动并不大,随刚度增大其先逐渐减小后增大,阻尼则减小增大循环多次;刚度递增后轮胎动载荷波动较大,先逐渐减小后不断增大,阻尼增大后轮胎动载荷总体呈下降趋势;橡胶衬套的刚度与阻尼均有使3个车辆平顺性指标分别最小的值存在.
4.2 模型优化及验证多目标优化函数通常存在一个难以比较优劣的解集,称为非支配解或Pareto最优解,而求解多目标优化的主要目的为无偏好地找到尽可能多的Pareto最优解[15-16].由动力吸振器参数对车辆平顺性影响规律可知,单影响因素均有合理数值使其较优,而综合3个平顺性指标最优的数值还未能确定,故根据改进的NSGA-Ⅱ算法[17]进行优化设计.以橡胶衬套的刚度k3和阻尼c3为设计变量,控制悬架动挠度fd和车轮相对动载荷Fd/G作为约束条件,即σfd≤ [fd] /3, σFd/G≤1/3,以车身加速度、悬架动行程和轮胎动载荷3个车辆平顺性指标的均方根值最小为目标函数,其表达式为
|
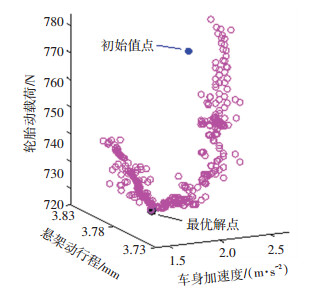
图 15 Pareto最优解 Fig. 15 Pareto optimal solution |
图 15中初始值点为橡胶衬套刚度k3=40 kN/m,阻尼c3=1 kN/(m·s-1),优化后的结果为k3=23.647 kN/m,c3=167 N/(m·s-1),此时可得到车身加速度、悬架动行程和轮胎动载荷均方根值的Pareto最优解.优化前后橡胶衬套刚度和阻尼变化量和各性能功率谱密度对比结果如图 16所示.
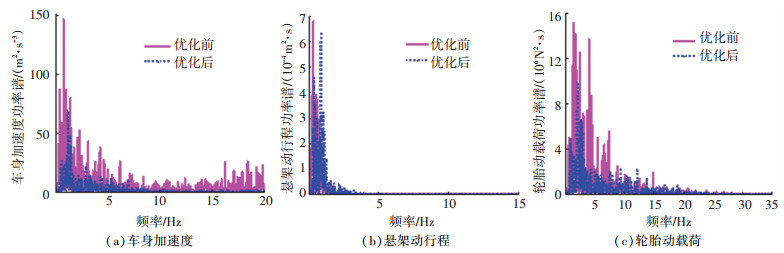
|
图 16 整体悬置型IWM-EV优化对比 Fig. 16 Optimization comparison of whole motor suspended IWM-EV |
图 16中,优化后的轮毂电机整体悬置式电动汽车对3个平顺性指标均有不同程度的改善,尤其是在5 Hz及以上频段,车身与车轮的共振频率均被减小,并显著改善人体敏感频段4~12.5 Hz的车辆垂向振动性能.经计算可得,优化前后车身加速度均方根值从2.551 m/s2下降为1.568 m/s2,悬架动行程均方根值从0.003 79 m下降为0.003 75 m,轮胎动载荷均方根值从784.695 N降为722.378 N,3种指标均方根值的改善程度由大到小依次为车身加速度38.53%、轮胎动载荷7.94%、悬架动行程1.06%.因此,经过优化后,该轮毂电机整体悬置式电动汽车对解决非簧载质量过大和路面电机双重激励带来的平顺性问题有重要意义.
5 结论1) 为解决轮毂电机引入电动汽车使车辆垂向负效应加剧的问题,研究路面激励和电机垂向激励耦合下车辆垂向性能,建立集成电动汽车、常规轮毂电机驱动汽车和加置动态吸振器的轮毂电机驱动电动汽车模型,讨论了垂向性能影响因素.仿真结果表明,加置动态吸振器后能显著改善车辆的车身加速度和轮胎动载荷,进而根据动态吸振器质量元件影响规律提出两种电机悬置方案.
2) 针对两种电机悬置方案,分析比较双重激励下车辆垂向振动规律以及车速、定转子相对位移等影响,较优选择电机整体悬置方案.对整体悬置方案中加置的橡胶衬套刚度和阻尼进行优化设计,仿真结果显示优化后的电机整体悬置方案减缓了车轮共振频率区域的平顺性,并降低车身加速度和轮胎动载荷,进而验证了优化的有效性.
| [1] |
LI X H, QIAN H. The present status and future trends of in-wheel motors for electric vehicles[J]. Advanced Materials Research, 2012, 433-440: 6943. DOI:10.4028/www.scientific.net/AMR.433-440.6943 |
| [2] |
TAN D, LU C. The influence of the magnetic force generated by the in-wheel motor on the vertical and lateral coupling dynamics of electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4655. DOI:10.1109/TVT.2015.2461635 |
| [3] |
HROVAT D. Influence of unsprung weight on vehicle ride quality[J]. Journal of Sound and Vibration, 1988, 124(3): 497. DOI:10.1016/S0022-460X(88)81391-9 |
| [4] |
NAGAYA G, WAKAO Y, ABE A. Development of an in-wheel drive with advanced dynamic-damper mechanism[J]. JSAE Review, 2003, 24(4): 477. DOI:10.1016/S0389-4304(03)00077-8 |
| [5] |
梁锐, 余卓平, 宁国宝. 基于吸振原理的轮边驱动电动车垂向振动负效应的抑制[J]. 机械设计, 2008, 25(1): 28. LIANG Rui, YU Zhuoping, NING Guobao. Restraint of negative effect on vertical vibration of wheel rim driven motor vehicle based on shake absorption principle[J]. Journal of Machine Design, 2008, 25(1): 28. DOI:10.3321/j.issn:1003-8728.2008.01.007 |
| [6] |
赵艳娥, 张建武, 韩旭. 轮毂电机独立驱动电动汽车动力减振机构设计与研究[J]. 机械科学与技术, 2008, 27(3): 395. ZHAO Yan'e, ZHANG Jianwu, HAN Xu. Design and study on the dynamic-damper mechanism for an in-wheel motor individual drive electric vehicle[J]. Mechanical Science and Technology for Aerospace Engineering, 2008, 27(3): 395. DOI:10.3321/j.issn:1003-8728.2008.03.027 |
| [7] |
钟银辉, 李以农, 杨超, 等. 基于主动悬架控制轮边驱动电动车垂向振动研究[J]. 振动与冲击, 2017, 36(11): 242. ZHONG Yinhui, LI Yinong, YANG Chao, et al. Vertical vibration of in-wheel motor electric vehicles based onactive suspension control[J]. Journal of Vibration and Shock, 2017, 36(11): 242. |
| [8] |
LUO Y T, TAN D. Study on the dynamics of the in-wheel motor system[J]. IEEE Transactions on Vehicular Technology, 2012, 61(8): 3510. DOI:10.1109/TVT.2012.2207414 |
| [9] |
韩以伦, 李国珊, 王强, 等. 基于垂向振动负效应的新型轮毂电机电动汽车平顺性影响[J]. 科学技术与工程, 2019, 19(16): 363. HAN Yilun, LI Guoshan, WANG Qiang, et al. Ride comfort of a new in-wheel motor driving electric vehicle based on the negative effect of vertical vibration[J]. Science Technology and Engineering, 2019, 19(16): 363. DOI:10.3969/j.issn.1671-1815.2019.16.057 |
| [10] |
赵旗, 王培德, 罗兰, 等. 路面激励Simulink模型的建立及其应用[J]. 科学技术与工程, 2018, 18(1): 128. ZHAO Qi, WANG Peide, LUO Lan, et al. Establishment of Simulink model for road excitation and its application[J]. Science Technology and Engineering, 2018, 18(1): 128. DOI:10.3969/j.issn.1671-1815.2018.01.022 |
| [11] |
邓文哲, 左曙光, 林福, 等. 偏心条件下轴向磁通轮毂电机不平衡弯矩建模与分析[J]. 电工技术学报, 2017, 32(13): 153. DENG Wenzhe, ZUO Shuguang, LIN Fu, et al. Modeling and analysis of unbalanced moment for an axial-flux in-wheel motor with eccentricity[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 153. |
| [12] |
ZHU Z Q, HOWE D. Instantaneous magnetic field distribution in permanent magnet brushless dc motors, part IV: magnetic field on load[J]. IEEE Transactions on Magnetics, 1993, 29(1): 152. DOI:10.1109/20.195560 |
| [13] |
ZHU Z Q, XIA Z P, WU L J, et al. Influence of slot and pole number combination on radial force and vibration modes in fractional slot PM brushless machines having single- and double-layer windings[C]//Proceedings of 2009 IEEE Energy Conversion Congress and Exposition. San Jose, CA: IEEE, 2009: 3443
|
| [14] |
SUN X, XUE Z, ZHU J, et al. Suspension force modeling for a bearingless permanent magnet synchronous motor using Maxwell stress tensor method[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): 1. |
| [15] |
HOSSEIN B, ALAVIDOOST M H, FAZEL Z M H, et al. An enhanced NSGA-Ⅱ algorithm for fuzzy bi-objective assembly line balancing problems[J]. Computers & Industrial Engineering, 2018, 123(9): 189. |
| [16] |
ELARBI M, BECHIKH S, GUPTA A, et al. A new decomposition-based NSGA-Ⅱ for many-objective optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(7): 1191. DOI:10.1109/TSMC.2017.2654301 |
| [17] |
刘伟, 史文库, 方德广, 等. 汽车动力学分析及悬架子系统优化设计[J]. 哈尔滨工业大学学报, 2012, 44(3): 96. LIU Wei, SHI Wenku, FANG Deguang, et al. Vehicle dynamics analysis and optimization of suspension design[J]. Journal of Harbin Institute of Technology, 2012, 44(3): 96. |
 2020, Vol. 52
2020, Vol. 52


