2. 先进加工技术国防重点学科实验室(北京理工大学), 北京 100081
2. Key Laboratory of Fundamental Science for Advanced Machining(Beijing Institute of Technology), Beijing 100081, China
大型铝合金构件广泛应用于航空、航天领域, 由于其几何尺寸和材料去除量庞大, 传统数控机床往往无法满足其加工需求.工业机器人具有加工区域大、灵活性高、制造成本低等优势, 正被逐步用于大型铝合金构件整体制造领域, 特别是在大型构件的预加工和粗加工方面[1-4].
然而, 工业机器人的系统刚度远低于数控机床, 切削加工中容易在切削力的激励作用下发生颤振, 降低加工精度甚至严重损坏加工设备[5].为改善机器人切削加工性能, 提高加工质量, 诸多学者就机器人切削颤振产生机理及颤振抑制[6-7]、机器人位姿与走刀轨迹优化[8-9]、切削参数优化[10-11]、误差补偿[12]、新工艺[13-14]等方面展开了大量的研究, 但是已发表文献中却鲜有涉及提高机器人切削加工效率的研究, 当前普遍的做法是适当减小切削深度和每齿进给量的同时增大主轴转速[4, 11].限于高速电主轴的设计制造困难, 采用这种方法提高加工效率的成本较高且提升空间有限, 难以满足材料去除体积比高的大型铝合金构件高效加工的要求.
行星复合铣削方法(铣-铣复合加工方法)是由王西彬教授[15]提出的一种通过驱动多把立铣刀同时高速行星转动将面铣和端铣复合, 实现难加工材料高效切削的新方法.研究表明, 相对于传统面铣加工, 行星复合铣削方法切削力小, 加工质量好, 刀具整体寿命长, 利于断屑.从切削机理上分析, 行星复合铣削切削力大幅降低是由于立铣刀螺旋角改善了实际有效前角[16].
然而, 上述研究工作并未对加工效率展开深入讨论, 且仅对比分析了传统数控机床上行星复合铣削与传统面铣加工的切削性能差异.行星复合铣削方法是否同样适用于大型铝合金构件整体加工, 以及相对于同样采用立铣刀的机器人端铣, 是否仍然具有突出优势, 均有待验证.鉴于机器人铣削加工中多采用端铣加工方式, 且工业机器人和传统机床之间的动力学特性存在显著差异, 即使采取相同的工艺, 切削性能也往往不同[17].因此, 本文在之前研究的基础上进一步开展实验研究, 验证行星复合铣削方法在机器人切削加工中的优势与可行性.
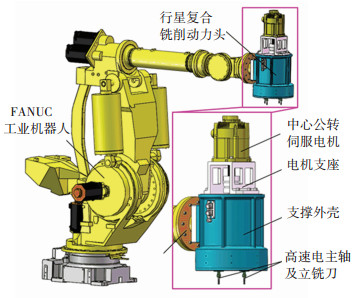
1 机器人行星复合铣削原理 1.1 机器人行星复合铣削系统机器人行星复合铣削是指采用机器人行星复合铣削工具系统进行材料去除的加工方法.如图 1所示, 该系统的硬件部分主要包括工业机器人和作为末端执行器的行星复合铣削动力头[18], 还包括电气控制单元和冷却系统(如工业冷水机)等[19].行星复合铣削动力头主要由中心公转伺服电机、电机支座、支撑外壳、高速电主轴及立铣刀等部件组成, 并通过连接法兰与工业机器人末端连接.
|
图 1 机器人行星复合铣削工具系统组成 Fig. 1 Composition of RPCM system |
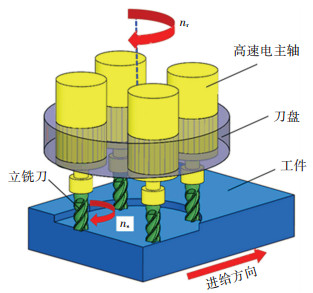
当使用机器人行星复合铣削工具系统进行切削加工时, 首先调整机器人位姿, 使其靠近待加工表面, 然后启动行星复合铣削动力头并给定公转转速和自转转速, 最后操控机器人按照给定切削深度和走刀路径实现材料的切削去除.在原有设计基础上, 结合机器人服役环境与接口形式, 对行星复合铣削动力头进行了改进设计, 其基本工作原理如图 2所示.
|
图 2 行星复合铣削动力头的工作原理 Fig. 2 Working principle of planetary compound milling power head |
以四铣刀结构为例, 4个高速电主轴圆周均布固定在刀盘上, 4把立铣刀分别安装在高速电主轴上.给定公转转速, 中心公转伺服电机驱动刀盘实现公转转动, 高速电主轴则分别驱动对应立铣刀实现自转转动.
相对于采用单个高速电主轴的机器人端铣, 行星复合铣削动力头通过自身机构提供的冗余自由度实现行星复合铣削, 不会因为占用工业机器人的自由度而影响其灵活性, 并且多把立铣刀有序参与切削加工, 显著提高了材料去除效率.同时, 当行星复合铣削动力头采用左旋立铣刀和右旋立铣刀相间均匀布置的结构且径向切削宽度足够大时, 同一时刻参与材料切削的相邻两把立铣刀的切削分力因为方向相反而相互抵消, 机器人末端所受到的合外力减轻, 一定程度上减小了机器人末端的力致变形, 有利于提高机器人铣削加工精度[15].
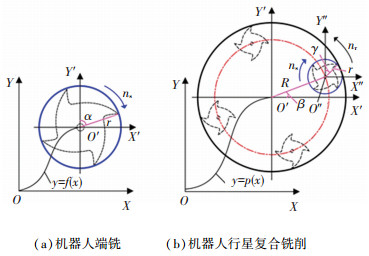
1.2 刀尖运动轨迹建模刀尖轨迹是切削加工中的重要特征之一, 也是进行切削机理分析的基础.根据机器人端铣和机器人行星复合铣削的运动特征, 在工件坐标系XOY中做出两种铣削方式沿任意路径OO′进给时, 任意刀齿数和任意刀具数的通用刀尖运动轨迹模型如图 3所示, 以常用的右旋立铣刀为例, 机器人端铣加工(如图 3(a))的刀尖运动轨迹参数方程为:
|
图 3 刀尖运动轨迹建模 Fig. 3 Modeling of tool nose trajectories of (a) REM and (b) RPCM |
| $ \left\{ {\begin{array}{*{20}{l}} {{x_1} = r\sin \left[ {2{\rm{ \mathsf{ π} }}{n_{\rm{s}}}t - \eta } \right] + {f_x}(t), }\\ {{y_1} = r\cos \left[ {2{\rm{ \mathsf{ π} }}{n_{\rm{s}}}t - \eta } \right] + {f_y}(t), } \end{array}} \right. $ |
| $ \eta = 2{\rm{ \mathsf{ π} }}(i - 1)/Z. $ |
式中:r为立铣刀半径(mm), ns为主轴转速(r/min), t为切削时间(min), Z为刀齿数量, i为刀齿序号(1≤ i ≤ Z), η为第i个刀齿与第1个刀齿间的圆心角(rad), fx(t)、fy(t)为进给路径函数y=f(x)在t时刻的坐标分量.
同理, 如图 3(b)所示, 当机器人行星复合铣削同样采用右旋立铣刀时, 其通用刀尖运动轨迹参数方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_2} = R\cos \left[ {2{\rm{ \mathsf{ π} }}{n_{\rm{r}}}t - \varphi } \right] + r\sin \left[ {2{\rm{ \mathsf{ π} }}{n_{\rm{s}}}t - \eta } \right] + {p_x}(t), }\\ {{y_2} = R\sin \left[ {2{\rm{ \mathsf{ π} }}{n_{\rm{r}}}t - \varphi } \right] + r\cos \left[ {2{\rm{ \mathsf{ π} }}{n_{\rm{s}}}t - \eta } \right] + {p_y}(t), } \end{array}} \right. $ |
| $ \varphi = 2{\rm{ \mathsf{ π} }}(k - 1)/{N_{\rm{T}}}. $ |
式中:R为立铣刀公转半径(mm), nr为立铣刀公转转速(r/min), NT为立铣刀数量, k为立铣刀序号(1≤k≤NT), φ为第k把立铣刀与第1把立铣刀间的圆心角(rad), px(t)、py(t)为进给路径函数y=p(x)在t时刻的坐标分量.
以直线进给为例, 进一步比较机器人端铣与机器人行星复合铣削的刀尖运动轨迹特征.当两种铣削方式均沿工件坐标系XOY的X轴匀速进给时, 上述刀尖运动轨迹方程中的进给分量分别为:
| $ \begin{array}{*{20}{l}} {{f_x}(t) = {f_z}Z{n_{\rm{s}}}t, }\\ {{p_x}(t) = {f_{\rm{p}}}{N_{\rm{T}}}{n_{\rm{r}}}t, }\\ {{f_y}(t) = {p_y}(t) = 0.} \end{array} $ |
式中:fz为机器人端铣每齿进给量, fp为机器人行星复合铣削每刀进给量, 即立铣刀公转一周沿进给方向移动的距离.
每齿进给量是进行铣削力与表面形貌分析和工艺参数制定的重要参数.根据单位时间内立铣刀的总进给量等于立铣刀轴心所经过的路径长度, 推导得到机器人行星复合铣削加工沿直线进给时, 铣刀的实际每齿进给量为
| $ {f_{\rm{e}}} = \frac{{{n_{\rm{r}}}}}{{Z{k_{\rm{m}}}}}\int_0^{\rm{T}} {\sqrt {4{\rm{ \mathsf{ π} }}{R^2}\left[ {{\rm{ \mathsf{ π} }} + {N_{\rm{T}}}{f_{\rm{p}}}\sin \left( {2{\rm{ \mathsf{ π} }}{n_{\rm{r}}}t} \right)} \right] + N_{\rm{T}}^2f_{\rm{p}}^2} }\; {\rm{d}}t. $ |
式中:T为公转周期(min), T=1/nr; km为转速比, 表示铣刀自转转速与公转转速的比值, 即km=ns/nr.
因此, 当行星复合铣削动力头结构与立铣刀型号确定时, 刀齿数Z、公转半径R和刀具数量NT随之确定, 立铣刀实际每齿进给量fe是刀盘每转进给量fp、自转转速ns和公转转速nr的函数, 表示为
| $ f_{\mathrm{e}}=F\left(n_{\mathrm{s}}, n_{\mathrm{r}}, f_{\mathrm{p}}\right). $ |
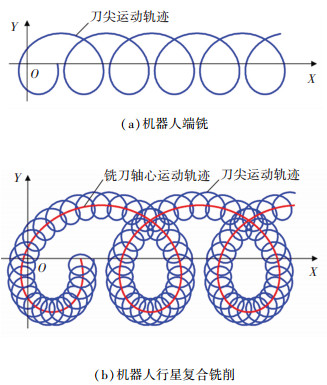
根据以上分析画出机器人端铣中第i个刀尖和机器人行星复合铣削中第k把刀上第i个刀尖的运动轨迹, 如图 4所示, 为了清晰对比, 对细节部分进行了适当的放大.
|
图 4 刀尖运动轨迹对比 Fig. 4 Comparison of tool nose trajectories of REM and RPCM |
机器人端铣多采用单轴形式的高速电主轴作为末端执行器, 因仅能装夹一把刀具, 所以每个刀尖点的运动轨迹都是沿着进给方向分布的余摆线, 相邻刀尖点的运动轨迹存在固定的相位差, 如图 4(a)所示.机器人行星复合铣削中, 刀具绕其轴心自转的同时围绕刀盘轴心公转, 因此刀尖点运动轨迹是沿着刀具轴心运动轨迹均匀分布的余摆线, 如图 4(b)所示, 而不同刀具轴心运动轨迹的差别仅在于初始相位角的不同.因此, 从刀尖运动轨迹的角度而言, 机器人行星复合铣削相当于多个间隔固定相位角的摆线铣削的有序组合.
2 机器人铣削对比实验 2.1 实验平台工艺研究是进行新技术开发与设备研制的重要基础, 为探究机器人行星复合铣削与机器人端铣在实际加工效率、切削力和加工质量等方面的差异, 同时为行星复合动力头的结构设计提供工艺数据支持, 搭建了机器人铣削加工实验平台, 如图 5所示.其中FANUC工业机器人的型号为M-20iA/35MT, 额定负载35 kg, 重复定位精度为±0.03 mm; 末端电主轴额定功率3.5 kW, 最高转速为18 000 r/min.工业机器人和工作台底部采用地脚螺栓固定, Kistler平板测力仪固定在工作台上, 用于实时采集铣削过程中工件受到的切削力.设置机器人用户坐标系与测力仪坐标系相同.

|
图 5 机器人铣削实验平台 Fig. 5 Robot milling experimental platform |
实验所用的刀具均为2刃Φ10 mm无涂层硬质合金立铣刀, 螺旋角为50°.工件材料为铝合金, 牌号为2024, 其主要化学成分如表 1所示[20]. Al-2024因具有较高的强度和良好的切削性能等特点而被广泛应用于航空航天领域.为避免机器人空间位姿突变引起系统刚度变化影响实验结果, 工件尺寸设计为100 mm×65 mm×20 mm, 并假设机器人位姿刚度在较小空间范围内恒定[21].
| 表 1 铝合金2024主要化学成分(质量分数) Tab. 1 Chemical composition of aluminum 2024 |
实验方案采用单因素对比实验, 除铣削方式不同外的其他实验条件均应尽可能保持一致.为避免机器人模态耦合效应的影响, 将主轴转速设置为10 000 r/min[22], 其余实验参数如表 2所示, 表中符号的含义与1.2小节一致, 切削方式均为顺铣.
| 表 2 单因素铣削实验工艺参数 Tab. 2 Process parameters of single-factor milling experiment |
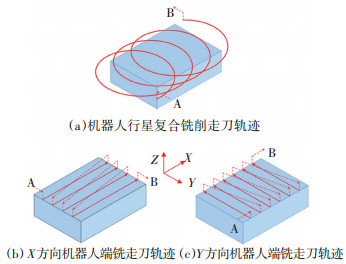
当采用以上实验参数时, 同一时刻仅有单个切削刃参与机器人端铣或单把立铣刀参与机器人行星复合铣削.因此本文借鉴文献[16]中的做法, 采用单把立铣刀沿余摆线轨迹进给的方式等效模拟机器人行星复合铣削4把铣刀时的实际加工状态.为全面对比, 同时考虑机器人端铣沿不同方向进给时的情况.实验走刀轨迹规划方案如图 6所示, (a)为机器人行星复合铣削单把立铣刀的走刀轨迹, (b)和(c)分别为沿X和Y方向进给时机器人端铣的走刀轨迹.记录去除每层材料的时间, 并实时采集切削力.
|
图 6 走刀轨迹设计 Fig. 6 Design of tool paths in experiments |
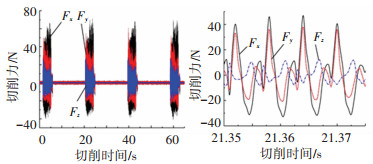
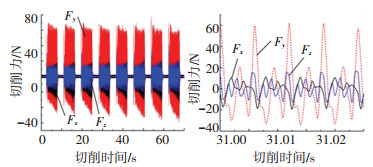
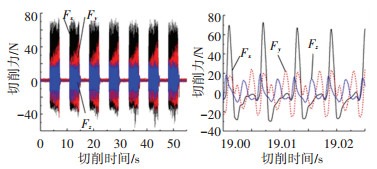
采用低通FFT滤波法去除铣削力信号中的低频噪声后, 机器人行星复合铣削和X或Y方向机器人端铣的切削力信号分别如图 7~9所示, 两种机器人铣削方式的三向切削分力均呈现明显周期性.
|
图 7 机器人行星复合铣削切削力 Fig. 7 Cutting force of RPCM |
|
图 8 X方向机器人端铣切削力 Fig. 8 Cutting force of REM along X direction |
|
图 9 Y方向机器人端铣切削力 Fig. 9 Cutting force of REM along Y direction |
从最大铣削力分量幅值的角度对比分析, 两种铣削方式中, 机器人行星复合铣削的最大切削力分量Fx幅值最小, 其次是沿X方向进给的机器人端铣切削力分量Fy, 沿Y方向进给的机器人端铣切削力分量Fx幅值最大.但两种铣削方式的最大切削力分量的波谷值相差并不大, 均为-30 ~-40 N(负号仅表示瞬时切削力方向不同).
机器人行星复合铣削中切削力分量Fx与Fy幅值相近, 而X或Y方向机器人端铣切削力分量Fx与Fy幅值差异较大, 主要原因是不同的走刀轨迹和进给方向导致主切削力方向与测力仪坐标轴之间夹角不同.
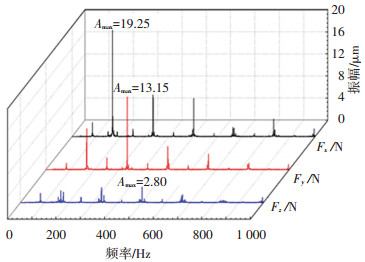
振幅大小能够反映切削力在对应频率的强弱, 截取两种铣削方式平稳切削时的切削力信号, 并分别对其进行FFT变换(快速傅里叶变换), 结果见图 10~12.由于实验中的主轴转速均为10 000 r/min, 对应的主轴转动频率约为166.67 Hz, 刀齿通过频率约为333.33 Hz.
|
图 10 机器人行星复合铣削切削力FFT变换 Fig. 10 FFT transform for cutting force of RPCM |
|
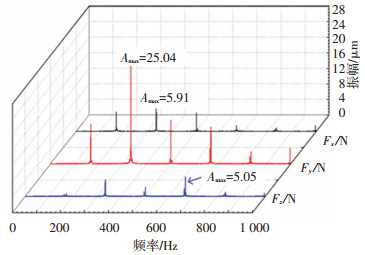
图 11 X方向机器人端铣切削力FFT变换 Fig. 11 FFT transform for cutting force of REM along X direction |
|
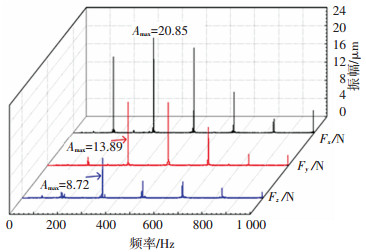
图 12 Y方向机器人端铣切削力FFT变换 Fig. 12 FFT transform for cutting force of REM along Y direction |
对比发现, 两种铣削方式的切削力均具有相似的频谱结构, 各切削力分量的能量主要集中分布在中低频分量, 并以主轴转动频率和刀齿通过频率占优, 谱峰值均出现在对应最大切削力分量的频谱曲线中.机器人行星复合铣削最大切削力分量的谱峰值最小, 其次是Y方向机器人端铣, X方向机器人普通铣削最大切削力分量谱峰值最大.
刀具轴向跳动是影响被加工表面加工质量的重要因素, 轴向切削力的强弱能够侧面反映轴向跳动量的大小.根据两种铣削方式的频谱图, 机器人行星复合铣削的轴向切削力分量Fz的谱峰值最小, 其次是X方向机器人端铣, Y方向机器人端铣的Fz的谱峰值最大.可以预见这种趋势也会同样体现在已加工表面的表面质量上.
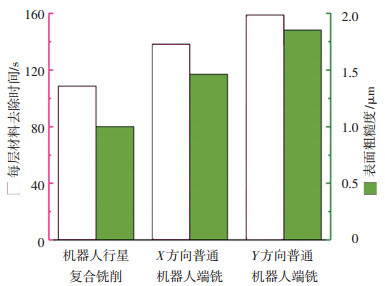
3.2 加工效率与表面粗糙度从立铣刀切入工件的瞬间开始计时, 到完成每层材料去除的切出瞬间停止计时, 计算5次重复实验的平均时间, 结果如图 13所示.
|
图 13 去除每层材料所用切削时间与表面粗糙度对比 Fig. 13 Contrast between cutting time for removing each material layer and surface roughness |
由于实验中采用单把立铣刀等效模拟机器人行星复合铣削中4把立铣刀的实际加工状态, 所以实验测得的平均每层材料去除时间(435 s)是采用真实机器人行星复合铣削时长的4倍, 这里取处理后的数据作为最终材料去除时间.机器人行星复合铣削与机器人端铣平均去除每层材料所用的时间分别为108.75、138.25和158.75 s, 相对于X和Y方向机器人端铣, 机器人行星复合铣削的加工效率分别提升了21.34%和31.50%.由于机器人端铣中沿Y方向进给时的走刀空行程数比沿X方向进给时的更多, 所以沿Y方向进给的每层材料去除时间也更长.
以表面粗糙度作为标准衡量已加工表面的表面质量, 均匀选取试件已加工表面上的5个样点, 重复测量3次每个样点处的表面粗糙度值, 并计算平均值作为该试件已加工表面的最终表面粗糙度值, 如图 13所示.
机器人行星复合铣削中已加工表面的表面粗糙度值最小, 其次是X方向机器人端铣, Y方向机器人端铣表面粗糙度最大, 这与3.1小节中的分析结果相同.相对于X和Y方向机器人端铣, 机器人行星复合铣削已加工表面的表面粗糙度分别降低了33.33%和47.37%.
4 结论1) 本文提出一种应用于大型铝合金构件高效铣削加工的机器人行星复合铣削工具系统, 建立了理论模型, 比较了机器人行星复合铣削与机器人端铣的刀尖运动轨迹特征, 发现机器人行星复合铣削相当于多个间隔固定相位角的摆线铣削的有序组合.
2) 机器人铣削对比实验结果表明, 相对于单把立铣刀的X和Y方向机器人端铣, 采用4把立铣刀结构的机器人行星复合铣削的最大切削力分量幅值和轴向切削力分量谱峰值更小, 加工效率分别提升了21.34%和31.50%, 同时表面粗糙度值分别降低了33.33%和47.37%, 证明了机器人行星复合铣削能够在提高铣削加工效率的同时改善加工质量.
3) 相对于机器人端铣加工, 机器人行星复合铣削的切削力优势能够有效抑制机械臂的变形和轴向跳动对加工质量的影响, 从而为提高大型铝合金构件机器人铣削的加工质量提供可靠保证.同时, 其加工效率的优势为切削参数提供了更大的选择范围, 使其能够在不降低加工效率的前提下, 通过调整工艺参数提高加工稳定性和加工质量, 从而为实现大型铝合金构件高效机器人铣削提供了新方案.
| [1] |
王战玺, 张晓宇, 李飞飞, 等. 机器人加工系统及其切削颤振问题研究进展[J]. 振动与冲击, 2017, 36(14): 147. WANG Zhanxi, ZHANG Xiaoyu, LI Feifei, et al. Review on the research developments of robot machining systems and cutting chatter behaviors[J]. Journal of Vibration and Shock, 2017, 36(14): 147. DOI:10.13465/j.cnki.jvs.2017.14.024 |
| [2] |
周莹皓, 张加波, 乐毅, 等. 移动机器人技术在航天制造业中的应用[J]. 机械设计与制造工程, 2018, 47(2): 87. ZHOU Yinghao, ZHANG Jiabo, LE Yi, et al. Application of mobile robot technology in the aerospace manufacturing industry[J]. Machine Design and Manufacturing Engineering, 2018, 47(2): 87. DOI:10.3969/j.issn.2095-509X.2018.02.020 |
| [3] |
IGLESIAS I, SEBASTIáN M A, ARES J E. Overview of the state of robotic machining: Current situation and future potential[J]. Procedia Engineering, 2015, 132: 912. DOI:10.1016/j.proeng.2015.12.577 |
| [4] |
URRESTI I, ARRAZOLA P J, ∅RSKOV K B, et al. High productivity mould robotic milling in Al-5083[J]. AIP Conference Proceedings, 2018, 1960(1): 070026. DOI:10.1063/1.5034922 |
| [5] |
MEJRI S, GAGNOL V, LE T P, et al. Dynamic characterization of machining robot and stability analysis[J]. The International Journal of Advanced Manufacturing Technology, 2016, 82(1/2/3/4): 351. DOI:10.1007/s00170-015-7336-3 |
| [6] |
PAN Zengxi, ZHANG Hui, ZHU Zhenqi, et al. Chatter analysis of robotic machining process[J]. Journal of Materials Processing Technology, 2006, 173(3): 301. DOI:10.1016/j.jmatprotec.2005.11.033 |
| [7] |
YUAN Lei, SUN Shuaishuai, PAN Zengxi, et al. Mode coupling chatter suppression for robotic machining using semi-active magnetor- heological elastomers absorber[J]. Mechanical Systems and Signal Processing, 2019, 117: 221. DOI:10.1016/j.ymssp.2018.07.051 |
| [8] |
KARIM A, SCHMID S, VERL A. Pose and feed-direction dependency analysis for milling tasks with industrial robots[J]. DEStech Transactions on Engineering and Technology Research, 2017, 555. DOI:10.12783/dtetr/icpr2017/17670 |
| [9] |
HE Fengxia, LIU Yu, LIU Kuo. A chatter-free path optimization algorithm based on stiffness orientation method for robotic milling[J]. The International Journal of Advanced Manufacturing Technology, 2019, 101(9/10/11/12): 2750. DOI:10.1007/s00170-018-3099-y |
| [10] |
SLAMANI M, GAUTHIER S, CHATELAIN J F. A study of the combined effects of machining parameters on cutting force components during high speed robotic trimming of CFRPs[J]. Measurement, 2015, 59: 268. DOI:10.1016/j.measurement.2014.09.052 |
| [11] |
MATSUOKA S, SHIMIZU K, YAMAZAKI N, et al. High-speed end milling of an articulated robot and its characteristics[J]. Journal of Materials Processing Technology, 1999, 95(1/2/3): 83. DOI:10.1016/S0924-0136(99)00315-5 |
| [12] |
SLAVKOVIC N R, MILUTINOVIC D S, GLAVONJIC M M. A method for off-line compensation of cutting force-induced errors in robotic machining by tool path modification[J]. The International Journal of Advanced Manufacturing Technology, 2014, 70(9/10/11/12): 2083. DOI:10.1007/s00170-013-5421-z |
| [13] |
FANG Qiang, PAN Zemin, FEI Shaohua, et al. A novel helical milling end-effector and its application[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(6): 3112. DOI:10.1109/TMECH.2015.2409986 |
| [14] |
GUO Yingjie, DONG Huiyue, WANG Guifeng, et al. A robotic boring system for intersection holes in aircraft assembly[J]. The Industrial Robot, 2018, 45(3): 328. DOI:10.1108/IR-09-2017-0176 |
| [15] |
LI Shenwang, WANG Xibin, XIE Lijing, et al. The milling-milling machining method and its realization[J]. The International Journal of Advanced Manufacturing Technology, 2015, 76(5/6/7/8): 1151. DOI:10.1007/s00170-014-6345-y |
| [16] |
李慎旺.难加工材料高效切削新方法及刀具结构研究[D].北京: 北京理工大学, 2015 LI Shenwang. Study on new method and tool structure for efficient cutting of difficult-to-cut materials[D]. Beijing: Beijing Institute of Technology, 2015 |
| [17] |
YUAN Lei, PAN Zengxi, DING Donghong, et al. A review on chatter in robotic machining process regarding both regenerative and mode coupling mechanism[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(5): 2240. DOI:10.1109/TMECH.2018.2864652 |
| [18] |
焦黎, 李晨旭, 王西彬.基于铣-铣复合加工原理的高柔性加工系统和加工方法: CN201810685286.X[P]. 2018-11-07
|
| [19] |
王西彬, 李晨旭, 焦黎.一种复合加工工具铣-铣动力头: CN201810685302.5[P]. 2018-11-06
|
| [20] |
DING Zhongfen. Mechanistic study of thin film sulfuric acid anodizing rate difference between Al2024 T3 and Al6061 T6[J]. Surface and Coatings Technology, 2019, 357: 287. DOI:10.1016/j.surfcoat.2018.09.083 |
| [21] |
LI Jing, LI Biao, SHEN Nanyan, et al. Effect of the cutter path and the workpiece clamping position on the stability of the robotic milling system[J]. The International Journal of Advanced Manufacturing Technology, 2017, 89(9/10/11/12): 2921. DOI:10.1007/s00170-016-9759-x |
| [22] |
CORDES M, HINTZE W, ALTINTAS Y. Chatter stability in robotic milling[J]. Robotics and Computer-Integrated Manufacturing, 2019, 55(Part A): 17. DOI:10.1016/j.rcim.2018.07.004 |
 2021, Vol. 53
2021, Vol. 53


