滚动轴承在各类机电一体化设备中使用广泛, 由于工作过程中长时间旋转磨损、高温等原因, 轴承故障是常发故障之一.轴承发生故障可能造成严重的经济损失或人员伤亡, 因此提高诊断效率和准确率十分重要.轴承故障诊断方法经历了人工经验判断、信号时域分析[1]、频域谱分析[2]、时频域分析[3]、模态分析[4]等阶段, 目前应用广泛的方法有人工经验判断, 如经验丰富的工人通过听机器响动判断工作状态; 时域指标分析如峭度值、平滑指数、基尼指数等; 频域分析如傅里叶变换包络分析; 时频域分析如短时傅里叶变换、小波变换、S变换等; 模态分析即信号通过一定规则分解, 得到模态分量后分析的方法, 如EMD分解后包络谱分析等.目前, 机电一体化产品日益增多, 而传统的故障诊断方法要求人员具有较高的经验知识, 且需多指标联合分析后得出诊断结论, 无法满足自动化诊断的需求.
随着人工智能技术的发展, 应用决策树[5]、支持向量机[6]、朴素贝叶斯[7]等机器学习手段开展故障诊断日益增多, 特别是以卷积神经网络为代表的深度学习方法的使用, 使故障诊断逐步走向智能化、自动化. ZHANG Wei等[8]提出了一种基于一维深度卷积网络的故障诊断模型, 实现了基于一维卷积神经网络端到端的诊断模式; 黄驰城[9]利用时频变换和三种经典卷积神经网络模型, 实现了二维卷积神经网络在轴承故障诊断中的应用.虽然一维、二维卷积神经网络均在故障诊断中取得了一定的效果, 但存在神经元输入输出采用标量形式导致的细节特征提取不足, 池化层丢失部分有用信息, 较大规模网络才能提取更详细特征等一系列问题, 因此提出许多改进方案.本文采用的基础胶囊网络结构由Hinton等提出, 主要思想为将神经元标量输入输出改为向量形式, 网络结构保留空间位置等信息, 舍弃池化层结构, 从而实现更好的效果. Hinton等提出的胶囊网络特征提取部分仅采用单层卷积, 在此基础上杨平等[10]提出了双卷积层胶囊网络的诊断方法, 相较于单卷积层取得了一定的改进, 但双卷积层胶囊网络仅增加了一个卷积层, 卷积层之间采用串联式连接, 没有从原始图像数据中进一步提取特征, 细节特征仍存在丢失, 特征提取能力需进一步优化.
本文利用胶囊结构的同时, 采用多尺度Inception结构, 配合空间注意力机制, 从原始图像数据中, 进行多尺度的特征提取和关键信息的识别, 配合损失值计算方法的优化, 达到更好的分类诊断效果, 通过低信噪比实验, 证明了方法的适用性.
1 基本原理 1.1 卷积结构卷积神经网络特征提取过程主要由卷积结构完成, 采用共享卷积核的形式对输入图像或矩阵进行局部卷积运算, 得到结果经激活函数非线性化输入下一层.采用k×k卷积核的卷积过程公式为
| $ a_{i, j}=f\left(\sum\limits_{m=0}^{k} \sum\limits_{n=0}^{k} \omega_{m, n} \cdot x_{i+m, j+n}+b\right). $ |
式中:ai, j为输出值, xi, j为第i行j列的元素, ωm, n为第m行n列的权重, 参数b为偏置项, f为激活函数, 常用的激活函数有sigmoid、tanh、Relu等, 其中Relu函数表达式为
| $ y=\max (0, x). $ |
式中y为输出值, x为输入值.
Relu函数为分段线性函数, 所有的负值和0输出为0, 所有的正值输出原值不变, 这种操作为单侧抑制, 实现稀疏后更好地挖掘相关特征, 加速模型收敛.
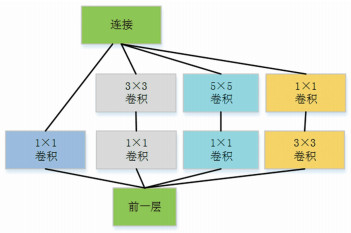
1.2 Inception结构2012年, AlexNet采用Relu激活函数、全局池化层、Dropout方式得到性能优良的成果后, 主流的网络结构突破大致是网络更深(层数), 但是纯粹的增大网络存在容易过拟合, 计算复杂, 梯度弥散等问题.为解决这些问题, GoogleLeNet采用了Inception结构, 初始V1结构如图 1所示.
|
图 1 多尺度卷积结构 Fig. 1 Inception V1 structure |
Inception结构[11]通过改深度增加为宽度增加的方法, 解决梯度弥散等问题, 但宽度增加同样增加了参数量, 在后续的改进过程中, V2和V3结构均采用卷积核拆分的方式, V2采用3个3×3的卷积核代替7×7卷积, V3采用1×7和7×1卷积核代替7×7卷积, 达到了减小网络结构的目的. Inception结构展示了特征提取过程中, 采用卷积核由小到大的方式可以提取更多的细节特征; 多层卷积核通过激活函数的增多, 非线性表达能力进一步得到提高; 宽度代替深度的增加可以避免一定的梯度弥散.
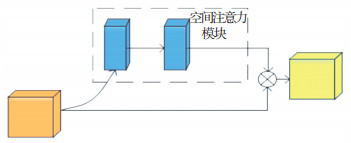
1.3 空间注意力机制注意力机制模仿人观察事物关注重点部位的特点[12], 广泛应用于图像识别、自然语言处理等领域.空间注意力机制将原始图像信息变换到另外一个空间, 通过训练空间转换模块输出与原信息的叠加实现关键信息的识别, 空间转换模块采用类池化的方式, 关注重点区域, 与原图像或矩阵的融合保证重点信息不丢失, 其结构如图 2所示.
|
图 2 空间注意力模块 Fig. 2 Spatial attention module |
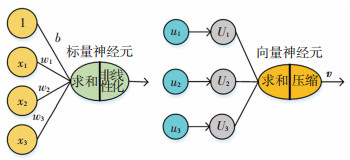
胶囊网络的概念在2017年由Hinton提出, 主要思想为将神经元的输入输出由标量形式改为向量形式, 从而拥有空间位置特征提取能力, 胶囊向量神经元与普通标量神经元类比如图 3所示.
|
图 3 标量与向量神经元 Fig. 3 Scalar and vector neurons |
向量神经元与标量神经元主要区别在于输入输出数据的结构形式, 采用向量结构具有更丰富的特征表达能力; 神经元之间采用动态路由的方式进行特征传递, 通过相关性计算, 特征得到很好的归类, 更加符合现实场景的需要; 动态路由每次迭代以0初始化参数, 参数规模得到了优化, 压缩向量的尺度, 保证了每一层向量神经元之间权重的一致性.算法过程如下:
1) 初始化l层第i个胶囊和l+1层第j个胶囊间特征传递参数bi, j为0;
2) 利用softmax方式计算两层胶囊间权重ci, j, 具体公式为
| $ c_{i, j}=\frac{\exp \left(b_{i, j}\right)}{\sum \exp \left(b_{i, j}\right)}; $ |
3) 低层胶囊特征ui传递至高层胶囊, 得到高层特征
| $ s_{j}=\sum c_{i, j} \cdot u_{i}; $ |
4) 压缩高层胶囊特征, 得到压缩后的特征
| $ v_{j}=\frac{\left\|s_{j}\right\|^{2}}{1+\left\|s_{j}\right\|^{2}} \cdot \frac{s_{j}}{\left\|s_{j}\right\|}; $ |
5) 迭代更新为
| $ b_{i, j}=b_{i, j}+u_{i} \cdot v_{j}. $ |
动态路由实现低层胶囊结构与高层胶囊之间的向量式传递, 通过二者标量积来度量相关性, 向量的模长代表实体的存在性, 构建了空间位置等关键特征.
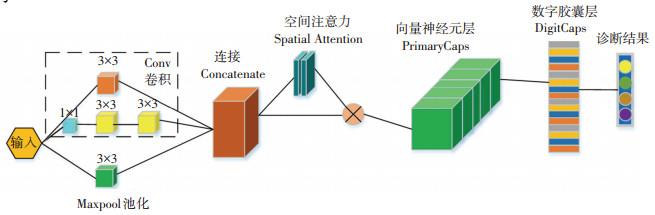
2 改进胶囊网络诊断方法 2.1 模型结构为提高胶囊网络的特征提取能力, 本文改进胶囊网络的单一卷积结构为多尺度卷积Inception模块和空间注意力模块的结合体, 构建更加全面丰富、特征突出的特征提取单元, 与初始胶囊结构和数字胶囊结构结合, 提出了一种前端特征提取提升的改进胶囊网络SAP- CapsNets(Start ability promotion capsule network), 其结构如图 4所示.
|
图 4 改进胶囊网络 Fig. 4 SAP-CapsNets |
SAP-CapsNets输入数据为振动信号时频分析(短时傅里叶变换)得到的二维时频域数据(数组非图像), 网络前端采用Inception结构配合空间注意力模块进行特征提取, 保证信息提取的充分性, 同时具有较强的抗噪声作用, 特征采集作用明显; 后端采用胶囊结构构造向量神经元, 通过动态路由实现特征传递; 激活函数采用Relu函数.
2.2 损失函数损失函数采用间隔损失和重构损失结合计算总损失的方式, 间隔损失表示为
| $ L_{k}=T_{k} \cdot\left(\max (0, m)-\left\|v_{k}\right\|\right)^{2}+\\\lambda \cdot\left(1-T_{k}\right) \cdot \max \left(0, \left\|v_{k}\right\|-m\right). $ |
式中: k是分类数, Tk是分类的指示函数(存在为1, 不存在为0); m+为上界, 惩罚假阳性; m-为下界, 惩罚假阴性; λ比例系数, 调整两者比重.
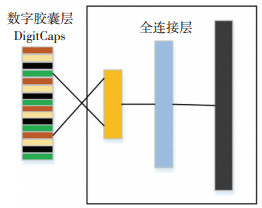
重构损失计算方法为胶囊层后构造3层全连接层如图 5所示, 得到与原数据数据点数相同的输出值, 计算原数据与输出数据距离平方和, 作为损失值.
|
图 5 重构结构 Fig. 5 Refactoring structure |
总损失为间隔损失和λ倍重构损失的和, λ平衡二者比重, 取0.01左右.
3 算例及结果分析 3.1 数据介绍和预处理为验证方法模型的效果, 采用凯斯西储大学轴承公开数据集.轴承的损伤为电火花加工的单点损伤, 人工制造故障的方式, 故障特征相对实际工况明显, 故本文采用人工降低信号信噪比的方法, 模拟噪声工况环境, 开展实验分析.数据为原始数据12 kHz采样频率下的驱动端轴承故障, 包含1 797、1 772、1 750和1 730 r/min这4种转速数据; 轴承状态为健康、内圈故障、滚动体故障和外圈故障.
深度学习网络参数量大, 需大样本数据驱动得到模型, 且轴承数据集中正常状态相对其他故障状态的样本较少, 样本存在不均衡问题.因此本文采用单个数据文件重复采样的方式减小样本间的不平衡问题.本文实验中采用单个数据文件中单次选取6 000个点, 每次向后移动500个点的形式进行采样, 采样后数据进行时频变换(短时傅里叶变换[13]), 由一维数据变换为二维数据, 短时傅里叶变换公式为
| $ S=\int f(t) g(t-\tau) \mathrm{e}^{-\mathrm{j} \omega t} \mathrm{~d} t. $ | (8) |
式中:f和g为信号和窗函数, 输出结果S为时频域数据, 自变量为时间, 变量ω为频率, 变量τ为移动窗口设置量.
变换二维后, 为避免数据转图像格式容易出现格式转换误差的问题, 本文将数据直接按数组形式保存使用, 不转换图像类型, 避免格式在转换过程中引起的原始数据特征损失.样本分布情况如表 1所示.
| 表 1 数据样本类型分布 Tab. 1 Distribution of data sample types |
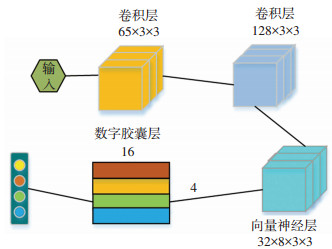
为验证模型的优劣性, 采用双卷积胶囊网络和传统卷积神经网络[14]作为对比分析, 二者结构如图 6、7所示.
|
图 6 双卷积层胶囊网络 Fig. 6 Double convolutional layer capsule network |

|
图 7 卷积神经网络 Fig. 7 Convolutional neural network |
模型均采用Relu激活函数; 双卷积胶囊网络将传统胶囊结构单卷积层扩展为双卷积层, 结合了卷积网络和胶囊网络的特点; 传统卷积神经网络为适应时频变换后的数据结构, 采用了一个4×3卷积核, 通过卷积和池化的方式, 逐层特征提取和压缩.
3.3 训练验证样本按8:2的比例随机划分训练集和验证集.训练过程采用未做处理的原始信号二维数据. 3种方法均采用Adam优化方法, 学习率0.001, 训练时单次读入数据量batch_size为50, 全部样本迭代次数epoch设置为20, 均运行3次取平均结果, 改进胶囊网络(SAP-CapsNets)、双卷积神经网络(CNN-CapsNets)和传统卷积神经网络(CNN)3种模型训练结果如表 2所示.
| 表 2 模型训练结果 Tab. 2 Model training results |
从表 2中可得, 改进胶囊网络在模型训练时间上没有明显的增加, 训练集正确率有了一定的提升.
验证过程首先采用未做处理的验证集数据试验, 3个模型验证集准确率分别为98.2%、96.2%和95.1, 从验证集结果看, 模型均达到了训练效果.
采用添加不同幅值高斯白噪声, 降低信噪比的方式, 对训练集和验证集进行处理, 信噪比公式为
| $ R=10 \lg \left(P_{\mathrm{s}} / P_{\mathrm{n}}\right). $ |
式中Ps为信号有效功率, Pn为噪声功率, R为信噪比.
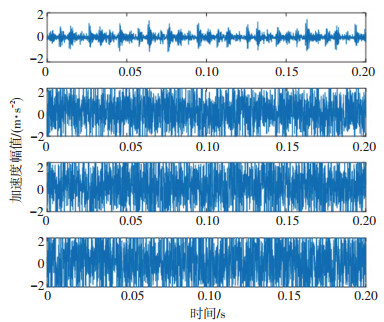
相同坐标下, 降低西储大学轴承数据集中的内圈故障信号信噪比, 信号时域图变化如图 8所示.
|
图 8 不同信噪比状态(原始、-1、-2、-3dB)时域图 Fig. 8 Time domain diagram of signals with different SNRs: original, -1, -2, and -3 dB |
统计图 8中几种不同信噪比状态信号, 统计指标使用敏感度较高的时域峭度值[15]、方差、歪度, 结果如表 3所示.
| 表 3 不同信噪比状态时域指标 Tab. 3 Time domain indicators of signals with different SNRs |
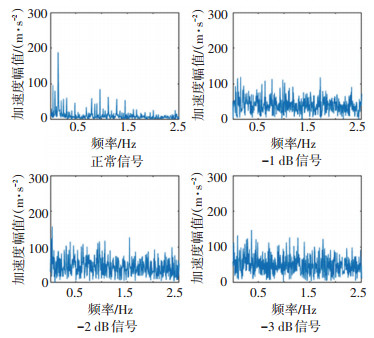
采用希尔伯特变换构造4种状态下信号的解析函数, 得到包络信号, 求解包络谱[16], 观察信噪比调整过程中信号频域的幅值变化情况, 得到包络谱如图 9所示.
|
图 9 几种信噪比信号包络谱 Fig. 9 Envelope spectra of signals with different SNRs |
从时域指标统计和包络谱图信号幅值变换情况分析得出, 信噪比降低后信号的时域、频域变化较大, 噪声严重影响了原始信号本身的特征, 采用简单的分析方法, 难以直接提取故障特征和判断故障类型.
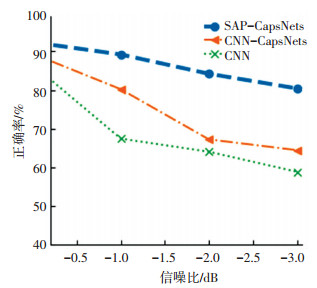
采用上文正常信噪比信号为训练集样本, 训练好的卷积神经网络、双卷积胶囊网络和改进胶囊网络3个模型, 输入调整3种不同信噪比的数据作为诊断验证集, 模型的诊断情况如图 10.
|
图 10 几种信噪比验证集正确率 Fig. 10 Accuracy rates of different SNR verification sets |
从图 10可以看出SAP-CapsNets具有一定的抗噪能力, 在信噪比-3 dB的情况下, 仍能达到80%以上的正确率, 相比双卷积层胶囊网络和传统的卷积神经网络能达到更好的特征提取和故障诊断效果.
为进一步验证改进方法的效果, 训练集数据直接采用降低信噪比后数据, 将-1、-2、-3 dB数据混合作为训练集样本, 模型训练过程正确率71%, 验证集采用正常信噪比数据正确率为64%, 模型结果较差.分析原因后认为:直接采用低信噪比数据训练模型, 受噪声影响, 训练时模型未能准确学习轴承故障主要特征, 因此对正常信噪比数据分类正确率仍较低.采用正常信噪比数据开展训练, 以低信噪比数据进行验证的方式, 具有更好的效果, 且当前可用实际工况数据较少, 研究实验室信噪比条件下模型训练, 逐步迁移至实际工况的意义更加明显.
4 结论本文提出了一种前端特征提取模块提升的胶囊网络模型(SAP-CapsNets), 实验对比在噪声环境下的特征提取能力, 实验结果表明:
1) 噪声环境影响信号的整体指标, 深度学习模型识别效果同样受到严重影响.
2) 相比双卷积层胶囊网络, 本文改进胶囊网络通过Inception模块和空间注意力模块的结合, 起到抗噪和特征提取能力提升的作用, 模型稳定性和泛化能力更好.
3) 本文提出的模型还需进一步优化, 在实验中模型各层参数经过调整, 才取得了较好的结果, 后续进一步优化分析, 提高模型参数选择的稳定性和通用性.
| [1] |
SAMANTA B, AL-BALUSHI K R. Use of time domain features for the neural network based fault diagnosis of a machine tool coolant system[J]. Journal of Systems and Control Engineering, 2001, 215(3): 13. DOI:10.1243/0959651011540987 |
| [2] |
YUAN Haodong, CHEN Jin, DONG Guangming. An improved initialization method of D-KSVD algorithm for bearing fault diagnosis[J]. Journal of Mechanical Science and Technology, 2017, 31(11): 5161. DOI:10.1007/s12206-017-1010-7 |
| [3] |
SAXENA M, BANNET O O, GUPTA M, et al. Bearing fault monitoring using CWT based vibration signature[J]. Procedia Engineering, 2016, 144(3): 234. DOI:10.1016/j.proeng.2016.05.029 |
| [4] |
XIONG Qing, XU Yanhai, PENG Yiqiang, et al. Low-speed rolling bearing fault diagnosis based on EMD denoising and parameter estimate with alpha stable distribution[J]. Journal of Mechanical Science and Technology, 2017, 31(4): 1587. DOI:10.1007/s12206-017-0306-y |
| [5] |
王飞.决策树算法在机械设备故障诊断系统中的应用[D].武汉: 华中科技大学, 2013 WANG Fei. The application of decision tree algorithm on fault diagnosis system for mechanical equipments[D]. Wuhan: Huazhong University of Science and Technology, 2013 |
| [6] |
YANG Yu, YU Dejie, CHENG Junsheng. A fault diagnosis approach for roller bearing based on IMF envelope spectrum and SVM[J]. Measurement, 2006, 40(9/10): 943. DOI:10.1016/j.measurement.2006.10.010 |
| [7] |
祝世丰.贝叶斯网络分类模型研究及其在小样本故障诊断中的应用[D].哈尔滨: 哈尔滨工业大学, 2009 ZHU Shifeng. Research on Bayesian network classification models and its application in small sample fault diagnosis[D]. Harbin: Harbin Institute of Technology, 2009 |
| [8] |
ZHANG Wei, LI Chuanhao, PENG Gaoliang, et al. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load[J]. Mechanical Systems and Signal Processing, 2018, 100: 439. DOI:10.1016/j.ymssp.2017.06.022 |
| [9] |
黄驰城.结合时频分析和卷积神经网络的滚动轴承故障诊断优化方法研究[D].杭州: 浙江大学, 2019 HUANG Chicheng. Research on fault diagnosis and optimization method of rolling bearing based on time-frequency analysis and con-volutional neural network[D]. Hangzhou: Zhejiang University, 2009 |
| [10] |
杨平, 苏燕辰, 张振. 基于卷积胶囊网络的滚动轴承故障诊断研究[J]. 振动与冲击, 2020, 39(4): 55. YANG Ping, SU Yanchen, ZHANG Zhen. A study on rolling bearing fault diagnosis based on convolution capsule network[J]. Journal of Vibration and Shock, 2020, 39(4): 55. DOI:10.13465/j.cnki.jvs.2020.04.006 |
| [11] |
GUAN Qing, WAN Xiaochun, LU Hongtao, et al. Deep convolutional neural network Inception-v3 model for differential diagnosing of lymph node in cytological images: A pilot study[J]. Annals of Translational Medicine, 2019, 7(14): 34. DOI:10.21037/atm.2019.06.29 |
| [12] |
LI Mingxuan, LI Ou, LIU Guangyi, et al. An automatic modulation recognition method with low parameter estimation dependence based on spatial transformer networks[J]. Applied Sciences, 2019, 9(5): 1010. DOI:10.3390/app9051010 |
| [13] |
GAO Huizhong, LIANG Lin, CHEN Xiaoguang, et al. Feature extraction and recognition for rolling element bearing fault utilizing short-time Fourier transform and non-negative matrix factorization[J]. Chinese Journal of Mechanical Engineering, 2015, 28(1): 96. DOI:10.3901/CJME.2014.1103.166 |
| [14] |
杨观赐, 杨静, 李少波, 等. 基于Dropout与ADAM优化器的改进CNN算法[J]. 华中科技大学学报(自然科学版), 2018, 46(7): 122. YANG Guanci, YANG Jing, LI Shaobo, et al. Modified CNN algorithm based on Dropout and ADAM optimizer[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2018, 46(7): 122. DOI:10.13245/j.hust.180723 |
| [15] |
WANG Dong. Some further thoughts about spectral kurtosis, spectral L2/L1 norm, spectral smoothness index and spectral Gini index for characterizing repetitive transients[J]. Mechanical Systems and Signal Processing, 2018, 108(1): 360. DOI:10.1016/j.ymssp.2018.02.034 |
| [16] |
APPANA D K, PROSVIRIN A, KIM J M. Reliable fault diagnosis of bearings with varying rotational speeds using envelope spectrum and convolution neural networks[J]. Soft Computing, 2018, 22(20): 6719. DOI:10.1007/s00500-018-3256-0 |
 2021, Vol. 53
2021, Vol. 53


