2. 大连理工大学 运载工程与力学学部汽车工程学院, 辽宁 大连 116024
2. School of Automotive Engineering, Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, Dalian 116024, Liaoning, China
随着环境污染与能源危机的不断加剧, 电动汽车逐渐受到大众的关注.锂离子电池具有能量密度高、循环寿命长、自放电率小等优点, 被广泛应用于电动汽车领域[1-2].在电池管理系统中, 如果不能准确估计电池的健康状态(SOH), 电池充放电控制就没有足够的参考依据, 就不能保证电池容量的有效发挥, 导致电池性能和寿命的降低.
通常情况下, 锂离子电池的应用阶段主要分为两大梯度:第一梯度应用于电动汽车等电动装置中, 健康状态区间为100%~80%;第二梯度中健康状态区间为80%~60%, 此时电池的充放电性能不足以满足汽车行驶的要求, 主要应用于电网和新能源发电等储能装置中[3].当电池容量降为原容量的60%后电池将失去其重要价值[4], 因此, 在电池健康状态为100%~60%的全寿命周期内进行健康状态的高精度估计对于电池健康管理和故障预警至关重要, 而目前大多数研究只对电池的第一梯度进行健康状态估计[5-8].锂离子电池健康状态的估计方法主要分为:实验法[9]、模型法[10-11]、数据驱动法[12]及融合法[13].其中, 实验法需要特殊的实验设备或实验条件[14-15]; 模型法中, 电化学模型[16]具有结构复杂、计算量大的缺点, 等效电路模型[17]往往计算精度不高, 经验模型[18]的通用性一般较差; 数据驱动法一般以锂离子电池的电压、电流、温度等参数为基础, 结合粒子群算法[19]、卡尔曼滤波[20-21]、粒子滤波[22]、神经网络[23]等智能算法[24-25]实现健康状态估计, 具有高效、实用的特点, 是未来研究电池健康状态估计的重要方向.
采用数据驱动法, 一些学者基于固定电压区间充电电量进行了健康状态估计的研究, 例如, 林甜甜等[8]选取充电周期内两恒定压差下的时间间隔作为健康状态估计的健康因子, Park等[26]选取恒流充电过程中固定荷电状态区间对应的所充电量作为健康状态估计的健康因子, 而上述研究未对区间进行优选, 较难实现健康因子对健康状态的高效估计; 戴海峰等[27]通过计算充电过程中电池衰减容量与充电曲线特征的相关系数来确定电压区间, 并建立相关向量机模型来进行健康状态估计, Zheng等[19]在恒流充电过程中通过粒子群算法选取电压区间, 并建立电池容量和健康因子的齐次线性关系, 这些研究仅在电池的100%~80%健康状态区间展开, 因此未能实现在电池100%~60%健康状态的全梯度区间进行健康状态的高精度估计.
本文提供一种在全寿命周期内通过计算电池容量来在线估计电池健康状态的方法.首先, 本文采用数据驱动法, 把恒流充电条件下某固定电压区间所充的电量作为电池容量估算的等效健康因子; 其次, 利用遗传算法寻找最优的充电电压片段, 在电池健康状态为100%~60%的全生命周期进行电池容量的精确在线估算; 最后, 通过容量与健康状态的线性转换以实现电池健康状态的精确在线估计.
1 等效健康因子的建立在复杂的车用环境下, 很少存在恒流放电的情况, 在放电工况下进行电池容量的估算存在着很大的难度, 而充电工况下充电电流较稳定, 应该在电池充电工况下选择电池等效健康因子, 因此本文选取电池充电过程中某段充电电压(VA→VB)下电池所充电量作为电池实际容量和健康状态估计的等效健康因子.
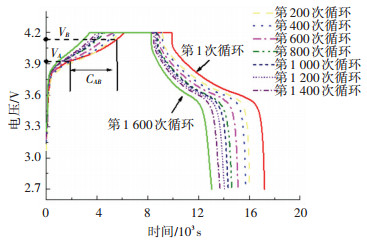
对容量为1.35 A·h锂离子电池进行充放电老化实验, 直到电池的健康状态低于60%, 其充电工况为标准的恒流恒压模式, 首先0.5 C恒流充电, 电压达到上截止电压4.2 V后进行恒压充电, 一直到电流小于0.05 A充电结束; 放电工况为0.5 C恒流放电, 电压达到下截止电压2.7 V放电结束.其中, 第1、200、400、…、1 600次循环的充放电电压曲线如图 1所示.
|
图 1 1.35 A·h锂离子电池的充放电电压曲线 Fig. 1 Charge and discharge voltage curves of 1.35 A·h lithium-ion battery |
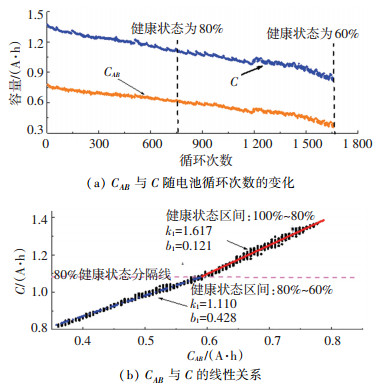
为了验证等效健康因子的有效性, 选取充电电压区间VA=3.85 V, VB=4.10 V, 令C为该电池的实际最大可用容量, CAB为该电池在充电电压VA→VB下的电池所充电量, 该电池在100%~60%健康状态区间CAB与C的对应关系如图 2所示.从图 2(b)中可以看出, 在100%~80%健康状态区间CAB与C近似是线性相关的, 拟合的线性方程的斜率为1.617, 截距为0.121;在80%~60%健康状态区间, CAB与C近似是线性相关的, 拟合的线性方程的斜率为1.110, 截距为0.428.
|
图 2 CAB与C的对应关系 Fig. 2 Relationship between CAB and C |
本文通过计算CAB与C在两个健康状态区间的Pearson指数和Spearman指数, 来进一步验证CAB与C在两个健康状态区间的线性相关性, 计算公式为:
| $ r_{\mathrm{P}}=\frac{E_{x y}-E_{x} E_{y}}{\sqrt{E_{x^{2}}-E_{y^{2}}} \sqrt{E_{y^{2}}-E_{y}^{2}}};\\r_{\mathrm{S}}=\frac{\sum_{i}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum_{i}\left(x_{i}-\bar{x}\right)^{2}} \sqrt{\sum_{i}\left(y_{i}-\bar{y}\right)^{2}}}. $ |
Pearson指数和Spearman指数越接近于1, 表明两变量的线性相关性越强.计算结果见表 1, 结果显示CAB与C在两个健康状态区间的Pearson指数和Spearman指数非常接近于1, 说明CAB与C在两个健康状态区间均有很强的线性相关性, 这同样验证了本文所选取等效健康因子的有效性.
| 表 1 CAB与C的Pearson和Spearman指数 Tab. 1 Pearson and Spearman indices of CAB and C |
因此, 本文假设在充电工况下某段充电电压区间VA→VB下的所充电量与该电池的实际可用容量是线性关系, 即满足下述方程:
| $ C_{k}=C_{k}^{A B} \cdot k_{0}+b_{0}. $ |
式中:Ck为电池在第k循环的实际可用容量, CkAB为电池在第k循环从VA到VB的充电电量, k0为由同类电池训练得到的平均斜率常数, b0为由同类电池训练得到的平均截距常数.
2 选择最优的充电电压片段 2.1 遗传算法遗传算法是一种模拟生物进化过程来寻找最优解的启发式优化算法[28-30].其具体流程如下:
1) 确定输入变量的边界条件, 设置遗传算法的参数.
2) 种群初始化.初始化一个种群S={s1, s2, …, sn}, n为种群大小, s为各个染色体.
3) 适应度计算.通过适应度函数评价种群S中每个染色体的适应度, 分别为f1, f2, …, fn.
4) 双亲选择.通过染色体的适应度计算每个染色体被选为亲代染色体的概率为
| $ p_{i}=f_{i} / \sum\limits_{k=1}^{n} f_{k}. $ |
5) 基因交叉.基因交叉是将两个亲代染色体各自的基因拆解开再重新结合的过程, 最后形成两个全新的染色体.基因交叉重组的方法为:
| $ \begin{aligned} X_{A}^{\prime} &=\alpha X_{A}+(1-\alpha) X_{B} ;\\ X_{B}^{\prime} &=\alpha X_{B}+(1-\alpha) X_{A}. \end{aligned} $ |
式中:XA、XB为基因交叉前的个体, XA′、XB′为基因交叉后的个体, α为[0, 1]的随机数.
6) 基因变异.基因变异是将某个体染色体基因序列中的某个基因位, 在边界条件的范围内随机变动形成新个体的过程.基因变异的方法为
| $ X_{A}^{\prime \prime}=\left\{\begin{array}{l} X_{A}+\beta\left(X_{\max }-X_{A}\right) r, \text { if } r \% 2=0; \\ X_{A}-\beta\left(X_{A}-X_{\min }\right) r, \text { if } r \% 2=1. \end{array}\right. $ |
式中:XA″为基因变异的个体, r为随机数, β为[0, 1]的随机数, Xmax、Xmin分别为该基因位的上下限.
重复2)~6)直到满足终止条件, 最后选择种群中适应度最大的染色体以及其对应的解作为最优解.在本文中, 设置遗传算法的参数为:种群大小为50, 停滞次数为30, 交叉概率为0.6, 变异概率为0.4.
2.2 最优充电电压片段的选择本文选择充电电压片段的初始电压VA和终止电压VB作为遗传算法的输入函数, 通过遗传算法来找到合适的充电电压片段, 方法原理图如图 3所示.

|
图 3 选择最优充电电压片段方法的原理图 Fig. 3 Schematic diagram for selecting the optimal charging voltage segment |
在电动汽车的实际使用过程中, 充电不一定是满充满放的.根据图 1所示的电池充放电曲线, 当电压为3.80 V时, 对应的电池荷电状态约为20%, 当电压为4.15 V时, 对应的电池荷电状态约为77%, 为了增加所提出方法的实际可用性, 本文在电池常用的中等荷电状态区间范围内选择充电电压片段来提取等效健康因子, 因此选择3.80≤VA, VB≤4.15.
另一方面, 如果充电电压片段对应的电池充电容量太少, 则此健康因子来估算电池实际可用容量的鲁棒性不高, 因此选择VB-VA≥0.15;如果充电电压片段范围太大, 则此健康因子在实际车用条件下的适用性不高, 因此选择VB-VA≤0.20.综上所述, 输入变量的边界条件确定如下:
| $ \begin{array}{c} 0.15 \leqslant V_{B}-V_{A} \leqslant 0.20 ;\\ 3.80 \leqslant V_{A} \leqslant 4.00; \\ 3.95 \leqslant V_{B} \leqslant 4.15. \end{array} $ |
在使用遗传算法寻找最佳充电片段时, 首先确定训练集中电池序号为i=1, 2, …, n, 每一个电池在第k个电池循环的实际可用容量为C1, k, C2, k, …, Cn, k, 每一个电池在第k个电池循环充电电压片段对应的充电电量为C1, kAB, C2, kAB, …, Cn, kAB, 用最小二乘法对Ci, kAB、Ci, k作线性拟合为
| $ C_{i, k}=C_{i, k}^{A B} \cdot k_{i}+b_{i}. $ |
式中:ki、bi分别为对第i个电池的Ci, kAB、Ci, k作线性拟合得到的斜率和截距.
其次, 取训练集中n个电池的平均斜率和平均截距为:
| $ \begin{array}{l} \bar{k}=\left(k_{1}+k_{2}+\ldots+k_{n}\right) / n , \\ \bar{b}=\left(b_{1}+b_{2}+\ldots+b_{n}\right) / n. \end{array} $ |
计算训练集中每个电池的估算电池容量为
| $ C_{i, k}^{\prime}=C_{i, k}^{A B} \cdot \bar{k}+\bar{b}, \quad i=1, 2, \ldots, n. $ |
计算训练集中第i个电池的估算电池容量的均方根误差为
| $ G_{i}=\sqrt{\frac{1}{m} \sum\limits_{k=1}^{m}\left(\frac{C_{i, k}^{\prime}}{C_{i, k}}-1\right)^{2}}, \quad i=1, 2, \ldots, n. $ |
确定遗传算法的目标函数为
| $ G=\frac{1}{n} \sum\limits_{i=1}^{n} G_{i}. $ |
如图 3所示, 通过遗传算法和训练集获得最优充电电压片段(VA→VB)、平均斜率k和平均截距b, 测试集的电池序号为j=1, 2, …, s, j电池在第k个循环下的实际可用容量为Cj, k, j电池在第k个循环下(VA→VB)对应的充电容量为Cj, kAB, j电池在第k个循环下的估算容量计算如下:
| $ C_{j, k}^{\prime}=C_{j, k}^{A B} \cdot \bar{k}+\bar{b}, \quad j=1, 2, \ldots, s. $ |
本文通过估算容量/健康状态与真实容量/健康状态的百分比误差CE、平均绝对误差CMAE、均方根误差CRMSE来评价所提出方法的效果:
| $ \begin{array}{c} C_{\mathrm{E}_{j, k}}=\left(C_{j, k}^{\prime}-C_{j, k}\right) / C_{j, k}, j=1, 2, \ldots, s ;\\ C_{\mathrm{MAE}_{j}}=\frac{1}{m} \sum\limits_{k=1}^{m}\left|\frac{C_{j, k}^{\prime}}{C_{j, k}}-1\right|, j=1, 2, \ldots, s; \\ C_{\mathrm{RMSE}_{j}}=\sqrt{\frac{1}{m} \sum\limits_{k=1}^{m}\left(\frac{C_{j, k}^{\prime}}{C_{j, k}}-1\right)^{2}}, j=1, 2, \ldots, s. \end{array} $ |
式中:CEj, k为j电池在第k个循环的容量(健康状态)百分比误差, CMAEj为j电池的容量(健康状态)平均绝对误差, CRMSEj为j电池的容量(健康状态)均方根误差.
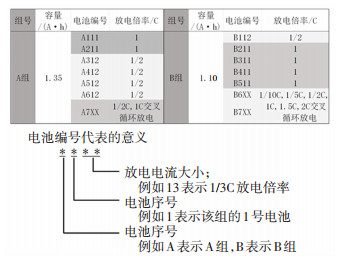
3 实验分析 3.1 实验的设定针对两种不同容量的锂电池分别设定不同的放电电流[31-32], 循环放电直到电池容量低于60%, 来验证所提出方法在不同的放电电流下和不同的电池老化阶段对电池健康状态的估计效果, 测试系统的型号为Arbin BT2000, 两种锂电池的阴极材料均为LiCoO2, 上截止电压为4.2 V, 下截止电压为2.7 V, 充电工况为典型的恒流恒压模式, 放电工况为恒流模式, 如图 1, 各组电池的实验条件如图 4.
|
图 4 两组电池的实验条件 Fig. 4 Experiment conditions of two groups of batteries |
本文构建了8个实验验证算例, 如表 2.其中, 设置#A-1、#A-2、#A-3、#A-4的实验对象为容量为1.35 A·h的锂离子电池, #B-1、#B-2、#B-3、#B-4的实验对象为容量1.1 A·h的锂离子电池, 用于验证本文所提出方法对不同型号锂电池的健康状态估计效果; 设置#A-1、#A-2、#B-1、#B-2在锂离子的健康状态处于80%~100%的生命周期进行估算, #A-3、#A-4、#B-3、#B-4在锂离子的健康状态处于60%~80%的生命周期进行估算, 用于验证本文所提出方法对锂电池在不同生命周期的健康状态估计效果; 设置8个实验算例的训练集、测试集中电池的放电电流倍率不同, 用于验证选取的最优电压片段在不同倍率放电工况下的健康状态估计效果.
| 表 2 构建验证所提出方法的算例及其验证结果 Tab. 2 Numerical examplesfor verifying the proposed method and corresponding results |
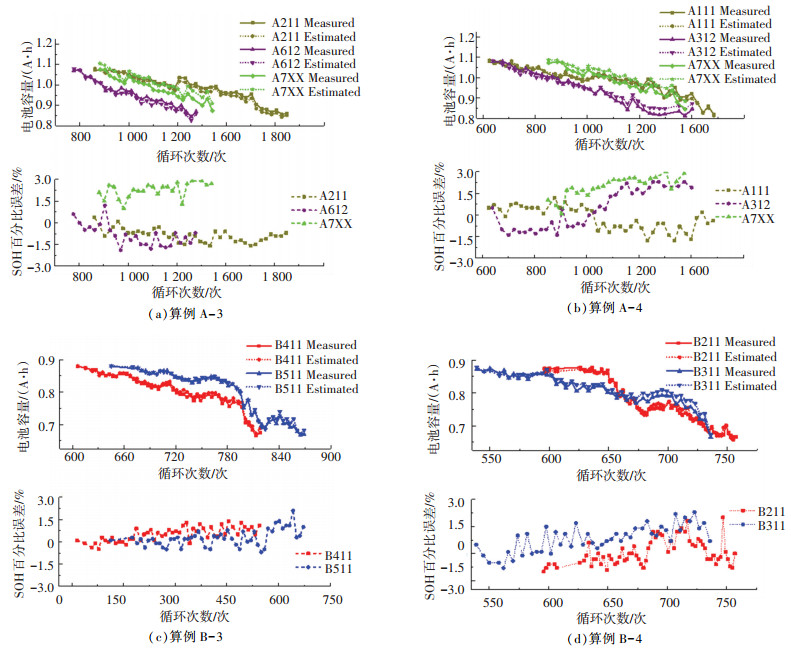
8个验证算例的验证结果如表 2和图 5、6所示, 其中, 表 2记录了各个算例里通过遗传算法训练得到的最优充电电压片段, 以及在该充电电压片段下训练集电池和测试集电池的健康状态估算误差(CRMSE & CMAE), 图 5、6记录了各个算例里在最优充电电压片段下测试集中每个电池的实际容量、估算容量, 以及健康状态估计百分比误差.

|
图 5 4个算例#A-1、#A-2、#B-1、#B-2(健康状态处于100%~80%)的估算效果 Fig. 5 Estimated results of four numerical examples: #A-1, #A-2, #B-1, and #B-2 (SOH between 100% and 80%) |
|
图 6 #A-3、#A-4、#B-3、#B-4算例(健康状态处于80%~60%)的估算效果 Fig. 6 Estimated results of four numerical examples: #A-3, #A-4, #B-3, and #B-4 (SOH between 80% and 60%) |
如表 2和图 5所示, #A-1、#A-2、#B-1、#B-2这4个算例中的锂离子电池均处于100%~80%健康状态区间, 在此区间进行健康状态估计时, 测试集电池健康状态估计的CRMSE < 1.20%, CMAE < 1.00%, 每次电池循环健康状态估计的百分比误差在3%之内, 与其他论文中的健康状态估计方法相比, 本文所提出的方法具有较高的精度.算例#A-1、#A-2中锂电池的容量为1.35 A·h, 算例#B-1、#B-2中锂电池的容量为1.1 A·h, 两类锂电池的健康状态估计效果都很好, 表明本文所提出方法在100%~80%健康状态区间, 适用于不同种类的电池.算例#A-1、#A-2、#B-1、#B-2中, 训练集电池和测试集电池的放电倍率不是相同的, 表明对于电池的100%~80%健康状态区间, 在某一放电倍率工况下训练出来的结果同样适用于其他放电倍率工况, 这进一步增加了本文所提出方法的适用性.
同样地, 如表 2和图 6所示, #A-3、#A-4、#B-3、#B-4这4个算例中的锂离子电池均处于80%~60%健康状态区间, 在此区间进行健康状态估计时, 测试集电池健康状态估计的CRMSE、CMAE < 1.55%, 每次电池循环健康状态估计的百分比误差在3%之内, 表明本文所提出方法不仅在学者研究较为广泛的电池100%~80%健康状态范围有很好的估算精度, 而且在学者研究较少的电池80%~60%健康状态范围也有很好的估算精度, 有助于电池的梯次利用.算例#A-3、#A-4中锂电池的容量为1.35 A·h, 算例#B-3、#B-4中锂电池的容量为1.1 A·h, 两类锂电池的健康状态估计效果都很好, 表明本文所提出方法在80%~60%健康状态区间, 同样适用于不同种类的电池.算例#A-3、#A-4、#B-3、#B-4中, 训练集电池和测试集电池的放电倍率不是相同的, 表明对于电池的80%~60%健康状态区间, 在某一放电倍率工况下训练出来的结果同样适用于其他放电倍率工况, 这进一步增加了本文所提出方法的适用性.
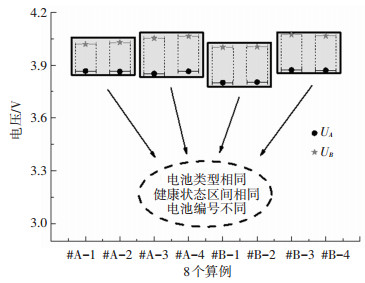
图 7列出了所有实验算例中通过遗传算法训练得到的最优电压片段.其中, #A-1/#A-2的训练集为同一电池类型、同一健康状态区间, 但是有不同编号的电池, #A-3/#A-4、#B-1/#B-2、#B-3/#B-4亦然.从表 2、图 7中可看出, #A-1/#A-2、#A-3/#A-4、#B-1/#B-2、#B-3/#B-4的最优电压片段几乎是一致的.这表明, 对于同一电池类型、同一健康状态区间的电池进行健康状态估计时, 训练集不同对选取最优电压区间的影响不大, 这样就可以随机选择某些单体电池作为训练集来估算其他单体电池, 增大了本文所提出方法对不同单体电池的适用性.所有实验算例中的最优电压片段均位于电池的可用电压区间的中后段, 为电池常用电压区间, 使本文所提出方法更具可行性及有效性.
|
图 7 8个算例中的最优电压片段 Fig. 7 Optimal voltage segments in eight numerical examples |
本文提出一种在线计算的采用数据驱动的基于等效健康因子的健康状态估计方法.通过在充电过程中选取某固定电压片段内所充电量作为电池容量估算的等效健康因子, 利用遗传算法选择最优的充电电压片段, 并基于等效健康因子估算电池容量, 继而完成电池健康状态的估计.
1) 在两类锂电池的验证算例中, 训练集与测试集电池的放电电流倍率不同, 电池健康状态估计的百分比误差均在3%之内, 大部分在2%之内, 平均绝对误差与均方根误差均低于1.55%, 大部分在1%之内, 表明本文所提出方法在不同的放电电流下对不同种类的锂电池具有广泛的适用性.
2) 该方法不仅在学者研究较为广泛的健康状态为100%~80%的电池生命区间, 而且是在学者研究较少的健康状态为80%~60%的电池生命区间, 电池健康状态估计的准确度都很高, 有助于电池的梯次利用.
3) 在所有验证算例中, 选取的最优电压片段均位于电池可用电压区间的常用段, 保证了本文所提出方法的可行性及有效性.
| [1] |
ZHU Xiaoyuan, LI Wei. Takagi-Sugeno fuzzy model based shaft torque estimation for integrated motor-transmission system[J]. ISA Transactions, 2019, 93: 14. DOI:10.1016/j.isatra.2019.03.002 |
| [2] |
王宏宇, 尹鸽平, 徐宇虹, 等. 锂离子电池硅/石墨/碳负极材料性能[J]. 哈尔滨工业大学学报, 2010, 42(12): 1916. WANG Hongyu, YIN Geping, XU Yuhong, et al. Properties of silicon/graphite/carbon anode for Li-ion battery[J]. Journal of Harbin Institute of Technology, 2010, 42(12): 1916. DOI:10.11918/j.issn.0367-6234.2010.12.015 |
| [3] |
VISWANATHAN V V, KINTNER-MEYER M. Second use of transportation batteries: Maximizing the value of batteries for transportation and grid services[J]. IEEE Transactions on Vehicular Technology, 2011, 60(7): 2963. DOI:10.1109/tvt.2011.2160378 |
| [4] |
陶志军, 贾晓峰. 中国动力电池回收利用产业商业模式研究[J]. 汽车工业研究, 2018(10): 33. TAO Zhijun, JIA Xiaofeng. Research on the business model of power battery recycling industry in China[J]. Auto Industry Research, 2018(10): 33. DOI:10.3969/j.issn.1009-847X.2018.10.006 |
| [5] |
BAEK K W, HONG E S, CHA S W. Capacity fade modeling of a Lithium-ion battery for electric vehicles[J]. International Journal of Automotive Technology, 2015, 16(2): 309. DOI:10.1007/s12239-015-0033-2 |
| [6] |
RAMESH S, KRISHNAMURTHY B. A mathematical model to study capacity fading in lithium ion batteries: Formation and dissolution reactions[J]. Journal of the Electrochemical Society, 2015, 162(4): A546. DOI:10.1149/2.0221504jes |
| [7] |
SCHMIDT A P, BITZER M, IMRE Á W, et al. Model-based distinction and quantification of capacity loss and rate capability fade in Li-ion batteries[J]. Journal of Power Sources, 2010, 195(22): 7634. DOI:10.1016/j.jpowsour.2010.06.011 |
| [8] |
林甜甜, 陈自强, 刘健. 基于等幅度充电时间的锂离子电池健康状态估计[J]. 装备环境工程, 2018, 15(12): 65. LIN Tiantian, CHEN Ziqiang, LIU Jian. Health state estimation of lithium-ion battery based on equal time interval charging[J]. Equipment Environmental Engineering, 2018, 15(12): 65. |
| [9] |
SCIPIONI R, J∅RGENSEN P S, STROE D I, et al. Complementary analyses of aging in a commercial LiFePO4/graphite 26650 cell[J]. Electrochimica Acta, 2018, 284: 454. DOI:10.1016/j.electacta.2018.07.124 |
| [10] |
COUTO L D, SCHORSCH J, JOB N, et al. State of health estimation for lithium ion batteries based on an equivalent-hydraulic model: An iron phosphate application[J]. Journal of Energy Storage, 2019, 21: 259. DOI:10.1016/j.est.2018.11.001 |
| [11] |
WENG Caihao, FENG Xuning, SUN Jing, et al. State-of-health monitoring of lithium-ion battery modules and packs via incremental capacity peak tracking[J]. Applied Energy, 2016, 180: 360. DOI:10.1016/j.apenergy.2016.07.126 |
| [12] |
MA Zeyu, YANG Ruixin, WANG Zhenpo. A novel data-model fusion state-of-health estimation approach for lithium-ion batteries[J]. Applied Energy, 2019, 237: 836. DOI:10.1016/j.apenergy.2018.12.071 |
| [13] |
WANG Zengkai, ZENG Shengkui, GUO Jianbin, et al. State of health estimation of lithium-ion batteries based on the constant voltage charging curve[J]. Energy, 2019, 167: 661. DOI:10.1016/j.energy.2018.11.008 |
| [14] |
ABRAHAM D P, KNUTH J L, DEES D W, et al. Performance degradation of high-power lithium-ion cells: Electrochemistry of harvested electrodes[J]. Journal of Power Sources, 2007, 170(2): 465. DOI:10.1016/j.jpowsour.2007.03.071 |
| [15] |
ZHANG Lingling, MA Yulin, CHENG Xinqun, et al. Degradation mechanism of over-charged LiCoO2/mesocarbon microbeads battery during shallow depth of discharge cycling[J]. Journal of Power Sources, 2016, 329: 255. DOI:10.1016/j.jpowsour.2016.08.030 |
| [16] |
VONLVDERS C, KEIL J, WEBERSBERGER M, et al. Modeling of lithium plating and lithium stripping in lithium-ion batteries[J]. Journal of Power Sources, 2019, 414: 41. DOI:10.1016/j.jpowsour.2018.12.084 |
| [17] |
LAI Xin, GAO Wenkai, ZHENG Yuejiu, et al. A comparative study of global optimization methods for parameter identification of different equivalent circuit models for Li-ion batteries[J]. Electrochimica Acta, 2019, 295: 1057. DOI:10.1016/j.electacta.2018.11.134 |
| [18] |
RECHKEMMER S K, ZANG Xiaoyun, ZHANG Weimin, et al. Empirical Li-ion aging model derived from single particle model[J]. Journal of Energy Storage, 2019, 21: 773. DOI:10.1016/j.est.2019.01.005 |
| [19] |
ZHENG Yuejiu, WANG Jingjing, QIN Chao, et al. A novel capacity estimation method based on charging curve sections for lithium-ion batteries in electric vehicles[J]. Energy, 2019, 185: 361. DOI:10.1016/j.energy.2019.07.059 |
| [20] |
ZHENG Xiujuan, FANG Huajing. An integrated unscented Kalman filter and relevance vector regression approach for lithium-ion battery remaining useful life and short-term capacity prediction[J]. Reliability Engineering & System Safety, 2015, 144: 74. DOI:10.1016/j.ress.2015.07.013 |
| [21] |
TRAN N T, KHAN A B, CHOI W. State of charge and state of health estimation of AGM VRLA batteries by employing a dual extended Kalman filter and an ARX model for online parameter estimation[J]. Energies, 2017, 10(1): 137. DOI:10.3390/en10010137 |
| [22] |
WEI Jingwen, DONG Guangzhong, CHEN Zonghai. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5634. DOI:10.1109/TIE.2017.2782224 |
| [23] |
ANDRE D, NUHIC A, SOCZKA-GUTH T, et al. Comparative study of a structured neural network and an extended Kalman filter for state of health determination of lithium-ion batteries in hybrid electric vehicles[J]. Engineering Applications of Artificial Intelligence, 2013, 26(3): 951. DOI:10.1016/j.engappai.2012.09.013 |
| [24] |
PATIL M A, TAGADE P, HARIHARAN K S, et al. A novel multistage Support Vector Machine based approach for Li ion battery remaining useful life estimation[J]. Applied Energy, 2015, 159: 285. DOI:10.1016/j.apenergy.2015.08.119 |
| [25] |
LIU Datong, ZHOU Jianbao, LIAO Haitao, et al. A health indicator extraction and optimization framework for lithium-ion battery degradation modeling and prognostics[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, 45(6): 915. DOI:10.1109/tsmc.2015.2389757 |
| [26] |
PARK M, SEO M, SONG M, et al. Capacity estimation of Li-ion battery using constant current charging voltage[C]// 2019 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS). Bangkok: IEEE, 2019: 202. DOI: 10.1109/APCCAS47518.2019.8953137
|
| [27] |
戴海峰, 姜波, 魏学哲, 等. 基于充电曲线特征的锂离子电池容量估计[J]. 机械工程学报, 2019, 55(20): 52. DAI Haifeng, JIANG Bo, WEI Xuezhe, et al. Capacity estimation of Lithium-ion batteries based on charging curve features[J]. Journal of Mechanical Engineering, 2019, 55(20): 52. DOI:10.3901/JME.2019.20.052 |
| [28] |
刘皓, 胡明昕, 朱一亨, 等. 基于遗传算法和支持向量回归的锂电池健康状态预测[J]. 南京理工大学学报, 2018, 42(3): 329. LIU Hao, HU Mingxi, ZHU Yiheng, et al. Prediction for state of health of lithium-ion batteries by genetic algorithm and support vector regression[J]. Journal of Nanjing University of Science and Technology, 2018, 42(3): 329. DOI:10.14177/j.cnki.32-1397n.2018.42.03.011 |
| [29] |
国强, 孙宇枭. 改进的双链量子遗传算法在图像去噪中的应用[J]. 哈尔滨工业大学学报, 2016, 48(5): 140. GUO Qiang, SUN Yuxiao. Improved quantum genetic algorithm with double chains in image denoising[J]. Journal of Harbin Institute of Technology, 2016, 48(5): 140. DOI:10.11918/j.issn.0367-6234.2015.05.023 |
| [30] |
刘玥, 钱霙婧, 马林, 等. 月球低能返回轨道设计的混合自适应遗传算法[J]. 哈尔滨工业大学学报, 2016, 48(4): 79. LIU Yue, QIAN Yingjing, MA Lin, et al. An adaptive genetic algorithm for low energy lunar return trajectory design[J]. Journal of Harbin Institute of Technology, 2016, 48(4): 79. DOI:10.11918/j.issn.0367-6234.2016.04.013 |
| [31] |
XING Yinjiao, MA E W M, TSUI K L, et al. An ensemble model for predicting the remaining useful performance of lithium-ion batteries[J]. Microelectronics Reliability, 2013, 53(6): 811. DOI:10.1016/j.microrel.2012.12.003 |
| [32] |
HE Wei, WILLIARD N, OSTERMAN M, et al. Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method[J]. Journal of Power Sources, 2011, 196(23): 10314. DOI:10.1016/j.jpowsour.2011.08.040 |
 2021, Vol. 53
2021, Vol. 53


