弹药传输机械臂是坦克炮弹药自动装填系统的重要组成部分,其作用是将弹药轴线协调到与待发射炮管轴线平行的位置[1].坦克在运动时由于路面不平度的激励,车体会产生基础振动,基础振动对安装在车体上的弹药传输机械臂的定位精度产生严重影响.现有的弹药传输机械臂控制器设计大多基于固定参数的PID控制,鲁棒性较差[2].因此,如何构造弹药传输机械臂的鲁棒控制器是一个亟待解决的难题.弹药传输机械臂是一种受扰动的不确定性系统.文献[2-3]根据一种特殊的Lyapunov函数构造了弹药传输机械臂的控制策略,仿真研究了有振动干扰的弹药传输机械臂位置控制,但是没有进行实验研究.
滑模控制是一类特殊的非线性控制方法,由于对匹配性模型不确定具有不变性,因而广泛应用在受扰动不确定系统中[4-5].普通线性滑模在系统状态抵达滑模面后,只能无限逼近平衡点,不能有限时间收敛;而终端滑模可使系统状态有限时间收敛,且比线性滑模具有更好的收敛性能,但是普通终端滑模存在奇异问题.为了使绳驱动机械臂在复杂不确定工况下获得满意的控制性能,文献[6]设计了新型非奇异终端滑模方法,确保系统有限时间收敛,实现了两自由度绳驱动机械臂高精度控制.为了解决高超声速飞行器在受外界扰动下的飞行控制问题,文献[7]构造了一种时变滑模方法,理论推导证明了系统所有状态有限时间收敛,仿真验证了控制的有效性.
固定时间控制是一类特殊的有限时间控制,这类控制的收敛时间和系统初始条件情况无关,能够固定时间收敛.和一般的有限时间控制相比,固定时间控制中因为同时包含大于1和小于1的分数幂项,所以无论系统初始状态是在平衡点附近还是远离平衡点处,都能改善系统状态的收敛速度,保证系统在固定时间内收敛.文献[8]构造了新型固定时间快速终端滑模面,使滑模面的收敛时间不依赖系统初始条件,和传统的终端滑模控制器相比具有更好的收敛性能.文献[9]针对航天器受外界干扰下的位置姿态耦合控制问题,基于固定时间概念构造了终端滑模自适应控制策略,能较好地控制航天器的相对位置和姿态,干扰抑制能力好.文献[10]针对机动目标的末制导拦截问题,构造了一种新型固定时间终端滑模制导律,和有限时间制导律相比,收敛时间独立于系统初始条件,可以根据制导律预先给定,优化系统收敛速率,缩短拦截时间,提高拦截精度.文献[11]针对再入飞行器飞行环境复杂多变的特征,设计了全局滑模跟踪制导律,实现了固定时间收敛的鲁棒跟踪控制.文献[12]针对受海风海浪等扰动情况下潜射导弹姿态跟踪控制问题,设计了一种新型固定时间终端滑模控制器,典型导弹发射轨迹的仿真证明了控制策略鲁棒性良好.
在控制系统设计中联合干扰观测器技术形成复合控制,是解决不确定系统控制问题的有效方法之一.通过估计包含外界干扰及不确定性的复合扰动并加以补偿,可以有效抑制系统抖振.文献[13]针对无人机中存在不确定干扰问题,采用滑模干扰观测器对干扰进行估计,实现了无人机对期望指令的有限时间跟踪.文献[14]针对目标拦截过程中存在不确定性和建模误差的问题,构造了基于固定时间收敛干扰观测器的终端滑模制导律,仿真表明所设计的制导律有良好的收敛性能和抖振抑制能力.针对受有界扰动的动力学系统,文献[15]和文献[16]设计了一种基于超螺旋算法的固定时间干扰观测器,使得收敛时间不依赖系统初始状态,计算结果证明了控制策略有效.文献[17]针对含有参数摄动、外界干扰的某飞行器弹性模型含有强不确定性问题,采用固定时间超螺旋扰动观测器估计系统的不确定性并补偿到控制中,改善了控制器的鲁棒性.
为了解决弹药传输机械臂在基础振动情况下的准确定位问题,本文以某坦克弹药传输机械臂为研究背景,针对某弹药传输机械臂原理样机,设计了一种基于固定时间干扰观测器和固定时间终端滑模控制相结合的复合控制策略.固定时间干扰观测器用于估计和补偿系统总的干扰,改善系统的抗干扰性能.固定时间终端滑模用于设计弹药传输机械臂的主控制器,避免了传统终端滑模的奇异问题,并且使得系统状态的收敛时间存在和系统初始状态无关的可估计上界.采用Lyapunov稳定理论证明了系统固定时间收敛. 3种不同振动工况下的原理样机实验表明,与传统固定参数PID控制器相比,复合控制策略鲁棒性更强,精度更高,算法先进有效.
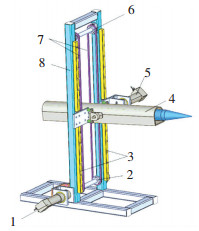
1 动力学模型图 1为弹药传输机械臂原理样机的工作原理.弹药传输机械臂主要由机架、升降部分、翻转部分组成.升降电机驱动主动链轮、传动链条、从动链轮转动,传动链条带动升降部分沿升降导轨进行升降运动.翻转部分由翻转电机驱动支臂进行回转运动.
|
1—升降电机;2—主动链轮;3—升降导轨;4—支臂;5—翻转电机;6—从动链轮;7—传动链条;8—机架 图 1 弹药传输机械臂原理样机 Fig. 1 Prototype model of ammunition transfer manipulator |
为便于分析,此处只考虑弹药传输机械臂在垂直平面内运动的动力学模型,如图 2所示.其中,XOY为笛卡尔坐标系;B1、B2、B3分别表示安装机架、升降部分与翻转部分,C2与C3分别为B2与B3的质心;假设B3的转轴过C2点,yr1为安装机架的基础振动位移;yr2为B2相对B1的位移;θ3为弹药传输机械臂支臂绕C2的翻转角位移;L3为C2和C3之间的距离.

|
图 2 弹药传输机械臂的简化动力学模型 Fig. 2 Simplified dynamics model of ammunition transfer manipulator |
设B2与B3的质量分别为m2与m3,B3相对其质心的转动惯量为J3.选择q=[yr2, θ3]T为系统的广义坐标,则由第二类Lagrange方程可得弹药传输机械臂的动力学模型为
| $ \mathit{\boldsymbol{H}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) = \mathit{\boldsymbol{U}} + \mathit{\boldsymbol{D}}. $ | (1) |
式中:H(q)为系统的惯性矩阵;
| $ \mathit{\boldsymbol{H}}(\mathit{\boldsymbol{q}}) = \left[ {\begin{array}{*{20}{c}} {{m_2} + {m_3}}&{{m_3}{L_3}\cos {\theta _3}}\\ {{m_3}{L_3}\cos {\theta _3}}&{{m_3}L_3^2 + {J_3}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}) = \left[ {\begin{array}{*{20}{c}} 0&{ - {m_3}{L_3}{{\dot \theta }_3}\sin {\theta _3}}\\ 0&0 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) = \left[ {\begin{array}{*{20}{l}} {({m_2} + {m_3})g}\\ {{m_3}g{L_3}\cos {\theta _3}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{l}} {{K_{T2}}{I_2}{i_2}{\eta _2}}\\ {{K_{T3}}{I_3}{i_3}{\eta _3}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{l}} { - ({m_2} + {m_3}){{\ddot y}_{r1}}}\\ { - {m_3}{L_3}\cos {\theta _3}{{\ddot y}_{r1}}} \end{array}} \right]. $ |
式中:KT2、KT3分别为升降电机和翻转电机的转矩系数;I2、I3分别为升降电机和翻转电机的控制电流;i2、i3分别为升降部分和翻转部分的传动比;η2、η3分别为升降部分和翻转部分的传动效率.
2 固定时间控制器设计令
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot q}}}_1} = {\mathit{\boldsymbol{q}}_2},}\\ {{{\mathit{\boldsymbol{\dot q}}}_2} = {\mathit{\boldsymbol{H}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{U}} - {\mathit{\boldsymbol{H}}^{ - 1}}(\mathit{\boldsymbol{q}})[\mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) + \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}}] + {\mathit{\boldsymbol{D}}_1}.} \end{array}} \right. $ | (2) |
式中:D1为系统总的不确定扰动项,D1=H-1(q)D=diag(D11、D12);
受文献[18]启发,固定时间干扰观测器可设计为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot {\hat q}}}}_2} = {\mathit{\boldsymbol{H}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{U}} - {\mathit{\boldsymbol{H}}^{ - 1}}(\mathit{\boldsymbol{q}})[\mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}})] + {{\mathit{\boldsymbol{\hat D}}}_1},}\\ {\mathit{\boldsymbol{\sigma }} = {\mathit{\boldsymbol{q}}_2} - {{\mathit{\boldsymbol{\hat q}}}_2},}\\ {{{\mathit{\boldsymbol{\hat D}}}_1} = {k_1} {\rm{sig}}{ ^{1/2}}(\mathit{\boldsymbol{\sigma }}) + {k_2} {\rm{sig}}{ ^p}(\mathit{\boldsymbol{\sigma }}) + {k_3}\int_0^t {{\rm{ sign }}} (\mathit{\boldsymbol{\sigma }}){\rm{d}}\tau .} \end{array}} \right. $ | (3) |
式中:
定理1 对于系统(2),若干扰观测器设计为式(3),则观测器的估计误差σ固定时间收敛到原点,收敛时间T1满足
| $ \begin{array}{l} {T_1} \le \max \left\{ {{T_{1i}} = \left( {\frac{{2{\varepsilon ^{1/2}}}}{{{k_1}}} + \frac{1}{{{k_2}(p - 1){\varepsilon ^{p - 1}}}}} \right) \times } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {1 + \frac{1}{{{w_i}\left( {\frac{1}{{{W_i}}} - \frac{{{h_1}({k_1})}}{{{k_1}}}} \right)}}} \right),(i = 1,2)} \right\}. \end{array} $ |
式中:wi=k3-Ai, Wi=k3+Ai,
证明 对σ求导,代入式(2)和式(3)可得
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot \sigma }} = {{\mathit{\boldsymbol{\dot q}}}_2} - {{\mathit{\boldsymbol{\dot {\hat q}}}}_2} = {\mathit{\boldsymbol{H}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{U}} - {\mathit{\boldsymbol{H}}^{ - 1}}(\mathit{\boldsymbol{q}})[\mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}})] + {\mathit{\boldsymbol{D}}_1} - \{ {\mathit{\boldsymbol{H}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{U}} - {\mathit{\boldsymbol{H}}^{ - 1}}(\mathit{\boldsymbol{q}})[\mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}})] + {{\mathit{\boldsymbol{\hat D}}}_1}\} = {\mathit{\boldsymbol{D}}_1} - {{\mathit{\boldsymbol{\hat D}}}_1}.} \end{array} $ |
代入式(3)可得
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot \sigma }} = - {k_1} {\rm{sig}}{ ^{\frac{1}{2}}}(\mathit{\boldsymbol{\sigma }}) - {k_2} {\rm{sig}}{ ^p}(\mathit{\boldsymbol{\sigma }}) + \psi ,}\\ {\mathit{\boldsymbol{\dot \psi }} = - {k_3} {\rm{sign}} (\mathit{\boldsymbol{\sigma }}) + {{\mathit{\boldsymbol{\dot D}}}_1}.} \end{array}} \right. $ |
由文献[18]可知,观测误差σ在固定时间T1内收敛到原点,T1满足
| $ \begin{array}{l} {T_1} \le \max \left\{ {{T_{1i}} = \left( {\frac{{2{\varepsilon ^{1/2}}}}{{{k_1}}} + \frac{1}{{{k_2}(p - 1){\varepsilon ^{p - 1}}}}} \right) \times } \right.\\ {\kern 1pt} \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {1 + \frac{1}{{{w_i}\left( {\frac{1}{{{W_i}}} - \frac{{{h_1}({k_1})}}{{{k_1}}}} \right)}}} \right),(i = 1,2)} \right\}. \end{array} $ |
即固定时间T1后,
定义e1=q1-qd,
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{e}}_1}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{e}}_1} + {\rm{sig}}{ ^{{r_2}}}({\mathit{\boldsymbol{e}}_2}). $ | (4) |
式中:φ(e1)=diag(φ(e11), φ(e12))为对称矩阵,其元素为
定义非负函数ϕ(x)为
| $ \mathit{\boldsymbol{\phi}} (x) = \left\{ {\begin{array}{*{20}{l}} {\sin ({\rm{ \mathsf{ π} }}{x^2}/(2{\tau ^2})),}&{|x| \le \tau ;}\\ {1,}&{|x| > \tau .} \end{array}} \right. $ |
式中:τ为常数,τ>0,函数ϕ(x)满足x→0, (ϕ(x))/x→0.
结合固定时间收敛双幂次趋近律[19],则固定时间终端滑模控制律可设计为
| $ \begin{array}{l} \mathit{\boldsymbol{U}} = - \mathit{\boldsymbol{H}}(\mathit{\boldsymbol{q}})\{ (1/{r_2})[\mathit{\boldsymbol{\bar \varphi }}({\mathit{\boldsymbol{e}}_1}) + \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{e}}_1})] {\rm{sig}}{ ^{2 - {r_2}}}({\mathit{\boldsymbol{e}}_2}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {(1/{r_2}) {\rm{diag}} (\mathit{\boldsymbol{\phi}} (|{\mathit{\boldsymbol{e}}_2}{|^{{r_2} - 1}})) {\rm{diag}} (|{\mathit{\boldsymbol{e}}_2}{|^{1 - {r_2}}}) \times }\\ {[{l_1} {\rm{sig}}{ ^{{a_1}}}(\mathit{\boldsymbol{s}}) + {l_2} {\rm{sig}}{ ^{{a_2}}}(\mathit{\boldsymbol{s}})] - }\\ {{\mathit{\boldsymbol{H}}^{ - 1}}(\mathit{\boldsymbol{q}})[\mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}})] + }\\ {{{\mathit{\boldsymbol{\hat D}}}_1} + \eta {\rm{sign}} (\mathit{\boldsymbol{s}}) - {{\mathit{\boldsymbol{\ddot q}}}_d}\} .} \end{array} \end{array} $ | (5) |
式中:l1、l2、a1、a2、η为常数,且l1、l2>0, a1>1, 0 < a2 < 1, η>0;φ(e1)=diag(φ(e11), φ(e12))为对称矩阵,其元素为
| $ \begin{array}{l} \bar \varphi ({e_{1i}}) = k{r_2}{(\alpha |{e_{1i}}{|^{{g_1} - 1/(k{r_2})}} + \beta |{e_{1i}}{|^{{g_2} - 1/(k{r_2})}})^{k{r_2} - 1}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{l}} {\alpha ({g_1} - 1/(k{r_2}))|{e_{1i}}{|^{{g_1} - 1/(k{r_2})}} + }\\ {\beta ({g_2} - 1/(k{r_2}))|{e_{1i}}{|^{{g_2} - 1/(k{r_2})}}} \end{array}} \right],i = 1,2. \end{array} $ |
定理2 对于式(2),若采用固定时间观测器(3)、滑模面式(4)和控制律(5),则系统误差在时间T内收敛到原点,收敛时间T满足
| $ T \le {T_1} + {T_2} + {T_3}. $ |
式中:
证明 取Lyapunov函数为V=0.5sTs,对其求导得
| $ \begin{array}{l} \mathit{\boldsymbol{\dot V}} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{s}}^{\rm{T}}}\left[ {\frac{{{\rm{d}}\mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{e}}_1})}}{{{\rm{d}}t}}{\mathit{\boldsymbol{e}}_1} + \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{e}}_1}){\mathit{\boldsymbol{e}}_2} + {r_2} {\rm{diag}} (|{\mathit{\boldsymbol{e}}_2}{|^{{r_2} - 1}}){{\mathit{\boldsymbol{\dot e}}}_2}} \right] = }\\ {{\mathit{\boldsymbol{s}}^{\rm{T}}}[\mathit{\boldsymbol{\bar \varphi }}({\mathit{\boldsymbol{e}}_1}){\mathit{\boldsymbol{e}}_2} + \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{e}}_1}){\mathit{\boldsymbol{e}}_2} + {r_2} {\rm{diag}} (|{\mathit{\boldsymbol{e}}_2}{|^{{r_2} - 1}})({{\mathit{\boldsymbol{\dot q}}}_2} - {{\mathit{\boldsymbol{\ddot q}}}_{\rm{d}}})] = }\\ {{\mathit{\boldsymbol{s}}^{\rm{T}}}\{ - {\rm{diag}} (\mathit{\boldsymbol{\phi}} (|{\mathit{\boldsymbol{e}}_2}{|^{{r_2} - 1}}))[{l_1} {\rm{sig}}{ ^{{a_1}}}(\mathit{\boldsymbol{s}}) + {l_2} {\rm{sig}}{ ^{{a_2}}}(\mathit{\boldsymbol{s}})] + }\\ {{r_2} {\rm{diag}} (|{e_2}{|^{{r_2} - 1}})[{\mathit{\boldsymbol{D}}_1} - {{\mathit{\boldsymbol{\hat D}}}_1} - \eta {\rm{sign}} (\mathit{\boldsymbol{s}})]\} .} \end{array} \end{array} $ | (6) |
经过T1时间后,由定理1知,
| $ \begin{array}{l} \mathit{\boldsymbol{\dot V}} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\{ - {\rm{diag}} (\mathit{\boldsymbol{\phi}} (|{\mathit{\boldsymbol{e}}_2}{|^{{r_2} - 1}}))[{l_1} {\rm{sig}}{ ^{{a_1}}}(\mathit{\boldsymbol{s}}) + {l_2} {\rm{sig}}{ ^{{a_2}}}(\mathit{\boldsymbol{s}})] - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{r_2} {\rm{diag}} (|{\mathit{\boldsymbol{e}}_2}{|^{{r_2} - 1}})\eta {\rm{sign}} (\mathit{\boldsymbol{s}})\} = }\\ { - \sum\limits_{i = 1}^2 \mathit{\boldsymbol{\phi}} (|{\mathit{\boldsymbol{e}}_{2i}}{|^{{r_2} - 1}})({l_1}|{s_i}{|^{{a_1} + 1}} + {l_2}|{s_i}{|^{{a_2} + 1}}) - } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{r_2}\eta \sum\limits_{i = 1}^2 | {e_{2i}}{|^{{r_2} - 1}}|{s_i}| \le - \min (\mathit{\boldsymbol{\phi}} (|{e_{2i}}{|^{{r_2} - 1}})) \cdot }\\ {\sum\limits_{i = 1}^2 {({l_1}|{s_i}{|^{{a_1} + 1}} + {l_2}|{s_i}{|^{{a_2} + 1}})} ,} \end{array} \end{array} $ |
即
| $ \mathit{\boldsymbol{\dot V}} \le - \min (\mathit{\boldsymbol{\phi}} (|{e_{2i}}{|^{{r_2} - 1}}))({2^{\frac{{{a_1} + 1}}{2}}}{l_1}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{V}}^{1 + \frac{{{a_1} - 1}}{2}}} + {2^{\frac{{1 + {a_2}}}{2}}}{l_2}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{V}}^{1 - \frac{{1 - {a_2}}}{2}}}). $ |
如果e2i≠0则ϕ(e2ir2-1)>0, (i=1, 2),系统状态空间被划分如下两个区域:
| $ {{\varOmega _1} = \{ ({e_{1i}},{e_{2i}})||{e_{2i}}{|^{{r_2} - 1}} > \tau ,i = 1,2\} ,} $ |
| $ {{\varOmega _2} = \{ ({e_{1i}},{e_{2i}})||{e_{2i}}{|^{{r_2} - 1}} \le \tau ,i = 1,2\} .} $ |
当系统状态在区域Ω1时,ϕ(e2ir2-1)=1,
| $ {T_s} = [2/({2^{\frac{{{a_1} + 1}}{2}}}{l_1}({a_1} - 1))] + [2/({2^{\frac{{1 + {a_2}}}{2}}}{l_2}(1 - {a_2}))] $ |
内到达滑模面[12].
当系统状态在区域Ω2时,代入控制律(5)到系统(2)中可得
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot e}}}_2} = - \frac{1}{{{r_2}}}[\mathit{\boldsymbol{\bar \varphi }}({\mathit{\boldsymbol{e}}_1}) + \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{e}}_1})] {\rm{sig}}{ ^{2 - {r_2}}}({\mathit{\boldsymbol{e}}_2}) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\mathit{\boldsymbol{r}}_2^{ - 1} {\rm{diag}} (\mathit{\boldsymbol{\phi}} (|{\mathit{\boldsymbol{e}}_2}{|^{{r_2} - 1}})) {\rm{diag}} (|{\mathit{\boldsymbol{e}}_2}{|^{1 - {r_2}}}) \times }\\ {[{l_1} {\rm{sig}}{ ^{{a_1}}}(\mathit{\boldsymbol{s}}) + {l_2} {\rm{sig}}{ ^{{a_2}}}(\mathit{\boldsymbol{s}})] - \eta {\rm{sign}} (\mathit{\boldsymbol{s}}) \cdot } \end{array} \end{array} $ | (7) |
当e2i→0,式(7)可化简为
当系统状态到达滑模面后,由滑模面(4)可知,
| $ {\mathit{\boldsymbol{\dot e}}_1} = - {\rm{sig}}{ ^k}(\alpha {\rm{sig}}{ ^{{g_1}}}({\mathit{\boldsymbol{e}}_1}) + \beta {\rm{sig}}{ ^{{g_2}}}({\mathit{\boldsymbol{e}}_1})). $ | (8) |
定义辅助变量χi=|e1i1-g1k|, (i=1, 2),则式(8)可以改写成
| $ {\dot \chi _i} = - (1 - {g_1}k){(\alpha + \beta \chi _i^\mu )^k}. $ | (9) |
式中μ=(g2-g1)/(1-g1k).
对式(9)进行积分,可得
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{T_3} = \mathop {\lim }\limits_{{\chi _i} \to \infty } \frac{1}{{1 - {g_1}k}}\int_0^{{\chi _i}} {\frac{1}{{{{(\alpha + \beta \chi _i^\mu )}^k}}}} {\rm{d}}{\chi _i} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {\lim }\limits_{{\chi _i} \to \infty } \frac{1}{{1 - {g_1}k}}(\int_1^{{\chi _i}} {\frac{1}{{{{(\alpha + \beta \chi _i^\mu )}^k}}}} {\rm{d}}{\chi _i} + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\kern 1pt} \int_0^1 {\frac{1}{{{{(\alpha + \beta \chi _i^\mu )}^k}}}} {\rm{d}}{\chi _i}) \le }\\ {\mathop {\lim }\limits_{{\chi _i} \to \infty } \frac{1}{{1 - {g_1}k}}\left( {\int_1^{{\chi _i}} {\frac{1}{{\beta \chi _i^{\mu k}}}} {\rm{d}}{\chi _i} + \int_0^1 {\frac{1}{{{\alpha ^k}}}} {\rm{d}}{\chi _i}} \right) = }\\ {\frac{1}{{1 - {g_1}k}}\left[ {\frac{1}{{{\beta ^k}(\mu k - 1)}} + \frac{1}{{{\alpha ^k}}}} \right] = \frac{1}{{{\alpha ^k}(1 - {g_1}k)}} + }\\ {\frac{1}{{{\beta ^k}({g_2}k - 1)}}.} \end{array} \end{array} $ |
故系统状态到达滑模面后在固定时间T3内到达原点.
综上所述,系统状态在固定时间T≤T1+T2+T3内收敛到原点.证毕.
为了说明本文所采用滑模面的优越性,选取传统非奇异终端滑模面和文献[21]的非奇异快速终端滑模面与本文的非奇异固定时间终端滑模面进行仿真对比研究.
1) 传统非奇异终端滑模面为
| $ {s_1} = x + {\sigma _1} {\rm{sig}}{ ^{{r_2}}}(\dot x). $ |
式中:σ1为大于0的常数.
2) 文献[21]的非奇异快速终端滑模面为
| $ {s_2} = x + {\sigma _2} {\rm{sig}}{ ^{{r_3}}}(x) + {\sigma _1} {\rm{sig}}{ ^{{r_2}}}(\dot x). $ |
式中:σ2、r3为大于0的常数,且r3>r2.
为了便于公平比较,仿真中选取系数α=β=1, k=2, r2=5/3, g1=3/10, g2=7/10, σ1=σ2=1, r3=7/3.则本文的非奇异固定时间终端滑模面可化为
| $ s = {(|x{|^{\frac{3}{{10}}}} + |x{|^{\frac{7}{{10}}}})^{\frac{{10}}{3}}} {\rm{sign}} (x) + {\rm{sig}}{ ^{\frac{5}{3}}}(\dot x), $ |
传统非奇异终端滑模面可化为
| $ {s_1} = x + {\rm{sig}}{ ^{\frac{5}{3}}}(\dot x), $ |
文献[21]的非奇异快速终端滑模面可化为
| $ {s_2} = x + {\rm{sig}}{ ^{\frac{7}{3}}}(x) + {\rm{sig}}{ ^{\frac{5}{3}}}(\dot x). $ |
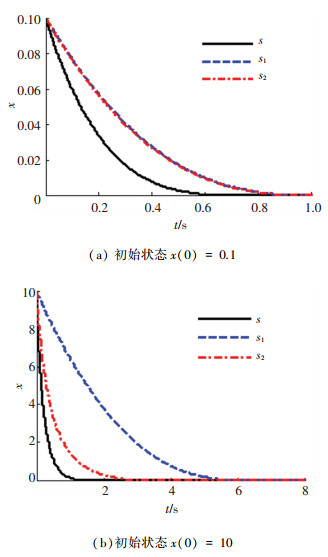
仿真选取初始状态x(0)=0.1 (状态变量距离平衡点较近)和x(0)=10 (状态变量距离平衡点较远)两种情况进行对比.仿真结果如图 3所示.
|
图 3 不同滑模面下状态变量x的收敛曲线 Fig. 3 Convergence curves of state variable x under three sliding mode surfaces |
从图 3(a)和3(b)可以看出,与滑模面s1、s2相比,本文采用的固定时间终端滑模面无论系统初始状态是在平衡点附近还是远离平衡点处,都能改善系统状态的收敛速度,具有更快的收敛速度.证明了本文固定时间终端滑模的优越性.
3 实验验证为检验提出的控制器的有效性,搭建了如图 4所示的弹药传输机械臂样机实验装置.基础振动台用来模拟路面产生的激励.

|
图 4 弹药传输机械臂实验装置 Fig. 4 Experimental setup of ammunition transfer manipulator |
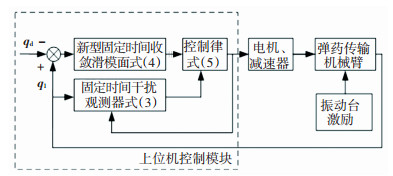
图 5为弹药传输机械臂系统控制框图.实验控制算法在上位机中采用LabVIEW编写,执行电机选用Maxon公司的EC45型无刷直流电机,控制器采用70/10型EPOS2数字位置控制器,控制器通过USB和上位机进行通讯交换数据,编码器采用HEDL9140型光电编码器,电机工作在电流模式下.
|
图 5 弹药传输机械臂系统控制框图 Fig. 5 Control block diagram of ammunition transfer manipulator system |
弹药传输机械臂样机参数如下:m2=8.6 kg, m3=3.6 kg, J3=1.6 kg·m2, L3=0.25 m,g=9.8 m/s2,KT2=KT3=45.5 mN·m/A, η2=η3=0.9, i2=113, i3=353.控制器参数设置为:k1=20, k2=15, k3=5, p=3, α=1, β=1, k=2, r2=16/15, g1=5/12, g2=1, l1=1, l2=2, a1=2, a2=1/2, η=1, τ=0.005.
为说明所设计方法的实用性和优越性,选取工程上弹药传输机械臂系统常用的固定参数PID控制方法进行对比实验.升降部分的PID控制参数取值为Kp1=4 400, Ki1=1 200, Kd1=1 800;翻转部分的PID控制参数取值为Kp2=290, Ki2=40, Kd2=40.
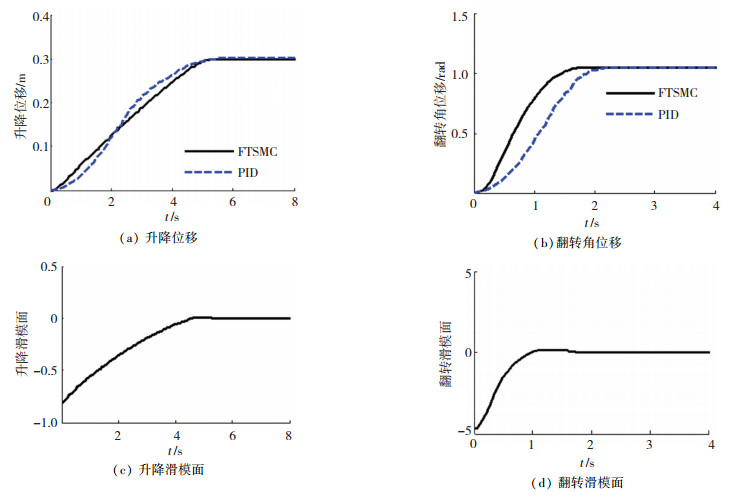
进行考虑3种不同正弦垂直振动工况下的定位实验,工况1:振动台振幅为10 mm,频率为1 Hz;工况2:振动台振幅为20 mm,频率为1 Hz;工况3:振动台振幅为50 mm,频率为0.5 Hz.升降定位目标为0.3 m,翻转定位目标为π/3·rad. 3种工况实验结果分别如图 6~8所示.
|
图 6 工况1实验结果 Fig. 6 Experimental results under working condition 1 |
|
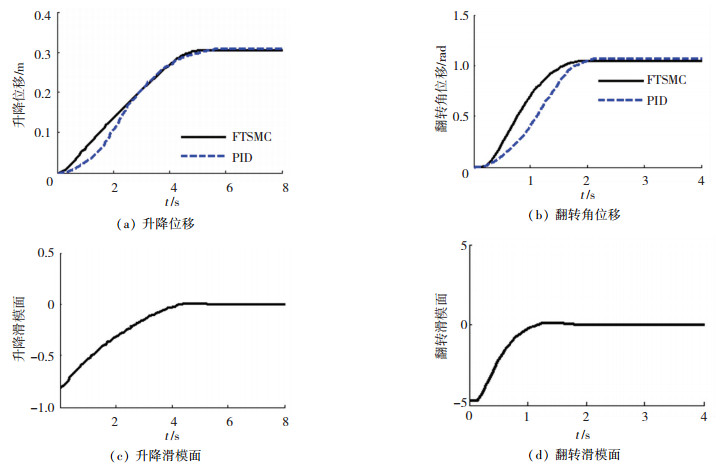
图 7 工况2实验结果 Fig. 7 Experimental results under working condition 2 |
|
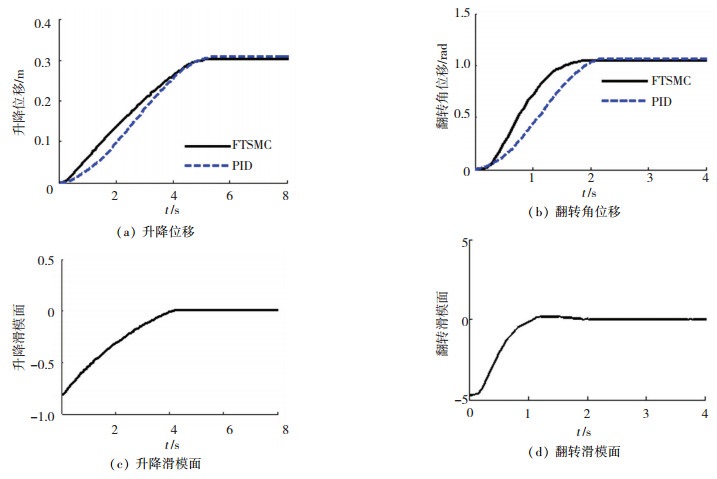
图 8 工况3下的实验结果 Fig. 8 Experimental results under working condition 3 |
由图 6(a)和6(b)可以看出,工况1振动下,FTSMC算法和PID算法都能使得弹药传输机械臂快速准确定位到位.这是因为PID算法的控制参数是在工况1下整定得到,因而PID算法也有较好的控制精度.但是,结合固定时间收敛干扰观测器的FTSMC算法的升降和翻转定位时间都要明显小于PID算法相应的定位时间,表明结合固定时间收敛干扰观测器的FTSMC算法收敛速度更快.
对比3种振动工况的实验结果可知,3种振动工况下FTSMC算法的升降和翻转定位误差都要小于PID算法相应的定位误差,并且随着基础振动的加强,FTSMC算法的升降和翻转定位误差都没有明显增加,说明设计的固定时间收敛干扰观测器能够有效地估计和补偿外界的振动激励影响,表明结合固定时间收敛干扰观测器的FTSMC算法具有很强的鲁棒性.相比之下,由图 7(a)、7(b)、8(a)和8(b)可知,PID算法在基础振动加强后,升降和翻转的定位误差都有明显增加,特别是图 7(b)和8(b)翻转部分的定位误差已趋于恶化,分别为0.016 rad和0.021 rad,远远高于FTSMC算法的0.005 rad和0.003 rad.说明当外界振动激励增强后,PID算法控制精度大大下降,抗干扰能力较差.同时,3种工况下结合固定时间收敛干扰观测器的FTSMC算法的升降和翻转定位时间都要小于PID算法相应的定位时间,再次验证了结合固定时间收敛干扰观测器的FTSMC算法收敛速度更快.升降滑模面和翻转滑模面都能在固定时间内收敛,验证了定理2的结论.
综上所述,本文提出的FTSMC算法在定位误差精度和时间上都要明显优于传统固定参数的PID控制算法,所设计的固定时间控制律能够使弹药传输机械臂在更短的时间内收敛到期望位置,振动抑制效果明显优于传统固定参数PID算法,鲁棒性强,更有利于实际工程应用。
4 结论1) 针对弹药传输机械臂在路面激励外界扰动下的位置控制问题,基于拉格朗日方程,建立了考虑垂直基础振动的弹药传输机械臂动力学方程.
2) 提出了固定时间观测器和固定时间终端滑模相结合的复合控制策略,固定时间观测器用于估计和补偿外界的总干扰项,固定时间终端滑模用于设计弹药传输机械臂的主控制器,采用Lyapunov稳定理论证明了系统固定时间收敛.
3) 实验结果验证了所设计算法的有效性和强鲁棒性.与固定参数PID控制算法相比,本文提出的算法具有更高的控制精度和干扰抑制能力,对其他具有基础振动的机械臂控制器设计有工程实际参考意义.
| [1] |
侯保林, 樵军谋, 韩宏潮. 弹丸传输机械臂结构与控制的综合设计方法[J]. 兵工学报, 2006, 27(5): 788. HOU Baolin, QIAO Junmou, HAN Hongchao. Integration design method of structure and control for a shell transfer arm[J]. Acta Armamentarii, 2006, 27(5): 788. DOI:10.3321/j.issn:1000-1093.2006.05.005 |
| [2] |
郭宇飞, 侯保林. 车体振动弹药传输机械臂的有界轨迹跟踪控制[J]. 北京理工大学学报, 2017, 37(5): 455. GUO Yufei, HOU Baolin. Bounded tracking control of ammunition transfer manipulators with chassis oscillation[J]. Transactions of Beijing Institute of Technology, 2017, 37(5): 455. DOI:10.15918/j.tbit1001-0645.2017.05.004 |
| [3] |
郭宇飞, 侯保林. 弹药协调器结构和位置控制动力学分析[J]. 兵工学报, 2013, 34(4): 392. GUO Yufei, HOU Baolin. Dynamics analysis of structure and positioning control of an ammunition coordinator[J]. Acta Armamentarii, 2013, 34(4): 392. |
| [4] |
陈霄, 刘忠, 罗亚松, 等. 海洋环境下欠驱动无人艇航迹跟踪控制算法[J]. 哈尔滨工业大学学报, 2018, 50(10): 116. CHEN Xiao, LIU Zhong, LUO Yasong, et al. Path tracking control algorithm for the underactuated USV in the marine environment[J]. Journal of Harbin Institute of Technology, 2018, 50(10): 116. DOI:10.11918/j.issn.0367-6234.201709067 |
| [5] |
姚绪梁, 王晓伟, 蒋晓刚, 等. 海流干扰下的欠驱动AUV三维路径跟踪控制[J]. 哈尔滨工业大学学报, 2019, 51(3): 43. YAO Xuliang, WANG Xiaowei, JIANG Xiaogang, et al. Control for 3D path-following of underactuated autonomous underwater vehicle under current disturbance[J]. Journal of Harbin Institute of Technology, 2019, 51(3): 43. DOI:10.11918/j.issn.0367-6234.201709002 |
| [6] |
WANG Yaoyao, JIANG Surong, CHEN Bai, et al. A new continuous fractional-order nonsingular terminal sliding mode control for cable-driven manipulators[J]. Advances in Engineering Software, 2018, 119: 21. DOI:10.1016/j.advengsoft.2018.01.011 |
| [7] |
赵阳, 蔡光斌, 张胜修, 等. 高超声速飞行器有限时间LPV滑模控制器设计[J]. 哈尔滨工业大学学报, 2019, 51(4): 113. ZHAO Yang, CAI Guangbin, ZHANG Shengxiu, et al. Design of finite-time LPV sliding mode controller for hypersonic vehicle[J]. Journal of Harbin Institute of Technology, 2019, 51(4): 113. DOI:10.11918/j.issn.0367-6234.201805110 |
| [8] |
HUANG Yi, JIA Yingmin. Fixed-time consensus tracking control for second-order multi-agent systems with bounded input uncertainties via NFFTSM[J]. IET Control Theory & Applications, 2017, 11(16): 2900. DOI:10.1049/iet-cta.2017.0304 |
| [9] |
袁利, 马广富, 董经纬, 等. 航天器近距离交会的固定时间终端滑模控制[J]. 宇航学报, 2018, 39(2): 195. YUAN Li, MA Guangfu, DONG Jingwei, et al. Fixed-time terminal sliding mode control for close-range rendezvous[J]. Journal of Astronautics, 2018, 39(2): 195. DOI:10.3873/j.issn.1000-1328.2018.02.010 |
| [10] |
赵国荣, 李晓宝, 刘帅, 等. 自适应非奇异快速终端滑模固定时间收敛制导律[J]. 北京航空航天大学学报, 2019, 45(6): 1059. ZHAO Guorong, LI Xiaobao, LIU Shuai, et al. Adaptive nonsingular fast terminal sliding mode guidance law with fixed-time convergence[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(6): 1059. DOI:10.13700/j.bh.1001-5965.2018.0621 |
| [11] |
王伯平, 王亮, 盛永智. 固定时间收敛的再入飞行器全局滑模跟踪制导律[J]. 宇航学报, 2017, 38(3): 296. WANG Boping, WANG Liang, SHENG Yongzhi. A global sliding mode based tracking guidance law with fixed-time convergence for reentry vehicle[J]. Journal of Astronautics, 2017, 38(3): 296. DOI:10.3873/j.issn.1000-1328.2017.03.010 |
| [12] |
ZHANG Liang, WEI Changzhu, JING Liang, et al. Fixed-time sliding mode attitude tracking control for a submarine-launched missile with multiple disturbances[J]. Nonlinear Dynamics, 2018, 93(4): 2543. DOI:10.1007/s11071-018-4341-8 |
| [13] |
宗群, 张睿隆, 董琦, 等. 固定翼无人机自适应滑模控制[J]. 哈尔滨工业大学学报, 2018, 50(9): 153. ZONG Qun, ZHANG Ruilong, DONG Qi, et al. Adaptive sliding mode control for fixed-wing unmanned aerial vehicle[J]. Journal of Harbin Institute ofTechnology, 2018, 50(9): 153. DOI:10.11918/j.issn.0367-6234.201705155 |
| [14] |
景亮, 张忠阳, 崔乃刚, 等. 固定时间收敛扰动观测终端滑模制导律设计[J]. 系统工程与电子技术, 2019, 41(8): 1820. JING Liang, ZHANG Zhongyang, CUI Naigang, et al. Fixed-time disturbance observer based terminal sliding mode guidance law[J]. Systems Engineering and Electronics, 2019, 41(8): 1820. DOI:10.3969/j.issn.1001-506X.2019.08.20 |
| [15] |
BASIN M, AVELLANEDA F G. Continuous fixed-time controller design for dynamic systems with unmeasurable states subject to unbounded disturbances[J]. Asian Journal of Control, 2019, 21(1): 194. DOI:10.1002/asjc.1869 |
| [16] |
BASIN M, RODRIGUEZ-RAMIREZ P, GARZA-ALONSO A. Continuous fixed-time convergent super-twisting algorithm in case of unknown state and disturbance initial conditions[J]. Asian Journal of Control, 2019, 21(1): 323. DOI:10.1002/asjc.1924 |
| [17] |
WANG Xiao, GUO Jie, TANG Shengjing, et al. Fixed-time disturbance observer based fixed-time back-stepping control for an air-breathing hypersonic vehicle[J]. ISA Transactions, 2019, 88: 233. DOI:10.1016/j.isatra.2018.12.013 |
| [18] |
SHTESSEL Y, BASIN M, PANATHULA C B. Multivariable conti-nuous fixed-time second-order sliding mode control: design and convergence time estimation[J]. IET Control Theory & Applications, 2017, 11(8): 1104. DOI:10.1049/iet-cta.2016.0572 |
| [19] |
李慧洁, 蔡远利. 基于双幂次趋近律的滑模控制方法[J]. 控制与决策, 2016, 31(3): 498. LI Huijie, CAI Yuanli. Sliding mode control with double power reaching law[J]. Control and Decision, 2016, 31(3): 498. DOI:10.13195/j.kzyjc.2014.1908 |
| [20] |
POLYAKOV A, FRIDMAN L. Stability notions and Lyapunov functions for sliding mode control systems[J]. Journal of the Franklin Institute, 2014, 351(4): 1831. DOI:10.1016/j.jfranklin.2014.01.002 |
| [21] |
YANG Ling, YANG Jianying. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems[J]. International Journal of Robust & Nonlinear Control, 2011, 21(16): 1865. DOI:10.1002/rnc.1666 |
 2021, Vol. 53
2021, Vol. 53


