燃气轮机周向拉杆转子是通过数对环状分布的拉杆,由预紧力将轮盘压紧而组合成的复杂结构.轮盘间由预紧力引起的接触效应、机组结构的非连续性是燃机转子非线性行为的主要来源.因此,为准确描述原模型特征,在建模过程中须考虑轮盘接触效应的影响.
Greenwood和Williamson提出了一种基于统计学分布的粗糙面弹性接触模型(GW模型),给出了接触变形与表面形貌的关系,建立了弹性及塑性接触的判别准则,该模型可较为准确地反映粗糙表面的接触特性[1]. Pullen和Williamson提出了塑性接触处理方法,详细推导了高度分布的关系并与实验观测的进行对比,研究了粗糙表面塑性接触的特性[2].汪光明等提出了一种将拉杆转子部件相互连接处虚拟成铰接头和抗弯弹簧的力学模型,用动态子结构法对拉杆转子的横向振动进行理论计算[3].李辉光等基于弹塑性理论对具有粗糙表面的长方微元体有限元接触分析,给出了计算粗糙面接触刚度的方法[4].程礼等将接触面虚拟为具有非线性刚度项的抗弯弹簧,动力学结果表明转子结构的不连续和接触效应是造成转子振动双稳态特征的主要因素[5].石坤等针对机械结合部提出了一种观念虚拟材料的参数化模型,根据GW模型和Hertz接触理论,推导出了虚拟材料的弹性模量和泊松比[6].
目前的接触效应处理大多只考虑弹性或塑性过程,忽略了以弹塑性变形为主的接触过程.且大多学者将轮盘接触条件处理为抗弯弹簧-铰链,在有限元模型编制时处理较为复杂.对此,本文考虑弹性-弹塑性-塑性全部变形过程,发展了一种基于虚拟材料层的燃机转子轮盘接触模型.通过控制虚拟材料层的材料参数(弹性模量、泊松比、密度、厚度)变化反映转子轮盘的力学接触特性.
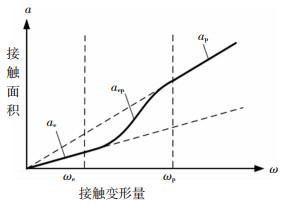
1 轮盘表面单峰接触模型在单微凸体的接触中,接触法向变形量ω的变化对接触面积、接触载荷、接触刚度影响很大.随着变形量ω的增大,接触状态由弹性接触到弹塑性接触,再到塑性接触变化.弹性接触和塑性接触可采用赫兹接触理论解释,而弹塑性接触理论涉及诸多不确定因素,很难通过现有理论解释.然而,在接触状态发生变化时,其力学性质和变形量是连续且光滑过渡的,这为弹塑性的接触理论提供了一个解决思路,接触面积随变形量变化的示意图如图 1所示.
|
图 1 接触状态过渡示意图 Fig. 1 Transition diagram of contact state |
当变形量ω小于弹性转为弹塑性变形的临界点ωe时,接触区域发生完全弹性变形,根据Hertz接触理论,接触面积、接触载荷、平均接触压力可表示为
| $ {{a_e} = {\rm{ \mathsf{ π} }}{R^\prime }\omega ,} $ | (1) |
| $ {{f_{\rm{e}}} = \frac{4}{3}{E^\prime }{R^{\prime \frac{1}{2}}}{\omega ^{\frac{3}{2}}},} $ | (2) |
| $ {{p_{\rm{e}}} = \frac{{{f_e}}}{{{a_e}}} = \frac{4}{{3{\rm{ \mathsf{ π} }}}}{E^\prime }{R^{\prime - \frac{1}{2}}}{\omega ^{\frac{1}{2}}}.} $ | (3) |
式中: R′为模型简化后微凸球的半径,E′为模型简化后的弹性模量.
1.2 单峰塑性接触阶段当变形量ω大于弹塑性转为塑性变形的临界点ωp时,接触区域发生完全塑性变形,材料力学性能将不能完全恢复到变形前状态[7].根据塑性变形接触理论,接触面积、接触载荷、平均接触压力可表示为
| $ {{a_{\rm{p}}} = 2{\rm{ \mathsf{ π} }}{R^\prime }\omega ,} $ | (4) |
| $ {{f_{\rm{p}}} = H{a_{\rm{p}}},} $ | (5) |
| $ {{p_{\rm{p}}} = \frac{{{f_{\rm{e}}}}}{{{a_{\rm{e}}}}} = H.} $ | (6) |
式中,H为两接触体中表面硬度较低值.
1.3 单峰弹塑性接触理论在弹塑性过渡临界点ωe和ωp处,接触面积和平均接触压力的过渡是连续且平滑的,不会产生突变,接触面积和平均接触压力的数值和其变化率分别等于弹性状态和塑性状态下的值.构造关于接触面积aep的三次Hermite插值多项式aep(ω):
| $ \;\;\;\;\;\;\;{{a_{{\rm{ep}}}}(\omega ) = {\rm{ \mathsf{ π} }}R\varGamma (\omega ),}\\ {\varGamma (\omega ) = {a_1}{\omega ^3} + {a_2}{\omega ^2} + {a_3}\omega + {a_4}.} $ | (7) |
代入边界条件,求解得Γ(ω)中各系数为
| $ {{a_1} = \frac{{({\omega _{\rm{e}}} + {\omega _{\rm{p}}})}}{{{{({\omega _{\rm{e}}} - {\omega _{\rm{p}}})}^3}}},} $ |
| $ {a_2} = - \frac{{2(\omega _{\rm{e}}^2 + {\omega _{\rm{e}}}{\omega _{\rm{p}}} + \omega _{\rm{p}}^2)}}{{{{({\omega _{\rm{e}}} - {\omega _{\rm{p}}})}^3}}}, $ |
| $ {{a_3} = \frac{{2\omega _{\rm{e}}^3 - 2\omega _{\rm{e}}^2{\omega _{\rm{p}}} + 7{\omega _{\rm{e}}}\omega _{\rm{p}}^2 - \omega _{\rm{p}}^3}}{{{{({\omega _{\rm{e}}} - {\omega _{\rm{p}}})}^3}}},} $ |
| $ {{a_4} = - \frac{{2\omega _{\rm{e}}^2\omega _{\rm{p}}^2}}{{({\omega _{\rm{e}}} - {\omega _{\rm{p}}})(\omega _{\rm{e}}^2 - 2{\omega _{\rm{e}}}{\omega _{\rm{p}}} + \omega _{\rm{p}}^2)}}.} $ |
假设接触圆区域的半径rep与接触变形量ω的关系为
| $ {r_{{\rm{ep}}}} = {(\delta {R^\prime }\omega )^{\frac{1}{2}}},({\omega _{\rm{e}}} \le \omega \le {\omega _{\rm{p}}}) $ | (8) |
式中,δ是弹塑性接触半径的变系数.
根据接触力学理论[8],弹塑性阶段平均接触压力pep和变形量ω的有如下关系:
| $ {p_{{\rm{ep}}}} = {m_1} + {m_2}\ln \frac{\omega }{{{r_{{\rm{ep}}}}}}, $ | (9) |
式中,m1和m2是与接触半径rep相关的常量.
将式(8)代入式(9)整理得
| $ {p_{{\rm{ep}}}} = {m_3} + {m_4}\ln \omega . $ | (10) |
根据平均接触压力的过渡平顺且光滑的条件,可得平均接触压力的边界方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{m_3} + {m_4}\ln {\omega _{\rm{e}}} = kH,}&{\omega = {\omega _{\rm{e}}};}\\ {{m_3} + {m_4}\ln {\omega _{\rm{p}}} = H;}&{\omega = {\omega _{\rm{p}}}.} \end{array}} \right. $ | (11) |
联立式(11)两方程,求解系数m3、m4并代入式(10)得
| $ {p_{{\rm{ep}}}} = H\left[ {1 - (1 - k)\frac{{\ln {\omega _{\rm{p}}} - \ln \omega }}{{\ln {\omega _{\rm{p}}} - \ln {\omega _{\rm{e}}}}}} \right]. $ | (12) |
弹塑性阶段接触载荷的表达式为
| $ \begin{array}{l} {f_{{\rm{ep}}}} = {a_{{\rm{ep}}}} \cdot {p_{{\rm{ep}}}} = \\ {\rm{ \mathsf{ π} }}R\varGamma (\omega ) \cdot H\left[ {1 - (1 - k)\frac{{\ln {\omega _{\rm{p}}} - \ln \omega }}{{\ln {\omega _{\rm{p}}} - \ln {\omega _{\rm{e}}}}}} \right]. \end{array} $ | (13) |
假设轮盘接触面的名义接触面积为An,其表面的单峰微凸体个数为N, 则在超过一定高度范围内,单峰微凸体的数量期望为nd.
| $ {N = \eta {A_n},} $ | (14) |
| $ {{n_d} = N\int_d^\infty \varPhi (z){\rm{d}}z = \eta {A_n}\int_d^\infty \varPhi (z){\rm{d}}z.} $ | (15) |
式中: η为微凸体个数分布的面积密度,Φ(z)为概率密度函数,d为微凸球平均表面与另一表面的距离.
大量实验结果表明,接触面各微凸体的高度值服从高斯正态分布.概率密度函数Φ(z)可用正态分布函数表示为
| $ \varPhi (z) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }}\exp \left( { - \frac{{{{(z - \mu )}^2}}}{{2{\sigma ^2}}}} \right). $ | (16) |
式中: μ为两轮盘接触面的平均高度,z为微凸体高度,σ为两接触面间高度分布标准差.
接触面的整体力学特性是全部单峰微凸体力学特性按照分布函数的积分,因此接触面整体力学特性可表示为弹性阶段、弹塑性阶段和塑性阶段的积分之和.
轮盘接触面的实际接触面积为
| $ \begin{array}{*{20}{l}} {{A_{{\rm{ real }}}} = {A_{\rm{e}}} + {A_{{\rm{ep}}}} + {A_{\rm{p}}} = \eta {A_n}[\int_d^{d + {\omega _{\rm{e}}}} {{a_{\rm{e}}}} \varPhi (z){\rm{d}}z + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{d + {\omega _{\rm{e}}}}^{d + {\omega _{\rm{p}}}} {{a_{{\rm{ep}}}}} \varPhi (z){\rm{d}}z + \int_{d + {\omega _{\rm{p}}}}^{ + \infty } {{a_{\rm{p}}}} \varPhi (z){\rm{d}}z].} \end{array} $ | (17) |
轮盘接触面的实际接触载荷为
| $ \begin{array}{*{20}{l}} {{F_{{\rm{ real }}}} = {F_{\rm{e}}} + {F_{{\rm{ep}}}} + {F_{\rm{p}}} = \eta {A_n}[\int_d^{d + {\omega _{\rm{e}}}} {{f_{\rm{e}}}} \varPhi (z){\rm{d}}z + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{d + {\omega _{\rm{e}}}}^{d + {\omega _{\rm{p}}}} {{f_{{\rm{ep}}}}} \varPhi (z){\rm{d}}z + \int_{d + {\omega _{\rm{p}}}}^{ + \infty } {{f_{\rm{p}}}} \varPhi (z){\rm{d}}z].} \end{array} $ | (18) |
根据法向刚度的定义,轮盘接触面的法向接触刚度为:
| $ {k_c} = \frac{{\partial f}}{{\partial \omega }}. $ | (19) |
将式(13)代入上式,整理轮盘接触面的法向接触刚度为
| $ \begin{array}{*{20}{l}} {{K_{{\rm{ real }}}} = {K_{\rm{e}}} + {K_{{\rm{ep}}}} + {K_{\rm{p}}} = \eta {A_n}[\int_d^{d + {\omega _{\rm{e}}}} {{k_{\rm{e}}}} \varPhi (z){\rm{d}}z + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{d + {\omega _{\rm{e}}}}^{d + {\omega _{\rm{p}}}} {{k_{{\rm{ep}}}}} \varPhi (z){\rm{d}}z + \int_{d + {\omega _{\rm{p}}}}^{ + \infty } {{k_{\rm{p}}}} \varPhi (z){\rm{d}}z].} \end{array} $ | (20) |
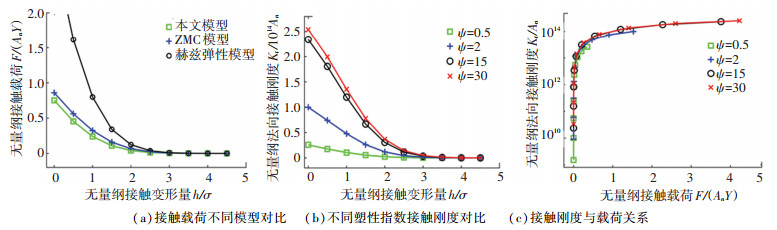
图 2(a)给出了本文模型、ZMC模型和赫兹弹性模型的接触刚度随无量纲变形量变化关系的对比,结果表明赫兹弹性模型未考虑弹塑性变形,结果具有较大误差.本文模型相较于ZMC模型而言,对弹塑性及塑性变形的发生更为敏感,能够良好地反映实际接触状态.
|
图 2 多峰接触分析 Fig. 2 Multipeak contact analysis |
单位面积接触刚度在不同塑性指数下变化规律如图 2(b)所示,接触刚度反映了接触载荷对变形量变化的敏感程度.在塑性指数较低时,轮盘接触面的法向接触刚度的变化率较小,随着塑性指数的不断增加,法向接触刚度的变化率逐渐变大.
在给定接触面的材料参数和表面形貌参数后,其接触的法向刚度与接触载荷为一一对应的关系,如图 2(c)所示,在接触变形量较小时,即接触载荷较小时,法向接触刚度值迅速增加,随着接触载荷逐渐增大,法向接触刚度的变化趋势区域平稳.对于高塑性的材料,法向接触刚度在接触载荷足够大时几乎相等,而对于低塑性材料,法向接触刚度在接触载荷足够大时值分离度较大.
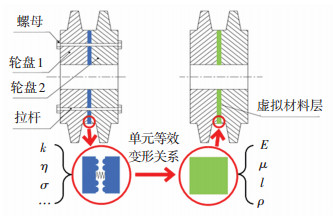
3 虚拟材料层参数计算目前对燃机转子接触效应的研究大多是将接触面的刚度转换为无厚度的铰链-弹簧模型,但此模型需要实验标定刚度参数且不足以全面反映轮盘接触面的力学特征.另外,刚度不是材料的固有参数,弹性模量、剪切模量、泊松比、密度才是材料的固有弹性参数[9].本文引入虚拟材料层建立轮盘接触面模型,通过虚拟层的材料参数(弹性模量E、泊松比μ、密度ρ、厚度l)表征接触力学特性(图 3).
|
图 3 含虚拟材料的接触界面示意图 Fig. 3 Schematic diagram of contact interface with virtual materials |
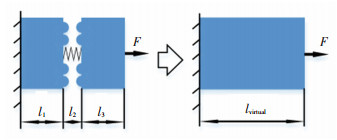
根据原接触层及等效的虚拟材料层在变形前后的法向变形量相等的关系,推导虚拟材料层弹性模量E的表达式.建立变形关系模型如图 4所示.
|
图 4 虚拟材料层等效变形量示意图 Fig. 4 Schematic diagram of equivalent deformation of virtual material layer |
在实际轮盘接触层中,对模型单元施加法向载荷,总形变Δlfact由三部分组成:左轮盘材料的变形Δl1、接触层刚度单元变形Δl2和右轮盘材料变形Δl3,其中弹性层的厚度远远小于左右轮盘单元的厚度,将其近似为无厚度的弹簧.在虚拟材料层中,由法向载荷引起的变形为Δlvirtual.各变形量为
| $ \varDelta {l_{{\rm{fact}}}} = \varDelta {l_1} + \varDelta {l_2} + \varDelta {l_3} = \frac{{F{l_1}}}{{EA}} + \frac{F}{K} + \frac{{F{l_3}}}{{EA}}, $ | (21) |
| $ \varDelta {l_{{\rm{ virtual }}}} = \frac{{F{l_{{\rm{ virtual }}}}}}{{\bar EA}}. $ | (22) |
式中: A为两轮盘名义接触面积,K为轮盘实际接触面接触刚度(K=k·A,k为接触层单位面积接触刚度).
根据等效为虚拟材料层前后的变形量不变的关系Δlfact=Δlvirtual,并假设l1=l3=l,lvirtual=l1+l3,整理可得虚拟材料层的弹性模量E为
| $ \bar E = \left( {\frac{{2lK}}{{2lK + EA}}} \right)E = \left( {\frac{{2lk}}{{2lk + E}}} \right)E. $ | (23) |
根据原接触层及等效的虚拟材料层在变形前后的法向形变量与横向形变量恒定的关系,推导虚拟材料层泊松比μ的表达式.
在实际轮盘接触中,法向应变为εfact,横向应变为εfact′,两者关系为
| $ \begin{array}{*{20}{l}} {{\varepsilon _{{\rm{ fact }}}}^\prime = \mu \cdot {\varepsilon _{{\rm{ fact }}}} = \mu \frac{{\varDelta l}}{{({l_1} + {l_3})}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mu \left( {\frac{{F{l_1}}}{{EA}} + \frac{F}{K} + \frac{{F{l_3}}}{{EA}}} \right)/({l_1} + {l_3}),} \end{array} $ | (24) |
式中,Δl为实际轮盘接触单元的变形量.
在等效的虚拟材料层中,法向应变为εvirtual,横向应变为εvirtual′,两者关系为
| $ {\varepsilon _{{\rm{virtual }}}}^\prime = \bar \mu \cdot {\varepsilon _{{\rm{virtual }}}} = \frac{{F\bar \mu }}{{\bar EA}}. $ | (25) |
根据原轮盘接触层及等效为虚拟材料层后在变形前后的法向形变量与横向形变量不变的关系εfact′=εvirtual′,并假设l1=l3=l,整理可得虚拟材料层的泊松比μ为
| $ \bar \mu = \left( {\frac{{\bar E}}{E} + \frac{{\bar EA}}{{2lk}}} \right)\mu . $ | (26) |
假定轮盘表面的微凸体高度值服从高斯正态分布,微凸体高度在[-3σ, 3σ]的范围内能够涵盖99.7%的微凸体数量分布,当虚拟材料层厚度h>6σ时,可认为已包括所有的接触微凸体[10].而在实际的固体微观表层结构中,材料表面组织状态、形貌轮廓、油脂附着等均会产生一定厚度,因此虚拟材料层的厚度要结合轮盘微观表层结构进行选择[9].
虚拟材料层将覆盖从表面污染层到轻微变形层,总厚度表达式为
| $ {l_{\max }} = \sum\limits_{i = 1}^n {\max } ({l_i}). $ | (27) |
取左右轮盘虚拟材料层的厚度相等,单侧虚拟材料层厚度应大于lmax,故整体虚拟材料层厚度应大于2lmax.
3.4 虚拟材料层密度根据接触面处两端的质量在等效为虚拟材料层前后保持不变的关系,推导得出虚拟材料层密度的表达式.假设左右轮盘单元的长度分别为l1、l2,质量分别为m1、m2,虚拟材料层的长度为l,质量为m,各段质量为:
| $ \left\{ {\begin{array}{*{20}{l}} {{m_1} = {\rho _1} \cdot V({l_1}),}\\ {{m_2} = {\rho _2} \cdot V({l_2}),}\\ {m = {\rho _{{\rm{ virtual }}}} \cdot V(l).} \end{array}} \right. $ | (28) |
根据单元质量在等效为虚拟材料层前后保持不变的关系m=m1+m2,因假设l1=l2=l、ρ1=ρ2=ρ,整理可得虚拟材料层的密度ρvirtual为
| $ {\rho _{{\rm{ virtual }}}} = \frac{{\rho \cdot V(l) + \rho \cdot V(l)}}{{V(2l)}} = \rho . $ | (29) |
本文建立了总长1 000 mm,具有5个压气机轮盘、1个涡轮盘的燃机拉杆转子模型,如图 5所示. 表 1给出了本文燃气轮机周向拉杆转子模型的各轮盘接触面积的参数.
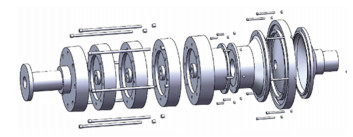
|
图 5 燃气轮机拉杆转子模型爆炸图 Fig. 5 Explosion diagram of gas turbine pull-rod rotor model |
| 表 1 接触面的尺寸参数 Tab. 1 Dimension parameters of contact surface |
| 表 2 预紧力F=50 kN时各轮盘虚拟材料层材料参数 Tab. 2 Material parameters of virtual material layer of each wheel (preload force F= 50 kN) |
根据虚拟材料层参数的计算公式,结合所建立的燃机拉杆转子模型,可计算得到各虚拟材料层的参数.其中,虚拟材料层的厚度和密度为与原转子尺寸材料相关的固定值,设虚拟材料层厚度l= 0.005 m,密度ρvirtual= 7 800 kg/m3.
根据图 6结果可以发现,随着预紧力的增大,虚拟材料层弹性模量和泊松比均呈上升趋势.虚拟层1、2、3、4由于轮盘接触面积较为接近,等效后参数值也较为接近,虚拟层6、7接触面积一致,等效后弹性模量和泊松比数值相等.
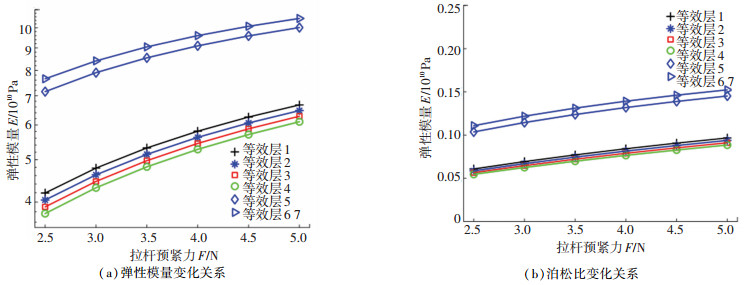
|
图 6 虚拟材料层参数与拉杆预紧力关系 Fig. 6 Relationship between parameters of virtual material layer and preload force |
表 3给出了在刚性支撑下不同预紧力下及实体转子的临界转速结果,可以发现,随着预紧力增大,转子一阶、三阶、四阶临界转速均出现上升趋势.其中四阶临界转速数值变化波动最大,在一定范围内的预紧力变化导致的临界转速最大偏差达2.31%.对于不考虑接触效应的实体转子,其整体刚度提升,各阶转速发生明显变化.结果表明由拉杆预紧力引起接触效应对临界转速变化有明显影响.
| 表 3 不同预紧力下临界转速 Tab. 3 Critical speed under different preload forces |
为进一步深入探究拉杆预紧力对轴系动态特性的影响,引入Capone轴承模型,考虑轴系在非线性油膜力作用下动态特性.采用Newmark-β数值积分法求解动力学方程,并通过分岔图直观表现动力学行为. 表 4给出了轴系的部分计算参数.
| 表 4 转子轴系部分参数 Tab. 4 Some parameters of rotor system |
选取三种预紧力大小(F= 30 kN、F= 40 kN、F= 50 kN)与实体的轴段,探究一定转速范围内预紧力导致的接触效应对轴系动态特性的影响.
如图 7所示给出了不同预紧力条件下转子的分岔图.在考虑预紧力的情况下,随着转速的增加,转子从周期1运动进入周期2运动状态,之后出现了带有周期2特征的混动运动,转速达到10 000 r/min附近重新回到周期2运动,之后出现了混沌或概周期的运动状态.分析不同预紧力大小可以发现,预紧力较小时,维持周期1运动的范围较大,且刚刚出现概周期运动时不宜转化为混沌状态.因此,可根据转子实际工作转速调节拉杆预紧力,避开混沌或概周期运动状态.在图 7(d)实体接触状态的分岔图中,转子首先进入概周期分岔运动,之后便式中处于混沌状态,随着转速增加,混动运动的无量纲复杂呈现发散的状态,此时出现了油膜振荡失稳.
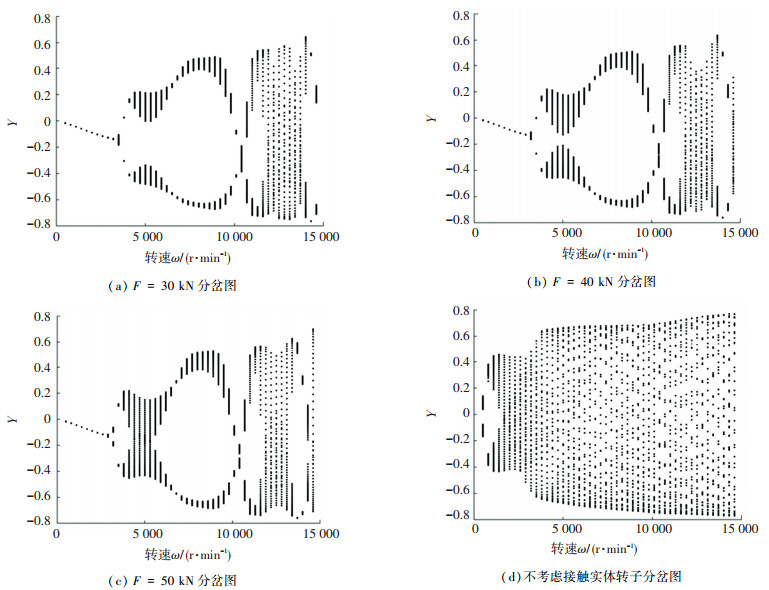
|
图 7 不同预紧力转子分岔图 Fig. 7 Bifurcation diagram of rotors under different preload forces |
1) 结合赫兹接触理论和变形光滑的边界条件,推导了弹塑性接触阶段接触面积、平均接触压力和接触载荷的表达式.分析了不同塑性指数下法向接触刚度与变形量、接触载荷的关系,发现塑性指数较大的材料,法向接触刚度对接触间距的变化更为敏感.
2) 引入虚拟材料层反映轮盘接触界面的接触效应,基于材料力学变形关系得到虚拟材料层的参数表征,分析结果表明虚拟材料层弹性模量和泊松比随预紧力的增大而增大,且对接触面积影响显著.
3) 刚性支撑下预紧力变化导致的接触效应对第四阶临界转速的影响较为明显,转速最大偏差达2.31%,而不考虑接触效应的实体转子临界转速会出现较大偏差.
4) 引入非线性油膜力,轴系动力学分岔图显示预紧力增大导致运动状态提前发生,实体转子与考虑预紧力接触的转子动态结果有较大分歧.
| [1] |
GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences (1934-1990), 1966, 295(1442). |
| [2] |
PULLEN J, WILLIAMSON J B P. On the plastic contact of rough surfaces[J]. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences (1934-1990), 1972, 327(1569). |
| [3] |
汪光明, 饶柱石, 夏松波, 等. 拉杆转子力学模型的研究[J]. 航空学报, 1993, 14(8): 419. WANG Guangming, RAO Zhushi, XIA Songbo, et al. The analysis of mechanical model of rod fastening rotor[J]. Acta Aeronautica ET Astronautica Sinica, 1993, 14(8): 419. DOI:10.3321/j.issn:1000-6893.1993.08.017 |
| [4] |
李辉光, 刘恒, 虞烈. 粗糙机械结合面的接触刚度研究[J]. 西安交通大学学报, 2011, 45(6): 69. LI HuiGuang, LIU Heng, YU Lie. Contact stiffness of rough mechanical joint surface[J]. Journal of Xi'an Jiaotong University, 2011, 45(6): 69. |
| [5] |
程礼, 钱征文, 陈卫, 等. 结构参数对拉杆转子双稳态振动特性的影响[J]. 振动测试与诊断, 2012, 32(5): 767. CHENG Li, QIAN Zhengwen, CHEN Wei, et al. The influence of structural parameters on the bistable vibration characteristics of the tie rod rotor[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(5): 767. |
| [6] |
石坤, 宋俐, 师俊平. 机械结合部等效材料参数建立与试验[J]. 农业机械学报, 2014, 45(2): 297. SHI Kun, SONG Li, SHI Junping. Establishment and test of equivalent material parameters of mechanical joint[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(2): 297. |
| [7] |
赵永武, 吕彦明, 蒋建忠. 新的粗糙表面弹塑性接触模型[J]. 机械工程学报, 2007, 43(3): 95. ZHAO Rongwu, LÜ Yanming, JIANG Jianzhong. A new elastic-plastic contact model for rough surfaces[J]. Journal of Mechanical Engineering, 2007, 43(3): 95. DOI:10.3321/j.issn:0577-6686.2007.03.016 |
| [8] |
李玲, 蔡安江, 蔡力钢, 等. 螺栓结合面微观接触模型[J]. 机械工程学报, 2016, 52(7): 205. LI Ling, CAI Anjiang, CAI Ligang, et al. Micro-contact model of bolted-joint interface[J]. Journal of Mechanical Engineering, 2016, 52(7): 205. |
| [9] |
田红亮.机械结构固定结合部虚拟材料的动力学建模[D].武汉: 华中科技大学, 2011 TIAN Hongliang. Dynamic modeling on fixed joint interface virtual material in mechanical structure[D]. Wuhan: Huazhong University of Science and Technology, 2011 |
| [10] |
肖会芳, 孙韵韵, 徐金梧, 等. 螺栓固结界面接触刚度的虚拟材料建模[J]. 中南大学学报(自然科学版), 2019, 50(9): 2100. XIAO Huifang, SUN Yunyun, XU Jinwu, et al. Virtual material based modeling for contact stiffness characteristics of bolted joint interface[J]. Journal of Central South University (Science and Technology), 2019, 50(9): 2100. |
 2021, Vol. 53
2021, Vol. 53


