2. 北京科技大学 流体与物质相互作用教育部重点实验室, 北京 100083;
3. 中国航天科工集团有限公司磁悬浮与电磁推进技术研究院, 北京 100143;
4. 天津航天机电设备研究所,天津 300301
2. The Key Laboratory of Fluid and Matter Interaction, University of Science and Technology Beijing, Beijing 100083, China;
3. China Aerospace Science and Industry Corporation Limited Institute of Magnetic Levitation and Electromagnetic Propulsion, Beijing 100143, China;
4. Tianjin Aerospace Electromechanical Equipment Research Institute, Tianjin 300301, China
高超声速飞行器服役时,由于空气压缩,产生大量内能,同时气流与热防护材料表面剧烈摩擦,产生大量摩擦热,在材料表面形成一个高温高压的极端环境,导致飞行器结构内部产生大温度梯度,进而引起飞行器结构材料失效.材料失效会降低飞行稳定性,影响飞行器服役安全,因此研究热防护材料在多物理场耦合作用下的失效问题具有重大意义.为了深入分析材料失效,本文将开始实验至D6AC钢材料破坏的时长定义为安全飞行时间[1-3].
Ognjanovic等[4]利用ANSYS Workbench建立了导弹结构的热流固耦合分析模型,研究了在2.3和3.7马赫数下气动力和气动热对结构变形的影响,并通过静态结构试验对模拟结果进行了验证,结果表明气动热对结构变形的影响远大于气动力.董维中等[5-7]建立了初步的表面温度分布与气动热耦合计算方法,以C-C为表面材料,考虑热化学非平衡和表面温度分布的因素,研究了C-C烧蚀对再入体头部区域的壁面温度和热流分布的影响,而后又采用多种气体模型算法,并讨论了它们对激波脱体距离、壁面热流、温度和密度分布等的影响.李桦等[8]运用了Baldwin-Lomax湍流模型,计算了在攻角为5°时钝锥体迎风面的压力分布和横向喷流干扰流场的数值解.刘建霞等[9]分析了高超声速滑翔飞行器表面流场特征,并对典型工况下的气动性能开展数值模拟研究,发现飞行器表面受热存在明显的分区特征,应进行不同的热处理方法.
目前的研究主要针对较低马赫数下的工况,且没有试验进行对比和佐证.本文基于高超声速气动力学和结构力学基本理论,建立高超声速热防护结构的多物理场耦合理论模型,通过数值模拟得到D6AC钢在不同飞行环境中的安全飞行时间,并对模拟结果进行风洞试验验证,形成高超声速飞行器多物理场耦合分析方法,以降低飞行试验和风洞试验实施困难及高成本的问题,同时以此方法为基础,深入探究在不同飞行速度、飞行迎角、飞行高度以及飞行器形状下的安全飞行时间.
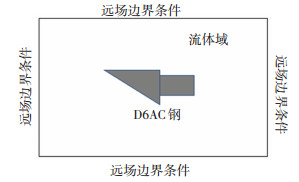
1 高超声速环境下D6AC钢多场耦合理论模型将高超声速热防护材料结构的计算域分成流体域和D6AC固体域,如图 1所示.
|
图 1 D6AC钢结构计算区域示意图 Fig. 1 Calculation region of D6AC steel structure |
在高马赫数下,空气属于粘性可压缩流体,因此流场的运动满足纳维-斯托克斯(Navier-Stokes)方程,包括质量守恒方程、动量守恒方程和能量守恒方程.质量守恒方程的一般形式为[10]
| $ \frac{{\partial \rho }}{{\partial {\rm{t}}}} + \nabla \cdot (\rho V) = 0. $ | (1) |
这里
| $ \nabla \cdot (\rho V) \approx \frac{{\partial \rho u}}{{\partial x}} + \frac{{\partial \rho v}}{{\partial y}} + \frac{{\partial \rho w}}{{\partial z}}. $ | (2) |
式中: ρ为密度,单位kg·m-3;t为时间,单位s;
动量守恒方程的一般形式如式(3)所示:
| $ \left\{ {\begin{array}{*{20}{l}} {\rho \frac{{{\rm{D}}u}}{{{\rm{D}}t}} = - \frac{{\partial P}}{{\partial x}} + \rho {f_x} + \frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{xy}}}}{{\partial y}} + \frac{{\partial {\tau _{xz}}}}{{\partial z}}, }\\ {\rho \frac{{{\rm{D}}v}}{{{\rm{D}}t}} = - \frac{{\partial P}}{{\partial y}} + \rho {f_y} + \frac{{\partial {\tau _{xy}}}}{{\partial x}} + \frac{{\partial {\tau _{yy}}}}{{\partial y}} + \frac{{\partial {\tau _{yz}}}}{{\partial z}}, }\\ {\rho \frac{{{\rm{D}}w}}{{{\rm{D}}t}} = - \frac{{\partial P}}{{\partial z}} + \rho {f_z} + \frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{zy}}}}{{\partial y}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}}.} \end{array}} \right. $ | (3) |
式中:
根据剪切应力公式可以知道剪切应力与速度随距离的变化率成正比,如式(4)所示:
| $ \tau = \mu \frac{{{\rm{d}}u}}{{{\rm{d}}y}}. $ | (4) |
式中,μ为粘性系数,单位为N·s·m-2.
粘性应力的表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\tau _{xx}} = \lambda \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right) + 2\mu \frac{{\partial u}}{{\partial x}}, }\\ {{\tau _{xy}} = {\tau _{yx}} = \mu \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right), }\\ {{\tau _{xz}} = {\tau _{zx}} = \mu \left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right), }\\ {{\tau _{yy}} = \lambda \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right) + 2\mu \frac{{\partial v}}{{\partial y}}, }\\ {{\tau _{zy}} = {\tau _{yz}} = \mu \left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}} \right), }\\ {{\tau _{zz}} = \lambda \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right) + 2\mu \frac{{\partial w}}{{\partial z}}.} \end{array}} \right. $ | (5) |
式中,λ为体积粘性系数,在斯托克斯假设下,
高马赫数下的气体是可压缩、有粘度的,因此在守恒方程中有粘性力和压力做功.能量守恒方程如式(6)所示:
| $ \rho \frac{{{\rm{D}}E}}{{{\rm{D}}t}} = \frac{{\partial {Q_x}}}{{\partial x}} + \frac{{\partial {Q_y}}}{{\partial y}} + \frac{{\partial {Q_z}}}{{\partial z}} + \rho {f_w} - \frac{{\partial {q_x}}}{{\partial x}} - \frac{{\partial {q_y}}}{{\partial y}} - \frac{{\partial {q_z}}}{{\partial z}} + \rho \hat q. $ | (6) |
式中:
Q为3个方向的面积力做的功,如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{Q_x} = - pu + u{\tau _{xx}} + v{\tau _{xy}} + w{\tau _{xz}}, }\\ {{Q_y} = - pv + u{\tau _{yx}} + v{\tau _{yy}} + w{\tau _{yz}}, }\\ {{Q_z} = - pw + u{\tau _{zx}} + v{\tau _{zy}} + w{\tau _{zz}}.} \end{array}} \right. $ | (7) |
q为3个方向的传导热功率,由傅里叶定律给出,如式(8)所示[11]:
| $ \left\{ {\begin{array}{*{20}{l}} {{q_x} = - \kappa \frac{{\partial T}}{{\partial x}}, }\\ {{q_y} = - \kappa \frac{{\partial T}}{{\partial y}}, }\\ {{q_z} = - \kappa \frac{{\partial T}}{{\partial z}}.} \end{array}} \right. $ | (8) |
式中: κ为热传导系数,单位为W/(m·K);T为温度,单位为K.
在高马赫数下,温度会逐渐升高,粘性系数和热传导系数都是关于温度的单调递增函数,温度越高,空气中分子运动越剧烈,粘性和热传导系数也随之增大.粘性系数由萨特兰(Sutherland)公式确定,如式(9)所示:
| $ \frac{\mu }{{{\mu _0}}} = \frac{{{T_0} + C}}{{T + C}}{\left( {\frac{T}{{{T_0}}}} \right)^{1.5}}. $ | (9) |
式中: T0= 288.15 K,C= 110.4 K,μ0= 1.8247×10-5kg/m·s.由此可以确定在任意温度下空气的粘性系数值.
热传导系数由普朗特数Pr和粘性系数确定,如式(10)所示[12]:
| $ {P_r} = \frac{{\mu {c_p}}}{\kappa }. $ | (10) |
式中: cp为定压比热,单位为J/(kg·K).
剧烈的气动加热使得结构表面温度急剧升高,同时热传导使得结构内部出现温度梯度,由于热膨胀及结构约束的作用,结构会产生热应力,进而发生变形.结构的响应方程可表示为式(11):
| $ [\sigma ] = [D]\;[B]\delta = [S]\mathit{\boldsymbol{\delta }}. $ | (11) |
式中: [D]为弹性矩阵,[B]为应变矩阵,[S]为应力矩阵,δ为位移矩阵.在高超声速结构受到气动力和气动加热的共同作用,结构的总应变量既包括气动力引起的弹性应变,也包括气动热引起的热应变.
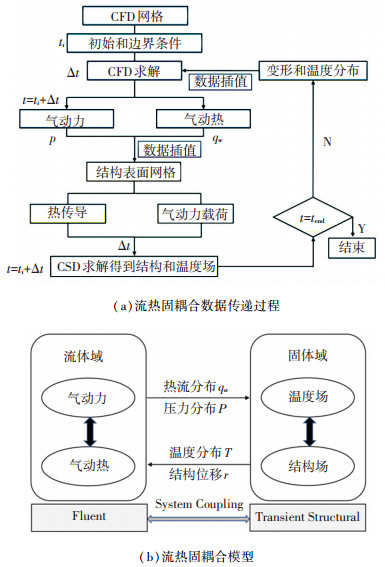
2 D6AC钢多场耦合模拟与验证D6AC钢结构工作时,气动加热过程是持续的、非稳态以及非线性的,流场、温度场和结构场之间相互耦合作用.以往的求解是将整个耦合作用过程分成三个部分来计算,但实际过程是连续的、反复循环的,使用拆分方法模拟出的结果有较大误差.所以本文采用流热固耦合解法进行高超声速结构多场耦合问题模拟,同时建立流体模型和结构模型,流体域和固体域在耦合面实时交换数据,实现流场和结构场的同步计算.耦合模拟过程如图 2(a)所示,给定初始的流体域温度、压强、来流速度及耦合面上的温度分布,固体壁面为无滑移边界条件,同时求解连续方程、动量和能量守恒方程,得到流体域的热流分布和压力分布;然后通过数据插值将流体域的热流和压力数据映射到结构域网格上,作为结构场求解的边界条件,基于有限元仿真得到结构温度分布及结构位移;再通过数据插值将结构场的温度分布和位移信息映射到流体域网格,作为边界条件进行流体域的求解,直至达到所需的耦合计算时间.流热固耦合模拟模型如图 2(b)所示,高超声速外流场求解采用基于有限体积法的Fluent求解器,结构场求解采用Ansys Workbench中的Transient Structural求解器,流固耦合面的数据交换通过System Coupling模块实现.仿真过程中,采用流体域和固体域一体化建模的方法,使得流体和固体区域在耦合面上的网格大小和节点位置均相同,避免了网格不匹配带来的数据差值传递误差,使计算结果更准确.
|
图 2 流热固耦合数值模拟方法 Fig. 2 Fluid-thermal-structural numerical simulation method |
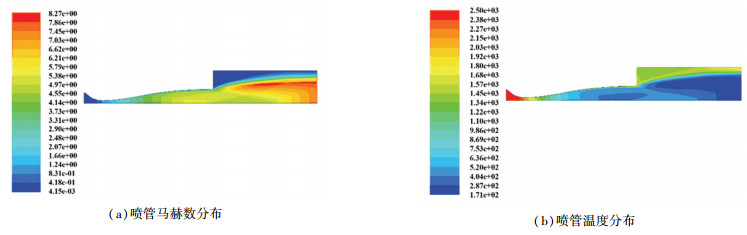
为验证本文D6AC钢耦合分析方法的适用性和准确性,针对风洞进行空载模拟和试验验证,得到出口流场参数,并将其作为D6AC钢结构多物理场耦合计算的边界条件,模拟流程如图 3所示.对风洞喷管进行结构化网格划分,网格数量为31826,质量均大于0.98.喷管入口边界条件为压力入口(Pressure-Inlet),出口边界条件为压力出口(Pressure-Outlet);壁面为绝热壁面边界条件(Wall);对称面为对称边界条件(Symmetry).通过数值模拟得到三组喷管出口参数,包括出口马赫数、出口温度和出口压强,如表 1所示.以表 1工况3为例,计算得到喷管出口处的马赫数分布和温度分布,如图 4所示.

|
图 3 D6AC钢模拟流程 Fig. 3 D6AC steel simulation process |
| 表 1 喷管流场参数 Tab. 1 Flow field parameters of nozzle |
|
图 4 工况3喷管流场参数分布 Fig. 4 Flow field parameters distribution of nozzle in condition 3 |
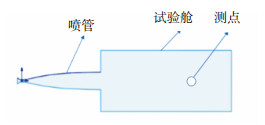
风洞喷管试验如图 5所示.由于皮托管本身对气流有阻碍作用,所以它测量的总压值是流场在产生激波后的流场总压值,而非实际总压值.根据式(12)可得到流场实际的总压值为
| $ {P_T} = {P_0} \times {1.2^6} \times {\left( {\frac{{M{a^{2.8}}}}{{1.4M{a^2} - 0.2}}} \right)^{2.5}}. $ | (12) |
|
图 5 风洞喷管示意图 Fig. 5 Nozzle schematic in wind tunnel test |
式中: PT为皮托管测量值,单位为MPa;P0为测点静压测量值,单位为Pa[13].
三种工况下喷管测点换算的静压值与模拟得到的静压值进行对比,如表 2所示.可以看出,在喷管测点静压误差分别为3.2%,3.5%,0.8%.
| 表 2 喷管模拟-试验静压对比 Tab. 2 Nozzle simulation-experiment comparison |
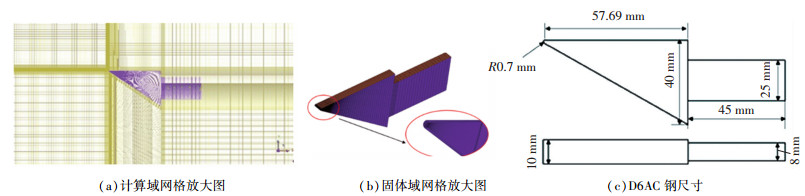
结构材料为超高强度合金结构钢D6AC,密度为7 900 kg·m-3,杨氏模量为1.2×1013 Pa,热膨胀系数为1.68×10-5 K-1,泊松比为0.3,其他材料参数如表 3所示.初始温度设置为300 K,流体为理想气体,具体参数如表 1所示,将喷管出口流场参数设置为远场压力边界条件,研究内部响应时,选择尾端作为固定面,将初始温度设置为300 K,流体为理想气体.几何尺寸如图 6所示,采用ICEM软件进行结构化网格划分,网格总数为831 246,其中D6AC钢结构网格数为94 826,流体域网格数为736 420.
| 表 3 D6AC钢主要参数 Tab. 3 D6AC steel properties |
|
图 6 D6AC钢结构计算模型 Fig. 6 Calculation model of D6AC steel structure |
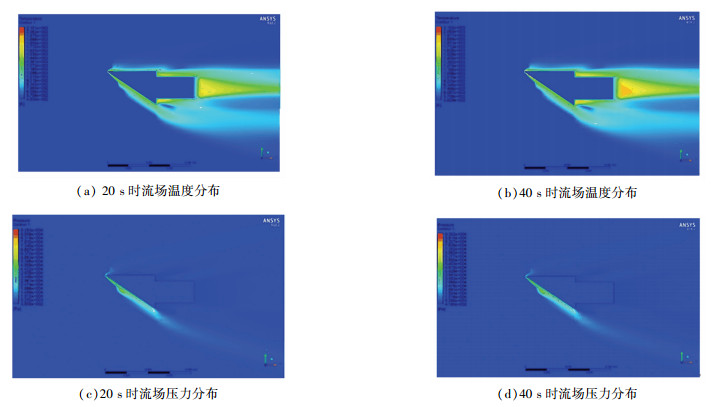
根据建立的模型进行计算,总计算时间为40 s.在不同工况下,D6AC钢外流场温度和压力分布的趋势相同,这里仅以表 1工况2为例.由于结构前缘倒角为0.7 mm,对来流的阻滞作用较弱,所以在前缘形成了附体激波,且斜激波为主要形式,正激波的范围较小,如图 7所示.激波后气流温度和压力发生急剧变化,在头部形成一个局部高温区.尾部下端不是平滑过渡,发生了激波与膨胀波的掺混和引射,并造成了附面层分离,贴近壁面的区域为低速流动,远离壁面的区域为高速流动,形成涡流.
|
图 7 外流场温度与压力分布 Fig. 7 Temperature and stress distribution of fluid domain |
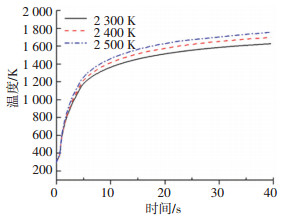
图 8为三种工况下结构前缘驻点温度随时间变化的曲线,可以看出驻点温度随时间的推移逐渐升高,这是由于在外流场气动加热作用下,气动加热产生的热量不断向结构内部传递,导致结构温度不断升高.开始时驻点温度升高地较快,之后逐渐降低,这是由于在气动加热初期,流体与结构温差较大,热流密度也较大,随着结构温度的升高,附面层内的温度梯度逐渐减小,使得壁面热流密度逐渐下降,温升速率也随之减小,最终结构的温度场将达到稳定状态.此外,来流温度越高,相应的驻点温度也越高.
|
图 8 前缘驻点温度随时间变化曲线 Fig. 8 Time history of temperature of stagnation point |
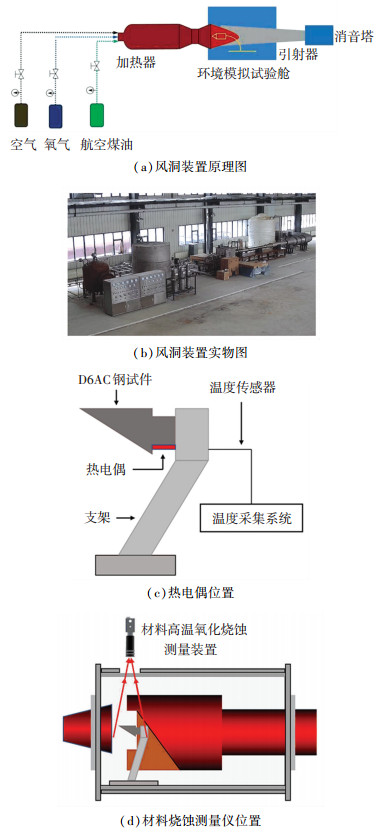
风洞试验采用北京科技大学“极端特殊环境下材料及构件实验评价科学装置”,如图 9(a)和图 9(b)所示,风洞尺寸与模拟计算相同,通过调节燃烧组分来控制试验温度,试验温度和来流速度与表 1三种工况下的入口温度和出口马赫数保持一致.试验中采用K型热电偶进行试件背风处温度测量[12],热电偶安装位置与数值模拟中的温度监测位置相同,如图 9(c)所示.结构形貌变化监测采用DY100A型高温氧化烧蚀测量仪,如图 9(d)所示,其测量原理是,基于高频率相机中形貌变化过程的图像,利用图像分析对比技术,对实测图像进行分析计算.
|
图 9 风洞试验装置示意图 Fig. 9 Schematic diagram of wind tunnel test device |
图 10为工况1下结构发生失效的形貌变化,可以看出,头部两侧最先失效,因为在两个端面产生的气动热数值最大,所以最先发生熔化,该过程与模拟结果一致.

|
图 10 风洞试验前后D6AC钢形貌对比 Fig. 10 Comparison of D6AC morphology before and after wind tunnel test |
风洞试验主要模拟10 km高空的实际环境,氧气含量极低,因此D6AC钢失效的主要形式是相变,由资料可知,D6AC钢熔点是1 625 K,根据熔点得到它的熔化时刻,如表 4所示.
| 表 4 D6AC钢相变开始时间 Tab. 4 Phase change starting time of D6AC steel |
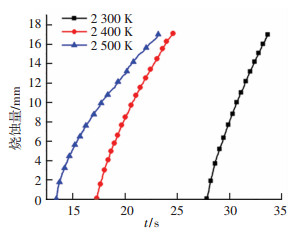
图 11为三种来流条件下结构烧蚀量随时间变化的模拟结果,可以看出,来流温度越高,开始烧蚀的时间越早.随着来流温度的升高,热流密度逐渐增大,单位时间内热量累积速率不断增大,因此试件开始熔化的时间依次提前.根据试验数据和模拟结果可知,以D6AC钢熔点为参考标准,达到熔点的时间与试验时间之间的误差分别为0.3%,0.6%,0.5%.
|
图 11 结构烧蚀量随时间的变化曲线 Fig. 11 Time history of ablation of the structure |
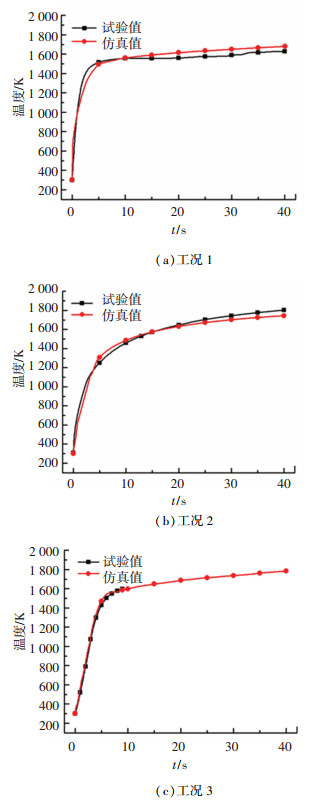
图 12为三种来流条件下风洞试验与模拟的监测点温度对比,可以看出,二者是相匹配的,模拟的最终温度(t= 40 s)也与试验结果吻合,三种工况下的模拟结果和试验结果在时间历程内的最大误差分别为3.13%、3.41%和2.14%.因此,本文采用的数值模拟方法对于高超环境下热防护材料气动热计算和疲劳破坏等相关试验具有普适性和准确性.
|
图 12 监测点温度随时间变化曲线 Fig. 12 Time history of temperature of monitoring point |
高超声速环境非常复杂,导致材料失效的因素很多,其中飞行高度、飞行速度、飞行迎角和飞行器形状的影响较为显著.运用之前证明过的耦合计算方法和D6AC钢尺寸模型,可以探究出不同高度、速度、迎角以及不同飞行器形状下气动热的数值大小.
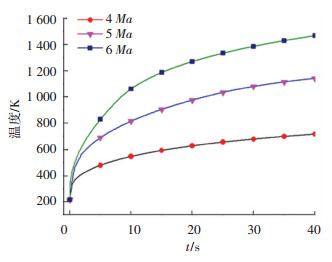
3.1 飞行速度对热防护材料的影响由于不同飞行速度会使结构头部对其前缘的空气产生不同的压缩效果,导致区域温度和热流分布情况不同,进而影响到结构内部的传热及变形情况,所以有必要分析不同速度下热防护材料的气动加热和结构响应过程.结构材料为D6AC钢,根据实际环境,以飞行高度20 km,迎角0°为初始条件,分别研究4 Ma、5 Ma、6 Ma下结构温度随时间的变化,最大温度值如表 5所示,结构前缘温度随时间变化曲线如图 13所示.可以看出,随着马赫数的增大,结构前缘驻点的温度也逐渐增大,但不同速度下,结构前缘的温度趋势是一致的,这将有利于预估更高马赫数下的气动加热.
| 表 5 不同速度条件温度最大值 Tab. 5 Maximum temperature at different speeds |
|
图 13 不同马赫数下结构前缘温度变化曲线 Fig. 13 Temperature-time curve of structure leading edge at different Mach numbers |
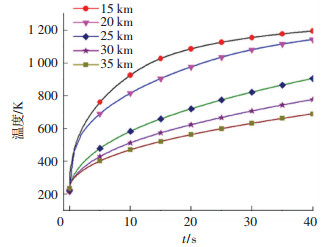
由于飞行器与目标之间的距离会产生变化,飞行高度也会进行调整.不同海拔高度下大气密度、温度等参数会有所不同,具体数据如表 6所示.以表 6参数为边界条件,飞行马赫数为5,迎角为0°,最大温度如表 7所示,温度随时间变化曲线如图 14所示.可以看出,在飞行速度,迎角一致的情况下,15~35 km海拔范围内,随着高度的增加,结构最大温度逐渐降低.主要原因是,随着高度增加,大气压强和密度逐渐减小,气流压缩和摩擦作用减小,气动加热作用减小,热量减小,致使结构温度和变形量都减小.
| 表 6 不同海拔大气属性 Tab. 6 Air properties at different altitudes |
| 表 7 不同高度条件温度最大值 Tab. 7 Maximum temperature at different altitudes |
|
图 14 不同飞行高度前缘温度变化曲线 Fig. 14 Temperature-time curve of structure leading edge at different altitudes |
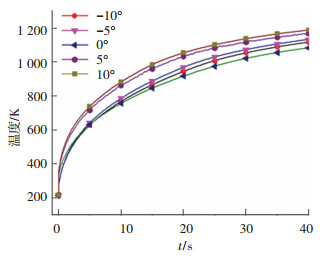
实际飞行中,飞行迎角会随着飞行姿态的改变而产生变化.迎角不同,将引起温度、压强等参数的改变,激波形状和位置也会受到影响.根据飞行特点,本文选择-10°、-5°、0°、5°、10°五种状态,分析飞行迎角对热防护结构影响,其中飞行高度20 km,飞行速度5Ma,以此得到最大温度值如表 8所示,结构前缘温度随时间的变化曲线如图 15所示.可以看出,随耦合时间的增加,结构前缘温度逐渐增加,针对本文所研究的尺寸结构,迎角为正时的结构温度要高于迎角为负时的结构温度,按照迎角由负到正的顺序,随着迎角的增大,结构的温度逐渐增加.
| 表 8 不同迎角条件温度最大值 Tab. 8 Maximum temperature at different attack angles |
|
图 15 不同飞行迎角前缘温度变化曲线 Fig. 15 Temperature-time curve of structure leading edge at different attack angles |
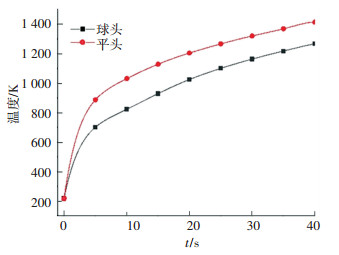
高马赫数环境飞行时存在着薄激波层和熵层,而不同飞行器形状会对激波层的形态和熵层产生影响,从而改变气动热数值大小.为对比不同结构形状对气动热的影响,本文考虑球头与平头两种形状,保持流体域尺寸和边界条件一致,分别采用长为37 mm,球头半径为7 mm的球头模型和长为37 mm的平头模型,飞行高度20 km,飞行速度5 Ma,迎角为0°,得到最大温度值如表 9所示,结构前缘温度随时间变化的曲线如图 16所示.可以看出,在相同马赫数下,结构前缘温度随耦合时间的增加而增大,且平头模型的最高温度大于球头模型.主要原因在于,球头模型激波与固体表面的距离大于平头模型,导致激波传热的耗散率高,传导至固体表面的热量少,而平头模型激波与固体表面距离小,气动热效果更剧烈.
| 表 9 不同飞行器形状下温度最大值 Tab. 9 Maximum temperature in different aircraft shapes |
|
图 16 不同飞行器形状前缘温度变化曲线 Fig. 16 Temperature-time curve of structure leading edge in different aircraft shapes |
1) 通过多物理场耦合数值模拟,分析了来流温度对D6AC钢结构气动加热和结构响应的影响,结果表明D6AC钢在服役状态下,前缘温度最高,最易发生失效;来流总温越高,服役时间越短.
2) 进行了地面风洞试验,D6AC钢相变开始时间和监测点温度变化与数值模拟相吻合,证明了本文采用的多物理场研究方法在高超声速环境下热流固耦合方法的适用性与准确性.
3) 根据多物理场研究方法对其他影响气动热的因素进行深入探究,模拟了不同飞行速度、飞行高度、飞行迎角以及飞行器形状下气动热数值的大小.研究发现,随着马赫数的升高,结构前缘温度逐渐升高;飞行海拔高度增加,空气稀薄,气动热减少;根据本文采用的D6AC模型,迎角为负时结构前缘表面的高温区逐渐变小;相同马赫数下,平头模型较球头模型的气动热效果更为显著.
| [1] |
姜贵庆, 刘连元. 高速气流传热与烧蚀热防护[M]. 北京: 国防工业出版社, 2003. JIANG G Q, LIU L Y. Heat transfer of hypersonic gas and ablation thermal protection[M]. Beijing: National Defense Industry Press, 2003. |
| [2] |
韩杰才, 洪长青, 张幸红, 等. 新型轻质热防护复合材料的研究进展[J]. 载人航天, 2015, 21(4): 315. HAN J C, HONG C Q, ZHANG X H, et al. Research progress of novel lightweight thermal protection composites[J]. Manned Spaceflight, 2015, 21(4): 315. DOI:10.3969/j.issn.1674-5825.2015.04.001 |
| [3] |
王文瑞, 王帅, 张佳明, 等. 航空发动机涡轮叶片多物理场探究及寿命分析[J]. 兵器装备工程学报, 2018, 39(12): 5. WANG W R, WANG S, ZHANG J M, et al. Multiphysics study and life analysis of aeroengine turbine blades[J]. Journal of Ordnance Equipment Engineering, 2018, 39(12): 5. DOI:10.11809/bqzbgcxb2018.12.002 |
| [4] |
OGNJANOVIĆ O V, MAKSIMOVIĆ S M, VIDANOVIĆ N D, et al. Numerical aerodynamic-thermal-structural analyses of missile fin configuration during supersonic flight conditions[J]. Thermal Science, 2017, 21(6B): 3037. |
| [5] |
董维中. 气体模型对高超声速再入钝体气动参数计算影响的研究[J]. 空气动力学学报, 2001, 19(2): 197. DONG W Z. Thermal and chemical model effect on the calculation of aerodynamic parameter for hypersonic reentry blunt body[J]. Acta Aerodynamica Sinica, 2001, 19(2): 197. DOI:10.3969/j.issn.0258-1825.2001.02.010 |
| [6] |
刘庆宗, 董维中, 丁明松, 等. 火星探测器气动热环境和气动力特性的数值模拟研究[J]. 空气动力学学报, 2018, 36(4): 642. LIU Q Z, DONG W Z, DING M S, et al. Numerical simulation of aerothermal environments and aerodynamic characterist ics for Mars entry capsules[J]. Acta Aerodynamica Sinica, 2018, 36(4): 642. DOI:10.7638/kqdlxxb-2016.0053 |
| [7] |
董维中, 高铁锁, 张巧芸. 高超声速三维碳-碳烧蚀流场的数值研究[J]. 空气动力学学报, 2001, 19(4): 388. DONG W Z, GAO T S, ZHANG Q Y. Numerical simulation of 3-D gmpllite ablation flowfields over a hypersonic reentry blunt body[J]. Acta Aerodynamica Sinica, 2001, 19(4): 388. DOI:10.3969/j.issn.0258-1825.2001.04.004 |
| [8] |
李桦, 王承尧. 有横向喷流的三维高超声速复杂流场的数值仿真[J]. 兵工学报, 2002, 23(3): 344. LI H, WANG C Y. Numerical simulation of three dimensional hypersonic complicated flowfield with a cross jet[J]. Acta Armamentarii, 2002, 23(3): 344. DOI:10.3321/j.issn:1000-1093.2002.03.014 |
| [9] |
刘建霞, 侯中喜, 陈小庆, 等. 高超声速滑翔飞行器气动性能的数值模拟研究[J]. 国防科技大学学报, 2012, 34(4): 22. LIU J X, HOU Z X, CHEN X Q, et al. Numerical simulation on the aerodynamic performance of hypersonic glide vehicle[J]. Journal of National University of Defense Technology, 2012, 34(4): 22. DOI:10.3969/j.issn.1001-2486.2012.04.005 |
| [10] |
TORO E F. Riemann solvers and numerical methods for fluid dynamics: a practical introduction[M]. Berlin: Springer Science & Business Media, 2013.
|
| [11] |
BERTIN J J. Hypersonic aerothermodynamics[M]. Washington: AIAA, 1994.
|
| [12] |
OCOKOLJIĆ G J, RAŠUO B P, BENGIN A Č. Aerodynamic shape optimization of guided missile based on wind tunnel testing and CFD simulation[J]. Thermal Science, 2017, 21(3): 1543. DOI:10.2298/TSCI150515184O |
| [13] |
傅职忠. 超音速时修正空速与马赫数的换算及加速度因子的计算[J]. 中国民航学院学报, 1996, 14(3): 10. FU Z Z. The conversion between the calibrated air speed and its corresponding mach number and the calculation of acceleration factor in supersonic flight[J]. Journal of Civil Aviation Institute of China, 1996, 14(3): 10. |
 2021, Vol. 53
2021, Vol. 53


