无刷直流电机具有优越的调速性能、无励磁损耗、低噪声等优点,应用在国民生产的各个领域,相关控制技术也快速发展.相对于带传感器的无刷直流电机,无位置传感器无刷直流电机具有结构简单、体积小、适应性强等优势[1],因而无位置控制技术得到了广泛的关注.
常用的转子位置检测算法主要有:反电动势过零检测法[2-3]、磁链估计法[4]、续流二极管电流检测[5]以及三次谐波检测法[6]等.而反电动势过零检测法作为其中最成熟、最易于实现的方法得到了广泛的应用[7].
由于反电动势检测存在低通滤波相移,需要进行相位延时补偿,因而限制了电机的运行转速与精度[8].为了提高位置检测精度,众多研究人员针对反电动势检测算法进行了改进.文献[9]在传统的反电动势检测环外增加了转子位置反馈环路,实现了闭环调节,提高了检测精度,但是需要增加采样电路.文献[10]设计了一种与电机转速无关的固定相位延时的开关电容低通滤波器,可以实现90°的固定延时,无需相位补偿,但是滤波器的设计较为复杂且需要准确的转速信息.文献[11]通过门电路进行逻辑操作获得无相位延时的过零点信号,但是需要增加较为复杂的逻辑电路.文献[12]通过避开PWM(Pulse Width Modulation)调制波形和换相续流的干扰进行转子位置检测,无需检测以及滤波电路,但是仍然存在相位延时问题.文献[13]利用软件锁相环设计了一种新的三次谐波反电动势检测方案,实现了一种高速运行时精确换相策略,缺点是需要采样电路,增加了系统的复杂性.文献[14]则提出一种改进的线反电势滑模观测器,可以获得无相位滞后位置信号, 但是依然存在需要采样电路的问题并且无法避免系统的抖动问题.
为了解决滤波延时以及相位补偿等问题,本文利用了形态学滤波对反电动势检测法进行了改进.通过对反电动势过零点的逻辑电平信号进行形态学滤波,实现固定时间的相位延时.同时利用锁相环改进了反电动势过零点30°延时算法,从而实现换相位置闭环调节.本文根据上述方法设计了无刷直流电机控制器,实验结果表明,本算法能有效且准确地检测反电动势过零点并跟踪换相位置,同时实现万分之一的调速精度.
1 反电动势检测法无刷直流电机控制系统框图如图 1所示.当电机处于BLDC模式时,通过检测反电动势过零点并延时30°即可获得准确的换相点,从而给出逆变桥开关信号对电机进行换相[15].

|
图 1 无刷直流电机控制系统 Fig. 1 Control system of brushless DC motor |
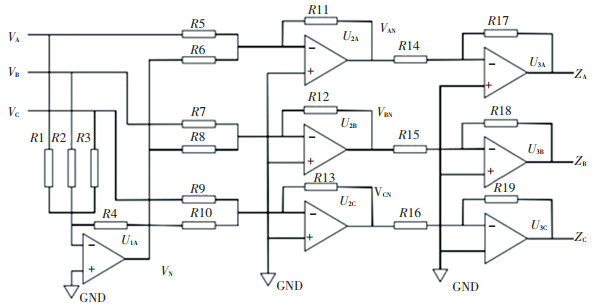
对于传统的反电动势检测算法来说,三相端电压与中性点电压的交点即是反电动势过零点,检测电路如图 2所示.
|
图 2 反电动势检测电路 Fig. 2 Detection circuit of back electromotive force |
对于梯形反电动势的无刷直流电机来说,其端电压及中性点电压波形如图 3所示.可以看到端电压中存在着由于换相续流引起的尖峰电压,直接送入比较器将会产生错误的过零点信号,如图 4中S1、S2所示.

|
图 3 三相端电压及虚拟中性点电压波形 Fig. 3 Three-phase terminal voltage and virtual neutral voltage waveforms |

|
图 4 三相过零点信号 Fig. 4 Zero-crossing of three-phase BEMF |
对于采用PWM调速的情况来说,反电动势中还将存在PWM调制信号.为了消除续流尖峰电压以及PWM调制信号的影响,反电动势检测一般需要低通滤波电路,从而造成相位延时.为了获得准确的换相位置,需要进行延时补偿,补偿公式如式(1)所示.
| $ \theta = \left\{ {\begin{array}{*{20}{c}} {30^\circ , }&{ - \varphi \left( \omega \right)\varphi \left( \omega \right) < {\rm{ \mathsf{ π} }}/6;}\\ {90^\circ , }&{ - \varphi \left( \omega \right)\varphi \left( \omega \right) > {\rm{ \mathsf{ π} }}/6.} \end{array}} \right. $ | (1) |
其中θ为延时角度,φ(ω)为滤波器相频特性.
对于传统的反电动势检测法来说,一般根据式(1)建立延时补偿表,根据转速信息查表获得延时补偿角度或采用线性拟合的方式进行补偿,不论采用哪一种方式,都无法避免计算误差并且补偿属于开环补偿, 容易受到干扰.
2 固定延时的形态学滤波算法针对上述问题,本文将数学形态学中的形态学滤波思想应用在二维信号的数据处理当中.数学形态学是一种非线性的信号处理算法,常用于图像处理,具有完整的理论方法和算法体系.
形态学滤波有两个基本运算,腐蚀和膨胀.腐蚀可以使目标区域变小,造成目标边界收缩,可以用来消除小且无意义的目标,其数学定义如式(2)所示.膨胀会使目标区域变大,造成目标边界扩大,可以减小目标区域内的谷域以及消除包含在目标区域中的噪声,定义如式(3)所示.可以将腐蚀运算看作是最小值滤波器,膨胀运算看作是最大值滤波器,它们可以分别获得数据的下包络和上包络.
| $ {A \ominus B = \left\{ {x, y|{{\left( B \right)}_{xy}} \subseteq A} \right\}, } $ | (2) |
| $ {A \oplus B = \left\{ {x, y|{{\left( B \right)}_{xy}} \cap A \ne \phi } \right\}.} $ | (3) |
由腐蚀和膨胀,我们可以获得闭运算即先膨胀再腐蚀.通过对反电动势方波信号进行闭运算可以初步滤除其中的调制信号.本文重新定义了方波信号中的腐蚀膨胀运算分别为f1、f2:
| $ \begin{array}{l} {f_1}\left( s \right) = s\& s\_{\rm{delay}}, \\ {f_2}\left( s \right) = s||s\_{\rm{delay}}. \end{array} $ | (4) |
则可得闭运算F为
| $ F = {f_1}\left( {{f_2}\left( s \right)} \right). $ | (5) |
其中:s为输入信号,s_delay为s延时t1的信号.
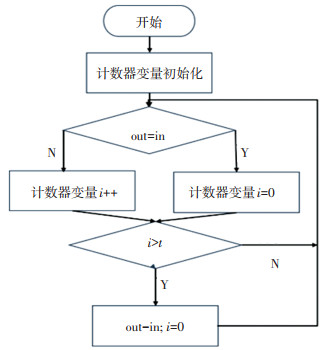
对于形态学滤波往往需要进行多次运算才能获得较好的效果,为此本文设计了一种形态学滤波后处理算法,可以保证在仅进行一次形态学滤波的情况下仍具有良好的滤波效果.算法程序框图如图 5所示,其本质是一个延时程序,宽度小于延时时间的脉冲将被消除,谷域将被填平.若设后处理算法的延时时间为t2, 则数字滤波算法的总延时时间为t=t1+t2.
|
图 5 形态学滤波后处理算法框图 Fig. 5 Morphological filtering post-processing algorithm |
由于后处理算法在信号边沿处效果较差,因而t1的选择需要保证形态学滤波后的信号在上升沿及下降沿处无过多的噪声信号;为了保证续流尖峰导致的脉冲被去除,t2的选择需要根据换相续流脉冲的宽度来确定,一般大于换相续流脉冲宽度的最大值即可.
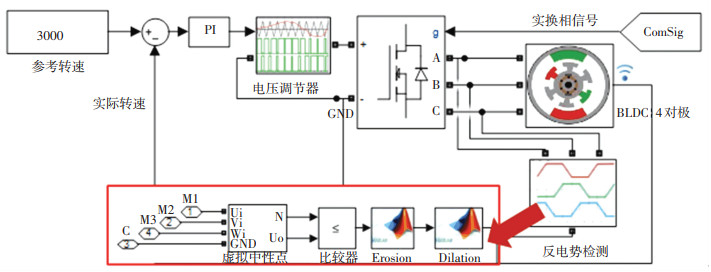
为了验证算法的可行性,在Simulink中建立算法的仿真模型,如图 6所示. Simulink模型通过检测BLDC的三相端电压然后构造出中性点,经过比较器形成反电动势过零点方波信号,Simulink将产生的反电动势过零点方波信号送入MATLAB函数写成的滤波算法模块.
|
图 6 Simulink仿真模型 Fig. 6 Simulation model in Simulink |
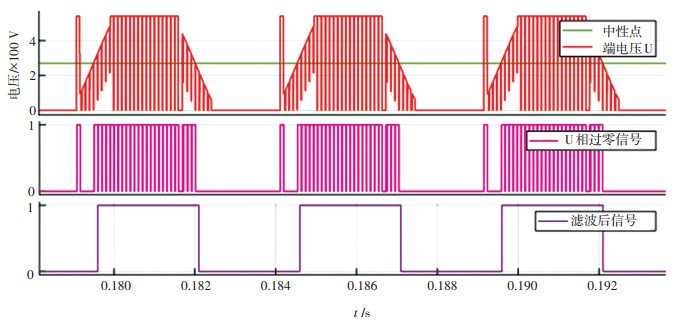
仿真结果如图 7所示, 可以看到采集到的端电压信号当中存在着换相续流引起的尖峰电压以及PWM的调制信号.端电压信号与虚拟中性点信号经过比较器之后形成的反电动势方波信号当中依然存在这些干扰信息.通过数字滤波处理之后,可以清楚地看到,这些干扰信号都被较好地滤除,滤波之后的信号可以非常良好地检测出反电动势过零点信号.值得一提的是,滤波之后的反电动势方波信号较原始信号是存在一个固定的时域延时的,由于仿真中的换相续流较小,所设定的延时时间较短,因而滤波信号较原始信号的延时不太明显.
|
图 7 滤波算法仿真结果 Fig. 7 Simulation results of filtering algorithm |
锁相环是一种相位跟踪系统,可以在噪声之中提取出几乎完全纯净的信号, 因而可以通过锁相环回路实现反电动势过零点的30°延时功能.锁相环主要由鉴相器、环路滤波器、压控振荡器组成.
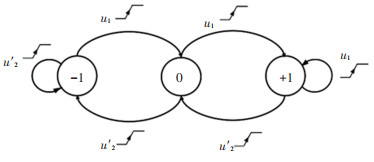
本文采用的鉴相器是鉴频鉴相器(PFD),它具有鉴频与鉴相的双重功能,因而输入带宽非常大,性能较好.如图 8所示,用状态转移图描述了PFD的基本原理.鉴频鉴相器的输出状态转移由u1和u2'的上升沿触发. u1的上升沿会使state跳向更高的状态,当已经处于最高的状态+1时,只会对u2'的上升沿进行响应.反之亦然.
|
图 8 鉴频鉴相器PFD原理图 Fig. 8 Schematic diagram of PFD |
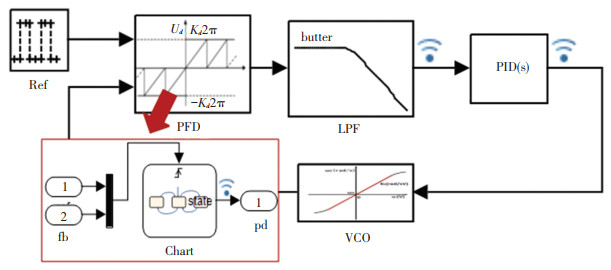
为了验证锁相环算法的功能,本文在simulink中搭建了锁相环的模型,使用stateflow设计了PFD鉴频鉴相器,如图 9所示PFD模块.使用FilterDesigner工具设计了滤波器,同时为环路加上PI控制器以使环路达到二阶锁相环性能.
|
图 9 Simulink锁相环模型 Fig. 9 Simulink phase-locked loop model |
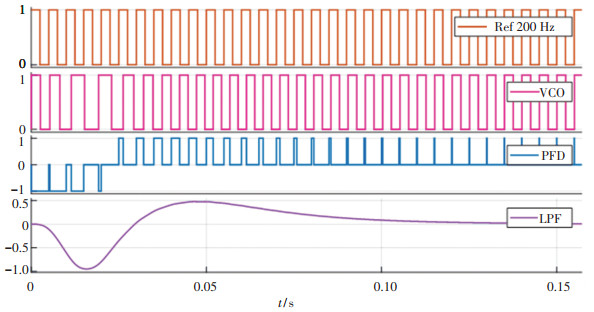
在输入信号为200 Hz的方波、VCO静态输出与输入无频差的情况下进行仿真,仿真结果如图 10所示.第一第二行分别为输入信号Ref和输出信号VCO,第三第四行分别为鉴频鉴相器输出信号PFD与环路滤波器输出LPF.可以看到,鉴频鉴相器以及环路滤波器都能正确地输出信号,锁相环系统能够快速锁相且无稳态误差.
|
图 10 锁相环模型仿真结果 Fig. 10 Simulation results of phase-locked loop model |
由于反电动势过零点延时30°才是准确的换相位置.现有的延时算法大多都是开环计算.本文改进了延时的算法,使用锁相环算法来跟踪换相位置,实现闭环调节.由于数字滤波器具有固定时域的延时,在一般情况下进行30°延时即可,在超高速情况下,若固定延时超过了30°可进行90°延时,为了说明算法的有效性,仿真实验进行90°延时.
为了验证锁相环延时算法的性能,搭建了仿真模型如图 11所示.其中PFD、LPF以及VCO是锁相环的基本组成,通过Delay模块对信号进行延时,设置鉴相器在相差为90°时输出为零,则VCO信号会锁定在与反电动势零点滞后90°电角度的位置.

|
图 11 30°延时锁相环模型 Fig. 11 Phase-locked loop model of 30° delay |
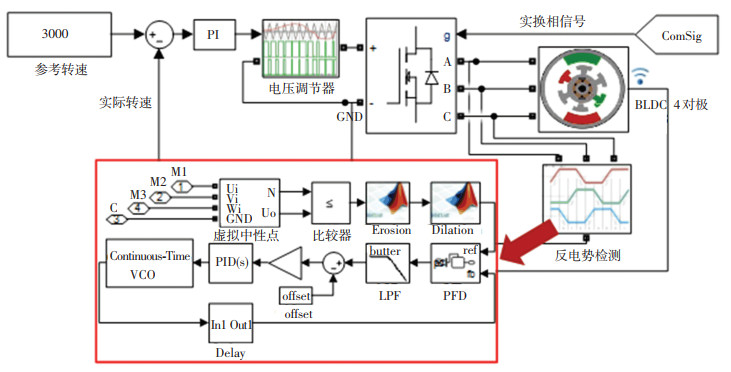
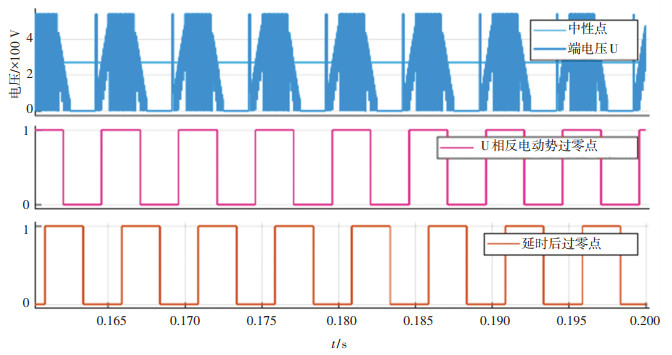
将延时模块与第2节中建立的电机控制模型一起进行仿真,仿真模型如图 12所示,滤波后的反电动势过零信号作为锁相环延时模块的参考输入,VCO输出延时信号.在3000转的目标转速下,仿真实验结果如图 13所示.第一、第二行为固定延时数字滤波算法的处理结果,第三行是进行了反电势过零点90°延时的结果.可以看到延时模块准确地跟踪了换相位置信号,具有较好的性能.
|
图 12 Simulink 30°延时仿真模型 Fig. 12 Simulink 30° delay simulation model |
|
图 13 延时模型仿真结果 Fig. 13 Simulation results of delay model |
为了验证算法的准确性,本文以CPLD MAX II为实验平台,搭载算法进行验证.实验装置如图 14所示,其中,图 14(a)为自行研制的无刷直流电机驱动器,图 14(b)为4对极无刷直流陀螺电机.使用(Yokogawa)DLM2054示波器对电机及驱动器运行状态进行监测和分析.

|
图 14 实验装置 Fig. 14 Experimental devices |
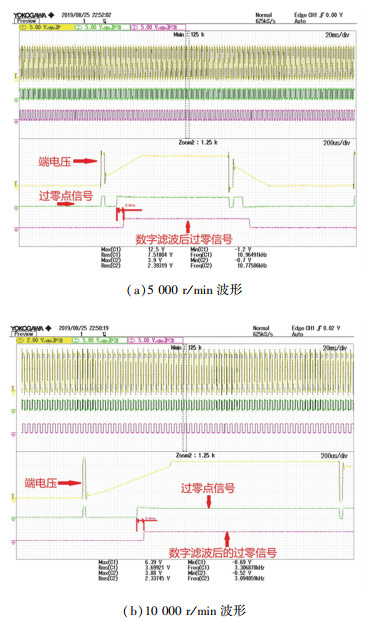
1) 固定延时滤波算法实验:为了验证本文设计的滤波算法的有效性,使电机分别运行在5 000 r/min和10 000 r/min进行实验.为了延时时间的测量方便,在满占空比条件下进行测量.实验结果如图 15所示,通道1为端电压信号,通道2为端电压与中性点比较所得的过零点方波信号.通道3为对通道2的方波信号进行数字滤波所得.可以看到端电压中存在由换相导致的续流尖峰并且直接造成了与中性点比较获得的过零信号中含有错误的过零信息.而滤波后的信号则完全消除了假过零点,说明该算法可以非常良好地去除虚假过零点,并且延时时间不随转速变化.在5 000 r/min和10 000 r/min的滤波延时都是0.4 ms.
|
图 15 端电压及反电动势过零信号波形 Fig. 15 Terminal voltage and zero-crossing signal waveforms |
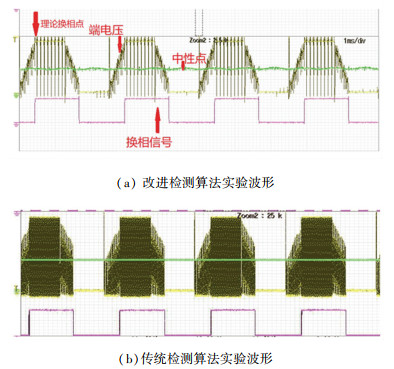
2) 反电势换相实验:为了获得换相位置,需要对过零信号进行延时. 图 16(a)为改进的检测算法的波形图.可以看到换相信号被准确地延时到理论换相位置,采集到的端电压波形也十分接近梯形,说明换相准确. 图 16(b)则为传统的反电动势检测算法波形,端电压出现畸变,梯形反电动势出现不对称.对比实验结果可以看到,改进算法可以有效地提高位置检测的精度.
|
图 16 反电动势换相波形 Fig. 16 Commutation waveform of BEMF |
3) 调速实验:由于锁相环的相位跟踪特性,可以将其运用在电机调速中.在本文的设计中,将电机反电动势与中性点比较得到的方波信号作为VCO输出,这样就构造出了锁相环回路.当给定参考信号,反电动势方波信号将被锁相到参考信号.这样即可实现锁相环调速.实验结果如图 17所示.

|
图 17 动态转速 Fig. 17 Dynamic speed |
其中显示的波形为光电传感器采集的电机实时转速,每转一圈一个数据点.平均转速指每30圈计算一次的转速为7 200.28 r/min,最大转速为25 s内电机最大的实时转速为7 201.25 r/min,最小转速为25 s内最低的实时转速为7 198.86 r/min.
则转速波动率:
| $ \delta = \frac{{{n_{{\rm{max}}}} - {n_{{\rm{min}}}}}}{{2*{n_{{\rm{ave}}}}}} = \frac{{7201.65 - 7198.86}}{{2 \times 7200.28}} = 1.94 \times {10^{ - 4}}. $ | (6) |
其中:nmax为转速最大值, nmin为转速最小值, nave为转速平均值.可以看到转速精度可以达到万分之一的数量级.
6 结论本文着重对反电动势检测算法进行了分析,建立了反电动势检测的数学模型并分析了反电势检测中存在的滤波延时问题.
1) 为了解决滤波延时问题,利用形态学滤波思想实现了固定时域延时的数字滤波算法并建立的Simulink仿真模型,通过仿真验证了算法的正确性.
2) 运用锁相环锁相的相位跟踪能力改进了反电动势过零点延时30°的算法.通过仿真验证了算法的性能并通过换相及调速实验验证了算法的实用性.
3) 设计开发了无刷直流电机控制器,采用上述算法,实现了转速波动在万分之一数量级的控制精度.
| [1] |
SHI Tingna, GUO Yuntao, SONG Peng, et al. A new approach of minimizing commutation torque ripple for brushless DC motor based on DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2010, 57(10): 3483. DOI:10.1109/TIE.2009.2038335 |
| [2] |
DAMODHARAN P, VASUDEVAN K. Sensorless brushless DC motor drive based on the zero-crossing detection of back electromotive force (EMF) from the line voltage difference[J]. IEEE Transactions on Energy Conversion, 2010, 25(3): 661. DOI:10.1109/TEC.2010.2041781 |
| [3] |
BI Chao, HLA N P, JIANG Quqan, et al. Back-EMF ZCP error induced by electromagnetic structure of spindle motor[J]. IEEE Transactions on Magnetics, 2011, 47(7): 1899. DOI:10.1109/TMAG.2011.2157895 |
| [4] |
NESIMI E. A new algorithm for sensorless operation of permanent magnet motors[J]. IEEE Trans. IA, 1994, 30(1): 414. |
| [5] |
OGASAWARA S, AKAGI H. An approach to position sensorless drive for brushless DC motors[J]. IEEE Transactions on Industry Applications, 1991, 27(5): 928. DOI:10.1109/28.90349 |
| [6] |
韦鲲, 任军军, 张仲超. 三次谐波检测无刷直流电机转子位置的研究[J]. 中国电机工程学报, 2004, 24(5): 167. WEI Kun, REN Junjun, ZHANG Zhongchao. Research on the scheme of sensing rotor position of BLDCM based on the third harmonic component[J]. Proceedings of the CSEE, 2004, 24(5): 163. |
| [7] |
朱俊杰, 粟梅, 陈程, 等. 无刷直流电机反电势过零检测新方法[J]. 仪器仪表学报, 2013, 34(2): 441. ZHU Junjie, SU Mei, CHEN Cheng, et al. Novel BEMF zero-crossing detecting method for brushless DC motor[J]. Chinese Journal of Scientific Instrument, 2013, 34(2): 441. |
| [8] |
李自成, 程善美. 无位置传感器无刷直流电机位置信号相位补偿[J]. 电力电子技术, 2010, 44(9): 55. LI Zicheng, CHENG Shanmei. Rotor position phase compensation for sensorless brushless DC Motors[J]. Power Electronics, 2010, 44(9): 55. |
| [9] |
吴小婧, 周波, 宋飞. 基于端电压对称的无位置传感器无刷直流电机位置信号相位校正[J]. 电工技术学报, 2009, 24(4): 54. WU Xiaoqian, ZHOU Bo, SONG Fei. A new control method to correct position phase for sensorless brushless DC motor[J]. Transartions of China Electrotechnical Socity, 2009, 24(4): 54. |
| [10] |
邹继斌, 江善林, 张洪亮. 一种新型的无位置传感器无刷直流电机转子位置检测方法[J]. 电工技术学报, 2009, 24(4): 48. ZHOU Jibin, JIANG Shanlin, ZHANG Hongliang. A novel method of detecting for rotor position of a sensorless brushless DC motor[J]. Transactions of China Electrotechnical Society, 2009, 24(4): 48. |
| [11] |
JIANG Quan, BI Chao, HUANG Ruoyu. A new phase-delay-free method to detect back EMF zero-crossing points for sensorless control of spindle motors[J]. IEEE Transactions on Magnetics, 2005, 41(7): 2287. DOI:10.1109/TMAG.2005.851841 |
| [12] |
王大方, 于知杉, 金毅, 等. 无位置传感器无刷直流电机无硬件滤波转子位置检测方法[J]. 电工技术学报, 2017, 32(19): 71. WANG Dafang, YU Zhishan, JIN Yi, et al. Research of rotor position detection for sensorless BLDCM without hardware filter circuit[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 71. |
| [13] |
FARQ M, ISHAK D. A new scheme sensorless control of BLDC motor using software PLL and third harmonic back-EMF[C]//IEEE Symposium on Industrial Electronics & Applications. Kuala Lumpur: IEEE, 2009.
|
| [14] |
史婷娜, 肖竹欣, 肖有文, 等. 基于改进型滑模观测器的无刷直流电机无位置传感器控制[J]. 中国电机工程学报, 2015, 35(8): 2043. SHI Tingna, XIAO Zhuxin, XIAO Youwen, et al. A position sensorless control strategy for BLDCM based on an improved sliding mode observer[J]. Proceedings of the CSEE, 2015, 35(8): 2043. |
| [15] |
张前, 冯明. 基于母线电流的无刷直流电机换相位置优化策略[J]. 北京航空航天大学学报, 2016, 42(7): 1441. ZHANG Qian, FENG Ming. BLDC motor commutation position optimization strategy based on bus current[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(7): 1441. |
 2021, Vol. 53
2021, Vol. 53


