2. 中南大学 轻合金研究院, 长沙 410012;
3. 中南大学 高性能复杂制造国家重点实验室, 长沙 410012
2. Light Alloys Research Institute, Central South University, Changsha 410012, China;
3. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410012, China
软体机器人具有环境适应性好、人机交互安全、系统设计简单等优点,因此获得了广泛的研究[1].现有软体驱动器驱动模式主要包括:流体驱动[2]、介电弹性体[3]、形状记忆合金[4]、化学过程驱动[5]、拉线驱动[6]等.
变刚度技术是软体机器人走向应用的重要使能技术,有效调控刚度对于软体机器人具有重要意义.目前软体机器人的变刚度实现机理包括拮抗原理[7-8]、电磁流变原理[9]、材料相变原理[10-11]及阻塞机制等,其中利用基于真空的颗粒阻塞机制由于结构简单、刚度调节速度快的优点近年来得到广泛的研究[12].
Cheng等[13]利用颗粒阻塞实现了微创手术柔性机械臂的局部刚度调控. Jiang等[14]提出了一种柔性机械手,采用颗粒阻塞和气动肌肉机构相结合的方法实现驱动和变刚度. Brown等[15-16]利用颗粒阻塞设计了一种通用软体抓手,能够在没有反馈的情况下抓取各种形状的物体,此抓手操作容易、结构简单,但是在抓取时,只能用力压向被抓物,从而被动地顺应被抓物形状,所以当被抓物较软或体积过大时,抓取效果不理想. Wei等[17]设计了一种包括气动层和颗粒层的双层结构软体手指,气动层实现驱动器的运动,而颗粒腔实现刚度调控.为避免使用复杂的真空系统,Li等[18]提出了一种被动颗粒阻塞的概念,在气动腔内施加正压,弯曲的驱动器会挤压松散的颗粒使之阻塞,故可通过控制气压即可调节软体驱动器的刚度.
在以上驱动器中,颗粒物质填充得比较松散,当发生阻塞转换时,驱动器姿态会有所变化,保形能力下降.为了解决这一问题,Li等[19]与韩奉林等[20]分别独立地提出了颗粒驱动软体驱动器,其中的颗粒物质始终充满软体型腔,颗粒的体积分数较高,所以在抽真空阻塞过程中,驱动器可以具有很好的形状保持能力.韩奉林等[20]发现通过调节腔内负压,可使驱动器的刚度提升约2.75倍,但颗粒充入型腔时,会堵塞在型腔入口附近,从而在驱动器根部产生较大的径向膨胀,导致驱动器弯角较小,需要通过结构优化进一步提升弯曲性能.
有限元法(Finite Element Method,FEM)是分析流体驱动软体机器人运动的常用方法,但由于颗粒物质的离散性,直接采用有限元方法分析颗粒驱动软体驱动器运动存在很大难度.韩奉林等[20]采用Mohr-Coulomb(M-C)模型将颗粒物质描述为连续介质,继而应用FEM方法成功分析了驱动器的变形过程,但由于M-C模型过度简化了颗粒物质,计算误差较大.在颗粒驱动软体驱动器中颗粒物质的运动具有离散性,其流动需要采用离散元(Discrete Element Method, DEM)仿真方法分析;而弹性腔壁的变形具有连续性,其变形需要采用非线性FEM仿真方法分析,因此必须采用FEM-DEM耦合方法才能处理此类复杂非线性边界问题.目前FEM-DEM已用于分析金属板材成型[21-22]、轮胎沙地接触[23]、岩石开凿[24]等问题,但是分析时更多的局限于单向耦合仿真,即DEM单向向FEM提供载荷,FEM不向DEM更新位移.而在颗粒驱动软体驱动器运动分析中,由于变形腔壁的大变形,必须使用FEM-DEM双向耦合分析方法.目前开展FEM-DEM双向耦合计算的主流方法是通过第三方平台为独立的FEM和DEM分析软件进行数据交换通道[25],但这种方法实施难度大、效率低,精度损失也比较大.
本文有两个目的:1)在单一ABAQUS平台下,实现了颗粒驱动软体机器人FEM-DEM的双向耦合运动分析,通过与单纯FEM分析和实验结果对比,验证这种方法的有益效果,并用这种方法研究了颗粒粒径对机器人运动的影响规律;2)设计了一种具有径向增强约束的软体型腔,通过仿真和实验,证明其可在不影响变刚度能力的前提下,增大机器人的运动范围.
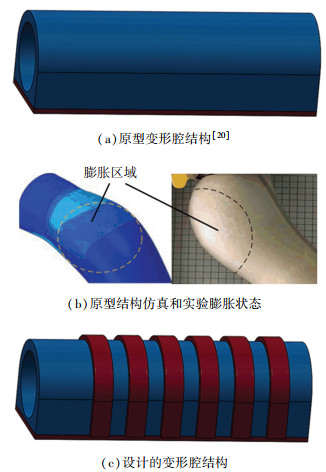
1 方法与材料 1.1 驱动器结构设计文献[20]中提出的颗粒驱动软体驱动器腔体的原型结构如图 1(a)所示,在一定程度上验证了颗粒驱动的可行性.但如图 1(b)所示,在仿真和实验中发现驱动器变形腔径向膨胀效应显著,造成弯曲角度较小.如果能够有效约束径向膨胀,则有可能进一步增加弯曲角度,提升弯曲性能.为此,本文设计了一种新型的结构如图 1(c)所示,在腔体外侧增加6个硬度较高的加强筋,以限制腔体的径向变形,增加颗粒对弯曲变形的作用效果.
|
图 1 软体驱动器腔体设计比较 Fig. 1 Comparison of soft actuator cavity designs |
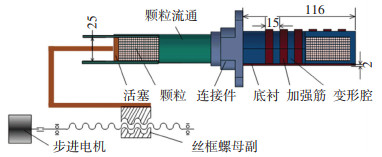
图 2展示了包含颗粒输送装置的完整的驱动器并且标示出了驱动器的关键尺寸.腔体与颗粒流道之间使用连接件进行连接.步进电机通过丝杠螺母副带动活塞在颗粒流道内往复移动.
|
图 2 驱动器结构 Fig. 2 Structure of actuator |
驱动器工作循环分为驱动变形、承载和卸载3个阶段.驱动时活塞向右运动,将颗粒压入变形腔,迫使驱动器开始驱动变形.变形至预定位置后,通过抽气孔将腔内抽成负压,提高承载能力.卸载时腔内与大气连通,活塞向左运动,颗粒在变形腔弹性恢复力挤压下流回颗粒流道.
1.2 驱动器材料选择和样机制备驱动器使用的材料如图 3所示.为了减小颗粒间的摩擦、提高颗粒的传压能力,选择质地较硬且表面光滑的ϕ2.8 mm的亚克力球作为填充颗粒,如图 3(a)所示.弹性变形腔体材料选择双组份硅胶Ecoflex 00-30(Smooth-on)材料(见图 3(b)),该材料邵氏硬度较低,可制造性及弹性好,在气动变形腔设计中应用较为广泛.为了起到更好的限制变形的效果,本文底衬和加强筋均选取邵氏硬度较高的聚氨酯材料(PU), 如图 3(c)所示.

|
图 3 驱动器材料 Fig. 3 Materials used in actuator |
驱动器制备过程见图 4.首先在CAD中建立浇注模具的模型,采用光固化3D打印技术打印模具如图 4(a)所示.分别量取等体积Ecoflex 00-30A、B组分硅胶均匀混合,随后放入真空除气装置中进行第一次脱气处理,将硅胶材料浇入模具内, 如图 4(b)所示.待浇注完成后,将模具放入真空除气装置内进行第二次除气处理.将模具静置成型3~4 h,待硅胶成型后做脱模处理(见图 4(c)),加强筋和底衬是由图 4(d)中的材料使用裁刀直接裁剪而成,然后使用硅胶专用胶(E300,佛山一滴强胶粘剂有限公司)将其与型腔粘接固定,图 4(e)中的连接件通过3D打印而成,将驱动器整体和连接件使用绑带固定,最后装配得到的驱动器如图 4(f)所示.

|
图 4 驱动器制备过程 Fig. 4 Actuator manufacturing process |
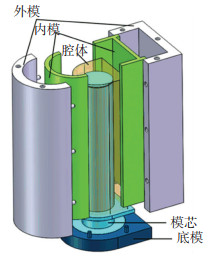
如图 5所示,用于浇注制造变形腔体的模具主要由四部分组成:内模(由内左、右模组成)、外模(由外左、右模组成)、底模和模芯.其中内模在浇注成型过程中形成腔体的外部形状,模芯在浇注过程中形成腔体的内部流道,外模和底模上布有定位销,起对内膜以及模芯的定位作用.
|
图 5 变形腔模具 Fig. 5 Actuator cavity manufacturing mold |
在ABAQUS中,提供了一种能够描述刚性颗粒的PD3D单元,此单元可以用于模拟大量离散颗粒相互接触运动,结合ABAQUS强大的非线性有限元功能可以有效进行DEM-FEM耦合仿真,故可以很好地用于颗粒驱动软体驱动器的颗粒充填型腔过程和驱动器变形过程的仿真研究.
为获得准确的仿真结果,需要建立超弹性材料的本构模型.超弹性材料本构模型参数值通过单轴拉伸试验获得,采用Ogden模型拟合出最优的聚氨酯材料、Ecoflex 00-30本构模型.参数见表 1.
| 表 1 超弹性模型参数 Tab. 1 Fitting parameters of hyperelastic model |
设置合理的接触模型是准确进行DEM仿真的前提.本文使用Hertz接触模型来定义颗粒的接触属性.对于同一种球型颗粒,由Hertz接触理论得出法向接触力与法向位移间的关系表达式为
| $ {F_n} = \frac{4}{3}{E^*}\sqrt R {\delta ^{\frac{3}{2}}}, $ | (1) |
颗粒接触刚度为
| $ {K_n} = \frac{4}{3}{E^*}\sqrt R . $ | (2) |
式中,
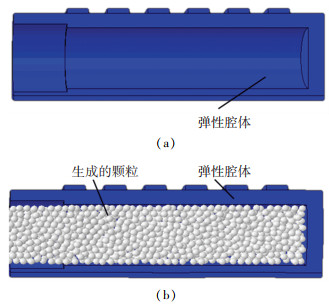
由于ABAQUS CAE可视化界面不支持PD3D单元的设置,故需要先在可视化界面中完成除颗粒外其余几何体的建模、材料属性的设置、网格的划分等前处理工作.在仿真中将活塞、颗粒流道、连接件设置为刚体.将变形腔、筋、底衬均设置为C3D8R单元,网格数目分别为4206、96、468.完成前处理设置后生成inp文件,然后需要对inp文件进行修改,以完成颗粒生成、颗粒属性设置等工作.修改inp文件主要流程见图 6,仿真采取颗粒生成器(Particle generator)的方法生成颗粒.首先定义活塞端面为颗粒生成器,颗粒最大数目定义为20000,然后定义颗粒直径、弹性模量、泊松比.再定义颗粒Hertz接触,最后定义颗粒生成速率、颗粒移动速率等.生成颗粒前后的型腔模型如图 7所示.

|
图 6 修改inp文件流程 Fig. 6 Process of modifying inp files |
|
图 7 生成颗粒前后的FEM模型 Fig. 7 FEM models before and after particles generating |
文献[20]中将颗粒物质作为连续体,提出了一种针对颗粒驱动软体驱动器的FEM仿真方法.为了对比FEM和DEM-FEM两种分析方法的准确性,采用FEM方法对设计的驱动器进行对比仿真分析.颗粒材料的本构模型采用弹性模型与M-C塑性模型的联合弹塑性模型.其中弹性模型参数弹性模量、泊松比见1.3节.
在塑性本构模型中,一般认为,颗粒材料的破坏符合粉体或土体的莫尔-库伦(Mohr-Coulomb,M-C)破坏准则. M-C强度理论公式为
| $ \tau = c + \sigma {\rm{tan}}\;\phi {\rm{.}} $ | (3) |
其中ϕ为法向应力,为τ剪应力.亚克力球的内摩擦角ϕ和黏聚力c通过快剪试验获得,实验中试样剪切速率0.64 mm/min,实验停止条件为试样轴向应变达到20%,测得的ϕ=26.1°,c=0.
1.5 软体驱动器性能测试实验 1.5.1 实验设计为验证所提出的仿真方法的有效性和设计方案的合理性,设计了两组实验研究颗粒驱动器的性能:第一组实验研究设计的驱动器结构的弯曲性能;第二组实验研究软体驱动器在不同真空负压状态下(阻塞)刚度变化情况.实验中使用颗粒的粒径为ϕ2.8 mm.
本研究中设计制造的用于分析驱动器弯角和刚度的实验装置如图 8所示.驱动器垂直放置,依靠连接件固定在台架上,两个直线模组分别沿水平和竖直方向安装,其上都安装有测力计.竖直直线模组带动测力计下移同时推动活塞移动,移动距离可通过计算机控制.将水平模组和测力计用于刚度试验.配备真空泵和真空调压阀,通过气管与驱动器连接,为其提供负压.

|
图 8 软体驱动器性能测试装置 Fig. 8 Experimental setup for measuring the performance of soft actuators |
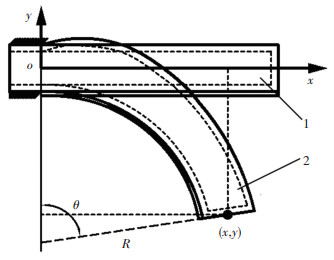
驱动器弯曲角θ的定义见图 9,其中状态1为驱动器的初始状态,状态2为变形后状态,弯曲角θ为驱动器端面与y轴的夹角.在实验中,由于实验条件的限制,活塞移动的最大距离为90 mm,每次将活塞移动10 mm,实验过程中使用相机采集驱动器图像,使用MATLAB图像处理功能测量弯曲角度并记录,重复9次测量过程直到活塞位移至90 mm.
|
图 9 驱动器弯曲角定义 Fig. 9 Definition of the actuator bending angle |
在文献[19]中,采用如下方法表征驱动器的弯曲刚度:通过测力计推动驱动器末端产生位移δy,此间驱动器弯角为δβ(β=arctan(y/x)为文献[19]中定义的弯曲角),测力计最大输出值为F,定义SR=Fδy/δβ表示驱动器的弯曲刚度.当β和δy较小时,驱动器末端的x坐标近似为常数,且δβ≈ y+δy /x-y/x=δy/x,因此,SR与F之间只差一个常系数.在本文中,为简单起见,直接以F作为弯曲刚度的表征参数.
实验中,首先使控制竖直直线模组移动60 mm距离,使驱动器产生对应的弯曲,然后启动真空泵使腔内产生负压并使颗粒阻塞.再控制水平直线模组移动,使测力计拉动驱动器匀速移动20 mm,重复3次并且记录每次实验的拉力的最大值,将3组最大拉力的平均值作为表征弯曲刚度的参数.然后改变真空泵的负压值,重复整个实验过程.本文选取负压为0、-20、-40、-60、-75 kPa的情况进行测量.
2 结果与讨论 2.1 弯曲性能仿真和实验结果为对比两种仿真方法分析计算驱动器变形的准确性,在本研究中使用FEM和FEM-DEM两种仿真方法分别对驱动器进行了分析并进行了实验.
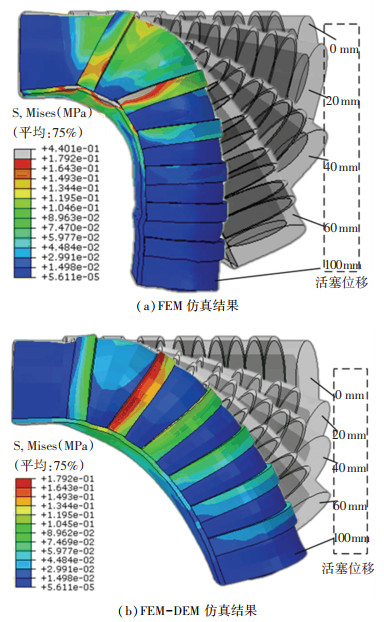
FEM仿真应力云图如图 10(a)所示,DEM-FEM仿真应力云图如图 10(b)所示,图 10中还展示出了在活塞位移分别为0、20、40、60、100 mm时驱动器的变形状态. 图 11是驱动器在不同活塞位移下的弯曲实验结果,仿真和实验结果对应的驱动器弯角与活塞位移关系曲线如图 12所示.实验中当活塞位移为90 mm时,驱动器弯曲角度为72.7°,对比文献[20]中原型驱动器结构角度48.9°,弯曲角度提升了48.7%.
|
图 10 驱动器仿真应力分布 Fig. 10 Stress distribution simulation results of actuator |

|
图 11 驱动器弯曲实验结果 Fig. 11 Experimental results of actuator bending |
|
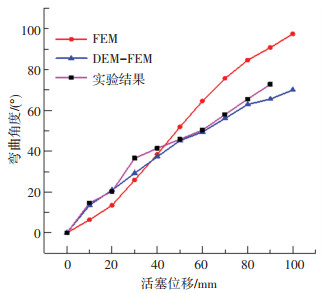
图 12 驱动器弯角与活塞位移关系的实验和仿真结果 Fig. 12 Experimental and simulation results of changes in the actuator bending angle versus piston displacement |
从图 12中曲线整体可看出, FEM-DEM仿真结果相对于FEM仿真结果更加接近于实际情况.除此之外,活塞位移90 mm时,驱动器的FEM仿真弯角为90.76,FEM-DEM仿真的弯曲角度为65.1°,对于驱动器采取FEM-DEM方法计算的弯曲角度与实验相比误差为10.5%. FEM仿真的误差为24.8%. FEM-DEM比FEM仿真结果驱动器弯曲角度更小,同时误差减小了14.3%.这可能是因为基于M-C模型的FEM方法过度简化了颗粒物质,造成计算误差较大.而FEM-DEM方法与实验仍存在误差的原因可能是仿真中设置的颗粒之间的摩擦特性、超弹材料的本构模型等条件与实际情况存在一定的差异.
从图 10(a)和(b)可以看出,FEM-DEM仿真中的驱动器应力分布较为均匀且驱动器末端也有着明显的应力,整体弯曲效果较为平滑,曲率变化较小.而FEM仿真中驱动器局部应力较大,应力和弯曲都集中在靠近驱动器根部的第一个筋和第二个筋之间且在驱动器末端应力很小.这可能是由于FEM-DEM仿真内部颗粒材料流动性较好,而FEM方法过高地估计了颗粒间的摩擦力导致腔体内部颗粒流动性较差.颗粒在驱动器根部堆积,局部产生了较大的应变,造成了局部弯曲.并且随着活塞位移的增加,堆积的颗粒越多,局部弯曲越大.
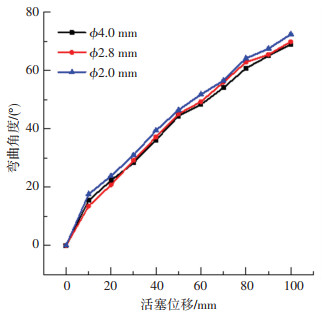
与单纯FEM方法相比,FEM-DEM方法的另一个优势在于可以研究颗粒粒径对驱动器变形的影响规律.本研究中使用FEM-DEM方法对颗粒直径为4、2.8、2 mm的情况进行仿真,仿真计算获得不同颗粒直径对于驱动器弯曲角度的影响关系如图 13所示.可以看出活塞位移超过10 mm后驱动器弯角呈现出近似线性的变化,这种现象可能是由于活塞移动一定的位移后驱动器内部颗粒变得更加紧凑造成的,当注入颗粒体积较小时,颗粒之间存在较大间隙,而当更多的颗粒被注入驱动器时, 弯曲角度的变化线性度更好.
|
图 13 颗粒直径对驱动器弯角-活塞位移关系的影响 Fig. 13 Simulation results of changes in actuator bending angle versus piston displacement when using particles with different diameters |
此外,可以看出使用直径为2 mm的颗粒的驱动器在活塞每一个位移状态下的弯角均是最大的,并且在活塞位移超过30 mm时,颗粒直径越小,驱动器弯曲角度越大.这种现象可能是因为对于相同的腔壁面积,直径较小的颗粒可以有更多的接触点数,而较大的颗粒分布更加稀疏,造成了传力效果的不均匀.
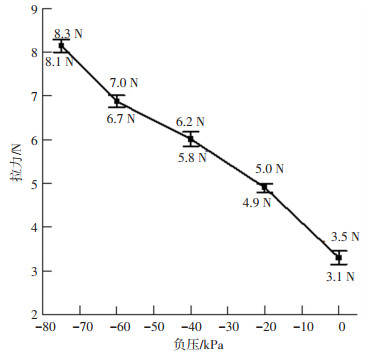
2.2 刚度变化实验结果图 14是驱动器在不同负压下,末端受拉产生20 mm位移过程中所施加的最大拉力,拉力越大则表明驱动器的刚性越强.从中可以看出, 随着负压力的增加驱动器所能够承受的拉力增大,且变化是近似线性的.除此之外,本研究中的驱动器在负压为0时最大拉力约为3.1~3.5 N,在负压为-75 kPa时最大拉力约为8.1~8.3 N,可知驱动器在阻塞前后承载力有着大约2.7倍的提升,即刚度变化也约2.7倍.相对于文献[20]中原型驱动器结构,本设计中增加的径向增强约束并没有削弱驱动器的刚度调节能力.
|
图 14 驱动器负压-拉力关系的实验结果 Fig. 14 Experimental results of pull force applied on the actuator at different negative pressures |
本文提出了一种以颗粒物质为介质驱动的软体驱动器,为减弱局部径向膨胀效应,其型腔设计有径向增强约束.为在设计阶段能更准确地预测驱动器地变形规律,将FEM-DEM双向耦合计算方法应用于驱动器的运动过程仿真,主要结论如下:
1) 在ABAQUS单一平台下,成功实现了颗粒驱动软体驱动器变形过程的FEM-DEM双向耦合仿真.
2) 与基于M-C模型的单纯FEM方法相比,DEM-FEM耦合计算所得的驱动器弯曲角度计算误差降低了14.3%,说明FEM-DEM双向耦合仿真能够更为真实地刻画颗粒物质流动与超弹型腔大变形之间的协同规律,是验证颗粒驱动软体机器人变形状态的较优手段.
3) 通过FEM-DEM双向耦合仿真研究发现, 较小的颗粒粒径可以增强机器人的变形能力.
4) 仿真和实验结果表明, 径向增强约束可使驱动器最大弯曲角度提升约48.7%,且对变刚度能力无不良影响.
5) 本文仅开展了颗粒驱动软体机器人运动和变刚度规律的初步研究,这种机器人在多次往复运动中的重复定位精度、刚度演化等重要规律还有待进一步研究.
| [1] |
ARNOLD T, SCHEUTZ M. The tactile ethics of soft robotics: designing wisely for human-robot interaction[J]. Soft Robotics, 2017, 4(2): 81. DOI:10.1089/SORO.2017.0032 |
| [2] |
滕燕, 高帅. 充气伸长型气动柔性驱动器刚度特性[J]. 哈尔滨工业大学学报, 2015, 47(5): 76. TENG Y, GAO S. Stiffness characteristic of elongation type pneumatic compliance actuator[J]. Journal of Harbin Institute of Technology, 2015, 47(5): 76. DOI:10.11918/J.ISSN.0367-6234.2015.05.013 |
| [3] |
郭闯强, 吴春亚, 邹添, 等. 介电弹性材料驱动器在机器人中的应用进展[J]. 哈尔滨工业大学学报, 2016, 48(1): 1. GUO C, WU C, ZOU T, et al. Application progress of dielectric elastomer actuators in robotsr[J]. Journal of Harbin Institute of Technology, 2016, 48(1): 1. DOI:10.11918/J.ISSN.0367-6234.2016.01.001ISSN.0367-6234.2016.01.001 |
| [4] |
MENCIASSI A, GORINI S, PERNORIO G, et al. A SMA actuated artificial earthworm[C]// Proceedings ICRA'04 2004. Piscataway, N J: IEEE, 2004: 3282. DOI: 10.1109/ROBOT.2004.1308760
|
| [5] |
WEHNER M, TRUBY R L, FITZGERALD D J, et al. An integrated design and fabrication strategy for entirely soft, autonomous robots[J]. Nature, 2016, 536(7617): 451. DOI:10.1038/NATURE19100 |
| [6] |
RENDA F, CIANCHETTIM, GIORELLI M, et al. A 3D steady-state model of atendon-driven continuum soft manipulator inspired by the octopus arm[J]. Bioinspiration & Biomimetics, 2012, 7(2): 025006. DOI:10.1088/1748-3182/7/2/025006 |
| [7] |
CIANCHETTI M, LICOFONTE A, FOLLADOR M, et al. Bioinspired soft actuation system using shape memory alloys[J]. Actuators, 2014, 3(3): 226. DOI:10.3390/ACT3030226 |
| [8] |
LASCHI C, CIANCHETTI M, MAZZOLAI B, et al. Soft robot arm inspired by the octopus[J]. Advanced Robotics, 2012, 26(7): 709. DOI:10.1163/156855312X626343 |
| [9] |
LI Y, LI J, TIAN T, et al. A highly adjustable magnetorheological elastomer base isolator for applications of real-time adaptive control[J]. Smart Materials and Structures, 2013, 22(9): 1. DOI:10.1088/0964-1726/22/9/095020 |
| [10] |
CAPADONA J R, SHANMUGANATHAN K, TYLER D J, et al. Stimuli-responsive polymer nanocomposites inspired by the sea cucumber dermis[J]. Science, 2008, 319(5868): 1370. DOI:10.1126/SCIENCE.1153307 |
| [11] |
SCHUBERT B E, FLOREANO D. Variable stiffness material based on rigid low-melting-point-alloy-microstructures embedded in soft poly(dimethylsiloxane) (PDMS)[J]. Rsc Advances, 2013, 3(46): 24671. DOI:10.1039/c3ra44412k |
| [12] |
闫继宏, 石培沛, 张新彬, 等. 软体机械臂仿生机理、驱动及建模控制研究发展综述[J]. 机械工程学报, 2018, 54(15): 1. YAN J, SHI P, ZHANG X, et al. Review of biomimetic mechanism, actuation, modeling and control in soft manipulators[J]. Journal of Mechanical Engineering, 2018, 54(15): 1. DOI:10.3901/JME.2018.15.001 |
| [13] |
CHENG N G, LOBOVSKY M B, KEATING S J, et al. Design and analysis of a robust, low-cost, highly articulated manipulator enabled by jamming of granular media[C]// 2012 IEEE International Conference on Robotics and Automation. Piscataway, N J: IEEE, 2012: 4328. DOI: 10.1109/ICRA.2012.6225373
|
| [14] |
JIANG A, XYNOGALAS G, DASGUPTA P, et al. Design of a variable stiffness flexible manipulator with composite granular jamming and membrane coupling[C]// 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, N J: IEEE, 2012: 2922. DOI: 10.1109/IROS.2012.6385696
|
| [15] |
AMEND J R, BROWN E, RODENBERG N, et al. A positive pressure universal gripper based on the jamming of granular material[J]. IEEE Transactions on Robotics, 2012, 28(2): 341. DOI:10.1109/TRO.2011.2171093 |
| [16] |
BROWN E, RODENBERG N, AMEND J, et al. Universal robotic gripper based on the jamming of granular material[J]. Proceedings of the National Academy of Sciences, 2010, 107(44): 18809. DOI:10.1073/PNAS.1003250107 |
| [17] |
WEI Y, CHEN Y, REN T, et al. A novel, variable stiffness robotic gripper based on integrated soft actuating and particle jamming[J]. Soft Robotics, 2016, 3(3): 134. DOI:10.1089/SORO.2016.0027 |
| [18] |
LI Y, CHEN Y, YANG Y, et al. Passive particle jamming and its stiffening of soft robotic grippers[J]. IEEE Transactions on Robotics, 2017, 33(2): 446. DOI:10.1109/TMECH.2019.2907045 |
| [19] |
LI Y, CHEN Y, YANG Y, et al. Soft robotic grippers based on particle transmission[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(1): 969. DOI:10.1109/TMECH.2019.2907045 |
| [20] |
韩奉林, 李鹏, 李明辉, 等. 颗粒流驱动变刚度弯曲软体驱动器的设计及运动仿真[J]. 中国机械工程, 2020, 31(8): 890. HAN F, LI P, LI M, et al. Design and motion simulation of the variable stiffness bending soft actuator driven by granular flow[J]. China Mechanical Engineering, 2020, 31(8): 890. DOI:10.3969/J.ISSN.1004-132X.2020.08.002 |
| [21] |
DONG G, ZHAO C, YA Y, et al. Discrete element and finite element coupling simulation and experiment of hot granule medium pressure forming[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(12): 4089. DOI:10.1016/S1003-6326(15)64060-2 |
| [22] |
曹秒艳, 李建超, 苑亚宁, 等. 基于DEM-FEM的AZ31B板材软模成形极限预测[J]. 中国有色金属学报, 2017, 27(4): 675. CAO M, LI J, YUAN Y, et al. Forming limit prediction in flexible die forming of AZ31B sheet based on combination of DEM-FEM[J]. The Chinese Journal of Nonferrous Metals, 2017, 27(4): 675. DOI:10.19476/J.YSXB.1004.0609.2017.04.001 |
| [23] |
赵春来, 臧孟炎. 基于FEM/DEM的轮胎一沙地相互作用的仿真[J]. 华南理工大学学报(自然科学版), 2015, 43(8): 75. ZHAO C, ZANG M. Simulation of tire—sand interactions based on FEM/DEM[J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(8): 75. DOI:10.3969/J.ISSN.1000-565X.2015.08.012 |
| [24] |
ONATE E, ROJEK J. Combination of discrete element and finite element methods for dynamic analysis of geomechanics problems[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(27/29): 3087. DOI:10.1016/J.CMA.2003.12.056 |
| [25] |
DEHNING C, BIERWISCH C, KRAFT T. Co-simulations of discrete and finite element codes[C]// Meshfree Methods for Partial Differential Equations Ⅶ. Cham, Switzerland: Springer, 2015: 61. DOI: 10.1007/978-3-319-06898-5_4
|
 2021, Vol. 53
2021, Vol. 53


