在流体力学的湍流研究中,壁湍流是一个重要的问题,其在理论研究和工业应用方面都具有关键意义,引起了人们极大的兴趣.在壁湍流的问题当中,槽道流由于具有简单的几何模型和边界条件,被视为一种非常有效的研究模型.
槽道湍流的实验研究与数值模拟研究成果非常丰富.直接数值模拟被认为是能够得到最准确数据的数值模拟方法. 1987年,Kim等[1]通过直接数值模拟的方式计算了Reτ≈180的槽道流,并将计算的结果与早前Eckemlmann等[2]的结果进行了对比.不过按照湍流研究的惯例,通常认为槽道流的内区为0.1个半槽道高度,而外区要大于50个壁面单位,Reτ必须足够高才会在存在内区与外区的交错段[3].同时Smits等[4]提出当Reτ达到103时湍流研究的结果接近工业上所需要的雷诺数,研究具有实际应用价值. Monty等[5]进行了最大Re=2 000的槽道湍流实验, 为Hoyas等[6]计算的Reτ=2000和Alamo等[7]计算的Reτ=1 000的结果提供实验验证数据. Schultz等[8]进行了1 000≤Reτ≤6 000的槽道流实验,主要的工作是测出不同雷诺数下的统计量,并且将新的数据与之前的DNS或者实验的数据进行对比.在数值模拟方面,Lozano等[9]计算了Reτ=4 200的槽道流,研究计算区域对数值模拟的影响,结论为计算区域(2πh×πh)在靠近壁面区域所得到的结果足够准确. Lee等[10]计算了Reτ=5 200的湍流槽道流,并且对之前的DNS与实验的结果进行了验证与总结.上面的计算均采用谱方法进行. Bernardini等[11]用二阶有限差分法计算了Reτ=4 000的湍流槽道流,对他人的计算结果进行了验证.除了Bernadini等人采用二阶有限差分法之外,Vela-Martin等[12]利用GPU对湍流槽道流开展计算,采用的方法为二阶有限差分法,计算的雷诺数达到Reτ=5300;Yamamoto等人[13]采用高阶精度的有限差分法,计算了Reτ=8 000的槽道流,但是由于计算的网格分辨率不够高,在速度脉动的计算上面与目前所认可的规律相比相差较大,目前对这组数据仍然存疑.目前最大雷诺数的槽道流算例是Hoyas等人[14]计算的雷诺数达到Reτ=10 000的槽道流,这组数据计算区域较小(2πh×πh),目的是为了得到槽道流湍流的单点统计规律.
减阻控制是湍流槽道流的研究热点和重点之一,实验与数值模拟都进行了大量的研究.湍流减阻具有代表性的工作包括Quadrio等[15]采用的壁面展向振动的方式、Luchini等[16]通过壁面沟槽限制了流向涡的展向流动以及Maden等[17]通过等离子体激励器控制的方式减小了槽道湍流的阻力等研究.
随着超级计算机性能与并行技术的提高,高Re数的槽道流DNS计算成为可能.本文结合所在课题组基于湍流热对流所建立的并行直接求解方法(PDM-DNS),将较高效的并行求解方法引入湍流槽道流计算当中,实现较高效并行的湍流槽道流DNS模拟计算.由于本文采用的计算方法是有限差分法,结合浸没边界法等计算技术,方便处理复杂的边界条件,较容易将槽道流的计算研究扩展到湍流流动控制等计算研究领域.
1 槽道流的计算方法由于计算规模巨大,高Re数湍流槽道流的DNS模拟往往需要使用高效并行计算技术并依托超级计算机进行.湍流槽道流的计算结果数据可以为壁湍流理论研究以及湍流流动控制等研究提供基础依据.
1.1 控制方程与其求解槽道流计算区域为上下为壁面的矩形区域.定义流向方向为x,展向方向为y,壁面法向方向为z,
不可压流动的控制方程为
| $ \nabla \cdot \overrightarrow u = 0, $ | (1) |
| $ \frac{{\partial \overrightarrow u }}{{\partial t}} + \left( {\overrightarrow u \nabla } \right)\overrightarrow u = - \nabla p + \frac{1}{{Re}}{\nabla ^2}\overrightarrow u . $ | (2) |
槽道流计算中,速度与压力在流向与展向方向采用周期边界条件, 上下壁面边界条件为速度无滑移和零压力梯度.计算网格在流向与展向方向采用等距网格,垂直壁面方向采用壁面附近加密的非等距网格.空间采用二阶精度中心差分格式,时间采用二阶精度的Runge-Kutta法进行计算.本文采用的计算步骤为投影法.
实际的槽道流是由压力驱动引起的流动.本文采用定流量计算(CFR, Constant Flow Rate),定流量指设定系统的流量恒定,系统的总流量不发生改变[18].控制流量的方法为在每个计算的单元内引入外加力Fx与Fy.设初始的流量为Q0, 计算n+1时刻的流量为Qn+1,所以有
| $ \left\{ \begin{array}{l} {F_x} = \left( {Q{{\left( x \right)}_0} - Q{{\left( x \right)}_{n + 1}}} \right) \times {\rm{d}}z, \\ {F_y} = \left( {Q{{\left( y \right)}_0} - Q{{\left( y \right)}_{n + 1}}} \right) \times {\rm{d}}z. \end{array} \right. $ | (3) |
对于流向与展向的速度u和v,通过引入外加力F修正以保证流量恒定.
1.2 直接并行求解方法与并行效率对于槽道流的DNS计算来说,当Re数增大就需要提高计算网格精度,所以采用高效的并行计算在高Re数湍流槽道流的DNS模拟中是不可缺少的.
课题组在之前为解决极高Ra数湍流热对流的DNS数值模拟,建立了直接并行求解方法PDM-DNS (Parallel Direct Method of Direct Numerical Simulation) [19],Direct Method指的是直接求解法,在求解的过程对于压力项的求解没有采用迭代的方式而是直接求解压力泊松方程得到压力.将这一计算方法引入到槽道流的计算中来,初步实现具有较高并行效率的湍流槽道流DNS模拟并行计算. PDM-DNS方法的计算特点是,采用OpenMP和MPI混编并行,可在“天河二号”超级计算机上运行.其中关键技术是压力泊松方程的高效并行求解,采用FFT解耦和PDD三对角方程并行求解技术.
表 1给出了在“天河二号”超级计算机上进行槽道流DNS计算并行效率测试结果.计算网格采用512×512×512,共1.34×109网格计算自由度.采用PDM-DNS方法分别在超级计算机上应用1~8个计算节点,即32~256计算核进行计算,所有计算都能达到95%以上的并行效率,并且具有很好的并行效率的线性延展性.因此,PDM-DNS方法可以给湍流槽道流DNS模拟提供较为高效的并行计算,使高Re数湍流槽道流的模拟得以实现并获得大量有效的数据.
| 表 1 在nx×ny×nz=512×512×512的网格下并行相关参数 Tab. 1 Parallelization parameters on the grid of nx×ny×nz= 512×512×512 |
槽道流以层流泊肃叶流动作为初场,通过添加速度扰动使其发展成为湍流槽道流.扰动大小幅值为初始速度大小的10%.在外加扰动的作用之下,流动逐渐从层流向湍流进行转变.
图 1给出了槽道流壁面摩擦系数随时间的变化过程.在不断添加人为的扰动速度影响下,槽道壁面的摩擦系数随着时间发生变化.在无量纲时间T<20的时候,壁面摩擦系数几乎是不变的;在20≤T≤35的阶段,壁面的摩擦系数会出现一个突增的情况;在T>35之后,壁面摩擦系数发展到另一个较大的数值并趋于平稳,此时流动发展进入湍流状态.在流动发展到湍流状态之后撤去人为的速度扰动,槽道流动不会回到层流流动而是稳定在湍流流动状态,继续计算最终得到充分发展的湍流槽道流,在此基础上可得到湍流槽道流的研究数据.

|
图 1 壁面摩擦系数随着时间的变化 Fig. 1 Variation of wall friction coefficient with time |
设定半槽道的宽度为h,为了验证程序的准确性,本文分别计算了Reτ≈180、550、1000、2 000时的4个算例,并且与相关的数值模拟进行对比.计算算例的主要参数具体如表 2所示.
| 表 2 槽道流算例的主要参数 Tab. 2 Parameters of channel flow simulations |
对于网格精度,x方向控制在10个壁面单位以内,y方向控制7个壁面单位以内.根据Jimenez等[9]的研究成果,计算区域取2πh×πh中等范围,可以保证槽道流内区的计算具有足够的准确性.本文所采用的对比数据是Lee[10]的DNS计算结果,他们的结果可靠性得到世界的认可.
2.1 平均速度在壁湍流的理论当中,一般认为在流动的内区到外区的平均流向速度是符合对数律的.对数律的公式可以写为
| $ {U^ + } = \frac{1}{\kappa } \cdot {\rm{log}}\;{z^ + } + B, $ | (4) |
其中,κ指卡门系数.在不同组的实验当中所测出来的κ值也有些许差异,Osterlund[20]测出κ=0.38,Monty[5]测出κ=0.37,Nagib[21]测出κ=0.39.由此可以认为κ在0.38附近,本文选取κ=0.38.
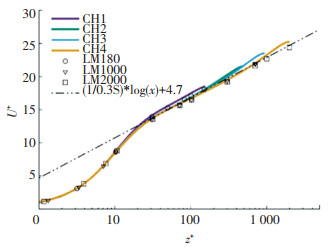
图 2给出了本文4个算例的平均速度剖面线,并给出相应的Lee[10]的DNS计算结果.从图 2可以看出, CH1的结果在对数段相比其它的结果略高,原因是在Reτ≈180下,当z+≈50时,z/δ≈0.28,当z+≈30时,z/δ≈0.17,所以在槽道流当中并不存在交错段(z+>50, z/δ<0.1),但是存在对数段(z+>30, z/δ<0.3).在Reτ≈550时,在z+=50下,z/δ≈0.09,所以在槽道流当中既存在交错段(z+>50, z/δ<0.1),也存在对数段(z+>30, z/δ<0.3).同样现象在Lee的数据当中也有所体现.在CH2~CH4的结果中都存在基本一致的对数段,且与Lee的结果相比较为接近,表明计算结果基本合理.
|
图 2 不同雷诺数下的平均速度曲线 Fig. 2 Mean velocity curves at different Reynolds numbers |
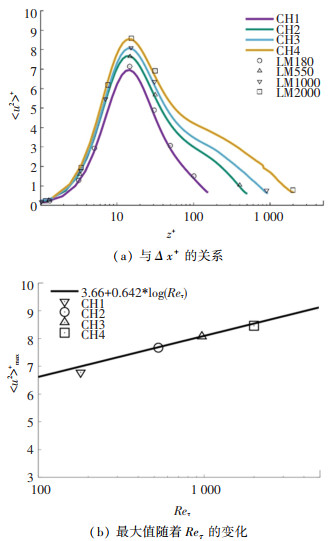
由于在雷诺应力的张量当中,< u′2>+是唯一一个可以与实验相比较的量,所以这个量对于验证湍流槽道流DNS的正确性十分重要. 图 3(a)是不同雷诺数下 < u′2>+随着壁法向方向的变化,图 3(b)是不同Reτ数下最大 < u′2>max+的变化.
|
图 3 不同雷诺数下流向方向雷诺正应力 Fig. 3 Mean-squared streamwise velocity fluctuations at different Reynolds numbers |
在比较 < u′2>+时同样将所有算例的雷诺应力与Lee的结果进行了对比.可以看出,雷诺正应力的最大值基本都出现在z+= 15的位置,而且随着Re数的增大,雷诺应力也随之增大.本文的结果与Lee在2015年的DNS结果相近,可以证明本文结果的准确性.
Lozano等人[9]在文章中指出,流向方向的雷诺应力最大值与雷诺应力之间满足以下关系:
| $ <{{u'}^2} > _{{\rm{max}}}^ + = 3.66 + 0.642 \cdot {\rm{log}}\left( {R{e_\tau }} \right). $ | (5) |
由于CH1所计算的Reτ较小,规律与CH2~CH4的结果相比有所区别.从图 3(b)上来看,本文CH2~CH4的结果同样也满足方程(5).
综上所述,平均速度与雷诺正应力结果的对比情况表明,本文湍流槽道流的DNS计算结果是可信的.
3 局部特殊壁面边界条件湍流流动控制是目前最热门的研究课题之一,壁面边界是湍流流动控制的研究重点.相较于常用的谱方法,速度压力法壁面边界条件易于处理是针对流动控制数值研究的一个优点,而计算精度问题则可以通过尽可能地提高计算规模来解决.借助类似浸没边界法等计算技术,粗糙壁面、滑移壁面以及各种吹吸气等壁面处技术都很容易实现.
为了探讨壁面边界条件变化对槽道湍流的影响,本文在CH1算例的基础上进行初步尝试.在下壁面加入三排微小毛刺,采用浸没边界法实现,计算壁面局部变化对槽道湍流流动的影响.本文采用离散力法计算浸没边界法中的力源项.在N-S方程中加入虚拟力源项,在控制方程中加入体积力来替代边界条件.在计算过程中求解完投影法的速度压力之后再加入虚拟力源项得到最终的速度.
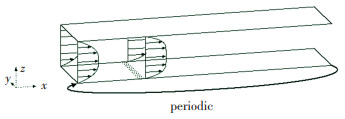
如图 4所示,在周期边界条件的槽道流中的1/4位置处,加入三排长宽约为0.044h(8个壁面单位)、高度约为0.022h(4个壁面单位)交错排列的微小毛刺.毛刺在整个展向具有微小间隔并均匀分布,在流向方向上对流动的影响只有局部作用.
|
图 4 槽道流加入粗糙毛刺示意图 Fig. 4 Simulation with rough burr in channel flow |
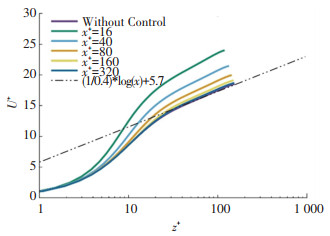
图 5给出的是在毛刺下游16个到320个壁面单位处的展向平均速度剖面,分别为毛刺高度4个壁面单位的4、10、20、40和80倍距离,同时给出了无毛刺时全场平均的速度分布.在毛刺的作用下,邻近位置的平均速度剖面线变化很大,平均速度曲线有所升高.当远离毛刺位置时,毛刺对湍流速度剖面的影响逐渐减小,到80倍毛刺高度距离位置处,湍流速度剖面已恢复到与无毛刺流动基本一致.可见壁面条件的改变对湍流流动影响显著.
|
图 5 加入毛刺后不同位置的平均速度曲线 Fig. 5 Mean velocity curves at different positions after adding rough burr |
由此可见,本文的速度压力法对湍流流动控制的研究,无论是加入展向的振动、壁面吹吸气还是改变槽道流的壁面形状都是易于实现的.加上本文方法具有高效并行特点,可以开展规模巨大的高Re数湍流槽道流DNS模拟计算,为湍流流动控制研究提供有效的计算工具和有价值的数据.
4 结论建立了槽道流DNS计算的PDM-DNS方法,在“天河二号”超级计算机上使用256个CPU核进行计算,其规模超过109自由度,计算并行效率超过95%,并得到良好的线性加速比.由此为开展高Re数湍流槽道流DNS模拟提供了有力的计算工具.
4个不同Re数的槽道流计算结果显示,速度剖面都具有粘性底层和对数段分布,并与湍流速度对数段的理论预测值分布一致,雷诺正应力分布合理,所有计算结果与他人的DNS结果吻合.本文提出的计算方法所得到的湍流槽道流计算结果和数据是合理可信的.
相较于谱方法,本文采用的速度压力差分求解方法方便于复杂边界条件的处理.在下壁面加入局部毛刺的算例结果展示,结合浸没边界法等计算技术,本文方法可以扩展到复杂壁面条件的湍流流动控制等研究中.
| [1] |
KIM J, MOIN P, MOSER R. Turbulence statistics in fully developed channel flow at low Reynolds number[J]. Journal of Fluid Mechanics, 1987, 177: 133. DOI:10.1017/S0022112087000892 |
| [2] |
ECKELMANN H. The structure of the viscous sublayer and the adjacent wall region in a turbulent channel flow[J]. Journal of Fluid Mechanics, 1974, 65(3): 439. DOI:10.1017/S0022112074001479 |
| [3] |
POPE S B. Turbulent flows[M]. Cambridge: Cabridge University Press, 2001: 273.
|
| [4] |
SMITS A J, MARUSIC I. Wall-bounded turbulence[J]. Physics Today, 2013, 66(9): 25. DOI:10.1063/PT.3.2114 |
| [5] |
MONTY J P, CHONG M S. Turbulent channel flow: comparison of streamwise velocity data from experiments and direct numerical simulation[J]. Journal of Fluid Mechanics, 2009, 633: 461. DOI:10.1017/S0022112009007769 |
| [6] |
HOYAS S, JIMENEZ J. Scaling of the velocity fluctuations in turbulent channels up to Reτ=2 003[J]. Physics of Fluids, 2006, 18(1): 011702. DOI:10.1063/1.2162185 |
| [7] |
DEL ALAMO J C, JIMENEZ J, ZANDONADE P, et al. Scaling of the energy spectra of turbulent channels[J]. Journal of Fluid Mechanics, 2004, 500: 135. DOI:10.1017/S002211200300733X |
| [8] |
SCHULTZ M P, FLACK K A. Reynolds-number scaling of turbulent channel flow[J]. Physics of Fluids, 2013, 25(2): 025104. DOI:10.1063/1.4791606 |
| [9] |
LOZANO-DURAN A, JIMENEZ J. Effect of the computational domain on direct simulations of turbulent channels up to Reτ=4 200[J]. Physics of Fluids, 2014, 26(1): 011702. DOI:10.1063/1.4862918 |
| [10] |
LEE M, MOSER R D. Direct numerical simulation of turbulent channel flow up to Reτ≈5 200[J]. Journal of Fluid Mechanics, 2015, 774: 395. DOI:10.1017/jfm.2015.268 |
| [11] |
BERNARDINI M, PIROZZOLI S, ORLANDI P. Velocity statistics in turbulent channel flow up to Reτ=4 000[J]. Journal of Fluid Mechanics, 2014, 742: 171. DOI:10.1017/jfm.2013.674 |
| [12] |
VELA-MARTIN A, ENCINAR M P, GARCIA-GUTIERREZ A, et al. A second-order consistent, low-storage method for time-resolved channel flow simulations up to Reτ=5 300[J]. arXiv, 2018: 1808.06461
|
| [13] |
YAMAMOTO Y, TSUJI Y. Numerical evidence of logarithmic regions in channel flow at Reτ=8 000[J]. Physical Review Fluids, 2018, 3(1): 012602. DOI:10.1103/PhysRevFluids.3.012602 |
| [14] |
HOYAS S, OBERLACK M, KRAHEBERGER S, et al. Turbulent channel flow at Reτ=10 000[C]//APS Division of Fluid Dynamics Meeting Abstracts 2019: H19. 001
|
| [15] |
QUADRIO M, RICCO P, VIOTTI C. Streamwise-travelling waves of spanwise wall velocity for turbulent drag reduction[J]. Journal of Fluid Mechanics, 2009, 627: 161. DOI:10.1017/S0022112009006077 |
| [16] |
LUCHINI P, MANZO F, POZZI A. Resistance of a grooved surface to parallel flow and cross-flow[J]. Journal ofFluid Mechanics, 1991, 228: 87. |
| [17] |
MADEN I, MADUTA R, KRIEGSEIS J, et al. Experimental and computational study of the flow induced by a plasma actuator[J]. International Journal of Heat and Fluid Flow, 2013, 41: 80. DOI:10.1016/j.ijheatfluidflow.2013.02.013 |
| [18] |
HASEGAWA Y, QUADRIO M, FROHNAPFEL B. Numerical simulation of turbulent duct flows with constant power input[J]. Journal of Fluid Mechanics, 2014, 750: 191. DOI:10.1017/jfm.2014.269 |
| [19] |
BAO Yun, LUO Jiahui, YE Mengxiang. Parallel direct method of DNS for two-dimensional turbulent rayleigh-benard convection[J]. Journal of Mechanics, 2018, 34(2): 159. DOI:10.1017/jmech.2017.54 |
| [20] |
OSTERLUND J M, JOHANSSON A V, NAGIB H M, et al. A note on the overlap region in turbulent boundary layers[J]. Physics of Fluids, 2000, 12(1): 1. DOI:10.1063/1.870250 |
| [21] |
NAGIB H M, CHAUHAN K A. Variations of von Karman coefficient in canonical flows[J]. Physics of Fluids, 2008, 20(10): 101518. DOI:10.1063/1.3006423 |
 2021, Vol. 53
2021, Vol. 53


