舰船旋转机械设备振动向外传播时会产生辐射噪声,其中包含了大量的低频线谱,不仅对自身声纳产生干扰,降低探测能力,还增强了水声辐射,降低声隐身性.各类旋转机械造成的低频线谱频率成分复杂,且存在频率波动现象,如何对低频线谱进行控制具有十分重要的意义[1].自适应控制算法不需要被控对象的精确模型[2],其中基于前馈控制的滤波最小均方算法(filtered-x least mean square, FxLMS),作为有限响应滤波器与LMS算法的结合使用,结构简单、易于工程实现,得到了广泛应用[3-4].
在实际工程应用中,前馈FxLMS算法存在许多局限性:1)多频线谱激励下,算法仅对其中1~2根线谱具备控制效果[5];2)线谱频率快速波动时,控制算法易出现相位失真现象[6];3)收敛性能和稳定性对于迭代步长的要求是相悖的,大步长导致稳态误差过大,小步长收敛速度较慢[7].对于上述问题,大量学者对其控制性能开展了研究.赵洪亮、Jeon等[8-9]使用窄带滤波法并行控制不同频率线谱,可解决多频线谱控制问题,但对窄带滤波器的要求较高.张志谊等[10]基于频率估计方法构造信号分量实现跟踪滤波,一旦出现频率失配,控制效果显著降低.李彦等[11]通过可在线调节的相位差补偿器抑制频率波动下最优解的波动,提高了控制系统鲁棒性.浦玉学、路翠华等[12-13]采用变步长算法提高控制前期的收敛速度,同时减小控制后的稳态误差.
小波包变换可描述信号和频率的局部特征,在任意的时间和空间域中分析信号[14-15].本文将小波包分解应用到多频波动线谱自适应控制中,保留了LMS算法的优势,将信号频带进行等间隔划分,对子频带信号进行并行控制,有效地改善了控制效果.确定了最优小波包基的选取原则,同时针对小波包分解造成的滤波器数量过大、计算复杂和子频带内虚有线谱等问题改进了小波包分解算法;基于改进的箕舌线函数设计变步长达到较快收敛速度和较小稳态误差.最后,搭建隔振试验台架和控制系统,验证所提算法的有效性.
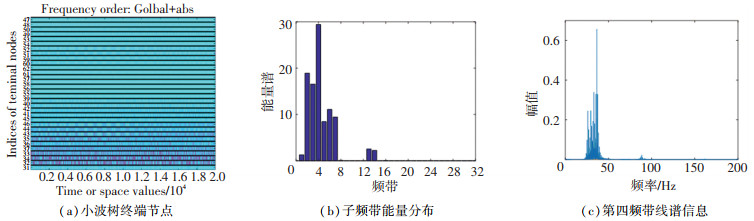
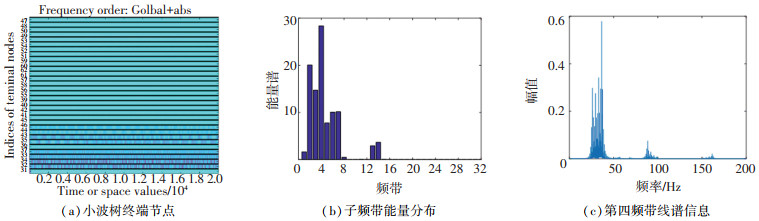
1 小波基的选择输入信号的分解情况会直接影响控制系统的收敛性和稳定性,由参考信号对控制算法的影响可知,要求分解后的子频带信号线谱能量集中、信号分解彻底且无明显端点效应.直接从小波函数性质分析分解信号的特性难以实现,因此,根据仿真结果反推小波基函数的影响,并确定最优小波基.初始激励信号设置为频率为28~31 Hz、35~38 Hz、58~61 Hz、108~111 Hz的扫频chirp信号,并叠加信噪比为40 dB的零均值高斯白噪声.分解层数为5,采样频率为1 kHz.分别使用Haar小波、db5小波、sym20小波、bior3.3小波和dmey小波对初始信号进行小波包分解,分解后的小波树终端节点、子频带能量分布和某一频带详细线谱信息如图 1~5所示.
|
图 1 Haar小波包基函数分解情况 Fig. 1 Decompositon of Haar wavelet packet basis function |
|
图 2 db5小波包基函数分解情况 Fig. 2 Decompositon of db5 wavelet packet basis function |

|
图 3 sym20小波包基函数分解情况 Fig. 3 Decompositon of sym20 wavelet packet basis function |
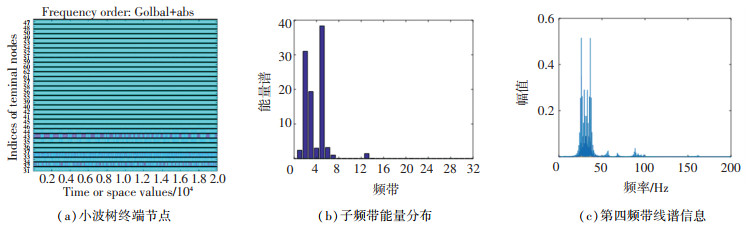
|
图 4 bior3.3小波包基函数分解情况 Fig. 4 Decompositon of bior3.3 wavelet packet basis function |
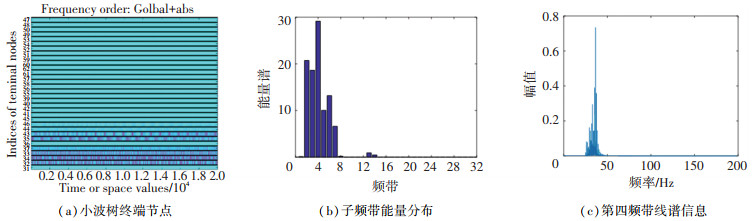
|
图 5 dmey小波包基函数分解情况 Fig. 5 Decompositon of dmey wavelet packet basis function |
纵观图 1~5可知,对参考信号中存在相近频率线谱进行小波包分解时,可得出以下结论:
1) Haar小波基函数分解后,线谱能量较为分散,在子频带内引起多根虚有线谱的振动,对于后续的自适应算法来说分解是失效的. 2)db5小波基函数分解后,线谱能量稍集中,但子频带内虚有线谱能量较大,不利于后续各个频带的并行控制策略. 3)sym20小波基函数分解后,线谱能量集中,子频带内虚有线谱能量较小,可用于后续控制算法实现. 4)bior3.3小波基函数分解后,线谱能量高度集中,导致某些含有目标线谱的频带能量过小,子频带内虚有线谱能量过大,分解失效. 5)dmey小波基函数分解后,线谱能量集中且近似均匀分布在含有目标线谱的频带内,子频带内主频能量高,虚有线谱能量很小,分解效果最佳.
综上所述,对于频率波动的复杂参考信号,dmey小波包基函数的分解效果最佳,sym20次之,其他小波基近似失效.根据上文仿真结果,小波包基函数的选择有以下标准:1)基函数在时频或频域内具有紧支撑正交性. 2)小波函数要具有近似对称性或对称性. 3)小波函数要具备良好的衰减性和快速收敛性.值得注意的是子频带中的虚有线谱,无论采取何种小波包均无法避免.
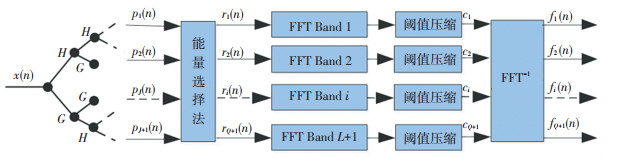
2 小波包最小均方算法 2.1 小波包分解改进算法小波包分解在频域内将频带进行等间隔线性划分,子频带中大部分不包含需要控制的线谱信息,对所有频带信号进行控制会极大增加滤波器个数和算法复杂度;且主线谱信号在自身频带或相邻频带内的能量映射导致频带内存在虚有线谱,会造成控制后出现其他线谱的振动.因此,需对小波包分解算法进行改进.
小波包分解过程中,数据量没有发生变化,仅把数据按照不同频带进行了分割.基于此,针对子频带数量过大的问题,使用能量选择法将子频带信号P1(n)、P2(n)...PJ(n) (J=2m)重新划分为Q+1个频带信号r1(n)、r2(n)...rQ+1(n),Q为需要控制的波动线谱个数.将原始子频带进行能量排序,按照从大到小的顺序取前Q个子频带作为划分后的新的第1~Q个子频带,剩余子频带信号叠加后作为第Q+1个新子频带. EPj(n)(j=1, ..., J)为原始子频带的能量值,Eri(n) (i=1, ..., Q+1)为划分后新的子频带的能量值.
假设j=k时,max EPj(n) =EPk(n),令
| $ {r_1}(n) = {P_k}(n), $ | (1) |
取出Pk(n),令
| $ {r_2}(n) = {P_s}(n)\;{\rm{max}}\left\{ {{E_{{P_{j(j \ne k)}}}}(n)} \right\} = {E_{{P_s}}}(n). $ | (2) |
以此类推,依次取出r3(n)、r4(n)...rQ(n).将剩余子频带叠加作为rQ+1(n).
此时,信号分解为Q+1个子频带信号,虚有线谱振动能量较小,可视为噪声,对子频带信号滤波要求只需保留子频带内较大线谱特征即可.使用阈值压缩进行滤波,消除虚有线谱对控制影响.虚有线谱本质上来说是能量映射或能量泄露造成的,进行阈值压缩后保留下来的线谱信号fi(n)与ri(n)相比,能量偏小.对阈值压缩后的各个子频带信号设置补偿系数ci,补偿系数由滤波前后子频带能量决定,能量计算时利用去相关性减小干扰噪声的影响.
| $ \begin{array}{l} {c_i} = {K_i} \cdot \frac{{{E_{{r_i}}}(n)}}{{{E_f}_i(n)}} = {K_i} \cdot \frac{{E\left[ {{r_i}(n){r_i}\left( {n - 1} \right)} \right]}}{{E\left[ {{f_i}(n){f_i}\left( {n - 1} \right)} \right]}}{\rm{ }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, 2, ..., Q + 1. \end{array} $ | (3) |
改进后的分解算法,不再直接将参考信号x(n)经小波包分解后的P1(n)、P2(n)...PJ(n)信号用于控制算法,小波包变换部分具体改进如图 6所示.
|
图 6 小波包改进分解算法 Fig. 6 Improved wavelet packet decomposition algorithm |
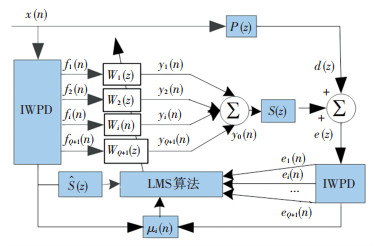
将小波包改进分解算法(Improved wavelet packet decomposition, IWPD)应用到FxLMS算法中,得到改进小波包自适应控制算法(Improved wavelet packet x-Least mean square, IWPx-LMS).算法结构如图 7所示.参考信号x(n)经IWPD分解为fi(n)(i=1, 2, ..., Q+1)一系列子频带信号.带频信号fi(n)与其对应控制器Wi(n)卷积即为此频带的控制输出信号yi(n), 叠加后即得到全频段控制输出信号y0(n),y0(n)经次级通道S(z)滤波后与经初级通道P(z)滤波得到的期望信号叠加形成了误差信号e(n). e(n)、变步长μ(n)和次级通道估计模型
|
图 7 IWPx-LMS算法结构图 Fig. 7 Algorithm structure diagram of IWPx-LMS |
设控制滤波器阶数为L时,辨识估计滤波器阶数为M, 则fi(n)的输入形式为
| $ {\mathit{\boldsymbol{f}}_i}(n) = {\left[ {{f_i}(n), {f_i}\left( {n - 1} \right), ..., {f_i}\left( {n - L + 1} \right)} \right]^{\rm{T}}}, $ | (4) |
第i个频带的控制滤波器Wi(n)可表示为
| $ {\mathit{\boldsymbol{W}}_i}(n) = {\left[ {{w_{i, 1}}, {w_{i, 2}}, ..., {w_{i, L}}} \right]^{\rm{T}}}, $ | (5) |
则有
| $ {y_i}(n) = \mathit{\boldsymbol{f}}_i^{\rm{T}}(n){\mathit{\boldsymbol{W}}_i}(n)\;\;\;\;\;i = 1, 2, ..., Q + 1, $ | (6) |
| $ \begin{array}{l} {e_i}(n) = {d_i}(n) + {\mathit{\boldsymbol{S}}^{\rm{T}}}(n){y_i}(n) = \\ \;\;\;\;\;\;\;\;\;\;\;{d_i}(n) + {\mathit{\boldsymbol{S}}^{\rm{T}}}(n)\mathit{\boldsymbol{f}}_i^{\rm{T}}(n){\mathit{\boldsymbol{W}}_i}(n). \end{array} $ | (7) |
根据梯度下降原理,控制器权系数更新如下:
| $ \begin{array}{l} {\mathit{\boldsymbol{W}}_i}(n + 1) = {\mathit{\boldsymbol{W}}_i}(n) - {u_i}(n){e_i}(n){{\mathit{\boldsymbol{\hat f}}}_i}(n)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, 2, ..., Q + 1, \end{array} $ | (8) |
其中,μi(n)为第i个频带的迭代步长,
| $ {{\mathit{\boldsymbol{\hat f}}}_i}(n) = \hat S(z){\mathit{\boldsymbol{f}}_i}(n) = \sum\limits_{j = 0}^{M - 1} {{{\hat s}_j}{f_i}(n - j)} . $ | (9) |
分解后的频带信号自相关矩阵特性不同,其迭代步长μi(n)的取值范围也不同.收敛速度和稳态误差对于μi(n)的要求本就是相悖的,缓解两者间的矛盾则要求控制前期采用较大步长获得较快收敛速度,后期基本稳定时采用小步长减小稳态误差.本文基于改进的箕舌线函数来设计迭代步长,将对应频带的参考信号和误差信号引入到迭代步长的更新中,即
| $ \begin{array}{l} {u_i}(n + 1) = {\alpha _i}{u_i}(n) + \\ \;\;\;\;\;{\beta _i}\left[ {1 - \frac{{{\rm{eps}}}}{{\mathit{\boldsymbol{f}}_i^{\rm{T}}(n){\mathit{\boldsymbol{f}}_i}(n) + {\gamma _i}{E_i}(n) + 1}}} \right]. \end{array} $ | (10) |
式中:αi、βi为可调参数;eps为常数,与分解信号Pi(n)输入特性相关;γi为控制残差影响因子,直接决定了步长的变化速度;为了减小误差信号中的干扰对迭代步长的影响,Ei(n)不再是误差信号能量,而是利用去相关性减小干扰的影响,Ei(n)=E[ei(n)ei(n-1)].
式(6)、式(8)~(10)即为各个子频带控制参数更新迭代过程,并联后即构成IWPx-LMS算法.
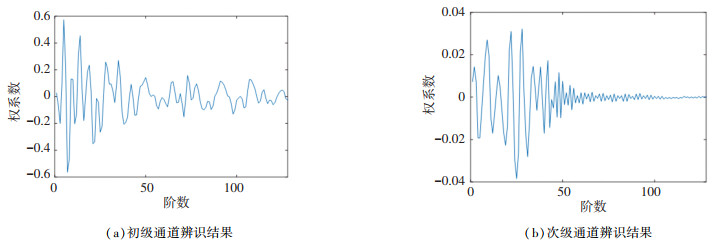
3 数值仿真分析为评价IWPx-LMS算法性能,基于matlab/simulink进行仿真分析,分别用前馈FxLMS算法和IWPx-LMS算法对四波动线谱激励进行主动控制仿真分析.为使仿真结果更加贴近试验,模型中所用初级通道和次级通道均通过实验数据辨识得到,阶数均为128阶,具体如图 8所示.
|
图 8 通道参数辨识 Fig. 8 Identification of path parameter |
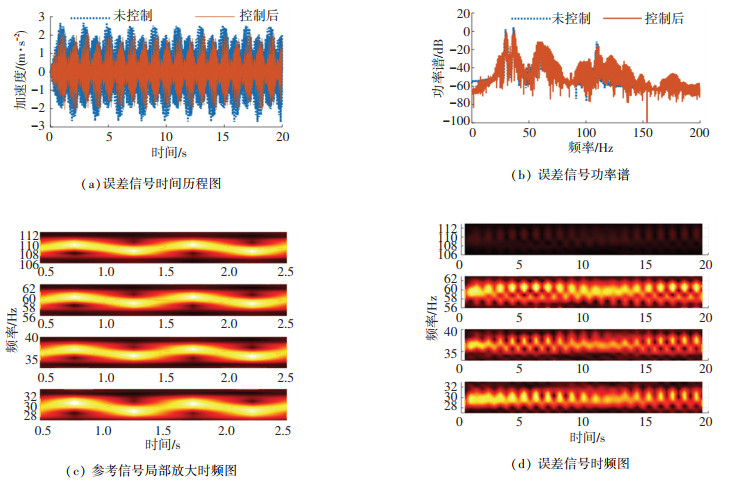
按照通道辨识结果设置初级通道和次级通道,控制滤波器阶数为128,采样频率1 kHz,小波包分解层数为5,小波基“dmey”. FxLMS算法步长5e-5,控制滤波器个数1;IWPx-LMS算法控制滤波器个数为5.仿真结果如图 9、图 10所示.
|
图 9 FxLMS算法控制效果 Fig. 9 Control effect of FxLMS algorithm |
|
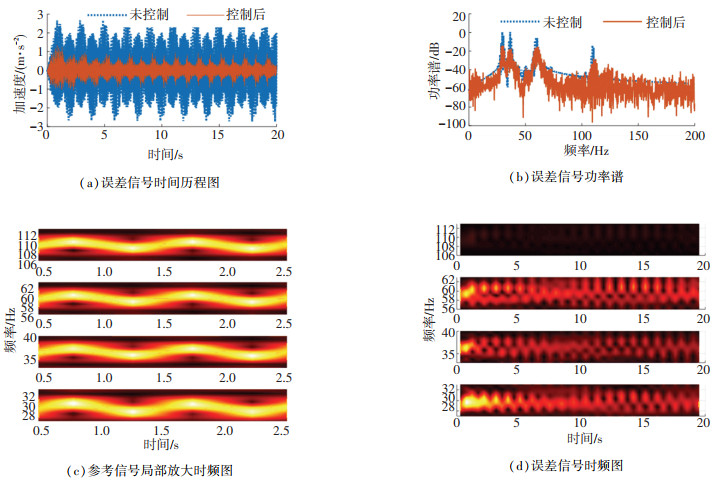
图 10 IWPx-LMS算法控制效果 Fig. 10 Control effect of IWPx-LMS algorithm |
由图 9、图 10可知:FxLMS算法对于多频波动线谱基本无控制效果,振幅无明显减小,控制后各线谱能量基本无衰减;IWPx-LMS算法控制后,振幅降幅达80%,各扫频线谱平均衰减可达19 dB,控制开启7 s后,时频图上的误差信号振动特征不再明显,控制效果良好.
4 试验研究搭建隔振试验台架,基于NI-PXIe控制系统进行主动控制试验.试验台架主要包括:激振器、主被动复合隔振器、加速度传感器、上层板、下层基座和立柱导轨等.测控系统主要包括:PXIe-8880控制器、A/D采集板卡PXI-4498、D/A输出板卡PXI-6733、机箱PXIe-1062Q、功率放大器Xenus XTL-230-36、接线盒、电缆等.激振器上的加速度信号作为参考信号,下层基座加速度信号为误差信号,将其控制前后的功率谱衰减作为振动评价指标.控制系统工作原理为:激励信号由控制器发出,经D/A输出至攻放,驱动激振器产生初始振动;采集参考信号和误差信号经A/D输入至控制器,经算法计算得出控制输出信号,经D/A输出至功放,驱动主被动一体化作动器产生控制力,抵消激振器产生的初始振动,控制完成.参数设置与仿真参数一致,连接实物图如图 11所示.

|
图 11 控制系统实物图和台架示意图 Fig. 11 Control system and schematic diagram of bench |
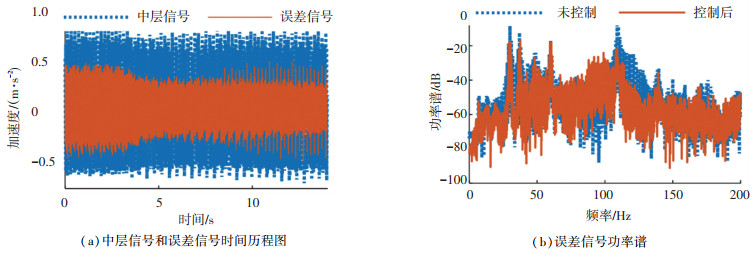
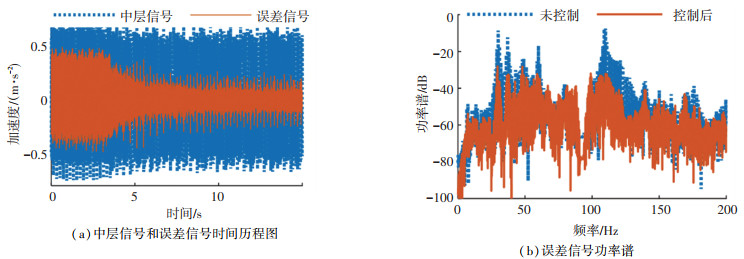
图 12和图 13分别是FxLMS算法和IWPx-LMS算法误差信号时间历程和功率谱. 3 s后施加控制,直到待控制点的振动响应得到抑制.
|
图 12 FxLMS算法试验结果 Fig. 12 Experimental effect of FxLMS algorithm |
|
图 13 IWPx-LMS算法试验结果 Fig. 13 Experimental effect of IWPx-LMS algorithm |
从时间历程图上可知,被动隔振下误差信号较之中层加速度信号有所衰减. FxLMS算法对于波动线谱几乎无控制效果,仅个别线谱稍有衰减. IWPx-LMS算法控制后,误差信号幅值降幅达82%,5 s内完成收敛,有较快的收敛速度;线谱功率谱衰减明显,平均可达22 dB.试验结果证明,基于“dmey”基函数的改进小波包分解算法,很好地改善了FxLMS算法的收敛性能,在多频波动线谱激励下,能够取得良好的控制效果.
5 结论多频波动线谱激励下,前馈FxLMS算法无法进行多频波动线谱的有效控制,基于此,本文提出了改进小波包自适应控制算法(IWPx-LMS),利用小波包分解将信号进行频带划分,然后采取并行控制的策略,在每个子频带中利用改进箕舌线函数设计迭代步长,搭建控制系统和试验台架验证算法的可行性,得出以下结论:
1) “dmey”小波基为IWPx-LMS算法最优小波基.小波包基函数选取原则:基函数在时频或频域内具有紧支撑正交性、近似对称性或对称性、良好的衰减性和快速收敛性.
2) 根据箕舌线函数设计变步长,使系统具有较快的收敛速度和较小的稳态误差.
3) 数值仿真和试验结果均表明,IWPx-LMS算法在多频波动线谱激励下能够取得良好的控制效果,线谱振动能量显著降低,平均降幅可达22 dB.
| [1] |
朱石坚, 何琳. 船舶机械振动控制[M]. 北京: 国防工业出版社, 2003.
|
| [2] |
FULLER C R, ELLIOTT S J, NELSON P A. Active control of vibration[M]. San Diego: Academic Press, 1996.
|
| [3] |
陈绍青, 王永, 魏璀璨, 等. 一类多频线谱激励下的主动隔振控制方法[J]. 振动与冲击, 2012, 31(23): 128. CHEN Shaoqing, WANG Yong, WEI Cuican, et al. An active vibration isolation control method under excitation of multi-line spectra[J]. Journal of Shock and Vibration, 2012, 31(23): 128. DOI:10.13465/j.cnki.jvs.2012.23.018 |
| [4] |
SUN H L, ZHANG P Q, GONG X L, et al. A novel kind of active resonator absorber and the simulation on its control effort[J]. Journal of Sound and Vibration, 2007, 300(2): 117. DOI:10.1016/j.jsv.2006.07.040 |
| [5] |
SNYDER S D. The effect of transfer function estimation errors on the filtered-x LMS algorithm[J]. IEEE Trans Signal Process, 1994, 42(4): 950. DOI:10.1109/78.285659 |
| [6] |
DALEY S, JOHNSON F A, PEARSON J B, et al. Active vibration control for marine application[J]. Control Engineering Practice, 2004(12): 465. DOI:10.1016/S0967-0661(03)00135-7 |
| [7] |
AN Fengyan, SUN Hongling, LI Xiaodong, et al. Optimization of parameters in decentralized adaptive control algorithm[J]. Journal of Vibration Engineering, 2013, 26(1): 48. DOI:10.16385/j.cnki.issn.1004-4523.2013.01.005 |
| [8] |
赵洪亮. 选频有源噪声控制系统控制算法的理论与实验研究[D]. 北京:中国科学院, 2004 ZHAO Hongliang.Theoretical and experimental research on control algorithm of active noise control based on frequency-selected filter[D]. Beijing: Chinese Academy of Sciences, 2004 |
| [9] |
JEON H J, CHANG T G, YU S, et al. A narrowband active noise control system with frequency corrector[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(4): 990. DOI:10.1109/TASL.2010.2073705 |
| [10] |
张志谊, 王俊芳, 周建鹏, 等. 基于跟踪滤波的自适应振动控制[J]. 振动与冲击, 2009, 28(2): 64. ZHANG Zhiyi, WANG Junfang, ZHOU Jianpeng, et al. A adaptive vibration control with tracking filters[J]. Journal of Shock and Vibration, 2009, 28(2): 64. DOI:10.13465/j.cnki.jvs.2009.02.043 |
| [11] |
LI Yan, HE Lin, SHUAI Changgeng. Time-domainfiltered-x-Newton narrowband algorithms for active isolation of frequency-fluctuating vibration[J]. Journal of Sound and Vibration, 2016, 367: 1. DOI:10.1016/j.jsv.2015.12.019 |
| [12] |
浦玉学, 张方, 姜金辉. 变步长自适应结构振动主动控制算法[J]. 振动与冲击, 2015, 34(10): 199. PU Yuxue, ZHANG Fang, JIANG Jinhui. A varying step adaptive algorithm for structural vibration active control[J]. Journal of Shock and Vibration, 2015, 34(10): 199. DOI:10.13465/j.cnki.jvs.2015.10.035 |
| [13] |
路翠华, 李国林, 周洪庆, 等. 基于相关特性的改进箕舌线变步长LMS算法[J]. 数据采集与处理, 2015, 30(4): 896. LU Cuihua, LI Guolin, ZHOU Hongqing, et al. Improved tonguelike curve variable step LMS algorithm based on correlation characteristic[J]. Journal of Data Acquisition and Processing, 2015, 30(4): 896. DOI:10.16337/j.1004-9037.2015.04.0023 |
| [14] |
侯新国, 牛超, 杨忠林. 基于最优Morlet小波自适应包络解调的弱故障特征提取方法[J]. 电机与控制学报, 2016, 20(10): 88. HOU Xingguo, NIU Cao, YANG Zhonglin. Method to extract weak fault feature based on optimal Morlet wavelet adaptive envelope demodulation[J]. Electric Machines and Control, 2016, 20(10): 88. DOI:10.15938/j.emc.2016.10.012 |
| [15] |
邢峰. 小波自适应算法在车身振动主动控制中的应用[J]. 农业工程学报, 2015, 31(20): 62. XING Feng. Application of adaptive wavelet algorithm in active vibration control for vehicle[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(20): 62. DOI:10.11975/j.issn.1002-6819.2015.20.009 |
 2021, Vol. 53
2021, Vol. 53


