2. 载运工具与装备教育部重点实验室(华东交通大学),南昌 330013;
3. 华南农业大学 工程学院,广州 510642;
4. 广东振声科技股份有限公司,广东 梅州 514700
2. Key Laboratory of Transportation Tools and Equipment, Ministry of Education(University of East China Jiaotong University), Nanchang 330013, China;
3. College of Engineering, University of South China Agricultural University, Guangzhou 510642, China;
4. Guangdong Zhensheng Technology Co. Ltd., Meizhou 514700, Guangdong, China
随着我国水果产业的壮大,实现果园运输机械化不仅仅是农业机械化的一个重要组成部分,同时也是水果产业不断发展的重要标志.传统的果园种植缺少科学合理规划,立地条件差,果树大多生长在难以形成较完善交通运输网,甚至是陡峭的梯田上.这就导致了常规的水果采运车难以在该环境下推广使用,直接给成熟果子的运输造成了较大的困难[1].目前,我国90%的柑橘种植在山地,土地条件差,山地果园机械化水平低,生产主要靠人力完成,劳动强度非常大.特别是山地果园肥料和果品运送方面主要靠肩挑或背篓背负,必须用机械化代替艰苦的劳动.柑橘产业要持续发展,农机农艺相融合是唯一出路.未来强壮的“果农”就是农机农艺融合[2].山地果园钢丝绳牵引式双轨运输机是一种由钢丝绳牵引,载物滑车沿着具有一定坡度的轨道行驶的运载工具,轨道由2条相互平行的圆管及辅助横梁焊接而成,轨道坡度集中在10°~40°之间[3].国内外已研制出多种山地果园轨道运输机械,山地果园牵引式双轨运输机是其中一种代表机型[4].该运输机缓解了山地地区果农的劳动强度,有效实现了果品及其他农资省力化运载需求[5].由于运输机作业环境复杂,运载果品时若频繁振荡,易造成钢丝绳振荡冲击损伤,因此有必要对该类运输机的牵引系统的失效行为及钢丝绳受力情况进行研究[6].
钢丝绳是一种金属结构,在许多工业工程、海洋工程和土木工程领域已经使用了很长一段时间[7-8],在吊桥、起重机、建筑电梯和矿井提升机等领域也有其应用[9-10].钢丝绳经常被使用,因为它们具有较高的抗拉强度和弯曲灵活性[11],而且与其他结构相比,它们具有更高的强度和更长的寿命[12].在理论推导、实验研究和有限元模拟这三种途径中,几何模型是研究钢丝绳力学模型及失效行为的研究基础.通过精确的数学表达式,建立钢丝绳的精确几何模型,从而进行相应的力学分析[13].王等[14]提出了钢丝绳和股线中心线的数学表示及其半径的计算方法, 给出了钢丝绳和股线缠绕关系的空间参数几何方程,并用经验值或迭代法以外的方法计算钢丝和钢绞线的半径是合理的. I.I. Argatov等[15]建立了基于Archard-Kragelsky磨损定律的微动磨损数学模型,并给出了磨损定律参数校准的示例. W. Ma等[16]首先推导出每根导线的质心轴(单、双或三螺旋)的坐标方程,然后利用MatlabTM生成形成该轴的控制点坐标的数据文件,最后根据得到的基螺旋的坐标方程,用递推法建立了高水平螺旋.吴等[17]利用Frenet框架和微分几何建立了钢丝绳二次螺旋的数学模型, 并在此基础上推导出二次螺旋线的几何参数,利用Love弹性细杆理论建立钢丝绳的等效力学模型,推导出钢丝绳的等效弹性模量和等效剪切模量的计算公式. Ivan Argatov[18]建立了简单螺旋钢丝绳股的精细离散数学模型,通过泊松比和局部接触变形(钢丝压扁)研究了钢绞线横向收缩的影响.
以上研究都对不同环境下的钢丝绳给出了精准的空间几何表达式,目的都是为了更好地研究钢丝绳力学性能及其失效行为,但针对山地轨道运载机牵引钢丝绳的空间几何表达式目前还没有明确的定论.因此,本文为了后续更深入研究山地轨道运载机牵引钢丝绳力学模型的建立与损伤机理的研究,对适用于山地轨道运载机牵引钢丝绳的空间几何结构进行数学公式推导,同时推导了曲率及挠率方程及其连续变化规律,这样有利于减少在不同参数和操作条件下进行昂贵的试验测试的需要.
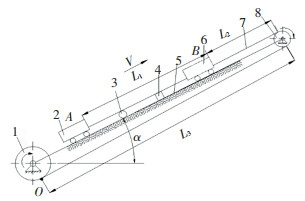
1 运输机钢丝绳选型及捻制特征 1.1 运输机钢丝绳选型山地轨道牵引式双轨运输机属于新式农用运输机,钢丝绳应用特点与矿山或港口起重机等有较大差别,需对钢丝绳绳径进行重新计算,避免绳径选择不适,造成浪费或强度不够.运输机钢丝绳作业时,钢丝绳在卷筒、约束轮及滑轮等约束下沿弯曲轨道转弯运行,应用工况与农用索道类似,选用圆股线接触右交互捻(SZ),型号为6×19+FC类钢丝绳[19].在前面研究中建立钢丝绳牵引系统虚拟样机模型[4],简化示意图如图 1所示,图 1中A点为载物滑车最低滑行位置,B点为载物滑车最高滑行位置.
|
1—卷筒; 2—载物滑车; 3—托辊; 4—横梁; 5—轨道; 6—载物滑车; 7—钢丝绳; 8—滑轮 图 1 运输机牵引系统示意图 Fig. 1 Structure of transport traction system |
钢丝绳最大有效长度与整绳最小破断拉力应满足式(1)、式(2)[20],当载物滑车运行至A点时,钢丝绳与卷筒相接处O点承受最大的静拉力如式(3)所示,钢丝绳质量如式(4)[20]所示,整绳最大静拉力如式(5)所示:
| $ {L = {L_1} + {L_2} + {L_3}, } $ | (1) |
| $ {{F_{\max }} = \frac{{{F_{\min }}}}{{{K_a}}}, } $ | (2) |
| $ {F_{\max }} - Mg(\sin \alpha + {f_1}\cos \alpha ) + mgL(\sin \alpha + {f_2}\cos \alpha ), $ | (3) |
| $ m = {K_g}{D^2}, $ | (4) |
| $ {F_{\max }} = Mg(\sin \alpha + {f_1}\cos \alpha ) + {K_g}{D^2}gL(\sin \alpha + {f_2}\cos \alpha ). $ | (5) |
式中:Fmax为整绳最大静拉力,kN;Fmin为钢丝绳最小破断拉力,kN;Ka为钢丝绳许用安全系数;L1为A、B两点间距离,m;L2为B点至顶端滑轮距离,m;L3为卷筒至顶端滑轮距离,m;M为载物滑车及所载物资总质量,kg;g为重力加速度,m/s2;α为轨道倾角,°;f1为轮轨间滚动摩擦系数;f2为钢丝绳与托辊间摩擦系数;m为钢丝绳质量,kg/m;D为钢丝绳公称直径,mm;Kg为钢丝绳重量系数,kg/100 m·mm2.
钢丝绳最小破断拉力Fn、钢丝绳破断拉力总和Fmin[21]为
| $ {{F_n} = {K_{\min }}{D^2}{E_t}, } $ | (6) |
| $ {{F_{\min }} = {K_h}{F_n}, } $ | (7) |
式中:Et为钢丝绳公称抗拉强度,MPa;Kmin为钢丝绳最小破断拉力系数;Kh为破断拉力换算系数.
将式(6)代入式(7)得
| $ {F_{\min }} = {K_h}{K_{\min }}{D^2}{E_t}, $ | (8) |
将式(5)及式(8)代入式(2)得如下关系式:
| $ \begin{array}{l} Mg(\sin \alpha + {f_1}\cos \alpha ) + {K_g}{D^2}gL(\sin \alpha + {f_2}\cos \alpha ) \le \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{K_h}{K_{\min }}{D^2}{E_t}}}{{{K_a}}}, \end{array} $ | (9) |
| $ d \ge \sqrt {\frac{{M(\sin \alpha + {f_1}\cos \alpha )}}{{\frac{{{K_h}{K_{\min }}{E_t}}}{{{K_a}g}} - {K_g}L(\sin \alpha + {f_2}\cos \alpha )}}} . $ | (10) |
对于6×19+FC钢丝绳,f1取0.05,f2取0.1[19];重量系数Kg取0.36,最小破断拉力系数Kmin取0.338,破断拉力换算系数Kh取1.214,g取9.8 m/s2;Ka取7,α取40°,M取500 kg,L取200 m;Et取1 670 MPa[20];于是
| $ \begin{array}{*{20}{l}} {d \ge \sqrt {\frac{{500(\sin {{40}^\circ } + 0.05\cos {{40}^\circ })}}{{\frac{{1.214 \times 0.338 \times 1670}}{{9.8 \times 7.1}} - 0.36 \times 2(\sin {{40}^\circ } + 0.1\cos {{40}^\circ })}}} \approx }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 6.03{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{mm}}{\rm{.}}} \end{array} $ |
查阅机械设计手册[19],选取钢丝绳的直径为7.7 mm.
1.2 钢丝绳捻制特征6×19+FC类圆股右交互捻钢丝绳由侧丝绕中心丝左旋捻制成单股,再由6侧股绕绳芯右旋捻制而成,侧股侧丝由内层丝及外层丝组成.所采用绳芯材质为纤维,因此该类钢丝绳只有螺旋股,无直股.钢丝绳捻制示意图如图 2所示,每股由1条中心丝,6条内层丝与12条外层丝捻制而成.为便于阐述钢丝间空间位置关系,对股及丝进行编号,以初始截面最左端为第1股,逆时针依次编为第1、2、3、4、5、6股;侧股中心丝逆时针依次编为1、2、3、4、5、6丝;侧股内层丝以每股中心线与绳芯中心线连线逆时针的第一钢丝中心为第01丝,逆时针依次编为第02、03、04、05、06丝;外层丝以每股中心线与绳芯中心线连线逆时针的第一钢丝中心为第07丝,逆时针依次编为第08、09、10、11、12、13、14、15、16、17、18丝.

|
1—侧股; 2—侧股单丝; 3—整绳; 4—纤维绳芯; r0—绳芯至股芯中心距; r1—内层丝芯至股芯中心距; r2—外层丝芯至股芯中心距 图 2 钢丝绳捻制示意图 Fig. 2 Wire rope twisting diagram |
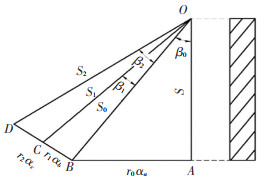
将整绳解剖后依次展开,如图 3所示,β0、β1、β2分别表示股在绳中、内层丝在股中、外层丝在股中的捻角;r0、r1、r2分别表示股在绳中螺旋半径(捻制半径)、内层丝在股中螺旋半径、外层丝在股中螺旋半径;S、S0、S1、S2分别表示整绳、侧股(中心丝)、侧股内层丝、侧股外层丝长度;αa、αb、αc分别表示钢丝绳在捻制过程中,股在绳中转过的角度、内层丝在股中转过的角度、外层丝在股中转过的角度.
|
图 3 钢丝绳展开示意图 Fig. 3 Wire rope expansion diagram |
由图 3几何位置可知:
| $ AB = {r_0}{\alpha _a}, BC = {r_1}{\alpha _b}, BD = {r_2}{\alpha _c}, $ | (11) |
由钢丝绳已知数据和几何关系可得
| $ {r_1} = 0.50{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{mm}}, {r_2} = 0.97{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{mm}}, {r_0} = 2.63{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{mm}}, $ |
| $ {\beta _0} = {18.30^\circ }, {\beta _1} = {7.16^\circ }, {\beta _2} = {13.10^\circ }. $ |
结合钢丝绳已求结构参数,型号为6×19+FC钢丝绳的关键几何参数,如表 1所示.
| 表 1 运输机钢丝绳几何参数 Tab. 1 Geometric parameters of transport wire rope |
直线段钢丝绳六侧股一次螺旋线的初始捻制角依次记为θ1、θ2、θ3、θ4、θ5及θ6,以逆时针为正,初始捻制角分别为0°、60°、120°、180°、240°、300°;侧股中6条内层丝二次螺旋线的初始捻制角θ01~θ06分别为45°、105°、165°、225°、285°、345°;侧股中12条外层丝二次螺旋线的初始捻制角θ07~θ18分别为0°、30°、60°、90°、120°、150°、180°、210°、240°、270°、300°、330°.
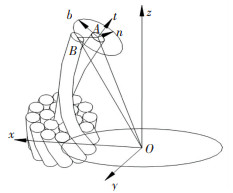
本文以第1股及第1股第18丝为研究对象,建立直线段钢丝绳空间曲线模型,如图 4所示. 图 4中侧股中心丝中心线上点A用向量OA表示,侧丝中心线上点B用OB表示,点A处的切向量、法向量、从法向量依次记为t、n、b.设向量AB为Frenet标架n-b-t内的平面矢量,则侧丝空间二次螺旋线可由向量OB=OA+AB表示.
|
图 4 钢丝绳第1股中心丝及其第18丝空间曲线模型 Fig. 4 Space curve model of first share center wire and its eighteenth wire |
令向量OA在x-y-z标架上为OAx,向量AB在n-b-t标架上为ABn,由图 4钢丝的位置关系及钢丝绳已知参数可得
| $ \mathit{\boldsymbol{O}}{\mathit{\boldsymbol{A}}^x} = \left\{ {\begin{array}{*{20}{l}} x\\ y\\ z \end{array}} \right\} = \left\{ {\begin{array}{*{20}{l}} {{r_0}\cos ({\theta _1} + {\alpha _a})}\\ {{r_0}\sin ({\theta _1} + {\alpha _a})}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{r_0}{\alpha _a}}}{{\tan {\beta _0}}}} \end{array}} \right\}, $ | (12) |
| $ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^n} = \left\{ {\begin{array}{*{20}{l}} n\\ b\\ t \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{r_2}\cos ({\theta _{18}} - {\alpha _c})}\\ {{r_2}\sin ({\theta _{18}} - {\alpha _c})}\\ 0 \end{array}} \right\}. $ | (13) |
侧股缠绕于绳芯转换矩阵[n, b, t]表达式为
| $ [n, b, t] = \left[ {\begin{array}{*{20}{c}} { - \cos ({\theta _1} + {\alpha _a})}&{\cos {\beta _0}\sin ({\theta _1} + {\alpha _a})}&{ - \sin {\beta _0}\sin ({\theta _1} + {\alpha _a})}\\ { - \sin ({\theta _1} + {\alpha _a})}&{ - \cos {\beta _0}\cos ({\theta _1} + {\alpha _a})}&{\sin {\beta _0}\cos ({\theta _1} + {\alpha _a})}\\ 0&{\sin {\beta _0}}&{\cos {\beta _0}} \end{array}} \right]. $ | (14) |
为求向量OB在坐标系x-y-z的表达式,ABn需转换为x-y-z标架表达式ABx.由空间坐标变换原理可知,向量AB在坐标系x-y-z中表达式可表示为
| $ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^x} = [n, b, t] \times \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^n}. $ | (15) |
将式(13)及(14)代入式(15)可得
| $ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^x} = [n, b, t] \times \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^n} = \left\{ {\begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {r_2}[\cos {\beta _0}\sin ({\theta _1} + {\alpha _a})\sin ({\theta _{18}} - {\alpha _c}) - \cos ({\theta _1} + {\alpha _a})\cos ({\theta _{18}} - {\alpha _c})]}\\ {{r_2}[ - \cos {\beta _0}\cos ({\theta _1} + {\alpha _a})\sin ({\theta _{18}} - {\alpha _c}) - \sin ({\theta _1} + {\alpha _a})\cos ({\theta _{18}} - {\alpha _c})]}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {r_2}\sin {\beta _0}\sin ({\theta _{18}} - {\alpha _c})} \end{array}} \right\}. $ | (16) |
由式(12)及(16)可知,向量OB在坐标系x-y-z中表达式为
| $ \mathit{\boldsymbol{O}}{\mathit{\boldsymbol{B}}^x} = \mathit{\boldsymbol{O}}{\mathit{\boldsymbol{A}}^x} + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^x} = \left\{ {\begin{array}{*{20}{c}} {{r_0}\cos ({\theta _1} + {\alpha _a}) + {r_2}[\cos {\beta _0}\sin ({\theta _1} + {\alpha _a})\sin ({\theta _{18}} - {\alpha _c}) - \cos ({\theta _1} + {\alpha _a})\cos ({\theta _{18}} - {\alpha _c})]}\\ {{r_0}\sin ({\theta _1} + {\alpha _a}) + {r_2}[ - \cos {\beta _0}\cos ({\theta _1} + {\alpha _a})\sin ({\theta _{18}} - {\alpha _c}) - \sin ({\theta _1} + {\alpha _a})\cos ({\theta _{18}} - {\alpha _c})]}\\ {\frac{{{r_0}{\alpha _a}}}{{\tan {\beta _0}}} + {r_2}\sin {\beta _0}\sin ({\theta _{18}} - {\alpha _c})} \end{array}} \right\}. $ | (17) |
令
| $ \left\{ {\begin{array}{*{20}{l}} {{e_1} = \frac{{{r_0}\tan {\beta _1}}}{{{r_1}\sin {\beta _0}}}, }\\ {{e_2} = \frac{{{r_0}\tan {\beta _2}}}{{{r_2}\sin {\beta _0}}}, } \end{array}} \right. $ | (18) |
由式(12)可得,直线段钢丝绳第i股中心丝方程表达式:
| $ \mathit{\boldsymbol{OA}}_i^x = \left\{ {\begin{array}{*{20}{l}} x\\ y\\ z \end{array}} \right\} = \left\{ {\begin{array}{*{20}{l}} {{r_0}\cos ({\theta _i} + {\alpha _a})}\\ {{r_0}\sin ({\theta _i} + {\alpha _a})}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{r_0}{\alpha _a}}}{{\tan {\beta _0}}}} \end{array}} \right\}. $ | (19) |
将式(18)带入(17)可得直线段钢丝绳第i股内层第j丝空间方程表达式与直线段钢丝绳第i股外层丝第k丝方程表达式:
| $ \mathit{\boldsymbol{OB}}_{ij}^x = \left[ {\begin{array}{*{20}{c}} {{r_0}\cos ({\theta _i} + {\alpha _a}) + {r_1}[\cos {\beta _0}\sin ({\theta _i} + {\alpha _a})\sin ({\theta _j} - {e_1}{\alpha _a}) - \cos ({\theta _i} + {\alpha _a})\cos ({\theta _j} - {e_1}{\alpha _a})]}\\ {{r_0}\sin ({\theta _i} + {\alpha _a}) + {r_1}[ - \cos {\beta _0}\cos ({\theta _i} + {\alpha _a})\sin ({\theta _j} - {e_1}{\alpha _a}) - \sin ({\theta _i} + {\alpha _a})\cos ({\theta _j} - {e_1}{\alpha _a})]}\\ {\frac{{{r_0}{\alpha _a}}}{{\tan {\beta _0}}} + {r_1}\sin {\beta _0}\sin ({\theta _j} - {e_1}{\alpha _a})} \end{array}} \right], $ | (20) |
| $ \mathit{\boldsymbol{OB}}_{ik}^x = \left[ {\begin{array}{*{20}{c}} {{r_0}\cos ({\theta _i} + {\alpha _a}) + {r_2}[\cos {\beta _0}\sin ({\theta _i} + {\alpha _a})\sin ({\theta _k} - {e_2}{\alpha _a}) - \cos ({\theta _i} + {\alpha _a})\cos ({\theta _k} - {e_2}{\alpha _a})]}\\ {{r_0}\sin ({\theta _i} + {\alpha _a}) + {r_2}[ - \cos {\beta _0}\cos ({\theta _i} + {\alpha _a})\sin ({\theta _k} - {e_2}{\alpha _a}) - \sin ({\theta _i} + {\alpha _a})\cos ({\theta _k} - {e_2}{\alpha _a})]}\\ {\frac{{{r_0}{\alpha _a}}}{{\tan {\beta _0}}} + {r_2}\sin {\beta _0}\sin ({\theta _k} - {e_2}{\alpha _a})} \end{array}} \right]. $ | (21) |
运输机钢丝绳弯曲段体现在钢丝绳与约束轮、滑轮及卷筒接触,如图 5所示.为研究钢丝绳弯曲段空间螺旋方程,以钢丝绳绕过滑轮为例进行说明.绳与轮接触时,绳中心轴线呈弯曲圆弧状态,绳中各股股芯中心线绕滑轮圆弧呈空间一次螺旋线,侧股侧丝中心线绕圆弧呈二次螺旋线,如图 6所示.
|
图 5 弯曲段钢丝绳接触示意图 Fig. 5 Contact sketch of bending section of wire rope |
|
1—钢丝绳中心路径; 2—钢丝绳单股中心路径; 3—钢丝绳单股侧丝中心路径 图 6 过滑轮时钢丝绳钢丝缠绕示意图 Fig. 6 Contact diagram of wire rope when winding pulley |
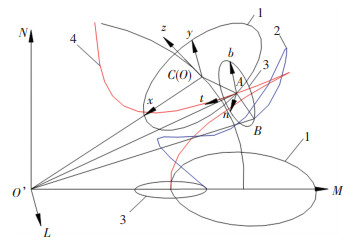
为构建弯曲段钢丝绳空间螺旋方程,建立绳轮接触空间曲线模型,如图 7所示.以动点C替代直线段钢丝绳坐标系原点O,建立弯曲段钢丝绳空间直角坐标系LMN. 图 7中一次螺旋线绕弧线旋转,二次螺旋线绕一次螺旋线旋转,弯曲状态侧丝中心线的二次螺旋线向量O′B的表达式为
| $ {\mathit{\boldsymbol{O}}^\prime }\mathit{\boldsymbol{B}} = {\mathit{\boldsymbol{O}}^\prime }\mathit{\boldsymbol{C}} + \mathit{\boldsymbol{CA}} + \mathit{\boldsymbol{AB}}. $ | (22) |
|
1—侧股螺旋半径(整绳螺旋半径)对应圆; 2—侧股侧丝中心线;3—侧股侧丝螺旋半径画出的圆; 4—侧股股芯中心线 图 7 过滑轮时钢丝绳空间曲线模型 Fig. 7 Wire rope space curve model when winding pulley |
图 7中,将x-y-z标架上的一次螺旋线与二次螺旋线分别视为建立在新标架L-M-N弯曲一次螺旋线与二次螺旋线,则向量O′C在标架L-M-N的表达式O′Cl为
| $ {\mathit{\boldsymbol{O}}^\prime }{\mathit{\boldsymbol{C}}^l} = \left\{ {\begin{array}{*{20}{l}} l\\ m\\ n \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} 0\\ {{r_3}\cos {\alpha _d}}\\ {{r_3}\sin {\alpha _d}} \end{array}} \right\}. $ | (23) |
式中:αd为钢丝绳在滑轮中转过角度;r3为滑轮圆心到钢丝绳绳芯距离.
标架x-y-z向标架L-M-N转换,对坐标系LMN的转换矩阵为
| $ [X, Y, Z] = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ { - \cos {\alpha _d}}&0&{ - \sin {\alpha _d}}\\ { - \sin {\alpha _d}}&0&{\cos {\alpha _d}} \end{array}} \right], $ | (24) |
标架n-b-t对坐标系LMN的转换矩阵[N, B, T]为
| $ \begin{array}{l} [N, B, T] = [X, Y, Z] \times [n, b, t] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} { - \sin ({\theta _1} + {\alpha _a})}&{ - \cos {\beta _0}\cos ({\theta _1} + {\alpha _a})}&{\sin {\beta _0}\cos ({\theta _1} + {\alpha _a})}\\ {\cos {\alpha _d}\cos ({\theta _1} + {\alpha _a})}&{ - \sin {\beta _0}\sin {\alpha _d} - \cos {\beta _0}\cos {\alpha _d}\sin ({\theta _1} + {\alpha _a})}&{ - \cos {\beta _0}\sin {\alpha _d} + \sin {\beta _0}\cos {\alpha _d}\sin ({\theta _1} + {\alpha _a})}\\ {\sin {\alpha _d}\cos ({\theta _1} + {\alpha _a})}&{\sin {\beta _0}\cos {\alpha _d} - \cos {\beta _0}\sin {\alpha _d}\sin ({\theta _1} + {\alpha _a})}&{\cos {\beta _0}\cos {\alpha _d} + \sin {\beta _0}\sin {\alpha _d}\sin ({\theta _1} + {\alpha _a})} \end{array}} \right]. \end{array} $ | (25) |
ABn转换为坐标系LMN上的表达式ABl为
| $ \begin{array}{l} \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^l} = [N, B, T] \times \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^n} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{c}} { - {r_2}\sin ({\theta _1} + {\alpha _a})\cos ({\theta _{18}} - {\alpha _c}) - {r_2}\cos {\beta _0}\cos ({\theta _1} + {\alpha _a})\sin ({\theta _{18}} - {\alpha _c})}\\ {{r_2}\cos {\alpha _d}\cos ({\theta _1} + {\alpha _a})\cos ({\theta _{18}} - {\alpha _c}) - {r_2}\sin ({\theta _{18}} - {\alpha _c})[\cos {\beta _0}\cos {\alpha _d}\sin ({\theta _1} + {\alpha _a}) - \sin {\beta _0}\sin {\alpha _d}]}\\ {{r_2}\sin {\alpha _d}\cos ({\theta _1} + {\alpha _a})\cos ({\theta _{18}} - {\alpha _c}) - {r_2}\sin ({\theta _{18}} - {\alpha _c})[\cos {\beta _0}\sin {\alpha _d}\sin ({\theta _1} + {\alpha _a}) + \sin {\beta _0}\cos {\alpha _d}]} \end{array}} \right\}. \end{array} $ | (26) |
由图 7可知,弯曲的一次螺旋线O′Al的向量方程表达式为
| $ {\mathit{\boldsymbol{O}}^\prime }{\mathit{\boldsymbol{A}}^l} = {\mathit{\boldsymbol{O}}^\prime }{\mathit{\boldsymbol{C}}^l} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^l}, $ | (27) |
| $ \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^x} = \left\{ {\begin{array}{*{20}{c}} {{r_0}\cos ({\theta _1} + {\alpha _a})}\\ {{r_0}\sin ({\theta _1} + {\alpha _a})}\\ 0 \end{array}} \right\}, $ | (28) |
CAx转换为坐标系LMN上的表达式CAl为
| $ \begin{array}{l} \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^l} = \left[ {X,Y,Z} \right] \times \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^x} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{c}} {{r_0}\sin ({\theta _1} + {\alpha _a})}\\ { - {r_0}\cos {\alpha _d}\cos ({\theta _1} + {\alpha _a})}\\ { - {r_0}\sin {\alpha _d}\cos ({\theta _1} + {\alpha _a})} \end{array}} \right\}, \end{array} $ | (29) |
| $ \begin{array}{l} {\mathit{\boldsymbol{O}}^\prime }{\mathit{\boldsymbol{A}}^l} = {\mathit{\boldsymbol{O}}^\prime }{\mathit{\boldsymbol{C}}^l} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^l} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{c}} {{r_0}\sin ({\theta _1} + {\alpha _a})}\\ {{r_3}\cos {\alpha _L} - {r_0}\cos {\alpha _d}\cos ({\theta _1} + {\alpha _a})}\\ {{r_3}\sin {\alpha _L} - {r_0}\sin {\alpha _d}\cos ({\theta _1} + {\alpha _a})} \end{array}} \right\}, \end{array} $ | (30) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{O}}^\prime }{\mathit{\boldsymbol{B}}^l} = {\mathit{\boldsymbol{O}}^\prime }{\mathit{\boldsymbol{C}}^l} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^l} + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^l} = \\ \left\{ {\begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin ({\theta _1} + {\alpha _a})[{r_0} - {r_2}\cos ({\theta _{18}} - {\alpha _c})] - {r_2}\cos {\beta _0}\cos ({\theta _1} + {\alpha _a})\sin ({\theta _{18}} - {\alpha _c})}\\ {{r_3}\cos {\alpha _d} - \cos {\alpha _d}\cos ({\theta _1} + {\alpha _a})[{r_0} + {r_2}\cos ({\theta _{18}} - {\alpha _c})] - {r_2}\sin ({\theta _{18}} - {\alpha _c})[\cos {\beta _0}\cos {\alpha _d}\sin ({\theta _1} + {\alpha _a}) - \sin {\beta _0}\sin {\alpha _d}]}\\ {{r_3}\sin {\alpha _d} - \sin {\alpha _d}\cos ({\theta _1} + {\alpha _a})[{r_0} + {r_2}\cos ({\theta _{18}} - {\alpha _c})] - {r_2}\sin ({\theta _{18}} - {\alpha _c})[\cos {\beta _0}\sin {\alpha _d}\sin ({\theta _1} + {\alpha _a}) + \sin {\beta _0}\cos {\alpha _d}]} \end{array}} \right\}. \end{array} $ | (31) |
图 8为钢丝绳侧股芯丝与滑轮接触示意图,式(31)中含有3个未知量,为求解式(31)关于αa的表达式,需求出图 8中各变量的相互关系.

|
图 8 钢丝绳侧股芯丝与滑轮接触示意图 Fig. 8 Contact diagram between side wire of wire rope and pulley |
在弯曲段钢丝绳中,αd与αa关系为
| $ {{\alpha _d} = \frac{{{r_0}}}{{{r_3}\tan {\beta _0}}}{\alpha _a}, } $ | (32) |
令
| $ {{e_3} = \frac{{{r_0}}}{{{r_3}\tan {\beta _0}}}, } $ | (33) |
将式(18)及式(33)代入式(30)可得弯曲段钢丝绳第i股中心丝方程表达式为
| $ {\mathit{\boldsymbol{O}}^\prime }\mathit{\boldsymbol{A}}_i^l = \left\{ {\begin{array}{*{20}{c}} {{r_0}\sin ({\theta _i} + {\alpha _a})}\\ {{r_3}\cos {e_3}{\alpha _a} - {r_0}\cos {e_3}{\alpha _a}\cos ({\theta _i} + {\alpha _a})}\\ {{r_3}\sin {e_3}{\alpha _a} - {r_0}\sin {e_3}{\alpha _a}\cos ({\theta _i} + {\alpha _a})} \end{array}} \right\}. $ | (34) |
将式(18)及式(33)代入式(31)可得弯曲段钢丝绳第i股内层第j丝方程为
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{O}}^\prime }\mathit{\boldsymbol{B}}_{ij}^l = }\\ {\quad \left\{ {\begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin ({\theta _i} + {\alpha _a})[{r_0} - {r_1}\cos ({\theta _j} - {e_1}{\alpha _a})] - {r_1}\cos {\beta _0}\cos ({\theta _i} + {\alpha _a})\sin ({\theta _j} - {e_1}{\alpha _a})}\\ {{r_3}\cos {e_3}{\alpha _a} - \cos {e_3}{\alpha _a}\cos ({\theta _i} + {\alpha _a})[{r_0} + {r_1}\cos ({\theta _j} - {e_1}{\alpha _a})] - {r_1}\sin ({\theta _j} - {e_1}{\alpha _a})[\cos {\beta _0}\cos {e_3}{\alpha _a}\sin ({\theta _i} + {\alpha _a}) - \sin {\beta _0}\sin {e_3}{\alpha _a}]}\\ {{r_3}\sin {e_3}{\alpha _a} - \sin {e_3}{\alpha _a}\cos ({\theta _i} + {\alpha _a})[{r_0} + {r_1}\cos ({\theta _j} - {e_1}{\alpha _a})] - {r_1}\sin ({\theta _j} - {e_1}{\alpha _a})[\cos {\beta _0}\sin {e_3}{\alpha _a}\sin ({\theta _i} + {\alpha _a}) + \sin {\beta _0}\cos {e_3}{\alpha _a}]} \end{array}} \right\}.} \end{array} $ | (35) |
将式(18)及式(33)代入式(31)可得弯曲段钢丝绳第i股外层第k丝方程为
| $ \begin{array}{l} {\mathit{\boldsymbol{O}}^\prime }\mathit{\boldsymbol{B}}_{ik}^l = \\ \left\{ {\begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin ({\theta _i} + {\alpha _a})[{r_0} - {r_1}\cos ({\theta _k} - {e_2}{\alpha _a})] - {r_1}\cos {\beta _0}\cos ({\theta _i} + {\alpha _a})\sin ({\theta _k} - {e_2}{\alpha _a})}\\ {{r_3}\cos {e_3}{\alpha _a} - \cos {e_3}{\alpha _a}\cos ({\theta _i} + {\alpha _a})[{r_0} + {r_1}\cos ({\theta _k} - {e_2}{\alpha _a})] - {r_1}\sin ({\theta _k} - {e_2}{\alpha _a})[\cos {\beta _0}\cos {e_3}{\alpha _a}\sin ({\theta _i} + {\alpha _a}) - \sin {\beta _0}\sin {e_3}{\alpha _a}]}\\ {{r_3}\sin {e_3}{\alpha _a} - \sin {e_3}{\alpha _a}\cos ({\theta _i} + {\alpha _a})[{r_0} + {r_1}\cos ({\theta _k} - {e_2}{\alpha _a})] - {r_1}\sin ({\theta _k} - {e_2}{\alpha _a})[\cos {\beta _0}\sin {e_3}{\alpha _a}\sin ({\theta _i} + {\alpha _a}) + \sin {\beta _0}\cos {e_3}{\alpha _a}]} \end{array}} \right\}. \end{array} $ | (36) |
钢丝绳空间螺旋方程、曲率和挠率变化规律是研究整绳三维实体建模及力学模型的基础,曲率是表示曲线在某点的弯曲程度,挠率是表示空间曲线的扭曲程度,钢丝绳空间螺旋曲线上任意点均有确定的曲率和挠率,整绳曲率及挠率具有一定变化规律.
钢丝绳曲率k、挠率τ与空间螺旋曲线方程f(αa)的关系如下[22]:
| $ \begin{array}{l} k = \frac{{\left\| {f{{({\alpha _a})}^\prime } \times f{{({\alpha _a})}^{\prime \prime }}} \right\|}}{{{{\left\| {f{{({\alpha _a})}^\prime }} \right\|}^3}}} = \\ \frac{{\sqrt {{{({y^\prime }{z^{\prime \prime }} - {z^\prime }{y^{\prime \prime }})}^2} + {{({z^\prime }{x^{\prime \prime }} - {x^\prime }{z^{\prime \prime }})}^2} + {{({x^\prime }{y^{\prime \prime }} - {y^\prime }{x^{\prime \prime }})}^2}} }}{{{{({{({x^\prime })}^2} + {{({y^\prime })}^2} + {{({z^\prime })}^2})}^{3/2}}}}, \end{array} $ | (37) |
| $ \begin{array}{l} \tau = \frac{{(f{{({\alpha _a})}^\prime }, f{{({\alpha _a})}^{\prime \prime }}, f{{({\alpha _a})}^{\prime \prime \prime }})}}{{{{\left\| {f{{({\alpha _a})}^\prime } \times f{{({\alpha _a})}^{\prime \prime }}} \right\|}^2}}} = \\ \frac{{{x^\prime }{y^{\prime \prime }}{z^{\prime \prime \prime }} + {x^{\prime \prime \prime }}{y^{\prime \prime }}{z^\prime } + {x^{\prime \prime }}{y^{\prime \prime \prime }}{z^\prime } - {x^{\prime \prime \prime }}{y^{\prime \prime }}{z^\prime } - {x^\prime }{y^{\prime \prime \prime }}{z^{\prime \prime }} - {x^{\prime \prime }}{y^\prime }{z^{\prime \prime \prime }}}}{{{{({y^\prime }{z^{\prime \prime }} - {z^\prime }{y^{\prime \prime }})}^2} + {{({z^\prime }{x^{\prime \prime }} - {x^\prime }{z^{\prime \prime }})}^2} + {{({x^\prime }{y^{\prime \prime }} - {y^\prime }{x^{\prime \prime }})}^2}}}. \end{array} $ | (38) |
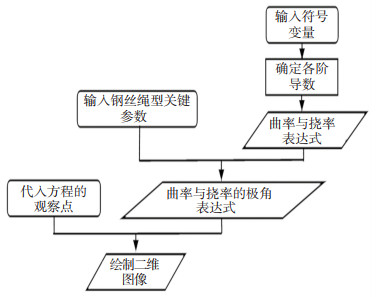
式中:f(αa)为钢丝绳空间螺旋曲线方程,x、y、z为对应的极角αa的函数.由式(37)及式(38),可分别求出直线段、弯曲段钢丝绳各钢丝的曲率与挠率空间表达式,但由于钢丝绳空间螺旋曲线方程较为复杂,求三次导后更为复杂,表示较困难.应用MATLAB软件语言符号功能对钢丝绳的曲率与挠率进行求解,在求解弯曲段钢丝的曲率及挠率时,设定滑轮直径为180 mm.钢丝绳曲率及挠率在MATLAB中的计算流程如图 9所示.
|
图 9 钢丝绳曲率及挠率在MATLAB中计算流程 Fig. 9 Wire rope curvature and torsion calculation flow in MATLAB |
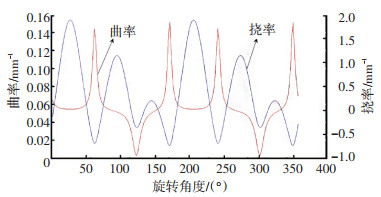
将钢丝绳直立及弯曲段的二维曲线函数图像导入Photoshop进行合并,得到直立与弯曲段钢丝绳曲率与挠率关系图,如图 10及11所示.在图 10中,直线段钢丝绳的曲率与挠率呈明显的周期性变化规律,变化周期均为180°;挠率峰值均出现于曲率的波谷处,曲率处于波峰时,挠率变化较为平缓;曲率与挠率的极值较明显.在图 11中,弯曲段钢丝绳曲率与挠率同样具有明显的周期性变化规律,变化周期均为360°;曲率处于波峰时,挠率发生突变;曲率处于波谷时,挠率变化率最大;曲率和挠率的极值大小明显.
|
图 10 直线段钢丝绳外层丝曲率与挠率变化规律 Fig. 10 Curvature and torsion variation of straight section of wire rope outer wires |

|
图 11 弯曲段钢丝绳外层丝曲率与挠率变化规律 Fig. 11 Curvature and torsion variation of bending section of wire rope outer wires |
上文推导了钢丝绳的空间数学方程、曲率和挠率表达式,分析了钢丝绳在直立及弯曲状态,侧股中侧丝的曲率及挠率的连续变化规律.为更直观了解该类钢丝绳的结构,通过已建立钢丝绳空间数学模型,运用MATLAB参数化功能及Solidworks软件曲线、扫描和实体阵列等功能建立钢丝绳三维实体模型.
应用SolidWorks曲线及扫描功能建立钢丝绳侧股芯丝,通过Matlab获取钢丝绳侧股侧丝的二次螺旋线参考点坐标,制成txt文件,如表 2为第1股第18丝参考点系列坐标;然后运用Solidworks“XYZ曲线”功能,在参数输入设置中导入已制好的坐标文件;最后应用SolidWorks扫描、装配及实体阵列建立钢丝绳整绳三维几何模型. 图 12~14分别为单丝、丝与丝缠绕、直立段及绳轮处钢丝绳三维几何模型.
| 表 2 第1股第18丝参考点系列坐标 Tab. 2 Reference point coordinate of first share eighteenth wire |

|
图 12 单丝与单丝缠绕几何实体模型 Fig. 12 Winding geometry entity model between single wire and single wire |

|
图 13 直立状态钢丝绳整绳三维实体模型 Fig. 13 Three-dimensional entity model of upright wire rope |

|
图 14 弯曲段钢丝绳三维实体模型 Fig. 14 Three-dimensional entity model of bending section of wire rope |
经过参数设计及三维建模最后得出第1股第18丝参考点系列坐标表格如表 2所示。
5 结论1) 在确定运输机钢丝绳型号及直径基础上,对钢丝绳股、丝进行编号,运用微分几何学及空间坐标变换原理,推导了6×19+FC类钢丝绳在直立及弯曲状态的空间螺旋方程,并推导了该类钢丝绳侧股外层钢丝曲率及挠率的连续变化规律,为钢丝绳在各种载荷下的工作状态的数值分析和实验分析提供理论依据.
2) 图 10结果表明:直线段钢丝绳的曲率与挠率呈明显的周期性变化规律,变化周期均为180°;挠率峰值均出现于曲率的波谷处,曲率处于波峰时,挠率变化较为平缓;曲率与挠率的极值较明显. 图 11结果表明:弯曲段钢丝绳曲率与挠率同样具有明显的周期性变化规律,变化周期均为360°;曲率处于波峰时,挠率发生突变;曲率处于波谷时,挠率变化率最大;曲率和挠率的极值大小明显.
3) 根据所推导的钢丝绳空间螺旋方程、曲率及挠率表达式,运用MATLAB参数化及SolidWorks曲线、扫描及装配等功能,绘制了运输机钢丝绳直立及弯曲状态的三维几何模型,并得到运输机钢丝绳股、丝参考点系列坐标,为后续建立钢丝绳力学模型及分析结构参数对钢丝绳损伤的影响奠定基础.
| [1] |
粘雅玲, 沈嵘枫, 张小珍, 等. 果园运输机械研究进展[J]. 农业技术与装备, 2014(22): 24. NIAN Yaling, SHENG Rongfeng, ZHANG Xiaozhen, et al. Research progress of orchard transportation machinery[J]. Agricultural Technology & Equipment, 2014(22): 24. DOI:10.3969/j.issn.1673-887X.2014.22.011 |
| [2] |
洪添胜.农机农艺融合就是"未来强壮的果农"[N].农民日报, 2015-11-19(008) HONG Tiansheng. The integration of agricultural machinery and agronomy is "the strong fruit farmers in the future"[N]. Farmers' Daily, 2015-11-19(008 |
| [3] |
欧阳玉平, 洪添胜, 苏建, 等. 山地果园牵引式双轨运输机断绳制动装置设计与试验[J]. 农业工程学报, 2014, 30(18): 22. OUYANG Yuping, HONG Tiansheng, SU Jian, et al. Design and test of rope breaking braking device of traction type double track transporter in mountain orchard[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(18): 22. DOI:10.3969/j.issn.1002-6819.2014.18.003 |
| [4] |
欧阳玉平, 洪添胜, 马煜东. 山地果园双轨运输机牵引系统动力学仿真与试验[J]. 系统仿真学报, 2015, 27(7): 1502. OUYANG yuping, HONG Tiansheng, MA Yudong. Dynamic simulation and test of mountain orchard double-track transport traction system[J]. Journal of System Simulation, 2015, 27(7): 1502. DOI:10.16182/j.cnki.joss.2015.07.013 |
| [5] |
欧阳玉平, 洪添胜, 苏建, 等. 山地果园牵引式双轨运输机排绳装置的设计[J]. 华中农业大学学报, 2014, 33(5): 123. OUYANG Yuping, HONG Tiansheng, SU Jian, et al. Design of rope arrangement device of traction type double track conveyor in mountain orchard[J]. Journal of Huazhong Agricultural University, 2014, 33(5): 123. DOI:10.13300/j.cnki.hnlkxb.2014.05.046 |
| [6] |
洪添胜, 苏建, 朱余清. 山地橘园链式循环货运索道设计[J]. 农业机械学报, 2011, 42(6): 108. HONG Tiansheng, SU Jian, ZHU Yuqing. Design of chain cycle freight ropeway in mountain orangery[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(6): 108. |
| [7] |
PÉRIERA V, DIENG L, GAILLET L, et al. Influence of an aqueous environment on the fretting behaviour of steel wire sused in civil engineering cables[J]. Wear, 2011, 271(9-10): 1585. DOI:10.1016/j.wear.2011.01.095 |
| [8] |
WAHID A, MOUHIB N, OUARDI A, et al. Experimental prediction of wire rope damage by energy method[J]. Engineering Structures, 2019, 201: 1. DOI:10.1016/j.engstruct.2019.109794 |
| [9] |
BELTRÁN J F, DE VICO E. Assessment of static rope behavior with asymmetric damage distribution[J]. Eng Struct, 2015, 86: 84. DOI:10.1016/j.engstruct.2014.12.026 |
| [10] |
赵敏, 张东来, 周智慧. 钢丝绳缺陷漏磁信号的通道均衡化方法[J]. 哈尔滨工业大学学报, 2013, 45(9): 47. ZHAO Min, ZHANG Donglai, ZHOU Zhihui. Channel equalization method for MFL signals of wire rope defects[J]. Journal of Harbin Institute of Technology, 2013, 45(9): 47. |
| [11] |
FONTANARI V, BENEDETTI M, MONELLI B D. Elasto-plastic behavior of a warrington-seale rope: experimental analysis and finite element modeling[J]. Eng Struct, 2015, 82: 113. DOI:10.1016/j.engstruct.2014.10.032 |
| [12] |
PETERKA P, KREŠÁK J, KROPUCH S, et al. Failure analysis of hoisting steel wire rope[J]. Eng Fail Anal, 2014, 45: 96. DOI:10.1016/j.engfailanal.2014.06.005 |
| [13] |
ZHANG Peng, DUAN Menglan, MA Jianmin, et al. A precise mathematical model for geometric modeling of wire rope strands structure[J]. Applied Mathematical Modelling, 2019, 76. DOI:10.1016/j.apm.2019.06.005 |
| [14] |
WANG Xiaoyu, MENG Xiangbao, WANG Jixin, et al. Mathematical modeling and geometric analysis for wire rope strands[J]. Applied Mathematical Modelling, 2015, 39(3-4): 1019. DOI:10.1016/j.apm.2014.07.015 |
| [15] |
ARGATOV I I, GÓMEZ X, TATO W, et al. Wear evolution in a stranded rope under cyclic bending: implications to fatigue life estimation[J]. Wear, 2011, 271(11): 2857. DOI:10.1016/j.wear.2011.05.045 |
| [16] |
MA W, ZHU Z C, PENG Y X, et al. Computer-aided modeling of wire ropes bent over a sheave[J]. Advances in Engineering Software, 2015, 90: 11. DOI:10.1016/j.advengsoft.2015.06.006 |
| [17] |
WU Weiguo, CAO Xin. Mechanics model and its equation of wire rope based on elastic thin rod theory[J]. International Journal of Solids and Structures, 2016, 102-103: 21. DOI:10.1016/j.ijsolstr.2016.10.021 |
| [18] |
ARGATOV I. Response of a wire rope strand to axial and torsional loads: asymptotic modeling of the effect of interwire contact deformations[J]. International Journal of Solids and Structures, 2011, 48(10): 1413. DOI:10.1016/j.ijsolstr.2016.10.021 |
| [19] |
闻邦椿, 张义民, 鄂中凯, 等. 机械设计手册[M]. 第五版. 北京: 机械工业出版社, 2010. WEN Bangchun, ZHANG Yimin, E Zhongkai. Mechanical design manual[M]. Fifth Edition. Beijing: China Machine Press, 2010. |
| [20] |
张德英, 李广宇, 向卫国. 斜井提升用钢丝绳的选择方法[J]. 煤矿机电, 2005(2): 69. ZHANG Deying, LI Guangyu, XIANG Weiguo. Selection method of steel wire rope for inclined shaft lifting[J]. Coal Mine Electrical, 2005(2): 69. DOI:10.16545/j.cnki.cmet.2005.02.027 |
| [21] |
苏世晨, 苏永春. 矿井提升钢丝绳直径计算新公式[J]. 煤矿安全, 2003, 34(6): 32. SU Shichen, SU Yongchun. New formula for calculating the diameter of mine hoisting wire rope[J]. Coal Mine Safety, 2003, 34(6): 32. DOI:10.13347/j.cnki.mkaq.2003.06.013 |
| [22] |
张惠波.提升钢丝绳几何特性及有限元分析研究[D].阜新: 辽宁工程技术大学, 2011 ZHANG Huibo. Research on geometric characteristics and finite element analysis of hoisting steel wire rope[D]. Fuxin: Liaoning University of Engineering and Technology, 2011 |
 2021, Vol. 53
2021, Vol. 53


