混凝土局压承载力计算方法深化研究

引用本文

盖立琦, 郑文忠, 李胜, 王英. 混凝土局压承载力计算方法深化研究[J]. 哈尔滨工业大学学报, 2021, 53(10): 1-11. DOI: 10.11918/202011118.

GAI Liqi, ZHENG Wenzhong, LI Sheng, WANG Ying. In-depth study on calculation method of local bearing capacity of concrete[J]. Journal of Harbin Institute of Technology, 2021, 53(10): 1-11. DOI: 10.11918/202011118.

基金项目

国家自然科学基金(51678190)

作者简介

盖立琦(1995—)，女，硕士研究生;
郑文忠(1965—)，男，教授，博士生导师

通信作者

郑文忠，hitwzzheng@163.com

文章历史

收稿日期: 2021-11-29

Abstract Full text Figures/Tables PDF

混凝土局压承载力计算方法深化研究

盖立琦^1,2, 郑文忠^1,2, 李胜^1,2, 王英^1,2

1. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学)，哈尔滨 150090;
2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学)，哈尔滨 150090

收稿日期: 2021-11-29

基金项目: 国家自然科学基金(51678190)

作者简介: 盖立琦(1995—)，女，硕士研究生; 郑文忠(1965—)，男，教授，博士生导师

通信作者: 郑文忠，hitwzzheng@163.com

摘要: 为探究混凝土达到局部受压承载力时间接钢筋能否屈服，间接钢筋不屈服时拉应力如何取值，以及网格式间接钢筋在楔形体外如何实现合理锚固等问题，完成了18个配置螺旋式间接钢筋和18个配置网格式间接钢筋的混凝土试件的局压试验。试验结果表明: 当混凝土发生局压破坏时，局压影响区范围内间接钢筋存在达不到屈服的现象；基于试验结果，获得了不同强度等级热轧钢筋(HPB300、HRB400、HRB500、HRB600)配置的螺旋式间接钢筋和网格式间接钢筋屈服所对应的间接钢筋体积配筋率；建立了发生局压破坏时未屈服的网格式间接钢筋与楔形体外侧面相交处拉应力的计算方法。

关键词: 混凝土螺旋式间接钢筋网格式间接钢筋合理锚固体积配筋率局压承载力

In-depth study on calculation method of local bearing capacity of concrete

GAI Liqi^1,2, ZHENG Wenzhong^1,2, LI Sheng^1,2, WANG Ying^1,2

1. Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150090, China;
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China

Abstract: To investigate whether the indirect steel bar is capable of yielding when the concrete reaches local bearing capacity, the calculation method of tensile stress when the indirect steel bar could not yield, and the possibility of reasonable anchoring of meshed indirect steel bar outside the wedge, 18 specimens reinforced with spiral indirect steel bars and 18 with meshed indirect steel bars were experimentally evaluated, subjected to local compression forces. Results show that when the concrete reached the ultimate load, non-yielding occurred in the indirect steel bars in the area affected by the local pressure. Based on the test results, the volumetric ratios of indirect steel bars corresponding to the yielding of the spiral and meshed indirect steel bars for hot-rolled steel bars with different strength grades (HPB300, HRB400, HRB500, HRB600) were obtained. A calculation method of the tensile stress at the intersection of the meshed indirect steel bar and the outer side of the wedge was established for the situation that the meshed indirect steel bar does not yield under local pressure.

Keywords: concrete spiral indirect steel bar reasonable anchoring of meshed indirect steel bar volumetric ratio of indirect steel bars local bearing capacity

混凝土局部受压是一种常见的受力形式，但混凝土局压破坏引发的工程事故屡见不鲜。目前，在工程实际施工中，通常采用配置螺旋式或网格式间接钢筋的方法来提高混凝土局压承载力，控制局压影响区裂缝^[1]。苏联学者捷尔万纳巴巴首次提出采用二项式来表示配筋混凝土的局部受压承载力^[2]，但此公式未考虑间接钢筋在局压破坏时可能达不到屈服的问题。文献[2]总结其公式不足并基于套箍强化理论和极限平衡理论提出了新的混凝土局压承载力计算公式，但此公式在推导中假定局压试件到达极限状态时，局压影响区范围内的间接钢筋可以达到屈服，未考虑发生局压破坏时存在间接钢筋达不到屈服的问题。文献[3-8]通过大量的混凝土局压试验，提出了混凝土局压破坏理论和承载力计算方法，指出当间接钢筋的配量适当时，间接钢筋先达到屈服后发生混凝土局压破坏；而当间接钢筋配置过多时，间接钢筋达不到屈服。文献[9-12]通过12个配置高强螺旋式间接钢筋的活性粉末混凝土局压试验发现，当混凝土达到局压破坏荷载时，约50%的局压试件破坏时间接钢筋拉应力低于其比例极限；通过12个配置网格式间接钢筋的活性粉末混凝土局压试验发现，局压影响区网格式间接钢筋(屈服强度为408 MPa)只有部分能够达到屈服。

基于研究成果发现，发生局压破坏的原因可能有：一是达到混凝土局压承载力时间接钢筋的强度没有充分发挥；二是楔形体与网格式间接钢筋的相交点以外锚固长度不足。针对现行混凝土结构设计规范中假定局压影响区范围内的间接钢筋屈服，而实际上混凝土发生局压破坏时会出现间接钢筋达不到其屈服强度的问题，提出不同强度等级热轧钢筋配置的间接钢筋屈服所对应的间接钢筋体积配筋率，并建立间接钢筋未屈服时拉应力的计算方法；针对网格式间接钢筋所辖面积一般不大于局压计算底面积的客观事实，而间接钢筋在局部受压过程中要充分发挥作用，自楔形体与网格式间接钢筋的交点算起需有合适的锚固长度的问题，提出将网格式间接钢筋自由边端伸长后弯折、焊接。

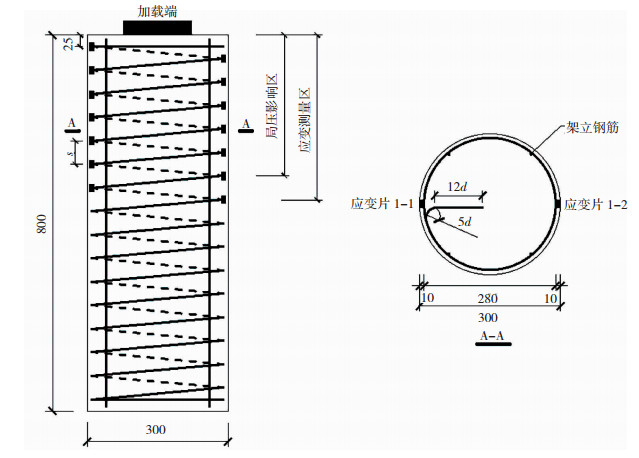
1 试验概况

18个配置螺旋式间接钢筋的圆形截面混凝土局压试件的试件设计见表 1，试件直径300 mm、高800 mm。方形承压板边长为145 mm、厚度为30 mm，局压面积比(A_b /A_l)为3.36。螺旋式间接钢筋在混凝土局压试件全高范围内布置。纵筋采用4根直径8 mm的HRB400热轧钢筋，保护层厚度10 mm。螺旋式间接钢筋在靠近承压端将1个水平圈压平，距离试件上表面25 mm。螺旋式间接钢筋应变测点布置形式为：在局压影响区300 mm高度范围内，每圈螺旋式间接钢筋对称布置2个应变片，如第一圈螺旋式间接钢筋两个测点分别表示为1-1和1-2，取两测点应变平均值作为第一圈间接钢筋的应变值记为ε₃₆，下角标表示第一圈间接钢筋距离加载端36 mm(加载端至1-1、1-2两测点中间位置的距离)，其余同理。应变测量圈数按局压试件间接钢筋间距计算确定，以保证应变测量区高度超过局压影响区。螺旋式间接钢筋布置及应变测点布置见图 1，各试件应变片具体粘贴情况见表 2。

表 1 配置螺旋式间接钢筋的混凝土试件参数 Tab. 1 Parameters of concrete specimens with spiral indirect steel bars

图 1 螺旋式间接钢筋布置及应变测点示意(mm) Fig. 1 Schematic diagram of spiral indirect steel bar and layout of strain measurement points(mm)

表 2 螺旋式间接钢筋应变片粘贴情况 Tab. 2 Pasting situations of spiral indirect steel bar strain gauges

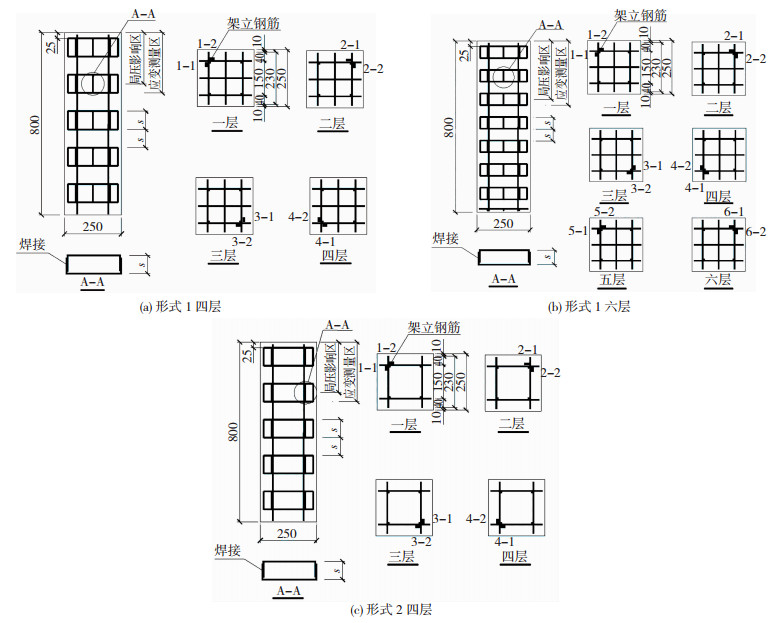
18个配置网格式间接钢筋的方形截面混凝土局压试件的设计见表 3，试件的截面边长250 mm、高800 mm。采用边长为120 mm、厚度为30 mm的方形承压板，计算底面积与局压面积之比(A_b/A_l)为4.34。网格式间接钢筋在方形混凝土局压试件全高范围内布置。试件在角部配置4根直径为8 mm的HRB400钢筋，间接钢筋保护层厚度为10 mm，第一层网格式间接钢筋距加载端部25 mm。网格式间接钢筋自由边端伸长后弯折、焊接。网格式间接钢筋应变测点布置形式为：在局压影响区250 mm高度范围内，每层网格式间接钢筋角部布置2个应变片，形式1网格式间接钢筋粘贴4层或6层应变片，形式2粘贴4层应变片。以第一层网格式间接钢筋为例，应变片1-1、1-2量测平均值作为第一层间接钢筋的角部钢筋实测应变值ε₂₅(下角标表示网格式间接钢筋距离加载端距离为25 mm)，其余同理。应变测量层数按局压试件间接钢筋间距计算确定，以保证应变测量区高度超过局压影响区。网格式间接钢筋布置及应变测点布置见图 2，各试件应变片具体粘贴情况见表 4。

表 3 配置网格式间接钢筋的混凝土试件参数 Tab. 3 Parameters of concrete specimens with meshed indirect steel bars

试件编号	混凝土强度等级	间接钢筋种类	间接钢筋直径d/mm	网格形式	间接钢筋间距s/mm	间接钢筋体积配筋率ρ_v/%
F-1	C40	HRB600	6	1	80	0.90
F-2	C40	HRB500	8	2	85	1.00
F-3	C40	HRB400	8	2	75	1.20
F-4	C40	HPB300	6	1	50	1.50
F-5	C40	HRB400	8	2	85	1.00
F-6	C40	HRB400	8	2	80	1.10
F-7	C40	HRB400	8	2	65	1.35
F-8	C40	HRB400	8	2	60	1.50
F-9	C60	HRB600	6	1	80	0.90
F-10	C60	HRB500	8	2	85	1.00
F-11	C60	HRB400	8	2	75	1.20
F-12	C60	HPB300	6	1	50	1.50
F-13	C60	HRB400	8	2	85	1.00
F-14	C60	HPB300	8	2	85	1.00
F-15	C80	HRB600	6	1	80	0.90
F-16	C80	HRB500	8	2	85	1.00
F-17	C80	HRB400	8	2	75	1.20
F-18	C80	HPB300	6	1	50	1.50

表 3 配置网格式间接钢筋的混凝土试件参数 Tab. 3 Parameters of concrete specimens with meshed indirect steel bars

图 2 网格式间接钢筋布置及应变测点示意(mm) Fig. 2 Schematic diagram of meshed indirect steel bar and layout of strain measurement points(mm)

表 4 网格式间接钢筋应变片粘贴情况 Tab. 4 Pasting situations of meshed indirect steel bar strain gauges

试验用混凝土和钢筋的基本力学性能见表 5、6。

表 5 混凝土基本力学性能 Tab. 5 Basic mechanical properties of concrete

表 6 钢筋基本力学性能 Tab. 6 Basic mechanical properties of steel bars

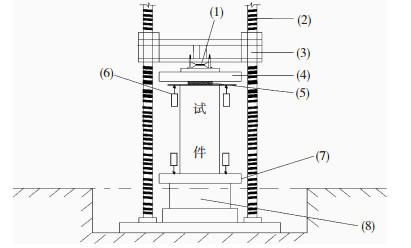
局压试验加载制度为：正式加载过程中，加载制度采用先力后位移双控制。当不超过预估荷载的70%时由力控制加载，加载速率为3 kN/s，此阶段加载采用分级加载制度，每级荷载按照不大于预估破坏荷载的10%加荷，每加载一级持荷1 min后进行下一级加载。之后由位移控制加载，以3 mm/min的速率进行局压加载，加载至局压承载力峰值后，将加载速率调整为5 mm/min，持续以此速率加载至低于局压破坏荷载的40%时结束加载。局压试验加载装置见图 3。局压荷载是由万能压力机的上压头通过传递局部压力的钢板来传递的。万能压力机的上压头比试件端面大，传递局压荷载的钢板比试件端面小。因此，局压钢板向试件传递的压力是均匀的。

注：(1)球铰；(2)压力机立柱；(3)可移动横梁；(4)压力机上压头；(5)承压板；(6)位移计；(7)压力机下压头；(8)液压加载器图 3 局压试验加载装置 Fig. 3 Local compression test loading device

2 试验现象 2.1 裂缝发展与分布

配置螺旋式间接钢筋和网格式间接钢筋的混凝土局压试件裂缝分布情况见图 4和图 5。配置螺旋式间接钢筋与网格式间接钢筋的混凝土试件在局压荷载作用下，裂缝发展与分布情况基本相同。在达到开裂荷载之前，试件无明显现象。继续加载，试件侧面至加载端距离约为承压板边长的高度处出现短小纵向裂缝，随着荷载的缓慢增大，裂缝由中间向两端发展，向上延伸发展至试件顶面。荷载继续增大，在其临近位置有少量新的纵向裂缝出现，已有裂缝不断发展变宽。达到局压破坏荷载时，侧面新裂缝不断出现且发展较快，四周纵向裂缝较多，呈“上宽下窄”的形态。卸载后，观察到加载端承压板明显压陷，加载端处裂缝集中出现在方形承压板对称轴及四角处，呈“外宽内窄”的形态。

图 4 配置螺旋式间接钢筋的混凝土试件裂缝分布 Fig. 4 Distribution of cracks in concrete specimens with spiral indirect steel bars

图 5 配置网格式间接钢筋的混凝土试件裂缝分布 Fig. 5 Distribution of cracks in concrete specimens with meshed indirect steel bars

综合分析配置两类间接钢筋的混凝土试件在局压荷载作用下的开裂情况，裂缝主要分为三类：第一类主要裂缝为承压板下纵向裂缝，主要集中于局压影响区范围内(截面高度范围内)，靠近承压板四周侧面；第二类主要裂缝为纵向劈裂裂缝，由于楔形体滑移产生；第三类主要裂缝为加载端面裂缝，主要集中在方形承压板中部或其临近位置及四角处，四角处裂缝主要由于应力集中产生，加载端面裂缝呈“内窄外宽”。

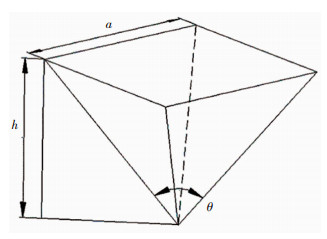
2.2 破坏形态与特征

各试件均表现为先开裂后破坏的破坏模式，且局压开裂荷载与破坏荷载数值相差较大，存在较为明显的裂缝发展阶段，具有较好延性，配置螺旋式间接钢筋和网格式间接钢筋的混凝土局压试件破坏形态与特征分别见图 6、7。发生局压破坏后，试验机的荷载示值不断减小，混凝土保护层开始剥落。当荷载降低至局压破坏荷载的40%左右时，螺旋式间接钢筋出现崩断现象，荷载示值突然大幅度直线下降，钢筋崩断位置为第三、四圈螺旋式间接钢筋，此位置大致位于楔形体楔尖处。而网格式间接钢筋未出现崩断现象，说明其相比于螺旋式间接钢筋约束效果略差。卸载后，发现两类间接钢筋均呈外鼓形态，且临近加载端试件四周混凝土脱落相对严重。将外围混凝土剥离后，两类间接钢筋加载端下部均存在明显的楔形体特征。楔形体近似呈四角锥体，其端面边长为承压板边长，图 6(b)和图 7(b)为试件剥离出的楔形体，图 8为楔形体特征模型。通过测量与计算得出配置螺旋式间接钢筋的混凝土试件楔形体劈尖夹角约为48°~62°，配置网格式间接钢筋的混凝土试件楔形体劈尖夹角约为46°~57°。

图 6 配置螺旋式间接钢筋的混凝土试件破坏形态和特征 Fig. 6 Failure characteristics of concrete specimens with spiral indirect steel bars

图 7 配置网格式间接钢筋的混凝土试件破坏形态和特征 Fig. 7 Failure characteristics of concrete specimens with meshed indirect steel bars

图 8 楔形体特征模型 Fig. 8 Wedge feature model

3 试验结果与分析 3.1 破坏荷载下螺旋式间接钢筋应力水平分析与计算

对18个配置螺旋式间接钢筋的圆形截面混凝土试件局压试验结果与数据进行统计分析，见表 7。采用配置螺旋式间接钢筋的混凝土试件达到破坏荷载时间接钢筋屈服的试件数据，以ρ_vβ_cor和间接钢筋受拉屈服应变ε_yv为横轴，以混凝土局压破坏荷载和混凝土局压净面积之比(f_cl=N_u/A_l)与未配置间接钢筋素混凝土局压强度β_cβ_lf_c的差值Δf=N_u/A_l-β_cβ_lf_c为纵轴，建立三维坐标系，进行三维拟合，选用一次多项式模型z=ax+by+z₀，得到Δf、ρ_vβ_cor和ε_yv的三维拟合关系见图 9，其拟合下包曲面见图 10。

表 7 配置螺旋式间接钢筋混凝土局压试验数据 Tab. 7 Local compression test data of concrete with spiral indirect steel bars

试件编号	f_c/MPa	f_yv/MPa	ρ_v/%	β_cor	N_u/kN	ε_yv/10^-6	ε_{sv, max}/10^-6	应变位置	是否屈服	Δf/MPa
C-1	28.2	660	0.90	1.64	1 712.2	3 300	4 522	ε₁₂₆	是	29.83
C-2	28.2	560	1.00	1.61	1 746.4	2 800	3 908	ε₁₉₄	是	31.46
C-3	28.2	480	1.20	1.61	1 756.2	2 400	3 682	ε₂₃₆	是	31.92
C-4	28.2	340	1.50	1.61	1 838.0	1 620	3 898	ε₂₈₈	是	35.81
C-5	28.2	480	1.00	1.61	1 698.8	2 400	2 879	ε₁₉₄	是	29.19
C-6	28.2	480	1.10	1.61	1 760.8	2 400	2 682	ε₁₁₃	是	32.14
C-7	28.2	480	1.35	1.61	1 814.6	2 400	2 529	ε₁₄₉	是	34.70
C-8	28.2	480	1.50	1.61	1 842.6	2 400	2 493	ε₂₃₈	是	36.03
C-9	41.3	660	0.90	1.64	2 262.8	3 300	3 515	ε₁₂₆	是	33.10
C-10	41.3	560	1.00	1.61	2 420.2	2 800	2 475	ε₂₆₉	否	40.59
C-11	41.3	480	1.20	1.61	2 274.0	2 400	3 093	ε₁₇₁	是	33.64
C-12	41.3	340	1.50	1.61	2 286.8	1 620	2 641	ε₁₈₈	是	34.24
C-13	41.3	480	1.00	1.61	2 253.6	2 400	3 168	ε₁₉₄	是	32.67
C-14	41.3	340	1.00	1.61	2 228.4	1 620	2 672	ε₂₆₉	是	31.47
C-15	59.2	660	0.90	1.64	2 667.0	3 300	3 409	ε₁₂₆	是	32.60
C-16	59.2	560	1.00	1.61	2 646.0	2 800	2 765	ε₁₉₄	否	31.60
C-17	59.2	480	1.20	1.61	2 700.4	2 400	3 035	ε₁₀₆	是	34.19
C-18	59.2	340	1.50	1.61	2 722.0	1 620	2 451	ε₁₈₈	是	35.21
注：ε_{sv, max}为破坏荷载下螺旋式间接钢筋拉应变实测最大值；ε₁₂₆表示距离加载端126 mm高度处的应变值。

表 7 配置螺旋式间接钢筋混凝土局压试验数据 Tab. 7 Local compression test data of concrete with spiral indirect steel bars

图 9 配置螺旋式间接钢筋试件拟合曲面 Fig. 9 Surface fitting of specimens with spiral indirect steel bars

图 10 配置螺旋式间接钢筋试件拟合曲面及下包曲面 Fig. 10 Surface fitting and lower envelope of specimens with spiral indirect steel bars

根据图 9、10，得到配置螺旋式间接钢筋的混凝土抗压强度拟合计算式和下包曲面计算公式：

$ f_{\mathrm{cl}, \mathrm{f}}=20.40+544.13 \beta_{\mathrm{cor}} \rho_{\mathrm{v}}+956.16 \varepsilon_{\mathrm{yv}}+\beta_{\mathrm{l}} \beta_{\mathrm{c}} f_{\mathrm{c}} $

(1)

$ f_{\mathrm{cl}, \mathrm{n}}=18.00+544.13 \beta_{\mathrm{cor}} \rho_{\mathrm{v}}+956.16 \varepsilon_{\mathrm{yv}}+\beta_{\mathrm{l}} \beta_{\mathrm{c}} f_{\mathrm{c}} $

(2)

式中：f_{cl, f}为配置螺旋式间接钢筋的混凝土抗压强度预估计算值；f_{cl, n}为具有95%保证率的配置螺旋式间接钢筋的混凝土抗压强度；β_cor为配置间接钢筋的局部受压承载力提高系数；ρ_v为间接钢筋体积配筋率；ε_yv为间接钢筋屈服应变。

将由式(1)计算得到的配置螺旋式间接钢筋的混凝土抗压强度预估计算值f_{cl, f}与其相应的试验值f_{cl, t}进行比较，见表 8。经统计分析，f_{cl, f}与f_{cl, t}比值的平均值为1.001，标准差为0.011，变异系数为0.011，吻合情况良好。

表 8 配置螺旋式间接钢筋的混凝土抗压强度实测值与计算值对比 Tab. 8 Comparison of measured and calculated compressive strengths of concrete with spiral indirect steel bars

若当配置螺旋式间接钢筋的混凝土发生局压破坏时，间接钢筋达到屈服，则可根据间接钢筋的屈服应变，计算间接钢筋的应力水平发挥。则此时间接钢筋的侧向约束应力为

$ \sigma_{1}=\frac{\rho_{\mathrm{v}}}{2} \beta_{\mathrm{cor}} E_{\mathrm{sv}} \varepsilon_{\mathrm{yv}} $

(3)

式中σ_l、E_sv为间接钢筋侧向约束应力和间接钢筋弹性模量。

根据Richart经验公式^[13]，基于“套箍强化理论”、约束混凝土的性质与现行混凝土规范中混凝土局压承载力计算公式推导得到

$ f_{\mathrm{cl}}=\beta_{\mathrm{c}} \beta_{\mathrm{l}} f_{\mathrm{c}}+2.1 \rho_{\mathrm{v}} \beta_{\mathrm{cor}} f_{\mathrm{yv}} $

(4)

当配置螺旋式间接钢筋的混凝土达到局压破坏荷载时间接钢筋屈服，由拟合计算式(1)、(4)联立推导可得出间接钢筋屈服应变ε_yv和间接钢筋体积配筋率上限试验值ρ_{v, max}的计算关系式为

$ \rho_{\mathrm{v}, \max }=\frac{20.40+956.16 \varepsilon_{\mathrm{yv}}}{-544.13 \beta_{\mathrm{cor}}+2.1 \beta_{\mathrm{cor}} E_{\mathrm{sv}} \varepsilon_{\mathrm{yv}}} $

(5)

经计算得到不同强度等级的螺旋式间接钢筋达到屈服时体积配筋率上限试验值，结果见表 9。

表 9 不同等级螺旋式间接钢筋屈服时的体积配筋率上限试验值 Tab. 9 Upper limit test values of volume reinforcement ratio of spiral indirect steel bars with different grades under yielding

当配置螺旋式间接钢筋的混凝土达到局压破坏荷载时间接钢筋屈服，由下包曲面计算式(2)和式(4)联立推导可得出间接钢筋屈服应变ε_yv和间接钢筋体积配筋率上限设计值ρ_{v, max}的关系式为

$ \rho_{\mathrm{v}, \mathrm{max}}=\frac{18.00+956.16 \varepsilon_{\mathrm{yv}}}{-544.13 \beta_{\mathrm{cor}}+2.1 \beta_{\mathrm{cor}} E_{\mathrm{sv}} \varepsilon_{\mathrm{yv}}} $

(6)

式中所有参数均为本文试件的试验值。经计算得到与本试验参数相同情况时不同强度等级的螺旋式间接钢筋达到屈服时体积配筋率上限设计值，供设计参考, 结果见表 10。

表 10 不同等级螺旋式间接钢筋屈服时的体积配筋率上限设计值 Tab. 10 Upper limit design values of volume reinforcement ratio of spiral indirect steel bars with different grades under yielding

这里需要特别说明的是，表 7中C-16试件螺旋式间接钢筋实测应变基本达到屈服应变，故认为其屈服并已将其作为拟合数据点。针对C-10试件，将其试验参数代入式(6)中进行验证，计算得到发生局压破坏时间接钢筋应变近似预估值为4 608×10^-6，超过其屈服应变2 800×10^-6。故认为试验应变值未达到屈服是应变片量测误差导致的。

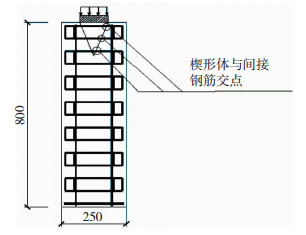
3.2 破坏荷载下网格式间接钢筋应力水平分析与计算

根据配置间接钢筋混凝土局压试件的裂缝发展模式与破坏机理可知，网格式间接钢筋与楔形体外侧面相交处及楔尖下方的拉应力最大，见图 11。配置网格式间接钢筋的局压试件楔形体劈尖夹角平均值约为50°，故取劈尖夹角为50°的楔形体模型。基于钢筋-混凝土黏结滑移本构关系理论，将实测应变值通过理论计算得到网格式间接钢筋与楔形体外侧面相交处及楔尖下方的应变值^[14]。以下分析与计算均采用网格式间接钢筋与楔形体外侧面相交处及楔尖下方的最大应变值ε_{sv, max}′。

图 11 网格式间接钢筋拉应力最大处示意(mm) Fig. 11 Schematic diagram of the maximum tensile stress of meshed indirect steel bar(mm)

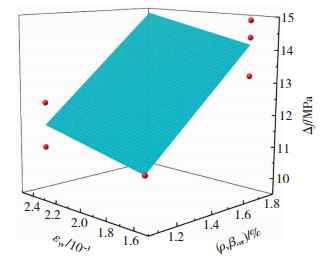
对18个配置网格式间接钢筋的方形截面混凝土局压试件的试验结果与数据进行统计分析，见表 11。采用配置网格式间接钢筋的混凝土试件达到破坏荷载时间接钢筋屈服的试件数据，以ρ_vβ_cor和间接钢筋受拉屈服应变ε_yv为横轴，以混凝土局压破坏荷载和混凝土局部受压净面积之比(f_cl=N_u /A_l)与未配置间接钢筋素混凝土局压强度β_c β_l f_c的差值Δf=N_u /A_l -β_c β_l f_c为纵轴，进行三维拟合，选用一次多项式模型z=ax+by+z₀，得到Δf、ρ_vβ_cor和ε_yv的三维拟合关系见图 12，其拟合下包曲面见图 13。

表 11 配置网格式间接钢筋混凝土局压试验数据 Tab. 11 Local compression test data of concrete with meshed indirect steel bars

试件编号	f_c/MPa	f_yv/MPa	ρ_v/%	β_cor	N_u/kN	ε_yv/10^-6	ε_{sv, max}′/10^-6	应变位置	是否屈服	Δf/MPa
F-1	28.2	660	0.90	1.15	1 011.6	3 300	2 572	ε₁₈₅′	否	11.59
F-2	28.2	560	1.00	1.12	1 009.2	2 800	2 210	ε₁₉₅′	否	11.43
F-3	28.2	480	1.20	1.12	1 026.2	2 400	2 146	ε₁₇₅′	否	12.61
F-4	28.2	340	1.50	1.15	1 059.0	1 620	2 843	ε₁₂₅′	是	14.89
F-5	28.2	480	1.00	1.12	1 002.6	2 400	2 830	ε₁₉₅′	是	10.97
F-6	28.2	480	1.10	1.12	974.6	2 400	2 269	ε₁₈₅′	否	9.02
F-7	28.2	480	1.35	1.12	994.8	2 400	2 132	ε₉₀′	否	10.43
F-8	28.2	480	1.50	1.12	1 023.2	2 400	1 997	ε₁₄₅′	否	12.40
F-9	41.3	660	0.90	1.15	1 388.4	3 300	2 202	ε₁₀₅′	否	11.72
F-10	41.3	560	1.00	1.12	1 422.0	2 800	2 011	ε₁₉₅′	否	14.05
F-11	41.3	480	1.20	1.12	1 405.0	2 400	2 111	ε₁₇₅′	否	12.87
F-12	41.3	340	1.50	1.15	1 409.6	1 620	2 729	ε₁₂₅′	是	13.19
F-13	41.3	480	1.00	1.12	1 397.6	2 400	2 784	ε₁₉₅′	是	12.35
F-14	41.3	340	1.00	1.12	1 377.0	1 620	2 081	ε₁₉₅′	是	10.92
F-15	59.2	660	0.90	1.15	1 694.0	3 300	2 059	ε₁₈₅′	否	10.51
F-16	59.2	560	1.00	1.12	1 696.4	2 800	1 851	ε₁₁₀′	否	10.68
F-17	59.2	480	1.20	1.12	1 748.0	2 400	1 811	ε₁₀₀′	否	14.26
F-18	59.2	340	1.50	1.15	1 749.6	1 620	2 152	ε₁₂₅′	是	14.37
注：ε_{sv, max}′为破坏荷载下网格式间接钢筋与楔形体外侧面相交处及楔尖下方拉应变最大值; ε₁₈₅′表示距离加载端185 mm高度处的应变值。

表 11 配置网格式间接钢筋混凝土局压试验数据 Tab. 11 Local compression test data of concrete with meshed indirect steel bars

图 12 配置网格式间接钢筋试件拟合曲面 Fig. 12 Surface fitting of specimens with meshed indirect steel bars

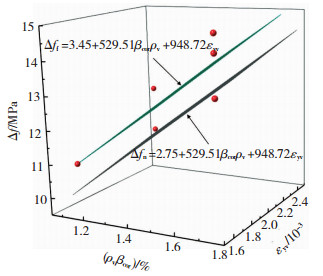
图 13 配置网格式间接钢筋试件拟合曲面及下包曲面 Fig. 13 Surface fitting and lower envelope of specimens with meshed indirect steel bars

根据图 12、13，配置网格式间接钢筋的混凝土抗压强度拟合计算式和具有95%保证率的拟合计算公式为：

$ f_{\mathrm{cl}, \mathrm{f}}=3.45+529.51 \beta_{\mathrm{cor}} \rho_{\mathrm{v}}+948.72 \varepsilon_{\mathrm{yv}}+\beta_{\mathrm{l}} \beta_{\mathrm{c}} f_{\mathrm{c}} $

(7)

$ f_{\mathrm{cl}, \mathrm{n}}=2.75+529.51 \beta_{\mathrm{cor}} \rho_{\mathrm{v}}+948.72 \varepsilon_{\mathrm{yv}}+\beta_{1} \beta_{\mathrm{c}} f_{\mathrm{c}} $

(8)

式中f_{cl, f}、f_{cl, n}为配置网格式间接钢筋的混凝土抗压强度预估计算值和具有95%保证率的配置网格式间接钢筋的混凝土抗压强度。

当配置网格式间接钢筋的混凝土发生局压破坏时，若间接钢筋达到屈服，则可根据间接钢筋的屈服应变，计算间接钢筋的应力发挥水平。则此时间接钢筋的侧向约束应力为

$ \sigma_{1}=\frac{\rho_{\mathrm{v}}}{2} \beta_{\mathrm{cor}} E_{\mathrm{sv}} \varepsilon_{\mathrm{yv}} $

(3)

根据Richart经验公式，基于“套箍强化理论”、约束混凝土的性质与现行混凝土规范中混凝土局压承载力计算公式推导得到

$ f_{\mathrm{cl}}=\beta_{\mathrm{c}} \beta_{\mathrm{l}} f_{\mathrm{c}}+2.1 \rho_{\mathrm{v}} \beta_{\mathrm{cor}} f_{\mathrm{yv}} $

(4)

当配置网格式间接钢筋的混凝土达到局压破坏荷载时间接钢筋屈服，由拟合计算式(7)、(4)联立推导可得出间接钢筋屈服应变ε_yv和间接钢筋体积配筋率上限试验值ρ_{v, max}的计算关系式为

$ \rho_{\mathrm{v}, \max }=\frac{3.45+948.72 \varepsilon_{\mathrm{yv}}}{-529.51 \beta_{\mathrm{cor}}+2.1 \beta_{\mathrm{cor}} E_{\mathrm{sv}} \varepsilon_{\mathrm{yv}}} $

(9)

经过计算可得到不同强度等级的网格式间接钢筋达到屈服时体积配筋率上限试验值，结果见表 12。

表 12 不同等级网格式间接钢筋屈服时的体积配筋率上限试验值 Tab. 12 Upper limit test values of volume reinforcement ratio of meshed indirect steel bars with different grades under yielding

当配置网格式间接钢筋的混凝土试件发生局压破坏时间接钢筋屈服，由下包曲面计算式(8)、(4)联立推导可得出间接钢筋屈服应变ε_yv和间接钢筋体积配筋率上限设计值ρ_{v, max}的关系式为

$ \rho_{\mathrm{v}, \max }=\frac{2.75+948.72 \varepsilon_{\mathrm{yv}}}{-529.51 \beta_{\mathrm{cor}}+2.1 \beta_{\mathrm{cor}} E_{\mathrm{sv}} \varepsilon_{\mathrm{yv}}} $

(10)

得到不同强度等级的网格式间接钢筋达到屈服时体积配筋率上限设计值，供设计参考。结果见表 13。

表 13 不同等级网格式间接钢筋的体积配筋率上限设计值 Tab. 13 Upper limit design values of volume reinforcement ratio of meshed indirect steel bars with different grades under yielding

当配置网格式间接钢筋的混凝土发生局压破坏时，若间接钢筋未达到屈服，采用统一的钢筋抗拉屈服强度计算配筋混凝土的局压承载力并不准确^[15]，计算结果偏于不安全。通过计算钢筋的实际拉应力得到的局压承载力更为准确且安全。

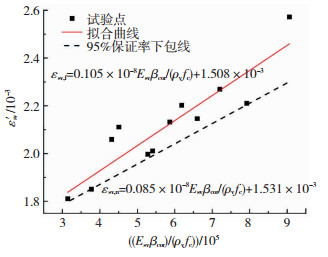
根据统计的试验数据，采用混凝土达到局压破坏时配置网格式间接钢筋尚未屈服的试件，以参数(E_sv β_cor)/(ρ_v f_c)为横坐标，以达到局压破坏时间接钢筋的拉应变ε_sv′为纵坐标拟合。观察发现各试验点在二维坐标系中近似线性分布，故采用线性拟合，获得了当混凝土发生局压破坏时，网格式间接钢筋拉应变拟合曲线和数学表达以及具有95%保证率的下包线和数学表达，见图 14。

图 14 混凝土发生局压破坏时网格式间接钢筋拉应变拟合曲线及具有95%保证率的下包曲线 Fig. 14 Fitting curve and lower envelope curve (with 95% guarantee rate) of tensile strain of meshed indirect steel bars when concrete fails under local pressure

当混凝土试件发生局压破坏时，网格式间接钢筋拉应变拟合计算式及具有95%保证率的间接钢筋拉应变计算式为：

$ \varepsilon_{\mathrm{sv}, \mathrm{f}}=0.105 \times 10^{-8} \frac{E_{\mathrm{sv}} \beta_{\mathrm{cor}}}{\rho_{\mathrm{k}} f_{\mathrm{c}}}+1.508 \times 10^{-3} $

(11)

$ \varepsilon_{\mathrm{sv}, \mathrm{n}}=0.085 \times 10^{-8} \frac{E_{\mathrm{sv}} \beta_{\mathrm{cor}}}{\rho_{\mathrm{v}} f_{\mathrm{c}}}+1.531 \times 10^{-3} $

(12)

式中：ε_{sv, f}、ε_{sv, n}为混凝土发生局压破坏时网格式间接钢筋拉应变预估值和具有95%保证率的混凝土发生局压破坏时网格式间接钢筋拉应变。

将由式(11)计算得到的混凝土发生局压破坏时网格式间接钢筋拉应变预估值ε_{sv, f}与试验值ε_{sv, t}进行比较，见表 14。经统计分析，二者比值的平均值为1.005，标准差为0.032，变异系数为0.032，吻合情况良好。

表 14 配置网格式间接钢筋拉应变预估值与试验值比较 Tab. 14 Comparison of estimated and test values of tensile strain of meshed indirect steel bar

当配置网格式间接钢筋的混凝土发生局压破坏时，若间接钢筋未达到屈服，可根据虎克定律计算间接钢筋应力发挥水平。网格式间接钢筋提供的侧向约束应力为

$ \sigma_{1}=\frac{\rho_{\mathrm{v}}}{2} \beta_{\mathrm{cor}} E_{\mathrm{sv}} \varepsilon_{\mathrm{sv}} $

(13)

式中ε_sv为未屈服间接钢筋拉应变预估值，按式(11)计算。

4 结论

1) 通过18个配置螺旋式间接钢筋和18个配置网格式间接钢筋的混凝土局压试件的试验结果发现，当混凝土发生局压破坏时，局压影响区范围内间接钢筋会存在达不到屈服的现象。

2) 基于18个配置螺旋式间接钢筋的混凝土局压试件试验数据，研究配置螺旋式间接钢筋的混凝土局压区间接钢筋应力发挥水平和合理配置问题。采用达到局压破坏时螺旋式间接钢筋达到屈服的试件数据，获得了不同强度等级(HPB300、HRB400、HRB500、HRB600)热轧钢筋配置的螺旋式间接钢筋屈服所对应的间接钢筋体积配筋率。

3) 为使间接钢筋在局部受压过程中充分发挥作用，自楔形体与网格式间接钢筋的交点算起实现合理锚固。本文提出了将网格式间接钢筋自由边端伸长并弯折，将相邻二网格钢筋焊接的新思路，为解决网格式间接钢筋的合理锚固问题提供建议与参考。

4) 基于18个配置网格式间接钢筋的混凝土局压试件的试验数据，采用达到局压破坏时螺旋式间接钢筋达到屈服的试件，获得了不同强度等级(HPB300、HRB400、HRB500、HRB600)热轧钢筋配置的网格式间接钢筋屈服所对应的间接钢筋体积配筋率；采用混凝土达到局压破坏时网格式间接钢筋尚未屈服的试件，推导了发生局压破坏时网格式间接钢筋未屈服时，网格式间接钢筋与楔形体外侧面相交处拉应变计算公式；建立了网格式间接钢筋与楔形体外侧面相交处拉应力计算方法。

参考文献

[1]	杨熙坤, 杨冰, 孟凡石. 混凝土及钢筋混凝土局部承压若干问题[J]. 低温建筑技术, 1999, 19(1): 8. YANG Xikun, YANG Bing, MENG Fanshi. Several problems on local compression of concrete and reinforced concrete[J]. Low Temperature Architecture Technology, 1999, 19(1): 8.
[2]	蔡绍怀. 混凝土及配筋混凝土的局部承压强度[J]. 土木工程学报, 1963, 9(6): 1. CAI Shaohuai. Local compressive strength of concrete and reinforced concrete[J]. China Civil Engineering Journal, 1963, 9(6): 1. DOI:10.15951/j.tmgcxb.1963.06.002
[3]	曹声远, 杨熙坤, 钮长仁. 混凝土轴心局部承压破坏及强度的试验研究[J]. 哈尔滨建筑工程学院学报, 1980(1): 61. CAO Shengyuan, YANG Xikun, NIU Changren. Experimental study on local bearing failure and strength of concrete under axial local pressure[J]. Journal of Harbin University of Civil Engineering and Architecture, 1980(1): 61.
[4]	曹声远, 杨熙坤, 钮长仁. 混凝土轴心局部承压变形的试验研究[J]. 哈尔滨建筑工程学院学报, 1980(1): 83. CAO Shengyuan, YANG Xikun, NIU Changren. Experimental study on local axial compression deformation of concrete[J]. Journal of Harbin University of Civil Engineering and Architecture, 1980(1): 83.
[5]	曹声远, 杨熙坤. 混凝土局部承压的工作机理及强度理论[J]. 哈尔滨建筑工程学院学报, 1982(3): 44. CAO Shengyuan, YANG Xikun. Working mechanism and strength theory of concrete under local pressure[J]. Journal of Harbin University of Civil Engineering and Architecture, 1982(3): 44.
[6]	刘永颐, 关建光, 王传志. 混凝土局部承压强度及破坏机理[J]. 土木工程学报, 1985(2): 53. LIU Yongyi, GUAN Jianguang, WANG Chuanzhi. Bearing strength of concrete and its failure mechanism[J]. China Civil Engineering Journal, 1985(2): 53. DOI:10.15951/j.tmgcxb.1985.02.005
[7]	曹声远, 杨熙坤, 徐凯怡. 钢筋混凝土局部承压的试验研究[J]. 哈尔滨建筑工程学院学报, 1983(2): 13. CAO Shengyuan, YANG Xikun, XU Kaiyi. Experimental study on local bearing capacity of reinforced concrete[J]. Journal of Harbin University of Civil Engineering and Architecture, 1983(2): 13.
[8]	曹声远, 杨熙坤, 徐凯怡. 钢筋混凝土局部承压强度理论[J]. 哈尔滨建筑工程学院学报, 1984(2): 25. CAO Shengyuan, YANG Xikun, XU Kaiyi. Local compressive strength theory of reinforced concrete[J]. Journal of Harbin University of Civil Engineering and Architecture, 1984(2): 25.
[9]	周威, 郑文忠, 胡海波. 钢筋网片约束活性粉末混凝土局压性能试验研究[J]. 建筑结构学报, 2013, 19(11): 148. ZHOU Wei, ZHENG Wenzhong, HU Haibo. Bearing capacity of reactive powder concrete reinforced by orthogonal ties[J]. Journal of Building Structures, 2013, 19(11): 148. DOI:10.14006/j.jzjgxb.2013.11.019
[10]	周威, 胡海波, 郑文忠. 高强螺旋筋约束活性粉末混凝土局压承载力试验[J]. 土木工程学报, 2014, 47(8): 70. ZHOU Wei, HU Haibo, ZHENG Wenzhong. Bearing capacity of reactive powder concrete reinforced by high-strength steel spirals[J]. China Civil Engineering Journal, 2014, 47(8): 70. DOI:10.15951/j.tmgcxb.2014.08.033
[11]	ZHOU Wei, HU Haibo. Bearing capacity of steel fiber reinforced reactive powder concrete confined by spirals[J]. Materials and Structures, 2015, 48(8): 2613. DOI:10.1617/s11527-014-0341-4
[12]	GENG Xiangri, ZHOU Wei, YAN Jiachuan. Reinforcement of orthogonal ties in steel-fiber-reinforced reactive powder concrete anchorage zone[J]. Advances in Structural Engineering, 2019, 22(10): 2311. DOI:10.1177/1369433219838085
[13]	RICHART E F, BRANDZAEG A, BROWN L R. A study of the failure of concrete under combined compressive stress[R]. Urbana: University of Illinois, 1928
[14]	郑文忠, 苗天鸣, 王识宇, 等. 锚固力在钢筋黏结和端板承压间的分配规律[J]. 哈尔滨工业大学学报, 2018, 50(6): 152. ZHENG Wenzhong, MIAO Tianming, WANG Shiyu, et al. Distribution regulation of the reinforcement force between bond and headed bars[J]. Journal of Harbin Institute of Technology, 2018, 50(6): 152. DOI:10.11918/j.issn.0367-6234.201710053
[15]	RAZVI S, SAATCIOGLU M. Confinement model for high-strength concrete[J]. Journal of Structural Engineering, 1999, 125(3): 281. DOI:10.1061/(ASCE)0733-9445(1999)125:3(281)