2. 中国地震局地震工程与工程振动重点实验室(中国地震局工程力学研究所),哈尔滨 150080
2. Key Lab of Earthquake Engineering and Engineering Vibration of China Earthquake Administration(Institute of Engineering Mechanics, China Earthquake Administration), Harbin 150080, China
水平荷载作用下,联肢墙中的连梁约束相邻墙肢变形,梁端剪力传递给墙肢形成附加轴力。在受力上与整体墙仅靠截面受弯承载力抵抗水平倾覆力矩相比,联肢墙是依靠各墙肢弯矩和两侧墙肢附加轴力组成的拉压力偶共同承担总倾覆力矩[1](见图 1),图中N为墙肢基底的附加轴力,不包括初始轴力G。这种在水平荷载作用下联肢墙墙肢产生附加轴力的现象在其试验中[2-6]得到了验证,附加轴力形成的拉压力偶可以有效地降低各墙肢的抗弯需求,同时也改变了各墙肢的轴力,如图 1(b)联肢墙,左右墙肢的总轴力分别为G-N和G+N。

|
图 1 水平荷载下剪力墙结构受力状态 Fig. 1 Shear wall structures undergoing lateral loads |
钢筋混凝土(RC)剪力墙的轴力是影响其力学性能的重要因素。文献[7-10]通过单片RC墙肢试验研究表明,轴拉力会降低墙肢的弯剪承载力及其抗侧刚度;较大的轴压力对其延性产生不利的影响,当墙肢进入小偏心受压状态后,继续增加轴力会降低墙肢的受弯承载力。在中国JGJ 3—2010《高层建筑混凝土结构技术规程》[11](以下简称《高规》)中,RC墙的受弯和受剪承载力计算公式均与其轴力有关。国内外设计和评估标准[11-13]均对RC墙肢的轴压比进行限制,以保证其具有足够的延性。因此,准确高效地计算墙肢附加轴力和详细地分析其对联肢墙受力性能的影响是实现联肢墙合理设计和安全评估的必要前提。
目前,在联肢墙内力计算中,通常采用两种方法得到墙肢的附加轴力。一是数值模拟方法,需要通过复杂的有限元建模分析,该方法费时费力。二是解析方法,该类方法均是基于连续连杆法建立的。其中,中国方法[14-15]以梁端约束弯矩为未知函数建立微分方程,其计算过程较为繁琐,需首先计算连梁的约束弯矩,然后折算成梁端剪力,最后对其求和得到墙肢附加轴力;国外方法[16]虽然以附加轴力为未知函数建立微分方程,但仅有针对水平均布荷载的附加轴力计算公式,缺少适用于集中力,特别是建筑结构中常用的倒三角荷载的情况,并且其坐标系选取不合理,推导出的公式相对较复杂。
鉴于墙肢附加轴力的重要性,针对目前存在的问题,本文基于连续连杆法,通过选取合适的坐标系,以墙肢附加轴力为未知函数建立微分方程,给出三种不同形式水平荷载下墙肢附加轴力的简便实用计算方法;并通过算例验证了本文方法的有效性,分析了附加轴力的控制因素及附加轴力对联肢墙承载力的影响。根据本文研究结果,可快速准确计算出墙肢附加轴力,深入了解其对联肢墙承载力的影响,进而为实现联肢墙的合理设计和安全评估提供参考。
1 联肢墙墙肢附加轴力计算方法本文基于连续连杆法建立以联肢墙墙肢附加轴力为未知函数的微分方程,同时借鉴了文献[15]坐标系的选取方法,将坐标系的z轴方向选为沿结构竖直向下,从而避免了文献[16]由于坐标系z轴向上而导致的倾覆力矩复杂的表达形式及微分方程繁琐的求解过程。在此基础上,推导了三种不同水平荷载形式下,墙肢附加轴力的计算公式,提出了简便实用计算方法。
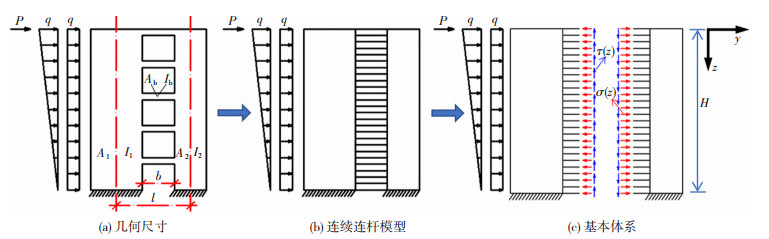
1.1 微分方程的建立选取联肢墙中典型的双肢墙进行受力分析,其几何尺寸见图 2(a)。由于联肢墙的墙梁刚度比较大,故可采用连续连杆法进行求解[15-16]。该方法假设为:1)每一层的连梁都转换为均布在整个楼层高度上的连续连杆;2)忽略连梁轴向变形,假定墙肢相同高度处的水平位移相同,两墙肢的转角和曲率是相等的,并假定连梁的反弯点在梁的跨中;3)层高h,墙肢形心间距离l,连梁跨度b,和墙肢与连梁的惯性矩I1、I2、Ib及面积A1、A2、Ab等参数沿建筑高度均为常数,且各层层高与墙肢和连梁的截面尺寸均相同。
|
图 2 联肢墙连续连杆模型 Fig. 2 Continous connecting links model of CWs |
首先将连梁转换为沿墙肢高度方向的无限连杆,见图 2(b);然后从连梁反弯点(即连杆中点)截开,每根连杆的边界受到正应力和切应力的作用,见图 2(c)。最后沿墙肢任意截面Z截开,得到水平作用下双肢墙计算模型的墙肢内力图,见图 3,z为该截面距离墙肢顶部的距离,N为水平荷载下墙肢的附加轴力。附加轴力N与连杆切口处切应力τ之间存在的关系为

|
图 3 墙肢计算模型内力图 Fig. 3 Internal force in CW calculation model |
| $ \tau(z)=\mathrm{d} N / \mathrm{d} z $ | (1) |
在图 3中,连杆在反弯点处切断,故连杆切口两端的竖向总位移应为零。水平荷载作用下,连杆切断处的竖向位移由墙肢的弯曲变形、轴向变形和连梁切口处的弯剪变形共同决定。因此,根据切断点处的位移协调条件可得
| $ \begin{aligned} \delta=& \delta_{1}+\delta_{2}+\delta_{3}=l \frac{\mathrm{d} y}{\mathrm{~d} z}+\frac{1}{E}\left(\frac{1}{A_{1}}+\frac{1}{A_{2}}\right) \int_{z}^{H} N(z) \mathrm{d} z+\\ & \frac{b^{3} h}{12 E I_{\mathrm{br}}} \frac{\mathrm{d} N}{\mathrm{~d} z}=0 \end{aligned} $ | (2) |
式中:δ1、δ2和δ3分别为由墙肢的弯曲变形、轴向变形和连梁切口处的弯剪变形所引起连梁切口端的竖向位移,y为墙肢水平位移,E为墙肢弹性模量,Ibr为连梁考虑剪切变形后的折算惯性矩,其计算公式为
| $ I_{\mathrm{br}}=\frac{I_{\mathrm{b}}}{1+\frac{12 \mu E_{\mathrm{b}} I_{\mathrm{b}}}{b^{2} G_{\mathrm{b}} A_{\mathrm{b}}}}=\frac{I_{\mathrm{b}}}{1+3\left(\frac{h_{\mathrm{b}}}{b}\right)^{2}} $ | (3) |
式中:Eb和Gb分别为连梁弹性模量和剪切模量,当材料为混凝土时,其比值取Gb/Eb = 0.4[17];hb为连梁高度; μ为截面上剪应力分布不均匀系数,矩形截面时,μ=1.2。
对式(2)求一阶导数:
| $ l \frac{\mathrm{d}^{2} y}{\mathrm{~d} z^{2}}+\frac{1}{E}\left(\frac{1}{A_{1}}+\frac{1}{A_{2}}\right) N(z)+\frac{b^{3} h}{12 E I_{\mathrm{br}}} \frac{\mathrm{d}^{2} N}{\mathrm{~d} z^{2}}=0 $ | (4) |
在图 3中,在墙肢任意Z截面处,由受力平衡条件可得
| $ M_{1}+M_{2}=M_{\mathrm{p}}(z)-l N(z) $ | (5) |
式中:M1和M2分别为两片墙肢Z截面处的弯矩,Mp(z)为外荷载对Z截面处的总外力矩,N(z)为墙肢Z截面处的附加轴力。
由梁的弯曲理论M = EIθ″以及该方法假设2,即两墙肢的曲率相等,可将式(5)表示为
| $ E\left(I_{1}+I_{2}\right) \frac{\mathrm{d}^{2} y}{\mathrm{~d} z^{2}}=M_{\mathrm{p}}(z)-{lN}(z) $ | (6) |
将式(4)与(6)联立,消去d2y/dz2,即可建立关于附加轴力N(z)的微分方程:
| $ \frac{\mathrm{d}^{2} N}{\mathrm{~d} z^{2}}-\left(k \alpha_{1}\right)^{2} N(z)=-\frac{\alpha_{1}^{2}}{l} M_{\mathrm{p}}(z) $ | (7) |
式中:
采用中国常用的整体参数α = kα1H和墙肢轴向变形影响参数T = 1/k2[15],式(7)可以变为
| $ \frac{\mathrm{d}^{2} N}{\mathrm{~d} z^{2}}-\frac{\alpha^{2}}{H^{2}} N(z)=-\frac{\alpha^{2} T}{l H^{2}} M_{\mathrm{p}}(z) $ | (8) |
将上式中截面高度z转化为相对高度ξ = z/H,则有
| $ \frac{\mathrm{d}^{2} N}{\mathrm{~d} \xi^{2}}-\alpha^{2} N(\xi)=-\frac{\alpha^{2} T}{l} M_{\mathrm{p}}(\xi) $ | (9) |
式中Mp(ξ)为三种水平荷载形式下结构相对高度为ξ处的外力矩,其表达式为
| $ M_{\mathrm{p}}(\xi)=V_{0} H f_{\mathrm{M}}(\xi) $ | (10) |
式中fM(ξ)的计算公式为
| $ f_{\mathrm{M}}(\xi)= \begin{cases}\left(3 \xi^{2}-\xi^{3}\right) / 3, & \text { 倒三角荷载 } \\ \xi^{2} / 2, & \text { 均布荷载 } \\ \xi, & \text { 顶部集中力 }\end{cases} $ | (11) |
值得说明的是,选择坐标系以联肢墙顶部为原点,z轴正方向竖直向下(图 2),简化了倾覆力矩Mp(ξ)的表达式,这对后续设定微分方程特解,简化方程求解至关重要。
1.2 微分方程的求解微分方程(9)解的一般形式为
| $ \begin{aligned} N(\xi)&=C_{1} \operatorname{ch}(\alpha \xi)+C_{2} \operatorname{sh}(\alpha \xi)- \\ &\frac{1}{\alpha^{2}}\left[1+\frac{\mathrm{D}^{2}}{\alpha^{2}}+\frac{\mathrm{D}^{4}}{\alpha^{4}}+\cdots\right]\left(\frac{T \alpha^{2}}{l} M_{\mathrm{p}}(\xi)\right) \end{aligned} $ | (12) |
式中:前两项为方程的通解,C1和C2为待定系数;最后一项为微分方程的特解,D是微分算子d/dz。对于常见的倒三角荷载、均布荷载和顶部集中力三种水平荷载形式,其特解为
| $ \begin{aligned} &N^{*}(\xi)= \begin{cases}- \frac{1}{\alpha^{2}}\left(\frac{1}{3}\left(3 \xi^{2}-\xi^{3}\right)+\frac{2-2 \xi}{\alpha^{2}}\right) \frac{T \alpha^{2}}{l} V_{0} H, & & \text { 倒三角荷载 } \\ -\frac{1}{\alpha^{2}}\left(\frac{1}{2} \xi^{2}+\frac{1}{\alpha^{2}}\right) \frac{T \alpha^{2}}{l} V_{0} H, & & \text { 均布荷载 } \\ -\frac{\xi}{\alpha^{2}} \frac{T \alpha^{2}}{l} V_{0} H, & & \text { 顶部集中力 }\end{cases} \end{aligned} $ | (13) |
该微分方程满足如下两个边界条件。
1) 联肢墙顶部的轴力为零,因此可得边界条件:
| $ \xi=0, N(\xi)=0 $ |
2) 联肢墙底部两片墙肢的弯曲变形和轴向变形均为零,因此,当z=H,即ξ=1时,式(2)中第一和二项均为零,故第三项中轴力的一阶导数也为零,即
| $ \xi=1, \frac{\mathrm{d} N(\xi)}{\mathrm{d} \xi}=0 $ |
根据以上两个边界条件,可以确定式(12)中待定系数,从而可得三种水平荷载下墙肢附加轴力解析公式为
| $ N(\xi)=\frac{T V_{0} H}{l} g(\xi, \alpha) $ | (14) |
式中g(ξ, α)是关于联肢墙整体参数α和截面相对高度ξ的函数,其表达式为
| $ \begin{array}{ll} g(\xi, \alpha)=\begin{cases}- \frac{2 \operatorname{ch}(\alpha \xi)}{\alpha^{2}}+\left(\frac{2 \operatorname{sh} \alpha}{\alpha}+\frac{2}{\alpha^{2}}-1\right) \frac{\operatorname{sh}(\alpha \xi)}{\alpha \operatorname{ch} \alpha}+\left(-\frac{1}{3} \xi^{3}+\xi^{2}+\frac{2-2 \xi}{\alpha^{2}}\right), & \text { 倒三角荷载 } \\ -\frac{\operatorname{ch}(\alpha \xi)}{\alpha^{2}}+\left(\frac{\operatorname{sh} \alpha}{\alpha}-1\right) \frac{\operatorname{sh}(\alpha \xi)}{\alpha \operatorname{ch} \alpha}+\left(\frac{1}{2} \xi^{2}+\frac{1}{\alpha^{2}}\right), & \text { 均布荷载 } \\ \xi-\frac{\operatorname{sh}(\alpha \xi)}{\alpha \operatorname{ch} \alpha}, & \text { 顶部集中力 }\end{cases} \end{array} $ | (15) |
综上,如果已知联肢墙的几何信息,以及水平荷载的形式,便可方便地得到联肢墙的整体参数α和基底剪力V0,进而快速计算出墙肢的附加轴力,从而避免了目前在计算附加轴力时,数值方法复杂的建模分析,以及解析方法繁琐的换算求和。本文方法的计算流程见图 4。

|
图 4 墙肢附加轴力计算流程 Fig. 4 Flowchart of calculation procedure for AAF of a wall pier |
为了检验本文提出的联肢墙墙肢附加轴力计算方法,参照文献[18]中18层和10层联肢墙进行重新设计并作为本文算例,其中10层算例为非对称双肢墙。基于OpenSees平台对算例进行有限元模拟分析,根据所得结果对本文方法进行验证,并与国内现有附加轴力计算方法[14-15]进行对比。18层和10层联肢墙算例分别命名为CW-18与CW-10,每层截面的几何信息相同,见表 1、2。
| 表 1 联肢墙算例几何信息 Tab. 1 Geometric information of typical CWs |
| 表 2 联肢墙算例截面设计信息 Tab. 2 Reinforcement details of typical CWsmm |
按照本文计算流程图 4,可分为三步完成墙肢附加轴力计算。以计算CW-18墙肢基底附加轴力为例,第一步可根据墙肢和连梁的几何信息,快速计算和统计出所需信息,见表 3。
| 表 3 算例CW-18所需计算信息 Tab. 3 Required calculation parameters for CW-18 |
第二步计算墙肢轴向变形影响参数T和整体参数α,其中,Ibr为考虑剪切变形影响的连梁惯性矩,按式(3)计算。
| $ k^{2}=1+\frac{\left(A_{1}+A_{2}\right)\left(I_{1}+I_{2}\right)}{A_{1} A_{2} l^{2}}=1.148 $ |
| $ T=\frac{1}{k^{2}}=0.871 $ |
| $ \alpha_{1}^{2}=\frac{12 I_{\mathrm{br}} l^{2}}{b^{3} h \sum I_{i}}=0.013 $ |
| $ \alpha=k \alpha_{1} H=8.004 $ |
第三步计算不同水平荷载形式下的墙肢附加轴力。为了使不同形式下的基底剪力保持一致,三种水平荷载形式的合力均假定为100 kN,即基底剪力V0均为100 kN。根据计算楼层选取截面相对高度,墙肢基底取ξ = 1,带入式(14)即可计算得到墙肢基底附加轴力值。
| $ N(\xi=1)= \begin{cases}342.15 \mathrm{~kN} & \text { 倒三角荷载 } \\ 233.98 \mathrm{~kN} & \text { 均布荷载 } \\ 548.75 \mathrm{~kN} & \text { 顶部集中力 }\end{cases} $ |
其余楼层的附加轴力只需根据楼层高度调整截面相对高度ξ即可得到。
2.2 本文方法验证在OpenSees平台单元库中,选用多竖板单元模拟墙肢,进而可以考虑RC墙的弯剪耦合效应[19],混凝土和钢筋的材料本构分别采用ConcreteCM模型和SteelMPF模型;选用连接单元模拟连梁,连梁通过弦转角表征其受力行为,故只考虑连接单元中的剪切弹簧u2,其恢复力模型仅针对弹性阶段,同时考虑弯曲和剪切变形后的弹性刚度按式(16)计算。联肢墙分析模型建立方式见图 5。为了直观地对比附加轴力的大小,本文模型未考虑竖向荷载,即忽略墙肢重力等产生的初始轴力。水平荷载采用与2.1节相同的三种形式,模拟不同水平荷载形式下算例模型的反应。

|
图 5 联肢墙分析模型 Fig. 5 Analytical model of a typical CW |
| $ K_{\mathrm{b}}=\frac{12 E_{\mathrm{b}} I_{\mathrm{br}}}{b^{3}} $ | (16) |
为了验证本文方法的有效性和合理性,分别采用本文方法、中国现有方法[14-15](以下简称现有方法)和有限元模拟计算在三种常用水平荷载形式下CW-18与CW-10墙肢的附加轴力,两个算例在所有工况下的基底剪力均假定为100 kN,对比结果见图 6。从图 6可看出,在均布荷载与倒三角荷载下,三种方法计算结果吻合程度较高;在顶部集中力下,本文方法和现有方法的计算结果整体均大于模拟结果,楼层较高时,本文方法与现有方法计算结果较为一致,随着楼层的降低,本文方法计算结果更趋近于数值模拟结果。为了进一步对比本文方法与现有方法的计算结果,图 7为两种解析方法下附加轴力的相对误差,其中相对误差=100×(解析方法结果-模拟结果)/模拟结果%。从图 7可看出,三种水平荷载形式下,算例CW-18与CW-10的相对误差呈现出相同的分布规律,本文方法为随着楼层的降低,相对误差逐渐减小,最大相对误差均出现在顶层墙肢,且计算结果整体略大于模拟结果,从工程应用的角度看,本文方法计算所得结果偏保守,是安全的;现有方法则为先下降后增加的趋势。在倒三角荷载与均布荷载下,两种解析方法的最大相对误差均不超过10%;而顶部集中力下,其最大相对误差均大于25%,且都发生于顶层,其原因为,顶层附加轴力较小,进而易于导致顶层相对误差较大;二者不同在于,在较低楼层,本文方法的相对误差明显小于现有方法。

|
图 6 三种水平荷载形式下墙肢附加轴力计算结果 Fig. 6 Calculated AAFs in CW piers under three types of lateral loads |

|
图 7 三种水平荷载形式下墙肢附加轴力计算相对误差 Fig. 7 Relative error of AAFs in CW piers under three types of lateral loads |
在联肢墙中,整体参数α反映了连梁相对刚度的大小,α越大,连梁的相对刚度越大。本文算例CW-18与CW-10的整体参数α分别为8.004和4.616,说明CW-18连梁的相对刚度较大,从图 6可看出,CW-18的墙肢附加轴力是大于CW-10的。因而,连梁和墙肢的刚度对附加轴力有直接的影响,在水平荷载形式和大小相同时,连梁相对刚度越大,墙肢附加轴力通常越大。
从图 6还可看出,对于同一个联肢墙,当基底剪力相同时,不同形式水平荷载作用下,墙肢的附加轴力差距较为显著。在本文算例中,当基底剪力均为100 kN时,CW-18墙肢基底附加轴力在水平均布荷载下约为250 kN,而顶部集中荷载下将近550 kN;CW-10墙肢基底附加轴力在均布荷载与顶部集中力下分别约为120 kN和270 kN。对于CW-18或CW-10,顶部集中力下墙肢基底的附加轴力均约为均布荷载下的2.2倍。分析其原因可知,联肢墙在抵抗水平荷载时,会将自身承担总倾覆力矩的一部分转化为由墙肢附加轴力形成的拉压力偶。因而可以推断,相比基底剪力,水平荷载对联肢墙产生的总倾覆力矩是影响墙肢附加轴力大小的主要因素。联肢墙在三种不同形式的水平荷载作用下,当墙肢基底剪力,即水平荷载合力相同时,所引起联肢墙总倾覆力矩的比值应为各自合力点至基底距离的比值。本文中均布荷载、倒三角荷载和顶部集中力的合力点到基底的距离分别为H/2、2H/3和H,因此,联肢墙在这三种水平荷载下基底的倾覆力矩之比应为3∶4∶6。提取2.2节本文计算方法所得结果,三种水平荷载形式下墙肢基底附加轴力的比例关系见表 4,可以看出,基底的附加轴力与倾覆力矩的比例关系较为一致。
| 表 4 不同水平荷载形式下倾覆力矩与附加轴力比例关系 Tab. 4 Comparion of OTM and AAF ratios under different types of lateral loads |
为进一步验证附加轴力与总倾覆力矩的关系,根据三种水平荷载合力点至基底距离的比例关系,分别令均布荷载、倒三角荷载和顶部集中力的合力为400 kN、300 kN和200 kN,此时三种水平荷载形式下CW-18和CW-10的总倾覆力矩分别均为12 960 kN·m和7 200 kN·m。当倾覆力矩相同时,本文方法得到的三种不同水平荷载形式下算例CW-18和CW-10每层墙肢的附加轴力,见图 8。

|
图 8 不同水平荷载形式下附加轴力计算结果对比 Fig. 8 Comparison of AAFs of CW piers under different lateral loads |
从图 8可以看出,当三种不同水平荷载引起的总倾覆力矩相同时,墙肢附加轴力的整体趋势和大小较为一致。因此,对于同一个联肢墙,在不同形式水平荷载作用下,墙肢附加轴力的主要控制因素为水平荷载引起联肢墙的总倾覆力矩,而非基底剪力。
3 附加轴力对联肢墙承载力影响分析联肢墙的整体受弯承载力由两片墙肢的总受弯承载力(M1 + M2)和其附加轴力形成的拉压力偶(Nl)共同组成,详见图 1(b),其整体受弯承载力按式(17)计算。为此,附加轴力的大小将直接决定了拉压力偶的大小,进而影响联肢墙整体受弯承载力。此外,根据《高规》[11]规定的RC墙受弯和受剪承载力公式可得其弯矩-轴力和剪力-轴力关系,见图 9。从图 9可看出,轴力直接影响了RC墙肢截面的受弯和受剪承载力。对于联肢墙,两侧墙肢的总轴力分别为G - N和G + N,所以,附加轴力同时也改变了每片墙肢自身的弯剪承载力。因此,本节将结合联肢墙的承载力公式,通过受弯和受剪强度指标分析附加轴力对联肢墙承载力的影响。

|
图 9 考虑轴力影响的RC墙受弯和受剪承载力 Fig. 9 Flexural and shear strengths of RC walls under the influence of axial forces |
| $ M=M_{1}+M_{2}+N l $ | (17) |
本节以算例CW-18和CW-10的底层墙肢为例,为考虑不同初始轴力对RC墙肢承载力的影响,分别设置了0.1、0.2和0.4三种初始轴压比。值得说明的是,根据《高规》[11]规定的RC墙受剪承载力公式,当墙肢的轴压比大于等于0.2时,其受剪承载力将保持不变,见图 9(b);为了考虑这一现象,特取0.2为以上三种初始轴压比的中间值。本文墙肢轴压比均选用混凝土抗压强度标准值计算,由于CW-10左右墙肢为非对称,初始轴力以截面尺寸较小墙肢的目标轴压比进行确定。在不同初始轴压比的分析中,附加轴力的最大值均为受到附加轴拉力墙肢的轴力G-N达到Tmax时(见图 9(a)),即引起墙肢发生轴拉破坏时的附加轴力大小。
3.1 附加轴力对联肢墙受弯承载力影响分析为了清晰直观地分析附加轴力对联肢墙两片墙肢总受弯承载力的影响,Lequesne[20]提出了墙肢强度指标(wall strength index,WSI)的概念,其定义式为
| $ I_{\mathrm{WS}}=\frac{M_{1}+M_{2}}{M_{\mathrm{o1}}+M_{\mathrm{o} 2}} $ | (18) |
式中:IWS为墙肢强度指标;M1和M2分别为联肢墙左右墙肢截面的受弯承载力,其应考虑附加轴力的影响;Mo1和Mo2分别为只考虑初始轴力下左右墙肢截面的受弯承载力。随着附加轴力的变化,M1和M2随之发生改变,Mo1和Mo2保持不变,因而通过IWS可以直观地得到附加轴力对两片墙肢总受弯承载力的影响。图 10为算例CW-18和CW-10的IWS随附加轴力的变化曲线,墙肢截面受弯承载力采用截面设计软件XTRACT计算获得。

|
图 10 算例IWS随附加轴力变化曲线 Fig. 10 Variation of WSI with AAF of typical CWs |
从图 10可看出,当附加轴力较小时,IWS约等于1,此时附加轴力并未明显改变两片墙肢的总受弯承载力;随着附加轴力的增加,IWS开始不断下降,且下降速率随之增加,说明附加轴力越大,两片墙肢的总受弯承载力下降越明显。上述由IWS得到的规律也可通过图 9(a)进行解释,当墙肢轴力远小于Pu时,随着轴力的变化,受弯承载力近似成线性变化,此时当附加轴力较小时,两片墙肢的总受弯承载力M1 + M2几乎不改变,其中,Pu为RC墙达到大小偏心界限受压状态时的轴力;而当一片墙肢的轴力G + N接近或大于Pu时,其受弯承载力将不再随着轴力的增加而近似成线性增大,导致轴力为G-N墙肢的受弯承载力减小值ΔM1大于轴力为G+N墙肢的受弯承载力增加值ΔM2,此时随着附加轴力的增加,两片墙肢的总受弯承载力M1+M2将小于其在初始轴压力G下的总受弯承载力2Mo。
但是,对于联肢墙整体,其受弯承载力等于两片墙肢总受弯承载力加上附加轴力形成的拉压力偶,见式(17),因而仅通过IWS判断附加轴力对联肢墙抵抗总倾覆力矩能力的影响是有局限的。为此,本文提出联肢墙强度指标(coupled wall strength index,CWSI)的概念,其定义式为
| $ I_{\mathrm{CWS}}=\frac{M}{M_{\mathrm{o}}}=\frac{M_{1}+M_{2}+N l}{M_{\mathrm{o} 1}+M_{\mathrm{o} 2}} $ | (19) |
式中,ICWS为联肢墙强度指标。从该式可看出,相比IWS,ICWS可以更准确地反映附加轴力对联肢墙整体受弯承载力的影响。图 11为ICWS随附加轴力的变化曲线,从图 11可看出,随附加轴力的增加,ICWS近似呈线性增长;墙肢的初始轴压比越小时,ICWS的增长速率越大;在不同轴压比下,ICWS最大值近似相等,其中CW-18均约等于4,而CW-10左右墙肢不对称,不同轴压比下ICWS最大值差距相对略大,初始轴压比从小到大对应的ICWS依次为7.0、7.7和8.4。由此可得,随着附加轴力的增加,联肢墙整体受弯承载力近似呈线性增加,当墙肢初始轴力越小时,其增长速率越快。

|
图 11 算例ICWS随附加轴力变化曲线 Fig. 11 Variation of CWSI with AAF of typical CWs |
联肢墙的受剪承载力等于每片墙肢的受剪承载力之和,因而本文提出墙肢受剪强度指标(wall shear strength index,WSSI),并通过该指标分析附加轴力对联肢墙受剪承载力的影响,其定义式为
| $ I_{\mathrm{WSS}}=\frac{V_{1}+V_{2}}{V_{\mathrm{o1}}+V_{\mathrm{o} 2}} $ | (20) |
式中:IWSS为墙肢受剪强度指标;V1和V2分别为联肢墙左右墙肢的受剪承载力,其应考虑附加轴力的影响;Vo1和Vo2分别为只考虑初始轴力下左右墙肢的受剪承载力。通过《高规》[11]规定的RC墙肢受剪承载力公式计算墙肢的受剪承载力,进而可得出IWSS随附加轴力的变化曲线,见图 12。

|
图 12 算例IWSS随附加轴力变化曲线 Fig. 12 Variation of WSSI with AAF of typical CWs |
从图 12中可看出,对于算例CW-18和CW-10,IWSS呈现出相同的变化规律,即随着附加轴力增加,IWSS会出现线性下降的现象;当墙肢初始轴压比等于0.2时,IWSS在附加轴力出现后便开始下降,而其余初始轴压比下IWSS先保持不变,随后开始下降,且不同初始轴压比下的IWSS下降速率相同。以上规律可通过图 9(b)进行解释,当一片墙肢的轴力G+N大于0.2倍的截面抗压强度时,其受剪承载力将保持不变,而另一片墙肢轴力G-N小于0.2倍的截面抗压强度时,该侧墙肢的受剪承载力将会随着附加轴力的增加而线性降低,故造成了IWSS线性下降;此外,当初始轴压比不等于0.2时,随着附加轴力的增加,两侧墙肢的受剪承载力将沿着直线变化,故IWSS先保持不变;而当任一墙肢的轴压比经过0.2后,一片墙肢受剪承载力将保持不变,另一片墙肢受剪承载力开始降低,IWSS将开始下降。从图 12中还可看出,当墙肢初始轴压比大于等于0.2时,IWSS的最小值相同,其原因为,轴力较大墙肢的受剪承载力已达到最大值,不再随着附加轴力的增加而改变,而对于另一片墙肢,由附加轴拉力降低其受剪承载力的最大值是一定的,因为使其受剪承载力下降的轴力变化范围均为由0.2倍截面抗压强度变化至墙肢被拉坏时的轴力Tmax。在本文算例中,IWSS的最小值均约为0.85,附加轴力最多削弱了联肢墙受剪承载力的15%。
4 结论本文基于连续连杆法,通过选取合适的坐标系,建立了以墙肢附加轴力为未知函数的微分方程,推导了三种水平荷载形式下直接计算墙肢附加轴力的公式,给出了高效计算方法,并采用数值模拟进行了验证,最后详细分析附加轴力对联肢墙承载力的影响规律,主要结论如下:
1) 选取坐标系z轴正方向沿结构竖直向下,建立以墙肢附加轴力为未知函数的微分方程,不仅可以简化倾覆力矩的表达式,便于后续微分方程特解的求解,而且可直接推导出三种水平荷载形式下墙肢附加轴力的计算公式,避免了国内现有解析方法计算附加轴力时需对连梁约束弯矩换算成剪力并求和的过程,本文方法计算时更加实用高效。
2) 本文方法只需已知联肢墙的几何尺寸与水平荷载形式和大小即可快速准确地计算其附加轴力,避免了复杂的有限元建模分析过程。
3) 针对同一个联肢墙,不同形式水平荷载作用下,墙肢附加轴力大小的主要控制因素为水平荷载引起联肢墙的总倾覆力矩,而非其基底剪力。
4) 随着附加轴力的增加,虽然两片墙肢的总受弯承载力会降低,但联肢墙整体受弯承载力近似呈线性增加,且墙肢初始轴压比越小,其整体受弯承载力随附加轴力增长的速率越大。附加轴力会降低联肢墙受剪承载力,在本文算例中,受剪承载力最多被其削弱了15%。
| [1] |
陈云涛, 吕西林. 联肢剪力墙抗震性能研究—试验和理论分析[J]. 建筑结构学报, 2003, 24(4): 25. CHEN Yuntao, LV Xilin. Seismic behavior of coupled shear walls—experiment and theoretical analysis[J]. Journal of Building Structures, 2003, 24(4): 25. DOI:10.3321/j.issn:1000-6869.2003.04.004 |
| [2] |
SANTHAKUMAR A R. The ductility of coupled shear walls[D]. Christchurch: University of Canterbury, 1974
|
| [3] |
AKTAN A E, BERTERO V V. Seismic response of R/C frame-wall structures[J]. Journal of Structural Engineering, 1984, 110(8): 1814. DOI:10.1061/(ASCE)0733-9445(1984)110:8(1803) |
| [4] |
OZSELCUK A R. Experimental and analytical studies of coupled wall structures[D]. Berkeley: University of California, Berkeley, 1989
|
| [5] |
SUGAYA K, TESHIGAWARA M, KATO M, et al. Experimental study on carrying shear force ratio of 12-storey coupled shear wall[C]//12th WCEE. Auckland: NESEE, 2000: 2152
|
| [6] |
LEHMAN D E, TURGEON J A, BIRELY A C, et al. Seismic behavior of a modern concrete coupled wall[J]. Journal of Structural Engineering, 2013, 139(8): 1380. DOI:10.1061/(ASCE)ST.1943-541X.0000853 |
| [7] |
方鄂华. 高层建筑钢筋混凝土结构概念设计[M]. 北京: 机械工业出版社, 2004: 151. FANG Ehua. Conceptual design for high rise RC structures[M]. Beijing: China Machinery Press, 2004: 151. |
| [8] |
李宏男, 李兵. 钢筋混凝土剪力墙抗震恢复力模型及试验研究[J]. 建筑结构学报, 2004, 25(5): 42. LI Hongnan, LI Bing. Experimental study on seismic restoring performance of reinforced concrete shear walls[J]. Journal of Building Structures, 2004, 25(5): 42. DOI:10.3321/j.issn:1000-6869.2004.05.006 |
| [9] |
JI Xiaodong, CHENG Xiaowei, XU Mengchao. Coupled axial tension-shear behavior of reinforced concrete walls[J]. Engineering Structures, 2018, 167: 142. DOI:10.1016/j.engstruct.2018.04.015 |
| [10] |
CHENG Xiaowei, JI Xiaodong, HENRY R S, et al. Coupled axial tension-flexure behavior of slender reinforced concrete walls[J]. Engineering Structures, 2019, 188: 275. DOI:10.1016/j.engstruct.2019.03.026 |
| [11] |
高层建筑混凝土结构技术规程: JGJ 3—2010[S]. 北京: 中国建筑工业出版社, 2010 Technical specification for concrete structures of tall building: JGJ 3—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [12] |
建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [13] |
Prestandard and commentary for the seismic rehabilitation of buildings: FEMA—356[S]. Washington DC: Building Seismic Safety Council, 2000
|
| [14] |
刘韬, 张令心, 陈永盛. 水平荷载下联肢剪力墙墙肢附加轴力计算公式[J]. 建筑结构, 2009, 49. LIU Tao, ZHANG Lingxin, CHEN Yongsheng. Computation formula for additional axial force of coupling wall piers under horizontal loads[J]. Building Structure, 2009, 49(S2): 221. |
| [15] |
包世华, 张铜生. 高层建筑结构设计和计算(上册)[M]. 2版. 北京: 清华大学出版社, 2013: 126. BAO Shihua, ZHANG Tongsheng. Design and calculation of high-rise building structure (Volume I)[M]. 2nd ed. Beijing: Tsinghua University Press, 2013: 126. |
| [16] |
SMITH B S, COULL A. Tall building structures: analysis and design[M]. New York: Wiley InterScience, 1991: 213.
|
| [17] |
施士昇. 混凝土的抗剪强度、剪切模量和弹性模量[J]. 土木工程学报, 1999, 32(2): 51. SHI Shisheng. Shear strength, modulus of rigidity and Young's modulus of concrete[J]. China Journal of Civil Engineering, 1999, 32(2): 51. DOI:10.3321/j.issn:1000-131X.1999.02.008 |
| [18] |
缪志伟. 钢筋混凝土框架剪力墙结构基于能量抗震设计方法研究[D]. 北京: 清华大学, 2009 MIAO Zhiwei. Study on energy-based seismic design methodology for reinforced concrete frame-shear wall structures[D]. Beijing: Tsinghua University, 2009 |
| [19] |
KOLOZVARI K, ORAKCAL K, WALLACE J W. Shear-flexure interaction modeling of reinforced concrete structural walls and columns under reversed cyclic loading[R]. Berkeley: Pacific Earthquake Engineering Research Center, University of California, Berkeley, 2015
|
| [20] |
LEQUESNE R D. Behavior and design of high-performance fiber-reinforced concrete coupling beams and coupled-wall systems[D]. Ann Arbor: University of Michigan-Ann Arbor, 2011
|
 2021, Vol. 53
2021, Vol. 53



 25
25