2. 中国电力科学研究院有限公司,北京 100192
2. China Electric Power Research Institute, Beijing 100192, China
大跨越输电铁塔中,钢管混凝土结构具备解决大直径钢管局部屈曲、改善法兰连接等问题的优势,已逐渐成为主材构件[1]。钢管混凝土柱作为主要承载构件,受多种荷载作用,复杂的受力状态对钢管和混凝土的协同工作性能提出了更高的要求[2-3]。钢-混界面黏结性能是二者协同工作的基础,因此有必要深入研究[4-6]。
钢-混界面黏结力由化学胶结力、机械咬合力和摩擦力三部分组成[7-8];宏观试验方法主要为推出试验,从力学性能研究界面黏结破坏过程[9-11]。随着商业有限元软件的日臻完善和普及,越来越多的学者采用数值方法研究钢-混界面的黏结-滑移行为。康希良等[12]采用接触分析模拟了钢管与混凝土界面作用,结果表明库伦摩擦滑动准则适用于模拟钢-混界面的切向力学行为。王振等[13]通过在同一节点处设置两个切向和一个法向弹簧单元来模拟钢管节点与混凝土节点的相互作用,发现考虑黏结-滑移时与试验结果较为接近。Hwang等[14]提出了等效刚度合并法连接钢管和混凝土界面的有限元模型,得到了当钢管径厚比小于100时必须考虑界面黏结作用的结论。文献[15]采用声发射技术对推出过程中钢-混界面黏结-滑移过程进行实时监测,结果显示化学胶结力随推出荷载的增大逐步丧失,钢-混界面的破坏是一个逐步剥离的过程。
目前,国内外学者针对钢-混界面的有限元模型主要有两类:1)在界面定义固定模式的非线性弹簧,这种模型的主要问题是无法反映推出过程的时变状态;2)利用基于库伦摩擦滑动准则的接触分析模型,然而库伦摩擦滑动准则定义的黏聚力(化学胶结力)一直存在,与推出过程中界面剥离的现象相违背。此外,对于输电杆塔中应用的直缝焊接钢管,经过辊压、焊接等工艺成型后存在明显初始几何缺陷[16],现有的有限元模型未能对此充分考虑。本文采用ANSYS参数化语言,通过钢管特征屈曲模态引入了钢管几何缺陷,采用面-面接触分析研究了钢管与混凝土界面的力学行为。模型可对每级荷载步进行检测,自动识别化学胶结力丧失的接触对,利用ANSYS重启动分析功能在荷载步之间自动修正界面库伦摩擦滑动准则,对钢管混凝土试件推出过程进行了精细化有限元数值模拟,以探讨钢管与混凝土界面黏结机理。
1 有限元模型介绍 1.1 材料本构关系混凝土单轴受压的应力-应变关系根据《混凝土结构设计规范》[17]确定:
| $ {\sigma _{\rm{c}}} = \left\{ \begin{array}{l} {f_{{\rm{ck}}}}\left[ {1 - {{\left( {1 - \frac{{{\varepsilon _{\rm{c}}}}}{{{\varepsilon _0}}}} \right)}^n}} \right], {\varepsilon _{\rm{c}}} \le {\varepsilon _0}\\ {f_{{\rm{ck}}}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\varepsilon _0} < {\varepsilon _{\rm{c}}} \le {\varepsilon _{{\rm{cu}}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{array} \right. $ | (1) |
| $ {n = 2 - \frac{1}{{60}}\left( {{f_{{\rm{ck}}}} - 50} \right)} $ | (2) |
| $ {{\varepsilon _0} = 0.002 + 0.5\left( {{f_{{\rm{ck}}}} - 50} \right) \times {{10}^{ - 5}}} $ | (3) |
| $ {{\varepsilon _{{\rm{cu}}}} = 0.003\;3 - 0.5\left( {{f_{{\rm{ck}}}} - 50} \right) \times {{10}^{ - 5}}} $ | (4) |
式中:fck采用混凝土28 d抗压强度实测值,当n大于2.0时取2.0,ε0为混凝土压应力为fck时的压应变,当小于0.002时取0.002,εcu为混凝土极限压应变,当大于0.003 3时取0.003 3。
混凝土单轴受拉应力-应变关系:
| $ {\sigma _{\rm{t}}} = \left\{ {\begin{array}{*{20}{l}} {{E_0}{\varepsilon _{{\rm{t}}0}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\varepsilon _{\rm{t}}} < {\varepsilon _{{\rm{t}}0}}}&{}\\ {0.6{f_{{\rm{ct}}}}\left( {1.2 - 0.2\frac{{{\varepsilon _{\rm{t}}}}}{{{\varepsilon _{{\rm{t}}0}}}}} \right), {\varepsilon _{{\rm{t}}0}} < {\varepsilon _{\rm{t}}} < {\varepsilon _{{\rm{tu}}}}}&{} \end{array}} \right. $ | (5) |
式中:混凝土单轴拉力达到抗拉强度后(此时拉应变为εt0),拉应力释放到0.6倍抗拉强度,当拉应变达到6εt0后,拉应力降为0,E0为式(1)在原点切线模量,fct=1.8×((fck+8)/18)0.6[18],fct为混凝土抗拉强度。混凝土的单轴应力-应变关系曲线见图 1。钢材采用理想弹塑性模型,泊松比为0.3, 弹性模量为2.06×105 MPa。

|
图 1 混凝土的单轴应力-应变曲线 Fig. 1 Uniaxial stress-strain curve of concrete |
混凝土采用8结点Solid65单元模拟,每个结点有3个平动自由度,单元具备开裂、塑性变形等功能;当最大主拉应力超过抗拉强度时,在垂直于主拉应力的方向上形成弥散裂缝,计算时关闭压碎功能。
钢管采用4结点Shell181单元模拟,每个结点有3个平动自由度和3个转动自由度,单元支持Mises屈服准则,适用于分析薄到中厚壳结构;非线性分析中考虑了壳体厚度的变化,壳面通过SECOFFSET命令进行偏移,以减少几何模型建模误差,带厚度的壳面偏移后的位置见图 2。

|
图 2 壳面偏移后位置 Fig. 2 Position of shell surface after offsetting |
钢管与混凝土界面插入面-面接触单元,分别是敷在钢管单元内表面的Targe170和混凝土单元表面的Conta174。Conta174单元通过数字输出接触状态(黏结或滑动),为判断黏结界面的黏结-滑移状态提供依据。
1.3 黏结界面的库伦摩擦滑动准则钢管和混凝土的切向力学行为用库仑摩擦滑动准则[19]模拟,等效剪力计算式为
| $ \tau=\tau_{\mathrm{a}}+\mu P $ | (6) |
式中:τa为化学胶结力,μ为钢-混界面摩擦系数,取室温下轧制钢与混凝土间摩擦系数测试均值0.281[18],P为法向压力。接触面滑动前界面处于黏结状态,当界面间化学胶结力τa与初始摩擦力μP之和超过容许剪应力τmax后进入滑动状态,如图 3所示的库伦摩擦滑动准则。

|
图 3 库伦摩擦滑动准则 Fig. 3 Coulomb friction and sliding criterion |
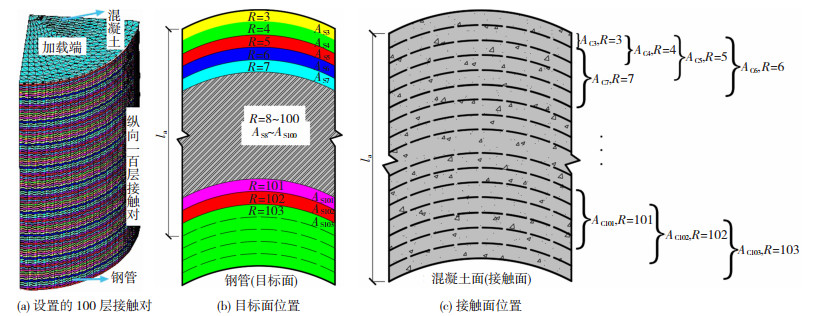
根据库伦摩擦滑动准则,接触面发生滑动后化学胶结力τa仍存在,故不能反映化学胶结力随滑移而丧失的实际情况。本文从加载端到自由端共建立100层接触对(图 4(a)),当某一层黏结界面发生滑移,则使本层界面单元中τa=0。
|
图 4 接触对的设置方式 Fig. 4 Setting of contact pairs |
钢管从加载端到自由端平均分为100层目标面,目标面前99层纵向高度为la/100,第100层纵向高度为5la/100(为混凝土推出预留空间,混凝土最大位移≤4la/100),每一层面积用(AS3~AS103)表示,见图 4(b)。混凝土表面覆盖100层接触面,与钢管目标面通过实常数(R=3~103)形成接触对,图 4(c)显示了每一层接触面位置,接触面面积与目标面面积关系:AC3=AS3、AC4=2AS4、AC5=3AS5、ACi=4ASi(i=6~103)。
接触分析中,仅实常数相同的接触对会在目标面对应位置计算黏结-滑移行为。在混凝土加载端最大位移4la/100范围内:仅当混凝土加载端位移s≤la/100,目标面AS3层与接触面AC3计算黏结-滑移行为;仅当加载端位移s≤2la/100,目标面AS4层与接触面AC4计算黏结-滑移行为;仅当加载端位移s≤3la/100,目标面AS5层与接触面AC5计算黏结-滑移行为;当加载端位移s≤4la/100,目标面ASi层始终与接触面ACi(i=6~103)计算黏结-滑移行为。
1.4 直缝焊接钢管加工偏差几何模型概化直缝焊接钢管生产工艺主要包括:钢板洗边、卷曲、合缝、焊接等。在运输、吊装等过程钢管会产生缺陷,焊接会导致残余变形。根据行业规范T/CEC 136—2017《输电线路钢管塔用直缝焊管》[20],直缝焊管外径制作允许偏差为±0.5%钢管外径D。钢管制作偏差包括钢管整体内径尺寸沿纵向不一致等整体几何缺陷和钢管局部发生鼓曲、凹陷等局部几何缺陷。有限元模型引入钢管几何缺陷的步骤如下:
1) 建立理想钢管模型,对钢管进行特征值屈曲分析。本文以图 5(a)中低阶屈曲模态表征整体几何缺陷,以图 5(b)中高阶屈曲模态表征局部几何缺陷。

|
图 5 特征屈曲模态(缺陷放大50倍) Fig. 5 Characteristic buckling modes (defects magnified by a factor of 50) |
2) 用ANSYS参数化设计语言,将钢管低、高阶屈曲模态分析结果的节点位移值存入数组,并将低、高阶屈曲模态的节点位移值叠加,使得钢管最大几何缺陷为±0.5%钢管外径D,以此作为钢管初始节点坐标更新钢管几何模型。钢管施加几何缺陷后,四边形壳单元的4个结点不一定保持共面,更新几何模型时无法生成面,故需用三角形单元对壳单元进行离散,从而解决结点共面的问题。
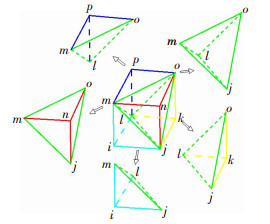
3) 在钢管所有节点位置再次建立混凝土节点,并依次向混凝土内部建立节点,通过节点依次生成混凝土体单元。每个钢管壳单元与混凝土单元的一个表面几何位置对应,由于钢管被离散为三角形单元,故混凝土宜采用四面体单元模拟。四面体单元可由六面体单元拆分得到,图 6为六面体拆分示意。
|
图 6 六面体单元拆分示意 Fig. 6 Splitting schematic of hexahedral element |
创建混凝土单元时先找到更新模型前可构成六面体的8个节点编号(模型更新前后节点编号保持不变),再在8个节点间依次通过节点直接生成四面体单元,以此原则在所有节点间循环生成全部混凝土单元,钢管混凝土横截面网格划分结果见图 7(a)。混凝土下端建立空腔段,为混凝土推出预留空间,钢管混凝土有限元模型见图 7(b)。求解时钢管和混凝土对称面施加对称边界条件,钢管底面施加竖向约束,混凝土顶面节点耦合于圆心正上方作为加载点。

|
图 7 有限元模型 Fig. 7 Finite element model |
有限元模型通过特征屈曲模态引入钢管几何缺陷,加载时在荷载步间自动修正库伦摩擦滑动准则并去除发生滑移接触对的化学胶结力,有限元模型计算流程见图 8。重启动分析[21]在计算荷载步间允许修改参数并继续分析,可实现在原来分析的基础上继续计算,图 8中在计算荷载步间对化学胶结力赋值为0的过程由重启动分析功能实现。

|
图 8 有限元模型计算过程 Fig. 8 Calculation process of the finite element model |
为研究直缝焊接钢管与混凝土界面黏结性能,文献[15]以界面黏结长度、混凝土强度、钢管径厚比为主要研究参数,进行了9个钢管混凝土试件的推出试验,试件设计参数列于表 1。
| 表 1 试件设计参数 Tab. 1 Design parameters of specimens |
试验加载采用1 000 kN单轴伺服液压试验机,混凝土加载端放置一块直径略小于钢管内径的圆形钢垫块,加载时直接作用于混凝土上端,通过界面黏结力传递给周围钢管,混凝土自由端设置空腔段,为混凝土推出预留空间,加载装置见图 9(a)。混凝土加载端的位移由位移计D1和D2测定,自由端端位移由D7测定,D3和D4测量钢管顶面的竖向位移,D5和D6测量底部支座沉降位移,测点布置见图 9(b)。

|
图 9 加载装置 Fig. 9 Test setup |
数值模拟得到的加载端荷载-滑移曲线与文献[15]的试验结果对比于图 10,图 10中数值模拟得到的曲线可分为Ⅰ类(形成拐点后呈下降趋势)、和Ⅱ类(形成拐点后持续上升),为了使对比结果更加清晰可见,Ⅰ类曲线对比结果分两张图给出。从图 10可得,有限元模型比较准确地反映了钢-混界面黏结-滑移行为,有限元分析结果与试验结果吻合良好。

|
图 10 荷载-滑移曲线FEM计算值与试验值比较 Fig. 10 Comparison of load-slip curves between FEM calculation results and test results |
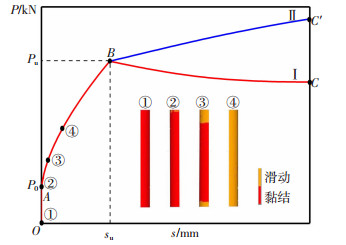
图 11为数值模拟的Ⅰ类、Ⅱ类曲线黏结界面接触状态随加载端位移变化过程,其中Ⅰ类、Ⅱ类加载端荷载-滑移曲线包括胶结段(OA)、非线性初滑移段(AB)和滑移段(BC、BC′),定义荷载-滑移曲线上界面发生初滑移时(A点)对应荷载为初始滑移荷载P0,拐点(B点)对应的荷载为Pu。有限元分析结果得到的各阶段黏结机理如下:
|
图 11 黏结界面滑移发展过程 Fig. 11 Development process of bond interface slippage |
胶结段(OA):从图 11中①处接触状态可得,加载初期界面处于黏结状态,加载端混凝土和钢管均发生等量的弹性压缩变形,界面无相对滑移产生。
非线性初滑移段(AB):图 11中②处接触状态表明,当加载端荷载达到P0,加载端黏结界面先发生相对滑移并逐步向混凝土中部发展,黏结界面发生滑移是由于混凝土与钢管发生了不协调变形。随着加载端荷载增大,自由端黏结界面开始出现相对滑移,见图 11中③处接触状态。加载端荷载逐渐增大,钢-混黏结界面由两端向中部逐步剥离,最终发展为全截面剥离,见图 11中④处接触状态。
滑移段(BC、BC′):Ⅰ类曲线在滑移段呈下降趋势。Ⅰ类曲线试件钢管整体几何缺陷特征为:钢管母线为直线,如图 12所示,为更直观表示缺陷的形式和位置,图中显示的缺陷变形值是实际缺陷的50倍。

|
图 12 Ⅰ类曲线整体几何缺陷(缺陷放大50倍) Fig. 12 Overall geometric defects of typeⅠcurves (defects magnified by a factor of 50) |
混凝土推出过程中有限元计算的钢管纵向应力分布如图 13(a)所示,在钢管局部凸起或者凹陷处纵向应力较大。钢-混界面产生相对滑移时,钢管几何缺陷受到挤压产生法向应力P,提供一定的机械咬合力和摩擦应力μP,应力大小主要与缺陷大小与形状相关,见图 13(b)。图 14为Ⅰ类曲线滑移段摩擦应力随滑移变化过程,从图 14得,滑移段状态⑥处摩擦应力比状态⑤处分布均匀,且摩擦应力数值小于状态⑤中的摩擦应力。由于滑移量增大,混凝土与钢管界面契合程度降低,整体几何缺陷形式也导致钢管约束能力降低,摩擦应力逐步分布均匀,局部摩擦应力受几何缺陷大小和形状影响而降低。在滑移段,由于机械咬合力与摩阻力两者之和小于荷载Pu,Ⅰ类曲线达到荷载Pu后出现下降段。

|
图 13 滑移后纵向应力的分布与产生机理(缺陷放大50倍) Fig. 13 Distribution and mechanism of longitudinal stress after slipping (defects magnified by a factor of 50) |

|
图 14 Ⅰ类曲线摩擦应力发展过程 Fig. 14 Development process of friction stress in type Ⅰ curves |
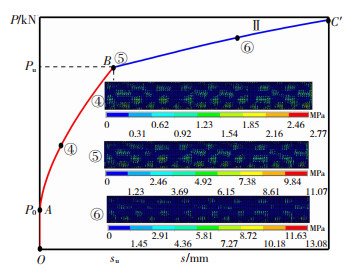
Ⅱ类曲线在滑移段持续上升。Ⅱ类曲线试件钢管整体几何缺陷特征:钢管母线为曲线,见图 15。当加载端荷载达到Pu后,钢管存在明显的锥楔作用,混凝土推出时钢管整体约束能力增强。图 16为Ⅱ类曲线滑移段摩擦应力随滑移变化过程,从图 16得,状态⑥局部摩擦应力略大于状态⑤中的摩擦应力,但比状态⑤分布均匀。由于滑移量增大,混凝土与钢管界面契合程度降低,钢管对混凝土约束能力降低,削弱了整体几何缺陷的锥楔作用,摩擦应力逐步分布均匀,局部摩擦应力的大小受几何缺陷影响增大。滑移段由于机械咬合力和摩阻力之和大于荷载Pu,Ⅱ类曲线达到荷载Pu后持续上升。

|
图 15 Ⅱ类曲线整体几何缺陷(缺陷放大50倍) Fig. 15 Overall geometric defects of typeⅡcurves (defects magnified by a factor of 50) |
|
图 16 Ⅱ类曲线摩擦应力发展过程 Fig. 16 Development process of friction stress in type Ⅱ curves |
随着黏结界面发生滑移,加载端黏结界面混凝土出现裂缝后自由端混凝土也出现裂缝,最终发展至整个黏结界面,如图 17中显示的混凝土裂缝发展过程。混凝土界面裂缝分布并不均匀,在钢管几何缺陷较大、密集区域更为明显。由于钢管存在几何缺陷,混凝土发生整体滑移时界面受到缺陷的反复挤压,混凝土裂缝会由黏结界面发展至混凝土内部,见图 17中⑤处混凝土裂缝分布。

|
图 17 混凝土裂缝发展过程 Fig. 17 Development process of concrete cracks |
实测几何缺陷是最可靠的方法,但对于庞大的工程结构实体既不经济也不现实。参考中国GB 50017—2017《钢结构设计标准》[22]中柱引入初始缺陷的方法,柱面的初始缺陷可按低阶整体屈曲模态采用:柱初弯曲取为柱高的1/1 000。对于直缝焊接钢管,钢管加工偏差包括整体几何缺陷和局部几何缺陷,只采用低阶屈曲模态引入缺陷,不能对局部几何缺陷进行考虑,对钢管实际存在的缺陷考虑不够全面,仍有完善的空间。本文根据规范钢管特征屈曲模态计算缺陷的方法,共对9个考虑初始缺陷的钢管混凝土进行了计算并完成试验验证,旨在提出经验性选取钢管几何缺陷的方式,为实际应用考虑几何缺陷方法提供参考。
钢管几何缺陷引入方法包括整体几何缺陷、局部几何缺陷引入方法。从2.2节试算知,直缝焊接钢管荷载-滑移曲线类型与钢管几何缺陷形式相关。整体几何缺陷根据低阶屈曲模态引入,Ⅰ类曲线试件钢管整体几何缺陷可引入低阶屈曲模态中钢管母线为直线的模型,Ⅱ类曲线试件可引入低阶屈曲模态中钢管母线为曲线的模型。
局部几何缺陷根据高阶屈曲模态引入,结合试算结果归纳各个试件高阶屈曲模态,发现试件高阶屈曲模态均呈显著波浪状,见图 18。将图 18中局部几何缺陷定义为周期性波峰状缺陷,完整的波峰定义为一个,钢管端部不完整的波峰定义为半个,则图 18中每一纵列波峰个数均相同(7个),并将图 18中纵向每一列波峰数目定义为波峰数量NCAL。

|
图 18 周期性波峰状缺陷(缺陷放大50倍) Fig. 18 Periodic wave crest-like defects (defects magnified by a factor of 50) |
为研究钢管局部几何缺陷引入方法,建立试件径厚比D/t、界面黏结长度la、混凝土强度fcu与波峰数量NCAL经验关系式,见式(7)。公式计算的波峰数目与有限元模型采用的波峰数目对比于图 19,整体误差较小。公式可作为高阶屈曲模态选取方式的计算原则,具体方法是先根据公式计算不同试件周期性波峰状缺陷的数目(四舍五入取整数),匹配对应的高阶屈曲模态阶数,再作为局部几何缺陷引入。
| $ \begin{array}{*{20}{c}} {{N_{{\rm{CAL}}}} = \left( {0.002\;82D/t + 0.006\;43{l_{\rm{a}}} + } \right.}\\ {1.56969)\left( {f_{{\rm{cu}}}^{0.5} - 4.430\;31} \right)} \end{array} $ | (7) |

|
图 19 波峰数量对比结果 Fig. 19 Comparison of crests numbers |
本文建立了9个含几何缺陷的钢管混凝土有限元模型,对推出过程钢-混界面时变状态进行检测并在荷载步之间修正库伦摩擦滑动准则,对钢-混界面黏结机理进行了分析,得到如下结论:
1) 数值模拟结果与试验曲线对比表明,本文有限元模拟方法具有较好的适用性,实现了钢管混凝土构件随加载端荷载增大黏结界面由两端向中部逐步发生剥离,混凝土裂缝由黏结界面向截面中心发展的变化机制。
2) 有限元细部分析结果可弥补宏观试验的不足,模拟结果表明钢管局部缺陷处纵向应力更显著,摩擦应力不均匀程度明显,摩擦应力随着界面滑移值增大逐渐趋于均匀分布。
3) 低阶屈曲模态可以表征钢管整体几何缺陷,Ⅰ类曲线(形成拐点后呈下降趋势)钢管整体几何缺陷的特点是钢管母线为直线,Ⅱ类曲线(形成拐点后仍缓慢上升)钢管整体几何缺陷的特点是钢管母线为曲线。
4) 高阶屈曲模态可以表征钢管局部几何缺陷,钢管局部几何缺陷为周期性波峰状缺陷,提出了波峰数目与径厚比、界面黏结长度、混凝土强度等参数的经验计算式。
| [1] |
朱瑞元, 李喜来, 廖宗高, 等. 大跨越钢管混凝土输电塔抗震性能分析[J]. 电力勘测设计, 2018, 25(增刊2): 137. ZHU Ruiyuan, LI Xilai, LIAO Zonggao, et al. Seismic performance analysis of a long-span concrete filled steel-tube transmission tower[J]. Electric Power Survey & Design, 2018, 25(S2): 137. DOI:10.13500/j.cnki.11-4908/tk.2018.s2.025 |
| [2] |
练其安, 雷东, 张大伟, 等. 钢管混凝土中型钢与混凝土黏结性能试验研究[J]. 钢结构, 2018, 33(9): 49. LIAN Qi'an, LEI Dong, ZHANG Dawei, et al. Experimental research on bond property between profile steel and concrete in concrete filled steel tube[J]. Steel Construction, 2018, 33(9): 49. DOI:10.13206/j.gjg201809009 |
| [3] |
韩林海. 钢管混凝土结构[M]. 北京: 科学出版社, 2016: 34. HAN Linhai. Concrete filled steel tubular structure[M]. Beijing: Science Press, 2016: 34. |
| [4] |
FU Zhaoqing, GE Hanbin, JI Bohai, et al. Interface bond behavior between circular steel tube and lightweight aggregate concrete[J]. Advanced Steel Construction, 2018, 14(3): 424. DOI:10.18057/IJASC.2018.14.3.7 |
| [5] |
ZHOU Xuhong, YAN Biao, LIU Jiepeng. Behavior of square tubed steel reinforced-concrete (SRC) columns under eccentric compression[J]. Thin-Walled Structures, 2015, 91: 129. DOI:10.1016/j.tws.2015.01.022 |
| [6] |
赵卫平, 雷永旺, 王振兴, 等. 钢管混凝土中内配钢骨与混凝土黏结性能试验[J]. 哈尔滨工业大学学报, 2020, 52(8): 121. ZHAO Weiping, LEI Yongwang, WANG Zhenxing, et al. Experimental study on bond performance between internal steel and concrete in concrete filled steel tube[J]. Journal of Harbin Institute of Technology, 2020, 52(8): 121. DOI:10.11918/202002049 |
| [7] |
康希良, 赵鸿铁, 薛建阳, 等. 钢管混凝土粘结滑移问题综述分析[J]. 西安建筑科技大学学报, 2006, 38(3): 321. KANG Xiliang, ZHAO Hongtie, XUE Jianyang, et al. Summarized review of the bond-slip problems of concrete filled steel tubes (CFST)[J]. Journal of Xi'an University of Architecture and Technology, 2006, 38(3): 321. DOI:10.3969/j.issn.1006-7930.2006.03.005 |
| [8] |
许开成, 毕丽苹, 陈梦成. 钢管混凝土界面黏结应力-滑移本构关系试验研究[J]. 建筑结构学报, 2015, 36(增刊1): 410. XU Kaicheng, BI Liping, CHEN Mengcheng. Experimental study on bond stress-slip constitutive relationship for CFST[J]. Journal of Building Structures, 2015, 36(S1): 410. DOI:10.14006/j.jzjgxb.2015.S1.062 |
| [9] |
陈宗平, 徐金俊, 薛建阳, 等. 钢管再生混凝土黏结滑移推出试验及黏结强度计算[J]. 土木工程学报, 2013, 46(3): 49. CHEN Zongping, XU Jinjun, XUE Jianyang, et al. Push-out test on the interface bond-slip behavior and calculation on bond strength between steel tube and recycled aggregate concrete in RACFST structures[J]. Journal of Civil Engineering, 2013, 46(3): 49. DOI:10.15951/j.tmgcxb.2013.03.016 |
| [10] |
TAO Zhong, SONG Tianyi, UY B, et al. Bond behavior in concrete-filled steel tubes[J]. Journal of Constructional Steel Research, 2016, 120: 81. DOI:10.1016/j.jcsr.2015.12.030 |
| [11] |
YU Chen, FENG Ran, SHAO Yongbo, et al. Bond-slip behaviour of concrete-filled stainless steel circular hollow section tubes[J]. Journal of Constructional Steel Research, 2017, 130: 248. DOI:10.1016/j.jcsr.2016.12.012 |
| [12] |
康希良, 程耀芳, 涂昀, 等. 钢管混凝土粘结-滑移性能试验研究及数值分析[J]. 工程力学, 2010, 27(9): 103. KANG Xiliang, CHENG Yaofang, TU Yun, et al. Experimental study and numerical analysis of bond-slip performance for concrete filled steel tube[J]. Engineering Mechanics, 2010, 27(9): 103. |
| [13] |
王振, 张宁. 钢管混凝土的界面黏结-滑移性能数值分析研究[J]. 中国公路学报, 2018, 38(1): 192. WANG Zhen, ZHANG Ning. Numerical analysis on bond-slip behavior of concrete-filled steel tubes[J]. China Journal of Highway and Transport, 2018, 38(1): 192. DOI:10.14048/j.issn.1671-2579.2018.01.041 |
| [14] |
HWANG J Y, KWAK H G, KWON Y. A numerical model for considering the bond-slip effect in axially loaded circular concrete-filled tube columns[J]. Advances in Structural Engineering, 2018, 21(12): 1933. DOI:10.1177/1369433218759779 |
| [15] |
赵卫平, 雷永旺, 尹鹏, 等. 钢管混凝土界面黏结破坏的声发射特征及时空演化机制[J/OL]. [2020-11-26]. https://doi.org/10.14006/j.jzjgxb.2020.0052 ZHAO Weiping, LEI Yongwang, YIN Peng, et al. Investigation on acoustic emission characteristics and time-space evolution mechanism of interfacial bond failure of concrete-filled steel tube[J/OL]. [2020-11-26]. https://doi.org/10.14006/j.jzjgxb.2020.0052 |
| [16] |
董家顺, 王兴东, 李殿杰, 等. 基于改进K-means算法的钢管表面缺陷视觉检测方法[J]. 武汉科技大学学报, 2020, 43(6): 440. DONG Jiashun, WANG Xingdong, LI Dianjie, et al. Visual inspection method for surface defects of steel tubes based on improved K-means algorithm[J]. Journal of Wuhan University of Science and Technology, 2020, 43(6): 440. DOI:10.3969/j.issn.1674-3644.2020.06.007 |
| [17] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2015 Code for design of concrete structures: GB 50010—2010[S]. Beijing: Chinese Architecture and Building Press, 2015 |
| [18] |
赵卫平, 朱彬荣. 高温后HSC粘结滑移基础参数测量与3D有限元数值模拟[J]. 工程力学, 2017, 34(4): 180. ZHAO Weiping, ZHU Binrong. Basic parameters test and 3D modelling of bond in HSC after elevated temperatures[J]. Engineering Mechanics, 2017, 34(4): 180. DOI:10.6052/j.issn.1000-4750.2015.11.0898 |
| [19] |
赵卫平. 基于ANSYS接触分析的粘结-滑移数值模拟[J]. 建筑科学与工程学报, 2011, 28(2): 47. ZHAO Weiping. Bond-slip numerical simulation based on ANSYS contact analysis[J]. Journal of Architecture and Civil Engineering, 2011, 28(2): 47. DOI:10.19815/j.jace.2011.02.008 |
| [20] |
中国电力企业联合会. 输电线路钢管塔用直缝焊管: T/CEC 136—2017[S]. 北京: 中国电力出版社, 2017 China Electricity Council (CEC). Longitudinal welding pipe for transmission line steel tubular tower: T/CEC 136—2017[S]. Beijing: China Electric Power Press, 2017 |
| [21] |
王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007: 281. WANG Xinmin. Numerical analysis of engineering structure on ANSYS[M]. Beijing: China Communications Press, 2007: 281. |
| [22] |
钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2017 Standard for design of steel structures: GB 50017—2017[S]. Beijing: Chinese Architecture and Building Press, 2017 |
 2021, Vol. 53
2021, Vol. 53


