2. 深圳市市政设计研究院有限公司,广东 深圳 518029
2. Shenzhen Municipal Design & Research Institute Co. Ltd., Shenzhen 518029, Guangdong, China
随着结构形式的不断推陈出新,钢板剪力墙逐渐受到重视和发展,但薄钢板剪力墙易失稳而厚钢板剪力墙成本较高。波纹钢板因波折的几何形式很好的弥补薄钢板易失稳的缺点,且相对厚钢板更薄,故部分学者着力于研究波纹钢板剪力墙等波纹板构件的抗侧性能。波纹钢腹板梁方面,Johnson等[1]基于有限元分析和试验研究了波纹钢腹板梁剪切弹性刚度和极限承载力。集装箱方面,查晓雄等[2]基于蒙皮理论推导了波纹板的抗侧刚度。波纹钢板剪力墙方面,李靓姣[3]对波浪形钢板墙在不同受力条件下的性能进行分析;孙军浩[4]理论分析了波纹钢板剪力墙抗侧承载力的计算方法,并得出了抗侧承载力计算公式。李雅楠[5]理论分析了波纹钢板剪力墙体系的抗侧性能并进行了有限元模拟。赵秋红等[6]研究了不同波纹钢板连接方式、设计参数、竖向荷载对波纹钢板剪力墙抗侧性能的影响。可发现,波纹钢板的抗侧刚度公式虽已由Johnson等[1]经试验得出,但公式的理论解释尚不完善,准确性和适用范围仍有待提高和扩大。
基于正交各向异性板理论,推导了波纹钢板剪力墙弹性抗侧刚度统一公式, 并验证公式的可靠性,后将公式计算结果与多种波纹钢板剪力墙ABAQUS有限元模拟结果进行对比,验证了公式的统一性,最后明确了公式的适用范围。
1 波纹钢板剪力墙弹性抗侧刚度的理论分析考虑波纹钢板剪力墙框架对抗侧刚度的贡献,波纹钢板剪力墙剪切弹性抗侧刚度由框架抗侧刚度Kf和波纹钢板抗侧刚度Kp两部分叠加组成:
| $ K=K_{\mathrm{p}}+K_{\mathrm{f}} $ | (1) |
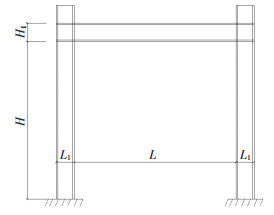
考虑单层波纹钢板剪力墙框架柱底部固接情形,框架样式见图 1。其中L、H分别为波纹钢板宽度和高度,L1、H1分别为框架柱截面高度和框架梁截面高度。
|
图 1 框架简图 Fig. 1 Frame sketch |
根据李雅楠[5]对波纹钢板剪力墙框架抗侧刚度的研究,假设框架梁是刚性的,框架的初始刚度计算公式为
| $ K_{\mathrm{f}}=18 \frac{E I_{\mathrm{c}}}{H^{3}} $ | (2) |
式中Ic是单根框架柱横截面绕强轴惯性矩,E是框架钢材弹性模量。
1.2 波纹钢板抗侧刚度公式推导相对于平钢板剪力墙,波纹钢板剪力墙有更好的弹性屈曲性能,且能避开传递到墙板上的重力荷载[7]。根据波纹钢板以上特点,将波纹钢板等效成一块宽为L、高为H、板厚度为t的正交各向异性平板,该异性板遵循如下基本假定[8]:
1) 忽略剪应变τxz和τyz,因而弯曲前垂直于中面的直线在弯曲过程中保持直线并仍然垂直于中面。
2) 略去法向应力σz及其相应的应变εz,因此任何点(x, y, z)的侧向挠度与中面上对应点(x, y, 0)的侧向挠度相等。
3) 与薄板的厚度相比,侧向挠度是微小的,因而略去弯曲引起的中面伸长,即与弯曲相比略去弯曲引起的薄膜作用。
4) 板的材质均匀、各向异性并且服从胡克定律。
正交各向异性材料在纯剪切状态下的侧移刚度等于其剪切刚度:
| $ D=\frac{G_{x y} A}{H}=\frac{G_{x y} t L}{H} $ | (3) |
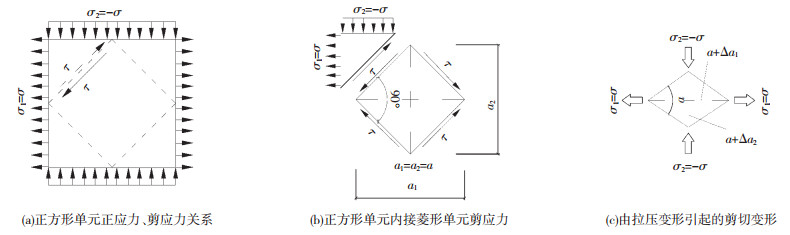
将波纹钢板等效为正交各向异性板时,其材料参数服从材料力学中正交各向异性体的规则[9]。对于各向同性材料,其弹性模量E、剪切模量G及材料泊松比ν存在简单关系。类似,在正交各向异性体中弹性模量与剪切模量之间依然存在关系,谢一环[10]给出了正交各向异性板弹性模量、剪切模量、泊松比之间的关系推导。如图 2(a)所示,正方形正交各向异性材料单元,其受主应力主方向为: σ2=-σ竖向受压,σ1=σ水平方向受拉。
|
图 2 正方形单元内接正方形正应力、剪应力、变形之间的关系 Fig. 2 Relationship between normal stress, shear stress, and deformation of inscribed square in square element |
根据力的平衡,该单元内接菱形应力状态为纯剪应力状态,且τ=σ,见图 2(b)。根据变形协调条件,内接菱形单元最终会变形成略扁的菱形,如图 2(c)所示,夹角会从π/2变成α, 剪切变形为γ=π/2-α。由图 2(c)可知变形后菱形夹角一半α/2的正切值为
| $ \tan \frac{\alpha}{2}=\frac{\left(a+\varDelta a_{2}\right) / 2}{\left(a+\varDelta a_{1}\right) / 2}=\frac{1+\varDelta a_{2} / a}{1+\varDelta a_{1} / a}=\frac{1+\varepsilon_{2}}{1+\varepsilon_{1}} $ | (4) |
式中ε1为第一主应力σ1方向上的应变,ε2为第二主应力σ2方向上的应变。
| $ \tan \left(\frac{{\rm{ \mathsf{ π} }}}{4}-\frac{\gamma}{2}\right)=\frac{1+\varepsilon_{2}}{1+\varepsilon_{1}} $ | (5) |
根据式(5)左侧对γ按一阶麦克劳林式展开得:
| $ \tan \left(\frac{{\rm{ \mathsf{ π} }}}{4}-\frac{\gamma}{2}\right)=1+\gamma+O(\gamma) $ | (6) |
根据式(5)右侧对ε1、ε2按二元函数f(ε1, ε2)=
| $ \frac{1+\varepsilon_{2}}{1+\varepsilon_{1}}=1-\varepsilon_{1}+\varepsilon_{2}+O\left(\varepsilon_{1}, \varepsilon_{2}\right) $ | (7) |
因此:
| $ 1-\gamma+O(\gamma)=1-\varepsilon_{1}+\varepsilon_{2}+O\left(\varepsilon_{1}, \varepsilon_{2}\right) $ | (8) |
式中
将式(8)省略高阶项并运算得:
| $ G_{12}=\frac{E_{1} E_{2}}{E_{1}\left(1+\nu_{21}\right)+E_{2}\left(1+\nu_{12}\right)} $ | (9) |
根据正交各向异性体工程弹性常数的互等关系:
| $ \nu_{12}=\frac{E_{1} \nu_{21}}{E_{2}} $ | (10) |
得正交各向异性平板沿板长方向的剪切模量表达式:
| $ G_{12}=\frac{E_{1} E_{2}}{E_{1}\left(1+\nu_{21}\right)+E_{2}} $ | (11) |
将波纹钢板等效为正交各向异性板,式(11)中E1、E2分别为波纹钢板x和y轴方向的等效弹性模量, 该模量受波纹钢板抗弯刚度影响显著。Briassoulis[11]给出计算波纹钢板绕波折边线弯曲的抗弯刚度计算公式:
| $ D_{y}=\frac{C_{1}}{S_{c}} \frac{E t^{3}}{12\left(1-\nu^{2}\right)} $ | (12) |
式中:C1是钢板波纹一个周期的宽度,Sc是钢板波纹一个周期展开后的宽度,t是波纹钢板厚度,ν是钢材泊松比。
绕波纹垂直方向的波纹钢板抗弯刚度计算公式:
| $ D_{x}=\frac{E I_{x}}{C_{1}} $ | (13) |
式中Ix是波纹钢板波纹横截面绕中性轴单个周期的惯性矩,Ix的表达式随钢板波纹形状的不同而改变。
等效正交各向异性板厚度为t,其绕板长和板宽方向中性轴单位长度的截面惯性矩均为I=t3/12,而相应抗弯刚度Dx、Dy已知,如式(12)、(13)所示,故根据截面抗弯刚度公式D=EI反推x和y轴方向的等效弹性模量E1和E2:
| $ \left\{\begin{array}{l} E_{1}=D_{x} / I=\frac{12 E I}{C_{1} t^{3}} \\ E_{2}=D_{y} / I=E \frac{C_{1}}{S_{\mathrm{c}}\left(1-\nu^{2}\right)} \end{array}\right. $ | (14) |
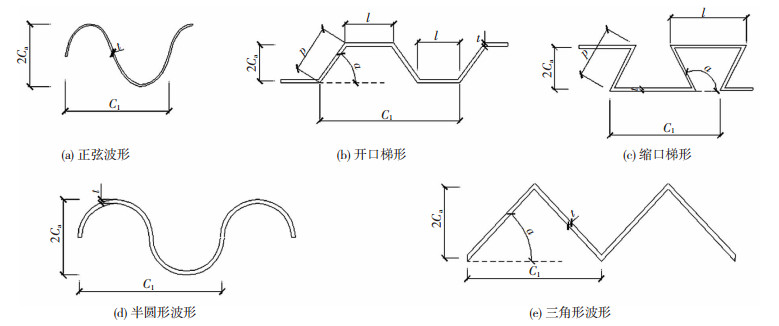
工程中波纹钢板常用波形有正弦形波纹钢板、梯形波纹钢板、半圆形波纹钢板、三角形波纹钢板,见图 3。
|
图 3 波纹钢板常用波形示意 Fig. 3 Commonly used wave forms of corrugated steel plates |
若波纹形状为正弦形,采用窦超等[12]给出的相应惯性矩和单周期波纹展开长度计算公式:
| $ I_{x}=C_{1} C_{\mathrm{a}}^{2} t \sqrt{\frac{0.250+2.35\left(C_{\mathrm{a}} / C_{1}\right)^{2}}{1+0.342\left(C_{\mathrm{a}} / C_{1}\right)^{2}}} $ | (15) |
| $ S_{\mathrm{c}}=C_{1} \sqrt{1+16.3\left(C_{\mathrm{a}} / C_{1}\right)^{1.92}} $ | (16) |
将式(15)代入式(14)计算后得:
| $ \left\{\begin{array}{l} E_{1}=\frac{12 E C_{\mathrm{a}}^{2} \sqrt{\frac{0.250+2.35\left(C_{\mathrm{a}} / C_{1}\right)^{2}}{1+0.342\left(C_{\mathrm{a}} / C_{1}\right)^{2}}}}{t^{2}} \\ E_{2}=E \frac{C_{1}}{\left(1-\nu^{2}\right) S_{\mathrm{c}}} \end{array}\right. $ | (17) |
将式(17)代入式(11):
| $ \begin{gathered} G_{12}= \\ \frac{12 C_{\mathrm{a}}^{2} E \sqrt{\frac{0.250+2.35\left(C_{\mathrm{a}} / C_{1}\right)^{2}}{1+0.342\left(C_{\mathrm{a}} / C_{1}\right)^{2}}} \frac{C_{1}}{\left(1-\nu^{2}\right) S_{\mathrm{c}}}}{12 C_{\mathrm{a}}^{2} \sqrt{\frac{0.250+2.35\left(C_{\mathrm{a}} / C_{1}\right)^{2}}{1+0.342\left(C_{\mathrm{a}} / C_{1}\right)^{2}}}\left(1+2 \nu_{21}\right)+\frac{C_{1} t^{2}}{\left(1-\nu^{2}\right) S_{\mathrm{c}}}} \end{gathered} $ | (18) |
因正交各向异性板未知泊松比ν21≥0,并且式(18)分母中
| $ G_{12}=\frac{2 G}{\left(1+2 \nu_{21}\right)(1-\nu)} \frac{C_{1}}{S_{\mathrm{c}}} $ | (19) |
若波纹形状为梯形,则相应的Sc和Ix计算表达式:
| $ S_{\mathrm{c}}=2 l+\frac{4 C_{\mathrm{a}}}{\sin \alpha}=2 l+2 p $ | (20) |
| $ I_{x}=2 l t C_{\mathrm{a}}^{2}+\frac{4 t C_{\mathrm{a}}^{3}}{3 \sin \alpha}=2 t C_{\mathrm{a}}^{2}(l+p / 3) $ | (21) |
将式(21)代入式(14)得:
| $ \left\{\begin{array}{l} E_{1}=D_{x} / I=\frac{24 E C_{\mathrm{a}}^{2}(l+p / 3)}{C_{1} t^{2}} \\ E_{2}=D_{y} / I=E \frac{C_{1}}{\left(1-\nu^{2}\right) S_{\mathrm{c}}} \end{array}\right. $ | (22) |
将式(22)代入式(11)得:
| $ G_{12}=\frac{\frac{24 E C_{\mathrm{a}}^{2}(l+p / 3)}{C_{1}} \frac{C_{1}}{\left(1-\nu^{2}\right) S_{\mathrm{c}}}}{\frac{24 C_{\mathrm{a}}^{2}(l+p / 3)}{C_{1}}\left(1+2 \nu_{21}\right)+t^{2} \frac{C_{1}}{\left(1-\nu^{2}\right) S_{\mathrm{c}}}} $ | (23) |
因未知泊松比ν21≥0,且式(23)分母中
| $ G_{12}=\frac{2 G}{\left(1+2 \nu_{21}\right)(1-\nu)} \frac{C_{1}}{S_{\mathrm{c}}} $ | (24) |
半圆形波纹钢板相应的Sc和Ix计算表达式:
| $ S_{\mathrm{c}}={\rm{ \mathsf{ π} }} D $ | (25) |
| $ \begin{gathered} I_{x}=\frac{{\rm{ \mathsf{ π} }}\left(D^{4}-d^{4}\right)}{64}=\frac{{\rm{ \mathsf{ π} }} t\left(D^{2}+d^{2}\right)(D+d)}{64}= \\ \frac{{\rm{ \mathsf{ π} }} t\left(16 C_{\mathrm{a}}^{2}-2 d D\right) C_{1}}{64} \end{gathered} $ | (26) |
式中D是半圆形波纹钢板外直径,d是半圆形波纹钢板内直径。
特别的,半圆形波纹钢板具有C1=4Ca=D+d的特性,故将式(26)代入式(14),再代入式(11)化简得:
| $ G_{12}=\frac{\frac{3 {\rm{ \mathsf{ π} }} E\left(16 C_{\mathrm{a}}^{2}-2 d D\right)}{16} \frac{C_{1}}{\left(1-\nu^{2}\right) S_{\mathrm{c}}}}{\frac{3 {\rm{ \mathsf{ π} }}\left(16 C_{\mathrm{a}}^{2}-2 d D\right)}{16}\left(1+2 \nu_{21}\right)+t^{2} \frac{C_{1}}{\left(1-\nu^{2}\right) S_{\mathrm{c}}}} $ | (27) |
同理,泊松比ν21≥0,式(27)分母中的16Ca2-2dD≥16Ca2-(D+d)2/2=8Ca2,故式(27)分母左项最小值取1.5πCa2。又因式(27)分母右项永远小于1.1t2,故式(27)分母中的二项式左项比右项比值永远大于1.36πCa2/t2。当Ca=2t时,式(27)分母左项比右项大于17。式(27)省略
| $ G_{12}=\frac{2 G}{\left(1+2 \nu_{21}\right)(1-\nu)} \frac{C_{1}}{S_{\mathrm{c}}} $ | (28) |
当波纹钢板波形为三角形时,相应的Sc和Ix为:
| $ S_{\mathrm{c}}=2 p $ | (29) |
| $ I_{x}=\frac{4}{3} t p C_{\mathrm{a}}^{2} $ | (30) |
将式(30)代入式(14)计算,再代入式(11)得:
| $ G_{12}=\frac{\frac{16 E p C_{\mathrm{a}}^{2}}{C_{1}} \frac{C_{1}}{\left(1-\nu^{2}\right) S_{\mathrm{c}}}}{\frac{16 p C_{\mathrm{a}}^{2}}{C_{1}}\left(1+2 \nu_{21}\right)+t^{2} \frac{C_{1}}{\left(1-\nu^{2}\right) S_{\mathrm{c}}}} $ | (31) |
同理,泊松比ν21≥0,式(31)分母中的
| $ G_{12}=\frac{2 G}{\left(1+2 \nu_{21}\right)(1-\nu)} \frac{C_{1}}{S_{\mathrm{c}}} $ | (32) |
如式(19)、(24)、(28)、(32)所示,各波形剪切模量G12计算式统一,且存在未知泊松比ν21,假设ν21在弹性阶段为常数。当波纹钢板退化为平钢板时,平钢板也可看作是一种波纹钢板,即G12=G,此时
| $ G_{12}=\frac{G}{1.428(1-\nu)} \frac{C_{1}}{S_{\mathrm{c}}} $ | (33) |
根据郭彦林等[13]及陆铁坚等[14]的分析,不考虑面外变形的前提下,防屈曲钢板剪力墙板和厚钢板剪力墙板在剪切弹性阶段受力特征为均匀剪切,其弹性抗侧刚度计算公式:
| $ K=\frac{G t L}{1.2 H} $ | (34) |
式中G是钢板剪切模量,1.2是钢板矩形形状系数。
因式(33)推导的前提条件是板均匀剪切,已知式(34)满足计算均匀剪切状态时平钢板弹性抗侧刚度的条件,同时平钢板也可看作是一种波纹钢板,故将波纹钢板剪切模量G12代替式(34)中的G计算波纹钢板弹性抗侧刚度是合理可行的,公式为
| $ K_{\mathrm{p}}=\frac{G_{12} t L}{1.2 H}=\frac{G t L}{1.714 H(1-\nu)} \frac{C_{1}}{S_{\mathrm{c}}} $ | (35) |
故根据式(1)、式(2)、式(35)得波纹钢板剪力墙弹性抗侧刚度计算统一公式:
| $ K=K_{\mathrm{p}}+K_{\mathrm{f}}=\frac{G t L}{1.714 H(1-\nu)} \frac{C_{1}}{S_{\mathrm{c}}}+18 \frac{E I_{\mathrm{c}}}{H^{3}} $ | (36) |
由前面公式推知,正弦形、梯形、半圆形、三角形等波形的波纹钢板剪力墙的弹性抗侧刚度表达式形式是统一的,见式(36)。式(36)中有关波形的参数仅有C1/Sc,然而与波形相关的变量较多,不只有C1/Sc。故理论上为认为在C1/Sc不变的情形下,周期性波形形状的改变对波纹钢板剪力墙弹性抗侧刚度无影响。
2 理论公式可靠性分析影响波纹钢板剪力墙弹性抗侧刚度的主要部分是波纹钢板抗侧刚度,而不是框架抗侧刚度,因此验证统一公式的可靠性主要是验证式(35)波纹钢板弹性刚度计算的可靠性。式(35)由波纹钢板剪切模量G12计算公式(33)转化得来,故核心是验证波纹钢板剪切模量G12计算的可靠性。Johnson等[1]根据波纹钢腹板梁抗剪试验数据提出了波纹钢板剪切模量G12计算公式,其可靠性已足够:
| $ G_{12}=G \frac{l+p \cos \alpha}{l+p}=G \frac{C_{1}}{S_{\mathrm{c}}} $ | (37) |
故只需将式(37)与式(33)进行比较,即可验证式(33)的可靠性,进而验证式(36)的可靠性。钢板泊松比ν=0.3时,将式(33)化简得:
| $ G_{12}=G \frac{C_{1}}{1.001 S_{\mathrm{c}}} $ | (38) |
显然,式(38)与式(37)形式相同,且式(37)是式(38)的1.001倍,因此式(38)是可靠的,进而式(36)是可靠的。
3 波纹钢板剪力墙弹性抗侧刚度有限元验证 3.1 有限元模型有限元分析采用赵秋红等[15]建立的模型为基本模型。框架梁截面为:H500 mm×300 mm×11 mm×15 mm,框架柱截面为:H400 mm×400 mm×13 mm×21 mm;框架梁柱采用Q345B级钢材,波纹钢板采用Q235B级钢材。钢材本构关系为双线性强化模型,弹性模量为2.06×105 MPa,强化阶段模量为0.01弹性模量,泊松比取0.3。所有模型均采用壳单元、S4R单元建模。框架和波纹钢板模型的网格均采用四边形单元进行划分,如图 4所示,其中框架模型单元的单元大小统一为15 cm,而波纹钢板模型单元大小根据波形尺寸的变化选择2~5 cm。柱底和波纹钢板底部各方向自由度受约束,梁腹板和梁柱节点区无平面外位移,梁柱连接方式为刚接。为模拟四边连接的波纹钢板与梁柱焊接连接的情形,有限元模型中波纹板与梁柱通过tie连接方式刚性连接在一起。

|
图 4 波纹钢板剪力墙模型网格划分示意 Fig. 4 Grid division of corrugated steel plate shear wall model |
波纹钢板初始缺陷按照结构弹性屈曲的一阶屈曲模态施加,缺陷幅值为H/750。最后对结构进行非线性推覆分析。
3.2 理论结果与有限元分析结果对比为验证理论公式的统一性,有限元模型中波纹钢板采用了开口和缩口梯形波纹钢板、正弦形波纹钢板、三角形波纹钢板、半圆形波纹钢板5种波形,并在波形基础上改变各形状参数值进行模拟。波纹尺寸数据见表 1~3。
| 表 1 梯形波纹钢板剪力墙抗侧刚度对比 Tab. 1 Comparison of lateral-resistant stiffness of trapezoidal corrugated steel plate shear wall |
| 表 2 正弦波纹钢板剪力墙抗侧刚度对比 Tab. 2 Comparison of lateral-resistant stiffness of sinusoidal corrugated steel plate shear wall |
| 表 3 三角形和半圆形波纹钢板剪力墙抗侧刚度对比 Tab. 3 Comparison of lateral-resistant stiffness of triangular and semicircular corrugated steel plate shear walls |
根据对上述模型的有限元分析得水平荷载-位移曲线,通过取该曲线的第一条上升段斜率获得剪力墙的弹性抗侧刚度K模拟值。选取编号T3梯形波纹钢板剪力墙模型的荷载-位移曲线为典型,如图 5所示,红色虚线段为水平荷载-位移曲线的第一条上升段,是一条斜直线,且所有有限元分析所得的水平荷载-位移曲线第一条上升段都为斜直线,故计算该线段斜率得剪力墙的弹性抗侧刚度K模拟值。

|
图 5 水平荷载下波纹钢板剪力墙荷载-位移曲线 Fig. 5 Load-displacement curve of corrugated steel plate shear wall under horizontal load |
波纹钢板剪力墙模型共建立70个,根据钢板波形的不同,分为梯形波形36个,正弦波形17个,三角形波形9个,半圆形波形8个以验证理论公式的统一性。
表 1~3中K计算值结果即波纹钢板剪力墙弹性抗侧刚度计算值,是由波纹钢板弹性抗侧刚度计算值和框架抗侧刚度计算值简单叠加而成的组合值,计算公式见式(36)。
值得注意的是,波纹钢板弹性刚度理论计算省略了公式分母中的小项,未考虑初始缺陷,未考虑框架的弯曲变形且理论假定认为等效正交各向异性板处于纯剪应力状态;而有限元模型不仅考虑了初始缺陷和框架的弯曲变形,且剪力墙中的波纹钢板并非纯剪应力状态等,这使K计算值普遍大于K模拟值,在表 1~3中都有体现。表 2中正弦波纹钢板剪力墙刚度对比存在个别K计算值略小的情形,且偏小的程度不明显,属于个例。
图 6中,紫色正三角形点代表各梯形波纹钢板剪力墙,橙色圆点代表正弦波纹钢板剪力墙,棕色空心菱形点代表三角形波纹钢板剪力墙,红色五角星形点代表半圆形波纹钢板剪力墙。波纹钢板剪力墙计算值和模拟值比值的均值为1.111,绝大部分点落在0%实线以上,说明波纹钢板剪力墙弹性刚度计算值比模拟值总体偏大,在计算剪力墙地震剪力时,钢板剪力墙实际分担的地震剪力小于计算地震剪力,相对偏安全;方差为0.006 4,说明计算值与模拟值总体吻合良好,离散性小;表明所提出的波纹钢板剪力墙弹性刚度统一计算公式具有明显的统一性。

|
图 6 理论计算值与模拟值对比 Fig. 6 Comparison between theoretical calculation results and simulation results |
由于波纹钢板本身的抗侧刚度受与周边框架的连接形式影响较大,故需在已有的四边连接水平波纹钢板剪力墙仅受单调水平荷载时的弹性抗侧刚度统一公式基础上讨论波纹钢板边界条件、竖向荷载、波纹钢板放置方向对波纹钢板剪力墙抗侧刚度的影响,明确统一公式的适用范围。
根据赵秋红等[6]的研究,波纹横放和波纹竖放的四边连接波纹钢板剪力墙与和波折边两边连接的竖向波纹钢板剪力墙初始刚度非常相近,而两边连接的水平波纹钢板剪力墙初始刚度显著降低,见图 7。此外,李雅楠[5]的研究发现,各轴压比下的竖向荷载对四边连接的波纹钢板剪力墙结构的初始刚度基本无影响。由此明确所推导的统一公式同时适用于计算边界条件为四边连接的波纹钢板剪力墙在受单独水平荷载和水平荷载、竖向荷载共同作用下的弹性抗侧刚度。

|
图 7 不同边界条件下的波纹钢板剪力墙示意 Fig. 7 Corrugated steel plate shear wall with different boundary conditions |
本文在考虑边缘框架抗侧刚度贡献的基础上通过正交各向异性板理论对弹性阶段的波纹钢板等效平板在纯剪和纯主应力作用下的面内变形的比较分析,推导了波纹钢板剪力墙弹性抗侧刚度统一公式,通过已有的波纹钢板剪切模量公式对比验证了统一公式是可靠的,并根据有限元分析验证了公式的统一性,最后明确了公式的适用范围,主要结论如下:
1) 从理论角度分析了波纹钢板剪力墙弹性抗侧刚度,推导了波纹钢板剪力墙弹性抗侧刚度统一公式。该公式理论性在于:公式完全由理论推导得出,有限元模拟用于验证公式的统一性,而非修正公式参数。
2) 波纹钢板剪力墙弹性抗侧刚度统一公式的统一性和适用范围:钢板波形为梯形、正弦形、半圆形、三角形等周期性形状;波纹钢板放置方向为竖向或横向;波纹钢板与周边框架的边界条件为四边连接;波纹钢板剪力墙受力条件为单独受水平荷载或同时受水平荷载和竖向荷载。
3) 在不变的情形下,钢板波形变化对波纹钢板剪力墙剪切弹性抗侧刚度影响不明显。
| [1] |
JOHNSON R P, CAFOLLA J, BERNARD C. Corrugated webs in plate girders for bridges[J]. Structures and Buildings, 1997, 122(2): 161. DOI:10.1680/istbu.1997.29305 |
| [2] |
ZHA Xiaoxiong, ZUO Yang. Theoretical and experimental studies on in-plane stiffness of integrated container structure[J]. Advances in Mechanical Engineering, 2016, 8(3): 3. DOI:10.1177/1687814016637522 |
| [3] |
李靓姣. 波浪形钢板墙的受力性能及设计方法研究[D]. 北京: 清华大学, 2012 LI Jingjiao. Research on behaviour and design methods of sinusoidal steel plate wall[D]. Beijing: Tsinghua University, 2012 |
| [4] |
孙军浩. 波纹钢板剪力墙的抗侧及抗震性能研究[D]. 天津: 天津大学, 2016 SUN Junhao. Research on lateral performance and seismic behavior of corrugated steel plate shear walls[D]. Tianjin: Tianjin University, 2016 |
| [5] |
李雅楠. 波纹钢板剪力墙体系的抗侧性能分析及设计方法研究[D]. 天津: 天津大学, 2017 LI Yanan. Lateral behavior and design method of corrugated steel plate shear walls[D]. Tianjin: Tianjin University, 2017 |
| [6] |
赵秋红, 邱静, 郝博超, 等. 两边连接竖向波纹钢板剪力墙的抗侧性能[J]. 天津大学学报(自然科学与工程技术版), 2019, 52(增刊2): 50. ZHAO Qiuhong, QIU Jing, HAO Bochao, et al. Lateral behavior of vertically-corrugated steel plate shear walls connected with beams only[J]. Journal of Tianjin University (Science and Technology), 2019, 52(S2): 50. DOI:10.11784/tdxbz201904083 |
| [7] |
ZHAO Q, SUN J, LI Y, et al. Cyclic analyses of corrugated steel plate shear walls[J]. The Structural Design of Tall and Special Buildings, 2017, 26(16): 1. DOI:10.1002/tal.1351 |
| [8] |
CHAJES A. Principles of structural stability theory[M]. New Jersey: Prentice Hall, 1974: 240.
|
| [9] |
王震鸣. 复合材料力学和复合材料结构力学[M]. 北京: 机械工业出版社, 1991: 101. WANG Zhenming. Mechanics of composite materials and composite structures[M]. Beijing: China Machine Press, 1991: 101. |
| [10] |
谢一环. 纸张材料弹性模量与剪切模量的关系[J]. 包装工程, 2012, 33(21): 38. XIE Yihuan. Relationship between elastic modulus and shear modulus of paper[J]. Packaging Engineering, 2012, 33(21): 38. |
| [11] |
BRIASSOULIS D. Equivalent orthotropic properties of corrugated sheets[J]. Computers & Structures, 1986, 23(2): 131. DOI:10.1016/0045-7949(86)90207-5 |
| [12] |
DOU Chao, JIANG Ziqin, PI Yonglin, et al. Elastic shear buckling of sinusoidally corrugated steel plate shear wall[J]. Engineering Structures, 2016, 121: 139. DOI:10.1016/j.engstruct.2016.04.047 |
| [13] |
郭彦林, 周明, 董全利. 防屈曲钢板剪力墙弹塑性抗剪极限承载力与滞回性能研究[J]. 工程力学, 2009, 26(2): 112. GUO Yanlin, ZHOU Ming, DONG Quanli. Hysteretic behavior of buckling-restrained steel plate shear wall[J]. Engineering Mechanics, 2009, 26(2): 112. |
| [14] |
陆铁坚, 姚赞, 杨诗龙. 钢板剪力墙弹性抗侧刚度分析[J]. 工业建筑, 2017, 47(1): 160. LU Tiejian, YAO Zan, YANG Shilong. Analysis on elastic lateral-resistant stiffness of steel plate shear wall[J]. Industrial Conctrustion, 2017, 47(1): 160. |
| [15] |
赵秋红, 李楠, 孙军浩. 波纹钢板剪力墙结构的抗侧性能分析[J]. 天津大学学报(自然科学与工程技术版), 2016, 49(增刊1): 153. ZHAO Qiuhong, LI Nan, SUN Junhao. Analysis on lateral performance of sinusoidally corrugated steel plate shear walls[J]. Journal of Tianjin University (Science and Technology), 2016, 49(S1): 153. DOI:10.11784/tdxbz201605012 |
 2021, Vol. 53
2021, Vol. 53


