由漩涡脱落引起的结构横风向响应是高层建筑抗风设计中面临的主要难题。通过改变建筑物截面形状或整体造型的气动优化措施(例如角部修正[1-2]、扭转[3]、锥度化[4-5]、开洞[6-8]等)已被证实能有效减小结构风荷载及风振响应。然而大多数气动优化方案往往会对建筑外形与空间效率带来不利影响[9],这也是气动优化设计在实际工程中遇到的最大挑战。因而优良的气动优化方案不应当仅局限于空气动力学方面的效率,也应当考虑如何将气动优化设计与建筑物的其他性能化设计结合起来,通过“一举多得”的方式,实现高效率的设计一体化“Integrated design”。
作为建筑可持续化的一部分,建筑物的节能低碳指标正得到日益重视。据联合国可持续建筑和气候组织(UNEP-SBCI)的资料[10],全球温室气体排放中约1/3来自于建筑物,建筑物的能耗占全球总量约40%,而这其中建筑覆面是影响建筑能耗最大的因素。在这一共识下,近几十年来建筑覆面的相关技术有了长足进步,特别是促进了双层幕墙系统与遮阳系统的研究[11-12]。
图 1所示的新型建筑覆面称为“镂空双层幕墙系统”(porous double skin façade system,简称“porous DSF”),由内玻璃幕墙与外镂空墙组成,且两者之间存在一定空隙。镂空双层幕墙系统不但具有建筑美学功能,还具有遮阳作用,能改善建筑能耗指标,柔化室内自然照明,消除室外眩光,减少城市光污染,因而得到日益重视与普及。

|
图 1 镂空双层幕墙系统 Fig. 1 Porous double skin façade system |
显然,镂空双层幕墙系统使气流在建筑表面的绕流过程发生了变化,从而将改变建筑物的气动特性。目前研究主要关注镂空双层幕墙系统对于幕墙风压的影响[13-14],试验发现[15-16]镂空双层幕墙能有效降低玻璃幕墙的覆面正负风压达40%左右,而对其中的最大负风压则能降低63%左右。镂空双层幕墙系统除了影响建筑表面风压,也势必会影响气流分离与涡脱强度,进而弱化建筑物的横风向风振,但相关工作则报道不多。在建筑迎风面上设置竖向开槽的双层幕墙风洞试验可以认为是与此较为接近的研究工作[17]。结果表明迎风面上设置竖向开槽的双层幕墙可以有效减低横风向风振响应,但对顺风向响应的作用则可以忽略不计。
本文对具有镂空双层幕墙系统的高层建筑抗风性能进行了详细的规律性研究,探讨将该类建筑覆面用于结构气动优化的可能性。通过风洞试验方法研究了镂空双层幕墙系统的覆盖面积与覆盖位置对抗风效率的影响,并考察不同风速情况下的减振效率,此外还对不同周边场地情况的影响做了分析。
1 风洞试验概况 1.1 试验模型以一实际工程项目为背景,制作了1∶400比例的缩尺模型,并在浙江大学ZD-1边界层风洞实验室(试验段尺寸为4 m宽×3 m高)中完成高频测力天平试验。通过高频基底天平测得建筑模型上的平均风荷载与脉动风荷载,然后与结构动力特性参数相结合,求解随机振动方程,最后得到风致振动响应。建筑物足尺高度374 m,截面为边长52 m的正方形,高宽比约为7.2,阻塞率约为1%,满足要求。由于建筑物中上部的气动力对一阶广义力和风振响应的贡献最大[18],所以试验仅在上部约1/3处(120 m)模拟了镂空双层幕墙系统。系统内外墙之间距离5 m(足尺),内墙密闭,外墙镂空。镂空部分参考了工程项目中外玻璃幕墙尺寸,设置为高3.5 m(典型层高)宽2 m的洞口,等间距排列,镂空率为43.75%。图 2为模型的风洞试验照片。

|
图 2 风洞试验 Fig. 2 Wind tunnel test |
为了研究镂空双层幕墙系统的覆盖面积与覆盖位置对抗风效率的影响,在模型上通过对洞口的封堵实现无镂空幕墙、上部1/6镂空、下部1/6镂空、角部镂空、上部1/3镂空5种工况,详见表 1与图 3。
| 表 1 工况说明 Tab. 1 Configurations of working conditions |

|
图 3 工况细节 Fig. 3 Details of working conditions |
利用尖劈、粗糙元等在风洞中模拟测试了开阔的A类地貌与城市的C类地貌。两种地貌的平均风速剖面、湍流度剖面及2/3楼顶高度(60 cm)顺风向归一化湍流功率谱见图 4、5。图 5中n为频率,Su为脉动风速功率谱密度,σ为脉动风速均方根,Lu为湍流积分尺度,U为该高度平均风速。

|
图 4 平均风速剖面与湍流度剖面 Fig. 4 Mean wind speed profile and turbulence profile |

|
图 5 60 cm高度处顺风向湍流功率谱 Fig. 5 Along-wind turbulence spectra at 60 cm height |
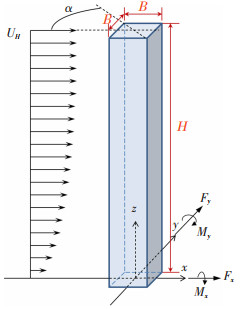
试验中参考点风速为8 m/s,雷诺数接近7×105。测试0°到90°以10°为间隔的10个风向角,同时考虑到风荷载在0°风向角附近变化较为剧烈,增加风向角为5°时的测试,共11个风向角。天平采样频率500 Hz,采样时长90 s。风洞试验坐标轴定义见图 6,与结构振型坐标轴保持一致,图中α代表风向角。为方便描述,文中将A类地貌下的5种工况分别记为A1~A5,C类地貌下的5种工况分别记为C1~C5。
|
图 6 风洞试验坐标轴定义 Fig. 6 Coordinate system definition of wind tunnel test |
为使研究结果具有一定的普适性,本文采用无量纲约化值的方式表达气动特性与风振响应。无量纲分析是结构风工程的一项基本技术,可以减少分析中不必要的物理量假设,突出空气动力学特性的影响,从而便于利用相似性原理演绎分析结果,对同类结构具有直接参考价值。
2.1 镂空双层幕墙对气动力的影响无量纲基底剪力系数与倾覆力矩系数分别定义为:
| $ C_{F x} =\frac{F_{x}}{0.5 \rho U_{H}^{2} B H}, C_{F y}=\frac{F_{y}}{0.5 \rho U_{H}^{2} B H} $ | (1) |
| $ C_{M x} =\frac{M_{x}}{0.5 \rho U_{H}^{2} B H^{2}}, C_{M y}=\frac{M_{y}}{0.5 \rho U_{H}^{2} B H^{2}} $ | (2) |
式中:Fx,Fy,Mx,My分别代表风洞试验得到的x方向与y方向的基底剪力与倾覆力矩,ρ为空气密度,UH为模型楼顶高度平均风速,B与H为模型迎风面的宽度和高度,见图 6。
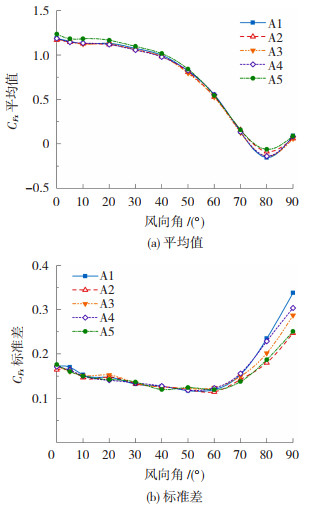
图 7为A1~A5在各风向角下基底剪力系数的平均值与标准差。平均值在0°风向角下达到最大正值,在80°风向角下出现较小的负值。在90°风向角时为0。与工况A1相比,A5会略微增大0°风向角下基底剪力系数的平均值,但增幅在4%以内,因此可认为平均基底剪力几乎不受镂空幕墙覆盖面积的影响。在横风向风振最剧烈的90°风向角下,镂空幕墙能明显降低模型基底剪力系数的标准差。其中A2与A5效果最好,与A1相比均能使基底剪力标准差降低约25%。A3对于基底剪力系数标准差的降低作用在15%左右,A4则在10%左右,效果相对较弱。从图 7可看出最不利风向角正对建筑立面,即0°和90°风向角。由于模型对称,后续结果均以0°风向角下的数据为例进行说明。
|
图 7 基底剪力系数 Fig. 7 Base shear coefficients |
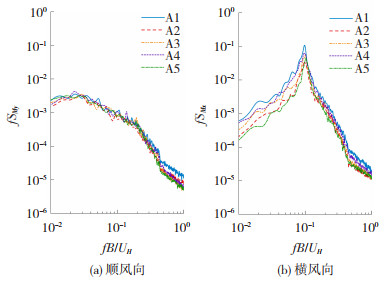
图 8给出各试验工况下顺风向与横风向无量纲倾覆力矩谱。图中横坐标采用约化频率fB/UH,频率f为变量,纵坐标采用式(2)定义的基底倾覆力矩系数的功率谱fS。不同覆盖面积的镂空双层幕墙对顺风向倾覆力矩谱不造成明显差别。但在约化频率 < 0.10时,镂空双层幕墙系统使得横风向倾覆力矩谱值明显变小。其中工况A2与A5的效果最好,能大幅降低尖峰峰值及低频段(约化频率 < 0.10)的谱值,A3与A4的效果则次之。在高频段(约化频率>0.10)时,不同镂空幕墙对降低倾覆力矩谱值仍有一定作用,但效果较弱。
|
图 8 A1~A5倾覆力矩系数谱 Fig. 8 Spectra of overturning moment coefficients of A1-A5 |
建筑物的横风向气动力主要由气流经过建筑物时产生的流动分离和交替脱离表面的旋涡引起。镂空双层幕墙使侧面的剪切层边界离建筑物较远,背风面尾流区域的循环气流区变长,由此导致侧面与背风面气动力的脉动分量降低[17]。此外,流动分离后产生的湍流风场中包括尺度大小不一的各种脉动分量,其中尺度较大的气流(低频段)容易被外层镂空幕墙过滤,而尺度较小的气流(高频段)则不易受到镂空幕墙的影响,因而镂空双层幕墙系统在低频段效果较好,在高频段效果较弱。
2.3 镂空双层幕墙建筑风振响应特性评估镂空双层幕墙系统的气动优化效果最直接的方法是考察结构的风振响应。结构风振响应的模态运动方程可表达为
| $ \ddot{\eta}_{j}(t)+2 \zeta \omega_{j} \dot{\eta}_{j}(t)+\omega_{j}^{2} \eta_{j}(t)=\frac{P_{j}(t)}{M_{j}} $ | (3) |
式中:
| $ {M_j} = \int\limits_0^H {m\left( z \right)\phi _j^2\left( z \right){\rm{d}}z} $ | (4) |
式中m(z)代表结构质量沿高度z的分布,ϕj(z)代表结构第j阶模态振型。
式(3)中的广义力采用文献[19-20]的方法以考虑高频测力天平方法中非线性振型的影响,计算公式为
| $ \begin{array}{l} {P_j}\left( t \right) = \left( {{Y_{jFx}} + {\mathit{\Lambda} _{jFx}}} \right){F_x}\left( t \right) + \left( {{Y_{jFy}} + {\mathit{\Lambda} _{jFy}}} \right){F_y}\left( t \right) + \\ \;\;\;\;\left( {{Y_{j{M_y}}} + {\mathit{\Lambda} _{j{M_y}}}} \right)\frac{{{M_y}\left( t \right)}}{h} + \left( {{Y_{jMx}} + {\mathit{\Lambda} _{jMx}}} \right)\frac{{{M_x}\left( t \right)}}{h} + \\ \;\;\;\;{Y_{jMz}}\frac{{{M_z}\left( t \right)}}{r} \end{array} $ | (5) |
式中Mz为基底扭矩,Yj[·]和Λj[·]为各荷载分量对广义气动力的贡献参数[19]。
在按式(5)求出广义力的时程数据并按照相似定律转化为足尺下的广义气动力时程后,代入式(3)并采用时域分析方法得到结构风振响应时程,最后通过统计分析方法得到响应的平均值、均方差、峰值等。选用四阶Runge-Kutta法,同时采用Newmark-β法进行验证,两者计算结果几乎完全吻合。时域分析方法与基于功率谱的频域分析方法在响应的均方值估计上几乎完全一致,但时域分析对响应的峰值的估计更为直接。
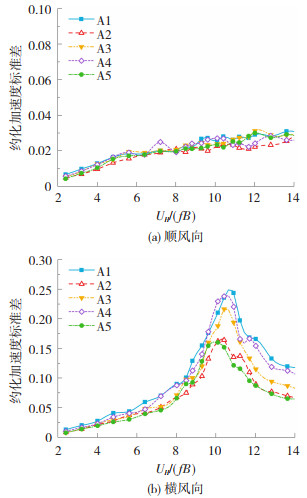
计算中依据工程经验假设结构1阶与2阶振型ϕ1y(z)=ϕ2x(z)=(z/H)1.2,阻尼比为1.5%。本文采用式(6)将楼顶加速度的标准差表示为无量纲的形式(约化加速度),结果见图 9,图中横坐标采用无量纲约化风速UH/(fB),f为结构自振频率,楼顶高度风速UH为变量,从而得到在指定自振频率下结构风振响应随风速的变化规律。
|
图 9 约化加速度标准差 Fig. 9 Standard deviations of normalized accelerations |
| $ \sigma_{a}^{*} \approx \frac{M_{j} \sqrt{\zeta}}{q_{r} B H} \sigma_{a} $ | (6) |
式中qr为楼顶高度的平均风压,σa为楼顶加速度标准差。
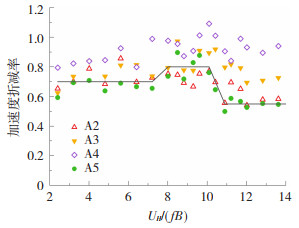
由图 9可知,镂空双层幕墙系统对顺风向响应的作用不明显,但对起主导作用的横风向响应则具有明显减振效果。而且减振效果不但与镂空工况有关,在不同约化风速下的表现也有所不同。为考察不同镂空工况在不同约化风速下的减振效率,可以将各镂空工况(A2~A5)的风振加速度与不设镂空幕墙的工况(A1)的风振加速度之比定义为“加速度折减率”。结果见图 10。图 10中黑色实线为A5工况加速度折减率的大致趋势,从而可以较为清晰地展现折减率数值随约化风速的变化关系。
|
图 10 A2~A5镂空双层幕墙对风振加速度的折减率 Fig. 10 Reductions in wind-induced accelerations by A2-A5 porous DSF system |
由图 10得知,除了角部镂空(A4)工况的效果不够理想外,其余镂空工况都能显著减少横风向风振,而且减振效果一般随约化风速的提高而增强。A5在约化风速>10.5时的折减率可达0.55,即楼顶1/3范围内设置镂空双层幕墙后的风振加速度仅为未设置前的55%,在约化风速7~10.5时的折减率约为0.8,而在约化风速 < 7时的折减率约为0.7。这说明设置镂空双层幕墙不但能大幅降低极端风下与横风向响应有关的结构设计风荷载,而且能改善常遇风下与横风向风振有关的居住舒适度。对居住舒适度的评估一般仅考虑1~10 a重现期下的风速,相应的约化风速相对较低。而现有的沿建筑高度收缩截面(锥度化)的气动优化方法虽能降低极端风下的设计风荷载,但在常遇风时效果较差,甚至有可能增加振动加速度[21]。相比而言,镂空双层幕墙对居住舒适度的气动优化效率更具优势。
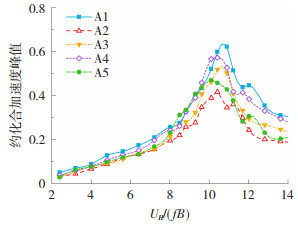
采用最佳线性无偏估计(best linear unbiased estimation,BLUE)方法[22]计算无量纲约化合加速度峰值,结果见图 11。由于在工程应用中主要关心峰值响应,所以选用峰值作为镂空双层幕墙系统的主要评估指标可能更为合适。约化合加速度峰值曲线的趋势与横风向约化加速度标准差曲线的趋势相近,设置镂空幕墙能有效减小响应峰值。在不同覆盖面积的镂空双层幕墙系统中,A2与A5的效果在涡激共振范围内明显优于A3与A4,由此推测镂空幕墙的覆盖面积越大降低横风向风振响应的效果越好,且设置在建筑物顶部比设置在其他位置的效果更好。
|
图 11 约化合加速度峰值 Fig. 11 Peak values of normalized total accelerations |
采用总倾覆力矩与总基底剪力为指标评估镂空双层幕墙对结构设计荷载的影响。总倾覆力矩与总基底剪力中包括三个组成部分:平均荷载、背景脉动荷载以及由风振引起的惯性荷载。背景荷载与惯性荷载同为动力荷载,但两者之间的相关性较弱,因而可采用SRSS方式进行组合。约化倾覆力矩和约化基底剪力为:
| $ \left\{ {\begin{array}{*{20}{l}} {M_k^* = \frac{{{M_k}}}{{0.5\rho U_H^2B{H^2}}} = {C_{Mk}} + g\sqrt {\sigma _{CMk}^2 + \frac{{\mu _{Mk}^2}}{\zeta }\sigma _{ak}^{*2}} }\\ {S_k^* = \frac{{{S_k}}}{{0.5\rho U_H^2BH}} = {C_{Fk}} + g\sqrt {\sigma _{CFk}^2 + \frac{{\mu _{Sk}^2}}{\zeta }\sigma _{ak}^{*2}} } \end{array}} \right., k = x, y $ | (7) |
式中:CMk与CFk分别为式(1)计算得到的x与y方向气动倾覆力矩和基底剪力系数的平均值,σCMk与σCFk为相应气动系数的脉动分量标准差,g为峰值系数,μMk与μSk为与质量和振型分布有关的参数,见式(8):
| $ \left\{ {\begin{array}{*{20}{l}} {{\mu _{Mk}} = \int\limits_H {m\left( z \right){\phi _k}\left( z \right)(z/H){\rm{d}}z} /\int\limits_H {m\left( z \right)\phi _k^2\left( z \right){\rm{d}}z} }\\ {{\mu _{{S_k}}} = \int\limits_H {m\left( z \right){\phi _k}\left( z \right){\rm{d}}z} /\int\limits_H {m\left( z \right)\phi _k^2\left( z \right){\rm{d}}z} } \end{array}} \right., k = x, y $ | (8) |
当各楼层质量相同且振型函数为指数型时,可以证明:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mu _{Mk}} = \frac{{2\beta + 1}}{{\beta + 2}}}\\ {{\mu _{Sk}} = \frac{{2\beta + 1}}{{\beta + 1}}} \end{array}, k = x, y} \right. $ | (9) |
式中β为振型指数,对高层建筑β通常在1.0~1.5。
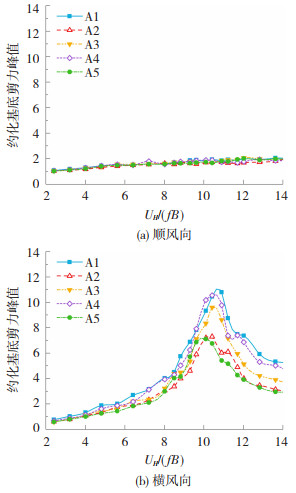
按前文假设的结构参数可得到不同镂空工况下顺风向与横风向总倾覆力矩和总基底剪力的约化值,见图 12、13。

|
图 12 约化倾覆力矩 Fig. 12 Normalized overturning moments |
|
图 13 约化基底剪力 Fig. 13 Normalized base shears |
可以看出,顺风向约化荷载(倾覆力矩和基底剪力)对约化风速不敏感,这代表实际的顺风向荷载与风速平方近似成正比关系。而横风向约化荷载则对约化风速非常敏感。为直观显示不同镂空工况的减载效率,将各镂空工况(A2~A5)的最大倾覆力矩和基底剪力与不设镂空幕墙的参照工况(A1)的最大倾覆力矩和基底剪力之比分别定义为“倾覆力矩折减率”和“基底剪力折减率”。结果见图 14。

|
图 14 A2~A5镂空工况倾覆力矩与基底剪力折减率 Fig. 14 Reductions in overturning moments and base shears by A2-A5 porous DSF system |
由图 14可以看出,在约化频率较低时,镂空双层幕墙的减载效率不够明显。这主要是因为在约化频率较小时,最大风荷载由顺风向控制,但是随着约化频率的增大,横风向荷载反超顺风向荷载并成为主导荷载(约化频率>5)[23],镂空双层幕墙对风荷载的折减效率逐渐接近对风振加速度的折减效率。当约化频率>10.5时,A5对倾覆力矩与基底剪力的最大折减率可达0.55,即结构总荷载最多能降至原结构的55%左右。
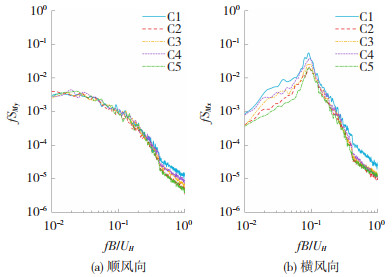
3 不同地貌对镂空双层幕墙减振效率的影响为比较不同地貌对镂空双层幕墙减振效率的影响,本文在典型C类地貌下对各工况进行试验。图 15给出C1~C5工况的顺风向与横风向无量纲倾覆力矩谱。与A类地貌下的结果类似,不同覆盖面积的镂空双层幕墙系统的顺风向倾覆力矩谱没有明显差别,但能显著降低横风向倾覆力矩谱的尖峰峰值及低频段(约化频率 < 0.10)的谱值。降低幅度最大的仍为工况C2与C5。
|
图 15 C1~C5倾覆力矩系数谱 Fig. 15 Spectra of overturning moment coefficients of C1-C5 |
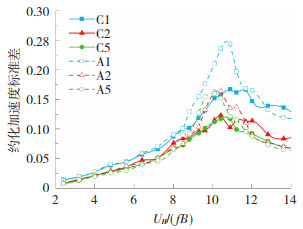
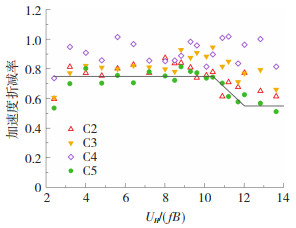
图 16比较了A类与C类地貌的无量纲约化加速度标准差,选取工况1(基本模型)与镂空双层幕墙效果较好的工况2与工况5进行说明。C类地貌下横风向风振响应明显低于A类地貌,工况2与工况5均能大幅降低加速度响应。图 17为C类地貌各镂空工况的加速度折减率结果。C5在约化风速 < 10.5时折减率约为0.75,在约化风速>12时折减率约为0.55,与A类地貌下的结果类似。证明镂空双层幕墙在常遇风下也能改善居住舒适度,且加速度折减率基本不受场地类别影响。
|
图 16 不同场地约化加速度标准差 Fig. 16 Standard deviations of normalized accelerations for different terrain conditions |
|
图 17 C2~C5镂空双层幕墙对风振加速度的折减率 Fig. 17 Reductions in wind-induced accelerations by C2-C5 porous DSF system |
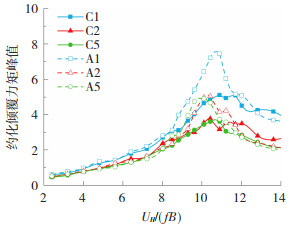
图 18展示A类与C类地貌的无量纲约化倾覆力矩峰值的结果,同样选取工况1、2、5进行说明。C类地貌下约化荷载明显低于A类地貌。约化风速较小时,镂空双层幕墙系统对于约化荷载的折减效果较弱,当约化风速接近或大于涡激共振临界风速时,镂空双层幕墙系统的气动优化效果开始显现。
|
图 18 不同场地约化倾覆力矩 Fig. 18 Normalized overturning moments for different terrain conditions |
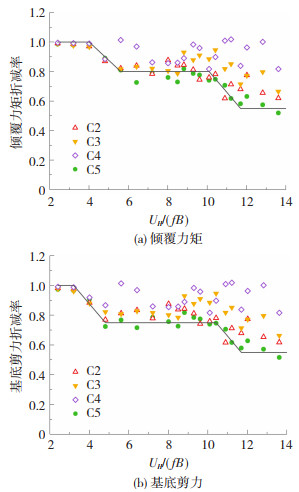
图 19展示了各镂空工况(C2~C5)的倾覆力矩折减率及基底剪力折减率,计算方法与A类地貌相同。在约化风速较低时,镂空双层幕墙的减载效率基本等于1。当约化风速在5~10.5时,C5的折减率达到0.75,而当约化风速>10.5时,C5对倾覆力矩与基底剪力的折减率可达到0.55,与A类地貌的结果一致。由此可见尽管横风向涡激振动的剧烈程度受场地类别影响,C类地貌下风振加速度和约化荷载在数值上比A类地貌要小,但镂空双层幕墙对于横风向风振加速度与结构风荷载的相对折减率基本不受场地类别影响。
|
图 19 C2~C5镂空工况倾覆力矩与基底剪力折减率 Fig. 19 Reductions in overturning moments and base shears by C2-C5 porous DSF system |
1) 镂空双层幕墙系统能有效降低高层建筑的横风向风振加速度与结构设计风荷载,且镂空双层幕墙的覆盖面积越大效果越好,设置在建筑物顶部效果更好。
2) 镂空双层幕墙系统的气动减振减载效率与约化风速有关。当约化风速≥10.5时,设置在建筑物上部1/3的镂空幕墙与设置在建筑物上部1/6的镂空幕墙能使风振加速度与总结构荷载降至原结构的55%左右。当约化风速 < 10.5时,镂空双层幕墙系统的效率会有所降低,但仍能降低风振响应20%~30%左右。在约化风速 < 5时,由于结构设计风荷载由顺风向响应控制,镂空双层幕墙系统的减载作用不明显。
3) 镂空双层幕墙系统不但可用于降低极端风情况下的结构设计风荷载,而且可用于控制常遇风时建筑物的风振加速度,提高建筑物的性能化指标。而现有的某些气动优化方法虽能降低极端风下的设计风荷载,但在常遇风时效果较差,甚至有可能增加振动加速度。相比而言,镂空双层幕墙对居住舒适度的气动优化效率更具优势。
4) 尽管横风向涡激振动的剧烈程度受场地类别影响,但镂空双层幕墙系统的气动优化效果基本不受场地类别影响,设置在建筑物上部1/3的镂空幕墙的相对减振减载效率在城市地貌下与开阔地貌下基本一致。
| [1] |
KAWAI H. Effect of corner modifications on aeroelastic instabilities of tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74/75/76: 719. DOI:10.1016/S0167-6105(98)00065-8 |
| [2] |
张正维, 全涌, 顾明, 等. 斜切角与圆角对方形截面高层建筑气动力系数的影响研究[J]. 土木工程学报, 2013, 46(9): 12. ZHANG Zhengwei, QUAN Yong, GU Ming, et al. Effects of corner chamfering and rounding modification on aerodynamic coefficients of square tall buildings[J]. China Civil Engineering Journal, 2013, 46(9): 12. DOI:10.15951/j.tmgcxb.2013.09.009 |
| [3] |
赵昕, 丁洁民, 孙华华, 等. 上海中心大厦结构抗风设计[J]. 建筑结构学报, 2011, 32(7): 1. ZHAO Xin, DING Jiemin, SUN Huahua, et al. Structural design of the Shanghai Tower for wind loads[J]. Journal of Building Structures, 2011, 32(7): 1. DOI:10.14006/j.jzjgxb.2011.07.002 |
| [4] |
KIM Y M, YOU K P. Dynamic responses of a tapered tall building to wind loads[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12): 1771. DOI:10.1016/S0167-6105(02)00286-6 |
| [5] |
KIM Y M, YOU K P, KO N H. Across-wind responses of an aeroelastic tapered tall building[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(8/9): 1307. DOI:10.1016/j.jweia.2008.02.038 |
| [6] |
KIKITSU H, OKADA H. Characteristics of across-wind response of tall building with open passage[C]//The 16th Proceedings of National Symposium on Wind Engineering. Yokohama: [s. n. ], 2000: 435
|
| [7] |
陈伏彬, 李秋胜. 大开洞对高层建筑风效应的影响研究[J]. 湖南大学学报(自然科学版), 2015, 42(3): 84. CHEN Fubin, LI Qiusheng. Investigation of the influence of openings on the wind effect of tall buildings[J]. Journal of Hunan University (Natural Sciences), 2015, 42(3): 84. DOI:10.16339/j.cnki.hdxbzkb.2015.03.013 |
| [8] |
王春刚, 张耀春, 秦云. 巨型高层开洞建筑刚性模型风洞试验研究[J]. 哈尔滨工业大学学报, 2004, 36(11): 1431. WANG Chungang, ZHANG Yaochun, QIN Yun. Wind tunnel tests study on mega tall buildings with opening rigidity models[J]. Journal of Harbin Institute of Technology, 2004, 36(11): 1431. |
| [9] |
TSE K T, HITCHCOCK P A, KWOK K C S, et al. Economic perspectives of aerodynamic treatments of square tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(9/10): 455. DOI:10.1016/j.jweia.2009.07.005 |
| [10] |
JAMES M. Façade-integrated sustainable technologies for tall buildings[J]. International Journal of Engineering Technology, Management and Applied Sciences, 2017, 5(5): 165. |
| [11] |
SHAMERI M A, ALGHOUL M A, SOPIAN K, et al. Perspectives of double skin façade systems in buildings and energy saving[J]. Renewable and Sustainable Energy Reviews, 2011, 15(3): 1468. DOI:10.1016/j.rser.2010.10.016 |
| [12] |
崔振华. 双层幕墙综合性评价[D]. 杭州: 浙江大学, 2014 CUI Zhenhua. A comprehensives evaluation on double skin façade[D]. Hangzhou: Zhejiang University, 2014 |
| [13] |
KEMPER F H, FELDMANN M. Wind load assumptions for permeable cladding elements considering the installation context[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 184: 277. DOI:10.1016/j.jweia.2018.10.011 |
| [14] |
LO Yuanlung, WU Yuting, FU Chunglin, et al. Wind load reduction effects on inner buildings by exterior porous façades[J]. Building and Environment, 2020, 183: 1. DOI:10.1016/j.buildenv.2020.107148 |
| [15] |
ZASSO A, PEROTTI F, ROSA L, et al. Wind pressure distribution on a porous double skin façade system[C]//Proceedings of the XV Conference of the Italian Association for Wind Engineering. Cham: Springer, 2019: 730. DOI: 10.1007/978-3-030-12815-9_55
|
| [16] |
POMARANZI G, DANIOTTI N, SCHITO P, et al. Experimental assessment of the effects of a porous double skin façade system on cladding loads[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 196: 14. DOI:10.1016/j.jweia.2019.104019 |
| [17] |
HU Gang, HASSANLI S, KWOK K C S, et al. Wind-induced responses of a tall building with a double-skin façade system[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017, 168: 91. DOI:10.1016/j.jweia.2017.05.008 |
| [18] |
邓挺. 500 m以上量级典型超高层建筑风效应研究[D]. 广州: 华南理工大学, 2016: 66 DENG Ting. Research on the wind effect of typical super-tall buildings beyond 500 m[D]. Guangzhou: South China University of Technology, 2016: 66 |
| [19] |
XIE Jiming, IRWIN P A. Application of the force balance technique to a building complex[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 77/78: 584. DOI:10.1016/S0167-6105(98)00174-3 |
| [20] |
XIE Jiming, GARBER J. HFFB technique and its validation studies[J]. Wind and Structures, An International Journal, 2014, 18(4): 376. DOI:10.12989/was.2014.18.4.375 |
| [21] |
XIE Jiming. Aerodynamic optimization of super-tall buildings and its effectiveness assessment[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 130(1): 95. DOI:10.1016/j.jweia.2014.04.004 |
| [22] |
杨肖悦, 谢霁明. 建筑覆面风致连锁损坏的概率风险评估[J]. 哈尔滨工业大学学报, 2019, 51(6): 189. YANG Xiaoyue, XIE Jiming. Probabilistic risk assessment of cascading damage for building cladding in strong wind[J]. Journal of Harbin Institute of Technology, 2019, 51(6): 189. DOI:10.11918/j.issn.0367-6234.201811105 |
| [23] |
XU Zhendong, XIE Jiming. Assessment of across-wind responses for aerodynamic optimization of tall buildings[J]. Wind and Structures, An International Journal, 2015, 21(5): 507. DOI:10.12989/was.2015.21.5.505 |
 2021, Vol. 53
2021, Vol. 53



