2. 中国铁塔股份有限公司, 北京 100142;
3. 同济大学建筑设计研究院(集团)有限公司, 上海 200092
2. China Tower Corporation Limited, Beijing 100142, China;
3. Architectural Design & Research Institute of Tongji University(Group) Co. Ltd., Shanghai 200092, China
随着通信行业的大规模发展,移动式通信塔的数量逐年增多,塔的形式也从传统的空间杆系结构向多种形式发展,主要分为角钢塔、多管塔、单管塔三种[1]。单管塔由于具有占地面积小、结构自重轻、施工速度快、人工要求低等优点,在国外被广泛使用。近几年单管塔在国内的使用也日益增多,但由于其在国内应用时间较短,还未形成一套关于单管塔的荷载取值、设计方法、制作要求等内容的完整体系。风荷载作为通信塔结构设计过程中的主要控制荷载,其设计取值主要参照《高耸结构设计规范》[2]和《建筑结构荷载规范》[3],对于典型的圆柱和简易几何外形所受阻力也可参照大多数的风荷载设计规范[4-5],不过由于单管塔的塔身直径、天线尺寸、外挑距离在实际应用中需要根据不同功能需求进行调整,如果直接参考规范取值可能存在较大误差。因此研究单管塔结构关键参数变化对所受风荷载及其变化规律影响能够为单管塔设计提供重要依据。
目前通信塔抗风研究的主要实现手段仍以风洞试验方法为主。张庆华等[6-7]通过高频测力天平对格构式塔架和典型输电塔塔头静气动力特征进行了研究,研究结论表明格构式输电塔头静气动力主要以顺风向阻力为主,紊流场对塔头模型平均力系数影响较小;Carril等[8]研究了风向角、遮蔽效应等对阻力系数的影响,也得到了紊流场对于平均气动力系数影响较小的结论;Martín等[9]基于高频测力天平风洞试验研究了微波天线数量及位置对格构式塔架所受风荷载的影响;邓洪洲等[10]通过高频测力天平技术得到了作用在模型上的平均风荷载和体型系数;Jatulis等[11]针对格构式塔架(格构件为圆钢)的静力风荷载进行了最优设计研究,给出了设计参考的优化建议;虞德群等[12]通过风洞试验对单管塔塔体美化外罩的体型系数进行了研究。近年来,国内外学者也开始通过CFD方法对此类结构的抗风性能进行研究。Naeeni等[13]通过二维CFD方法研究了太阳能发电设备的抛物型收集器在不同风速及风向角下的流场形态,并从微观角度解释了组成构件对抛物型收集器受力性能的影响。Pezo等[14]通过数值方法,采用三种不同湍流模型对不同雷诺数范围和不同攻角下拉索桅杆节段的阻力系数进行了测定。Fabre等[15]通过风洞试验及CFD方法对带有外挑结构的三角形格构式测风塔外部复杂流场结构进行了研究,数值计算结果与试验结构吻合较好。
Prud′homme等[16]选取格构式塔架结构上的单一遮蔽角钢构件为研究对象,通过风洞试验研究了雷诺数、构件外形、湍流度等对遮蔽角件上所受风荷载的影响,研究结果表明雷诺数取1.4×104与3.81×104对遮蔽角件的阻力系数和升力系数的影响几乎可以忽略不计。Schewe[17]通过风洞试验研究了Re=104~107范围内圆柱、梯形桥梁断面、翼型断面气动力系数随雷诺数的变化规律,发现适当的雷诺数改变会引起气动力系数和Strouhal数的剧烈变化。Georgakis等[18]通过全尺寸模型的风洞试验对不同外形的格构式桅杆随雷诺数及风向角的变化进行了研究,结果表明规范规定的阻力系数值需要修正,均匀流场中桅杆阻力系数被低估了,而在紊流场中阻力系数则被高估了。
上述这些风洞和数值试验研究对象主要是格构式刚性塔架模型和桅杆模型,然而对单管塔模型及其塔头构件的抗风研究却少有涉及。单管塔沿塔身分布的外形差异主要集中于顶部塔头,风力特性在塔头部位差异较大,因而对单管塔塔头模型进行风洞试验研究其阻力系数的不同影响因素是有必要的。此外,雷诺数对于结构阻力系数的影响也与结构几何外形密切相关,工程结构中受雷诺数影响显著并且受到工程师和科研工作者广泛关注的是圆柱绕流问题。光滑圆柱的阻力系数会随着雷诺数的变化出现急剧下降又缓慢上升的情况,单管塔作为类圆柱结构,其阻力系数的变化与雷诺数也密切相关。
基于上述背景,本文针对双轮式单管塔塔头分别设计了整体式和分离式两种模型,采用不同的塔身直径、天线尺寸、外挑距离等可变参数共13组模型,通过高频测力天平技术在均匀流场中进行风洞试验。对比不同模型随风速变化的阻力系数曲线,也即随雷诺数变化的曲线,研究这些参数对阻力系数的影响以及阻力系数在高雷诺数区间内的变化规律。通过对比整体和分离式模型,得到天线外形影响系数的变化规律,进而判断外部天线对塔头整体阻力的贡献。试验结果可为双轮式单管塔塔头设计选型提供参考和依据。
1 风洞试验简介 1.1 模型介绍本文研究对象为双轮式单管塔塔头模型,塔头由正十六边形塔身(TB)、支架(BM)和天线(A)组成,dTB、dWT和sH、sB、sD分别表示对应原型塔身直径、外挑距离和天线几何尺寸(高、长、宽),其中塔身直径、外挑距离及天线几何尺寸为可变参数,其余构件尺寸均保持不变。几何外形及可变参数取值见图 1,详细试验尺寸参数见表 1,其中模型净投影面积S为正对来流方向的模型塔身及天线的净投影面积。

|
图 1 单管塔塔头原型尺寸及布置形式(mm) Fig. 1 Prototype size and layout of head of monopole (mm) |
| 表 1 模型试验可变参数设置(缩尺比1∶4) Tab. 1 Variable parameters of model test (scale 1∶4) |
为使得天平-模型系统固有频率远高于作用荷载的主要频率范围,需保证模型具有足够的刚度和较轻的质量以及满足几何相似性要求,风洞试验模型塔身部分采用轻质高强铝合金制作,支架与天线部分采用不锈钢及玻璃钢制作,几何缩尺比1∶4,见图 2。其中模型在风洞中的最大阻塞比为4.5%,故无需考虑风洞阻塞比修正。

|
图 2 风洞试验单管塔双轮式塔头模型 Fig. 2 Model of head of monopole (two-wheel type) in wind-tunnel test |
本文试验将模型分成以下2种类型:1)整体式模型,模型塔身、支架和天线共同受力,天平测得模型整体受力,见图 2(a);2)分离式模型,模型塔身与支架、天线分离,天平仅与中间塔身连接,天平只测得塔身受力,见图 2(b)。整体式模型与分离式模型主要区别在于分离式模型去除了支架与塔身连接固定件,将外部天线通过底部附件连接件固定与铁质圆盘,并与建筑转盘通过螺栓连接,外部天线、支架不与塔身接触,见图 2(c)。对应表 1中模型1~3为整体式模型,模型4~6为分离式模型。
1.2 试验描述本文试验在同济大学土木工程防灾国家重点实验室TJ-2大气边界层风洞中进行,作用于模型上的气动力通过高频动态测力天平测得,试验采样频率300 Hz,采样时间20 s。风速按照稳转速方式施加,风速施加范围5~30 m/s;试验参考风速通过数字微压记采集风压换算得到,风速参考点位置位于建筑转盘前缘2 m,高0.64 m,距洞壁0.72 m,见图 3。

|
图 3 风速参考点位置 Fig. 3 Position of wind speed reference point |
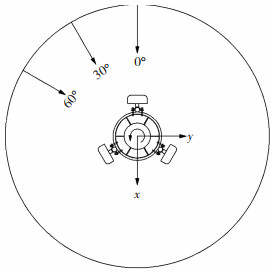
针对整体式模型,本文进一步研究了不同的塔身直径、天线尺寸、外挑距离对作用于模型上的阻力系数的影响。所有的试验工况均考虑了阻力系数随风向角的改变,其中风向角用ϕ表示,按逆时针方向施加。考虑到结构对称性,ϕ分别取为0°、30°和60°,天平坐标系及风向角见图 4。当ϕ=0°时,体轴、风轴与天平坐标系三轴重合。
|
图 4 风洞试验单管塔塔头模型风向角 Fig. 4 Wind direction angle of model of head of monopole in wind-tunnel test |
通过上述风洞试验获得作用在模型上的沿x方向和y方向的水平风荷载,以Fx和Fy表示,经式(1)~(3)变换后可得沿体轴方向的时均无量纲气动力系数CFx、CFy和沿风轴方向的时均无量纲平均风压力系数CD(本文CD均代表整体式模型所受顺风向阻力系数):
| $ C_{F_{x}}=\frac{1}{\tau} \int_{t_{0}}^{t_{0}+\tau} \frac{F_{x}(t)}{0.5 \rho V^{2} S} \mathrm{~d} t $ | (1) |
| $ C_{F_{y}}=\frac{1}{\tau} \int_{t_{0}}^{t_{0}+\tau} \frac{F_{y}(t)}{0.5 \rho V^{2} S} \mathrm{~d} t $ | (2) |
| $ C_{\mathrm{D}}=C_{F_{x}} \cos \phi+C_{F_{y}} \sin \phi $ | (3) |
式中:Fx(t)、Fy(t)分别为天平测得的对应x方向和y方向的瞬时气动力,V为经数字微压计换算所得试验参考风速,ρ为空气密度,S为模型参考面积。
2.1 塔身直径对阻力系数的影响图 5为整体模型阻力系数随雷诺数变化散点图,其中(a)、(b)、(c)分别对应原型塔身直径dTB为400、600和800 mm在不同风向角下阻力系数随雷诺数的变化规律。从图中可发现随着雷诺数的增大,阻力系数基本保持稳定,说明在试验雷诺数区间内,阻力系数对雷诺数的变化不敏感。因而本文通过对试验雷诺数区间内各测试点取均值得到了对应风向角下不同塔身直径模型阻力系数,见图 6。从中可发现对应风向角下,随着塔身直径增大,阻力系数降低,说明模型净投影面积增加部分未能产生与之相匹配的阻力,这是由于塔身与天线的相互干扰从而导致阻力产生一定的折减。

|
图 5 不同直径整体式模型阻力系数随雷诺数变化 Fig. 5 Relation between drag coefficient of integrated models with different diameters and Reynolds number |

|
图 6 不同塔身直径模型阻力系数对比 Fig. 6 Comparison of drag coefficient of integrated models with different monopole diameters |
此外,风向角的改变会引起模型周围空气绕流形态的改变,但由于本文选用的模型外挑距离较小,塔身与外部天线较近,从图 5中可看出绕流形态改变所引起的阻力系数在数值上的变化并不明显,但对阻力系数随雷诺数的变化趋势有所影响。图 6中,塔身直径dTB=400 mm时,风向角改变所引起的阻力系数趋势变化较为明显;塔身直径dTB=600 mm时,风向角改变所引起的阻力系数趋势变化较为不明显。这是由于在一定范围内,随着塔身直径增大,塔身在绕流系统中所起到的权重增大,阻力系数变化趋势随塔身直径增大逐渐趋于平缓。
图 7为分离式模型中塔身阻力系数随雷诺数变化规律,其中(a)、(b)、(c)分别对应塔身原型直径dTB为400、600和800 mm在不同风向角下阻力系数随雷诺数的变化规律,从图中可以发现风向角对于分离式模型塔身阻力系数影响十分显著。

|
图 7 不同直径分离式模型阻力系数随雷诺数变化 Fig. 7 Relation between drag coefficient of segregated models with different diameters and Reynolds number |
当ϕ=0°时,来流在前缘天线处产生分流,尾流对塔身阻力影响较弱,阻力系数随雷诺数的变化较为平缓;当ϕ=60°时,来流直接作用于塔身,塔身为近圆柱形,随着雷诺数增大,呈现类似于圆柱的阻力特性,但天线与塔身的相互干扰作用又会减弱这种特性,因而阻力系数最终表现为随着雷诺数的增加快速降低;当ϕ=30°时,模型沿来流方向呈非对称状态,流动复杂,阻力系数随雷诺数增加而减小,且其对应雷诺数下的阻力系数数值均处于ϕ=0°与ϕ=60°对应阻力系数之间。同时从图中可观察到阻力系数随雷诺数的变化近似呈线性下降趋势,因而为比较塔身直径对于阻力系数下降快慢的影响,对各风向角下的试验数据进行线形拟合。
表 2为通过线性拟合得到的不同塔身直径不同风向角下分离式模型的阻力系数随雷诺数变化的下降斜率。从中可以看出风向角固定时,随着塔身直径的增大,阻力系数随雷诺数的下降趋势逐渐变缓。
| 表 2 不同直径分离模型在不同风向角下阻力系数下降斜率 Tab. 2 Descending slope of drag coefficient of segregated models with different diameters under different wind direction angles |
为考察天线及支架对整体模型气动阻力的贡献,本文定义了一个天线外形影响系数fa,表示外部天线所受阻力与整体模型所受阻力之比,其中外部天线阻力通过整体模型阻力与分离模型塔身所受阻力之差得到。由于附加连接(底部固定件)仅对底部流场有所影响,对上部流场的影响几乎可以忽略不计,因而综合考虑认为当其他条件一致时,整体式模型受力减去分离式模型塔身受力得到外部天线与支架受力的方法是可行的。天线外形影响系数fa的计算公式为
| $ f_{\mathrm{a}}=\frac{\Delta F}{F_{\mathrm{D}}}=\frac{C_{\mathrm{D}}-C_{\mathrm{D}_{-} \mathrm{TB}}}{C_{\mathrm{D}}} $ | (4) |
式中CD和CD_TB分别表示同一外形下整体式模型与分离式模型的阻力系数。
图 8 (a)、(b)、(c)为不同风向角下,不同塔身直径的模型天线外形影响系数随雷诺数变化曲线。从图 8(a)中可看出,当ϕ=0°时,随雷诺数增大,三种塔直径模型的天线外形影响系数很快趋于稳定,天线对于模型阻力的贡献在ϕ=0°时受雷诺数影响较小;当ϕ=30°及ϕ=60°时,雷诺数对天线外形影响系数变化有较大影响,但随着雷诺数的增大,呈现与图 8(a)中天线外形影响系数类似的变化规律,在高雷诺数段逐渐趋向稳定,说明外部天线所受阻力在整体塔头风荷载中所占比例较大且随着雷诺数的增大而增大,最终在高雷诺数段趋于稳定。同时,随着塔身直径的增大,天线外形影响系数整体降低,即随着塔身直径的增大,塔身在绕流影响中所起到的权重增大,相对降低了天线对于模型整体阻力的贡献。

|
图 8 不同直径模型天线外形影响系数随雷诺数变化 Fig. 8 Relation between antenna shape influence coefficient of models with different diameters and Reynolds number |
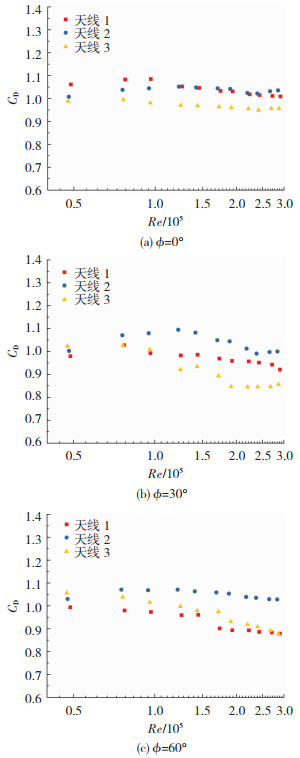
本文选取了实际使用中常用的三种天线进行单管塔塔头模型风洞试验,其中天线尺寸中高度为变化较大,长度及宽度变化相对较小,三种天线尺寸见图 1。图 9为不同风向角及天线尺寸下整体模型阻力系数随雷诺数变化曲线。
|
图 9 不同天线尺寸模型阻力系数随雷诺数变化 Fig. 9 Relation between drag coefficient of models with different antenna sizes and Reynolds number |
从图中可看出,当ϕ=0°时,对应不同天线的试验模型阻力系数均较为接近,受雷诺数变化的影响较小。当ϕ=30°及ϕ=60°时,阻力系数随雷诺数的增大呈整体下降趋势。但实际情况中所使用的天线在长宽高三个方面均有变化,加之天线与塔身组成的复杂三维绕流系统,本文试验并不能很好给出使单管塔塔头所受阻力最小的最优天线尺寸规格,只能从本文试验中定性判断天线3对应的尺寸为较优的天线尺寸规格。当ϕ=0°及ϕ=30°时,天线3所对应的阻力系数数值较另两种天线规格小;当ϕ=60°时,天线3与天线1分别对应的阻力系数数值较为接近。
2.3 外挑距离对阻力系数的影响图 10为不同的风向角及外挑距离下模型整体阻力系数随雷诺数变化曲线。

|
图 10 不同外挑距离模型阻力系数随雷诺数变化 Fig. 10 Relation between drag coefficient of models with different overhang distances and Reynolds number |
从图 10 (a)中可看出当ϕ=0°时,阻力系数随雷诺数变化较为平稳,其中当外挑距离位于122~693 mm时,阻力系数变化曲线几乎重合,说明当外挑距离处于该分布区间时,流场性质较为类似,外挑距离对于阻力系数的影响较小;当外挑距离继续增大时,阻力系数随雷诺数的变化仍保持较为平缓的变化趋势,阻力系数变化曲线上浮,阻力系数增大,这是由于当外挑距离逐渐增大时,由天线前缘分离引起的尾流流场对塔身的影响减弱;当ϕ=30°及ϕ=60°时,阻力系数随风速变化呈现较为规则的下降趋势,同时阻力系数变化曲线随着外挑距离增大逐渐上升,且随着外挑距离的增大,阻力系数在雷诺数逐渐增大的过程中下降趋势逐渐变缓。
3 结论1) 整体式模型阻力系数对雷诺数变化不敏感,阻力系数会随着塔身直径的增大而降低。风向角对阻力系数的变化趋势有所影响,在一定范围内,随着塔身直径增大,阻力系数变化趋势会逐渐趋于平缓。
2) 风向角对塔身所受阻力影响较显著,ϕ=0°时,阻力系数随雷诺数增加缓慢下降,ϕ≠0°时,阻力系数随雷诺数增加快速下降。同时随着塔身直径的增大,相同风向角下,阻力系数随雷诺数变化的下降斜率增加,下降趋势逐渐变缓。天线外形影响系数随着雷诺数的增加而增加,最终在高雷诺数段趋于稳定;塔身直径增大,天线外形影响系数整体降低,天线对于整体阻力的贡献减弱。
3) ϕ=0°时,天线尺寸对于阻力系数大小及变化趋势影响较小;ϕ≠0°时,阻力系数随雷诺数增加呈下降趋势。天线3为试验所采用的三种天线尺寸中较优的天线选型。
4) 阻力系数会随着外挑距离的增大而增大,且随雷诺数发展变化规律基本保持不变。其中ϕ=0°时,阻力系数随雷诺数变化基本保持平稳;ϕ≠0°时,阻力系数随雷诺数变化呈整体下降趋势。
| [1] |
屠黑男, 王肇民. 轻型通信塔设计[J]. 特种结构, 2001, 18(4): 24. TU Heinan, WANG Zhaomin. Design of light communication tower[J]. Special Structures, 2001, 18(4): 24. |
| [2] |
高耸结构设计规范: GB 50135—2006 [S]. 北京: 中国计划出版社, 2007 Code for design of high-rising structures: GB 50135—2006 [S]. Beijing: China Planning Press, 2007 |
| [3] |
建筑结构荷载规范: GB 50009—2012 [S]. 北京: 中国建筑工业出版社, 2012 Load code for the design of building structures: GB 50009—2012 [S]. Beijing: China Building Industry Press, 2012 |
| [4] |
Design of steel lattice towers and masts: AS 3995-1994 [S]. Homebush: Standards Australia, 1994
|
| [5] |
Lattice towers and masts: Code of practice for loading: BS 8100-1 [S]. London: British Standards Institution, 1986
|
| [6] |
张庆华, 顾明, 黄鹏. 典型输电塔塔头风力特性试验研究[J]. 振动工程学报, 2008, 21(5): 452. ZHANG Qinghua, GU Ming, HUANG Peng. Experiment on wind force on typical superstructures of latticed transmission tower[J]. Journal of Vibration Engineering, 2008, 21(5): 452. DOI:10.3969/j.issn.1004-4523.2008.05.005 |
| [7] |
张庆华, 顾明, 黄鹏. 格构式塔架风力特性试验研究[J]. 振动与冲击, 2009, 28(2): 1. ZHANG Qinghua, GU Ming, HUANG Peng. Experimental study of wind force on latticed tower[J]. Journal of Vibration and Shock, 2009, 28(2): 1. DOI:10.3969/j.issn.1000-3835.2009.02.001 |
| [8] |
CARRIL C F, ISYUMOV N, BRASIL R M. Experimental study of the wind forces on rectangular latticed communication towers with antennas[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(8): 1007. DOI:10.1016/S0167-6105(03)00049-7 |
| [9] |
MARTIN P, ELENA V B, LOREDO-SOUZA A M, et al. Experimental study of the effects of dish antennas on the wind loading of telecommunication towers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 149: 40. DOI:10.1016/j.jweia.2015.11.010 |
| [10] |
DENG Hongzhou, ZHANG Jianming, SHUAI Qun, et al. Wind-tunnel investigation on pressure coefficient of steel tubular transmission tower[J]. Power System Technology, 2010, 34(9): 190. DOI:10.3724/SP.J.1011.2010.01138 |
| [11] |
JATULIS D, JUOZAPAITIS A, VAINIUNAS P. Optimal design of lattice towers made up of solid round steel bars[C]//Modern Building Materials Structures and Technigues, 10th International Conference. Vilnius: [s. n. ], 2010: 641
|
| [12] |
虞德群, 屠海明, 栾壮壮. 单管塔美化外罩体型系数风洞试验研究[J]. 特种结构, 2016, 33(1): 34. YU Dequn, TU Haiming, LUAN Zhuangzhuang. Wind-tunnel experimental study on shape coefficient of single tube tower decorated cover[J]. Special Structures, 2016, 33(1): 34. |
| [13] |
NAEENI N, YAGHOUBI M. Analysis of wind flow around a parabolic collector (1) fluid flow[J]. Renewable Energy, 2006, 32(11): 1898. DOI:10.1016/j.renene.2006.10.004 |
| [14] |
PEZO M L, BAKI V V. Numerical determination of drag coefficient for guyed mast exposed to wind action[J]. Engineering Structures, 2014, 62: 98. DOI:10.1016/j.engstruct.2014.01.025 |
| [15] |
FABRE S, STICKLAND M, SCANLON T, et al. Measurement and simulation of the flow field around the FINO 3 triangular lattice meteorological mast[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 130: 99. DOI:10.1016/j.jweia.2014.04.002 |
| [16] |
PRUD'HOMME S, LEGERON F, LANEVILLE A, et al. Wind forces on single and shielded angle members in lattice structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 124: 20. DOI:10.1016/j.jweia.2013.10.003 |
| [17] |
SCHEWE G. Reynolds-number effects in flow around more-or-less bluff bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(14/15): 1267. DOI:10.1016/S0167-6105(01)00158-1 |
| [18] |
GEORGAKIS C T, STØTTRUP-ANDERSEN U, JOHNSEN M, et al. Drag coefficients of lattice masts from full-scale wind-tunnel tests[C]//Proceedings of the 5th European and African Conference on Wind Engineering-EACWE. Florence: EACWE, 2009: 5
|
 2021, Vol. 53
2021, Vol. 53


