2. 中国路桥工程有限责任公司,北京100011;
3. 武汉科技大学 城市建设学院,武汉 430081
2. China Road & Bridge Corporation, Beijing 100011, China;
3. School of Urban Construction, Wuhan University of Science and Technology, Wuhan 430081, China
风致稳定性是大跨度桥梁设计中的控制性因素,气动外形优化是改善桥梁气动性能最基本有效的方法[1-2]。桥梁工程领域中气动外形优化的经典方法是基于风洞试验的迭代启发式过程,此方法依赖于风洞试验室的资源消耗和研究人员的精力投入,导致优化设计的范围有限,效果欠佳[3]。近年来CFD技术的快速改进使其在应用工业领域大放异彩,并且早在1997年,将其与数学优化算法结合用于挑选最优气动外形的想法就已经开始引起科学家的关注与研究[4]。目前,在机械、汽车和航空航天领域,基于CFD和数学优化算法的气动外形优化方法已被应用于配置最佳几何外形车辆、飞机机身和机翼、压缩机叶片、层流和湍流扩散器等,这种方法不仅能够严谨彻底地搜索整个设计域,并且消除了经典方法固有的风洞试验资源耗费和迭代试错过程效率低下的缺点[5-7]。由于CFD在土木工程领域中引入较晚[6-7],导致这种结合数学策略的优化方法研究也有所滞后,因此关于将其移植到桥梁工程领域是否可行的研究显得需求迫切。
本文研究了基于数值计算与数学策略的流线型箱梁气动外形优化方法。数值计算是利用CFD模拟和颤振时域法进行计算,数学策略则是将试验设计、蚁群混合遗传算法与Kriging代理模型结合,通过求解某桥梁断面整个设计域中部分的解,构建和训练Kriging近似代理模型,得到满足一定精度的整个设计域所有的解,从而寻求最优断面。作为案例研究,以颤振性能为目标,优化苏通桥主梁截面外形。
1 优化准备 1.1 问题描述在工程上,流线型箱梁气动外形优化是指在满足行车、静力、稳定等要求的前提下,通过主梁几何外形的修剪使其具有最佳的气动性能。相应地在数学上,流线型箱梁气动外形优化是将其几何形状表达为梁高、梁宽、风嘴角度上下腹板倾角几个设计变量的集合,称为设计参数;设计变量本身有一定的限制,一般六车道使得桥面宽度满足相应的不等式,流线型要求上下腹板倾角满足相应的关系式等等,这些关系式表达为约束;气动性能分为颤振性能、涡振性能等,在数学上对应目标函数值。鉴于以上,流线型箱梁气动外形优化可表达为多目标多约束多设计变量下的数学优化问题。
1.2 优化流程由于主梁断面优化问题包含大变化范围的多设计变量、强敏感性的目标函数值,设计完全试验会产生巨量的试验次数;且风洞试验对人力、物力、时间成本消耗较大,因此在保证精度的前提下,需要寻找一种新的优化策略,流程见图 1。策略分为3个组成部分:(a) 前期准备选定断面气动外形敏感参数及优化范围,在设计域中进行试验设计;(b) 优化过程以数值模拟为工具计算风致响应并结合数学策略(近似代理模型建立、验证与更新)得到整个设计域内的风致响应;(c) 结果分析是对各个参数进行统计分析,深入探究机理,最终选出气动外形良好断面。
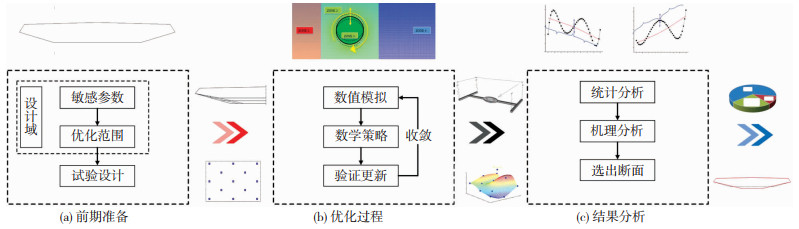
|
图 1 流线型箱梁气动外形优化流程 Fig. 1 Aerodynamic shape optimization process of streamlined box girder |
将流线型箱梁断面气动敏感变量分为断面端部变量如风嘴角度、上下腹板倾角等;断面中部变量如梁高、梁宽等。目前已建造的大跨度桥梁中,断面端部总是采用较长的下斜腹板,且下腹板倾角与风嘴角度、风嘴长度等相互关联,因此在端部外形变量中,下腹板倾角对气动性能影响占比大;断面中部的梁高和梁宽两个参数一般不宜做出较大改变,因其不仅对气动性能影响较大,且会引起主梁抗压弯静力性能、质量和惯性矩动力性能等发生变化,但考虑到优化效果,认为可在一定范围内变化[8];综上,选取主梁端部变量下腹板倾角A和中部变量梁高H作为设计变量。以苏通长江大桥主梁流线型箱梁断面为基准断面(A=13°, H=4.0 m) [9],A和H两参数的优化范围取80%~120%,1%为梯度,设计域为{H: [3.2, 4.8], A: [10.4, 15.6] }。
1.4 试验设计若在设计域中进行完全试验,则试验总次数为1 681次,故采取合理的试验设计方法制定抽样方案。典型试验设计方法有正交试验设计、均匀试验设计、(空间填充)拉丁超立方设计[10]等,示意见图 2。均匀试验设计能避免采样随机性、易于选取,且可以提供设计全空间的信息;序列探索是基于特定模型,Lin[11]提出了一种序列探索试验设计(sequential exploratory experiment design, SEED)方法产生新的样本点来更新Kriging模型;综上,采用均匀试验+序列探索试验设计方法制定抽样方案,示意见图 2(c)。

|
图 2 典型试验设计 Fig. 2 Typical experimental designs |
颤振临界风速采用混合数值计算。根据设计变量A/H变化,先通过CFD模拟竖弯和扭转强迫振动得到三分力系数时程,再用最小二乘法拟合颤振导数并建立气动力模型,最后建立有限元结构模型以二维时域方法求解颤振临界风速。以苏通桥原断面作为算例对计算方法进行说明并检验准确性。
2.1 网格及模型CFD数值模拟直接影响到近似模型响应面的精度和优化算法的效率, 是整个优化流程的基础。因此,合理的计算域划分与网格数量、湍流模型、雷诺数[12]等至关重要。二维模型计算域及网格划分见图 3,计算域的左侧设置为速度入口,右侧设置为压力出口,上下壁面设置为滑移壁面,其中B表示梁宽,在距断面中心10B位置处设置左右交界面以及在距断面中心5B位置处设置环形交界面。流线型箱梁断面中心距入口20B、出口30B、上下边界10B,出入口边界及上下壁面边界已远离断面,数值模拟能够反映真实物理环境。数值风洞入口风速12 m/s,雷诺数与苏通桥试验报告相同,取为4.64×105,湍流模型采用学界广泛应用的SST k-ω模型[2]。为合理划分网格并减少网格数量,整个计算域内采用分块划分网格的方式:ZONE1、ZONE2和ZONE4区域采用结构化网格,ZONE3区域采用结构化与非结构化混合网格,箱梁断面壁面边界层为结构化网格,网格厚度为2.5×10-5 m。将ZONE3设置为竖向和扭转区域,箱梁断面运动时,交界面内网格随之运动,保证了边界层的正确模拟,设定ZONE2为变形网格区域,应用局部网格重划与弹簧光顺法协调控制网格的变形。
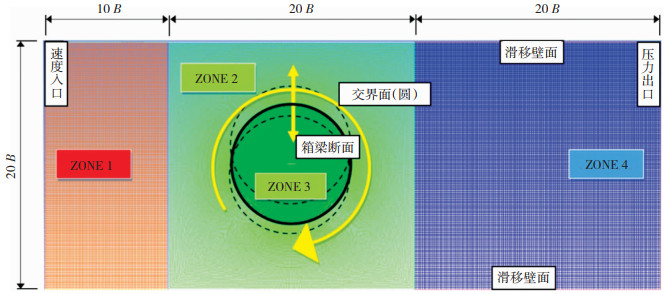
|
图 3 计算域及网格划分示意 Fig. 3 Schematic of computational domain and meshes |
计算域、网格划分方式及基本参数设定之后,在进行CFD计算之前,还需对不同的计算参数进行必要的试算,以期得到兼顾效率和准确性的最佳计算参数,网格无关性与时间无关性验证便是选取网格数量与时间步长的必经步骤。网格选取遵守双倍网格尺寸变化规则进行,对图 3所示网格,ZONE1、3、4分区网格数量不变,只对ZONE2进行网格重划分以得到不同总数的网格,ZONE2网格分辨率随着网格数量增加而增大。网格名称以Mesh为前缀、中间下划线、网格总数为后缀进行命名,不同网格及网格无关性验证结果(0°攻角)见表 1,误差在可接受范围内。基于桥梁断面长度与入口边界风速考量,选取计算步长为5×10-4 s、2×10-3 s和1×10-3 s,三者计算偏差在0.1%以内。最终选取计算网格总数为12万,时间步长为1×10-3 s。
| 表 1 不同网格数量及数值结果 Tab. 1 Grids of different quantities and numerical results |
国内外许多学者在颤振分析的计算方法中进行过深入探索,综合考虑计算效率与准确性,选用二维时域法[13]进行颤振临界风速计算。采用文献[14]的脉冲响应函数表达自激力,并将其施加于模拟节段模型风洞试验的有限元模型以计算颤振临界风速。
在Fluent平台对上述CFD计算模型分别进行竖弯和扭转强迫振动,竖弯振幅取0.2倍梁高,扭转振幅取1°,入口风速固定为12 m/s,雷诺数取值为4.76×105,通过改变折算频率实现折算风速变化,在对应实桥风速为0~300 m/s设置15个风速点。颤振导数识别方法为通过最小二乘法拟合CFD模拟监测到的CL和CM时程曲线,从而得到颤振导数[15]。如图 4所示,除H4*外,其他气动导数变化趋势和数值大小与风洞试验吻合较好,特别是流线型箱梁的几个重要的气动导数H1*、H3*(低折算风速)、A1*、A2*和A3* [15]。
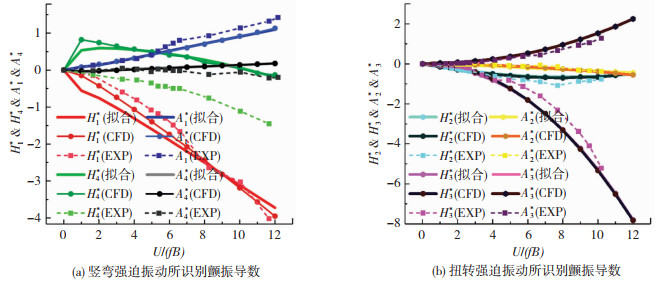
|
图 4 最小二乘拟合颤振导数 Fig. 4 Flutter derivatives by least squares fitting |
根据在正余弦振动形式下,脉冲响应函数表达的自激力与气动导数表达的自激力相等价的关系,Lin[11]导出了用脉冲响应函数表达的自激力的具体表达形式。即只要得到桥梁断面的气动导数,就可以在时域内获得任意运动形式下的自激力近似表达式,从而对结构振动响应进行分析。以最小二乘拟合上述颤振导数可得到脉冲响应函数特定系数近似值,即可获得自激力近似表达式,拟合结果见图 4,除H1*和H4*在较低折算风速时误差较大,其余拟合准确,认为可用于分析颤振临界风速发生。
2.4 颤振临界风速求解在ANSYS中建立有限元结构分析模型,参考风洞试验节段模型设计计算,如图 5所示,弹簧采用刚度相同杆单元BEAM4模拟,其余构件采用刚性杆单元模拟,每延米质量和转动惯量采用质量单元MASS21施加;箱梁断面几何缩尺比选用1∶70,风速比1∶8.367,各项参数见表 2;给定风速即可进行计算。
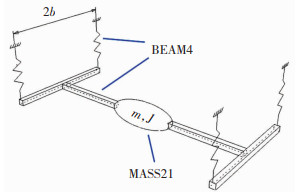
|
图 5 有限元结构分析模型 Fig. 5 Finite element model of structural analysis |
| 表 2 结构分析建模参数 Tab. 2 Structural analysis modeling parameters |
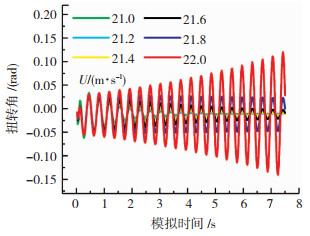
当风速取值为U=21~22 m/s时,扭转位移时程见图 6:在来流风速为21.8 m/s时接近于等幅振动但仍收敛,22 m/s时则明显运动发散,故认为颤振临界风速为21.9 m/s,此时换算实桥风速为182.5 m/s,节段模型试验结果为185 m/s,计算误差为1.4%,认为计算非常准确,耗时5~10 min。综上,二维时域法可以作为数值计算工具完成优化过程中每一轮新断面的颤振临界风速求解。
|
图 6 二维时域法计算扭转位移时程 Fig. 6 Torsional displacement time history calculated by two-dimensional time domain method |
数学策略优化思路为近似代理模型:首先用均匀试验设计结合数值计算构造元模型并验证精度,然后用序列探索试验设计方法搜索模型最优解和误差最大解并与真实数值计算值对比验证,若不满足精度要求则加入新计算的真实值更新模型,直到优化结束,更新模型转变为末模型。
3.1 元模型及验证统计学习的目的是使学到的近似代理模型不仅对已有数据有很好的拟合,更重要的是对新数据有很好的预测,因此选取合适的代理模型、评价指标、验证更新方法等至关重要[16]。
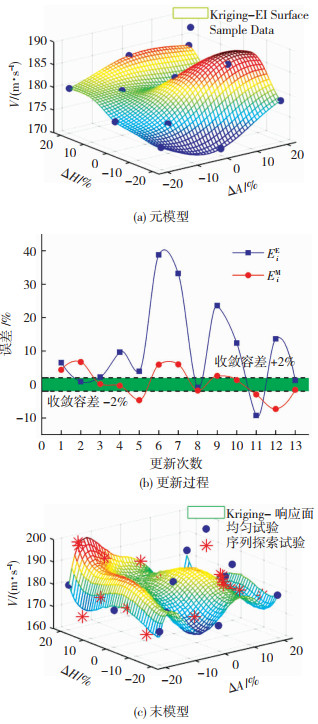
Kriging模型具有随机特性,可提供预测位置的预测值和预测误差,适用于全局优化算法[17],因此选取Kriging进行统计学习,得到元模型见图 7(a);进一步通过简洁而有效的留一交叉验证来合理评价模型精度[20]。选取相对误差、相对误差均值、标准差以及预测趋势作为评价指标。预测相对误差、相对误差均值与标准差为:
| $ e_{i}=\left|\frac{V_{i}^{\mathrm{C}}-V_{i}^{\mathrm{K}}}{V_{i}^{\mathrm{C}}}\right| $ | (1) |
| $ \bar e = \frac{1}{n}\sum\limits_{i = 1}^n {{e_i}} $ | (2) |
| $ \sigma = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{(e - \bar e)}^2}} }}{{n - 1}}} $ | (3) |
|
图 7 流线型箱梁-Kriging建立及更新 Fig. 7 Modeling and updating process of streamlined box girder-Kriging model |
式中:ei为样本点i上的相对误差,ViC和ViK分别为样本点i的颤振临界风速CFD计算值和Kriging近似模型预测值,e和σ为相对误差均值与标准差。Kriging模型预测误差见表 3,最大值与最小值分别为5.12%与0.12%,误差均值与标准差分别为2.20%和1.55%;预测趋势见图 7,前5个样本点略有误差,后8个样本点波动基本一致。综上,Kriging模型预测误差较小,但仍存在误差较大的点,预测趋势较准确,但仍存在趋势不符的区域。
| 表 3 留一交叉验证相对误差 Tab. 3 Relative error of leave-one-out cross-validation |
对于Kriging模型某些点(如采样点9)真实值与预测值偏差较大的问题,解决办法是采用序列探索试验设计方法增加采样点对模型进行更新。Kriging模型的预测值是一个随机变量,模型可以给出预测均值EI和均方误差MSE,基于这种随机预测特性,序列探索实验设计可以对模型的EI和MSE两个指标进行搜索以增加新的样本点,最终使得构建的模型能够捕捉到真正对象函数的趋势和变化[18]。
采用MATLAB编程实现混合蚁群遗传算法来搜索EI值最大和MSE值最大的更新点,这种算法能够结合蚁群算法的全局搜索能力强和遗传算法的计算效率高的优点[19]。同时进行新一轮的数值计算,并与预测值进行比较,对其误差设定收敛准则为EiE和EiM在2%以内,两者分别为按照EI和MSE搜索策略得到更新点的数值计算值与模型预测值的误差。更新过程见图 7(b)和表 4,经过13次更新完成收敛。更新过程波动较多,在第6次更新时,EI误差波动增至将近40%,模型预测失真严重,原因可能是气动外形优化问题的高度敏感性,后续随着样本点继续增加,模型预测能力逐渐恢复,误差不断减小直至满足收敛准则。
| 表 4 流线型箱梁-Kriging模型更新过程 Tab. 4 Updating process of streamlined box girder-Kriging model |
将初始样本点和所有的更新点用于建立Kriging模型,得到流线型箱梁-Kriging末模型见图 7(c)。由EI值响应面可直观得出最大值出现在左上角,而不是元模型的右下角,这也说明了模型更新的必要性。
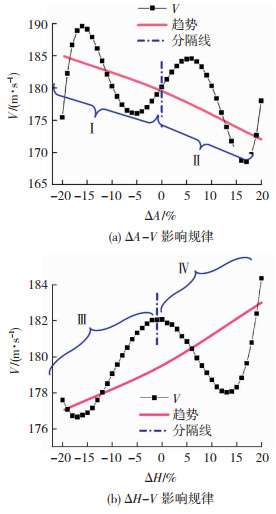
3.3 参数统计分析利用末模型得到设计域内每个采样点的颤振临界风速V预测值,根据文献[20]方法对优化参数A和H进行直观分析和方差分析,以探究它们对V的影响规律和程度,统计分析结果见图 8。图 8(a)给出ΔA对V的影响规律,V随A增加呈减小趋势,以分隔线为界趋势明显呈两个相似区间Ⅰ和Ⅱ,在各自区间内V类似呈正弦变化;图 8(b)给出了ΔH对V的影响规律,V随H增加呈增大趋势,以分隔线为界趋势呈两个相似区间Ⅲ和Ⅳ,在各自区间内V类似呈余弦变化。根据V变化范围来看,A影响区间为[165, 190],而H影响区间为[175, 185],所以A影响相对较大。
|
图 8 优化参数统计分析结果 Fig. 8 Statistical analysis results of optimized parameters |
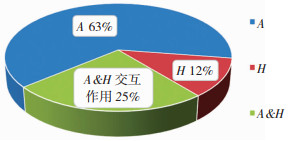
图 9给出了方差分析结果,扇形比例表示对应项的平均方差占平均方差总和的比例。根据方差分析理论,一个因素的平均方差所占比例越高,表明该因素对指标变化的影响越明显。A、H和A & H交互作用所占比例分别为63%、12%和25%,3个指标对颤振临界风速的影响依次递减,验证了直观分析所得结论。A和H两个参数不仅能各自独立对V产生影响,还会联合起来产生影响,这称为交互作用。如图 10所示,以ΔH=(-20%, 0, 20%)作为研究对象,探究ΔA=[-20%, 20%]变化范围内V变化趋势。ΔH=-20%和0时,曲线趋势同增同减,无明显的交互作用;在ΔH=20%,ΔA=[0, 7%]时,曲线呈下降趋势,另外两条则呈上升趋势,且3条曲线出现交叉,此时交互作用明显。原因可能是梁高较大的断面钝体特性明显,下腹板倾角产生的影响大。
|
图 9 平均方差分布 Fig. 9 Average variance distribution |

|
图 10 典型交互作用示意 Fig. 10 Schematic of typical interaction |
对上述统计分析总结并进行最值搜索,得到气动外形最优断面见图 11。虚线为原始苏通桥断面,实线为最优断面,梁高增加20%,即4.8 m,下腹板倾角减小17%,即10.79°,颤振临界风速为198 m/s,相比于原型断面增加了15 m/s。

|
图 11 流线型箱梁最优化断面与原断面对比 Fig. 11 Comparison of optimized section and original section of streamlined box girder |
以流线型箱梁气动外形优化数值策略为研究对象,将蚁群混合遗传算法、Kriging近似代理模型、CFD数值风洞模拟和ANSYS颤振时域法结合使用,得出一套完整的气动外形优化方法,并以苏通桥断面优化为例检验了优化方法可行性。主要结论如下:
1) 采用CFD进行强迫振动识别颤振导数和ANSYS颤振时域法计算颤振临界风速为182.5 m/s,与风洞试验185 m/s相差较小,数值计算手段准确性较高。
2) 结合蚁群混合遗传算法,Kriging数学代理模型更新13次后达到2%以内的预测误差,数学代理模型预测颤振响应可行性较高。
3) 借助统计分析数学手段进行优化分析表明,下腹板倾角A相对于梁高H对流线型箱梁断面颤振性能影响更大,两个参数存在交互作用。
4) 优化结果显示,基于苏通长江大桥的流线型箱梁最优参数匹配断面为梁高H=4.8 m,下腹板倾角A=10.79°。
5) 基于数值计算与数学策略的流线型箱梁气动外形优化策略能够应用于流线型箱梁断面气动外形优化,对今后桥梁断面选型具有借鉴意义。
| [1] |
LARSEN A, WALL A. Shaping of bridge box girders to avoid vortex shedding response[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104/105/106: 159. DOI:10.1016/j.jweia.2012.04.018 |
| [2] |
HU Chuanxin, ZHOU Zhiyong, JIANG Baosong. Effects of types of bridge decks on competitive relationships between aerostatic and flutter stability[J]. Wind and Structures, 2019, 28(4): 255. DOI:10.12989/was.2019.28.4.255 |
| [3] |
CID MONTOYA M, NIETO F, HERNÁNDEZ S, et al. CFD-based aeroelastic characterization of streamlined bridge deck cross-sections subject to shape modifications using surrogate models[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 177: 417. DOI:10.1016/j.jweia.2018.01.014 |
| [4] |
SOBIESZCZANSKI-SOBIESKI J, HAFTKA R T. Multidisciplinary aerospace design optimization: survey of recent developments[J]. Structural & Multidisciplinary Optimization, 1997, 14(1): 1. DOI:10.1007/bf01197554 |
| [5] |
MADSEN J I, SHYY W, HAFTKA R T. Response surface techniques for diffuser shape optimization[J]. AIAA Journal, 2000, 38(9): 1512. DOI:10.2514/3.14576 |
| [6] |
KAREEM A, BOBBY S, SPENCE S M J, et al. Optimizing the form of tall buildings to urban environments[C]//CTBUH 2014 International Conference. Shanghai: CTBUH, 2014: 1
|
| [7] |
DING F, AHSAN K. A multi-fidelity shape optimization via surrogate modeling for civil structures[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2018, 178: 49. DOI:10.1016/j.jweia.2018.04.022 |
| [8] |
王德智. 闭口钢梁箱几何外形的空气动力性能优化[D]. 上海: 同济大学, 2013 WANG Dezhi. Aerodynamic shape optimization of closed steel box girder[D]. Shanghai: Tongji University, 2013 |
| [9] |
秦鹏. 典型桥梁断面自激力非线性特性的数值模拟研究[D]. 上海: 同济大学, 2018 QIN Peng. Numerical study of nonlinear self-excited force characteristics for typical bridge decks[D]. Shanghai: Tongji University, 2018 |
| [10] |
魏昕. 基于元模型的全局优化算法研究[D]. 武汉: 华中科技大学, 2012 WEI Xin. Research of global optimization algorithm base on metamodel[D]. Wuhan: Huazhong University of Science & Technology, 2012 |
| [11] |
LIN Yao. An efficient robust concept exploration method and sequential exploratory experimental design[D]. Atlanta: Georgia Institute of Technology, 2004
|
| [12] |
李永乐, 汪斌, 黄林, 等. 平板气动力的CFD模拟及参数研究[J]. 工程力学, 2009, 26(3): 207. LI Yongle, WANG Bin, HUANG Lin, et al. CFD simulation and parameter study on aerodynamic force of flat plate[J]. Engineering Mechanics, 2009, 26(3): 207. |
| [13] |
曹映泓, 项海帆, 周颖. 大跨度桥梁非线性颤振和抖振时程分析[J]. 广东公路交通, 2000, 66(增刊): 41. CAO Yinghong, XIANG Haifan, ZHOU Ying. Time-domain analysis on nonlinear fluttering and buffeting of long-span cable-stayed bridge[J]. Guangdong Highway Communications, 2000, 66(S): 41. DOI:10.15951/j.tmgcxb.2000.05.010 |
| [14] |
LI Q C, LIN Y K. New stochastic theory for bridge stability in turbulent flow. Ⅱ[J]. Journal of Engineering Mechanics, 1995, 121(1): 1. DOI:10.1061/(ASCE)0733-9399(1995)121:1(102) |
| [15] |
陈政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005: 82. CHEN Zhengqing. Wind engineering of bridge[M]. Beijing: China Communications Press, 2005: 82. |
| [16] |
何柳, 单鹏. 基于环量分布的轴流双级风扇三维数值优化[J]. 航空动力学报, 2010, 25(12): 2660. HE Liu, SHAN Peng. Three-dimensional aerodynamic optimization for the two-stage axial-flow fan based on work distribution[J]. Journal of Aerospace Power, 2010, 25(12): 2660. DOI:10.13224/j.cnki.jasp.2010.12.008 |
| [17] |
BERNARDINI E, SPENCE S M J, WEI D, et al. Aerodynamic shape optimization of civil structures: A CFD-enabled Kriging-based approach[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2015, 144: 154. DOI:10.1016/j.jweia.2015.03.011 |
| [18] |
姚拴宝, 郭迪龙, 孙振旭, 等. 基于Kriging代理模型的高速列车头型多目标优化设计[J]. 中国科学: 技术科学, 2013, 43(2): 186. YAO Shuanbao, GUO Dilong, SUN Zhenxu, et al. Multi-objective optimization of the streamlined head of high-speed trains based on the Kriging model[J]. Scientia Sinica Technologica, 2013, 43(2): 186. DOI:10.1360/ze2013-43-2-186 |
| [19] |
张天骄, 李济生, 李晶, 等. 基于混合蚁群优化的天地一体化调度方法[J]. 系统工程与电子技术, 2016, 38(7): 1555. ZHANG Tianjiao, LI Jisheng, LI Jing, et al. Space ground integrated scheduling based on the hybrid ant colony optimization[J]. Systems Engineering and Electronics, 2016, 38(7): 1555. DOI:10.3969/j.issn.1001-506X.2016.07.12 |
| [20] |
辛益军. 方差分析与实验设计[M]. 北京: 中国财政经济出版社, 2002: 17. XIN Yijun. Analysis of variance and experimental design[M]. Beijing: Chinese Financial & Economic Publishing House, 2002: 17. |
 2021, Vol. 53
2021, Vol. 53


