2. 地震工程与工程振动重点实验室(中国地震局工程力学研究所),哈尔滨 150080
2. Key Lab of Earthquake Engineering and Engineering Vibration (Institute of Engineering Mechanics, China Earthquake Administration), Harbin 150080, China
近年来相关工程设计人员对强震记录的选取工作越来越重视,目前国内学者提出的记录选取方案[1-6],由于地震动记录信息的缺失,多为某一水平向的记录选取,从而对结构进行单方向的非线性时程分析。随着中国强震动记录的积累,结构进行双向非线性时程分析的需求越来越高,而对另一水平向的记录选取,只需按照中国GB 50011—2010《建筑抗震设计规范》[7]要求进行1∶0.85的比例放缩[8],但该方法并不满足地震动的物理意义,同时选取记录的可行性也有待商榷。
国外学者为解决工程中的相关问题,将观测到的两水平方向地震动转换为一个地震动参数指标,如ASCE/SEI 7-16[9]中两水平方向的地震动转换为最大方向谱,TEC 2007[10]中为几何平均谱,NEHRP[11]中为均方根谱。其中,最大方向谱的假设条件是结构的强度和刚度在各个方向完全相同,且最大方向的方位角与结构的主要方向重合[12],而均方根谱和几何平均谱更偏向数学意义上两个方向的合成与平均,并没有实际的物理意义。一般来说,地震动记录选取时所用的地震动参数与统计目标谱的地震动参数指标相同,然而利用中国抗震设计规范进行地震动记录选取时,并没有严格规定参数的选择,仅仅对选取记录与目标谱间的相对误差做出相关规定。
为研究以上三种不同地震动参数指标对地震动记录选取结果的影响,本文以GB 50011—2010《建筑抗震设计规范》中的规范设计谱为目标谱,以满足规范中选波规定为基础,采用全周期谱匹配法进行地震动记录的选取,并分别输入到4层和12层框架结构中,对比分析选取记录的结构响应以及地震动特性的差异,同时对地震动参数进行敏感性分析。
1 双向地震动记录选取流程本文随机选用了两种工况:罕遇地震设防烈度7度(0.15 g)、场地类别Ⅱ类、设计地震分组第二组(工况1),和罕遇地震设防烈度8度(0.20 g)、场地类别Ⅰ1类、设计地震分组第三组(工况2),进行地震动记录的选取与对比分析。
1.1 记录初选与调幅在记录选取前首先进行记录初选,现有研究已对记录的初选有较为全面的认识,并依据震级、距离、场地条件等指标确定了初选条件[13-14]。为保证初选记录库数量的充足,本文将初选震级Mw定为5.5~8级,场地条件仅由VS30的范围确定,从美国太平洋地震研究中心(PEER)的NGA-West1数据库中初选了330条记录。
为保证工程应用中的实用性,采用保持反应谱谱形不变的线性放缩,调幅目标谱为规范设计谱,调幅系数由满足规范目标峰值加速度APG的条件下确定。在调幅时应先分别计算每条地震动在不同地震动参数指标下的反应谱值,然后依据APG条件再进行放缩。美国抗震规范中的放缩系数上限值为2~4[15-16],而在中国工程应用中,放缩系数的上限值一般不大于5,且允许上限值为10。本文为保证选出的地震动记录与目标谱谱形的一致性,将放缩系数的上限定为10。值得注意的是,在谱匹配时记录的两个水平方向应采用相同的调幅系数,以保证地震动的本来特性。
1.2 反应谱匹配GB 50011—2010《建筑抗震设计规范》规定,在记录选取时“多组时程波的平均地震影响系数曲线与振型分解反应谱法所用的地震影响系数曲线相比,在对应于结构主要振型的周期点上相差不大于20%”。为满足上述规定,本文采用全周期匹配方法[17],匹配周期区间为0.01~6.0 s,每条记录反应谱与目标谱之间误差平方和的计算公式为
| $ \delta=\sum\limits_{i=1}^{N}\left|w\left(T_{i}\right)\left(\ln S_{\mathrm{a}}\left(T_{i}\right)-\ln S_{\mathrm{a}}^{1}\left(T_{i}\right)\right)^{2}\right| $ | (1) |
式中:δ为记录反应谱与目标谱的误差和,也是其与目标谱匹配度的唯一衡量标准,w(Ti)为周期点i处的权重系数,本文为保证记录选取工作的便捷性,w(Ti)均取为1,N为匹配区间内选取的匹配点数量,Sa(Ti)为记录在周期Ti处的加速度反应谱值,Sa1(Ti)为周期Ti处的目标谱值。将不同地震动参数指标下放缩后的反应谱与目标谱匹配,选出与目标谱匹配度最好的地震动。相较于其他匹配方法,全周期匹配法的同种工况可采用同一组记录选取结果,大大较小了工作量。为排除记录选取数量对选取结果的影响,每个工况中每个地震动参数下均依据误差平方和排序,分别选取δ最小的前20条地震动记录。记录选取的过程如图 1所示。两种工况在三种不同地震动参数指标下的选取结果见图 2,由图 2可知选取结果满足GB 50011—2010《建筑抗震设计规范》的选取要求。

|
图 1 地震动记录选取流程 Fig. 1 Selection procedure of ground motion records |

|
图 2 不同参数指标选取的地震动反应谱值 Fig. 2 Response spectrum values of ground motions selected by different parameter indexes |
本文进行时程分析的结构为徐朝阳等[8]中采用的结构,分别为4层(模型1)和12层(模型2)的两个三维混凝土框架模型,依据中国规范的设防烈度设计配筋。表 1给出了两个结构模型的相关结构参数,两个框架结构的一阶自振周期分别为0.61 s和1.96 s。
| 表 1 抗震模型参数 Tab. 1 Parameters of seismic models |
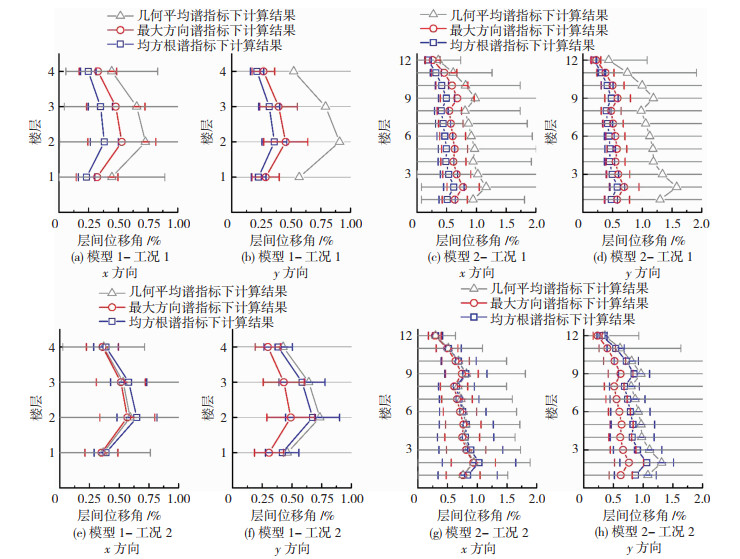
为比较三种不同参数指标选出的地震动对结构的影响,将第1节中两种工况下选出的地震动分别双向输入到两个结构模型中,输入方向与结构的正交方向一致,即本文的x方向和y方向,进行弹塑性时程分析,计算并对比结构的层间位移角和层间剪力,见图 3、4。
|
图 3 三种参数指标层间位移角的计算结果对比 Fig. 3 Comparison of story displacement angle of three kinds of parameter indexes |

|
图 4 三种参数指标层间剪力的计算结果对比 Fig. 4 Comparison of story shear force of three kinds of parameter indexes |
由对比结果可知,在模型1-工况2的x方向,均方根谱计算得到的层间位移角和层间剪力的平均值最大,几何平均谱的计算结果的平均值次之,最大方向谱的计算结果的平均值最小;在模型2-工况2的x方向,三种谱的计算结果的平均值无明显的排序;模型1-工况2和模型2-工况2的y方向,几何平均谱的计算结果平均值最大,均方根谱的计算结果平均值次之,最大方向谱的计算结果平均值最小;其余情况,几何平均谱的计算结果平均值最大,最大方向谱的计算结果平均值次之,均方根谱的计算结果平均值最小。虽然对于同一条地震动,最大方向谱相比于其他两种参数谱大,但由于采用APG线性调幅,导致另外两种参数谱的放缩系数比最大方向谱的大,尤其是几何平均谱,因此几何平均谱的计算结果比另外两参数大很多;由于双向地震动记录的选取本质是将水平双向地震动反应谱转化为单一反应谱,因此必然存在两个方向的反应谱差异性较大的情况,但三种地震动参数中最大方向谱的差异性相对较小,从而使得其在x、y两方向的计算结果大致相同。两工况中,几何平均谱的计算结果标准差最大,均方根谱的计算结果标准差次之,最大方向谱的计算结果标准差最小。其根本原因是双向地震动记录选取工作中的地震动参数选取不同所导致,并使得最大方向谱的离散性最小,几何平均谱的离散性最大。
3 地震动特性对比由于每条地震动在不同参数指标下的反应谱值不同,因此每种参数指标下选出的地震动不完全相同,即使是同一条地震动,放缩系数也完全不同。为更好的研究三种地震动参数指标对地震动记录选取结果的影响,本节以记录的放缩系数与地震动三要素特性为出发点,进行对比分析。
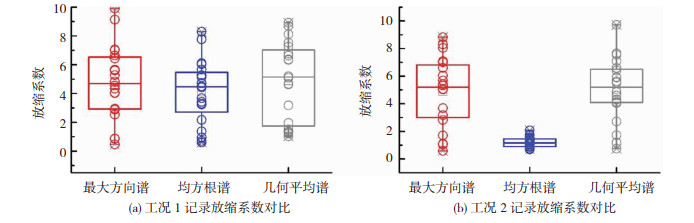
3.1 放缩系数对比虽然地震动特性不包含放缩系数,但是放缩系数仍是衡量记录选取工作的一个指标,在地震动记录反应谱与目标谱匹配度相差不大时,放缩系数接近1的地震动优先选取,也体现了对地震动本来特性的保证。现有研究[15]表明,一般记录选取时放缩系数的上限为4,但具体的上限依据实际工程需求确定[16],特殊情况时规定放缩系数小于2.5[18]。而中国在进行地震动的放缩时,调幅上限一般定为5[2],可视情况将上限提升至10。由于本文选取的记录数量较多,为保证与目标谱较高的匹配度,将调幅系数上限定为10。通过三种地震动参数选取的地震动放缩系数见图 5。
|
图 5 三种参数指标放缩系数对比 Fig. 5 Comparison of scaling coefficient of three kinds of parameter indexes |
由图 5可知,最大方向谱地震动参数选出的地震动放缩系数的均值和方差在两种工况下几乎相同,均方根谱放缩系数工况1的均值和方差明显大于工况2,几何平均谱放缩系数工况1的均值略大于工况2,工况1的标准差明显大于工况2。由此可见,通过最大方向谱参数选出的地震动的放缩系数更加稳定。
3.2 幅值特性对比对于部分记录,虽然加速度峰值比较大,但作用时间短、动量小,若削去个别突出的峰值,结构响应可能几乎不受影响,可能出现地震动峰值大而震害不严重的现象,另外由于本文选取的地震动记录是依据规范目标峰值加速度APG进行放缩的,因此对于记录峰值的对比是没有意义的。为更合理地运用加速度峰值表示地震动强度,本文采用有效峰值进行幅值特性的对比分析。其中有效值的概念考虑的是地震动总强度,而不是单个最大值的影响。有效峰值加速度和有效峰值速度的定义分别为:
| $ \begin{aligned} S_{\mathrm{EPA}}=S_{\mathrm{a}} / 2.5 \end{aligned} $ | (2) |
| $S_{\mathrm{EPV}}=S_{\mathrm{v}} / 2.5 $ | (3) |
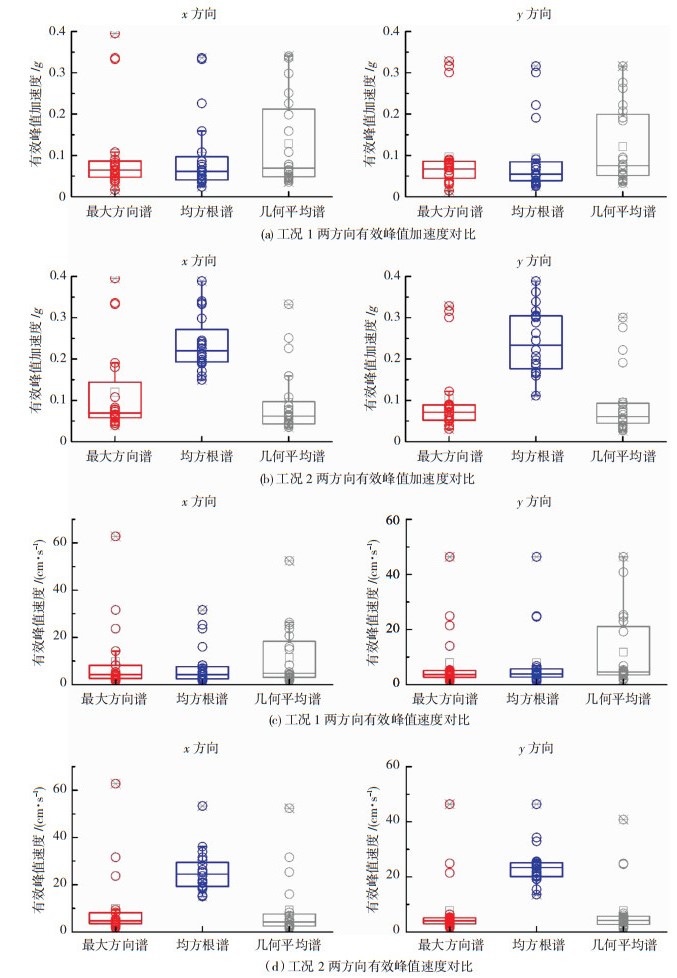
式中:Sa为阻尼比为5%的加速度反应谱在周期0.1~0.5 s之间平均值,Sv为阻尼比为5%的速度反应谱在1 s周期附近的平均值,常数2.5是一个经验系数,其物理意义是结构最大反应值对地震动峰值的放大倍数的平均值[19]。计算得到三种参数指标在两种工况下两个方向的有效峰值加速度和有效峰值速度见图 6。
|
图 6 两种工况下三种参数指标有效加速度和有效速度对比 Fig. 6 Comparison of EPA and EPV of three kinds of parameter indexes under two working conditions |
由对比结果可知,两种工况下,三种参数指标在两个方向上有效峰值加速度和有效峰值速度均值和方差几乎相同,但相比来说,最大方向谱在两方向的差异较小。在同一工况同一方向上,工况1中三种参数指标的有效峰值加速度和有效峰值速度均值几乎相同,工况2中均方根谱的均值最大,其余两种参数指标相差无几;除工况2中有效峰值速度两方向中均方根谱的标准差最大,几何平均谱次之,其余情况几何平均谱最大,均方根谱次之,但最大方向谱始终最小。说明通过最大方向谱选取的地震动在幅值特性上差异性较小。
3.3 频谱特性对比描述地震动频谱特性的主要频谱是傅里叶谱、反应谱和功率谱。傅里叶谱将地震动分解为随时间变化的具有物理意义的简谐运动。反应谱表征了地震动加速度过程作用于单自由度弹性体系的最大反应随体系的自振特性变化的函数关系。功率谱从随机振动的观点考察地震动,用功率谱密度函数描述随机振动中所包含的各频率分量强度与相应频率间的关系,一般功率谱与相关函数相联系。目前有关地震动记录的选取,大多依据地震动记录的反应谱与目标谱进行匹配,本文也不例外,因此本节主要对比各个地震动参数下的反应谱特性,见图 7。

|
图 7 三种地震动参数选出记录反应谱与目标谱比值 Fig. 7 Ratio of selected response spectrum to target spectrum under three kinds of parameter indexes |
经对比可知,三种地震动参数选出的记录反应谱平均值在整体上基本满足GB 50011—2010《建筑抗震设计规范》对记录选取的规定。在两种工况下的中短周期段处,最大方向谱的平均值大于目标谱,而均方根谱和几何平均谱的平均值小于目标谱;中长周期段处,最大方向谱的平均值基本与目标谱持平,而均方根谱和几何平均谱明显大于目标谱,甚至超过1.2倍目标谱。因此在中短周期段,通过最大方向谱地震动参数选取的记录相对保守,另外两种参数选取的记录不保守,存在安全隐患;而在中长周期段,通过另外两种参数选取的记录又过于保守。对于一般受低阶振型影响较大的结构,其一阶振型周期大多处于中短周期段,因此考虑频谱特性时,通过最大方向谱选取地震动记录相对合理。
3.4 持时特性对比结构屈服进入塑性状态时,持时直接影响结构的累积塑性耗能,对结构破坏和倒塌起很大作用。持时依据不同的强度定义和划分标准,可分为30余种类别,如括弧持时、一致持时、能量持时、反应持时等。由于结构地震反应和破坏程度与输入结构的地震动能量相关,用能量作为参数确定持时才有物理意义,因此本节对能量持时进行分析。能量持时的计算公式为
| $ E_{\mathrm{n}}(t)=\int_{0}^{t} a^{2}(t) \mathrm{d} t / \int_{0}^{T_{0}} a^{2}(t) \mathrm{d} t $ | (4) |
式中:a(t)为加速度时程,T0为总持续时间。En(t)的物理意义为单位质量的单自由度体系在地震动a(t)作用下,t时刻的能量与总能量之比。本文选取的能量比值下限和上限分别为5%和95%[19]。计算得到每种参数指标在两种工况下选出地震动的能量持时见图 8。

|
图 8 三种地震动参数选出记录能量持时对比 Fig. 8 Comparison of energy duration of three kinds of parameter indexes |
由图 8可知,两种工况下,通过最大方向谱参数选取的地震动能量持时均值最小,且在两个方向上差距不大,且选出的地震动之间能量持时的差异性较小;工况1中两个方向上几何平均谱能量持时均值最大,工况2中均方根谱能量持时均值最大;两种工况下几何平均谱选出的记录能量持时差异性最大,均方根谱差异性次之。因此通过最大方向谱参数指标选出的地震动记录在考虑能量持时时离散性较小。
4 地震动参数敏感性分析目前工程应用中最常用谱匹配方法进行地震动记录的选取,本文采用的全周期匹配法是谱匹配方法中较为常用的一种。除此之外,一些专家和工程人员在进行记录选取时也会考虑其他因素,例如,Özdemir等[20]在选取记录时为全面考虑工程需求,以峰值速度分组作为选取的参考指标之一,针对每个分组选取适量记录进行时程分析;Lancieri等[21]在Seifried等[22]的基础上,分别从地震学和工程学两个角度阐释了在时域选取地震动记录的可行性与可靠性,将匹配的重心从反应谱转移至加速度时程谱,此方法虽然相对繁琐,但是消除了反应谱匹配原理及振幅对结构响应的影响;冀昆[14]认为地震动的幅值特性和持时特性虽然会对地震动的输入产生影响,但是受限于地震动本身的不确定性和离散性,其无法作为工程人员选取记录的首选条件,只可作为谱形匹配思路的补充。本节以上述选取的参数指标为参考,旨在反应谱匹配的基础上考虑幅值和持时特性与频谱特性的相关性。
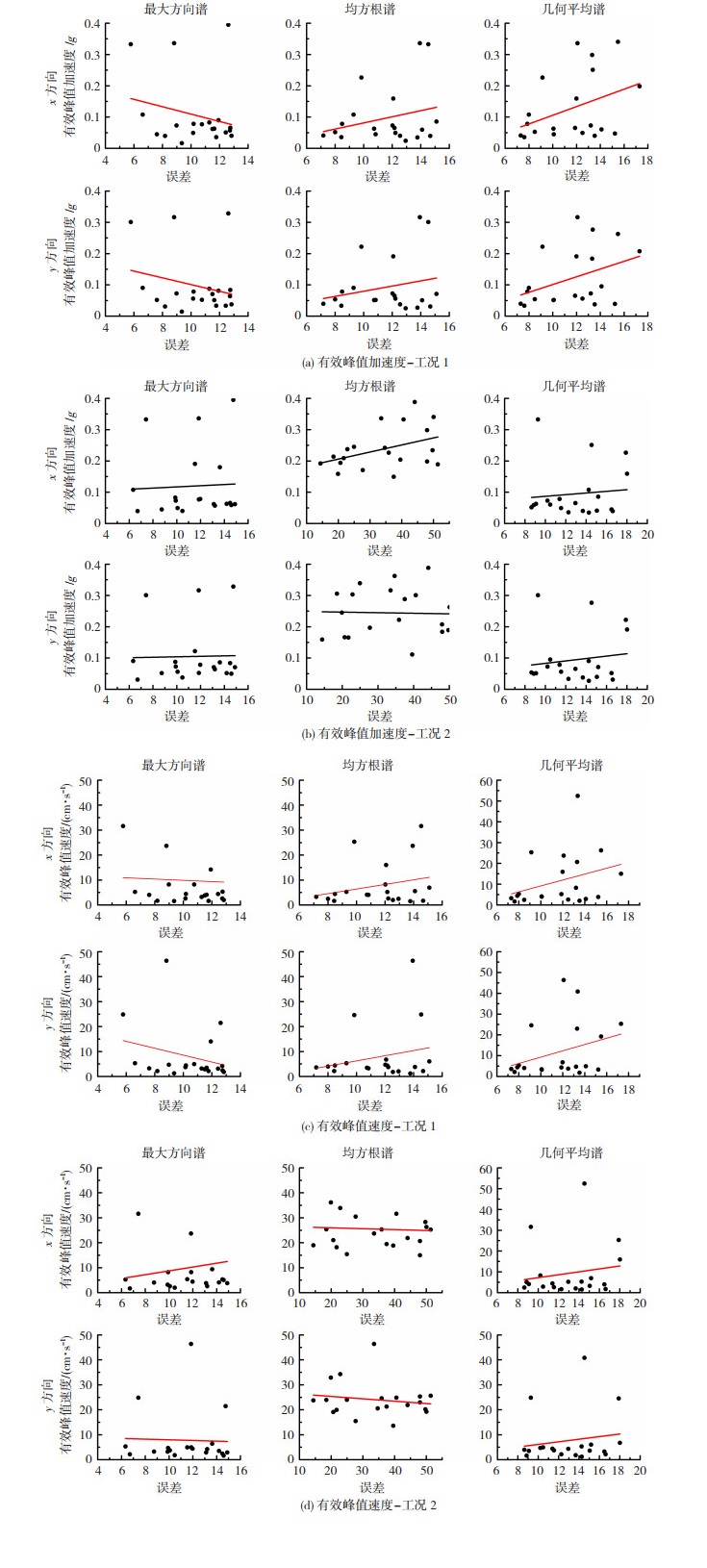
本小节比较了两种工况下,通过三种地震动参数指标选取记录的有效峰值加速度和有效峰值速度,其与每条记录与目标谱的误差之间的分布见图 9。
|
图 9 有效峰值加速度和有效峰值速度与误差的相关性 Fig. 9 Correlation between error, EPA, and EPV |
由图 9可知,随着记录反应谱与目标谱误差的增加,通过最大方向谱参数选出的记录两个方向的有效峰值加速度和有效峰值速度某工况下可能是正相关,也可能是负相关,但其相关性并不强,在整体上成持平状态;而通过另外两个参数选出的记录在两个方向的有效峰值加速度和有效峰值速度无明显的相关性,数据的离散性偏大。因此作为谱匹配记录选取工作的补充,建议用最大方向谱地震动参数进行谱匹配后,可适当考虑选出记录的有效峰值加速度和有效峰值速度,为保证选出记录在幅值特性上离散性较小,同时依据本节的敏感性分析,可将有效峰值加速度和有效峰值速度的上限分别定为0.2 g和20 cm/s,超过上限的记录可视情况剔除。
5 结论按照GB 50011—2010《建筑抗震设计规范》进行全周期地震动记录选取,以4层结构和12层结构为算例,选取记录的地震动特性为基础,对比了最大方向谱、均方根谱、几何平均谱三种地震动参数选取结果的表现,得到如下结论:
1) 相较于参数均方根谱和几何平均谱,最大方向谱选取结果的结构响应、放缩系数和地震动特性离散度更小,虽然同一条地震动可能两个方向差异性较大,但总体上通过最大方向谱参数选出的各条地震动差异性较小。
2) 参数最大方向谱可以更好地体现记录不同合成方向的最大谱响应,具有更符合实际的物理意义,但在谱匹配时可能获得偏保守的选取结果,尤其在中短周期,而参数均方根谱和几何平均谱的选取结果在中长周期偏保守,在中短周期不保守。
3) 谱匹配除考虑频谱特性外,还可适当考虑有效幅值,尤其采用参数最大方向谱选波时,在给定有效峰值加速度和有效峰值速度的上限内,可保证选取的地震动记录离散度更小,工程中的针对性更强。
在实际工程应用中,建议根据不同的结构采用不同的地震动参数进行记录选取,在保证目标谱相对误差范围内,尽量保证更好的经济性和实用性。
| [1] |
温瑞智, 冀昆, 任叶飞. 结构时程分析中多层次强震动记录输入选取研究综述[J]. 地震工程与工程振动, 2019, 39(5): 1. WEN Ruizhi, JI Kun, REN Yefei. Review on selection of strong ground motion input for structure time-history dynamic analysis[J]. Earthquake Engineering and Engineering Dynamics, 2019, 39(5): 1. DOI:10.13197/j.eeev.2019.05.1.wenrz.001 |
| [2] |
冀昆, 温瑞智, 任叶飞. 适用于我国抗震设计规范的天然强震记录选取[J]. 建筑结构学报, 2017, 38(12): 57. JI Kun, WEN Ruizhi, REN Yefei. Ground motion recordings selection for seismic design code[J]. Journal of Building Structures, 2017, 38(12): 57. DOI:10.14006/j.jzjgxb.2017.12.007 |
| [3] |
杨浦, 李英民, 赖明. 结构时程分析法输入地震波的选择控制指[J]. 土木工程学报, 2000, 33(6): 33. YANG Pu, LI Yingmin, LAI Ming. A new method for selecting input waves for time-history analysis[J]. China Civil Engineering Journal, 2000, 33(6): 33. DOI:10.15951/j.tmgcxb.2000.06.005 |
| [4] |
陈波, 温增平. 考虑目标谱不确定性及谱形的实际地震动记录优化选取和调整方法[J]. 建筑结构学报, 2015, 36(11): 99. CHEN Bo, WEN Zengping. Optimized real ground motion selection and scaling method considering uncertainty and spectral shape of target spectrum[J]. Journal of Building Structures, 2015, 36(11): 99. DOI:10.14006/j.jzjgxb.2015.11.013 |
| [5] |
李爽, 周洪圆, 刘向阳, 等. 基于中国规范的近断层区抗震设计谱研究[J]. 建筑结构学报, 2020, 41(2): 7. LI Shuang, ZHOU Hongyuan, LIU Xiangyang, et al. Study on near-fault seismic design spectra based on Chinese code for seismic design of buildings[J]. Journal of Building Structures, 2020, 41(2): 7. DOI:10.14006/j.jzjgxb.2018.0664 |
| [6] |
吕大刚, 刘亭亭, 李思雨, 等. 目标谱与调幅方法对地震动选择的影响分析[J]. 地震工程与工程振动, 2018, 38(4): 21. LÜ Dagang, LIU Tingting, LI Siyu, et al. Investigation of effects of target spectrum and amplitude scaling methods on selection of ground motion[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(4): 21. DOI:10.13197/j.eeev.2018.04.21.lvdg.004 |
| [7] |
建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Architecture and Buildings Press, 2010 |
| [8] |
徐朝阳, 温瑞智, 任叶飞, 等. 中美抗震规范地震记录选取比较[J]. 哈尔滨工业大学学报, 2020, 52(10): 61. XU Zhaoyang, WEN Ruizhi, REN Yefei, et al. Comparison of ground motion selection in seismic design codes between China and United States[J]. Journal of Harbin Institute of Technology, 2020, 52(10): 61. DOI:10.11918/202001083 |
| [9] |
Minimum design loads and associated criteria for buildings and other structures: ASCE 7-16[S]. Reston: American Society of Civil Engineers, 2016
|
| [10] |
Turkish earthquake code (TEC)[S]. Ankara: Afet ve Acil Durum Ba, skanlǐgı (in Turkish), 2007
|
| [11] |
NEHRP recommended seismic provisions for new buildings and other structures: FEMA P-750/2009 Edition[S]. Washington DC: Building Seismic Safety Council, 2009
|
| [12] |
REYES J C, KALKAN E. Significance of rotating ground motions on behavior of symmetric- and asymmetric-plan structures: Part I. Single-story structures[J]. Earthquake Spectra, 2015, 31(3): 1591. DOI:10.1193/072012EQS241M |
| [13] |
冀昆, 温瑞智, 任叶飞. 中国抗震规范强震记录选取的初选条件研究[J]. 防灾减灾工程学报, 2016, 36(1): 44. JI Kun, WEN Ruizhi, REN Yefei. Study on the initial of selection criteria strong motion records for Chinese seismic code[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(1): 44. DOI:10.13409/j.cnki.jdpme.2016.01.005 |
| [14] |
冀昆. 我国不同抗震设防需求下的强震动记录选取研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2018 JI Kun. Strong ground motion selection for multiple levels of seismic fortification demand in China[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2018 |
| [15] |
KWONG N S, CHOPRA A K. Determining bidirectional ground motions for nonlinear response history analysis of buildings at far-field sites[J]. Earthquake Spectra, 2018, 34(4): 1931. DOI:10.1193/052217EQS093M |
| [16] |
ZIMMERMAN R B, BAKER J W, HOOPER J D, et al. Response history analysis for the design of new buildings in the NEHRP provisions and ASCE/SEI 7 standard: Part Ⅲ-Example applications illustrating the recommended methodology[J]. Earthquake Spectra, 2017, 33: 419. DOI:10.1193/061814EQS087M |
| [17] |
CAVDAR E, OZDEMIR G, BAYHAN B. Significance of ground motion scaling parameters on amplitude of scale factors and seismic response of short- and long-period structures[J]. Earthquake Spectra, 2019, 35(4): 1663. DOI:10.1193/08178EQS204M |
| [18] |
URIBE R, SATTAR S, SPEICHER M S, et al. Effect of common U.S. ground motion selection methods on the structural response of steel moment frame buildings[J]. Earthquake Spectra, 2019, 35(4): 1611. DOI:10.1193/122917EQS268M |
| [19] |
袁一凡, 田启文. 工程地震学[M]. 北京: 地震出版社, 2012: 60. YUAN Yifan, TIAN Qiwen. Engineering seismology[M]. Beijing: Seismological Press, 2012: 60. |
| [20] |
ÖZDEMIR G, GVLKAN H P. Scaling legitimacy for design of lead rubber bearing isolated structures using a bounding analysis[J]. Earthquake Spectra, 2016, 32(1): 345. DOI:10.1193/123113EQS300M |
| [21] |
LANCIERI M, BAZZURRO P, SCOTTI O. Spectral matching in time domain: a seismological and engineering analysis[J]. Bulletin of Seismological Society America, 2018, 108(4): 1972. DOI:10.1785/0120170396 |
| [22] |
SEIFRIED A E, BAKER J W. Spectral variability and its relationship to structural response estimated from scaled and spectrum matched ground motions[J]. Earthquake Spectra, 2016, 32(4): 2191. DOI:10.1193/061515EQS094M |
 2021, Vol. 53
2021, Vol. 53


