2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
采用烧结黏土砖和砂浆砌筑而成的砖墙与混凝土楼/屋盖组成的混合结构,中国量大面广。当前大量砖砌体结构建筑因城镇更新、抗震设防和使用功能的提升,虽未达到设计使用年限,但已需要加固、改造或拆除。实际上拟拆除砖砌体结构房屋,并不完全因为结构损坏等安全问题,砌体墙片相对完整,承载能力较强。为此,对这些砖砌体墙片工业化拆除后再拼装,实现拆除墙片的再利用,具有重要意义。
国内针对具有历史价值和文物价值的砌体结构的迁移、改造和加固过程中,多涉及砖砌体墙片整体拆除后的拼装再利用。山东淄川中医院仿古门楼因道路拓宽采用动力牵引法进行了整体搬移[1];上海四明公所门楼因中国人寿大厦的筹建被整体平移;哈尔滨中央大街西九道街的“百年老墙”因旧城改造进行了移位和复位[2]。在保护建筑的加固改造过程中对墙体整体拆除和移位的技术,为砖砌体结构房屋的工业化拆除与砖墙片再利用提供了借鉴。
Quagliarini等[3]对拆下的砖块、砖碎片和砂浆的化学、物理和力学性能进行了分析,并对使用砖块和砖碎片制成的罗马式砖墙片进行了抗压强度试验,结果表明施工工艺对墙体的抗压强度和破坏模式有着较大的影响。Zhou等[4]采用锯切和冲孔两种方法实现了砖块与水泥砂浆的分离,并对拆除砖块和用拆除砖块制作的墙片进行了力学性能评价,结果表明拆除过程对砖块性能影响较小,用拆除砖块和新砖块制作的墙片的抗压强度相近。Ucer等[5]对拆除现场获得的砖块、砂浆块和砖墙片进行了基本力学性能试验,并对比分析了由砖块和砂浆强度推导出的砌体强度与砖墙实际强度,结果表明拆除获得的砖块和砖墙片均能达到标准规定的强度限值,而且墙片的破坏模式与常规砖墙相同。这些研究说明,在条件允许时采用合理的设计方法,被拆除的墙片可应用于工程建造。
总结国内外相关研究现状[6-12],对于砌体结构的研究较多集中在新型墙体和新的抗震措施等方面,对用拆除墙段建造的砖砌体结构抗震性能的研究有限。针对用拆除墙段建造的砖砌体结构抗震性能研究的不足,本文采用增量动力分析方法(简称IDA)对7个砖砌体结构模型进行了地震易损性分析,考察构造柱间距、结构层数和砌体强度对用拆除墙段建造的砖砌体结构抗震性能的影响,为用拆除墙段建造的砖砌体结构的抗震能力评估提供科学依据。
1 用拆除墙段建造的砖砌体结构在拆除砖砌体墙片前,首先要进行拟拆除砖墙所支承楼/屋盖的拆除。砖砌体墙片包括无洞口墙片和有洞口墙片;有洞口的墙片分为有窗洞口的墙片和有门洞口的墙片。为实现砌体结构建筑工业化拆除及再利用,引入装配式砌体建筑的相关设计方案,拆除墙段的尺寸和形状应符合装配式一体化设计的要求,且拆除墙段宜满足无支撑状态下的抗倾覆要求和吊装额定起重重量的要求。综合考虑相关资料,为避免墙段在运输及吊装过程中发生损坏,建议墙段长度不超过4.8 m,高度不超过3.6 m。
无洞口的墙片的裁分需根据裁分尺寸,确定拟拆除墙片的裁分方案。采用取芯机以孔孔相切的原则在拟拆除墙段两边成孔,安装夹持框并将夹持框与吊具的吊钩相连,最后在墙段下方成孔后吊离墙段,具体拆除示意见图 1。这里需要指出,在对墙片裁分之前需设置好可靠支撑。

|
图 1 无洞口墙片的拆除示意 Fig. 1 Removal of wall pieces without openings |
有窗洞口的墙片分为窗间墙与窗带墙。窗间墙和窗带墙的裁分需在窗间墙两侧由楼盖到窗台的高度范围之内和由窗顶至楼盖的高度范围之内采用取芯机以孔孔相切的原则成孔分割。这里需要注意,裁分由窗顶至楼盖的高度范围之内的窗带墙时,要设有必要的支顶来保证拆除过程中的安全。
有门洞口的墙片分为门上墙与门洞两侧墙。门洞两侧墙的裁分与无洞口的墙片的裁分方法相同。门上墙的裁分与窗顶至楼盖部分墙体的裁分方法相同。
拆除墙段间的连接包括水平连接和竖向连接。拆除墙段间通过砂浆层实现竖向连接。拆除墙段间通过“端面孔口+水平植筋+构造柱”实现水平连接,具体包括相邻墙段间的“一”形连接、“L”形连接和“T”形连接,以及窗间墙与窗带墙的连接和门上墙与两侧墙的连接,连接示意见图 2。

|
图 2 拆除墙段间的几种连接方式 Fig. 2 Several connection modes for removed walls |
需要指出,在用拆除墙段建造新的砌体结构房屋之前,应检测拟拆除房屋的砖墙、砖墙所用砖块和砌筑砂浆的力学性能;拆除墙段间通过“端面孔口+水平植筋+构造柱”实现水平连接,这种措施将导致用拆除墙段建造的砖砌体结构的构造柱间距较小,合理考虑构造措施对结构整体抗震性能的影响也是值得关注的问题。
2 分析模型本文主要考察构造柱间距、结构层数和砌体强度对用拆除墙段建造的砖砌体结构抗震性能的影响,所建立模型的平面布置相同,仅改变以上三种设计参数的取值,结构平面布置见图 3。

|
图 3 结构平面布置(mm) Fig. 3 Structure layout(mm) |
用拆除墙段建造的砖砌体结构模型轴线长36.0 m,宽14.4 m,各层层高均为3.0 m,墙厚240 mm。屋面和楼板厚度为120 mm,混凝土强度等级为C30。构造柱尺寸为240 mm×240 mm,混凝土强度等级为C20。拆除墙段所用砖强度等级为MU10,砂浆强度可由测得的砖砌体抗压强度平均值和砖强度计算得出。7个模型结构均满足现行《砌体结构设计规范》[13]的要求,模型的其他信息见表 1。
| 表 1 模型的基本信息 Tab. 1 Basic information of models |
增量动力分析可反映在不同地震动作用下结构的强度、刚度和变形能力的变化过程。本文基于Wilson-θ法进行弹塑性动力反应分析,采用串联多自由度的等效剪切模型对砌体结构进行模型建立,等效剪切模型见图 4。相比于微观模型,这种等效剪切模型既可满足易损性计算的要求,又减少了计算量,提高了计算效率。动力分析选用考虑刚度退化的三线性恢复力模型[14-15],恢复力模型见图 5。该模型可以较精确地描述带构造柱砖墙片的滞回关系,许多学者基于该模型对砌体结构进行了地震易损性分析并验证了可靠性[16-19]。
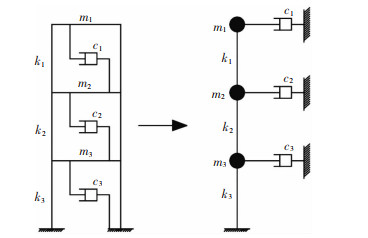
|
图 4 等效剪切模型 Fig. 4 Diagram of equivalent shear model |
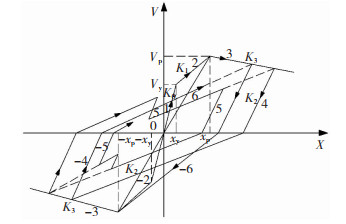
|
图 5 恢复力模型 Fig. 5 Resilience model |
为保证IDA分析计算的准确性,需确定一个合理有效的地震动强度指标和一个结构损伤指标[20]。
3.2 地震动的选择为减少地震动的不确定性对结构地震易损性分析的影响,参考美国ATC-63报告中建议的选波原则[21],在美国太平洋地震研究中心的强震动记录数据库中选取了20条地震动记录。选取的地震动记录见表 2。考虑到等效剪切模型计算速度较快和等步长法操作计算方式简单且易于在程序中实现的特点,本文采用等步长法,每个模型进行IDA分析时的调幅步长为0.025g。
| 表 2 选取的地震动记录 Tab. 2 Selected ground motion records |
根据相关研究,地震峰值加速度Apg指标在短周期建筑结构相关性较高,相关性随着结构周期的增大逐渐降低[22]。砌体结构周期一般不高于0.4 s,属于短周期结构,因此选取Apg作为地震动强度指标。
3.3 结构性能状态划分结构损伤指标的适用性和准确性直接影响着易损性曲线的形状及其条件超越概率。国内外学者多采用位移指标作为地震易损性的损伤指标。位移指标包括最大层间位移指标和最大层间位移角指标[23]。结构最大层间位移角θmax可以反映结构形式、材料、层高和损伤等因素的影响,因此本文选取最大层间位移角θmax作为结构损伤指标。基于中国《建筑抗震设计规范》[24]小震不坏、中震可修、大震不倒的三水准设防要求,结合李佳、熊立红对砌体墙片破坏等级的划分[25-26],在砌体房屋总高度与总宽度的最大比值不超过2.0时,本文把砌体结构的性能状态划分为4个等级,即正常使用、轻微破坏、中等破坏和严重破坏,各性能状态的层间位移角限值见表 3。
| 表 3 各性能状态的层间位移角限值 Tab. 3 Inter-story displacement angle limits for each performance status |
采用有限元软件对结构-地震动样本开展增量动力分析,可以获得在不同地震动强度下砌体结构的最大层间位移角θmax。地震动记录不同,IDA曲线会呈现出一定的离散性,为准确反映结构在不同
地震作用下的抗震能力,可根据IDA分析结果绘制易损性曲线,基于结构破坏概率来评估其抗震安全性能,从而降低这种离散性[20]。
地震易损性是指结构在不同地震动强度下,发生不同程度破坏的可能性,也就是结构达到某个预定极限状态或性能水平的概率,通常用易损性曲线或易损性矩阵来表示[27]。本文采用前面增量动力分析得到的最大层间位移角θmax和地震峰值加速度Apg来建立结构的地震易损性曲线[20]。
研究表明[28],结构最大层间位移角θmax和地震峰值加速度Apg服从式(1)。对增量动力分析得到的最大层间位移角θmax和地震峰值加速度Apg分别取对数,然后进行线性回归分析,可得到如式(2)所示的地震需求概率模型,式中a、b为回归系数。
| $ \theta_{\max }=a A_{\mathrm{pg}}^{b} $ | (1) |
| $ \ln \left(\theta_{\max }\right)=\ln (a)+b \ln \left(A_{\mathrm{pg}}\right) $ | (2) |
设结构最大层间位移角θmax和地震峰值加速度Apg均服从对数正态分布[29],结构在不同极限状态下的失效概率Pf为
| $ P_{\mathrm{f}}=\varphi\left[\frac{\ln \left(\hat{\theta_{\max }}\right)-\ln (\hat{C})}{\sqrt{\beta_{\mathrm{c}}^{2}+\beta_{\mathrm{d}}^{2}}}\right] $ | (3) |
式中:
选取地震峰值加速度Apg为横坐标,选取不同地震动强度作用下结构的最大层间位移角超越各个极限状态限值的条件概率作为纵坐标,即可进行结构地震易损性曲线的绘制[21]。
3.4.1 构造柱间距的影响为研究构造柱间距对用拆除墙段建造的砖砌体结构地震易损性的影响,以基本结构模型为基础并仅改变构造柱间距,1号、2号和3号模型的构造柱间距分别为2、3、6 m,由IDA分析得到的对应地震需求概率模型的数学表达式为:
| $ \ln \left(\theta_{\max -1}\right)=-6.014+0.927 \ln \left(A_{\mathrm{pg}}\right) $ | (4) |
| $ \ln \left(\theta_{\max -2}\right)=-6.101+0.930 \ln \left(A_{\mathrm{pg}}\right) $ | (5) |
| $ \ln \left(\theta_{\max -3}\right)=-6.153+0.932 \ln \left(A_{\mathrm{pg}}\right) $ | (6) |
计算分析所得的地震易损性曲线见图 6。

|
图 6 不同构造柱间距结构的易损性曲线 Fig. 6 Vulnerability curves of masonry structures with different column spacing |
根据图 6中的易损性曲线,作出不同构造柱间距砖砌体结构的地震破坏矩阵,具体见表 4。
| 表 4 不同构造柱间距结构的地震破坏矩阵 Tab. 4 Seismic damage matrix of masonry structures with different column spacing |
由图 6可以看出,随着Apg的增加,用拆除墙段建造的砖砌体结构模型发生破坏的超越概率逐渐增大。三个模型发生轻微破坏的易损性曲线的斜率均比较大,即结构在地震作用下,很容易就超过弹性极限状态。随着Apg的增加结构继续发生破坏,易损性曲线的斜率逐渐减小,结构开始进入屈服阶段继续抵抗地震作用。由表 4可知,当Apg为0.2g时,1号、2号和3号模型超越轻微破坏的概率分别为37.36%、29.05%和24.51%;当Apg为0.8g时,1号、2号和3号模型超越严重破坏的概率分别为9.79%、6.52%和5.02%。由此表明,随着构造柱间距的减小,砖砌体结构发生超越各个极限状态限值的概率逐渐降低,结构的抗震性能逐步提高,即合理设置构造柱可显著提高砌体结构的抗震性能。
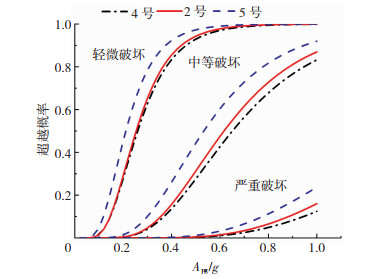
3.4.2 结构层数的影响为研究结构层数对用拆除墙段建造的砖砌体结构地震易损性的影响,以基本结构模型为基础并仅改变结构层数,4号、2号和5号模型的结构层数分别为4、5、6层,由IDA分析得到的对应地震需求概率模型的数学表达式为:
| $ \ln \left(\theta_{\max -4}\right)=-5.990+0.892 \ln \left(A_{\mathrm{pg}}\right) $ | (7) |
| $ \ln \left(\theta_{\max -2}\right)=-6.101+0.930 \ln \left(A_{\mathrm{pg}}\right) $ | (5) |
| $ \ln \left(\theta_{\max -5}\right)=-6.165+0.900 \ln \left(A_{\mathrm{pg}}\right) $ | (8) |
计算分析所得的地震易损性曲线见图 7。
|
图 7 不同层数结构的易损性曲线 Fig. 7 Vulnerability curves of masonry structures with different stories |
根据图 7中的易损性曲线,作出不同层数砌体结构的地震破坏矩阵,具体表 5。
| 表 5 不同层数结构的地震破坏矩阵 Tab. 5 Seismic damage matrix of masonry structures with different stories |
由图 7可以看出,随着Apg的增加,砖砌体结构房屋发生破坏的超越概率也逐渐增大,4号和2号模型的易损性曲线相差较小,与5号模型的易损性曲线相差较大。由表 5可知,当Apg为0.2g时,4号、2号和5号模型超越轻微破坏的概率分别为27.79%、29.05%和45.29%;当Apg为0.8g时,4号、2号和5号模型超越严重破坏的概率分别为4.89%、6.52%和11.26%。由对比可知,随着结构层数的增加,砌体结构的破坏概率逐渐增大,而且增大幅度较高。相关研究表明,相同地震烈度情况下,砖砌体结构的层数越多、总高度越大,砌体结构就越容易发生破损或倒塌。建议拆除墙段再利用时,结构总层数和总高度不宜超过GB 50011的规定,保证砌体结构的抗震性能。
3.4.3 砌体强度的影响为研究砖砌体强度对用拆除墙段建造的砖砌体结构地震易损性的影响,以基本结构模型为基础并仅改变拆除墙片的抗压强度平均值,6号、2号和7号模型墙片的抗压强度平均值分别为2.90、3.33、4.19 MPa,由IDA分析得到的对应地震需求概率模型的数学表达式为:
| $ \ln \left(\theta_{\max -6}\right)=-6.053+0.880 \ln \left(A_{\mathrm{pg}}\right) $ | (9) |
| $ \ln \left(\theta_{\max -2}\right)=-6.101+0.930 \ln \left(A_{\mathrm{pg}}\right) $ | (5) |
| $ \ln \left(\theta_{\max -7}\right)=-6.268+0.898 \ln \left(A_{\mathrm{pg}}\right) $ | (10) |
计算分析所得的地震易损性曲线见图 8。

|
图 8 不同砖砌体强度结构的易损性曲线 Fig. 8 Vulnerability curves of masonry structures with different strength of brick masonry |
根据图 8中的易损性曲线,作出不同砖砌体强度结构的地震破坏矩阵,具体见表 6。
| 表 6 不同砖砌体强度结构的地震破坏矩阵 Tab. 6 Seismic damage matrix of masonry structures with different strength of brick masonry |
由图 8可以看出,随着Apg的增加,砖砌体结构房屋发生破坏的超越概率也逐渐增大,6号和2号模型的易损性曲线相差较小,与7号模型的易损性曲线相差较大。由表 6可知,当Apg为0.2g时,6号、2号和7号模型超越轻微破坏的概率分别为40.98%、29.05%和20.09%;当Apg为0.8g时,6号、2号和7号模型超越严重破坏的概率分别为8.65%、6.52%和2.80%。由对比可知,在相同Apg的情况下,随着砖砌体强度的提高,砌体结构发生轻微破坏、中等破坏和严重破坏的概率显著降低。也就是说,砖砌体强度对砌体结构抗震性能有着较大的影响,用拆除墙段建造新的砖砌体结构实践中应避免低强度墙段的使用。
4 结论1) 构造柱间距的减小可明显提高砌体结构的抗震性能。拆除墙段间的水平连接是通过“端面孔口+水平植筋+构造柱”来实现的,与普通砌体结构相比,使用拆除墙段建造的砖砌体结构的构造柱间距较一般砌体结构小,在进行抗震设计时应合理考虑构造柱间距的减小对抗震性能的提高。
2) 相同地震烈度情况下,砌体结构的层数越多、总高度越大,砌体结构就越容易发生破损或倒塌。需要进一步研究不同设防烈度下不同设计地震分组用拆除墙段建造的砖砌体结构的层数限值和墙体的平均应力与抗压强度比限值。
3) 砖砌体强度对砌体结构的抗震性能有着较大的影响。为保证用拆除墙段建造的砖砌体结构的抗震性能,在用拆除墙段建造新的砌体结构房屋之前,应检测拟拆除房屋的砖墙、砖墙所用砖块和砌筑砂浆的力学性能,合理评定拆除墙段的力学性能及完好性,选择状况良好的墙片作为拆除再利用对象。
| [1] |
蒋传圣. 一座仿古门楼的整体搬移[J]. 建筑知识, 1992(4): 32. JIANG Chuansheng. A whole relocation of an antique gatehouse[J]. Architectural Knowledge, 1992(4): 32. |
| [2] |
郑文忠, 苏志明, 周威. 砌体结构房屋拆除技术进展与展望[J]. 哈尔滨工业大学学报, 2019, 51(12): 17. ZHENG Wenzhong, SU Zhiming, ZHOU Wei. Progress and prospect on demolition technology of masonry structures[J]. Journal of Harbin Institute of Technology, 2019, 51(12): 17. DOI:10.11918/j.issn.0367-6234.201812053 |
| [3] |
QUAGLIARINI E, LENCI S, PIATTONI Q, et al. Experimental analysis of Romanesque masonries made by tile and brick fragments found at the archaeological site of S. Maria in Portuno[J]. International Journal of Architectural Heritage, 2014, 8(2): 172. DOI:10.1080/15583058.2012.683132 |
| [4] |
ZHOU Kan, CHEN Hanmei, WANG Yong, et al. Developing advanced techniques to reclaim existing end of service life (EoSL) bricks—An assessment of reuse technical viability[J]. Developments in the Built Environment, 2020, 2: 7. DOI:10.1016/j.dibe.2020.100006 |
| [5] |
UCER D, ULYBIN A, ZUBKOV S, et al. Analysis on the mechanical properties of historical brick masonry after machinery demolition[J]. Construction and Building Materials, 2018, 161: 188. DOI:10.1016/j.conbuildmat.2017.11.090 |
| [6] |
高惠瑛, 别冬梅, 马建军, 等. 汶川地震区砖砌体住宅房屋易损性研究[J]. 世界地震工程, 2010, 26(4): 73. GAO Huiying, BIE Dongmei, MA Jianjun, et al. A research on vulnerability for brick-residence buildings in Wenchuan earthquake areas[J]. World Earthquake Engineering, 2010, 26(4): 73. |
| [7] |
谢贤鑫, 张令心, 曲哲. 基于修复性的砌体填充墙易损性研究[J]. 建筑结构学报, 2018, 39(12): 159. XIE Xianxin, ZHANG Lingxin, QU Zhe. Reparability-based fragility analysis of masonry infills in buildings[J]. Journal of Building Structures, 2018, 39(12): 159. DOI:10.14006/j.jzjgxb.2018.12.019 |
| [8] |
黄艺, 王睿喆. 墙体开洞影响下房屋砖砌体结构地震易损性分析[J]. 地震工程学报, 2019, 41(3): 574. HUANG Yi, WANG Ruizhe. Seismic vulnerability analysis of brick masonry structures with wall openings[J]. China Earthquake Engineering Journal, 2019, 41(3): 574. DOI:10.3969/j.issn.1000-0844.2019.03.574 |
| [9] |
程明超, 夏彦龙, 张秋石. 砌体结构易损性研究现状[J]. 砖瓦, 2017(3): 74. CHENG Mingchao, XIA Yanlong, ZHANG Qiushi. Research on vulnerability of masonry structure[J]. ZhuanWa, 2017(3): 74. DOI:10.16001/j.cnki.1001-6945.2017.03.018 |
| [10] |
LOURENCO P B, ROQUE J A. Simplified indexes for the seismic vulnerability of ancient masonry buildings[J]. Construction and Building Materials, 2006, 20: 200. DOI:10.1016/j.conbuildmat.2005.08.027 |
| [11] |
SAFAR M, GHOBARAH A. Inelastic response spectrum for simplified deformation-based seismic vulnerability assessment[J]. Journal of Earthquake Engineering, 2008, 12(2): 222. DOI:10.1080/13632460701457272 |
| [12] |
KARBASSI A, NOLLET M J. Performance-based seismic vulnerability evaluation of masonry buildings using applied element method in a nonlinear dynamic-based analytical procedure[J]. Earthquake Spectra, 2013, 29(2): 399. DOI:10.1193/1.4000148 |
| [13] |
砌体结构设计规范: GB 50003—2011[S]. 北京: 中国建筑工业出版社, 2011 Code for design of masonry structures: GB 50003—2011[S]. Beijing: China Architecture & Building Press, 2011 |
| [14] |
刘锡荟, 张鸿熙, 刘经伟, 等. 用钢筋混凝土构造柱加强砖房抗震性能的研究[J]. 建筑结构学报, 1981(6): 50. LIU Xihui, ZHANG Hongxi, LIU Jingwei, et al. A study of aseismic characteristics of masonry building with reinforced concrete tie-columns[J]. Journal of Building Structures, 1981(6): 50. DOI:10.14006/j.jzjgxb.1981.06.005 |
| [15] |
张令心, 江近仁, 刘洁平. 多层住宅砖房的地震易损性分析[J]. 地震工程与工程振动, 2002, 22(1): 54. ZHANG Lingxin, JIANG Jinren, LIU Jieping. Seismic vulnerability analysis of multistory dwelling brick buildings[J]. Earthquake Engineering and Engineering Vibration, 2002, 22(1): 54. DOI:10.13197/j.eeev.2002.01.009 |
| [16] |
张弘毅. 约束砌体结构地震易损性研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2017 ZHANG Hongyi. Research of seismic vulnerability of confined masonry buildings[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2017 |
| [17] |
赵河先. 设防砌体结构易损性模型相关参数修正[D]. 哈尔滨: 中国地震局工程力学研究所, 2017 ZHAO Hexian. The modification of the relative parameters of the structural vulnerability model of reinforced masonry structure[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2017 |
| [18] |
赵文哲. 砌体结构地震易损性研究[D]. 北京: 中国地震局地球物理研究所, 2018 ZHAO Wenzhe. Seismic fragility analysis of masonry building[D]. Beijing: Institute of Geophysics, China Earthquake Administration, 2018 |
| [19] |
鲁若帆. 分类分区砖砌体房屋地震易损性分析[D]. 哈尔滨: 中国地震局工程力学研究所, 2020 LU Ruofan. Seismic vulnerability analysis of brick masonry buildings with different types in different areas[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2020 |
| [20] |
马肖彤, 陆华, 何妍亭, 等. 基于性能的钢筋混凝土框架剪力墙结构地震易损性分析[J]. 地震工程学报, 2020, 42(6): 1387. MA Xiaotong, LU Hua, HE Yanting, et al. Performance-based seismic fragility analysis of a reinforce-concrete frame-shear wall structure[J]. China Earthquake Engineering Journal, 2020, 42(6): 1387. DOI:10.3969/j.issn.1000-0844.2020.06.1386 |
| [21] |
潘毅, 陈侠辉, 王涵平, 等. 无黏结预应力装配式框架结构地震易损性分析[J]. 哈尔滨工业大学学报, 2018, 50(6): 74. PAN Yi, CHEN Xiahui, WANG Hanping, et al. Seismic fragility analysis of unbonded post-tensioned fabricated RC frame structures[J]. Journal of Harbin Institute of Technology, 2018, 50(6): 74. DOI:10.11918/j.issn.0367-6234.201709017 |
| [22] |
叶列平, 马千里, 缪志伟. 结构抗震分析用地震动强度指标的研究[J]. 地震工程与工程振动, 2009, 29(4): 17. YE Lieping, MA Qianli, MIAO Zhiwei. Study on earthquake intensities for seismic analysis of structures[J]. Earthquake Engineering and Engineering Vibration, 2009, 29(4): 17. DOI:10.13197/j.eeev.2009.04.019 |
| [23] |
张秋石. 砌体结构地震易损性及其在保险中的应用研究[D]. 西安: 西安建筑科技大学, 2017 ZHANG Qiushi. Research on the earthquake vulnerability of masonry structure and its application to insurance[D]. Xi'an: Xi'an University of Architecture and Technology, 2017 |
| [24] |
建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [25] |
李佳. 基于数值模拟的砌体结构倒塌影响因素分析及抗倒塌措施初探[D]. 重庆: 重庆大学, 2013 LI Jia. The collapsed factors analysis of masonry structures and preliminary exploration about anti-collapse based numerical simulation[D]. Chongqing: Chongqing University, 2013 |
| [26] |
熊立红. 多层混凝土砌块结构性态抗震研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2005 XIONG Lihong. Study on seismic performance of small hollow concrete block buildings[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2005 |
| [27] |
吴轶, 何铭基, 蔡健, 等. 带耗能腋撑型钢混凝土转换框架结构地震易损性分析[J]. 工程力学, 2012, 29(10): 185. WU Yi, HE Mingji, CAI Jian, et al. Seismic fragility analysis of steel reinforced concrete transfer frame with energy dissipation haunch brace[J]. Engineering Mechanics, 2012, 29(10): 185. DOI:10.3969/j.issn.1000-565X.2011.12.025 |
| [28] |
李刚, 程耿东. 基于性能的结构抗震设计: 理论、方法与应用[M]. 北京: 科学出版社, 2004. LI Gang, CHENG Gengdong. Performance-based seismic design of structures: theory, methods and applications[M]. Beijing: Science Press, 2004. |
| [29] |
SUCUOGLU H, YUCEMEN S, GEZER A, et al. Statistical evaluation of the damage potential of earthquake ground motions[J]. Structural Safety, 1998, 20(4): 369. DOI:10.1016/S0167-4730(98)00018-6 |
| [30] |
刘蒙. 基于易损性的砌体结构抗震抗倒塌研究[D]. 长沙: 湖南大学, 2011 LIU Meng. Seismic collapse study of masonry structures based on fragility[D]. Changsha: Hunan University, 2011 |
 2021, Vol. 53
2021, Vol. 53


