随着复合地基在土木工程中的广泛应用,研究饱和复合地基的固结特性已成为国内外岩土工程界的热门课题[1-9]。郑俊杰等[1]和杨涛等[2]把饱和复合地基均质化,研究了不排水桩饱和复合地基的固结特性。Lang等[3]采用修正等应变假定,分析了不排水刚性桩饱和复合地基的固结解。Miao等[4]把未打穿深厚软土层的水泥搅拌桩加固地基视为双层地基,揭示了水泥搅拌桩饱和复合地基的固结特性。Wijerathna等[5]考虑了水泥搅拌桩的渗透性,利用饱和地基的固结规律通过组合法获得水泥搅拌桩饱和复合地基的近似固结解。张玉国等[6]和Castro等[7]研究了排水桩饱和复合地基的固结特性。Xie等[8]和卢萌盟等[9]考虑桩体压缩性对自身孔隙变形的影响,分别研究了排水桩和不排水桩饱和复合地基的固结特性。这些优秀研究成果有力地推动饱和复合地基固结理论的发展,深刻揭示了饱和复合地基独特的固结性质。
目前饱和复合地基固结分析均沿用天然地基固结理论的假设条件,认为复合地基与天然地基一样,在固结分析中可以近似地假定孔隙水体积模量无穷大。在此假定下,外荷载在施加时全部由孔隙水承担,土骨架承担的荷载为零,复合地基不会产生与外荷载作用同步的即时沉降。然而,为了充分发挥桩体高刚度和高强度的性质,通常在桩顶设置土工格栅或桩帽,确保桩体和桩间土共同作用,使桩体复合地基的等效压缩模型大大增加,从而显著降低复合地基的沉降量。为了反映桩土共同作用力学机制,通常认为复合地基中桩土之间满足等应变假定[1-2, 6-9],因此桩体复合地基的等效压缩模量可以比天然地基增加数倍至数十倍。同时,饱和土体属于天然材料,孔隙中或多或少含有一定量的空气,完全饱和的天然土体在实际工程中是很少存在的。研究表明[10-19],即使孔隙水中含有少量空气,由于空气的压缩系数远远大于水的压缩系数,含气孔隙水的体积模量也会大大下降。如当饱和度为97%时,含气水的体积模量只有纯水的1/300;当饱和度为95%时,含气水的体积模量只有纯水的1/500。因此,即使与天然地基相比,含气水也表现出一定的压缩性[9-14],对地基固结行为会产生较大影响[15-19]。更何况压缩模量为天然地基数倍至数十倍的桩体复合地基,更不能忽略孔隙流体(含气水)的压缩性。然而,目前考虑孔隙流体压缩性的复合地基固结特性分析还未见文献报道,流体压缩性对复合地基固结特性的影响规律如何,除含气水外是否需要进一步考虑纯水的压缩性,成为复合地基固结分析中一个至关重要的关键课题。
在自然界中,存在一种特殊的非饱和土:它们具有较高的饱和度,以至于气体以孤立封闭气泡的形式分散在孔隙水中,无法形成独立的连续气相介质。此时土中孔隙实际上仍被一种流体所充盈,只不过此时的流体是一种混合流体(含气水)而已。在岩土工程界,一般公认当饱和度大于95%后[15-18],孔隙中的水和气可视为一种混合流体,以准饱和的形式充盈在土体孔隙中。鉴于Terzaghi有效应力原理在这些高饱和度的非饱和土体中依然成立[10-19],岩土工程界把饱和度大于95%且小于100 %的土体称为准饱和土[16-18]。本文的研究目的是在考虑孔隙流体压缩变形的条件下,理论研究不排水桩加固准饱和复合地基的固结特性。
1 固结方程对于桩体按三角形和正四边形布置形式加固、大面积堆载的复合地基,它的固结特性可以选取一个桩-土单元来分析。图 1为不排水桩准饱和复合地基桩-土单元的固结分析简图。

|
图 1 固结分析模型 Fig. 1 Computing model for consolidation |
在推导固结方程时作了如下假定:①土和桩体满足线弹性本构方程。②土和桩体只有竖向变形而无侧向变形。上覆荷载由桩土共同承担,桩土之间满足等应变假定。③桩体不排水,土体竖向渗流满足达西定律。④不考虑土颗粒的压缩,但考虑孔隙水和气的压缩变形。⑤土体为准饱和或饱和土体,满足Terzaghi有效应力原理。⑥地基大面积堆载,外荷载产生的附加应力(总应力)σz(t)随深度z保持不变。⑦桩端坐落在不排水硬地层上,复合地基底部满足不排水边界条件。根据假定①和②,复合地基满足等应变假定,有
| $ \varepsilon_{z}=\left(\sigma_{\mathrm{s} z}-u_{\mathrm{s}}\right) / E_{\mathrm{s}}=\sigma_{\mathrm{p}z} / E_{\mathrm{p}} $ | (1) |
式中εz为复合地基的竖向应变,σsz为土体的竖向应力,σpz为桩体应力,us为土体的孔压,Es为原状土的压缩模量,Ep为桩体的压缩模量。令rp和re分别为桩体半径和影响半径,根据受力平衡方程有
| $ {\rm{ \mathsf{ π} }}\left(r_{\mathrm{e}}^{2}-r_{\mathrm{p}}^{2}\right) \sigma_{\mathrm{s} z}+{\rm{ \mathsf{ π} }} r_{\mathrm{p}}^{2} \sigma_{\mathrm{p} z}={\rm{ \mathsf{ π} }} r_{\mathrm{e}}^{2} \sigma_{z}(t) $ | (2) |
令井径比n=re/rp,Ec=[(n2-1)Es+Ep]/n2,Ec为复合地基的等效压缩模量,根据式(1)~(2)得
| $ \varepsilon_{z}=\left(1 / E_{\mathrm{c}}\right) \sigma_{z}(t)-\left[\left(1-1 / n^{2}\right) / E_{\mathrm{c}}\right] u_{\mathrm{s}} $ | (3) |
令Sr为饱和度,Sa=1-Sr为含气率,Fredlund等[19]提出含气水体积模量计算公式为
| $ 1 / K_{\mathrm{f}}=\left(S_{\mathrm{a}} / K_{\mathrm{g}}\right)+\left(1-S_{\mathrm{a}}\right) / K_{\mathrm{w}} $ | (4) |
式中:Kf为含气水的体积模量,Kg=0.2 MPa为气体的体积模量,Kw=2 000 MPa为纯水的体积模量。表 1给出了准饱和土中各种含气率下含气水的体积模量值。
| 表 1 水在各种含气率下的体积模量值 Tab. 1 Bulk modulus of water with various air contents |
从表 1知,当含气率Sa为1%~5%时,含气水的体积模量介于19.80~3.99 MPa。而不排水桩,如水泥搅拌桩的压缩模量介于31.80~73.40 MPa[20],管桩的压缩模量约30 000 MPa[3]。桩的压缩模量比准饱和土中含气水的体积模量大,因此在准饱和复合地基固结分析中需要考虑含气水的压缩性。设固相和流体应变以压为正,土体的孔隙率为φ,比流量ξ定义为单元体流体的渗出量与单元体体积之比,在一维压缩条件下有
| $ \xi=\varepsilon_{z}-\left(\varphi / K_{\mathrm{f}}\right) u_{\mathrm{s}} $ | (5) |
把式(3)代入式(5)得
| $ \xi=\left(1 / E_{\mathrm{c}}\right) \sigma_{z}(t)-\left[\left(1-1 / n^{2}\right) / E_{\mathrm{c}}+\varphi / K_{\mathrm{f}}\right] u_{\mathrm{s}} $ | (6) |
根据卢萌盟等[9]研究,不排水桩复合地基在固结过程中仅有竖向渗流而无径向渗流,根据假设③,孔隙流体的连续性方程可表示为
| $ \frac{\partial}{\partial z}\left(\frac{K_{\mathrm{v}}}{\gamma_{\mathrm{w}}} \frac{\partial u_{\mathrm{s}}}{\partial z}\right)=-\frac{\partial \xi}{\partial t} $ | (7) |
令χp=Ep/Es,χf=Ec/Ef和cv=EsKv/γw,cv为土体的竖向固结系数,α和β的定义为:
| $ \alpha=n^{2} /\left(n^{2}-1+n^{2} \varphi_{\mathrm{f}}\right), \quad \beta=\left(\alpha E_{\mathrm{c}} / E_{\mathrm{s}}\right) c_{\mathrm{v}} $ | (8) |
把式(6)代入式(7)可得
| $ \frac{\partial u_{\mathrm{s}}}{\partial t}=\beta \frac{\partial^{2} u_{\mathrm{s}}}{\partial z^{2}}+\alpha \frac{\partial \sigma_{z}(t)}{\partial t} $ | (9) |
因为顶面排水而底面不排水,所以边界条件为:
| $ \left\{\begin{array}{lc} z=0: & u_{\mathrm{s}}=0 \\ z=H: & \partial u_{\mathrm{s}} / \partial t=0 \end{array}\right. $ | (10) |
式中H为复合地基厚度。
现在来推导考虑流体压缩性时准饱和复合地基固结方程的初始条件。如图 1所示,在复合地基中桩和桩间准饱和土共同承受上覆荷载。t=0时施加的外荷载为σz(0)。在t=0荷载施加的瞬间,孔隙流体无时间从孔隙中流出,故桩间准饱和土处于不排水加载状态,比流量ξ=0。首先研究孔隙流体体积模量无穷大(Kf→∞)即不考虑流体压缩性的情形。由式(5)、ξ=0和Kf→∞可知土骨架应变εz等于零。由于桩体与土骨架之间满足等应变假定,故桩体应变亦等于零,相应地土骨架和桩体承担的荷载亦为零,上覆荷载只能由桩间土中的流体来承担。根据t=0时总应力σz(t)=σz(0),复合地基面积(等于桩与桩间土的面积之和)是桩间土面积的n2/(n2-1)倍,可知t=0时桩间土的孔压等于n2σz(0)/(n2-1),即瞬间加载复合地基产生的孔压比天然地基的要大一些,这一结果与卢萌盟等的研究结论一致[9]。其次研究流体存在压缩性的情形。设瞬时加载时孔隙流体在深度z处承受的孔压为us(z, 0),流体体积模量为Kf,则孔隙流体产生的应变为us(z, 0)/Kf,由式(5)和ξ=0可得土骨架的应变为
| $ \varepsilon_{z}(z, 0)=\left(\varphi / K_{\mathrm{f}}\right) u_{\mathrm{s}}(z, 0) $ | (11) |
根据假设⑤,准饱和土与饱和土一样满足有效应力原理,有
| $ \sigma_{\mathrm{s}z}(z, 0)-u_{\mathrm{s}}(z, 0)=E_{\mathrm{s}}\left(\varphi / K_{\mathrm{f}}\right) u_{\mathrm{s}}(z, 0) $ | (12) |
根据假设②,桩土之间满足等应变假定,故在深度z处桩体应变量也等于式(11),可知桩体承担的应力为
| $ \sigma_{\mathrm{p}z}(z, 0)=E_{\mathrm{p}} \varepsilon_{z}(z, 0)=\left(\varphi E_{\mathrm{p}} / K_{\mathrm{f}}\right) u_{\mathrm{s}}(z, 0) $ | (13) |
根据假说⑥和深度z处的受力平衡得
| $ {\rm{ \mathsf{ π} }}\left(r_{\mathrm{e}}^{2}-r_{\mathrm{p}}^{2}\right) \sigma_{\mathrm{s} z}(z, 0)+{\rm{ \mathsf{ π} }} r_{\mathrm{p}}^{2} \sigma_{\mathrm{p} z}(z, 0)={\rm{ \mathsf{ π} }} r_{\mathrm{e}}^{2} \sigma_{z}(0) $ | (14) |
把式(12)~(13)代入式(14)并利用n、χf和α的定义得
| $ u_{\mathrm{s}}(z, 0)=\alpha \sigma_{z}(0) $ | (15) |
式(15)是固结方程式(9)的初始条件。从式(15)的推导过程可知,当考虑流体压缩性时,施加σz(0)时不但使流体立即产生ασz(0)的即时孔压,而且使复合地基立即产生φus(z, 0)/Kf的即时应变,从而产生与施加荷载同步的即时沉降,这是不考虑孔隙流体压缩性的复合地基固结理论所无法揭示的一个重要性质。
2 瞬时加载时的固结解瞬时加载曲线见图 2,瞬时加载产生的总应力σz(t)为
| $ \sigma_{z}(t)=\sigma_{0}, t \geqslant 0 $ | (16) |
|
图 2 瞬时加载曲线 Fig. 2 Instant loading curve |
固结方程由式(9)和式(16)得
| $ \partial u_{\mathrm{s}} / \partial t=\beta\left(\partial^{2} u_{\mathrm{s}} / \partial z^{2}\right) $ | (17) |
边界条件见式(10),初始孔压由式(15)~ (16)得us(z, 0)=ασ0。求解式(17)可获得t时刻孔压为
| $ u_{\mathrm{s}}=\sum\limits_{m=1}^{\infty} \frac{2 \alpha \sigma_{0}}{M} \sin \left(\frac{M}{H} z\right) \mathrm{e}^{-\gamma_{m} t} $ | (18) |
式中的M=(2m-1)π/2,γm的表达式为
| $ \gamma_{m}=M^{2} \beta / H^{2}=\left(\alpha E_{\mathrm{c}} / E_{\mathrm{s}}\right)\left(M^{2} c_{\mathrm{v}} / H^{2}\right) $ | (19) |
为验证本文推导正确性,取Kf→∞,有α=n2/(n2-1),代入式(18)就可发现孔压表达式与文献[9]中的式(30)完全一致。根据式(18)可得t时刻复合地基的平均孔压为
| $ \bar{u}_{\mathrm{s}}(t)=\frac{1}{H} \int_{0}^{H} u_{\mathrm{s}}(z, t) \mathrm{d} z=\sum\limits_{m=1}^{\infty} \frac{2 \alpha \sigma_{0}}{M^{2}} \mathrm{e}^{-\gamma_{m} t} $ | (20) |
由于瞬时加载时外荷载在t=0时一次性加载完毕,故复合地基的即时应变等于瞬时加载瞬间产生的初始应变,由式(11)和式(15)~(16)得
| $ \varepsilon_{\mathrm{i}z}(z, t)=\varepsilon_{\mathrm{i} z}(z, 0)=\varphi \alpha \sigma_{0} / K_{\mathrm{f}} $ | (21) |
即时沉降由式(21)对复合地基沿深度积分得
| $ S_{\mathrm{i}}(t)=\int_{0}^{H} \varepsilon_{\mathrm{i}z} \mathrm{d} z=\alpha \varphi \chi_{\mathrm{f}}\left(\sigma_{0} H / E_{\mathrm{c}}\right) $ | (22) |
由式(3)、式(16)和式(18)可知t时刻复合地基沉降为
| $ S(t)=\int_{0}^{H} \varepsilon_{z} \mathrm{~d} z=\frac{\sigma_{0} H}{E_{\mathrm{c}}}\left[1-\frac{\alpha\left(n^{2}-1\right)}{n^{2}} \sum\limits_{m=1}^{\infty} \frac{2 \mathrm{e}^{-\gamma_{m} t}}{M^{2}}\right] $ | (23) |
把外荷载直接产生的孔压称为即时孔压,记为usp(z, t)。随着孔压消散,t时刻孔压变为us(z, t)。固结应变是孔压消散引起的应变。式(3)表明,孔压变化引起的应变等于[(n2-1)/(n2Ec)]Δus,Δus为即时孔压减去t时刻孔压的差值,由此可得孔压消散引起的复合地基固结应变为
| $ \varepsilon_{\mathrm{c}z}(z, t)=\frac{\left(n^{2}-1\right)\left[u_{\mathrm{sp}}(z, t)-u_{\mathrm{s}}(z, t)\right]}{n^{2} E_{\mathrm{c}}} $ | (24) |
瞬时加载时即时孔压等于初始孔压,usp(z, t)=us(z, 0)=ασ0,把它和式(18)代入式(24)后沿深度积分得
| $ S_{\mathrm{c}}(t)=\int_{0}^{H} \varepsilon_{\mathrm{c} z} \mathrm{~d} z=\alpha \frac{n^{2}-1}{n^{2}}\left(1-\sum\limits_{m=1}^{\infty} \frac{2}{M^{2}} \mathrm{e}^{-\gamma_{m} t}\right) \frac{\sigma_{0} H}{E_{\mathrm{c}}} $ | (25) |
根据上节式(10)~(15)之间的分析可知,当考虑流体压缩变形时,复合地基在加载期间同时产生即时沉降和即时孔压,随着孔压逐渐消散,复合地基出现随时间增长的固结沉降。故复合地基沉降由两部分组成,一部分是与加载同步产生的即时沉降,另一部分是随孔压消散引起的固结沉降,复合地基的沉降量等于即时沉降和固结沉降之和。故即时沉降也可由式(23)减去式(25)获得
| $ S_{\mathrm{i}}(t)=S(t)-S_{\mathrm{c}}(t)=\alpha \varphi \chi_{\mathrm{f}}\left(\sigma_{0} H / E_{\mathrm{c}}\right)=S_{\mathrm{i}}(0) $ | (26) |
式(26)与式(22)结果相同,说明不同方法获得的结果是一致的。
取t→∞,孔压为零,地基最终沉降和按当前应力计算的最终固结沉降由式(23)和式(25)得:
| $ S_{\infty}=\sigma_{0} H / E_{\mathrm{c}} $ | (27) |
| $ S_{\mathrm{c} \infty}=\alpha\left(1-1 / n^{2}\right)\left(\sigma_{0} H / E_{\mathrm{c}}\right) $ | (28) |
固结度反映的是固结沉降发展规律,故本文固结度的定义为t时刻的固结沉降与t时刻按当前应力计算的最终固结沉降之比,由式(25)和式(28)得
| $ U(t)=S_{\mathrm{c}}(t) / S_{\mathrm{c} \infty}=1-\sum\limits_{m=1}^{\infty}\left(2 / M^{2}\right) \mathrm{e}^{-\gamma_{m }t} $ | (29) |
根据式(23)和式(25)~(29),瞬时加载时t时刻的沉降量可由固结度表示为
| $ S(t)=S_{\mathrm{i}}(0)+U(t) S_{\mathrm{c} \infty} $ | (30) |
单级线性加载曲线见图 3,单级线性加载时外荷载产生的总应力σz(t)为
| $ \sigma_{z}(t)= \begin{cases}\sigma_{0} t / t_{0}, & 0 \leqslant t<t_{0} \\ \sigma_{0}, & t \geqslant t_{0}\end{cases} $ | (31) |

|
图 3 单级线性加载曲线 Fig. 3 Single ramp loading curve |
固结方程由式(9)和式(31)得
| $ \frac{\partial u_{\mathrm{s}}}{\partial t}=\left\{\begin{array}{l} \beta\left(\partial^{2} u_{\mathrm{s}} / \partial z^{2}\right)+\sigma_{0} t / t_{0}, 0 \leqslant t<t_{0} \\ \beta\left(\partial^{2} u_{\mathrm{s}} / \partial z^{2}\right), \quad t \geqslant t_{0} \end{array}\right. $ | (32) |
边界条件与式(10)相同,初始孔压由式(15)和式(31)得us(z, 0)=0。根据分离变量法对式(32)求解得
| $ u_{\mathrm{s}}(z, t)=\left\{\begin{array}{l} \frac{2 \alpha \sigma_{0}}{t_{0}} \sum\limits_{m=1}^{\infty} \frac{1-\mathrm{e}^{-\gamma_{m }t}}{M \gamma_{m}} \sin \left(\frac{M}{H} z\right), 0 \leqslant t<t_{0} \\ \frac{2 \alpha \sigma_{0}}{t_{0}} \sum\limits_{m=1}^{\infty} \frac{\mathrm{e}^{-\gamma_{m}\left(t-t_{0}\right)}-\mathrm{e}^{-\gamma_{m} t}}{M \gamma_{m}} \sin \left(\frac{M}{H} z\right), t \geqslant t_{0} \end{array}\right. $ | (33) |
为验证本文推导正确性,取Kf→∞,有α=n2/(n2-1),代入到式(33),发现孔压表达式与文献[9]中的式(46)和(48)完全一致。根据式(33)可得t时刻复合地基的平均孔压为
| $ -u_{\mathrm{s}}(t)=\left\{\begin{array}{l} \frac{2 \alpha \sigma_{0}}{t_{0}} \sum\limits_{m=1}^{\infty} \frac{1-\mathrm{e}^{-\gamma_{m} t}}{M^{2} \gamma_{m}}, 0 \leqslant t<t_{0} \\ \frac{2 \alpha \sigma_{0}}{t_{0}} \sum\limits_{m=1}^{\infty} \frac{\mathrm{e}^{-\gamma_{m}\left(t-t_{0}\right)}-\mathrm{e}^{-\gamma_{m} t}}{M^{2} \gamma_{m}}, t \geqslant t_{0} \end{array}\right. $ | (34) |
把式(31)和(33)代入到式(3)并把它沿深度积分可得复合地基的沉降为:
当0≤t<t0时,
| $ S(t)=\frac{\sigma_{0} H t}{E_{\mathrm{c}} t_{0}}-\frac{2\left(n^{2}-1\right) \alpha \sigma_{0} H}{n^{2} E_{\mathrm{c}} t_{0}} \sum\limits_{m=1}^{\infty} \frac{1-\mathrm{e}^{-\gamma_{m} t}}{M^{2} \gamma_{m}} $ | (35) |
当t≥t0时,
| $ \begin{gathered} S(t)=\frac{\sigma_{0} H}{E_{\mathrm{c}}}-\frac{2\left(n^{2}-1\right) \alpha \sigma_{0} H}{n^{2} E_{\mathrm{c}} t_{0}} \\ \sum\limits_{m=1}^{\infty} \frac{\mathrm{e}^{-\gamma_{m}\left(t-t_{0}\right)}-\mathrm{e}^{-\gamma_{m} t}}{M^{2} \gamma_{m}} \end{gathered} $ | (36) |
从式(9)的数学物理意义可知,等式右边第一项反映的是地基固结所引起的孔压消散,第二项反映的是施加外荷载直接产生的即时孔压usp,可得usp随时间的变化规律为
| $ \frac{\partial u_{\mathrm{sp}}(z, t)}{\partial t}=\alpha \frac{\partial \sigma_{z}(t)}{\partial t} $ | (37) |
式(37)还可以采用另一种方法获得:若复合地基不发生固结,则地基中的孔压不会消散,此时地基中的孔压等于外荷载直接产生的即时孔压;而地基不发生固结的条件是式(9)等式右边的第一式等于零,故可以得到式(37)。在推导式(37)时并没有用到单级线性加载这一条件,因此它对任何加载方式均成立。
在单级线性加载条件下,式(37)的初始条件为t=0时瞬时加载σz(0)引起的孔压,根据式(15)和式(31)可得usp(z, 0)=0。把式(31)代入式(37)并利用初始条件得
| $ u_{\mathrm{sp}}(z, t)=\left\{\begin{array}{l} \alpha \sigma_{0} t / t_{0}, 0 \leqslant t<t_{0} \\ \alpha \sigma_{0}, t \geqslant t_{0} \end{array}\right. $ | (38) |
外荷载产生的总应力等于式(31),而直接产生的即时孔压等于式(38),故复合地基产生与施加外荷载同步的即时沉降。根据式(3)、(31)和us=usp并沿深度进行积分可得t时刻的即时沉降为
| $ S_{\mathrm{i}}(t)=\left\{\begin{array}{l} \alpha \varphi \chi_{\mathrm{f}}\left[\sigma_{0} H t /\left(E_{\mathrm{c}} t_{0}\right)\right], 0 \leqslant t<t_{0} \\ \alpha \varphi \chi_{\mathrm{f}}\left(\sigma_{0} H / E_{\mathrm{c}}\right), t \geqslant t_{0} \end{array}\right. $ | (39) |
式(39)表明,伴随着单级线性加载,即时沉降在[0, t0]区间内随时间线性增加。把式(33)和(38)代入式(24)后沿深度积分,可得单级线性加载时复合地基的固结沉降为:
当0≤t<t0时,
| $ S_{\mathrm{c}}(t)=\frac{\left(n^{2}-1\right) \alpha \sigma_{0} H}{n^{2} E_{\mathrm{c}}}\left(\frac{t}{t_{0}}-2 \sum\limits_{m=1}^{\infty} \frac{1-\mathrm{e}^{-\gamma_{m} t}}{M^{2} \gamma_{m} t_{0}}\right) $ | (40) |
当t≥t0时,
| $ \begin{gathered} S_{\mathrm{c}}(t)=\frac{\left(n^{2}-1\right) \alpha \sigma_{0} H}{n^{2} E_{\mathrm{c}}} \\ \left(1-2 \sum\limits_{m=1}^{\infty} \frac{\mathrm{e}^{-\gamma_{m}\left(t-t_{0}\right)}-\mathrm{e}^{-\gamma_{m }t}}{M^{2} \gamma_{m} t_{0}}\right) \end{gathered} $ | (41) |
固结完成后孔压us(z, t)等于零,由式(24)和(38)并沿深度积分可得按当前应力计算的最终固结沉降为:
| $ S_{\mathrm{c} \infty}(t)=\left\{\begin{array}{l} \left(n^{2}-1\right) \alpha \sigma_{0} H t /\left(n^{2} E_{\mathrm{c}} t_{0}\right), 0 \leqslant t<t_{0} \\ \left(n^{2}-1\right) \alpha \sigma_{0} H /\left(n^{2} E_{\mathrm{c}}\right), t \geqslant t_{0} \end{array}\right. $ | (42) |
从式(42)可以看出,当0≤t<t0时,伴随着单级线性加载时当前应力随时间线性增大,按当前应力计算的最终固结沉降也随时间线性增大;当t≥t0后外荷载产生的当前应力保持不变,最终固结沉降也随之保持不变。
地基固结度U(t)定义为当前固结沉降与按当前应力计算的最终固结沉降之比,有
| $ U(t)=\frac{S_{\mathrm{c}}}{S_{\mathrm{c} \infty}}=\left\{\begin{array}{l} 1-\frac{2}{t} \sum\limits_{m=1}^{\infty} \frac{1-\mathrm{e}^{-\gamma_{m} t}}{M^{2} \gamma_{m}}, 0 \leqslant t<t_{0} \\ 1-\frac{2}{t_{0}} \sum\limits_{m=1}^{\infty} \frac{\mathrm{e}^{-\gamma_{m}\left(t-t_{0}\right)}-\mathrm{e}^{-\gamma_{m }t}}{M^{2} \gamma_{m}}, t \geqslant t_{0} \end{array}\right. $ | (43) |
根据式(35)~(36)和式(39)~(43),t时刻复合地基沉降可用固结度表示为
| $ S(t)=S_{\mathrm{i}}(t)+U(t) S_{\mathrm{c}\infty}(t) $ | (44) |
本节假定外荷载产生的总应力σz(t)随时间任意变化,以此来获取不排水桩复合地基固结的通解。首先,根据数学物理方法[21],结合边界条件式(10),可令
| $ u_{\mathrm{s}}=\sum\limits_{m=1}^{\infty} f_{m}(t) \sin (M z / H) $ | (45) |
把式(45)代入到式(9)并利用三角级数的正交性得
| $ \partial f_{m}(t) / \partial t+\gamma_{m} f_{m}(t)-2 \alpha \sigma_{z}(t) / M=0 $ | (46) |
对式(15)也按三角级数展开,可得式(46)的初始条件为fm(t)=2ασz(0)/M,对式(46)求解后代入式(45)得
| $ \begin{gathered} u_{\mathrm{s}}(z, t)=\sum\limits_{m=1}^{\infty} \frac{2 \alpha}{M} \sin \left(\frac{M}{H} z\right) \mathrm{e}^{-\gamma_{m} t} \\ {\left[\sigma_{z}(0)+\int_{0}^{t} \mathrm{e}^{\gamma_{m} \tau} \frac{\partial \sigma_{z}}{\partial \tau} \mathrm{d} \tau\right]} \end{gathered} $ | (47) |
根据式(47)可得t时刻复合地基的平均孔压为
| $ \bar{u}_{\mathrm{s}}(t)=\sum\limits_{m=1}^{\infty} \frac{2 \alpha}{M^{2}} \mathrm{e}^{-\gamma_{m }t}\left[\sigma_{z}(0)+\int_{0}^{t} \mathrm{e}^{\gamma_{m} \tau} \frac{\partial \sigma_{z}}{\partial \tau} \mathrm{d} \tau\right] $ | (48) |
t时刻复合地基的沉降由式(3)和式(47)得:
| $ \begin{aligned} &S(t)=\frac{\sigma_{z}(t)}{E_{\mathrm{c}}} H-\frac{\left(n^{2}-1\right) \alpha H}{n^{2} E_{\mathrm{c}}} \times \\ &\sum\limits_{m=1}^{\infty} \frac{2 \mathrm{e}^{-\gamma_{m} t}}{M^{2}}\left[\sigma_{z}(0)+\int_{0}^{t} \mathrm{e}^{\gamma_{m} \tau} \frac{\partial \sigma_{z}}{\partial \tau} \mathrm{d} \tau\right] \end{aligned} $ | (49) |
当总应力σz(t)随时间任意变化时,方程式(37)的初始孔压等于式(15),有t=0时usp(z, 0)=ασz(0),求解式(37)可得外荷载直接产生的即时孔压为
| $ u_{\mathrm{sp}}(z, t)=\alpha \sigma_{z}(t) $ | (50) |
外荷载产生的总应力为σz(t),而直接产生的即时孔压为式(50),故复合地基会产生与施加外荷载同步的即时沉降。根据式(3)、us=usp并沿深度进行积分可得t时刻的即时沉降为
| $ \begin{aligned} S_{\mathrm{i}}(t) &=\int_{0}^{H} \frac{n^{2} \sigma_{z}(t)-\left(n^{2}-1\right) u_{\mathrm{sp}}}{n^{2} E_{\mathrm{c}}} \mathrm{d} z \\ &=\alpha \varphi \chi_{\mathrm{f}} \frac{\sigma_{z}(t) H}{E_{\mathrm{c}}} \end{aligned} $ | (51) |
式(51)的推导过程中运用了式(8)中的第一式。随着孔压usp逐步消散,土骨架和桩体承受的荷载逐渐增加,复合地基沉降随之增大,由孔压消散产生的沉降为固结沉降。把式(47)和式(50)代入到式(24)后沿深度积分可得t时刻的固结沉降为
| $ \begin{gathered} S_{\mathrm{c}}(t)=\frac{\left(n^{2}-1\right) \alpha \sigma_{z}(t) H}{n^{2} E_{\mathrm{c}}}-\frac{\alpha\left(n^{2}-1\right) H}{n^{2} E_{\mathrm{c}}} \times \\ \sum\limits_{m=1}^{\infty} \frac{2 \mathrm{e}^{-\gamma_{m} t}}{M^{2}}\left[\sigma_{z}(0)+\int_{0}^{t} \mathrm{e}^{\gamma_{m} \tau} \frac{\partial \sigma_{z}}{\partial \tau} \mathrm{d} \tau\right] \end{gathered} $ | (52) |
利用式(49)、(51)~(52)可以验证S(t)=Si(t)+Sc(t)成立。注意到固结完成时复合地基的孔压us等于零,故根据式(3)、式(24)和式(50)可知按当前应力σz(t)计算的最终沉降和最终固结沉降为
| $ S_{\infty}(t)=\sigma_{z}(t) H / E_{\mathrm{c}} $ | (53) |
| $ S_{\mathrm{c} \infty}(t)=\left[\alpha\left(n^{2}-1\right) / n^{2}\right]\left[\sigma_{z}(t) H / E_{\mathrm{c}}\right] $ | (54) |
利用式(51)、式(53)~(54)可以验证S∞(t)=Si(t)+Sc∞(t)成立。根据固结度定义式U(t)=Sc/Sc∞,有
| $ U(t)=1-\sum\limits_{m=1}^{\infty} \frac{2 \mathrm{e}^{-\gamma_{m} t}}{M^{2} \sigma_{z}(t)}\left[\sigma_{z}(0)+\int_{0}^{t} \mathrm{e}^{\gamma_{m} \tau} \frac{\partial \sigma_{z}}{\partial \tau} \mathrm{d} \tau\right] $ | (55) |
根据式(49)和式(51)~(55),t时刻的沉降可用固结度表示为
| $ S(t)=S_{\mathrm{i}}(t)+U(t) S_{\mathrm{c}\infty}(t) $ | (56) |
为了验证式(47)~(56)理论推导的正确性,采用第2节“瞬时加载时的固结解”和《地基处理新技术》[20]中介绍的叠加法来推导任意加载条件下的固结解。令τ为外荷载施加时间,τ=0时的瞬间加载量为σz(0),由第2节式(18)可知该荷载消散到t时的孔压为
| $ u_{\mathrm{s} 1}=\sigma_{z}(0) \sum\limits_{m=1}^{\infty} \frac{2 \alpha}{M} \sin \left(\frac{M}{H} z\right) \mathrm{e}^{-\gamma_{m }t} $ | (57) |
τ时的瞬间加载量为
| $ u_{\mathrm{s} 2}=\sum\limits_{m=1}^{\infty} \int_{0}^{t} \frac{2 \alpha}{M} \sin \left(\frac{M}{H} z\right) \frac{\partial \sigma(\tau)}{\partial \tau} \mathrm{e}^{-\gamma_{m}(t-\tau)} \mathrm{d} \tau $ | (58) |
消散到t时的总孔压为式(57)~(58)之和,由此就可以再次得到式(47)。外荷载在t时的瞬间加载量为dσz(t),根据第2节式(26)可知,该荷载产生的即时沉降增量为
| $ \mathrm{d} S_{\mathrm{i}}(t)=\left(\alpha \varphi{\chi_{\mathrm{f}}} H / E_{\mathrm{c}}\right) \mathrm{d} \sigma_{z}(t) $ | (59) |
由式(26)可知初始即时沉降为
算例1:某场地原状土[20]孔隙率为0.459,厚度10 m,Es=2.6 MPa,cv=0.004 cm2/s。采用水泥搅拌桩进行地基加固,复合地基所要求的设计承载力为150 kPa,水泥掺量为15%,桩基压缩模量Ep为59 MPa,置换率为20%,折算成井径比n为2.24。令TV=cVt/H2为土体固结时间因数,现在来分析该场地的固结特性。
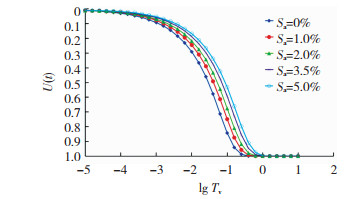
5.1 瞬时加载下的固结特性分析图 4~5给出了瞬时加载时水泥搅拌桩准饱和复合地基固结度和平均孔压随固结时间因数变化规律。图 4表明当固结时间因数相同时,复合地基固结度随着孔隙水含气率增加而逐渐减小。造成这一结果的原因是随着含气率增加,含气孔隙水的体积模量越小,复合地基的固结越慢,固结度亦相应减少。图 5表明当固结时间因数较小时,平均孔压随含气率增加而减小。随着固结时间因数增加,各含气率复合地基中的平均孔压逐渐接近直至相等,之后随着固结时间因数的进一步增加(Tv约大于0.99),含气率越大的平均孔压越大。出现这一规律的原因是随着含气率增大,α值大幅减小,即时孔压亦减小。如含气率为2%时,即时孔压约为外荷载的0.68倍,当含气率为5%时,即时孔压约为外荷载的0.41倍。受其影响,在固结初期,平均孔压随含气率的增大而减小;然而,由于含气率大的复合地基孔压消散慢,故随着固结时间因数进一步增长,各含气率的复合地基平均孔压逐渐接近,当固结接近完成时,平均孔压随含气率的增大而增大。值得指出的是,当考虑流体压缩性时,复合地基既有即时沉降又有固结沉降。即时沉降的产生机制与孔压消散的固结机理无关。本文把固结度定义为当前固结沉降和当前应力作用下的最终固结沉降之比,可以消除即时沉降对固结度的影响,从而更简明地反映准饱和复合地基中固结度随含气率的变化规律,更深刻地揭示考虑流体压缩性时复合地基的固结机理。
|
图 4 瞬时加载时按固结沉降定义的固结度随时间因数变化 Fig. 4 Consolidation degree defined by consolidation settlement varying with time factor subjected to an instant loading |

|
图 5 瞬时加载时平均孔压随时间因数变化 Fig. 5 Average pore pressure varying with time factor subjected to an instant loading |
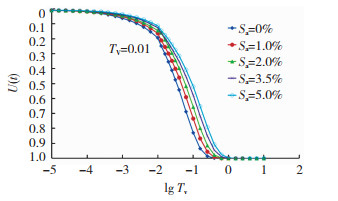
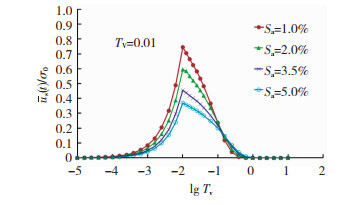
单级加载的固结规律与瞬时加载时基本一致。图 6给出了单级线性加载时固结度随固结时间因数变化规律,当固结时间因数相同时,水泥搅拌桩复合地基的固结度随着含气率增大而减小。图 7给出了单级线性加载时平均孔压随固结时间因数变化规律。
|
图 6 单级加载时按固结沉降定义的固结度随时间因数变化 Fig. 6 Consolidation degree defined by consolidation settlement varying with time factor subjected to a single ramp loading |
|
图 7 单级加载时平均孔压随时间因数变化 Fig. 7 Average pore pressure varying with time factor subjected to a single ramp loading |
从图 7可以看出,当固结时间因数较小时,平均孔压随含气率增大而减小。出现这一规律的原因是随着含气率增大,外荷载直接产生的即时孔压减小,造成最大平均孔压也相应减少。如当含气率为2%时,最大平均孔压约为外荷载的0.59倍,当含气率为5%时,最大平均孔压约为外荷载的0.36倍;然而,含气率大的复合地基孔压消散慢,故当固结接近完成时,平均孔压呈现出与固结初期相反,即随着含气率增大而增大的固结规律。
5.3 即时沉降和最终沉降之比分析与不考虑流体压缩性的解答不同,考虑孔隙流体压缩性的不排水桩复合地基存在即时沉降。由于最终沉降等于即时沉降和最终固结沉降之和,故即时沉降和最终沉降之比间接反映了地基固结沉降的大小,从而受到工程界的重视。本文把即时沉降与最终沉降之比称为即时沉降的占比率。从式(51)和式(53)可知,即时沉降的占比率等于αφχf,而与加载方式无关。为了分析桩体压缩模量对即时沉降占比率的影响,本节不局限于水泥搅拌桩,而让桩型和桩体压缩模量自由变化,半刚性桩到刚性桩的压缩模量大约介于30~30 000 MPa,现分析桩体压缩模量在这个范围变化时各种含气率下即时沉降占比率的变化规律。
分析选用的土体力学参数和桩体加固参数与前述算例1相同,只让桩体压缩模量发生变化,即时沉降占比率随桩体压缩模量的变化曲线见图 8。图 8表明,当含气率相同时,桩体压缩模量越大,即时沉降占比率也越大。首先研究不排水桩饱和复合地基即时沉降占比率的变化特性。当孔隙水含气率为0时,准饱和土变为饱和土。以往研究不排水桩饱和复合地基的固结特性时,依据直觉假定孔隙水不可压缩,即孔隙水的体积模量取无穷大,故理论上施加外荷载不会产生复合地基的即时沉降。但实际孔隙水也存在压缩性,孔隙水的体积模量等于2 000 MPa,故外荷载施加时不排水桩饱和复合地基实际上也会产生即时沉降。当桩体压缩模量不超过100 MPa时,由于孔隙水的体积模量远远大于桩体和土体的压缩模量,图 8显示即时沉降占比率小于0.7%,接近于零,此时把孔隙水视为体积模量无穷大,从而即时沉降等于零,产生的误差不大。但当桩体的压缩模量和孔隙水的体积模量相当或更大时,如桩体压缩模量大于2 000 MPa,由于复合地基满足等应变假定,即时沉降占比率大于10%。预应力管桩的压缩模量为30 000 MPa,即时沉降的占比率高达63%。上述研究表明,在不排水桩饱和复合地基中,对于半刚性桩,即时沉降可以忽略,故忽略孔隙水的压缩性对固结分析的影响不大。对于刚性桩,即时沉降占比率较大,即使是不含气的饱和土体,在固结分析时也必须考虑孔隙水的压缩性。其次研究不排水桩准饱和复合地基即时沉降占比率的变化特性。准饱和土中的孔隙水含有一定的气体,如表 1所示,含气水的等效体积模量大幅降低。从图 8可以看出,即使半刚性桩体压缩模量只有30 MPa,当含气率等于0.2%时,外荷载引起的准饱和复合地基的即时沉降占比率也达到5%;当含气率等于1%时,准饱和复合地基的即时沉降占比率达到20%;当含气率等于5%,即时沉降占比率达到58%;当水泥搅拌桩压缩模量为59 MPa时,含气率为5%的复合地基即时沉降占比率为66.7%。由于桩体压缩模量一般大于30 MPa,因此在不排水桩准饱和复合地基固结分析时,都不能忽略即时沉降占比率,即需要考虑含气孔隙流体的压缩量。刚性桩的压缩模量远大于半刚性桩,更需要考虑含气孔隙水的体积模量。如采用预应力管桩加固准饱和土时,由于管桩压缩模量有30 000 MPa,当含气率等于0.2%时,即时沉降占比率高达97.3%;当含气率等于1%,即时沉降占比率为99%,这说明对于刚性桩准饱和复合地基,主要表现为即时沉降,即时孔压和固结沉降只占很小比例,当含气率大于0.2%时,即时孔压和固结沉降小于外荷载的2.7%,因此可以忽略不计,无需进行管桩准饱和复合地基固结分析。如果像以往岩土学者那样在管桩复合地基固结分析时不考虑含气孔隙水的压缩性,由此得到的理论结果将是即时沉降占比率为0而固结沉降占100%,与本文结果相比南辕北辙。综上所说,对于准饱和复合地基,无论是半刚性桩还是刚性桩,均需要考虑含气孔隙水的压缩性,否则,理论与实际的即时沉降和固结沉降占比率相差较大。
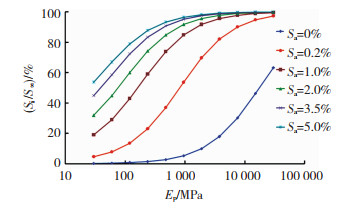
|
图 8 即时沉降占比率随桩体压缩模量变化 Fig. 8 Ratio of immediate settlement to final settlement varying with compressive modulus of pile |
1) 假定准饱和复合地基的桩土之间满足等应变假定,考虑孔隙流体压缩性,推导出不排水桩准饱和复合地基的固结方程。在假定地基底部不排水边界条件下,获得了瞬时加载,单级线性加载和随时间任意加载时复合地基孔压、即时沉降、固结沉降和固结度的解析解答。
2) 当固结时间因数相同时,随着孔隙水含气率的增加(即饱和度的减小),水泥搅拌桩复合地基的等效压缩模量变小,固结速率变慢,固结度减小。本文准饱和复合地基的固结度定义为当前固结沉降和当前应力作用下的最终固结沉降之比,荷载直接产生的即时沉降量和即时孔压量均不会影响决定孔压消散快慢的固结度大小。同时,含气率越大,外荷载直接产生的即时孔压越小;受其影响,在固结初期,复合地基的孔压随着含气率的增大而减小。
3) 在不排水桩准饱和复合地基中,施加外荷载会同步产生即时沉降,当外荷载随时间逐渐增大时,即时沉降也随时间逐渐增大,这是以往复合地基固结理论未曾揭示的新固结性质。即时沉降的占比率只与孔隙率,复合地基等效压缩模量与流体体积模量之比和孔压系数(即时孔压与外荷载之比)有关,而与加载方式无关。当桩体与流体的压缩模量相当或更大时,固结分析需要考虑孔隙流体的压缩性。对于管桩准饱和复合地基的沉降,主要表现为荷载施加时就产生的即时沉降,固结沉降和固结过程可以忽略而无需考虑固结特性。
| [1] |
郑俊杰, 刘志刚, 吴世明. 石灰桩复合地基固结分析[J]. 华中理工大学学报, 2000, 28(5): 111. ZHENG Junjie, LIU Zhigang, WU Shiming. Consolidation analysis of composite ground with lime-flyash pile[J]. Journal of Huazhong University of Science and Technology, 2000, 28(5): 111. DOI:10.3321/j.issn:1671-4512.2000.05.039 |
| [2] |
杨涛, 吉映竹, 杨欢. 悬浮刚-柔性长短桩复合地基固结解析解[J]. 建筑结构学报, 2020, 41(11): 176. YANG Tao, JI Yingzhu, YANG Huan. Analytical solution for consolidation of composite ground with floating rigid-flexible and long-short piles[J]. Journal of Building Structures, 2020, 41(11): 176. DOI:10.14006/j.jzjgxb.2019.0107 |
| [3] |
LANG R Q, YANG A W. A quasi-equal strain solution for the consolidation of a rigid pile composite foundation under embankment loading condition[J]. Computers and Geotechnics, 2020, 117: 103232. DOI:10.1016/j.compgeo.2019.103232 |
| [4] |
MIAO L C, WANG X H, KAVAZANJIAN E J. Consolidation of a double-layered compressible foundation partially penetrated by deep mixed columns[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(8): 1210. DOI:10.1061/(ASCE)1090-0241(2008)134:8(1210) |
| [5] |
WIJERATHNA M, LIYANAPATHIRANA D S, LEO C J. Analytical solution for the consolidation behavior of deep cement mixed column-improved ground[J]. International Journal of Geomechanics, 2017, 17(9): 04017065. DOI:10.1061/(ASCE)GM.1943-5622.0000954 |
| [6] |
张玉国, 杨晗玥, 段萌萌, 等. 真空-堆载联合预压条件下复合地基固结解析解[J]. 长江科学院院报, 2019, 36(5): 75. ZHANG Yuguo, YANG Hanyue, DUAN Mengmeng, et al. Analytical solution for consolidation of composite ground under vacuum-surcharge preloading[J]. Journal of Yangtze River Scientific Research Institute, 2019, 36(5): 75. |
| [7] |
CASTRO J, SAGASETA C. Consolidation around stone columns influence of column deformation rigid elevated caps[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(7): 851. DOI:10.1002/nag.745 |
| [8] |
XIE K H, LU M M, LIU G B. Equal strain consolidation for stone-column reinforced foundation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33: 1721. DOI:10.1002/nag.790 |
| [9] |
卢萌盟, 谢康和, 周国庆, 等. 不排水桩复合地基固结解析解[J]. 岩土工程学报, 2011, 11(4): 574. LU Mengmeng, XIE Kanghe, ZHOU Guoqing, et al. Analytical solution for consolidation of composite ground with impervious pile[J]. Chinese Journal of Geotechnical Engineering, 2011, 11(2): 574. |
| [10] |
VAZIRI H H, CHRISTIAN H A. Application of Terzaghi's consolidation theory to nearly saturated soils[J]. Canadian Geotechnical Journal, 1994, 31: 311. DOI:10.1139/t94-037 |
| [11] |
YUE Z Q, SELVADURAI A P S, LAW K T. Excess pore water pressure in a porelastic seabed saturated with a compressible fluid[J]. Canadian Geotechnical Journal, 1994, 31: 989. DOI:10.1139/t94-113 |
| [12] |
SUBHARTHI S, KAI G, RAJIB M, et al. Measuring near-saturated hydraulic conductivity of soils by quasi unit-gradient percolation: theory and numerical analysis[J]. Journal of Plant Nutrition and Soil Science, 2019, 182(4): 524. DOI:10.1002/jpln.201800382 |
| [13] |
高广运, 张其唯, 毕俊伟. 高铁荷载下准饱和分层地基环境振动特性研究[J]. 噪声与振动控制, 2020, 40(3): 181. GAO Guangyun, ZHANG Qiwei, BI Junwei. Analysis of ground vibration caused by high speed railway on quasi-saturated layered subgrade[J]. Noise and Vibration Control, 2020, 40(3): 181. |
| [14] |
刘忠玉, 徐传永, 朱新牧, 等. 考虑非Darcy渗流的砂井地基弹黏塑性固结分析[J]. 哈尔滨工业大学学报, 2021, 53(5): 113. LIU Zhongyu, XU Chuanyong, ZHU Xinmu, et al. Elasto-viscoplastic consolidation analysis of ground with sand drains considering non-Darcian flow[J]. Journal of Harbin Institute of Technology, 2021, 53(5): 113. DOI:10.11918/201907173 |
| [15] |
艾智勇, 吴超. 渗透各向异性可压缩地基固结的平面应变分析[J]. 力学学报, 2009, 41(5): 801. AI Zhiyong, WU Chao. Analysis on plane strain consolidation of a multi-layered soil with anisotropic permeability and compressibility constituents[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(5): 801. DOI:10.3321/j.issn:0459-1879.2009.05.025 |
| [16] |
徐进, 蔡正银, 王旭东. 孔隙流体可压缩各向异性土体三维固结半解析数值模拟[J]. 岩石力学与工程学报, 2012, 31(5): 1049. XU Jin, CAI Zhengyin, WANG Xudong. Semi-analytical numerical simulation for three-dimensional consolidation of compressible anisotropic soil with pore fluid[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(5): 1049. DOI:10.3969/j.issn.1000-6915.2012.05.023 |
| [17] |
徐进, 王旭东, 蔡正银. 抽水引起三维流固耦合问题的有限层法[J]. 岩土工程学报, 2013, 35(9): 1683. XU Jin, WANG Xudong, CAI Zhengyin. Finite layer method for 3D coupled flow-deformation response due to pumping[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(9): 1683. |
| [18] |
CHEN G J. Consolidation of multilayered half space with anisotropic permeability and compressible constituents[J]. International Journal of Solids and Structures, 2004, 41(16/17): 4567. |
| [19] |
FREDLUND D G, RAHARDJO H, FREDLUND M D. Unsaturated soil mechanics in engineering practice[M]. New York: John Wiley & Sons, 2012: 783.
|
| [20] |
龚晓南. 地基处理新技术[M]. 西安: 陕西科学技术出版社, 1997. GONG Xiaonan. New technique of ground treatment[M]. Xi'an: Shaanxi Science and Technology Press, 1997. |
| [21] |
李明奇, 田太心. 数学物理方程[M]. 成都: 电子科技大学出版社, 2014. LI Mingqi, TIAN Taixin. Equations of mathematical physics[M]. Chengdu: University of Electronic Science and Technology of China Press, 2014. |
 2021, Vol. 53
2021, Vol. 53


