2. 廊坊师范学院 建筑工程学院,河北 廊坊 065000;
3. 强震区轨道交通工程抗震研究北京市国际科技合作基地(北京科技大学),北京 100083;
4. 北京市住房和城乡建设科学技术研究所,北京 100083
2. School of Architecture and Civil Engineering, Langfang Normal University, Langfang 065000, Hebei, China;
3. Beijing International Cooperation Base for Science and Technology-Aseismic Research of the Rail Transit Engineering in the Strong Motion Area (University of Science and Technology Beijing), Beijing 100083, China;
4. Beijing Science and Technology Institute of Housing and Urban-Rural Development, Beijing 100083, China
中国既有老旧农宅分布广泛,且抗震性能差,为保障其内住户的生命财产安全,对既有老旧农宅进行修补与加固具有重要现实意义。近年来许多专家学者利用振动台对砌体结构的动力特性及抗震性能进行了研究。刘琛等[1]通过振动台试验验证了钢筋网水泥砂浆面层加固方法对砖砌体房屋整体加固的有效性。张明杰等[2]通过振动台试验表明,初始裂缝的存在使得碳纤维布在加固砌体结构时能够更加有效地发挥其加固性能。杨韬等[3]对加固与未加固的砌体结构模型进行了多种工况下的振动台试验,研究了钢筋-砂浆面层交叉条带法加固砌体结构的整体抗震性能。Benedetti等[4]对缩尺比例为1∶2的砖石建筑模型进行了受损和加固修复试验,其试验结果可评估所采用的各种加固技术的效率。Das等[5]通过振动台试验验证了无黏结纤维增强弹性隔震器能有效降低砌体结构的动力响应。Meoni等[6]提出了一种称为“智能砖”的新型传感技术,用于检测和定位未加筋砖房在振动台试验中的地震损伤。
钢框架与钢板带的设计依据是《北京市农村危房加固维修技术指南(试行)》[7]中的房屋增设内钢框架加固方式,该指南针对北京市农村地区20世纪80—90年代建造的典型农宅的结构特点,结合农村住宅抗震综合改造的实践经验,提供了一种加固方式,但并无具体的结构参考数值,本结构加固设计主要依据GB 50017—2017《钢结构设计标准》[8]和GB 50011—2010《建筑抗震设计规范》[9]中的相关规定。基于此思路本文提出了一种以内嵌式轻型钢框架加固为主,钢板带加固为辅的加固方法,设计了1/4的砌体结构振动台模型,采用振动台试验的方式,分析了加固前后砌体结构模型的抗震效果。
1 振动台试验模型设计 1.1 相似比设计在缩尺模型结构试验设计中,应优先满足非原型材料全质量相似比与原型材料全质量相似比[10],但通常由于振动台承载力的限制,全质量相似比设计存在困难,故常采用欠人工质量相似比,本文采用原型材料欠人工质量相似比,相似条件见表 1。
| 表 1 振动台模型试验中的相似条件 Tab. 1 Similarity conditions in shaking table model test |
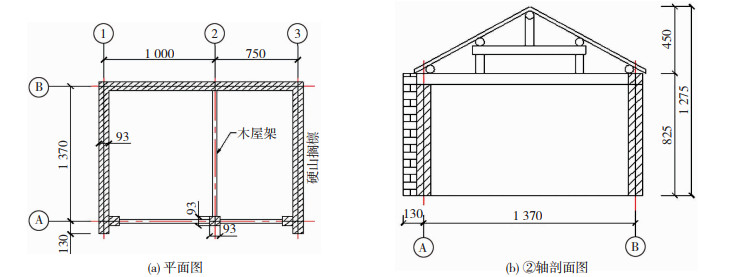
试验模型的几何长度相似比为1/4,模型不设内隔墙,根据振动台尺寸及承载能力,设计的砌体结构振动台模型见图 1。模型自重为0.85 t,按振动台试验模型质量相似比,模型质量应为1.7 t,所以约需加配重0.85 t。
|
图 1 缩尺后的农房平立剖面图(mm) Fig. 1 Cross section of farmhouse after scale reducing (mm) |
在结构长度与宽度方向采用1/4缩尺比,在厚度方向采用1/2缩尺比,即模型砖尺寸约为60 mm×28 mm×26 mm。厚度方向缩尺比的改变,可避免由于厚度方向过薄而易产生的拉弯复合应力下的破坏,并不影响结构的整体尺寸。砌筑模型时,灰缝厚度为3~5 mm,外墙采用切割后的小砖按照三七墙的砌筑方式进行砌筑,不设内隔墙。
考虑到双面坡屋顶不便于固定配重件,将配重质量等效到檐口高度处,同时为避免震动过程中模型与配重件的相互移动,将配重件简化为两块混凝土板,底层混凝土板与墙体砌筑在一起,在振动时不会发生滑移,底层混凝土板上浇筑平面尺寸小于自身的一层素混凝土以达到配重要求,最后基于底层配筋混凝土板完成山墙尖及屋盖的施工,具体增加配重方案见图 2。

|
图 2 配重方案(mm) Fig. 2 Counterweight scheme (mm) |
由于结构前后纵墙开洞不规则不对称,会使前后纵墙的刚度不对称,为增加房屋的抗震性能及整体的抗侧刚度,根据内框架加固的思路,确定加固方案如下:在房间的四角布置3.3 m高的钢柱,钢柱采用薄壁方钢管,其规格为B□150×5,钢梁采用窄翼缘H型钢,其规格为HN250×125×6×9,钢屋架采用等肢角钢,其规格为∟125×8。内框架结构示意图见图 3。框架柱的基础采用素混凝土基础,混凝土强度等级为C30,基础尺寸为300 mm×300 mm×500 mm,框架柱埋入混凝土基础中300 mm。

|
图 3 内嵌式轻型钢框架结构示意 Fig. 3 Schematic diagram of embedded light steel frame structure |
在进行加固施工时,通过手钻从结构内部打穿钢管并继而打穿墙体,随后采用穿墙螺栓进行固定。结构中沿墙体高度方向每隔1 000 mm设置一道螺栓。沿柱高方向均匀打两个孔用于固定,由于不设内隔墙,边柱沿两个方向打孔,中柱只沿Y向打孔。加固后的具体效果见图 4。

|
图 4 加固效果 Fig. 4 Reinforcement effect |
钢板采用厚度为0.5 mm的薄钢板,并将其裁为宽度为50 mm的钢板条,将钢板条对应于穿墙螺栓的位置打孔,将垫片、钢板条、墙体与内钢框架通过穿墙螺栓固定在一起,钢板条靠近墙体一侧用免钉胶与墙体进行加强粘接。本试验只在两侧山墙进行钢板条的加固,在山墙尖处围成三角形,下部围一矩形,并在其对角再拉接一道钢板条,前后纵墙不进行钢板条加固。
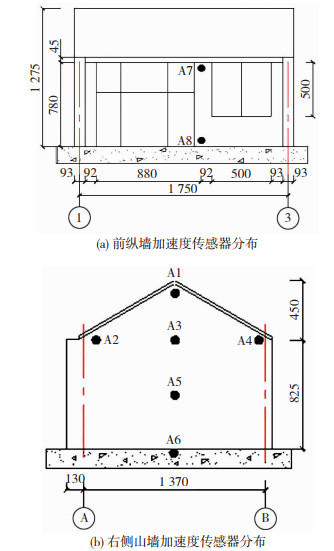
3 振动台试验方案 3.1 加速度传感器与位移传感器布置1) 加速度传感器共有8个,型号为LC0701-5M,编号为A1~A8。分别布置于右侧山墙前后檐口、前纵墙砖柱上下端与混凝土底座处,并在右侧山墙中部沿高度方向均布3个加速度传感器,具体布置形式见图 5。
|
图 5 加速度传感器分布(mm) Fig. 5 Distribution of acceleration sensors (mm) |
2) 位移传感器共有3个,型号为LXW-510 VOT 500,编号为U1~U3。分别布置于右侧山墙前后檐口处与山墙基底中部处,具体布置形式见图 6。

|
图 6 位移传感器分布(mm) Fig. 6 Distribution of displacement sensors (mm) |
根据GB 50011—2010《建筑抗震设计规范》中8度基本烈度的Ⅱ类及Ⅲ类场地的设计反应谱与地震波反应谱,反应谱曲线见图 7,在结构自振周期处,EL Centro波、Taft波及San Fernando地震波的反应谱能够和设计反应谱较好拟合,根据自振周期处不同地震波反应谱谱值大小,得出地震波输入顺序为EL Centro波、San Fernando波和Taft波。

|
图 7 加速度反应谱 Fig. 7 Acceleration response spectrum |
选取8度EL Centro小震、San Fernando小震、Taft小震、EL Centro中震及EL Centro大震共5组工况,沿着砌体结构的弱轴方向进行加震。在结构养护完成后,加震之前首先对结构进行锤击试验,来测定结构的自振频率,之后每次加震结束都采用锤击法测定其自振频率。对未加固的模型进行小震加载,随后采用穿墙螺栓将框架柱与墙体拧紧,并在山墙外侧粘贴钢板条,再进行中震与大震下的加载试验。具体加载工况见表 2。
| 表 2 加载工况一览表 Tab. 2 List of loading conditions |
首先对结构施加EL Centro波、San Fernando波及Taft波的小震作用,在此阶段不进行内钢框架的加固。由于地震荷载沿结构纵向施加,山墙易产生平面外破坏,结构右侧山墙出现了细微斜裂缝,裂缝宽度在1 mm之内,在左侧山墙的纵横墙交接处则产生了较大的裂缝,裂缝宽度大约为2~3 mm,而后纵墙几乎没有损伤。小震作用下结构损伤见图 8。

|
图 8 小震作用下结构损伤 Fig. 8 Structural damage under small earthquake |
在中震加载过程中,结构表面的石灰粉随着震动有少许脱落。由于内钢框架的加固作用,在震动时,纵横墙交接处的裂缝并未进一步向下发展,外部钢板带也阻止了左侧山墙墙体外闪,见图 9(a)。右侧山墙的裂缝主要集中在左上角,裂缝宽度进一步增大,由于钢板带与钢框架的加固作用,虽然裂缝宽度很大,但并未出现墙体砖块掉落的现象,在对角钢板带的下方出现了一条肉眼可见的新的斜裂缝,裂缝宽度在1 mm之内,见图 9(b)。

|
图 9 中震作用下结构损伤 Fig. 9 Structural damage under moderate earthquake |
大震加载时,结构前纵墙的左上角与砖柱破坏严重,并出现了墙体砖块掉落的现象,见图 10(a)。结构的后纵墙损伤较轻,但局部也产生了严重破坏,后纵墙左上角最大裂缝宽度达12 mm,墙角几乎要掉落,见图 10(b)。

|
图 10 大震作用下结构损伤 Fig. 10 Structural damage under large earthquake |
在大震加载过程中,可以明显观察到模型两侧的山墙发生左右晃动,但由于内框架与钢板带的约束作用,结构并未发生整体倒塌。大震过后结构的左侧山墙外倾程度更大,墙体左上角边缘外闪25 mm,但钢板条并未与墙体脱离,有效阻止了墙体倒塌。钢板带在墙体变形较大的位置发生局部屈曲,防止了墙体散落。大震作用下山墙的破坏损伤情况见图 11。

|
图 11 山墙损伤 Fig. 11 Gable damage |
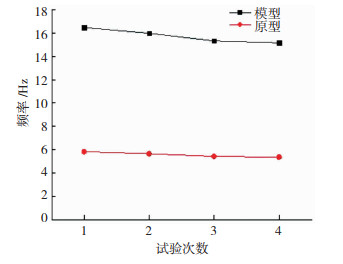
采用锤击法测定农宅结构的自振频率,在山墙的每个加速度传感器附近进行锤击,采集信号,取各个数值的平均值。模型的自振频率会随着地震波的加载逐渐发生变化,4次锤击试验的结果见表 3,模型与原型的自振频率变化见图 12。
| 表 3 模型自振频率 Tab. 3 Natural frequency of model |
|
图 12 自振频率变化 Fig. 12 Variation of natural frequency |
从锤击试验结果可知结构的自振频率在整体上随着地震波的加载呈现逐渐衰减的趋势,这是因为结构在逐次加载的过程中,损伤逐渐积累,裂缝不断发展,刚度逐渐降低,导致结构自振频率衰减。
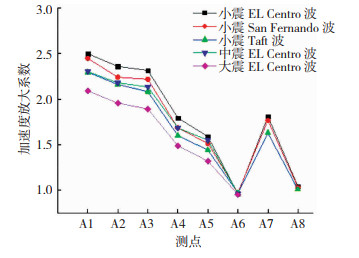
4.2.2 加速度响应分析记录A1~A8各测点在小震作用下的加速度数据,在小震作用下,基座的加速度响应峰值小于0.7 m/s2,振动台输出地震波小于输入地震波,由于中震及大震时结构前纵墙的砖柱发生了局部倒塌,因此不再记录前纵墙砖柱在中震及大震作用下的加速度数据。计算可得A1~A8各测点在不同地震波下的加速度放大系数,见图 13。山墙处6个测点的加速度放大系数随地震波加载工况变化情况见图 14。
|
图 13 A1~A8加速度响应 Fig. 13 Acceleration responses of A1-A8 |

|
图 14 A1~A6加速度响应 Fig. 14 Acceleration responses of A1-A6 |
从图 13、14可看出,结构的加速度放大系数随着测点高度的增加逐渐增大,随着地震强度的增加,在整体上呈现减小的趋势,在采用内嵌式钢框架与钢板带组合加固后,结构的加速度放大系数有微小的增大趋势。这是由于地震强度越大,墙体的塑性发展越快,结构发生破坏,墙体的抗侧刚度减小,频率减小的缘故。而中震时采取了加固措施,结构的刚度略微增加,因此加速度放大系数略有增大。
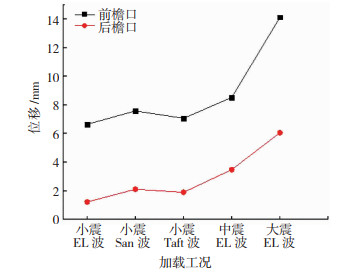
4.2.3 位移响应分析5次加震工况下结构前后檐口处的位移变化见图 15。
|
图 15 前后檐口位移变化 Fig. 15 Displacement variation of front and rear cornices |
从图 15可知,在8度EL Centro波小震作用下,前后檐口处的最大位移分别为6.63、1.2 mm,最大位移角分别为1/498、1/2 750;8度San Fernando波小震作用下,前后檐口处的最大位移分别为7.56、2.09 mm,最大位移角分别为1/437、1/1 579;8度Taft波小震作用下,前后檐口处的最大位移分别为7.06、1.87 mm,最大位移角分别为1/467、1/1 765;8度EL Centro波中震作用下,前后檐口处最大位移分别为8.5、3.46 mm,最大位移角分别为1/388、1/954;在8度EL Centro波大震作用下,前后檐口处的最大位移分别为14.1、6.04 mm,最大位移角分别为1/234、1/546。参考砌体结构位移角建议限值[11],见表 4。
| 表 4 砌体结构位移角建议限值 Tab. 4 Recommended limit values of displacement angle of masonry structure |
从表 4可知采用内钢框架与钢板带进行加固后,在8度大震作用下,结构并未达到“严重破坏”。该结构的前后纵墙刚度相差较大,从图 15可知结构的位移随着震级的增大而增大,且前檐口的位移很明显大于后檐口的位移,说明结构出现了扭转效应。
4.2.4 内嵌式钢框架试验现象大震过后内嵌式钢框架的试验现象见图 16,框架结构在大震后仍然保持未损坏的状态,框架柱底端伸入混凝土底座,可视为刚性固定端,大震过后钢框架柱与混凝土底座的连接依然非常牢固,并未出现框架柱倾倒或框架柱底端拔出的现象。框架梁柱节点连接牢固,未出现梁柱脱开现象。框架柱也未出现整体失稳或局部屈曲的现象。从试验结果可以推断出,大震过程中内钢框架一直处于弹性阶段,未出现明显的变形,使结构的安全性得以保障。

|
图 16 大震过后框架柱的试验现象 Fig. 16 Experimental phenomena of frame columns after large earthquake |
1) 本文根据内框架加固思路提出了一种以内嵌式轻型钢框架加固为主,钢板带加固为辅的加固方法,设计了相似比为1/4的砌体结构振动台模型,采用振动台试验的方式,分析验证了其可行性与实用性。
2) 砌体结构模型的主要损伤位置集中在前纵墙、两侧山墙以及纵横墙交接处。随着所加载的地震等级增大,结构的自振频率与加速度放大系数在整体上逐渐减小,结构前后纵墙刚度相差过大,前檐口的位移大于后檐口的位移,出现了扭转效应,但由于内钢框架的加固作用,结构并未达到“严重破坏”。
3) “钢框架-砖墙-钢板带”的组合可以优势互补,钢框架增加结构整体的抗弯强度,防止发生整体倒塌,钢板带约束墙体,增强墙体抗拉性能及整体性,三者的力学性能互为补充,使加固后的结构达到了“大震不倒”的设防目标。
| [1] |
刘琛, 刘洁平, 张令心, 等. 钢筋网水泥砂浆面层加固砖砌体结构振动台模型设计[J]. 结构工程师, 2012, 28(6): 72. LIU Chen, LIU Jieping, ZHANG Lingxin, et al. Shaking table model design for brick masonry structures strengthened with an externally steel reinforced mesh mortar layer[J]. Structural Engineers, 2012, 28(6): 72. DOI:10.15935/j.cnki.jggcs.2012.06.020 |
| [2] |
张明杰, 徐礼华, 陈乾浩, 等. 碳纤维布加固开裂砌体结构振动台试验[J]. 武汉大学学报(工学版), 2015, 48(3): 306. ZHANG Mingjie, XU Lihua, CHEN Qianhao, et al. Shaking table tests of CFRP-strengthened masonry structures with initial cracks[J]. Engineering Journal of Wuhan University, 2015, 48(3): 306. DOI:10.14188/j.1671-8844.2015-03-004 |
| [3] |
杨韬, 周献祥, 罗瑞, 等. 钢筋-砂浆面层交叉条带法加固砌体结构振动台试验研究[J]. 建筑结构, 2019, 49(5): 9. YANG Tao, ZHOU Xianxiang, LUO Rui, et al. Shaking table test study on masonry structure reinforced by using steel bar-mortar layer crossed strip method[J]. Building Structure, 2019, 49(5): 9. DOI:10.19701/j.jzjg.2019.05.002 |
| [4] |
BENEDETTI D, CARYDIS P, PEZZOLI P. Shaking table tests on 24 simple masonry buildings[J]. Earthquake Engineering & Structural Dynamics, 1998, 27(1): 67. DOI:10.1002/(SICI)1096-9845(199801)27:1<67::AID-EQE719>3.0.CO;2-K |
| [5] |
DAS A, DEB S K, DUTTA A. Shake table testing of un-reinforced brick masonry building test model isolated by U-FREI[J]. Earthquake Engineering & Structural Dynamics, 2016, 45(2): 253. DOI:10.1002/eqe.2626 |
| [6] |
MEONI A, D'ALESSANDRO A, CAVALAGLI N, et al. Shaking table tests on a masonry building monitored using smart bricks: Damage detection and localization[J]. Earthquake Engineering & Structural Dynamics, 2019, 48(8): 910. DOI:10.1002/eqe.3166 |
| [7] |
北京市农村危房加固维修技术指南(试行)[M]. 北京: 中国建筑工业出版社, 2016: 60 Technical guide for reinforcement and maintenance of rural dilapidated buildings in Beijing (trial version)[M]. Beijing: China Architecture & Building Press, 2016: 60 |
| [8] |
钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2017 Standard for design of steel structures: GB 50017—2017[S]. Beijing: China Architecture & Building Press, 2017 |
| [9] |
建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [10] |
陈再现, 陈芍桥, 吴斌, 等. 缩尺模型子结构混合模拟试验方法数值模拟研究[J]. 哈尔滨工业大学学报, 2016, 48(6): 51. CHEN Zaixian, CHEN Shaoqiao, WU Bin, et al. Numerical simulation of substructure hybrid simulation test method for the scale model[J]. Journal of Harbin Institute of Technology, 2016, 48(6): 51. DOI:10.11918/j.issn.0367-6234.2016.06.008 |
| [11] |
苏启旺, 许浒, 吴昊, 等. 砖砌体结构层间位移角的探讨[J]. 土木工程学报, 2013, 46(增刊1): 111. SU Qiwang, XU Hu, WU Hao, et al. Research on inter-story displacement angle of brick masonry structures[J]. China Civil Engineering Journal, 2013, 46(S1): 111. DOI:10.15951/j.tmgcxb.2013.s1.041 |
 2021, Vol. 53
2021, Vol. 53


