2. 同济大学 环境科学与工程学院,上海 200092
2. College of Environmental Science and Engineering, Tongji University, Shanghai 200092, China
随着城市化进程的加快,多水源供水格局日渐增多,管网水质风险点往往分布于混合供水带、老化管道和管网末梢[1-2]。其中,混合供水带是不同水质出厂水的交汇处,易引起营养互补和生物化学反应,造成余氯损耗。该区域水压不稳定,水流方向和流速频繁变化,管壁沉积物和生物膜易被冲起,会增大浊度、加速铁释放。此外,供水量改变、水压调节等均可能改变原有水力条件,使混合供水带波动或明显偏移,造成流经附近管道的水体突变,加大"黄水"风险[3-5]。准确预测混合供水带可以更有针对性地监测和改善局部水质问题。
混合供水带一般可用水力模型预测,部分研究中也辅以水质检测,修正预测结果。水力模型通常预测供水分界线,表征不同水厂的供水界限。李黎武等[6]利用拓扑理论,提出了一种在管网水力计算基础上,确定供水分界线的自动绘制方法。阎立华等[7]基于管网水力计算的平差结果,根据图论原理,得出了判断供水分界线的矩阵。EPANET等软件也常用于各类水力建模[8-9]。邢翔轩[10]选取水力模型预测分界线附近的一系列点做水质检测,根据不同水厂出水指标的显著差异,修正并确定了实际供水分界线及其漂移带。
建立水力模型需要大量管网数据,过程复杂,耗时较长[1]。而由于水源、处理工艺等区别,不同水厂出厂水可能存在差异较大的水质指标,如电导率、余氯、无机盐含量等,这些指标在管网中按一定规律分布,具有明显识别特征,可以作为特征指标,判断混合供水带位置。
采用空间插值法可以将样点水质指标等离散的测量数据转换为连续的数据曲面,包括空间内插和外推两种算法,在森林资源、气温、GDP、供水水压、土壤元素等空间分布分析中都有相关应用[11-12]。任学蓉等[13]利用克里金空间内插法研究了沙湖水质主要因子的空间分布特征。沙湖平面与地理空间相对应,直接利用空间插值法计算,所得结果与实际情况相近,但是对于按一定管道流动的管网水,直接按地理空间插值研究并不合适。
因此,以双水厂供水的H市为例,不同于常用的水力模型法,基于特征水质指标,采用空间插值法预测混合供水带。在插值过程中,考虑到管网分布与地理空间差异,对特征指标进行修正。得到预测混合供水带后,定义"虚拟中线",与水力模型模拟结果进行比较,并结合实际监测点的流速、流向等变化情况,验证该方法的合理性。
1 研究方法 1.1 特征水质指标水质指标是指水样中除水分子外所含杂质的种类和数量,是描述水质状况的一系列指标。定义特征水质指标为:多水源供水地区,不同水厂出厂水差异较大,在管网中按一定规律分布,可明显识别混合供水带的水质指标。具体来说应满足以下条件:
1) 在不同水厂出厂水中数值差异足够大(一般相差1倍以上),使其在混合供水带,由物理混掺引起的数值变化,远大于混掺前随水体流动而产生的其他增减变化,达到可明显识别混合带的要求。
2) 在管网中规律分布,随水体流动距离的增加而递增(减)或稳定不变,可做出较规律的带状插值图。部分指标如温度、pH、溶解氧等受环境因素影响大,在管网中分布杂乱,一般不作为特征指标。
3) 在混合供水带的数值变化以物理混掺影响为主。
根据特征水质指标在混合供水带的数值变化特征,又可将其分为一般特征指标和敏感特征指标。一般特征指标如电导率、硬度等,在混合供水带通常不会因物理混掺以外原因发生明显数值变化;而敏感特征指标如铁、余氯等,则可能因为混合供水带特殊的水力水质情况,发生化学、生物反应,出现数值特别大或特别小的异常点,需进一步修正插值结果,去除异常点的影响。在实际应用中,可根据水厂指标差异,合理选择特征指标。
H市主要由西侧的C水厂和东侧的T水厂供水,东西两侧供水区域之间存在混合供水带。连续一个月检测两水厂出厂水部分水质指标,并取平均值,如表 1所示。可以看出,两水厂出厂水浊度、余氯、电导率、硬度、总铁质量浓度等指标差异均较大(>100%),从中选取差异最大的两个指标——电导率和总铁质量浓度作为本次研究的特征水质指标。其中,总铁质量浓度为敏感特征指标,插值前需去除异常点的影响,具体修正方法见1.2。
| 表 1 出厂水水质指标对比 Tab. 1 Contrast of water quality indices of finished water |
在C、T两水厂间,相对均匀地选择采样点(相邻两点距离约2 km),并在预计可能的混合供水区域适当增加样点,使插值结果更准确。以电导率为例,初步分析其在管网中的变化规律,如图 1所示。横、纵坐标分别表示样点到C、T水厂的距离以及电导率大小。由图 1可知,两种水的电导率因在混合供水带混掺而发生突变,大小为200~230 μs/cm,变化幅度远大于混掺前的数值变化,符合特征水质指标要求。

|
图 1 电导率空间变化 Fig. 1 Spatial variation of electrical conductivity |
一般认为,不同出厂水均匀混掺区域(各水厂水所占比例相近)为主要的混合供水带影响区[3],故将C水厂与T水厂水按4∶ 6、5∶ 5、6∶ 4的比例进行混掺,进一步确定混合供水带电导率在200~250 μs/cm。
1.2 空间修正插值法克里金法是一种常用的空间插值方法,可以利用已知样本点的统计特性,量化它们之间的空间自相关性,并说明采样点在预测区域范围内的空间分布情况,是一种线性、无偏、方差最小的空间内插方法[14]。与反向距离权重法不同,其不仅考虑了预测点与样本点之间的位置关系,而且通过变异函数和结构分析,考虑了样本点之间的空间相关关系及与未知点的空间分布关系[11]。其实质是利用区域化变量的原始数据和变异函数的结构特点,对未知样本点进行线性无偏、最优估计。由于该方法有坚实的理论基础,插值效果往往更接近于实际情况。
克里金法的插值公式为
| $ {z^*}\left( {{x_0}} \right) = \sum\limits_{i = 1}^n {{\lambda _i}} z\left( {{x_i}} \right) $ | (1) |
式中:z*(x0)为未知点x0处的预测值,z(xi)为已知点xi处的检测值,λi为权重,与地理位置关系有关。
其估计值误差的方差为
| $ S = 2\sum\limits_{i = 1}^n {{\lambda _i}} \gamma \left( {{x_i} - {x_0}} \right) - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{\lambda _i}} } {\lambda _j}\gamma \left( {{x_i} - {x_j}} \right) $ | (2) |
| $ \sum\limits_{i = 1}^n {{\lambda _i}} = 1 $ | (3) |
| $ \gamma (h) = \frac{1}{{2{N_h}}}\sum\limits_{i = 1}^{{N_h}} {{{\left[ {z\left( {{x_i} + h} \right) - z\left( {{x_i}} \right)} \right]}^2}} $ | (4) |
式中:γ(h)为变异函数,h为分离距离,Nh为在(xi+h, xi)之间用来计算样本变异函数值的样本的对数。
在求估计方差的极小值时需引入一个拉格朗日乘数μ,即
| $ S = 2\sum\limits_{i = 1}^n {{\lambda _i}} \gamma \left( {{x_i} - {x_0}} \right) - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{\lambda _i}} } {\lambda _j}\gamma \left( {{x_i} - {x_j}} \right) - 2\mu \left( {\sum\limits_{i = 1}^n {{\lambda _i}} - 1} \right) $ | (5) |
为使估计方差最小,有
| $ \left\{ \begin{array}{l} \frac{{\partial S}}{{\partial {\lambda _1}}} = 0\\ \frac{{\partial S}}{{\partial {\lambda _2}}} = 0\\ \;\;\;\;\; \vdots \\ \frac{{\partial S}}{{\partial {\lambda _n}}} = 0 \end{array} \right. $ | (6) |
根据
| $ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 1}^n {{\lambda _i}} \gamma \left( {{x_i} - {x_j}} \right) + \mu = \gamma \left( {{x_j} - {x_0}} \right)}\\ {\sum\limits_{i = 1}^n {{\lambda _i}} = 1} \end{array}} \right. $ | (7) |
即
| $ \left| {\begin{array}{*{20}{c}} {{\gamma _{11}}}& \cdots &{{\gamma _{1n}}}&1\\ \vdots & \vdots & \vdots & \vdots \\ {{\gamma _{n1}}}& \cdots &{{\gamma _{nn}}}&1\\ 1& \cdots &1&0 \end{array}} \right|\left| {\begin{array}{*{20}{c}} {{\lambda _1}}\\ \vdots \\ {{\lambda _n}}\\ \mu \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {{\gamma _{01}}}\\ \vdots \\ {{\gamma _{0n}}}\\ 1 \end{array}} \right| $ | (8) |
得到所有的权重λ1,…, λn和拉格朗日乘数μ,其中,γij=γ(xi-xj),即距离为xi和xj之间的变异函数值。权重依赖于已知点和预测点之间的距离,同时也依赖于已知点之间的分布情况[15]。
本研究中,水在管网中流动,水质指标的数值分布不仅与地理空间有关,还与管网系统分布有关,故应先对插值方程中的相关系数进行修正。但是,管网系统分布复杂,管网点与水厂的地理直线距离和管网水实际流经管线距离的比值各不相同,难以推出统一的对应关系式,使得修正方程系数难以实现,故考虑直接修正水质指标数值,再进行空间插值分析。
引入地理直线距离和实际样点水流经管线距离的比值为修正系数ki,对各样点实测指标值进行修正。修正公式如下
| $ z{'_i} = {z_0} + \left( {{z_i} - {z_0}} \right) \times {k_i} $ | (9) |
| $ {k_i} = \frac{{{d_i}}}{{{s_i}}} $ | (10) |
式中:z0为出厂水水质指标实测值,zi为管网样点水质指标实测值,z′i为管网样点水质指标修正值,di为水厂与样点的地理直线距离,si为管网水从水厂到样点所流经管线距离。
si可通过已有的GIS系统统计得到,也可根据管网的余氯衰减规律推算。但是,余氯也是一个敏感指标,一般在混合供水带消耗较快,由此估算的混合供水区域样点si可能与实际值存在较大偏差,因此,结合GIS系统统计结果更为可靠。另外,管网系统分布复杂,从GIS图上看,从水厂到样点存在多条可能路径。目前借助EPANET等水力模型,可以模拟水流走向及节点流量分布等,以此模拟节点水龄,并较为准确地估算流经的管线距离。为了不借助水力模型,依据经济性原则,选取从水厂到样点的最短路径近似计算si;对于路径上个别节点间仍存在多条管线的情况取均值叠加。从研究结果来看,本文所用修正方法效果较好。
修正后的插值结果,各分布带对应的实际数值范围,可根据带内平均修正系数ki反推,分析整个管网区域水质指标分布规律时,以反推的实际数值范围为准。
1.3 水力模型及监测结果验证EPANET除了水力模拟功能外,还提供了水质模拟功能[9],包括模拟示踪剂随时间的变化情况,模拟反应物随时间的消耗和变化情况,计算水在管道中的停留时间,示踪从给定节点到任一节点的流量比例等。由此,EPANET可以研究不同水源的混合水、在整个系统中水的流动时间、余氯的衰减情况等[9]。
采集管网信息,用EPANET软件建立管网水力模型,通过示踪从给定节点到任一节点的流量比例,模拟管网混合供水带位置,其结果得到了较为广泛的认可[16]。另外,在所建模型中也可模拟各管段流速、流向情况,作为验证混合供水带的依据。
但是,由于水质指标受多种因素影响,据此插值预测的混合供水带边界可能不完全准确;而且不同水质指标与水力指标的变化梯度存在差异,可能使各预测结果的区域范围大小(即带宽)不同,导致难以比较。因此,本文定义带宽的中线为"虚拟中线",认为其在一定程度上标识了混合供水带的位置及走向特征。在进行结果比较时,分别取水力模型、特征水质指标空间插值预测结果的"虚拟中线"进行比较,若"虚拟中线"基本重合,则认为预测结果基本相符。
另外,设置在线监测点,根据实际流速、流向变化,可以更直观地验证混合供水带预测结果是否正确。同时,混合带内余氯、浊度等异常情况也可作为验证依据。
2 结果与讨论 2.1 一般特征指标预测结果以电导率为例,分别对修正前后的电导率插值分析,如图 2、3所示。图 2修正前混合供水带电导率在200~250 μs/cm,图 3修正后混合供水带电导率为190~240 μs/cm。图 2黑色虚线、图 3白色虚线分别为电导率修正前后预测的混合供水带"虚拟中线",所在带状区域宽度表示带宽。

|
图 2 电导率修正前混合供水带预测 Fig. 2 Prediction of mixed water supply zone before conductivity correction |

|
图 3 电导率修正后混合供水带预测 Fig. 3 Prediction of mixed water supply zone after conductivity correction |
对比图 2、3可知,修正前后电导率空间分布情况及变化规律相近。这也说明同一分布带的修正系数ki相近,根据带内平均修正系数ki反推实际数值范围较为合理。如图 3混合供水带电导率反推后仍为200~250 μs/cm。
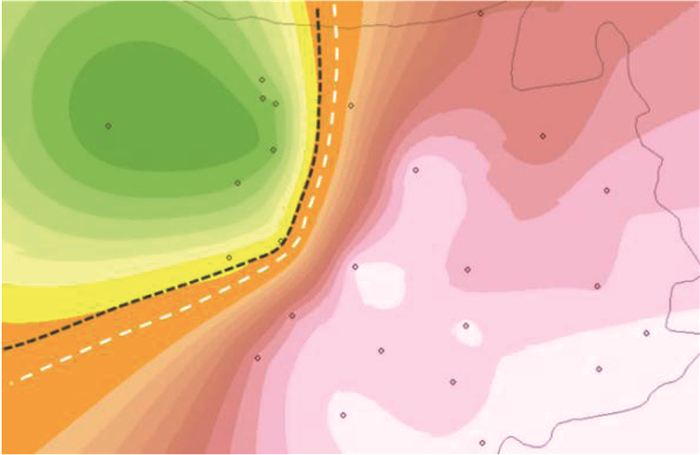
将两种插值结果加载至一张图中(如图 4所示),比较"虚拟中线"位置可知,修正后的预测结果较修正前整体向右侧偏移。
|
图 4 电导率修正前后预测结果对比 Fig. 4 Comparison of prediction results before and after conductivity correction |
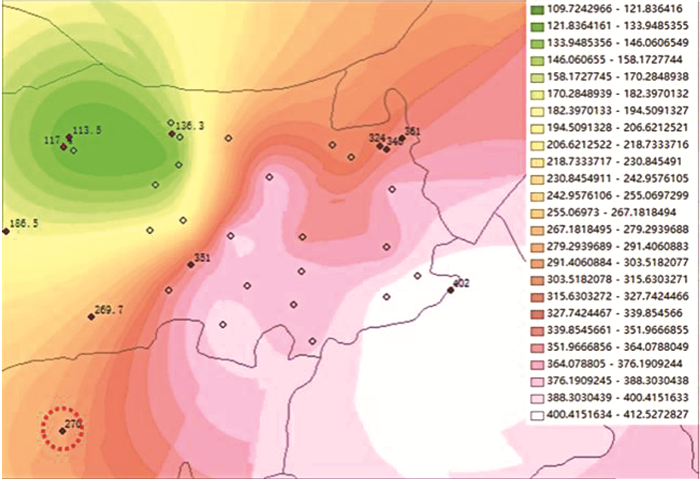
为检验克里金空间修正插值结果的可靠性,除上述插值点(26个样点)外,另取11个样点,验证其修正电导率值与预测结果是否一致,如图 5所示。图中空心点为插值点,实心点为检验点,具体检验结果见表 2。
|
图 5 插值精度检验(修正后) Fig. 5 Interpolation accuracy test (revised) |
| 表 2 插值精度检验 Tab. 2 Interpolation accuracy test |
11个检测点中有10个点(91%)的修正电导率值与预测插值带中值偏差小于5%。仅1个点偏差9.2%(图 5虚线圈所示位置),该点与水厂距离最远,从地图上看已在H市边缘地带。综合来看,本研究所采用的插值结果精度较好。
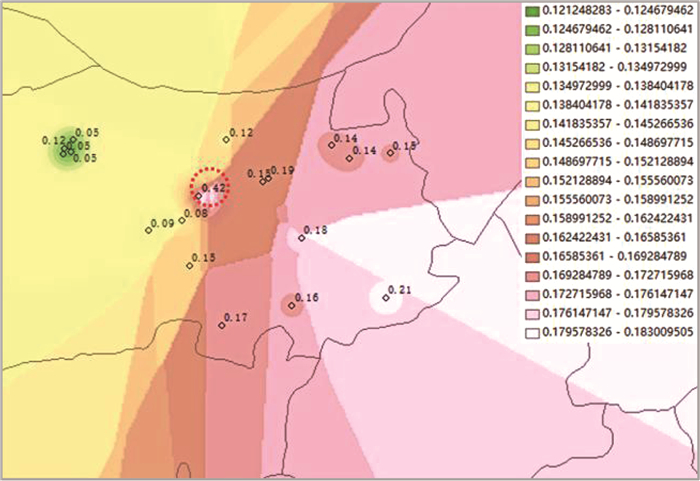
2.2 敏感特征指标预测结果同样地,根据各样点总铁质量浓度的修正值,可以得到初步预测结果,如图 6所示。总铁质量浓度属于敏感特征指标,部分位于混合供水带的样点,其总铁质量浓度可能因化学、生物反应发生明显变化,影响插值结果。图 6显示,未去除异常点的插值结果较为混乱,且没有预判数值为0.10~0.12 mg/L的混合带。
|
图 6 总铁质量浓度修正值空间插值预测结果(未去除异常点) Fig. 6 Spatial interpolation prediction of total iron concentration correction (no abnormal points removed) |
正常情况下,水质指标一般在管网中连续变化,少有突变点。若出现数值特别大或特别小的异常点,需考虑是否为测量误差(错误)或存在特殊变化(敏感点),无论是哪种情况,在插值处理前均应剔除这些异常点,再对其他数据进行插值分析。此后观察去除的异常点是否在预测的混合供水带内,可作为判断该点异常原因的一个依据;若在,则很可能是因化学生物反应发生"突变"的水质敏感点,需重点关注。
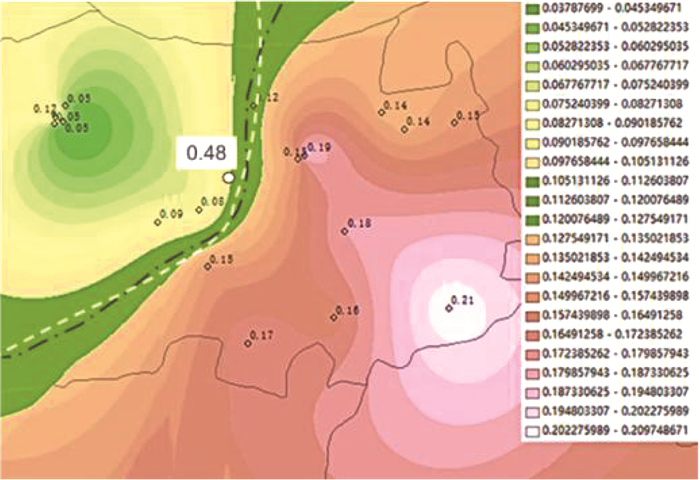
在H市各样点中,图 6虚线圈内0.42 mg/L样点数值远大于其他样点,是其附近样点总铁质量浓度(0.08、0.15 mg/L)的3~5倍,去除该异常点重新得到插值结果,如图 7所示。黑色点划线即为去除异常点后总铁质量浓度空间修正插值预测的混合供水带"虚拟中线",与修正后电导率预测"虚拟中线"(白色虚线)基本吻合。所去除点在预测混合供水带边缘,该点未修正前实测总铁质量浓度为0.48 mg/L,大于0.3 mg/L,需关注该点的铁释放异常情况。
|
图 7 总铁质量浓度修正值空间插值预测结果(去除异常点) Fig. 7 Spatial interpolation prediction of total iron concentration correction (abnormal points removed) |
沿"虚拟中线"再次采样检测,统计发现有50%的样点总铁质量浓度大于0.3 mg/L,30%在0.10~0.12 mg/L。可见,混合供水带不稳定的水力水质条件确实可能加速该区域部分管段的铁释放,造成局部铁质量浓度超标,但并非整个区域都会出现铁超标现象。超标与否可能与不同区域的管段情况、用水量大小、流速等因素相关。
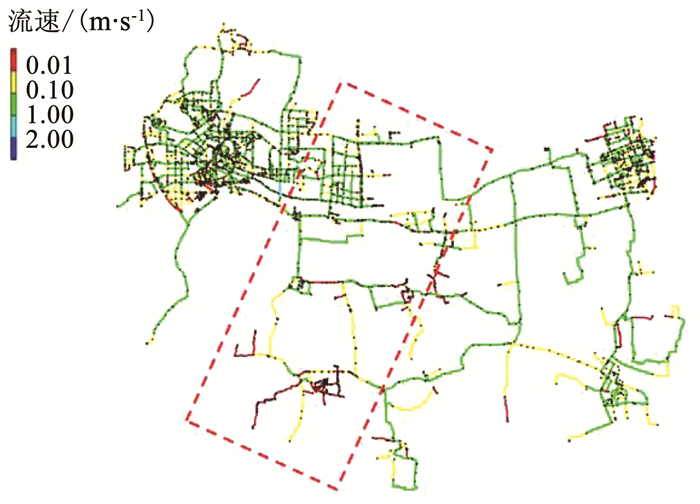
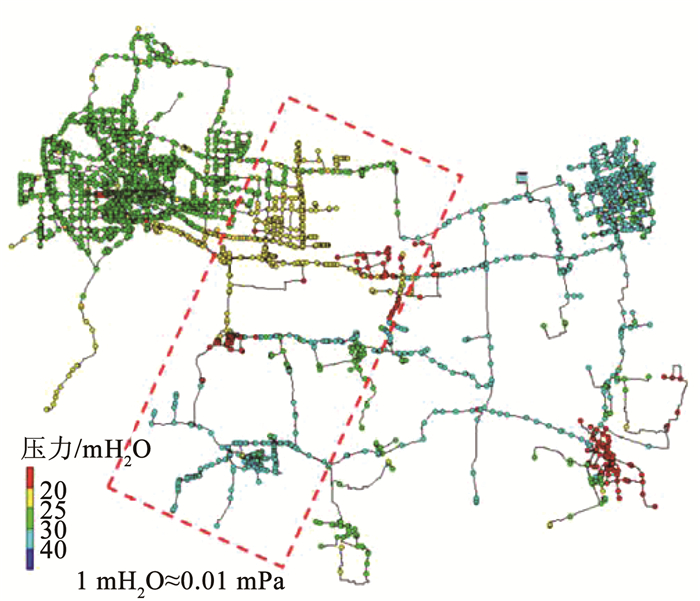
2.3 水力模型比较验证结果用EPANET软件建立H市供水管网模型,其管段流速分布、节点压力分布如图 8、9所示。由图 8、9可知,两水厂之间虚线框内区域存在压力较小且流速接近0(小于0.01)的节点和管段,符合混合供水带的水力特征。局部放大框内管段,观察其模拟流向,如图 10所示,图中箭头指向即为模拟水流方向。
|
图 8 管段流速模拟分布 Fig. 8 Simulated velocity distribution of pipe section |
|
图 9 节点压力模拟分布 Fig. 9 Simulated pressure distribution of nodes |
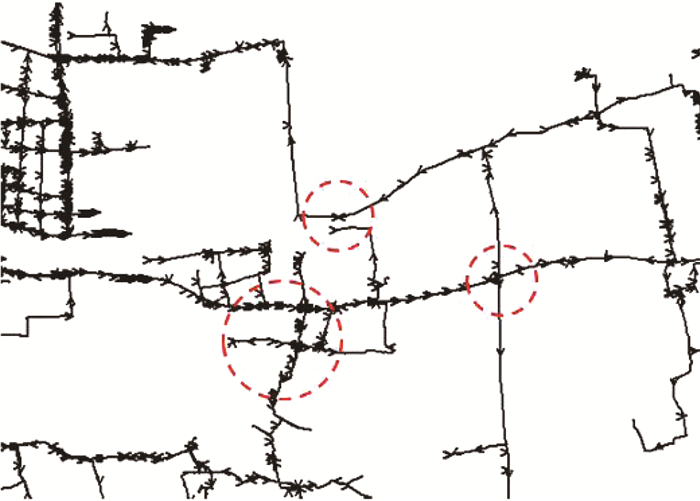
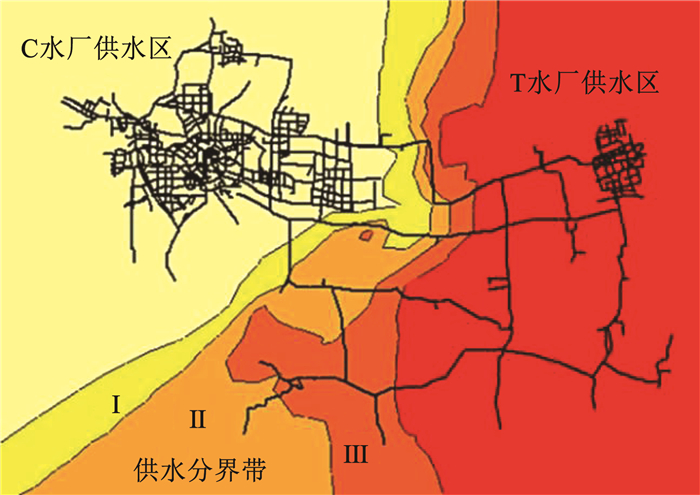
图 10中多处存在重叠管段上,有两个相反方向模拟水流的情况,符合混合供水带水力特征。综合图 8~10结果,可初步判断模拟混合供水带位于图示红色虚线框区域。示踪从给定节点到任一节点的流量比例,进一步更精确模拟混合供水带位置,结果如图 11所示。
|
图 10 局部模拟流向 Fig. 10 Local simulated flow direction |
|
图 11 水力模型模拟混合供水带 Fig. 11 Prediction of mixed water supply zone by hydraulic model |
图 11中Ⅱ区域即水力模型模拟的混合供水带主要影响区域(C水厂供水占比大于40%,小于60%),Ⅰ、Ⅲ为附近可能受影响区域,其余分别为两个水厂的单独供水区。
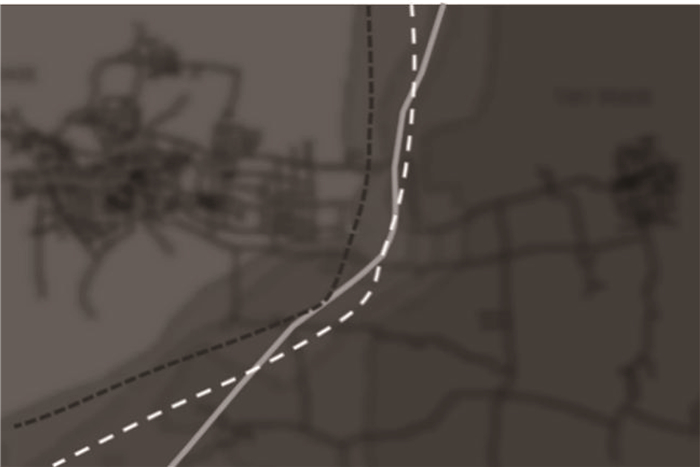
将修正前后的电导率空间插值预测结果与该结果对比,如图 12所示。修正后的"虚拟中线"(白色虚线)与水力模型"虚拟中线"(灰色实线)更接近。进一步考虑混合供水带重合面积,经对比,修正后电导率预测混合供水带与Ⅰ、Ⅱ、Ⅲ区均有重合,与Ⅱ区重合面积达86%;修正前混合供水带主要与Ⅰ、Ⅱ区重合,与Ⅱ区重合率约40%,整体偏左。综合来看,修正后的插值预测结果与水力模型预测结果更接近,二者基本吻合,但带宽等存在一定差异。
|
图 12 修正前后电导率插值预测结果与水力模型结果比较 Fig. 12 Comparison between results of hydraulic model and predicted results of conductivity interpolation before and after modification |
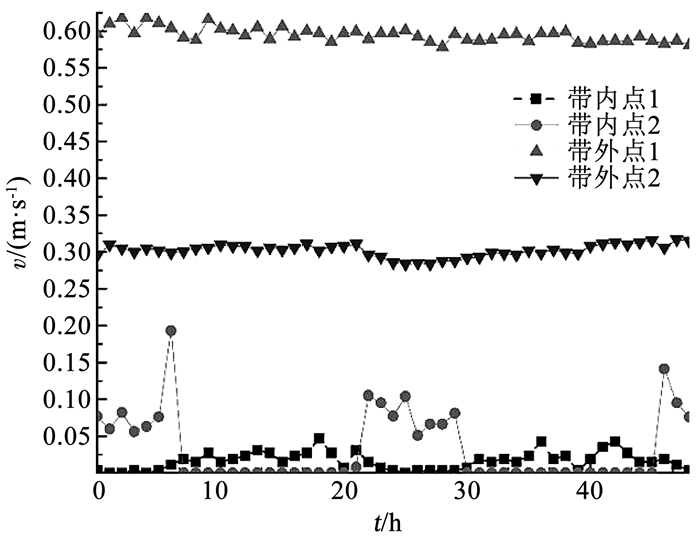
在本文所预测的混合供水带内设在线监测点,观测到流速、流向频繁变化,说明预测结果正确。图 13分别显示了带内、外4个监测点的单向流速变化,数据来自H市管网综合监测系统。其中,带外两点分别位于C、T水厂附近,带内两点则位于预测"虚拟中线"附近。带外点流速较快且稳定,流向不变;带内点流速慢且不稳定,流向频繁改变(流速为0)。监测流速由单向流量计数据计算得出,当流速为0时,说明原方向流量为0,发生了流向的改变。
|
图 13 混合供水带内外监测点流速变化 Fig. 13 Velocity variation at monitoring points inside and outside the mixed water supply zone |
混合供水带可能存在余氯偏低、浊度偏高问题,也可作为一个验证依据。图 14显示了H市余氯的空间分布情况(未引入修正系数,且未删除异常点)。可以看出,除距离C、T水厂较远的区域(图中下方绿色区域)余氯较低外,在两水厂之间预测混合带附近,余氯也呈较明显的带状分布,且质量浓度相对较低。

|
图 14 余氯插值结果 Fig. 14 Residual chlorine interpolation results |
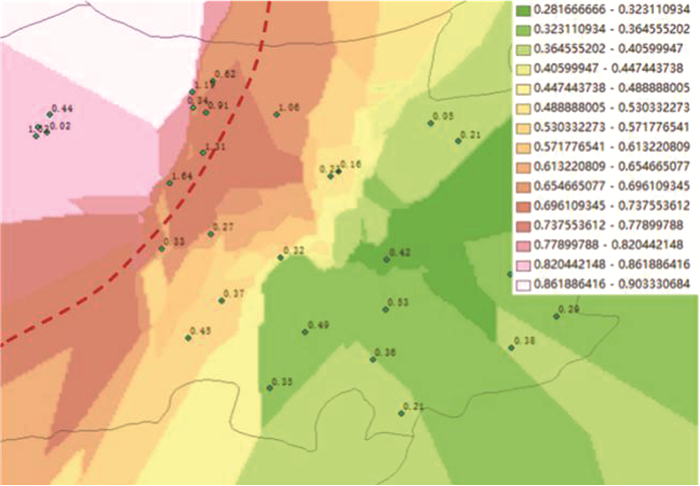
图 15为H市浊度空间分布情况(未引入修正系数,且未删除异常点),在预测混合带附近区域也近似呈带状分布,且数值偏高(0.65~0.77)。
|
图 15 浊度插值结果 Fig. 15 Turbidity interpolation results |
综合来看,余氯、浊度在预测混合带附近均近似呈带状分布,且存在数值不达标样点,说明预测结果正确。同时说明,混合供水带确实存在余氯偏低、浊度偏高的水质风险。
3 结论1) 提出了一种不依靠水力模型,利用水质检测和数据分析(空间修正及插值)来预测管网混合供水带位置的方法,并验证了其可行性。
2) 在分析特征水质指标时,注意到部分敏感指标在混合供水带的特殊变化,如铁、余氯等。这类指标预测混合供水带需进一步修正插值结果,去除异常点的影响。在空间插值分析前,考虑到管网分布与地理空间差异,根据地理直线距离与实际样点水流经管线距离的比值ki,修正了各样点实测指标数值,使插值预测结果更准确。
3) 提出的"特征水质指标空间修正插值法"预测的混合供水带区域,相比水力模型预测的物理混掺区域,更直接地反映了发生水质变化的混合带影响范围,对于实际监控可能存在水质问题的混合供水区域更具指导意义。该方法可用于城镇管网改扩建后,快速确定新的混合供水带位置,更有针对性地布置水质监测点,监控管网水力水质情况,改善局部水质问题。
| [1] |
任瑛. 城市供水管网风险分析与评价[D]. 西安: 西安建筑科技大学, 2011: 1 REN Ying. Risk analysis and evaluation on the municipal water supply network[D]. Xi'an: Xi'an University of Architecture and Technology, 2011: 1. DOI: 10.7666/d.d191534 |
| [2] |
YANG Q, LI H, WANG X, et al. Study on joint optimal operation of multi-source water supply of south-to-north water transfer project in Handan[J]. South-to-North Water Transfers and Water Science & Technology, 2007, 5: 37. |
| [3] |
黄廷林, 戴雪峰, 王旭冕, 等. 多水源供水管网中铁释放规律[J]. 环境工程学报, 2014, 8(3): 834. HUANG Tinglin, DAI Xuefeng, WANG Xumian, et al. Law of iron release in water supply network with multiple water resources[J]. Chinese Journal of Environmental Engineering, 2014, 8(3): 834. |
| [4] |
李礼, 李玉仙, 王敏, 等. 管垢差异对水源切换后铁释放程度的影响及其黄水风险判断[J]. 给水排水, 2016(增刊1): 273. LI Li, LI Yuxian, WANG Min, et al. The iron release rules of the pipes with different scale when water source switch and red water risk prediction[J]. Water & Wastewater Engineering, 2016(S1): 273. |
| [5] |
谭浩强, 何文杰, 韩宏大, 等. 水力条件对供水管网铁释放的影响研究[J]. 中国给水排水, 2014, 30(3): 56. TAN Haoqiang, HE Wenjie, HAN Hongda, et al. Effect of hydraulic conditions on iron release in water distribution system[J]. China Water & Wastewater, 2014, 30(3): 56. |
| [6] |
李黎武, 许仕荣, 施周. 多水源管网供水分界线及等水压线的动态模拟[J]. 湖南城建高等专科学校学报, 2001, 10(3): 46. LI Liwu, XU Shirong, SHI Zhou. A topological-based method for determination of source-serving districts and drawing pressure-contour in multi-source networks[J]. Journal of Hunan Urban Construction College, 2001, 10(3): 46. |
| [7] |
阎立华, 刘丽英, 马婷婷. 图论法研究多水源管网供水分区[J]. 沈阳建筑大学学报(自然科学版), 2007, 23(1): 113. YAN Lihua, LIU Liying, MA Tingting. Multi-source water supply network for subarea based on graphic theory[J]. Journal of Shenyang Jianzhu University (Natural Science), 2007, 23(1): 113. |
| [8] |
蒋仲安, 王佩, 施蕾蕾, 等. 基于低偏差序列的矿井供水管网可靠性[J]. 中南大学学报(自然科学版), 2014, 45(5): 1686. JIANG Zhongan, WANG Pei, SHI Leilei, et al. Mine water supply network reliability based on low deviation sequence[J]. Journal of Central South University (Science and Technology), 2014, 45(5): 1686. |
| [9] |
刘百仓, 林璐, 林佳琪, 等. EPANET在城市多水源供水管网水力及水质计算中的应用[J]. 给水排水, 2010, 46(增刊1): 416. LIU Baicang, LIN Lu, LIN Jiaqi, et al. Application of EPANET in hydraulic and water quality calculation of urban multi-source water supply network[J]. Water & Wastewater Engineering, 2010, 46(S1): 416. DOI:10.3969/j.issn.1002-8471.2010.z1.117 |
| [10] |
邢翔轩. 城市供水管网风险分析及评价[D]. 西安: 西安建筑科技大学, 2012: 1 XING Xiangxuan. Risk analysis and evaluation of urban water supply pipeline network[D]. Xi'an: Xi'an University of Architecture and Technology, 2012: 1. DOI: 10.7666/d.d244232 |
| [11] |
汪瑞清. 基于ArcGIS的供水水压插值法比较分析[J]. 净水技术, 2016, 35(4): 77. WANG Ruiqing. Analysis and comparison of several interpolation algorithms for supply pressure based on ArcGIS[J]. Water Purification Technology, 2016, 35(4): 77. DOI:10.3969/j.issn.1009-0177.2016.04.013 |
| [12] |
MURPHY R R, CURRIERO F C, BALL W P. Comparison of spatial interpolation methods for water quality evaluation in the Chesapeake Bay[J]. Journal of Environmental Engineering, 2010, 136(2): 160. DOI:10.1061/(ASCE)EE.1943-7870.0000121 |
| [13] |
任学蓉, 杨红. 沙湖水质的因子分析[J]. 宁夏工程技术, 2007, 6(1): 27. REN Xuerong, YANG Hong. Effect factor analysis of water quality in Shahu Lake of Ningxia[J]. Ningxia Engineering Technology, 2007, 6(1): 27. DOI:10.3969/j.issn.1671-7244.2007.01.009 |
| [14] |
KANG K, QIN C, LEE B, et al. Modified screening-based Kriging method with cross validation and application to engineering design[J]. Applied Mathematical Modelling, 2019, 70: 626. |
| [15] |
孙强, 薛雷, 王媛媛. 克里金参数估值法及其在参数估计分析中的应用[J]. 岩土力学, 2009, 30(增刊2): 371. SUN Qiang, XUE Lei, WANG Yuanyuan. Kriging method for parameter estimation and its application to geo-engineering[J]. Rock and Soil Mechanics, 2009, 30(S2): 371. |
| [16] |
SZUSTER-JANIACZYK A, BYLKA J. The effect of the mixing of water from different sources in the water supply system on tap water quality: a full-scale technical investigation case study[J]. Water Science and Technology: Water Supply, 2019, 19(1): 303. |
 2021, Vol. 53
2021, Vol. 53


