数值法可以计算分析复杂的动力模型，在高铁引起的环境振动问题研究中得到广泛应用。研究表明，2维模型忽略沿轨道方向的影响，计算结果不精确^[1]；3维模型计算效率低^[2]；2.5维模型假设沿轨道方向结构- 土体的几何形状和材料性质保持不变，对轨道方向和时间进行双重Fourier变换，将空间- 时间域的三维问题转化为波数- 频域内每个节点包含3个自由度的平面应变问题，只需选取垂直于轨道的结构- 土体截面进行离散求解，再通过Fourier逆变换求得时域- 空间域内解答。2.5维有限元法兼顾精度和效率^[3]。

2.5维有限元方法最早由Hwang等^[4]用于地震行波作用下地下结构动力响应问题研究。杨永斌等^[5]将该方法应用到列车运行引起的地面振动响应研究，提出2.5维FEM-IFEM，研究弹性半空间和分层地基的地面振动。之后，开发了包括多种地基类型和人工边界条件的2.5维有限元动力计算模型^[5]。Costa等^[8]运用此法结合等效线性分析方法研究动荷载作用下土体的非线性特性并开发出2.5维FEM-BEM，建立轮轨相互作用耦合模型，研究分层路基上的动力响应。边学成等^[10]开发与频率相关的黏壶单元吸收有限单元边界上的外行波，发展了高铁移动荷载作用下轨道和地基动力相互作用的2.5维有限元数值方法，模拟轨道和地面的振动及波的传播，并探讨了轨道不平顺因素的影响。Francois等^[12]提出完美匹配层方法(PML)，将其应用到2.5维有限元方法中，通过计算弹性半空间的格林函数位移验证了2.5D PML能够吸收所有不同入射角的波。基于此，Lopes等^[13]建立2.5D FEM-PML轨道- 隧道- 地基系统模型和振源附近的3D FEM建筑物模型，研究仅考虑地面土体- 结构之间的相互作用，表明某些垫层刚度会放大建筑楼板的垂直振动。高广运等^[15]开发出2.5维黏弹性边界条件，分析了高铁运行时分层地基、饱和分层地基、横观各向同性地基、饱和横观各向同性地基和非饱和地基的振动响应及波的传播特性。

综上，基于2.5维有限元法的研究均针对地基的振动响应，将地基简化为弹性体，忽略了地基因高铁运行产生的塑性变形。由于真实土体组构的复杂性，尚没有一个能真实描述土体塑性的本构模型，本文采用改进的摩尔- 库伦模型模拟地基土体。将问题视为材料非线性问题，引入切线刚度迭代法、后欧拉积分算法和一致切线模量算法，推导出适用于高铁荷载下弹塑性地基振动与变形分析的2.5维有限元方法。数值计算中将弹性理论得到的土体位移作为试探位移，经改进的摩尔- 库伦屈服准则判定屈服后，通过施加体荷载和更新土体刚度矩阵模拟弹塑性土体的变形。计算模型将轨道板视为铺设在地基上的欧拉梁，采用黏弹性边界模拟波在半无限空间中的传播，列车荷载采用连续轴重荷载模型和经英国轨道不平顺谱修正的随机激振荷载模型模拟。

1 弹塑性地基非线性理论

采用切线刚度迭代法表征材料的非线性。切线刚度迭代法采用定期更新总刚度矩阵和体荷载迭代相结合的方法获得刚度方程的收敛，该方法能够得到加载过程中的变形发展状况，适用于动态问题求解，近年来得到广泛应用。

1.1 体荷载生成

土体达到屈服条件后，通过迭代不断修改加载在系统上的荷载，并重复利用弹性求解方法获得刚度方程的收敛。在每一个荷载增量步中，位移增量值δ ⁱ由刚度方程(1)求得，即

$ {\boldsymbol{K}}{{\boldsymbol{\delta }}^i} = {{\boldsymbol{p}}^i} $

(1)

在进行应力重分布时，修改式(1)中的荷载增量矢量pⁱ。通常，该荷载增量矢量表达式为

$ {{\boldsymbol{p}}^i} = {{\boldsymbol{p}}_{\rm{a}}} + {\boldsymbol{p}}_{\rm{b}}^i $

(2)

式中：K为总刚度矩阵，δⁱ表示第i次迭代产生的位移增量值，pⁱ为外荷载与内荷载之和，p_a为实际加载的荷载增量，p_bⁱ为体荷载矢量，其值在相临的两次迭代间发生变化，矢量p_bⁱ必须是自平衡的，以避免其对加载净荷载的影响。体荷载的生成方法包括初始应变法和初始应力法，由于荷载已知，本文采用初始应力法。

弹塑性土体的应力增量- 应变增量显式关系式如下:

$ \Delta {\boldsymbol{\sigma }} = \left( {{{\boldsymbol{D}}^{\rm{e}}} - {{\boldsymbol{D}}^{\rm{p}}}} \right)\Delta {\boldsymbol{\varepsilon }} $

(3)

式中：Δσ为应力增量，Δε为应变增量，D^e为弹性矩阵，D^p为塑性矩阵。

假定应力状态已处于弹塑性材料的破坏面上，随后的应力改变能够使应力状态漂移到破坏面的另一个位置，且不超过原有破坏面，于是有

$ \frac{{\partial F}}{{\partial {\boldsymbol{\sigma }}}}\Delta {\boldsymbol{\sigma }} = 0 $

(4)

F为屈服函数。

假设应力改变仅由弹性应变分量引起，结合非关联流动法则，应力增量为

$ \Delta {\boldsymbol{\sigma }} = {{\boldsymbol{D}}^{\rm{e}}}\left( {\Delta {\boldsymbol{\varepsilon }} - \boldsymbol{\lambda }\frac{{\partial Q}}{{\partial {\boldsymbol{\sigma }}}}} \right) $

(5)

Q为塑性势函数。将式(5)代入式(4)得

$ {{\boldsymbol{D}}^{\rm{p}}} = \frac{{{{\boldsymbol{D}}^{\rm{e}}}\frac{{\partial Q}}{{\partial {\boldsymbol{\sigma }}}}{{\left( {\frac{{\partial F}}{{\partial {\boldsymbol{\sigma }}}}} \right)}^{\rm{T}}}{{\boldsymbol{D}}^{\rm{e}}}}}{{{{\left( {\frac{{\partial F}}{{\partial {\boldsymbol{\sigma }}}}} \right)}^{\rm{T}}}{{\boldsymbol{D}}^{\rm{e}}}\frac{{\partial Q}}{{\partial {\boldsymbol{\sigma }}}}}} $

(6)

引起应力重分布的体荷载p_bⁱ在每一次迭代中为所有包含高斯屈服点单元积分的和。即

$ {\boldsymbol{p}}_{\rm{b}}^i = \sum\limits_{{\rm{单元}}}^{{\rm{全部单元}}} {\int {{{\boldsymbol{B}}^{\rm{T}}}} } {\left( {f{{\boldsymbol{D}}^{\rm{p}}}\Delta {\boldsymbol{\varepsilon }}} \right)^i}{\rm{d}}{\boldsymbol{\Omega }} $

(7)

式中f为塑性矩阵D^p的修正因子，由线性插值方法求得。

1.2 改进摩尔-库伦屈服准则

摩尔-库伦屈服准则物理意义明确、使用简便，广泛应用于岩土工程分析。现有有限元法多采用简化模型不能对土体介质的塑性变形进行合理描述。因此，对能够合理描述土体微小塑性变形的改进摩尔- 库伦模型进行2.5维有限元实现，以达到高铁荷载作用下地基振动与变形的准确高效求解。本文规定拉应力为正，压应力为负。由应力不变量表示的摩尔- 库伦屈服准则：

$ F = {\sigma _{\rm{m}}}\sin \;\varphi + \sqrt {{J_2}} K(\theta ) - c\cos \;\varphi $

(8)

式中：c、φ分别为黏聚力和内摩擦角，σ_m为平均应力，$\sqrt {{J_2}} $为等效应力，θ为洛德角，$K\left( \theta \right) = \cos \;\theta - 1/\sqrt 3 \sin \;\varphi \sin \;\theta $。

摩尔库伦准则在π平面上为六边形，存在6个棱角奇异点，造成屈服函数和势函数不连续及梯度无法计算，导致奇异点附近数值计算繁琐和收敛缓慢。采用分段函数描述K(θ)，旨在消除摩尔-库伦屈服准则在π平面上的奇异点，使新屈服面在拐点处平滑连续。K(θ)的表达式如下^[19]：

$ K(\theta ) = \left\{ {\begin{array}{*{20}{l}} {A - B\sin \;3\theta , |\theta | > {\theta _{\rm{T}}}}\\ {\cos \theta - \frac{1}{{\sqrt 3 }}\sin \;\varphi \sin \;\theta , |\theta | \le {\theta _{\rm{T}}}} \end{array}} \right. $

(9)

式中：θ_T为过渡角，取25°；A、B的表达式详见文献[19]。

在子午平面上，采用双曲线近似模拟屈服面，消除顶点奇异性和子午面拐点不可导的问题。

修正后的摩尔-库伦准则屈服函数表达式为^[20]

$ F = {\sigma _{\rm{m}}}\sin \;\varphi + \sqrt {{J_2}{K^2}(\theta ) + {m^2}{c^2}{{\cos }^2}\;\varphi } - c\cos \;\varphi $

(10)

式中参数m的取值范围为[0, 1]，通过调整m的大小，可以反映双曲线对屈服函数的拟合程度和岩土介质抗拉强度的大小。

取塑性势函数和屈服函数的表示式一致^[20]，即

$ G = {\sigma _{\rm{m}}}\sin \;\psi + \sqrt {{J_2}{K^2}(\psi ) + {m^2}{c^2}{{\cos }^2}\;\psi } - c\cos \;\psi $

(11)

式中ψ为膨胀角，K(ψ)的表达式与K(θ)相同。

令矢量a和b分别表示屈服函数F和塑性势函数G关于应力的一阶偏导数：

$ {\boldsymbol{a}} = \frac{{\partial F}}{{\partial {\boldsymbol{\sigma }}}} = C_1^a\frac{{\partial {\sigma _{\rm{m}}}}}{{\partial {\boldsymbol{\sigma }}}} + C_2^a\frac{{\partial \sqrt {{J_2}} }}{{\partial {\boldsymbol{\sigma }}}} + C_3^a\frac{{\partial {J_3}}}{{\partial {\boldsymbol{\sigma }}}} $

(12)

$ {\boldsymbol{b}} = \frac{{\partial G}}{{\partial {\boldsymbol{\sigma }}}} = {C_1}\frac{{\partial {\sigma _{\rm{m}}}}}{{\partial {\boldsymbol{\sigma }}}} + {C_2}\frac{{\partial \sqrt {{J_2}} }}{{\partial {\boldsymbol{\sigma }}}} + {C_3}\frac{{\partial {J_3}}}{{\partial {\boldsymbol{\sigma }}}} $

(13)

式中各分量的具体表达式详见文献[20]。

后向欧拉算法需通过塑性势函数的二阶偏导数对节点应力进行更新，以判断土体是否达到屈服状态。塑性势函数的二阶偏导数表达式为^[20]

$ \begin{array}{l} \frac{{\partial {\boldsymbol{b}}}}{{\partial {\boldsymbol{\sigma }}}} = \frac{{{\partial ^2}{\boldsymbol{G}}}}{{\partial {{\boldsymbol{\sigma }}^2}}} = \frac{{\partial {C_2}}}{{\partial {\boldsymbol{\sigma }}}}\frac{{\partial \sqrt {{J_2}} }}{{\partial {\boldsymbol{\sigma }}}} + {C_2}\frac{{{\partial ^2}\sqrt {{J_2}} }}{{\partial {{\boldsymbol{\sigma }}^2}}} + \\ \;\;\;\;\;\;\;\;\frac{{\partial {C_3}}}{{\partial {\boldsymbol{\sigma }}}}\frac{{\partial {J_3}}}{{\partial {\boldsymbol{\sigma }}}} + {C_3}\frac{{{\partial ^2}{J_3}}}{{\partial {{\boldsymbol{\sigma }}^2}}} \end{array} $

(14)

式中各分量的表达式详见文献[20]，当|θ|>25°时，K(θ)=A－Bsin 3θ，代入式(14)可消除分母中的cos 3θ项，方便数值计算。

1.3 弹塑性本构积分算法

弹塑性理论以屈服函数判断土体所处状态。当屈服函数F>0时，土体处于塑性状态；当F＜0时，土体处于弹性状态。采用返回算法，进行初始弹性预测，设定增量步，判定土体应力状态所处位置(屈服面内或屈服面外)，对处于屈服面外的应力进行塑性修正，使之返回到屈服面上。

对屈服面外的应力进行塑性修正反映其真实的加载过程(偏应力随增量步的增加而增加)。根据正交流动法则，等效塑性应变率可表示为

$ {\dot {\bar \varepsilon} _{{\rm{pl}}}} = \dot \lambda B({\boldsymbol{\sigma }}) $

(15)

式中：$\boldsymbol{\dot \lambda }$为塑性流动因子；B(σ)为与屈服准则有关的量，Mises屈服准则B(σ)=1，其他屈服准则B(σ)≠1。

采用各向同性硬化法则，将黏聚力c看作等效塑性应变的函数，即

$ H = \frac{{\partial c}}{{\partial {{\bar \varepsilon }_{{\rm{pl}}}}}}, {\bar \varepsilon _{{\rm{pl}}}} = \smallint {\dot {\bar \varepsilon} _{{\rm{pl}}}} $

(16)

利用屈服函数的一致性条件结合式(15)、(16)整理为

$ \dot F = {{\boldsymbol{a}}^{\rm{T}}}{\boldsymbol{\sigma }} + \frac{{\partial F}}{{\partial c}}HB \boldsymbol{\dot \lambda } = {{\boldsymbol{a}}^{\rm{T}}}{\boldsymbol{\sigma }} - A'\boldsymbol{\dot \lambda } = 0 $

(17)

式中$A' = - \frac{{\partial F}}{{\partial c}}HB$，当A′=0时为理想弹塑性问题。

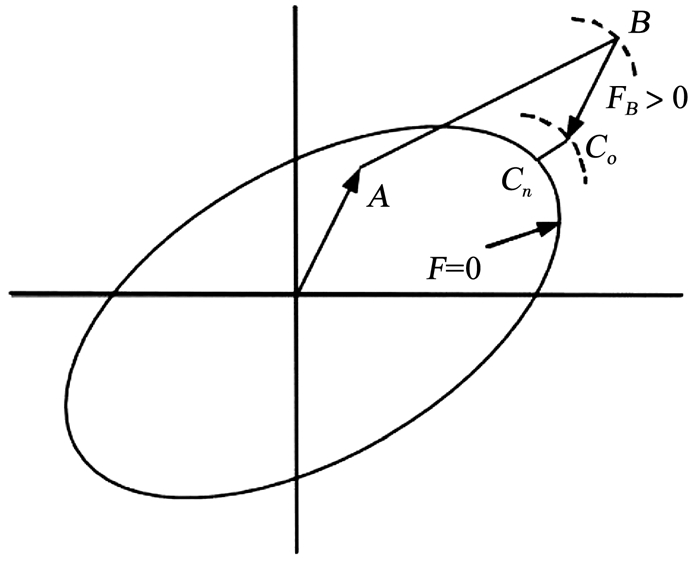
对如图 1所示的弹性试探应力σ_B进行塑性修正。定义应力改变量计算公式为

$ \Delta {\boldsymbol{\sigma }} = {{\boldsymbol{D}}^{\rm{e}}}\Delta {\boldsymbol{\varepsilon }} - \Delta \lambda {{\boldsymbol{D}}^{\rm{e}}}{\boldsymbol{b}} = \Delta {{\boldsymbol{\sigma }}_{\rm{e}}} - \Delta \lambda {{\boldsymbol{D}}^{\rm{e}}}{\boldsymbol{b}} $

(18)

式中Δσ_e为弹性应力增量。

将屈服函数F在B点进行一阶泰勒展开得

$ \Delta \lambda = \frac{{{F_B}}}{{{\boldsymbol{a}}_B^{\rm{T}}{{\boldsymbol{D}}^{\rm{e}}}{{\boldsymbol{b}}_B} + A{'_B}}} $

(19)

采用后向欧拉积分算法，通过迭代将σ_B拉回屈服面。后向欧拉应力(C点应力)表示为

$ {{\boldsymbol{\sigma }}_C} = {{\boldsymbol{\sigma }}_B} - \Delta \lambda {{\boldsymbol{D}}^{\rm{e}}}{\boldsymbol{b}} $

(20)

其初始估计值表示为

$ {{\boldsymbol{\sigma }}_C} = {{\boldsymbol{\sigma }}_B} - \Delta \lambda {{\boldsymbol{D}}^{\rm{e}}}{{\boldsymbol{b}}_B} $

(21)

定义矢量r为当前应力σ与后向欧拉应力的差值，即

$ {\boldsymbol{r}} = {\boldsymbol{\sigma }} - \left( {{{\boldsymbol{\sigma }}_B} - \Delta \lambda {{\boldsymbol{D}}^{\rm{e}}}{{\boldsymbol{b}}_C}} \right) = {\boldsymbol{\sigma }} - {{\boldsymbol{\sigma }}_B} + \Delta \lambda {{\boldsymbol{D}}^{\rm{e}}}{{\boldsymbol{b}}_C} $

(22)

r=0表示应力返回到屈服面上。

将σ_B固定，对r进行泰勒展开得

$ {{\boldsymbol{r}}_n} = {{\boldsymbol{r}}_0} + \mathop {\boldsymbol{\sigma }}\limits^. + \dot \lambda {{\boldsymbol{D}}^{\rm{e}}}{\boldsymbol{b}} + \Delta \lambda {{\boldsymbol{D}}^{\rm{e}}}\frac{{\partial {\boldsymbol{b}}}}{{\partial {\boldsymbol{\sigma }}}}{\boldsymbol{\dot \sigma }} $

(23)

式中${\boldsymbol{\dot \sigma }}$为σ的变化率，$\dot \lambda $为Δλ的变化率。

令r_n=0，则

$ \begin{array}{l} \mathop {\boldsymbol{\sigma }}\limits^. = - {\left( {{\boldsymbol{I}} + \Delta \lambda {{\boldsymbol{D}}^{\rm{e}}}\frac{{\partial {\boldsymbol{b}}}}{{\partial {\boldsymbol{\sigma }}}}} \right)^{ - 1}}\left( {{{\boldsymbol{r}}_0} + \Delta \lambda {{\boldsymbol{D}}^{\rm{e}}}{\boldsymbol{b}}} \right) = \\ \;\;\;\;\;\; - {{\boldsymbol{Q}}^{ - 1}}{{\boldsymbol{r}}_0} - \dot \lambda {{\boldsymbol{Q}}^{ - 1}}{{\boldsymbol{D}}^{\rm{e}}}{\boldsymbol{b}} \end{array} $

(24)

式中I为单位矩阵。

屈服函数F在C点的一阶泰勒展开式为

$ \begin{array}{l} {F_{Cn}} = {F_{C0}} + {\left( {\frac{{\partial F}}{{\partial {\boldsymbol{\sigma }}}}} \right)^{\rm{T}}}\mathop {\boldsymbol{\sigma }}\limits^. + \frac{{\partial F}}{{\partial {{\bar \varepsilon }_{{\rm{pl}}}}}}{{\dot {\bar \varepsilon} }_{{\rm{pl}}}} = \\ \;\;\;\;\;\;\;\;{F_{C0}} + {\boldsymbol{a}}_C^{\rm{T}}{\boldsymbol{\dot \sigma }} + A{'_C}\dot \lambda \end{array} $

(25)

将式(23)代入式(25)，可得

$ \dot \lambda = \frac{{{F_C} - {\boldsymbol{a}}_C^{\rm{T}}{{\boldsymbol{Q}}^{ - 1}}{{\boldsymbol{r}}_0}}}{{{\boldsymbol{a}}_C^{\rm{T}}{{\boldsymbol{Q}}^{ - 1}}{{\boldsymbol{D}}^{\rm{e}}}{\boldsymbol{b}} + A{'_C}}} $

(26)

将式(26)分别代入式(23)和(15)即可求得应力增量${\boldsymbol{\dot \sigma }}$和等效塑性应变增量${\dot {\bar \varepsilon} _{{\rm{pl}}}}$。

一致切线模量法能有效避免土体从弹性突变为塑性时可能引起的伪加载或伪卸载，保证计算程序的收敛性。

由式(21)可得标准隐式后向欧拉算法表达式

$ {\boldsymbol{\sigma }} = {{\boldsymbol{\sigma }}_B} - \Delta \lambda {{\boldsymbol{D}}^{\rm{e}}}{\boldsymbol{b}} $

(27)

对式(27)求微分，可得

$ \begin{array}{l} \mathop {\boldsymbol{\sigma }}\limits^. = {\left( {{\boldsymbol{I}} + \Delta \lambda {{\boldsymbol{D}}^{\rm{e}}}\frac{{\partial {\boldsymbol{b}}}}{{\partial {\boldsymbol{\sigma }}}}} \right)^{ - 1}}{{\boldsymbol{D}}^{\rm{e}}}(\mathop {\boldsymbol{\varepsilon }}\limits^. - {\boldsymbol{\dot \lambda b}}) = \\ \;\;\;\;\;\;{{\boldsymbol{Q}}^{ - 1}}{{\boldsymbol{D}}^{\rm{e}}}(\mathop {\boldsymbol{\varepsilon }}\limits^. - {\boldsymbol{\dot \lambda b}}) = {\boldsymbol{R}}(\mathop {\boldsymbol{\varepsilon }}\limits^. - {\boldsymbol{\dot \lambda b}}) \end{array} $

(28)

为使当前应力σ位于屈服面上，应满足条件$\dot F = 0$，即屈服函数F的一致性条件

$ \dot F = {{\boldsymbol{a}}^{\rm{T}}}{\boldsymbol{\sigma }} - A'\dot \lambda = 0 $

(29)

将式(28)代入式(29)并简化得

$ \dot \lambda = \frac{{{{\boldsymbol{a}}^{\rm{T}}}{\boldsymbol{R}}\mathop {\boldsymbol{\varepsilon }}\limits^. }}{{{{\boldsymbol{a}}^{\rm{T}}}{\boldsymbol{Rb}} + A'}} $

(30)

将式(30)代入式(28)并简化得

$ \mathop {\boldsymbol{\sigma }}\limits^. = \left( {{\boldsymbol{R}} - \frac{{{\boldsymbol{Rb}}{{\boldsymbol{a}}^{\rm{T}}}{{\boldsymbol{R}}^{\rm{T}}}}}{{{{\boldsymbol{a}}^{\rm{T}}}{\boldsymbol{Rb}} + A'}}} \right) \cdot {\boldsymbol{\varepsilon }} = {{\boldsymbol{D}}^{{\rm{ct}}}} \cdot {\boldsymbol{\dot \varepsilon }} $

(31)

式中D^ct为一致性刚度矩阵。当土体达屈服状态后，通过不断更新D^ct即可实现地基塑性变形的求解。

2 弹塑性地基2.5维有限元模型构建 2.1 弹塑性地基2.5维有限元

假定列车运行方向为x正方向，时间为t。定义变量关于x，t的双重Fourier变换为

$ \widetilde {\bar u}\left( {{\xi _x}, y, z, \omega } \right) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } u } (x, y, z, t){{\rm{e}}^{{\rm{i}}{\xi _x}x}}{{\rm{e}}^{ - {\rm{i}}\omega t}}{\rm{d}}x{\rm{d}}t $

(32)

式中：ω表示圆频率，ξ_x表示在x方向上的波数，上标"~"和"-"分别表示波数域和频域内的变量。

由第1节知，弹塑性地基非线性振动与变形求解采用切线刚度法解决材料非线性问题，土体经改进的摩尔- 库伦屈服准则判定屈服后，通过施加体荷载和更新土体刚度矩阵模拟弹塑性土体的塑性变形。因此，每一迭代步的计算均为弹性土体求解问题。

土体运动平衡微分方程为

$ {\sigma _{ij, i}} + {f_j} = \rho \;\;{\ddot u_j} $

(33)

式中：σ_{ij, i}为应力对相应分量的微分，f_j为体力，ρ为土体密度，${\ddot \mu _j}$表示位移对时间t的二次偏导数。

式(33)结合几何方程和物理方程，并对时间t作傅里叶变换，整理得频域内以位移表示的平衡微分方程

$ {\mu ^{\rm{c}}}{\bar u_{j, ii}} + \left( {{\lambda ^{\rm{c}}} + {\mu ^{\rm{c}}}} \right){\bar u_{i, ij}} + {\bar f_j} + {\omega ^2}\rho {\bar u_j} = 0 $

(34)

式中：λ^c和μ^c为考虑土体材料阻尼的拉梅常数，λ^c=λ(1+2βi)，μ^c=μ(1+2βi)，β为土体阻尼比，i为虚数单位。

频域内的应力边界条件

$ {\bar \sigma _{ij}}{n_i} - {\bar F_j} = 0 $

(35)

对式(34)和应力边界条件(35)应用虚功原理，引入虚位移δu_j^*，得控制方程

$ \int_v \delta u_j^*\left( {{{\bar \sigma }_{ij, i}} + {\omega ^2}\rho {{\bar u}_j}} \right){\rm{d}}v - \int_s \delta u_j^*\left( {{{\bar \sigma }_{ij}}{n_i} - {{\bar F}_j}} \right){\rm{d}}s = 0 $

(36)

对式(36)进行分部积分，运用高斯公式并对x方向进行傅里叶变换得频域- 波数域内的控制方程

$ \int_{s}{\delta }{{\widetilde{{\bar{\varepsilon }}}}^{*}}\bar{\sigma }\text{d}s=\int_{s}{{{\omega }^{2}}}\rho \delta {{\tilde{\bar{\mu }}}^{*}}\tilde{\bar{\mu }}\text{d}s+\int_{s}{\delta }{{\tilde{\bar{\mu }}}^{*}}\bar{f}\text{d}s $

(37)

式中：δu^*为虚位移，δε^*为虚位移对应的虚应变，上标"*"表示共轭复数。

对几何方程和物理方程作双重傅里叶变换，得频域- 波数域内的矩阵形式为

$ \widetilde {{\boldsymbol{\bar \varepsilon }}} = {\boldsymbol{B}}\widetilde {{\boldsymbol{\bar \mu }}} $

(38)

$ \widetilde {{\boldsymbol{\bar \sigma }}} = {\boldsymbol{D}}\widetilde {{\boldsymbol{\bar \varepsilon }}} $

(39)

式中：${\boldsymbol{B}} = {\left[ {\begin{array}{*{20}{c}} { - {\rm{i}}{\xi _x}}&0&0&{\frac{\partial }{{\partial y}}}&0&{\frac{\partial }{{\partial z}}}\\ 0&{\frac{\partial }{{\partial y}}}&0&{ - {\rm{i}}{\xi _x}}&{\frac{\partial }{{\partial z}}}&0\\ 0&{}&{\frac{\partial }{{\partial z}}}&0&{\frac{\partial }{{\partial y}}}&{ - {\rm{i}}{\xi _x}} \end{array}} \right]^{\rm{T}}}$ $\begin{array}{l} \widetilde {{\boldsymbol{\bar \varepsilon }}} = {\left[ {{{\widetilde {\bar \varepsilon }}_x}, {{\widetilde {\bar \varepsilon }}_y}, {{\widetilde {\bar \varepsilon }}_z}, {{\widetilde {\bar \gamma }}_{xy}}, {{\widetilde {\bar \gamma }}_{yz}}, {{\widetilde {\bar \gamma }}_{zx}}} \right]^{\rm{T}}}, \widetilde {{\boldsymbol{\bar u}}} = {[\widetilde {\bar u}, \widetilde {\bar v}, \widetilde {\bar w}]^{\rm{T}}}\\ \;\;\;\;\;\;\;\;\widetilde {{\boldsymbol{\bar \sigma }}} = {\left[ {{{\widetilde {\bar \sigma }}_x}, {{\widetilde {\bar \sigma }}_y}, {{\widetilde {\bar \sigma }}_z}, {{\widetilde {\bar \gamma }}_{xy}}, {{\widetilde {\bar \gamma }}_{yz}}, {{\widetilde {\bar \gamma }}_{zx}}} \right]^{\rm{T}}} \end{array}$ ${\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{\lambda ^{\rm{c}}} + 2{\mu ^{\rm{c}}}}&{{\lambda ^{\rm{c}}}}&{{\lambda ^{\rm{c}}}}&0&0&0\\ {{\lambda ^{\rm{c}}}}&{{\lambda ^{\rm{c}}} + 2{\mu ^{\rm{c}}}}&{{\lambda ^{\rm{c}}}}&0&0&0\\ {{\lambda ^{\rm{c}}}}&{{\lambda ^{\rm{c}}}}&{{\lambda ^{\rm{c}}} + 2{\mu ^{\rm{c}}}}&0&0&0\\ 0&0&0&{{\mu ^{\rm{c}}}}&0&0\\ 0&0&0&0&{{\mu ^{\rm{c}}}}&0\\ 0&0&0&0&0&{{\mu ^{\rm{c}}}} \end{array}} \right]$

用4节点等参单元进行离散，形函数表达式如下：

$ {N_i}(\eta , \varsigma ) = \frac{1}{4}\left( {1 + \eta {\eta _i}} \right)\left( {1 + \varsigma {\varsigma _i}} \right) $

(40)

式中η，ς为局部坐标系变量。单元位移u_i(i=x，y，z)由单元节点位移u_xj^e、u_yj^e、u_zj^e(j=1, 2, 3, 4)表示为

$ \begin{array}{l} {u_x} = \sum\limits_{j = 1}^4 {{N_j}} (\eta , \varsigma )u_{xj}^{\rm{e}}, {u_y} = \sum\limits_{j = 1}^4 {{N_j}} (\eta , \varsigma )u_{yj}^{\rm{e}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{u_z} = \sum\limits_{j = 1}^4 {{N_j}} (\eta , \varsigma )u_{zj}^{\rm{e}} \end{array} $

对式(37)引入形函数式(40)，可得弹塑性土体2.5维有限元方程的矩阵形

$ \left( {\widetilde {{\boldsymbol{\bar K}}} - {\omega ^2}{\boldsymbol{M}}} \right)\widetilde {{\boldsymbol{\bar U}}} = \widetilde {{\boldsymbol{\bar F}}} $

(41)

式中：M、${\widetilde {{\boldsymbol{\bar K}}}}$、$\widetilde {{\boldsymbol{\bar F}}}$分别为质量矩阵、刚度矩阵和节点载荷列阵，$\widetilde {{\boldsymbol{\bar U}}}$为单元位移节点列阵。

$ \begin{array}{l} \;\;\;\;\;{\boldsymbol{M}} = \sum\limits_e \rho \int_{ - 1}^1 {\int_{ - 1}^1 {{{\boldsymbol{N}}^{\rm{T}}}} } {\boldsymbol{N}}|{\boldsymbol{J}}|{\rm{d}}\eta {\rm{d}}\;\varsigma \\ \widetilde {{\boldsymbol{\bar K}}} = \sum\limits_e {\int_{ - 1}^1 {\int_{ - 1}^1 {{{\left( {{{\boldsymbol{B}}^*}{\boldsymbol{N}}} \right)}^{\rm{T}}}} } } {\boldsymbol{D}}({\boldsymbol{BN}})|{\boldsymbol{J}}|{\rm{d}}\eta {\rm{d}}\;\varsigma \\ \;\;\;\;\;\;\;\widetilde {{\boldsymbol{\bar F}}} = \sum\limits_e {\int_{ - 1}^1 {\int_{ - 1}^1 {{{\boldsymbol{N}}^{\rm{T}}}} } } \widetilde {{\boldsymbol{\bar f}}}|{\boldsymbol{J}}|{\rm{d}}\eta {\rm{d}}\;\varsigma \end{array} $

式中：e表示对所有单元进行集成，J为Jocobi矩阵，N为形函数矩阵，$\widetilde {{\boldsymbol{\bar f}}}$为单元等效节点载荷列阵。

2.2 无砟轨道模型

无砟轨道由钢轨、轨枕、扣件、道床、道岔等部分组成，共同承担列车轮轨的作用力。在列车荷载作用下，整个轨道系统可近似为整体变形，因此，可将轨道系统简化为铺设在地基上的欧拉梁。列车荷载等效为宽度3 m的均布荷载^[21]。

轨道梁的动力方程在频域- 波数域内可表达为

$ \left( {EI\xi _x^4 - m{\omega ^2}} \right)\widetilde {\bar u} = {\widetilde {\bar f}_{\rm{T}}}\left( {{\xi _x}, \omega } \right) + {\widetilde {\bar f}_{\rm{d}}}\left( {{\xi _x}, \omega } \right) $

(42)

式中：EI为轨道梁弯曲刚度，$\widetilde {\bar u}$为轨道振动位移，m为轨道系统综合质量，${\widetilde {\bar f}_{\rm{T}}}$为地基反力，${\widetilde {\bar f}_{\rm{d}}}$为列车荷载，其表达式如式(44)、(45b)所示。

采用位移协调条件耦合式(41)和(42)得轨道-地基的控制方程。

2.3 黏弹性人工边界

为在有限域内实现半无限空间的准确求解，设置合适的人工边界阻止外行波的反射。黏弹性人工边界具有稳定性好、易编程的优点。在有限元中，黏弹性边界是在边界节点的每个方向上施加一端固定的弹簧-阻尼元件，以黏性阻尼的吸波作用和弹簧的刚性复原作用模拟半无限空间。该边界对外行波的吸收取决于地基土体的材料特性和外行波的频率^[10]。吸收边界节点的系数由半无限区域材料性质决定，作用于边界节点上的荷载表达式为

$ {f_{{\rm{b}}j}} = {A_l}\left( {{K_j}{u_j} + {C_j}{{\dot u}_j}} \right), j = x, y, z $

(43a)

作双重傅里叶变换得

$ {\widetilde {\bar f}_{{\rm{b}}j}} = {A_l}\left( {{K_j} - {\rm{i}}\omega {C_j}} \right){\widetilde {\bar u}_j}, j = x, y, z $

(43b)

式中：${K_x} = {K_y} = \frac{G}{r}\frac{1}{{A + 1}}$，${K_z} = \frac{{\lambda + 2G}}{r}\frac{1}{{A + 1}}$，A_l为节点黏弹性边界应力作用范围，C_x=C_y=Bρv_s，C_z=Bρv_p。其中，A为刚度调节系数，B为阻尼调节系数，r为结构几何中心到人工边界的垂直距离。

2.4 列车荷载模型

列车运行引起的激振荷载包括准静态荷载和随机激振荷载两部分。准静态荷载由列车轴重引起，随机激振荷载涉及列车悬挂体系、轨道不平顺和地基的均匀性等方面。

2.4.1 准静态列车荷载

1节列车由1个车厢、两个转向架和4个轮对等组成，和谐号CRH380AL动车组列车由2拖14动组成，具体参数如表 1所示。假定列车以速度c沿x正方向运行，则频域-波数域内的连续轴重荷载表达式为

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\widetilde {\bar f}_{\rm{d}}}\left( {{\xi _x}, \omega } \right) = \frac{{2\pi }}{c}\delta \left( {{\xi _x} - \frac{\omega }{c}} \right) \cdot \\ \sum\limits_{n = 1}^{N - 1} {\left[ {{P_{n1}}\left( {1 + {{\rm{e}}^{ - {\rm{i}}{a_n}{\xi _x}}}} \right) + {P_{n2}}} \right.} \left. {\left( {{{\rm{e}}^{ - {\rm{i}}\left( {{a_n} + {b_n}} \right){\xi _x}}} + {{\rm{e}}^{ - {\rm{i}}\left( {2{a_n} + {b_n}} \right){\xi _x}}}} \right)} \right]{{\rm{e}}^{ - {\rm{i}}}}\sum\limits_{k = 0}^{N - 1} {{L_k}} {\xi _x} \end{array} $

(44)

式中：δ(x)为Dirac函数，P_n1和P_n2分别表示第n节车体前轮对和后轮对轴重，L_i表示车厢长度，a_n和b_n分别为第n节车体轮轴间距。

由Dirac函数性质可知，x≠0时δ(x)≡0，则式(44)中，只有当ξ_x=ω/c时${\widetilde {\bar f}_{\rm{d}}}\left( {{\xi _x}, \omega } \right) \ne 0$。因此，有限元编程计算中，关于ξ_x，ω的双重傅里叶逆变换转化为关于ω的一重逆变换。

2.4.2 修正列车荷载

准静态连续轴重荷载仅考虑列车轴重，不能考虑列车的随机激振部分。梁波等^[21]根据英国铁路技术中心的理论分析和试验研究，提出一个与高、中、低频相应的，反映轨道不平顺、附加动荷载和轨面波形磨耗效应的激励力模拟列车荷载，同时考虑了钢轨、轨枕的分散传递因素，该激励力模型包含了列车随机激振的主要组分。由该激励力表示的修正列车连续轴重荷载为

$ \begin{array}{l} {f_{\rm{d}}}(x, t) = {k_1}{k_2}\sum\limits_{n = 1}^N {\left( {{P_0} + {P_1}\sin {\omega _1}t + } \right.} \\ \;\;\left. {{P_2}\sin {\omega _2}t + {P_3}\sin {\omega _3}t} \right)\delta (x - ct) \end{array} $

(45a)

式(45a)涵盖了列车动荷载的一系列重要因素(车辆因素、轨道及轨下基础因素等)，能较好地表征真实列车荷载。其中：

$ \begin{array}{l} {P_0}\delta (x - ct) = {P_0}\delta \left( {x - ct + \sum\limits_{i = 0}^{n - 1} {{L_i}} } \right) + \\ \;\;\;\;\;{P_0}\delta \left( {x - ct + \sum\limits_{i = 0}^{n - 1} {{L_i}} + {a_n}} \right) + \\ \;\;\;\;{P_0}\delta \left( {x - ct + \sum\limits_{i = 0}^{n - 1} {{L_i}} + {a_n} + {b_n}} \right) + \\ \;\;\;\;{P_0}\delta \left( {x - ct + \sum\limits_{i = 0}^{n - 1} {{L_i}} + 2{a_n} + {b_n}} \right) \end{array} $

$ \begin{array}{l} {P_j}\sin {\omega _j}t\delta (x - ct) = {P_j}\sin {\omega _j}t\left[ {\delta \left( {x - ct + \sum\limits_{i = 0}^{n - 1} {{L_i}} } \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\delta \left( {x - ct + \sum\limits_{i = 0}^{n - 1} {{L_i}} + {a_n}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\delta \left( {x - ct + \sum\limits_{i = 0}^{n - 1} {{L_i}} + {a_n} + {b_n}} \right) + \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\delta \left( {x - ct + \sum\limits_{i = 0}^{n - 1} {{L_i}} + 2{a_n} + {b_n}} \right)} \right] \end{array} $

式中：k₁为临近车轮力在线路上的叠加系数，一般为1. 2 ~1. 7；k₂为钢轨及轨枕的分散系数，一般为0.6~0.9；P₀为车轮静载；P_i=m₀a_iω_i²(i=1，2，3)分别对应表 2控制条件中振动荷载的典型值；m₀为簧下质量；a_i为相应于不平稳控制条件下的几何不平顺矢高；ω_i=2πc/L_i为振动圆频率；c为列车运行速度；L_i为几何不平顺曲线波长。

对式(45a)作双重傅里叶变换，得修正列车荷载在频域- 波数内的表达式为

$ {{\tilde{\bar{f}}}_{\text{d}}}\left( {{\xi }_{x}},\omega \right)={{k}_{1}}{{k}_{2}}\frac{2\pi }{c}\left[ \delta \left( {{\xi }_{x}}-\frac{\omega }{c} \right){{\overset{2}{\mathop{\text{ }P}}\,}_{o}} \right.\left. \pm \text{i }\!\!\pi\!\!\text{ }\sum\limits_{j=1}^{3}{\delta }\left( {{\xi }_{x}}-\frac{\omega \pm {{\omega }_{j}}}{c} \right){{{\tilde{\bar{P}}}}_{j}} \right] $

(45b)

式中：当ω>0时为"+"，ω＜0时为"-"。

$ \begin{array}{l} {\widetilde {\bar P}_j} = \sum\limits_{n = 1}^N {\left[ {{P_j}\left( {1 + {{\rm{e}}^{ - {\rm{i}}{a_k}{\xi _x}}} + {{\rm{e}}^{ - {\rm{i}}\left( {{a_n} + {b_n}} \right){\xi _x}}}} \right.} \right.} \left. {\left. { + {{\rm{e}}^{ - {\rm{i}}\left( {2{a_n} + {b_n}} \right){\xi _x}}}} \right)} \right]{{\rm{e}}^{ - {\rm{i}}\sum\limits_{k = 0}^{N - 1} {{L_k}} {\xi _x}}}, \\ \;\;\;\;\;\;\;\;j = 0, 1, 2, 3, 4 \end{array} $

3 数值方法验证

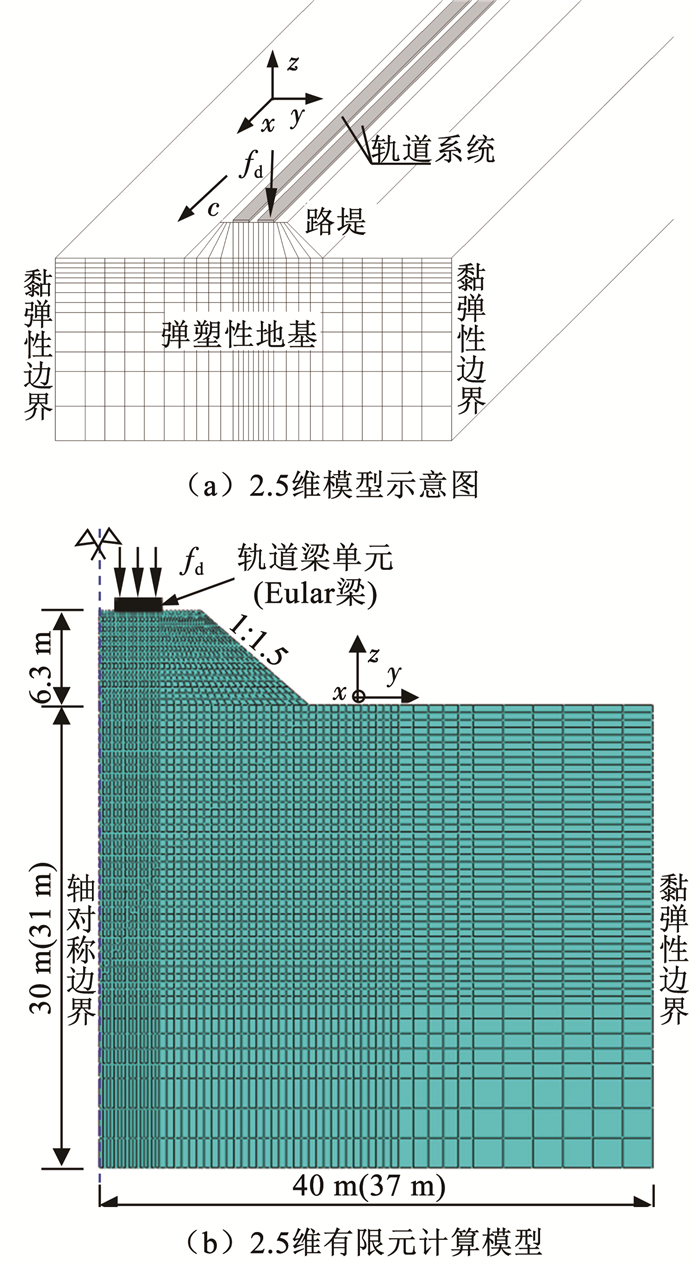
依托VS2013开发平台，编制高铁荷载下弹塑性地基2.5维有限元Fortran计算程序。计算模型如图 2所示。通过以下两种方法验证理论及计算模型的正确性：1)与移动点荷载作用下弹性半空间振动的解析解的退化验证；2)与京沪线上高铁运行引起的地面振动实测结果进行验证。

3.1 弹性半空间解析解验证

Eason^[23]推导出移动点荷载f_d(x, t)=P₀=δ(x-ct)作用下弹性半无限空间振动问题的解析解。建立基岩层上厚30 m、宽40 m的2.5维有限元计算模型，如图 2(b)，忽略路堤，假定荷载作用在有限元模型土体表面中心处，采用轴对称模型，模型两侧分别设置轴对称边界和黏弹性人工边，土体及荷载参数同文献[23]。当弹塑性模型中黏聚力趋近于无穷大时，土体不会屈服进入塑性状态，弹塑性土体退化为弹性土体。

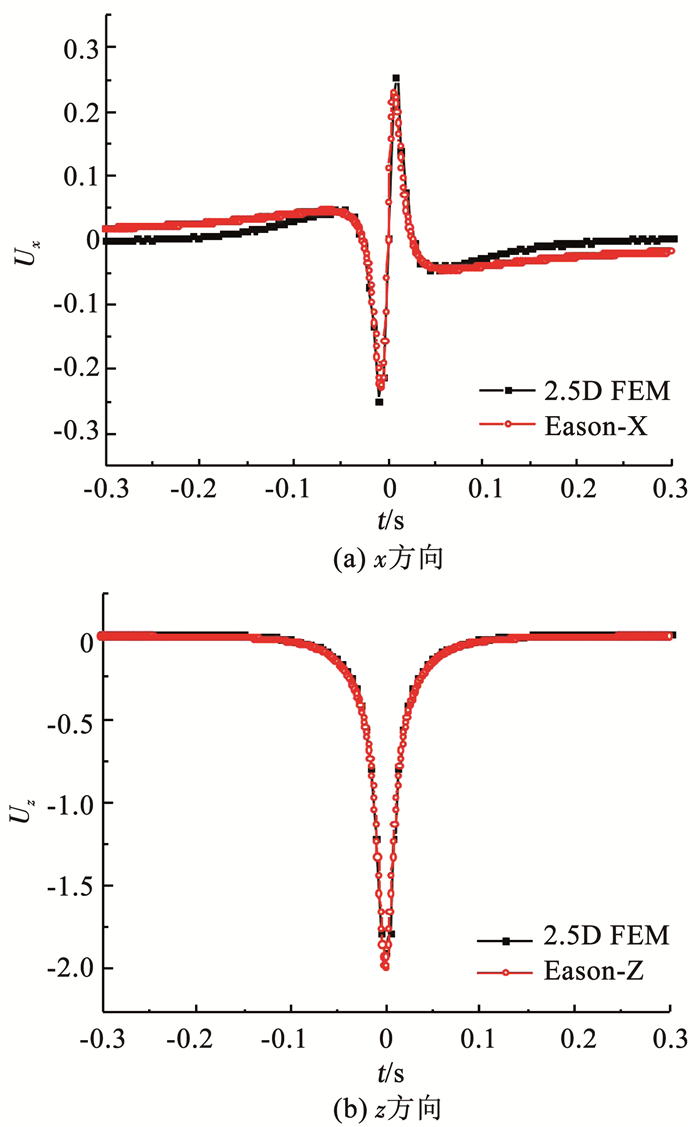
由图 3可知，本文算法得到的在荷载移动方向和竖向的振动幅值与解析解吻合较好，证明本文理论的正确性。

3.2 实测验证

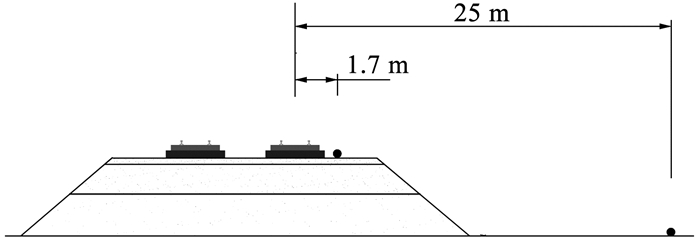
翟婉明等^[24]实测了京沪高铁苏州段的地面振动。如图 4所示，选取近轨道处(1. 7 m)和远轨道处(25 m)测点进行对比验证。

建立2.5维有限元计算模型如图 2(b)所示，对于双线路堤取一半结构建模分析，模型两侧分别设置轴对称边界和黏弹性人工边界，模型底部为固定边界。计算模型路堤高6.3 m、面宽4.3 m，地基宽37 m、深31 m。桩采用等代桩墙处理，列车荷载模型采用1拖7动，其表达式如式(45)，参数取值同文献[21]。土体及桩体参数同文献[24]。

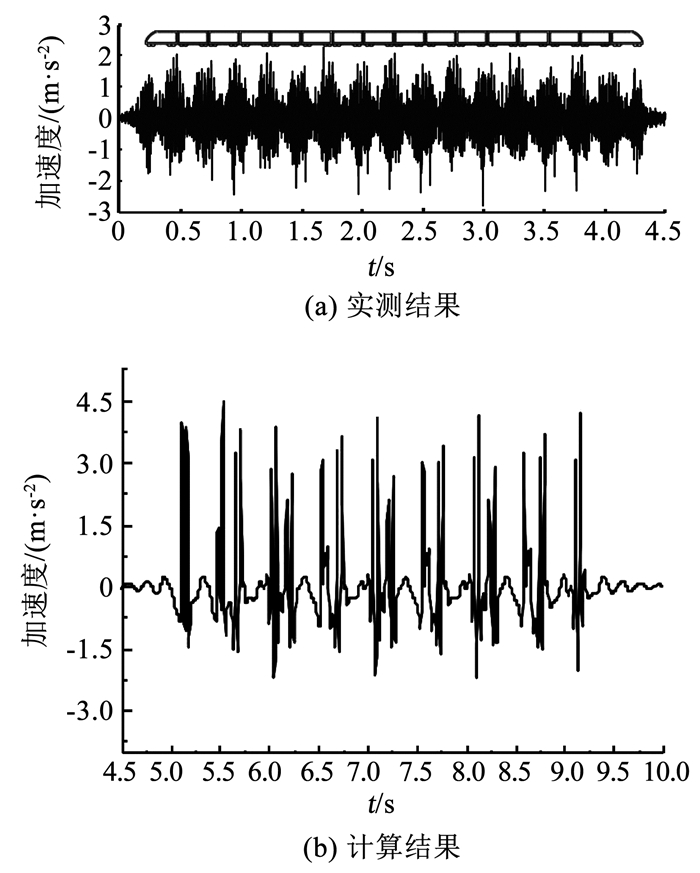
测点1.7 m处的振动加速度实测结果及本文计算结果如图 5所示。可以看出，本文计算结果频率成分稀疏，但能表征主要的频率成分。近轨道处，正向加速度峰值计算结果约为实测结果2倍。这是因为本文采用轴对称模型，默认另一半结构也有同样的荷载施加，对应双线轨道同时有高铁同向运行的最不利情况，而实测时只有一条轨道上有列车运行。另外，近轨道处的负向振动受荷载施加方式的抑制作用而使其负向加速度峰值小于正向峰值。

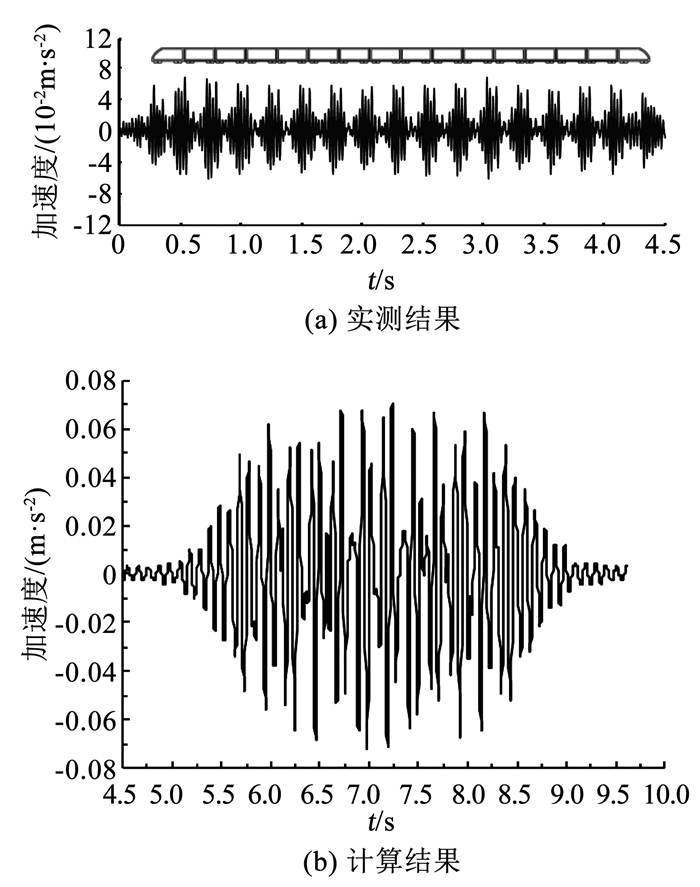
距轨道中心25 m处的实测加速度值及本文计算结果如图 6所示。远轨道处振动响应受荷载施加方式及振动叠加效应影响较小，计算结果接近实测结果。由图 6可知，正负加速度峰值和主频特性与实测结果吻合较好。总体而言，本文建立的计算模型能准确描述地基的振动峰值及主频特性，证明了计算模型应用的可靠性。

4 结论

1) 以弹性地基2.5维有限元法为基础，地基视为弹塑性，以切线刚度法表征地基土体非线性，引入改进的摩尔- 库伦屈服准则，以弹性理论得到的位移为试探位移，通过定期更新总体刚度矩阵和体荷载的方法实现高铁荷载下弹塑性地基变形求解。

2) 通过与移动点荷载引起的弹性半空间振动响应解析解对比，验证了本文理论的正确性。将修正的列车荷载模型应用到本文建立的弹塑性地基2.5维有限元模型中，构建高铁荷载下地基振动与变形分析模型，通过与实测结果对比，验证了本文模型应用的可靠性。