2. 广西防灾减灾与工程安全重点实验室(广西大学),南宁 530004
2. Guangxi Key Laboratory of Disaster Prevention and Engineering Safety (Guangxi University), Nanning 530004, China
近年来,国内外学者对楔形桩承载机理[1]进行了深入研究。Kodikara等[2]借助三维数值模型,考虑楔角、平均桩径等因素的影响,研究了软岩中多荷载作用下楔形桩的侧摩阻力分布。Lee等[3]通过圆锥贯入试验,对比分析了楔形桩和等截面圆桩的承载力。张可能等[4]和周航等[5]分别利用室内静力沉桩试验、圆孔扩张理论等手段,详细分析了沉桩深度、楔角等因素对沉桩过程的影响。孔纲强等[6-7]通过透明土模型对比试验,分别研究竖向荷载和水平荷载下楔形桩桩侧土的位移变化及破坏形式,详细分析了楔形桩的竖向承载特性与水平承载特性。进一步,周航等[8]基于Euler梁模型推导出水平荷载下楔形桩桩身水平位移和弯矩的解析表达式,并通过模型试验进行了分析和验证。
相对而言,关于楔形桩动力相互作用的研究仍不完善。蔡燕燕等[9]基于平面应变模型推导了成层地基中楔形桩纵向振动阻抗函数的解析解。吴文兵等[10-11]分别采用Rayleigh-Love杆模型和剪切复刚度传递模型考虑楔形桩的横向惯性效应及其桩侧土挤土效应,研究了楔形桩纵向振动响应规律。进一步,王奎华等[12-13]推导得到了考虑桩周土竖向波动效应和施工扰动效应时楔形桩桩顶纵向振动阻抗函数的解析解。随后,王奎华等[14-15]基于非等截面桩体模型,推导出楔形桩纵向振动响应半解析解,并且详细分析了缺陷楔形桩的纵向动力响应。综上可以看出,现有关楔形桩动力特性的研究主要是完善了楔形桩的纵向振动理论。
对于港口码头、基坑支护等工程,主要考虑桩体的水平动力特性,此内容也是抗震设计的核心。近年来,逐渐出现关于桩体水平动力特性的研究。栾鲁宝等[16]和郑长杰等[17]分别基于Timoshenko模型和土体三维波动理论推导了管桩的动力复阻抗解析表达式,详细分析了管桩的水平振动特性。进一步,栾鲁宝等[18]基于Biot动力固结理论研究了竖向荷载下桩体的水平动力响应。因此,对楔形桩而言,其水平承载特性的研究也不能仅从静力角度,需要考虑频率相关性和共振现象的桩土动力相互作用,但建立一个与实际工况相符的楔形桩水平振动响应模型比较困难。
综上,为了完善楔形桩振动理论,系统研究了黏弹性地基中水平简谐激振力作用下的楔形桩水平振动问题。基于Winkler地基和Timoshenko梁模型,建立了桩土横向耦合振动模型; 严格推导得到了桩体的水平位移、弯矩和剪力的解析表达式; 基于所得解,分析了桩土设计参数对楔形桩水平振动特性的影响,并通过与Euler梁模型对比验证了本文解的合理性。
1 数学模型Euler梁模型主要研究仅发生弯曲变形时的梁水平振动问题,但实际上梁在弯曲时也会发生剪切变形并且伴随着转动惯性的作用,忽略这两个因素会使结果产生较大误差。Timoshenko[19]在Euler梁模型上考虑了这两个因素并建立了与实际情况更接近的模型,大大减小了误差。进一步,陈镕等[20]对Timoshenko梁模型进行了频谱分析,发现转动惯量对模型最终结果的影响不大。因此,在不考虑转动惯量的情况下,采用Timoshenko梁模型对楔形桩水平振动问题进行求解与分析。
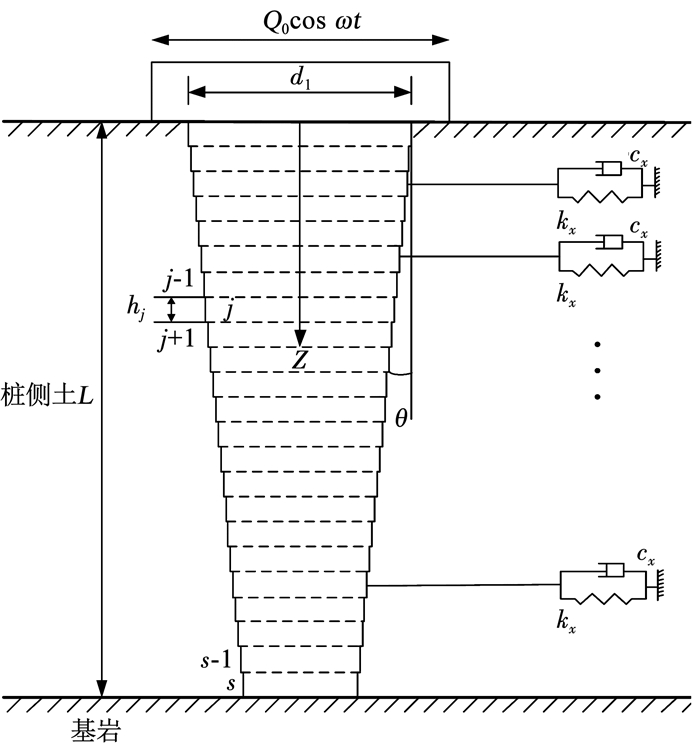
1.1 计算简图基于Winkler地基模型,本文的桩土横向耦合振动计算模型如图 1所示。其中,桩侧土为均匀地基,桩顶受到水平简谐激振力F(t)=Q0 cos ωt,Q0为外载荷幅值,ω为激振频率,楔角为θ,桩长为L,桩顶直径为d1,深度为z。
|
图 1 桩土横向耦合计算模型 Fig. 1 Lateral coupling calculation model of pile-soil system |
图 1中,桩土系统从桩顶到桩底划分成s个厚度相等的微元段,依次标记为1,2,…,s。图中hj表示第j段桩到桩顶的距离。当划分段数s足够大时,各微元段变得非常薄,足以将微元段视作等直径桩。
为便于后面公式的求解,统一规定坐标轴:对于所有的楔形桩微元段,均取坐标原点于第1微元段顶部的中点,其中Z轴正方向向下。
1.2 基本假设运用Winkler地基模型模拟楔形桩与桩侧土的相互作用。同时,为了便于求解且保证结果的普适性,作以下假设:1)桩侧土均匀、各向同性,可视为线性黏弹性连续介质; 2)桩体为自上而下截面逐渐变小的圆形变截面楔形体; 3)施加水平简谐激振力时仅认为桩土发生横向位移; 4)桩土界面无相对滑动,且不考虑承台作用; 5)同一个微元段水平振动方程中的土体刚度系数和阻尼系数为常数。
1.3 桩周土模型kx和cx分别为桩侧土的刚度系数和阻尼系数,并根据Gazetas等[21]的研究成果取值如下:
| $ \left\{\begin{array}{l} k_{x}=1.2 E_{\mathrm{s}} \\ c_{x} \approx 6.0 a_{j}^{-\frac{1}{4}} \rho_{\mathrm{s}} v_{\mathrm{s}} d_{j}+2 k_{x} \frac{\beta_{\mathrm{s}}}{\omega} \end{array}\right. $ | (1) |
式中:vs=
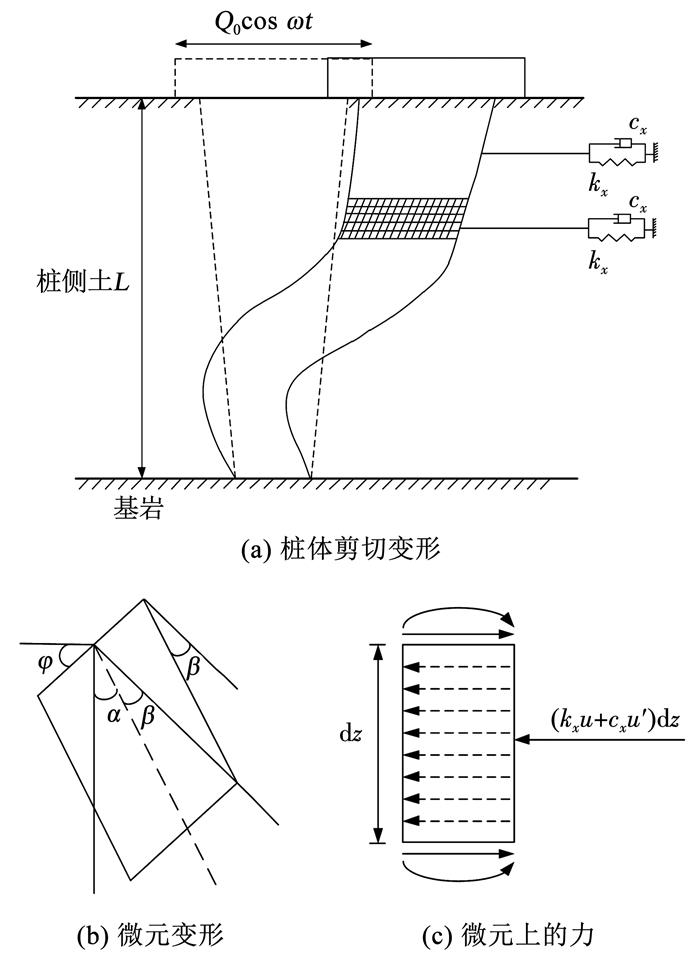
当给桩顶施加水平简谐激振力时,考虑了楔形桩的剪切变形,故微元段的变形与受力情况如图 2所示,其中φ为桩体横截面转角, α为弹性轴的倾角, β为剪切变形角。
|
图 2 桩体变形与受力 Fig. 2 Deformation and stress of pile |
则可得第j微元段的水平振动方程为
| $ \left\{\begin{array}{l} k^{\prime} A_{\mathrm{p}j} G_{\mathrm{p}}\left[\frac{\partial \varphi_{j}(z, t)}{\partial z}-\frac{\partial^{2} u_{j}(z, t)}{\partial z^{2}}\right]+k_{x} \cdot u_{j}(z, t)+ \\ c_{x} \cdot \frac{\partial u_{j}(z, t)}{\partial t}+m_{\mathrm{p} j} \cdot \frac{\partial^{2} u_{j}(z, t)}{\partial t^{2}}=0 \\ E_{\mathrm{p}} I_{\mathrm{p} j} \cdot \frac{\partial^{2} \varphi_{j}(z, t)}{\partial z^{2}}+k^{\prime} A_{\mathrm{p} j} G_{\mathrm{p}}\left[\frac{\partial u_{j}(z, t)}{\partial z}-\varphi_{j}(z, t)\right]=0 \end{array}\right. $ | (2) |
式中:uj(z, t)、φj(z, t)为第j微元段内某质点的水平位移和转角; Gp、Ep为桩体剪切模量和弹性模量; mpj、Apj、Ipj为第j微元段的质量、横截面积和转动惯性矩; k′为剪切形状系数,桩体截面为圆形时取0.75。
2.2 方程的求解从复频域内求解稳态简谐振动下的解析解时,采用分离变量法,可直接令
| $ \left\{\begin{array}{l} u_{j}(z, t)=U_{j}(z) \cdot \mathrm{e}^{\mathrm{i} \omega t} \\ \varphi_{j}(z, t)=\psi_{j}(z) \cdot \mathrm{e}^{\mathrm{i} \omega t} \end{array}\right. $ | (3) |
将式(3)代入式(2)中,可得
| $ \left\{\begin{array}{l} k^{\prime} A_{\mathrm{p} j} G_{\mathrm{p}} \mathrm{e}^{\mathrm{i} \omega t} \cdot\left[\frac{\mathrm{d} \psi_{j}(z)}{\mathrm{d} z}-\frac{\mathrm{d}^{2} U_{j}(z)}{\mathrm{d} z^{2}}\right]+ \\ \ \ \ \ U_{j}(z) \mathrm{e}^{\mathrm{i} \omega t} \cdot\left(k_{x}-m_{\mathrm{p} j} \omega^{2}+\mathrm{i} c_{x} \omega\right)=0 \\ E_{\mathrm{p}} I_{\mathrm{p} j} \mathrm{e}^{\mathrm{i} \omega t} \cdot \frac{\mathrm{d}^{2} \psi_{j}(z)}{\mathrm{d} z^{2}}+ \\ \ \ \ \ k^{\prime} A_{\mathrm{p}j} G_{\mathrm{p}} \mathrm{e}^{\mathrm{i} \omega t} \cdot\left[\frac{\mathrm{d} U_{j}(z)}{\mathrm{d} z}-\psi_{j}(z)\right]=0 \end{array}\right. $ | (4) |
由式(4)可以看出,对于楔形桩的第j微元段,Ipj、mpj和Apj均为常数。为简化计算过程,在等式两边同时除以eiωt,并且令
| $ \left\{\begin{array}{l} W_{\mathrm{p} j}=E_{\mathrm{p}} I_{\mathrm{p} j} \\ J_{\mathrm{p} j}=k^{\prime} A_{\mathrm{p} j} G_{\mathrm{p}} \\ k_{\mathrm{s} j}=k_{x}-m_{\mathrm{p} j} \omega^{2}+\mathrm{i} c_{x} \omega \end{array}\right. $ | (5) |
将式(5)代入式(4)中,通过消元可以得到一个四阶常微分方程:
| $ W_{\mathrm{p} j} \frac{\mathrm{d}^{4} U_{j}(z)}{\mathrm{d} z^{4}}-\frac{k_{\mathrm{s}j} W_{\mathrm{p} j}}{J_{\mathrm{p} j}} \frac{\mathrm{d}^{2} U_{j}(z)}{\mathrm{d} z^{2}}+k_{\mathrm{s} j} U_{j}(z)=0 $ | (6) |
进一步,转角ψj可以表示为
| $ \psi_{j}(z)=\frac{W_{\mathrm{p} j}}{J_{\mathrm{p} j}} \frac{\mathrm{d}^{3} U_{j}(z)}{\mathrm{d} z^{3}}+\left(1-\frac{k_{\mathrm{s}j} \cdot W_{\mathrm{p}j}}{J_{\mathrm{p}j}^{2}}\right) \frac{\mathrm{d} U_{j}(z)}{\mathrm{d} z} $ | (7) |
对方程(6)求解,可得其通解为
| $ \begin{aligned} U_{j}(z)=& \mathrm{e}^{\alpha_{j}z}\left(A_{1 j} \cos \beta_{j} z+B_{1 j} \sin \beta_{j} z\right)+\\ & \mathrm{e}^{-\alpha_{j}z}\left(C_{1 j} \cos \beta_{j} z+D_{1 j} \sin \beta_{j} z\right) \end{aligned} $ | (8) |
式中:A1j、B1j、C1j、D1j为待定系数,可由边界条件得到。系数αj和βj的表达式为
| $ \left\{\begin{array}{l} \alpha_{j}=\sqrt{\sqrt{\frac{k_{\mathrm{s} j}}{4 W_{\mathrm{p} j}}}+\frac{k_{\mathrm{s} j}}{4 J_{\mathrm{p} j}}} \\ \beta_{j}=\sqrt{\sqrt{\frac{k_{\mathrm{s}j}}{4 W_{\mathrm{p} j}}}}-\frac{k_{\mathrm{s} j}}{4 J_{\mathrm{p} j}} \end{array}\right. $ | (9) |
将式(8)代入式(7)中,整理得转角的表达式为
| $ \begin{aligned} \psi_{j}(z)=& \mathrm{e}^{\alpha_{j}z}\left(A_{2 j} \cos \beta_{j} z+B_{2 j} \sin \beta_{j} z\right)+\\ & \mathrm{e}^{-\alpha_{j} z}\left(C_{2 j} \cos \beta_{j} z+D_{2 j} \sin \beta_{j} z\right) \end{aligned} $ | (10) |
式中:A2j、B2j、C2j、D2j为待定系数。
同理,根据弯矩M、剪力Q与水平位移U、转角ψ之间的关系,依次可推得M、Q的解析表达式:
| $ \begin{gathered} M_{j}(z)=-W_{\mathrm{p} j} \frac{\mathrm{d} \psi_{j}(z)}{\mathrm{d} z}= \\ -W_{\mathrm{p} j}\left[\mathrm{e}^{\alpha_{j}z}\left(A_{3 j} \cos \beta_{j} z+B_{3 j} \sin \beta_{j} z\right)+\right. \\ \left.\mathrm{e}^{-\alpha_{j}z}\left(C_{3 j} \cos \beta_{j} z+D_{3 j} \sin \beta_{j} z\right)\right] \end{gathered} $ | (11) |
| $ \begin{gathered} Q_{j}(z)=J_{\mathrm{p} j}\left[\frac{\mathrm{d} U_{j}(z)}{\mathrm{d} z}-\psi_{j}(z)\right]= \\ W_{\mathrm{p} j}\left[\mathrm{e}^{\alpha_{j}z}\left(A_{4 j} \cos \beta_{j} z+B_{4 j} \sin \beta_{j} z\right)+\right. \\ \left.\mathrm{e}^{-\alpha_{j}z}\left(C_{4 j} \cos \beta_{j} z+D_{4 j} \sin \beta_{j} z\right)\right] \end{gathered} $ | (12) |
式中:A3j、B3j、C3j、D3j、A4j、B4j、C4j、D4j均为待定系数。
由于式(10)~(12)均由式(8)推导得到,其待定系数之间满足一定的等式关系,式(10)~(12)中的待定系数可以用式(8)中的待定系数A1j、B1j、C1j、D1j表示(j=1,…,s):
| $ \left\{\begin{array}{l} A_{2 j}=A_{1 j} \cdot t_{5 j}+B_{1 j} \cdot t_{6 j} \\ B_{2 j}=-A_{1 j} \cdot t_{6 j}+B_{1 j} \cdot t_{5 j} \\ C_{2 j}=-C_{1 j} \cdot t_{5 j}+D_{1 j} \cdot t_{6 j} \\ D_{2 j}=-C_{1 j} \cdot t_{6 j}-D_{1 j} \cdot t_{5 j} \end{array}\right. $ | (13) |
| $ \left\{\begin{array}{l} A_{3 j}=A_{1 j} \cdot t_{7 j}+B_{1 j} \cdot t_{8 j} \\ B_{3 j}=-A_{1 j} \cdot t_{8 j}+B_{1 j} \cdot t_{7 j} \\ C_{3 j}=C_{1 j} \cdot t_{7 j}-D_{1 j} \cdot t_{8 j} \\ D_{3 j}=C_{1 j} \cdot t_{8 j}+D_{1 j} \cdot t_{7 j} \end{array}\right. $ | (14) |
| $ \left\{\begin{array}{l} A_{4 j}=A_{1 j} \cdot t_{9 j}+B_{1 j} \cdot t_{0 j} \\ B_{4 j}=-A_{1 j} \cdot t_{0 j}+B_{1 j} \cdot t_{9 j} \\ C_{4 j}=-C_{1 j} \cdot t_{9 j}+D_{1 j} \cdot t_{0 j} \\ D_{4 j}=-C_{1 j} \cdot t_{0 j}-D_{1 j} \cdot t_{9 j} \end{array}\right. $ | (15) |
| $ \left\{\begin{array}{l} t_{1 j}=\mathrm{e}^{\alpha_{j}z} \cdot \cos \beta_{j} z, t_{2 j}=\mathrm{e}^{\alpha_{j}z} \cdot \sin \beta_{j} z \\ t_{3 j}=\mathrm{e}^{-\alpha_{j}z} \cdot \cos \beta_{j} z, t_{4 j}=\mathrm{e}^{-\alpha_{j} z} \cdot \sin \beta_{j} z \\ t_{5 j}=\alpha_{j}\left(1-\frac{k_{\mathrm{s} j} \cdot W_{\mathrm{p} j}}{J_{\mathrm{p} j}^{2}}\right)+\frac{W_{\mathrm{p} j}}{J_{\mathrm{p} j}}\left(\alpha_{j}^{3}-3 \alpha_{j} \beta_{j}^{2}\right) \\ t_{6 j}=\beta_{j}\left(1-\frac{k_{\mathrm{s} j} \cdot W_{\mathrm{p} j}}{J_{\mathrm{p} j}^{2}}\right)+\frac{W_{\mathrm{p} j}}{J_{\mathrm{p} j}}\left(-\beta_{j}^{3}+3 \alpha_{j}^{2} \beta_{j}\right) \\ t_{7 j}=\alpha_{j}^{2}-\beta_{j}^{2}-\frac{k_{\mathrm{s} j}}{J_{\mathrm{p} j}}, t_{8 j}=2 \alpha_{j} \beta_{j} \\ t_{9 j}=\alpha_{j} \frac{k_{\mathrm{s} j}}{J_{\mathrm{p} j}}-\alpha_{j}^{3}+3 \alpha_{j} \beta_{j}^{2}, t_{0 j}=\beta_{j} \frac{k_{\mathrm{s} j}}{J_{\mathrm{p} j}}+\beta_{j}^{3}-3 \alpha_{j}^{2} \beta_{j} \end{array}\right. $ | (16) |
式(8)中的待定系数A1j、B1j、C1j、D1j需通过桩体的边界条件进行求解,这里考虑桩顶约束转角、桩底固定的情况,其他的边界条件可以通过类似的方法进行求解。桩顶和桩底处的边界条件可分别表达为
| $ \left\{\begin{array}{l} \left.\psi_{1}(z)\right|_{z=0}=0,\left.Q_{1}(z)\right|_{z=0}=Q_{0} \\ \left.U_{\mathrm{s}}(z)\right|_{z=L}=0,\left.\psi_{\mathrm{s}}(z)\right|_{z=L}=0 \end{array}\right. $ | (17) |
在第j微元段与第j+1微元段的分界面处,楔形桩的水平位移、转角、弯矩和剪力满足连续条件,即
| $ \left\{\begin{array}{l} \left.U_{j}(z)\right|_{z=h_{j}}=\left.U_{j+1}(z)\right|_{z=h_{j}} \\ \left.\psi_{j}(z)\right|_{z=h_{j}}=\left.\psi_{j+1}(z)\right|_{z=h_{j}} \\ \left.M_{j}(z)\right|_{z=h_{j}}=\left.M_{j+1}(z)\right|_{z=h_{j}} \\ \left.Q_{j}(z)\right|_{z=h_{j}}=\left.Q_{j+1}(z)\right|_{z=h_{j}} \end{array}\right. $ | (18) |
将式(18)转化成矩阵关系可得
| $ \boldsymbol{T}_{j}\left(h_{j}\right) \boldsymbol{X}_{j}=\boldsymbol{T}_{j+1}\left(h_{j}\right) \boldsymbol{X}_{j+1} $ | (19) |
进一步可得
| $ \boldsymbol{X}_{j+1}=\boldsymbol{T}_{j+1}^{-1}\left(h_{j}\right) \boldsymbol{T}_{j}\left(h_{j}\right) \boldsymbol{X}_{j} $ | (20) |
其中,各项矩阵的详细表达如下:
| $ \boldsymbol{T}_{j}\left(h_{j}\right)=\left[\begin{array}{ccccc} t_{1 j} & t_{2 j} & t_{3 j} & t_{4 j} \\ t_{5 j} \cdot t_{1 j}-t_{6 j} \cdot t_{2 j} & t_{6 j} \cdot t_{1 j}+t_{5 j} \cdot t_{2 j} & -t_{5 j} \cdot t_{3 j}-t_{6 j} \cdot t_{4 j} & t_{6 j} \cdot t_{3 j}-t_{5 j} \cdot t_{4 j} \\ t_{7_{j}} \cdot t_{1 j}-t_{8 j} \cdot t_{2 j} & t_{8 j} \cdot t_{1 j}+t_{7 j} \cdot t_{2 j} & t_{7 j} \cdot t_{3 j}+t_{8 j} \cdot t_{4 j} & -t_{8 j} \cdot t_{3 j}+t_{7 j} \cdot t_{4 j} \\ t_{9 j} \cdot t_{1 j}-t_{0 j} \cdot t_{2 j} & t_{0 j} \cdot t_{1 j}+t_{9 j} \cdot t_{2 j} & -t_{9 j} \cdot t_{3 j}-t_{0 j} \cdot t_{4 j} & t_{0 j} \cdot t_{3 j}-t_{9 j} \cdot t_{4 j} \end{array}\right] $ | (21) |
| $ \boldsymbol{X}_{j}=\left[\begin{array}{llll} A_{1 j} & B_{1 j} & C_{1 j} & D_{1 j} \end{array}\right]^{\mathrm{T}} $ | (22) |
利用式(20)进行累乘可以得到矩阵Xs,即
| $ \boldsymbol{X}_{\mathrm{s}}=\left[\prod\limits_{j=s}^{1} \boldsymbol{T}_{j}^{-1}\left(h_{j-1}\right) \boldsymbol{T}_{j-1}\left(h_{j-1}\right)\right] \boldsymbol{X}_{1} $ | (23) |
将桩顶边界条件代入转角和剪力表达式中,转化成矩阵方程组,可以得到式(24);同理,由桩底边界条件可以得到式(25),即
| $ \left[\begin{array}{llll} t_{51} & t_{61} & -t_{51} & t_{61} \\ t_{91} & t_{01} & -t_{91} & t_{01} \end{array}\right] \boldsymbol{X}_{1}=\left[\begin{array}{c} 0 \\ \frac{Q_{0}}{W_{\mathrm{p} j}} \end{array}\right] $ | (24) |
| $ \left[\begin{array}{cccc} t_{1 \mathrm{s}} & t_{2 \mathrm{s}} & t_{3 \mathrm{s}} & t_{4 \mathrm{s}} \\ t_{5 \mathrm{s}} \cdot t_{1 \mathrm{s}}-t_{6 \mathrm{s}} \cdot t_{2 \mathrm{s}} & t_{6 \mathrm{s}} \cdot t_{1 \mathrm{s}}+t_{5 \mathrm{s}} \cdot t_{2 \mathrm{s}} & -t_{5 \mathrm{s}} \cdot t_{3 \mathrm{s}}-t_{6 \mathrm{s}} \cdot t_{4 \mathrm{s}} & t_{6 \mathrm{s}} \cdot t_{3 \mathrm{s}}-t_{5 \mathrm{s}} \cdot t_{4 \mathrm{s}} \end{array}\right] \boldsymbol{X}_{\mathrm{s}}=\left[\begin{array}{l} 0 \\ 0 \end{array}\right] $ | (25) |
将式(23)代入式(25)中,得到有关矩阵X1的两个方程,再结合式(24),便可以得到有关矩阵X1的4个方程,经过推导和整理后能够计算出X1,最后通过式(23)可以推导出每个微元段的Xj,于是得到整个楔形桩的水平位移函数,继而推导出转角、弯矩和剪力的表达式,利用分段函数则可以表示出整个楔形桩的动力响应表达式。
基于上述推导,可得式(8)中系数A1j、B1j、C1j、D1j的解析表达式:
| $ \left\{\begin{aligned} A_{1 j}=& \widetilde{Q_{0 j}} \cdot\left[t_{6 j}^{2}\left(\mathrm{e}^{-2 \alpha_{j} L}-1\right)+t_{5 j}^{2}\left(\cos 2 \beta_{j} L-1\right)-\right.\\ &\left.t_{5 j} \cdot t_{6 j} \cdot \sin 2 \beta_{j} L\right] / C_{j} \\ B_{1 j}=& \widetilde{Q_{0 j}} \cdot\left[t_{5 j} \cdot t_{6 j}\left(-\mathrm{e}^{-2 \alpha_{j} L}+\cos 2 \beta_{j} L\right)+\right.\\ &\left.t_{5 j}^{2} \cdot \sin 2 \beta_{j} L\right] / C_{j} \\ C_{1 j}=& \widetilde{Q_{0 j}} \cdot\left(t_{6 j}^{2} \cdot \mathrm{e}^{2 \alpha_{j} L}+t_{5 j}^{2} \cdot \cos 2 \beta_{j} L+\right.\\ &\left.t_{5 j} \cdot t_{6 j} \cdot \sin 2 \beta_{j} L-t_{5 j}^{2}-t_{6 j}^{2}\right) / C_{j} \\ D_{1 j}=& \widetilde{Q_{0 j}} \cdot\left[t_{5 j} \cdot t_{6 j}\left(\mathrm{e}^{2 \alpha_{j} L}-\cos 2 \beta_{j} L\right)+\right.\\ &\left.t_{5 j}^{2} \cdot \sin 2 \beta_{j} L\right] / C_{j} \end{aligned}\right. $ | (26) |
其中
| $ \widetilde{Q_{0 j}}=\frac{Q_{0}}{E_{\mathrm{p}} I_{\mathrm{p} j}\left(t_{5 j} \cdot t_{0 j}-t_{6 j} \cdot t_{9 j}\right)} $ | (27) |
| $ C_{j}=t_{6 j} \cdot\left(\mathrm{e}^{2 \alpha_{j} L}-\mathrm{e}^{-2 \alpha_{j} L}\right)+t_{5 j} \cdot\left(2 \sin 2 \beta_{j} L\right) $ | (28) |
因此,整个楔形桩的水平位移函数表达式为
| $ \left.u(z, t)\right|_{z=z_{0}}=\left.u_{j}(z, t)\right|_{z=z_{0}}, h_{j} \leqslant z_{0} \leqslant h_{j+1} $ | (29) |
本文求解的关键在于将楔形桩划分为s个厚度相等的薄微元段,然后对每个微元段建立水平振动方程进行求解,因此,桩体单元划分精度关乎整个模型的精度,首先研究桩体单元划分精度的问题。
如无特别说明,桩土设计参数的取值情况参考文献[22],如表 1所示。
| 表 1 桩土设计参数取值 Tab. 1 Design parameters of pile-soil system |
为了使结果更客观,令a0=ω·d1/vs,并且引入无量纲参数,将水平简谐激振下荷载为最大值时的桩身位移、弯矩和剪力无量纲化为
| $ \left\{\begin{array}{l} U_{j \max }(z)=E_{\mathrm{p}} d_{1} u_{j \max } /\left(500 Q_{0}\right) \\ M_{j \max }(z)=m_{j \max } /\left(2 Q_{0} d_{1}\right) \\ Q_{j \max }(z)=q_{j \max } / Q_{0} \end{array}\right. $ | (30) |
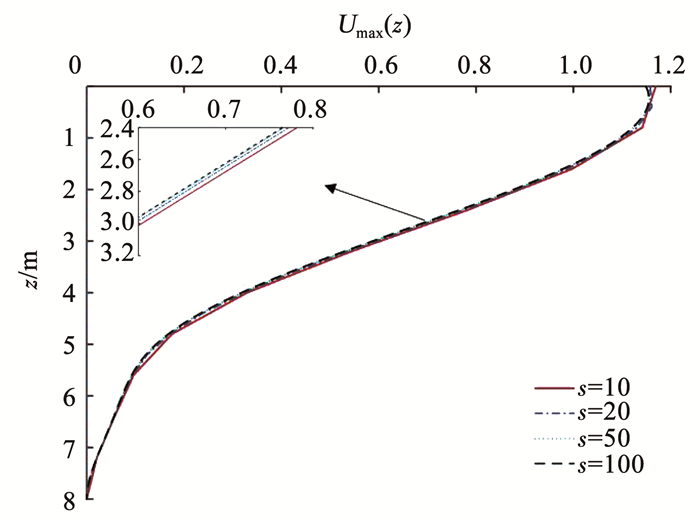
在研究桩体单元划分精度时,桩顶直径d1设置为0.6 m,桩长L设置为8 m,划分段数s分别设置为10、20、50和100,其余参数取值如表 1所示。图 3反映了桩体单元划分精度对桩体水平位移的影响,可以看出,划分段数s=100时,桩体水平位移曲线已经趋于稳定。通过试算多种工况下划分段数s对桩体水平位移、弯矩和剪力的影响,结果表明:当s>100时,计算结果已经稳定收敛。因此,如果不作特别说明,本文统一取桩身微元段厚度与楔形桩桩长的比值为1 /100。
|
图 3 桩体单元划分精度对桩体水平位移的影响 Fig. 3 Influence of dividing precision of pile element on horizontal displacement of pile |
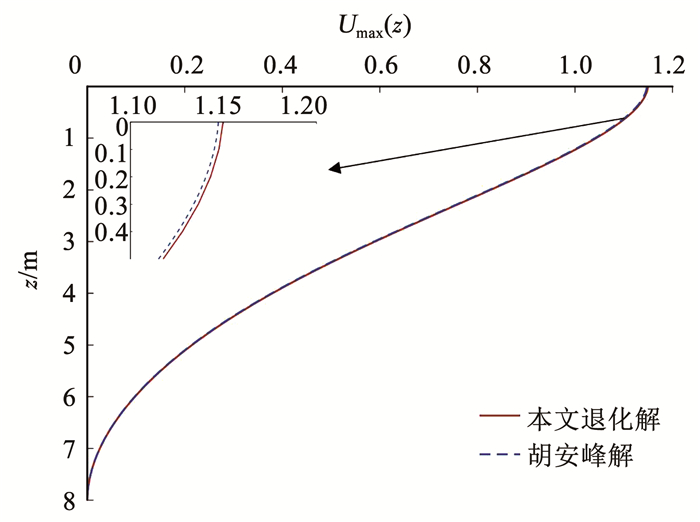
为了验证本文所建立模型的准确性和可靠性,将楔形桩- 土系统横向耦合振动模型与胡安峰等[22]建立的等直径桩水平振动模型进行对比分析。桩顶直径d1设置为0.6 m,桩长L设置为8 m,楔角为0°,其余参数取值如表 1所示。两种模型计算下的桩体水平位移如图 4所示,两种解基本吻合。通过计算多种工况时两种模型下的桩体水平位移、弯矩和剪力,两种解仍然基本吻合,从而验证了本文计算模型的正确性。
|
图 4 两种模型下桩体水平位移对比 Fig. 4 Comparison of horizontal displacement of pile under two models |
动力荷载作用下桩身不同深度处的水平位移、弯矩和剪力的最大值会对设计造成比较大的影响,是工程关注的重点内容,本节将详细讨论水平简谐激振下荷载为最大值时桩顶约束转角和桩底固定工况的楔形桩空间响应,其他边界条件可以通过类似的方法进行研究。
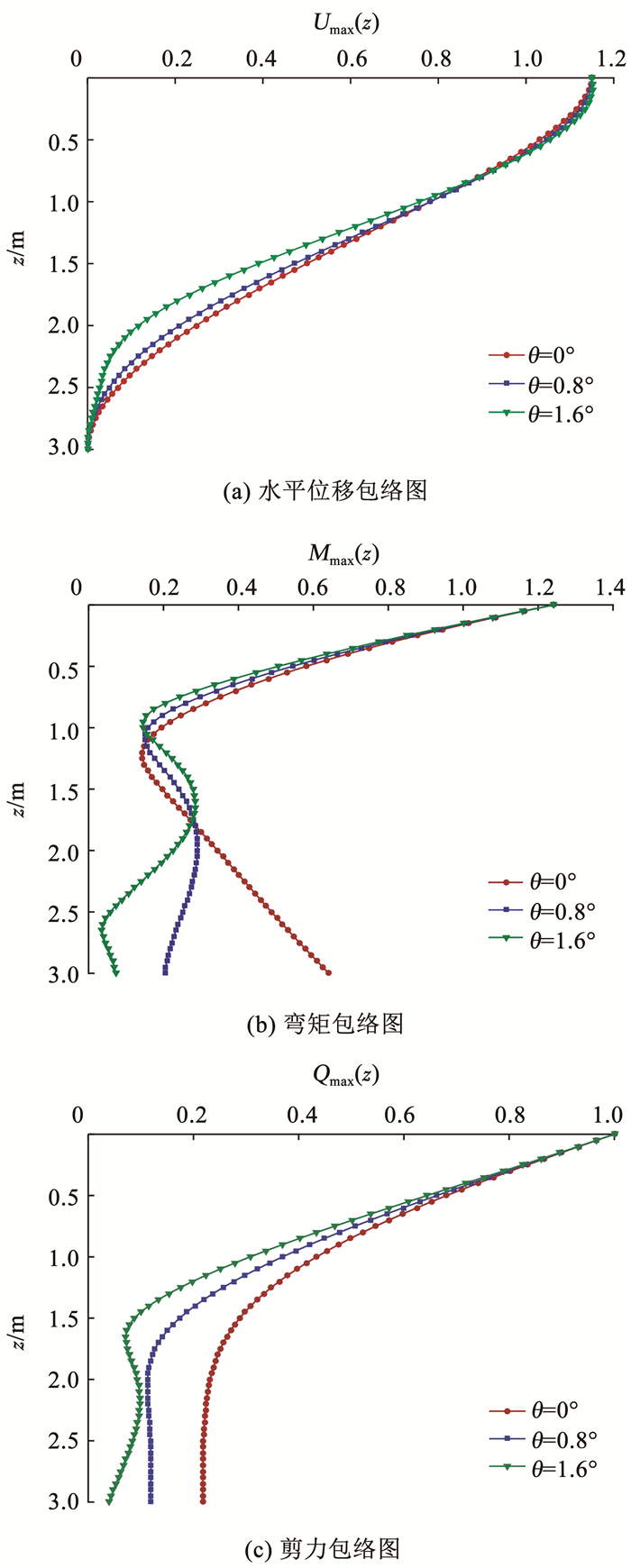
4.1 楔角对楔形桩空间响应的影响分析楔角对楔形桩空间响应的影响时,保持桩顶直径不变,楔角θ分别设置为0°、0.8°和1.6°,随着楔角的增大,桩身直径沿深度方向逐渐减小,其余参数取值如表 1所示。楔形桩位移包络图、弯矩包络图和剪力包络图如图 5所示,反映了楔角对桩体水平动力特性的影响,图中横坐标表示无量纲的水平位移、弯矩和剪力,纵坐标表示土体深度。
|
图 5 楔角对楔形桩空间响应的影响 Fig. 5 Influence of wedge angle on spatial response of tapered pile |
由图 5可知,在距离桩顶0.5 m内,楔角的变化对桩身的水平位移、弯矩和剪力的影响很小,基本可以忽略。随着楔角的增大,桩身水平位移沿深度方向衰减加快,桩身剪力逐渐减小; 桩身弯矩除桩中部外,均随着楔角的增大而减小。这是由于楔角对桩顶部直径的改变不明显,桩中部和底部直径发生较明显变化。
综上,楔角对桩顶部产生的影响很小,对桩中部和底部则会产生较大的影响。
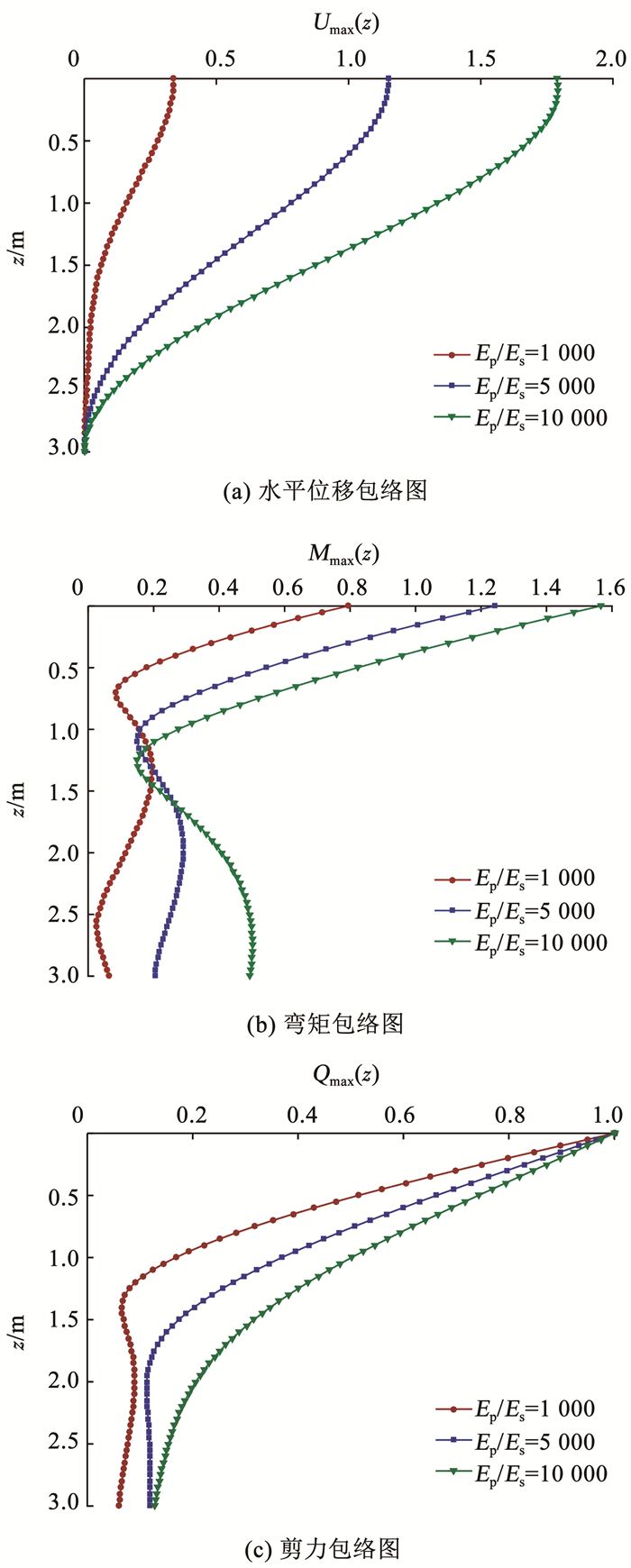
4.2 桩土刚度比对楔形桩空间响应的影响分析桩土刚度比对楔形桩空间响应的影响时,保持土体弹性模量不变,Ep/Es分别设置为1 000、5 000和10 000,其余参数取值如表 1所示。包络图如图 6所示,反映了桩土刚度比对楔形桩水平动力特性的影响。
|
图 6 桩土刚度比对楔形桩空间响应的影响 Fig. 6 Influence of pile-soil stiffness ratio on spatial response of tapered pile |
由图 6可知,整体上桩身的水平位移、弯矩和剪力都会随着桩土刚度比的增大而增大。桩底部的水平位移、剪力受桩土刚度比的影响很小; 随着桩土刚度比的减小,桩身水平位移、剪力沿深度方向衰减加快; 桩身弯矩除桩中部外,均随着桩土刚度比的增大而增大。这表明虽然增大了桩土刚度比,由于楔角的存在导致楔形桩桩顶部、桩中部和桩底部空间响应的变化仍然存在差异,并且该差异受桩土刚度比显著影响。
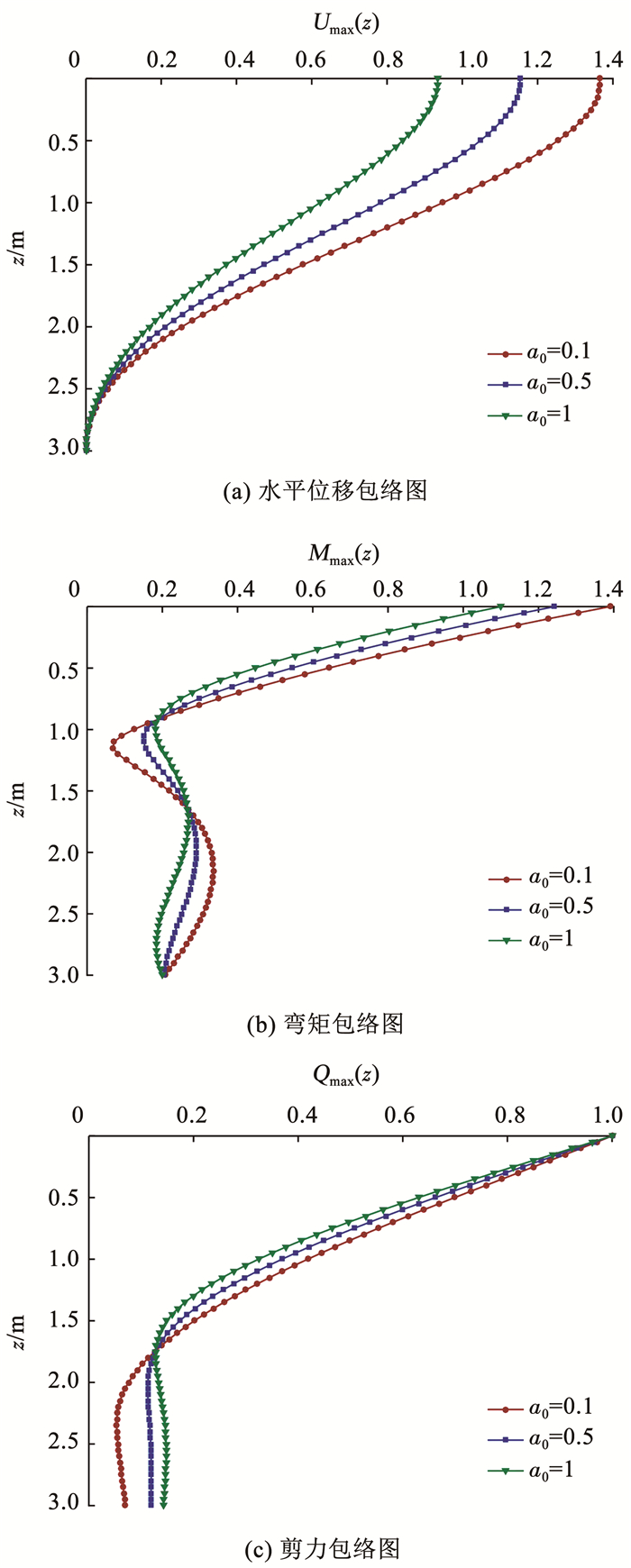
4.3 无量纲频率对楔形桩空间响应的影响在分析无量纲频率对楔形桩空间响应的影响时,a0分别设置为0.1、0.5和1,其余参数取值如表 1所示。包络图如图 7所示,反映了无量纲频率对楔形桩水平动力特性的影响。
|
图 7 无量纲频率对楔形桩空间响应的影响 Fig. 7 Influence of dimensionless frequency on spatial response of tapered pile |
由图 7可以看出,桩顶部、中部的水平位移、剪力随着无量纲频率的增大而减小; 桩底部的水平位移则基本不变,弯矩随着无量纲频率的增大而减小,剪力随着无量纲频率的增大而增大。这是由假设桩顶约束转角、桩底固定导致的。综上,无量纲频率对桩体的作用比较复杂,并且会产生明显的影响。
5 楔形桩时间响应分析前文详细研究了不同参数影响下的楔形桩水平位移、弯矩和剪力的空间变化规律,对设计有一定的指导作用。本节进一步研究桩体各部位的时间变化规律,探明楔形桩不同部位的时间响应规律。
进行楔形桩时间响应分析时,在桩顶部、桩中部和桩底部各选取一微元段为代表,以考虑无量纲频率对楔形桩时间响应的影响为例,其余设计参数的影响可作类似分析。假设桩长为10倍桩顶直径,分别取研究深度为z=0、1.5和3 m,历时多个周期。为了减少误差,引入无量纲参数,将桩身水平位移和弯矩无量纲化为
| $ \left\{\begin{array}{l} U_{j}(t)=E_{\mathrm{p}} d_{1} u_{j} /\left(500 Q_{0}\right) \\ M_{j}(t)=m_{j} /\left(2 Q_{0} d_{1}\right) \end{array}\right. $ | (31) |
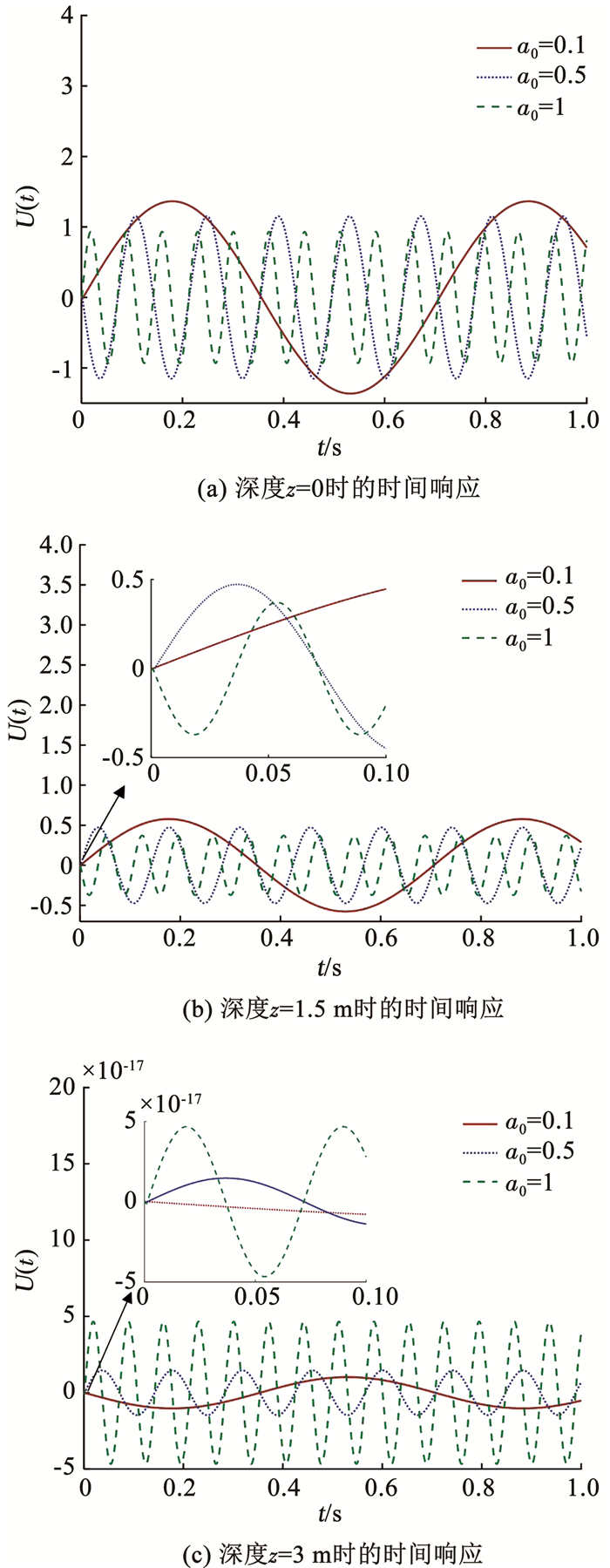
分析无量纲频率对桩身的影响时,a0分别设置为0.1、0.5和1,其余桩土设计参数的取值如表 1所示。桩顶部、桩中部和桩底部的桩身水平位移时间响应图如图 8所示,横坐标表示时间,纵坐标表示某深度的水平位移无量纲响应值。
|
图 8 桩身水平位移时间响应分析 Fig. 8 Time response analysis of horizontal displacement of pile |
由图 8可知,由于无量纲频率减小,激振频率ω相应减小,故整个桩体到达最大水平位移所需的时间相应增大。因此,桩顶部和桩中部的水平位移随着无量纲频率的增大而减小; 而由于假设桩底固定,桩底部的水平位移非常小以至于可以忽略。
综上,无量纲频率对桩体的动力性质有比较大的影响,并且影响随深度逐渐变弱。
5.2 桩身弯矩时间响应分析同理,图 9反映了不同深度桩身弯矩随时间的变化响应。可以看出,无量纲频率减小即激振频率ω减小,整个桩体到达最大弯矩所需的时间相应增大。由于假设桩顶约束转角,桩顶部的弯矩随着无量纲频率的增大而减小,桩中部和桩底部的弯矩基本不随无量纲频率改变。

|
图 9 桩身弯矩时间响应分析 Fig. 9 Time response analysis of bending moment of pile |
对于Euler梁模型,桩体分层后第j微元段的水平振动方程为
| $ \begin{aligned} &E_{\mathrm{p}} I_{\mathrm{p} j} \frac{\partial^{4} u_{j}(z, t)}{\partial z^{4}}+k_{x} \cdot u_{j}(z, t)+ \\ &c_{x} \cdot \frac{\partial u_{j}(z, t)}{\partial t}+m_{\mathrm{p} j} \frac{\partial^{2} u_{j}(z, t)}{\partial t^{2}}=F(t) \cdot \delta(z) \end{aligned} $ | (32) |
式中:δ(z)为广义狄拉克函数,其余符号的意义与之前相同。当式(2)中的k′ApjGp→∞,即不考虑桩体剪切变形的作用时,式(2)能够变成式(32)。
仍采用分离变量法在复频域内求解稳态振动,涉及的边界条件、连续条件与Timoshenko梁模型解法相同,其他边界条件可以通过类似的方法进行研究。
首先,令
| $ u_{j}(z, t)=U_{j}(z) \cdot \mathrm{e}^{\mathrm{i} \omega t} $ | (33) |
利用分离变量法和传递矩阵法,最后可以得到第j微元段的振幅函数如下:
| $ \begin{aligned} U_{j}(z)=& C_{1} \mathrm{e}^{\lambda z} \cos \lambda z+C_{2} \mathrm{e}^{\lambda z} \sin \lambda z+\\ & C_{3} \mathrm{e}^{-\lambda z} \cos \lambda z+C_{4} \mathrm{e}^{-\lambda z} \sin \lambda z \end{aligned} $ | (34) |
其中所涉及的系数分别为
| $ \lambda=\alpha\left(\cos \frac{\beta}{4}+\mathrm{i} \sin \frac{\beta}{4}\right) $ | (35) |
| $ \alpha=\sqrt[4]{\frac{\left[\left(k_{x}-m_{\mathrm{p} j} \omega^{2}\right)^{2}+c_{x}^{2} \omega^{2}\right]^{1 / 2}}{4 E_{\mathrm{p}} I_{\mathrm{p} j}}} $ | (36) |
| $ \beta=\arccos \frac{k_{x}-m_{\mathrm{p}j} \omega^{2}}{\sqrt{\left(k_{x}-m_{\mathrm{p}j} \omega^{2}\right)^{2}+c_{x}^{2} \omega^{2}}} $ | (37) |
| $ C=\mathrm{e}^{2 \lambda L}-\mathrm{e}^{-2 \lambda L}+2 \sin 2 \lambda L $ | (38) |
| $ C_{3}=Q_{2}\left(\mathrm{e}^{2 \lambda L}+\sin 2 \lambda L+\cos 2 \lambda L-2\right) / C $ | (39) |
| $ C_{4}=Q_{2}\left(\mathrm{e}^{2 \lambda L}+\sin 2 \lambda L-\cos 2 \lambda L\right) / C $ | (40) |
| $ C_{1}=C_{3}-Q_{2}, C_{2}=Q_{2}-C_{4} $ | (41) |
| $ Q_{2}=\frac{Q_{0}}{4 E_{\mathrm{p}} I_{\mathrm{p}j} \lambda^{3}} $ | (42) |
因此,将振幅函数代入式(33)可以求出第j微元段的水平位移函数uj(z, t)。
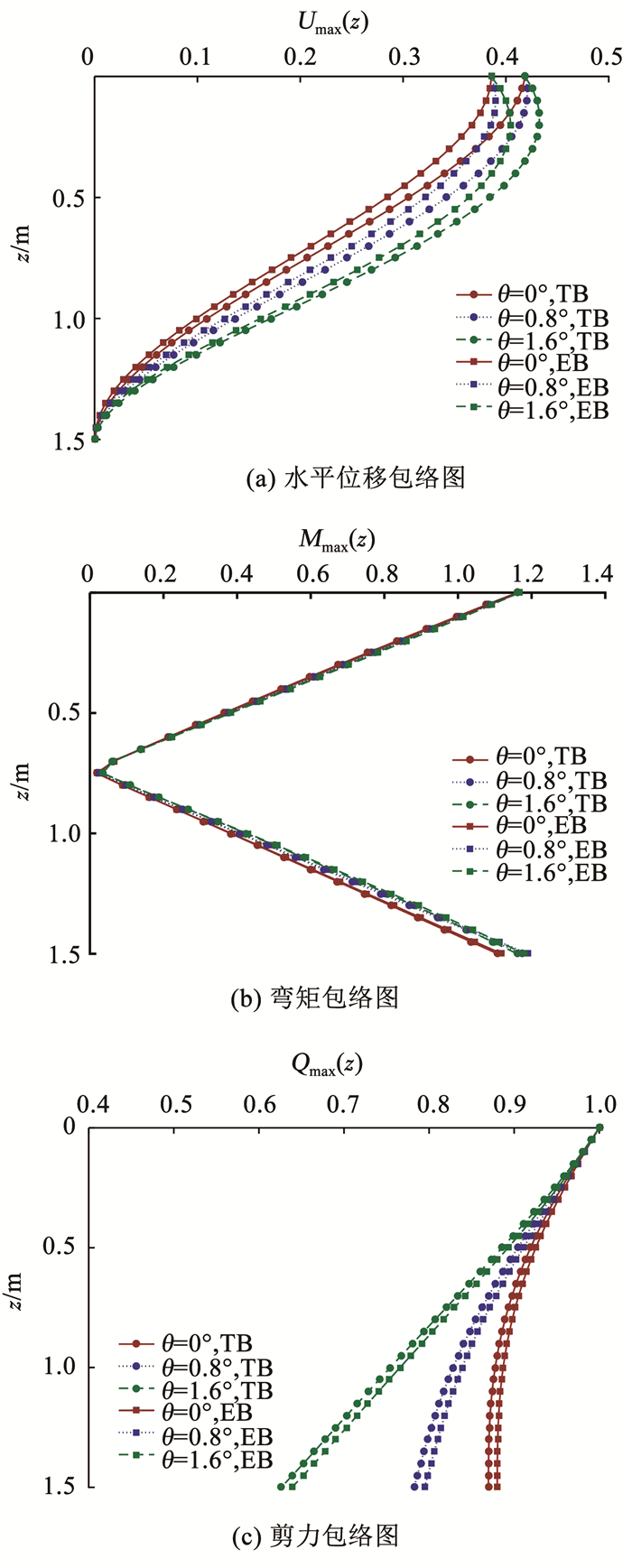
6.2 两种模型的差异对于长细构件,使用Timoshenko梁模型(简称TB)与Euler梁模型(简称EB)的计算结果非常接近,故本节将详细讨论小长径比下两种模型受楔角的影响,其他桩土设计参数的影响可作类似分析。令桩顶长径比L/d1为5,楔角θ分别设置为0°、0.8°和1.6°,其余桩土设计参数取值如表 1所示。
图 10反映了楔角对两种模型下桩体水平动力特性的影响。可以看出,两种模型下桩体动力响应的变化规律与第4节的分析基本一致; 弯矩先减小后增大,可能是由小长径比下桩中部的截面转角很小导致的; 两种模型下桩体的动力响应存在一定差异,但是楔角对两种模型造成的影响基本相同。
|
图 10 两种模型下楔形桩空间响应对比 Fig. 10 Comparison of spatial response of tapered pile under two models |
采用Winkler地基和Timoshenko梁模型,建立了桩顶水平简谐激振力作用下楔形桩- 土系统的控制方程,并得到了楔形桩水平位移、弯矩和剪力的解析解。基于所得解,详细分析了桩土设计参数对楔形桩空间响应和时间响应的影响,得出以下主要结论:
1) 桩顶部的动力响应受楔角改变的影响很小,桩中部和桩底部则随着楔角增大而明显减小。
2) 整个桩体的动力响应基本随桩土刚度比的增大而明显增大。
3) 随着无量纲频率的减小,整个桩体的动力响应到达最大值所需的时间也相应增大; 改变无量纲频率会使桩体各部位的动力响应发生明显不同的变化,作用比较复杂,并且影响随深度逐渐变弱。
4) 虽然Timoshenko梁模型与Euler梁模型在小长径比下存在一定差异,但楔角对两种模型造成的影响基本相同。
| [1] |
鹿文东, 玉利荣. 锥形钻孔灌注桩作用机理与承载力试验研究[J]. 地基基础工程, 2002, 12(3): 36. LU Wendong, YU Lirong. Experimental study on action mechanism and bearing capacity of tapered bored pile[J]. Foundation Engineering, 2002, 12(3): 36. |
| [2] |
KODIKARA J, KONG K H, HAQUE A. Numerical evaluation of side resistance of tapered piles in mudstone[J]. Geotechnique, 2006, 56(7): 505. DOI:10.1680/geot.2006.56.7.505 |
| [3] |
LEE J, PAIK K, KIM D, et al. Estimation of axial load capacity for bored tapered piles using CPT results in sand[J]. Journal of Geotechnical & Geoenvironmental Engineering, ASCE, 2009, 135(9): 1285. DOI:10.1061/(ASCE)GT.1943-5606.0000036 |
| [4] |
张可能, 何杰, 刘杰, 等. 静压楔形桩沉桩效应模型试验研究[J]. 中南大学学报(自然科学版), 2012, 43(2): 638. ZHANG Keneng, HE Jie, LIU Jie, et al. Experimental study on static pressure wedge-shaped pile sinking effect model[J]. Journal of Central South University (Natural Science Edition), 2012, 43(2): 638. |
| [5] |
周航, 孔纲强, 刘汉龙. 基于圆孔扩张理论的静压楔形桩沉桩挤土效应研究[J]. 中国公路学报, 2014, 27(4): 28. ZHOU Hang, KONG Gangqiang, LIU Hanlong. Study on soil squeezing effect of static pressure wedge-shaped pile sinking based on circular hole expansion theory[J]. Chinese Journal of Highways, 2014, 27(4): 28. DOI:10.19721/j.cnki.1001-7372.2014.04.004 |
| [6] |
孔纲强, 曹兆虎, 周航, 等. 极限荷载下纵向截面异形桩破坏形式对比模型试验研究[J]. 岩土力学, 2015, 36(5): 124. KONG Gangqiang, CAO Zhaohu, ZHOU Hang, et al. Experimental study on failure forms of abnormal piles with longitudinal section under ultimate load[J]. Rock and Soil Mechanics, 2015, 36(5): 124. DOI:10.16285/j.rsm.2015.05.013 |
| [7] |
孔纲强, 曹兆虎, 周航, 等. 水平荷载下扩底楔形桩承载力特性透明土模型试验[J]. 土木工程学报, 2015, 48(5): 83. KONG Gangqiang, CAO Zhaohu, ZHOU Hang, et al. Transparent soil model test of bearing capacity characteristics of wedge-shaped pile with enlarged bottom under horizontal load[J]. Chinese Journal of Civil Engineering, 2015, 48(5): 83. DOI:10.15951/j.tmgcxb.2015.05.010 |
| [8] |
周航, 孔纲强, 曹兆虎. 水平荷载下楔形桩桩- 土相互作用理论分析[J]. 中南大学学报(自然科学版), 2016, 47(3): 193. ZHOU Hang, KONG Gangqiang, CAO Zhaohu. Theoretical analysis of pile-soil interaction under horizontal load[J]. Journal of Central South University (Natural Science Edition), 2016, 47(3): 193. DOI:10.11817/j.issn.1672-7207.2016.03.024 |
| [9] |
蔡燕燕, 俞佳, 郑春婷, 等. 楔形桩桩顶纵向振动阻抗的解析解[J]. 岩土工程学报, 2011, 33(增刊2): 392. CAI Yanyan, YU Jia, ZHENG Chunting, et al. Analytical solution of longitudinal vibration impedance of wedge shaped pile top[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S2): 392. |
| [10] |
吴文兵, 王奎华, 武登辉, 等. 考虑横向惯性效应时楔形桩纵向振动阻抗研究[J]. 岩石力学与工程学报, 2011, 30(增刊2): 3618. WU Wenbing, WANG Kuihua, WU Denghui, et al. Study on longitudinal vibration impedance of wedge-shaped pile considering transverse inertia effect[J]. Journal of Rock Mechanics and Engineering, 2011, 30(S2): 3618. |
| [11] |
吴文兵, 谢帮华, 黄生根, 等. 考虑挤土效应时楔形桩纵向振动阻抗研究[J]. 地震工程学报, 2015, 37(4): 1042. WU Wenbing, XIE Banghua, HUANG Shenggen, et al. Study on longitudinal vibration impedance of wedge shaped pile considering soil compaction effect[J]. Journal of Seismic Engineering, 2015, 37(4): 1042. DOI:10.3969/j.issn.1000-0844.2015.04.1042 |
| [12] |
王奎华, 高柳, 肖偲, 等. 考虑桩周土竖向作用大直径楔形桩纵向振动特性[J]. 岩土力学, 2016, 37(增刊2): 232. WANG Kuihua, GAO Liu, XIAO Si, et al. Longitudinal vibration characteristics of large diameter wedge-shaped pile considering vertical action of soil around pile[J]. Rock and Soil Mechanics, 2016, 37(S2): 232. DOI:10.16285/j.rsm.2016.S2.027 |
| [13] |
高柳, 王奎华, 李振亚, 等. 考虑桩周土竖向作用和施工扰动效应时大直径楔形桩的纵向振动特性[J]. 振动与冲击, 2018, 37(2): 30. GAO Liu, WANG Kuihua, LI Zhenya, et al. Longitudinal vibration characteristics of large diameter wedge-shaped pile considering vertical action of soil around pile and construction disturbance effect[J]. Journal of Vibration and Impact, 2018, 37(2): 30. DOI:10.13465/j.cnki.jvs.2018.2.005 |
| [14] |
王奎华, 童魏烽. 基于非等截面桩体模型的楔形桩动力响应[J]. 哈尔滨工业大学学报, 2019, 51(8): 104. WANG Kuihua, TONG Weifeng. Dynamic response of wedge-shaped pile based on non-uniform section pile model[J]. Journal of Harbin Institute of Technology, 2019, 51(8): 104. DOI:10.11918/j.issn.0367-6234.201806076 |
| [15] |
王奎华, 童魏烽, 王磊. 基于非等截面桩体模型的缺陷楔形桩动力响应研究[J]. 天津大学学报(自然科学与工程技术版), 2018, 51(12): 26. WANG Kuihua, TONG Weifeng, WANG Lei. Study on dynamic response of faulted wedge pile based on non-uniform section pile model[J]. Journal of Tianjin University (Natural Science and Engineering Technology Edition), 2018, 51(12): 26. DOI:10.11784/tdxbz201803087 |
| [16] |
栾鲁宝, 丁选明, 刘汉龙, 等. 考虑剪切变形的PCC桩水平振动响应解析解[J]. 岩石力学与工程学报, 2016, 35(11): 2345. LUAN Lubao, DING Xuanming, LIU Hanlong, et al. Analytical solution of horizontal vibration response of PCC pile considering shear deformation[J]. Journal of Rock Mechanics and Engineering, 2016, 35(11): 2345. DOI:10.13722/j.cnki.jrme.2015.1487 |
| [17] |
郑长杰, 丁选明, 栾鲁宝. 黏弹性地基中管桩水平动力特性分析[J]. 岩土力学, 2017, 38(1): 26. ZHENG Changjie, DING Xuanming, LUAN Lubao. Analysis of horizontal dynamic characteristics of pipe piles in viscoelastic foundation[J]. Rock and Soil Mechanics, 2017, 38(1): 26. DOI:10.16285/j.rsm.2017.01.004 |
| [18] |
栾鲁宝, 丁选明, 瞿立明. 饱和土中考虑竖向荷载的端承桩水平振动响应解析解[J]. 防灾减灾工程学报, 2017, 37(3): 419. LUAN Lubao, DING Xuanming, QU Liming. Analytical solution of horizontal vibration response of end-bearing pile considering vertical load in saturated soil[J]. Chinese Journal of Disaster Prevention and Mitigation Engineering, 2017, 37(3): 419. DOI:10.13409/j.cnki.jdpme.2017.03.013 |
| [19] |
TIMOSHENKO S P. On the correction for shear of the differential equation for transverse vibration of prismatic bars[J]. Philosophical Magazine, 1921, 41: 744. DOI:10.1080/14786442108636264 |
| [20] |
陈镕, 万春风, 薛松涛, 等. Timoshenko梁运动方程的修正及其影响[J]. 同济大学学报(自然科学版), 2005, 33(6): 711. CHEN Rong, WAN Chunfeng, XUE Songtao, et al. Modification of motion equation of Timoshenko beam and its effect[J]. Journal of Tongji University (Natural Science Edition), 2005, 33(6): 711. |
| [21] |
GAZETAS G, DOBYR R. Horizontal response of piles in layered soils[J]. Journal of Geotechnical Engineering, 1984, 110(l): 20. DOI:10.1061/(ASCE)0733-9410(1984)110:1(20) |
| [22] |
胡安峰, 谢康和, 应宏伟, 等. 粘弹性地基中考虑桩体剪切变形的单桩水平振动解析理论[J]. 岩石力学与工程学报, 2004, 23(9): 1515. HU Anfeng, XIE Kanghe, YING Hongwei, et al. Analytic theory of horizontal vibration of single pile considering shear deformation of pile body in viscoelastic foundation[J]. Journal of Rock Mechanics and Engineering, 2004, 23(9): 1515. DOI:10.3321/j.issn:1000-6915.2004.09.020 |
 2021, Vol. 53
2021, Vol. 53


