2. 重载铁路工程结构教育部重点实验室(中南大学), 长沙 410075
2. Key Laboratory of Engineering Structures of Heavy Haul Railway (Central South University), Ministry of Education, Changsha 410075, China
土压平衡盾构法因其对地表影响程度低、占用地面空间小等优势广泛应用于城市隧道建设。盾构掘进时常往刀盘前方、土舱或螺旋输送机内添加改良剂把渣土改良成合适的塑流性状态,旨在保证进排土的顺畅以及控制进出土量的平衡[1-2],从而规避掘进参数波动幅度大、刀盘结泥饼、螺旋输送机喷涌、地层损失等风险[3-4]。为确保盾构安全高效掘进,需充分认识改良渣土力学行为,明确其合适改良状态的评价指标。因此,学者们研究了改良渣土塑流性及力学特征,通过分析渣土状态、盾构掘进参数或地层变位响应,提出了渣土合理状态的不同评价指标。研究手段主要如下:
1) 现场测试和坍落度试验。Quebaud等[5]提出了渣土的合理坍落度范围,Ye等[6]建立了坍落度与渣土含水率、改良参数的经验关系,制定了合适改良方案。然而,该手段缺乏对渣土理论模型的探讨而仅能做定性分析或提出针对特定地层的经验公式,而且坍落度试验是在大气压条件下开展,所得坍落度值是静态指标,不能准确反映土舱或螺旋输送机内带压状态下渣土的流动状态。
2) 缩尺模型试验。孟庆琳等[7]等建立了盾构掘进与进排土的试验模型,通过土舱压力分布特征、螺旋输送机扭矩以及沿程压力梯度来评价渣土的流动特性,但相关模型系统复杂、成本高昂,故操作难度大,数据采集量有限,评价指标具有唯象性且不能深入剖析流动介质特性对流态的影响。
3) 理论模型和数值模拟。通过单元试验分析改良渣土的力学行为,探讨其合理的理论模型,利用有限元、离散元等数值方法模拟盾构掘进时地层与渣土在复杂边界下的运动情况,分析渣土流态与流场分布情况及进排土效率[7]、渣土压力分布特征[8]、地层变位[9]等问题,进而确定合理改良参数。该手段通过改变模型参数,可适用于不同地层条件,亦能摒弃“试错”的传统方法。其中,盾构进排土效率优化与平衡控制着重于探讨渣土的宏观塑性流动,不考虑土颗粒与改良剂之间的相互作用,因此,此类问题可将改良渣土近似视为均匀连续的流体,采用连续介质模型表征盾构进排土过程中改良渣土的力学行为,基于计算流体力学(CFD)模拟改良渣土的塑性流动,重现或预测盾构进排土过程。
流变本构模型的准确搭建是CFD数值模拟真实反映盾构改良渣土宏观力学行为的关键。由坍落度试验可知,提筒后渣土在自重作用下缓慢流动坍落并最终达到某一稳定高度,表明渣土可近似看作非牛顿流体,当剪切应力大于屈服应力时,渣土似流体般发生剪切流动; 当剪切应力小于屈服应力时,渣土似固体般不发生变形[10]。至于渣土流变模型参数的获取,鲜有文献介绍测试原理及方法。采用参数反演法,Talebi等[11]将改良渣土视为Bingham流体,在螺旋输送机数值模型中输入工程使用的改良参数和掘进参数,反演得改良土流变参数。该方法物理意义不明确,且忽略高压力梯度下渣土流变参数的压力相关性,因而有必要采用试验环境还原盾构实际情况的室内试验,来分析带压环境下改良渣土力学特征及模型参数。通过旋转剪切仪,Moris等[12]探讨了改良渣土在不同法向压力、十字板转速、改良参数下的变形情况和剪切强度特性; 张檑[13]分析了十字板扭矩- 转速曲线,将砂卵石层改良渣土视为Bingham流体,拟合其流变参数,并用ICAR混凝土流变仪进行标定,然后通过数值模拟讨论了流变参数的压力相关性; 孟庆琳[7]将泡沫改良砂土视为可压缩的Bingham流体,分析了不同法向压力、改良参数下的渣土流变参数,并建立流变参数的压力相关性公式,然而流变参数的既有推导方法对流变学的认识不够充分。此外,渣土流变行为与其压缩性也密切关联,孟庆琳[7]通过非饱和土三轴压缩试验探讨了渣土的压缩性,建立了密度的压力相关性公式,然而制备过程中试样塑流性强难以直立且土内泡沫在负压成型时易被破坏,试验可靠度低; 盾构内渣土受土舱或螺旋输送机外壳侧向限制而仅发生沿进排土方向的压缩变形,且进排土过程中渣土来不及固结排水就被快速排出。Mori等[12]通过不排水侧限压缩试验分析了渣土的压缩特性,该试验还原了盾构内渣土所处的环境,具备探究盾构内渣土密度压力相关性的潜力。
综上,既有关于渣土流变行为的研究存在以下问题:仅描述试验现象,未搭建理论模型量化渣土力学特征; 设置的试验环境不切合盾构实况; 推导参数时对非牛顿流体力学理解不足,并且尚未开展对改良砾砂渣土流变力学行为的探究。因此,采用了加压式十字板剪切试验仪,针对昆明某地铁区间砾砂地层盾构泡沫改良渣土提出了详细的试验方案、流变理论模型和参数分析方法。通过侧限压缩试验和十字板剪切试验,探究了泡沫改良砾砂的压缩特性和剪切强度特性。基于流变力学理论,拟合并分析了试样的压缩系数和流变参数,提出了泡沫改良砾砂的密度、流变参数压力相关性公式。提出的改良渣土理论模型及压力相关性参数可直接用于土舱及螺旋输送机内渣土的流动规律及力学行为的数值模拟和计算。
1 流变试验方案 1.1 试验材料试验土样取自昆明地铁某区间盾构掘进状态理想的渣土,渣土级配曲线见图 1,参照《GB/T50123—2019土工试验方法标准》中土的工程分类,该土属于含细粒土砾。为改善渣土的塑流性状态,掘进时采用水和分散型泡沫剂对刀盘前方和土舱内切削土体进行改良,其中单环管片掘进水用量828 L,泡沫原液用量26 L,泡沫体积分数为3%,发泡倍率约为8。因此,获取的土样为泡沫改良渣土,其基本土性参数如表 1所示,改良渣土坍落体见图 2。

|
图 1 试验土样级配曲线 Fig. 1 Grain size distribution of soil sample |
| 表 1 试验土样的物理力学参数 Tab. 1 Physical characteristics of soil sample |

|
图 2 改良渣土坍落度试验 Fig. 2 Slump test of conditioned soil |
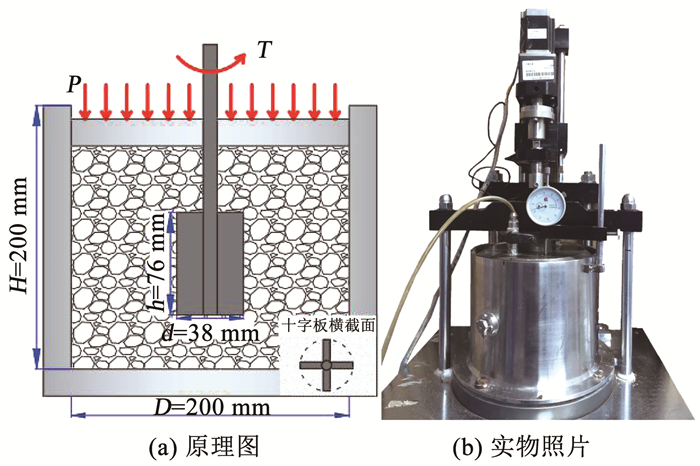
采用Liu等[14]开发的加压式十字板旋转剪切仪探究泡沫改良砾砂的力学特征,其原理及实物图(含尺寸)如图 3所示。仪器主要由试样腔、加压装置、剪切装置、传感装置等组成。其中,试样腔与外界没有气水交换; 加压装置采用气泵加压,压力施加在盖板上然后均匀传递到试样腔中的土样; 剪切装置是十字剪切板,十字板在电机驱动下以恒定转速旋转,额定扭矩为30 N·m; 传感装置包括压力传感器和扭矩传感器,实时监测并记录试样所受法向压力和十字板所受扭矩。此外,考虑到仪器与试样颗粒粒径的相对尺寸大小会影响测试结果精度,参照既有经验[15],叶片直径d应为试样最大粒径的2倍左右,叶片边缘至腔壁的距离(D-d)/2应为试样最大粒径的3倍以上。所用加压式十字板剪切仪叶片直径和高度分别为38、76 mm,试样腔内壁直径为200 mm,而试样最大粒径不超过10 mm,因此,所用的剪切仪满足对试样最大颗粒尺寸的要求。
|
图 3 加压式十字板旋转剪切仪 Fig. 3 Pressurized vane shear apparatus |
采用加压式十字板剪切仪对改良渣土试样进行不排水条件下的侧限压缩试验和十字板剪切试验,步骤如下:
1) 将试样分层均匀置入试样腔内并盖上圆形盖板,十字板穿过盖板中心圆孔插入到试样中,应控制叶片底部离试样腔底距离不小于0.5d,叶片顶部离试样上表面距离不小于d[15]。
2) 打开盖板排气阀,预加10 kPa法向压力,直至试样上方空气被排出,即盖板与试样上表面接触,保证压力通过盖板传递到试样,再关闭排气阀。
3) 继续加压,为使试样承受的法向压力达到设计值,加压方式参考Liu等[14]的试验方法,对盖板加压时多加10 kPa压力来抵消盖板边缘与试样腔内壁间摩擦力、盖板自重的影响。此外,安装百分表实时监测试样的法向位移,变形稳定后百分表读数差值为该法向压力下试样对应的压缩量。
4) 压缩稳定后,使十字板以恒定速率旋转,每转2°记录一次十字板所受扭矩M(N·m),十字板反复剪切试样失效面,直至扭矩减小至趋于稳定。为了消除盖板中心圆孔内壁对十字板轴身摩擦扭矩的干扰,需将各工况十字板扭矩测试值减去空腔情况下十字板扭矩,继而修正后扭矩可视为各工况十字板叶片克服试样剪切强度所需扭矩。
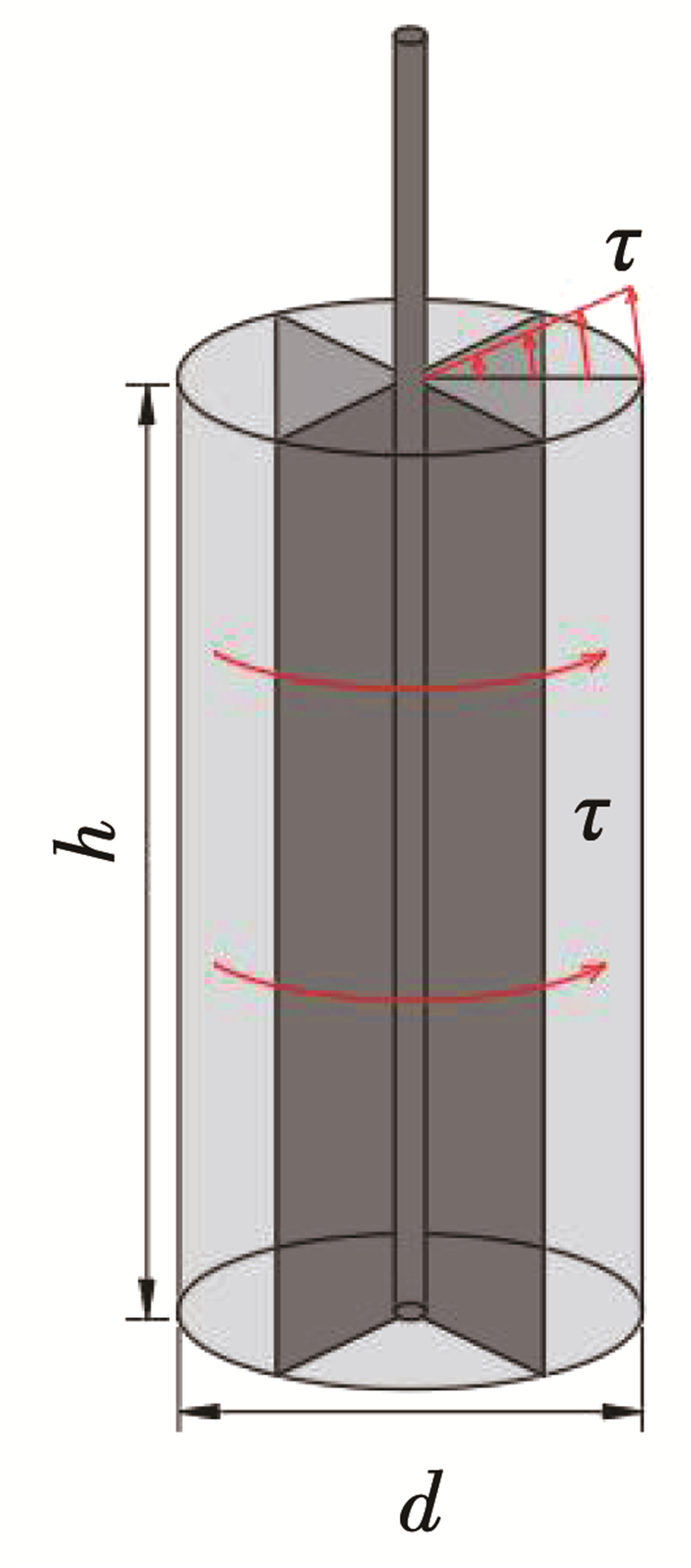
5) 依据ASTM D4648[16]推导叶片扭矩与试样剪切应力的关系,假设试样剪切失效面是由叶片直径和长度确定的圆柱上下表面和侧面(见图 4),失效面上剪切应力相等且均匀分布,将失效面上剪切应力积分可得阻力扭矩,而叶片驱动扭矩等于失效面上的阻力扭矩,因此,十字板扭矩可通过式(1)换算为剪切应力τ (Pa),进而可得试样剪切应力随位移的变化情况。此外,十字板转速n可通过式(2)换算为剪切应变率
| $ \tau = \frac{{6M}}{{{\rm{ \mathsf{ π} }}\left( {{d^3} + 3{d^2}h} \right)}} $ | (1) |
| $ \dot \gamma = \frac{{{\rm{ \mathsf{ π} }}n}}{{5400}} \times \frac{{{D^2}}}{{{D^2} - {d^2}}} $ | (2) |
|
图 4 试样剪切失效圆柱面示意 Fig. 4 Schematic of cylindrical shear failure interface |
盾构正常掘进时土舱和螺旋输送机内渣土压力一般维持在0~300 kPa,剪切应变率为4.36e-3~5.45e-2[7]。为了从试验中获取类似盾构工作环境下改良渣土试样的压缩和剪切强度等特性,将施加于土样上方的法向压力设为0、50、100、150、200、250、300 kPa,十字剪切板的转速设为15、30、45、60、90、120 (°)/min,共42种工况,不同十字板转速对应的剪切应变率如表 2所示。
| 表 2 十字板转速- 剪切应变率换算 Tab. 2 Conversion table of vane rotation speed and shear strain rate |
不排水条件下,试样腔内泡沫改良砾砂在法向压力的作用下发生一维压缩变形。试验安装的百分表可观察盖板法向位移的变化,待百分表读数稳定时可换算得到试样的法向压缩应变,即
| $ {\varepsilon _p} = \frac{{{h_0} - {h_p}}}{{{h_0}}} = \frac{{{h_0} - \left( {H - {H_l} - \Delta h} \right)}}{{{h_0}}} $ | (3) |
式中:εp为试样受到大小为p的法向压力压缩后的压缩应变,h0为试样初始高度,hp为试样受到大小为p的法向压力压缩后的高度稳定值,Hl为盖板厚度,Δh为百分表读数差值。
通过试验记录和公式换算可得试样法向压力下压缩应变稳定值,如表 3所示。
| 表 3 不同法向压力下的一维压缩应变 Tab. 3 Compression strain under different normal pressure |
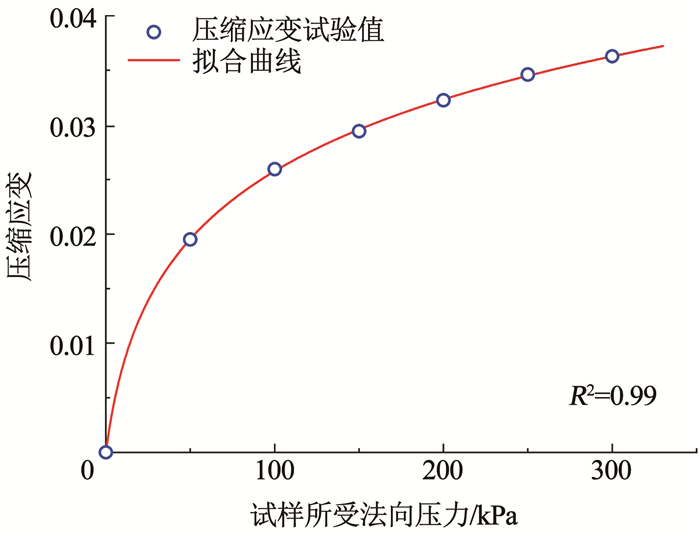
随着法向压力增加,试样压缩应变呈对数方式增加,其中压缩应变增量逐渐减小。原因是在不排水和侧限条件下,加压时土中泡沫无法排出,泡沫内外出现瞬时压差,泡沫内气体受到压缩,泡沫体积占比减小,试样土骨架随之压缩变形。随着法向压力增大,土颗粒排列越来越紧密,试样越来越难被压缩。通过最小二乘法,拟合法向压力- 压缩应变曲线如图 5所示,对数方程如下:
| $ \varepsilon \left( p \right) = 1.01 \times {10^{ - 2}} \times \ln \left( {1 + 0.119p} \right) $ | (4) |
|
图 5 法向压力- 压缩应变拟合曲线 Fig. 5 Fitting curve of normal pressure and compression strain |
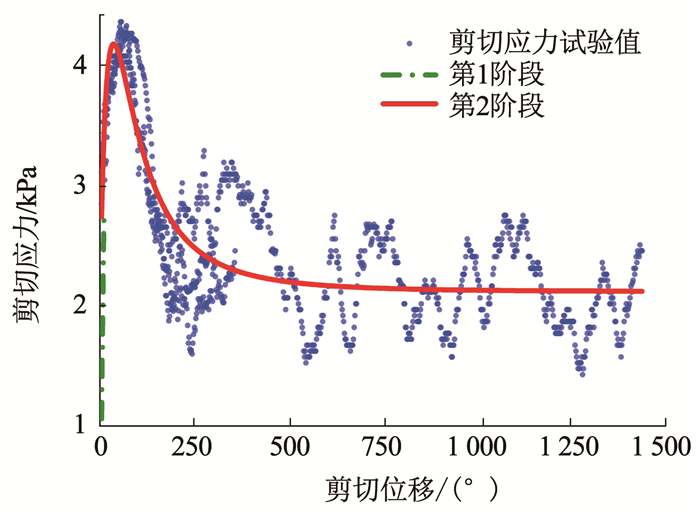
对泡沫改良砾砂进行多组十字板剪切试验,分析剪切过程中剪切应力的变化。以试验工况“p=100 kPa,n=120(°)/min”(以下简称“p-100,n-120”)为例,如图 6所示,十字板旋转使试样产生剪切应力,试样剪切破坏后十字板外周区域与随十字板旋转区域渣土试样发生相对剪切位移,且失效面附近粗颗粒要破坏原咬合状态而发生平移或翻滚等重排列现象,宏观表现为体应变增大的剪胀现象,剪胀损耗的能量由剪应力做功来补偿,故剪切应力随剪切位移增加而增加,当达到峰值时,表明试样被剪切破坏,其峰值剪切应力即土样的抗剪强度; 而后随剪切位移增大试样出现应变软化,剪切应力减小至趋于某一范围内正弦式波动,表明试样仍有残余强度,数据波动是由于泡沫溶液的润滑和粘结作用,加速了非均质性泡沫改良砾砂受剪时土颗粒错动和重新胶结,引起剪切面反复闭合和贯通,从而导致剪切强度产生较明显波动。
|
图 6 工况“p-100, n-120”剪切应力- 剪切位移曲线 Fig. 6 Shear stress and shear displacement curve (p=100 kPa, n=120 (°)/min) |
为消除试样非均质性产生的剪切应力变化曲线波动,参考曹文贵等[17]提出的模拟不同法向正应力下岩土体剪切变形全过程的统计损伤本构模型,取两次重复试验的剪切应力数据点,将剪切全过程拟合为两阶段(图 6曲线):1)线弹性阶段,从原点开始,试样所受剪切应力与剪切位移呈正线性关系; 2)非线性阶段,随着剪切位移增加,剪切应力非线性单调递增至峰值,随后剪切位移继续增加,但剪切应力呈非线性递减趋势,直至稳定值。该阶段可用含5个待定系数的函数式(5)表示。表 4为工况“p-100,n-120”的拟合剪切应力第2阶段曲线的函数待定系数取值和R2大小。
| 表 4 工况“p-100,n-120”拟合系数取值 Tab. 4 Value of fitting coefficient (p=100 kPa, n=120 (°)/min) |
| $ y = \left( {Ax - B} \right){{\rm{e}}^{ - \frac{{{{\left( {Ax - C} \right)}^E}}}{D}}} + B $ | (5) |
同理,其余工况剪切过程中的剪切应力峰值和最终稳定值亦可通过其对应工况剪切应力随位移变化的拟合曲线得到,如图 7所示。拟合的决定系数R2在0.5~0.8,这说明了不同工况下剪切应力变化曲线具有相似的特征,上述拟合方法适用于不同剪切工况。

|
图 7 不同工况剪切应力- 剪切位移拟合曲线 Fig. 7 Fitting curves of shear stress and shear displacement under different working conditions |
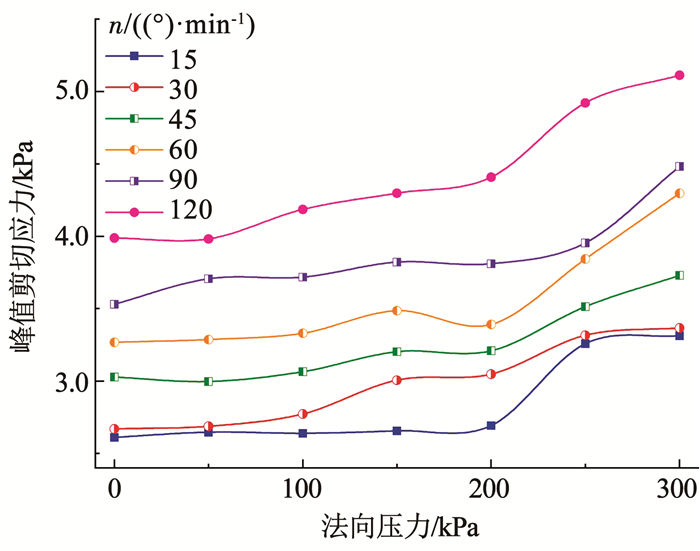
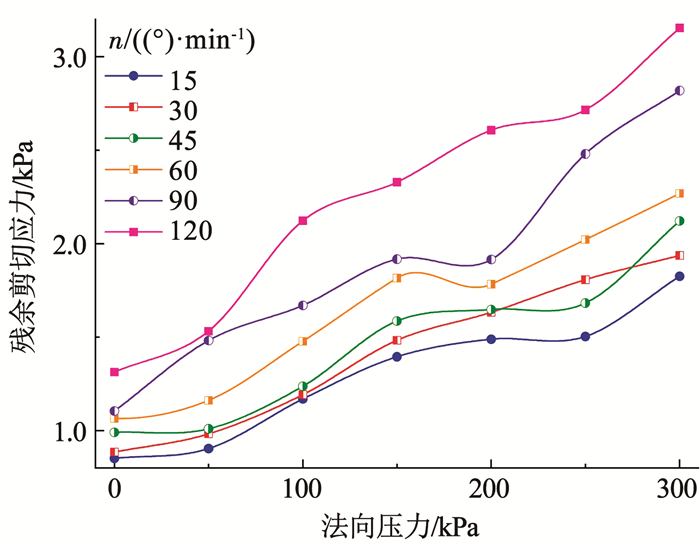
由图 7可知,试样达到剪切应力峰值或残余值时需发生一定的剪切位移,该剪切位移量与法向压力或十字板转速大小无相关性。进一步观察法向压力、十字板转速对试样峰值剪切应力和残余剪切应力的影响,结果见图 8、9,随试样所受法向压力增大,试样峰值和残余剪切应力均逐渐增大,原因是试样所受法向压力越大,泡沫体积压缩减小,土骨架收缩变形程度越大,试样孔隙率减小而密度增大,颗粒间咬合作用和胶结作用越强,剪胀需消耗更大的能量,十字板旋转需克服更大的扭矩,即试样破坏和变形需更大的剪切应力,反映试样抗剪能力的峰值剪切应力随法向压力增大而增大; 同时,法向压力越大,剪切过程中粗颗粒破碎更明显,破碎后细颗粒重排列使试样更密实,且受加压和剪切作用后泡沫体积减小或破灭增加了孔隙溶液的渗流通道,剪切失效区域细颗粒随溶液流动而迁移的能力增强,宏观表现为试样剪切破坏后自修复速率加快,则残余剪切应力随法向压力增大而增大。此外,随十字板转速的增加,十字板所受扭矩增大,即试样的峰值和残余剪切应力随剪切应变率的增加而增加,说明泡沫的注入使试样具有近似非牛顿流体的剪切流动特性,具体分析见3.2节。
|
图 8 峰值剪切应力随法向压力的变化 Fig. 8 Variation of peak shear stress with normal pressure |
|
图 9 残余剪切应力随法向压力的变化 Fig. 9 Variation of residual shear stress with normal pressure |
由试验结果分析可知,改良土试样可近似视为具有一定压缩性的非牛顿流体。以下从流变力学视角提出了考虑改良渣土压缩特性和剪切特性的理论模型,进一步分析试验数据求解了泡沫改良砾砂的压缩系数和流变参数的压力相关性公式。
3.1 泡沫改良砾砂密度的压力相关性公式由2.1可知,泡沫改良砾砂试样具有一定的压缩性,而在盾构带压环境下渣土的压缩性影响着土舱压力的波动程度和渣土的流动状态。将渣土近似看作可压流体,流体的压缩性一般用压缩系数来表征,压缩系数反映作用在流体上的压力变化引起流体单位体积变化的程度。根据式(4)计算得渣土的流体压缩系数κ(Pa-1),即
| $ \begin{aligned} \kappa(p)=&-\frac{\Delta V / V}{\Delta p}=-\frac{\Delta \varepsilon}{\Delta p}=-\frac{\varepsilon(p)-\varepsilon\left(p_{0}\right)}{p-p_{0}}=\\ & \frac{\ln \left(\frac{8.37+p_{0}}{8.37+p}\right)}{99.40 \times\left(p-p_{0}\right)} \end{aligned} $ | (6) |
式中:V为土舱与螺旋输送机容积,p0为参考压力,p为渣土所受绝对压力。
进一步地,盾构掘进时土舱和螺旋输送机内渣土体积恒定,压缩性表现为渣土密度发生变化,因此,假设渣土体积守恒,建立渣土在单向压缩时,密度与法向压力、流体压缩系数的关系式:
| $ \rho \left( p \right) = \frac{{{m_0}}}{{\left( {1 - \Delta \varepsilon } \right)V}} = \frac{{{\rho _0}}}{{1 + \Delta p \cdot \kappa \left( p \right)}} $ | (7) |
式中: m0和ρ0分别为参考压力p0下土舱和螺旋输送机内渣土的质量和密度。
取参考压力p0为常压值,代入试样在常压下密度和试验所得压缩系数,整理可得泡沫改良砾砂密度ρ(kg/m3)的压力相关性公式:
| $ \rho \left( p \right) = \frac{{2.015 \times {{10}^5}}}{{99.04 + \ln \left( {\frac{{8.37}}{{8.37 + p}}} \right)}} $ | (8) |
泡沫改良渣土常被假设为符合经典Bingham模型或Herschel-Bulkley模型的非牛顿流体,其本构关系是剪切应力与剪切应变率的关系,表达式如下。
Bingham模型:
| $ \begin{array}{l} \;\;\;\;\left| \tau \right| \le {\tau _y}, \dot \gamma = 0\\ \left| \tau \right| \ge {\tau _y}, \tau = {\tau _y} + \mu \dot \gamma \end{array} $ | (9a) |
Herschel-Bulkley模型:
| $ \begin{array}{l} \;\;\;\;\left| \tau \right| \le {\tau _y}, \dot \gamma = 0\\ \left| \tau \right| > {\tau _y}, \tau = {\tau _y} + \mu {{\dot \gamma }^n} \end{array} $ | (9b) |
式中:τy为屈服应力,表征渣土固、流体转换的临界应力状态; μ为塑性黏度,表征渣土处于流体状态时的流动难易程度; n为幂律指数。
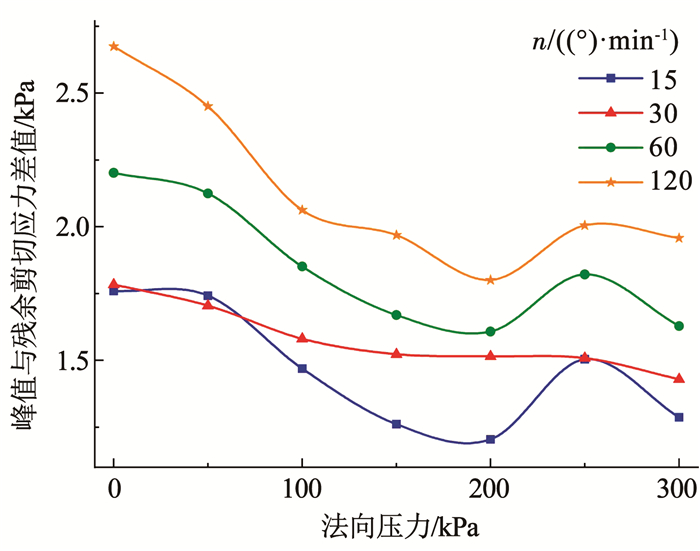
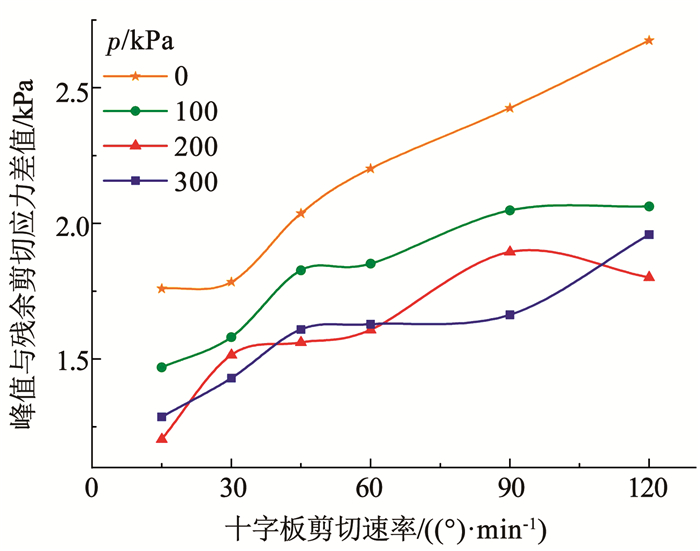
一般流体所受剪切应力与剪切应变率是一一对应的,然而由试验结果可知,十字板剪切破坏了试样的连续性,颗粒咬合和胶结作用减弱,导致破坏试样原有剪切强度无法修复,因此,同一剪切应变率下试样的剪切应力存在不同的峰值和残余值。以部分工况为例,图 10、11表明,试样所受法向压力越大、十字板转速越小时,其峰值与残余剪切应力的差值越小,试样应变软化程度减小,说明在高法向压力、低剪切应变率状态下,泡沫改良砾砂如前所述局部区域流动能力增强,即土样抗剪强度和连续性得到修复的能力越强,且低应变率使土样变形缓慢,强度和连续性可充分恢复,因此,宏观行为越接近流体。
|
图 10 峰值与残余剪切应力差值随法向压力的变化 Fig. 10 Variation of difference between peak and residual shear stress with normal pressure |
|
图 11 峰值与残余剪切应力差值随十字板转速的变化 Fig. 11 Variation of difference between peak and residual shear stress with vane rotation speed |
如何选取合适的剪切应力值以通过剪切应力- 剪切应变率相关性探究改良渣土的流变特性,尚未有定论。孟庆琳[7]的流变试验结果表明剪切应力- 剪切位移曲线存在峰值,故取峰值抗剪强度作为改良渣土以某剪切应变率变形时对应的剪切应力。张檑[13]认为改良渣土以某一剪切应变率变形时对应唯一的剪切应力,因此,流变试验时记录多次同一十字板转速下测得的扭矩并取其平均值。然而,笔者认为要使改良渣土以某一剪切应变率发生大剪切变形或塑性流动,不同情况下渣土流动需克服不同的剪切强度。渣土坍落度试验中,渣土体保持良好连续性,故在自重作用下,渣土体克服峰值剪切强度而坍落流动; 同理,当盾构以满舱模式缓慢掘进时,土舱内渣土在压力差作用下克服峰值抗剪强度而发生连续流动; 在刀具附近以及螺旋叶片附近区域,启动掘进时刀具切削和螺旋叶片旋转需克服渣土峰值抗剪强度以使区域附近渣土流动,然而在保持正常掘进和进排土时,渣土结构已彻底松动,尤其是螺旋输送机内渣土断续被排出,颗粒间咬合作用或胶结作用被完全破坏,从宏观上看,区域附近渣土克服残余剪切强度而继续发生体积恒定的变形流动。
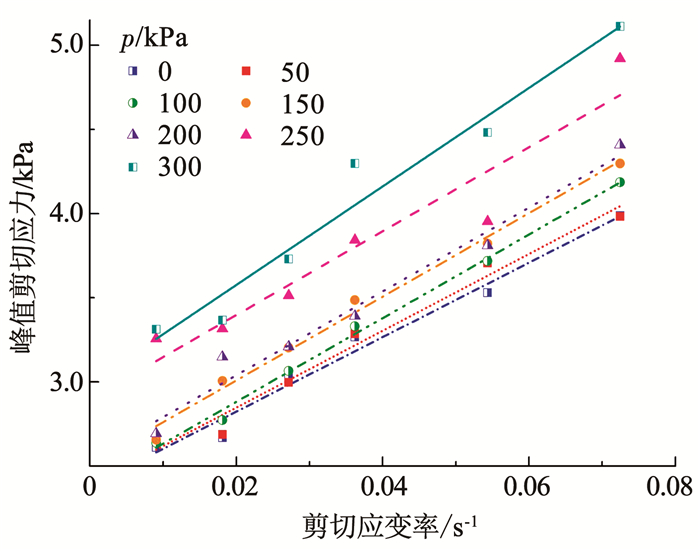
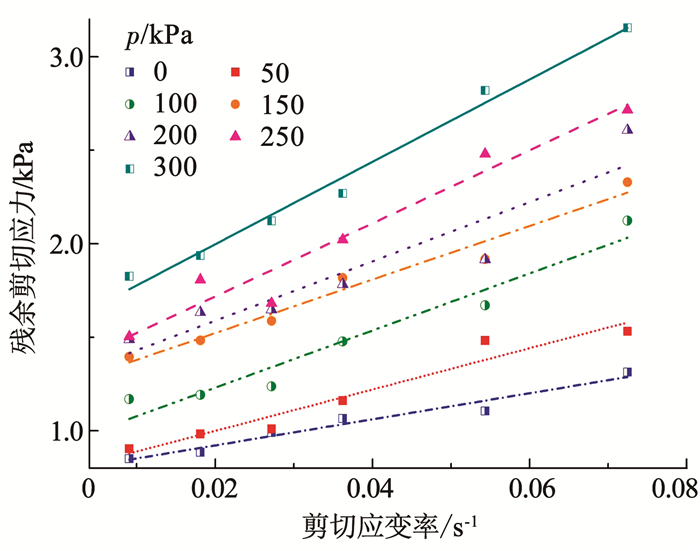
因此,为求解适用于不同情况的试样流变参数,分别对不同工况下的峰值剪切应力- 应变率、残余剪切应力- 应变率曲线进行Bingham和Herschel-Bulkley两种本构方程拟合。结果发现试样更符合Bingham流体,即试样的剪切应力与应变率呈线性递增关系(见图 12、13),这是因为十字板转速越大,试样变形的剪切应变率越大,剪胀现象越明显,峰值剪切应力越大,而试样破坏后失效面附近区域维持较大的流动速率需十字板克服更大的扭矩,即残余剪切应力与剪切应变率亦呈正相关关系。函数拟合得不同剪切应力对应的两类流变参数(屈服应力和塑性黏度)如表 5、6所示。
|
图 12 不同法向压力下峰值剪切应力- 应变率拟合曲线 Fig. 12 Fitting curves of peak shear stress and strain rate with different normal pressures |
|
图 13 不同法向压力下残余剪切应力- 应变率拟合曲线 Fig. 13 Fitting curves of residual shear stress and strain rate with different normal pressures |
| 表 5 Bingham模型流变参数拟合结果(基于峰值剪切应力) Tab. 5 Fitted rheological parameters of Bingham model (based on peak shear stress) |
| 表 6 Bingham模型流变参数拟合结果(基于残余剪切应力) Tab. 6 Fitted rheological parameters of Bingham model (based on residual shear stress) |
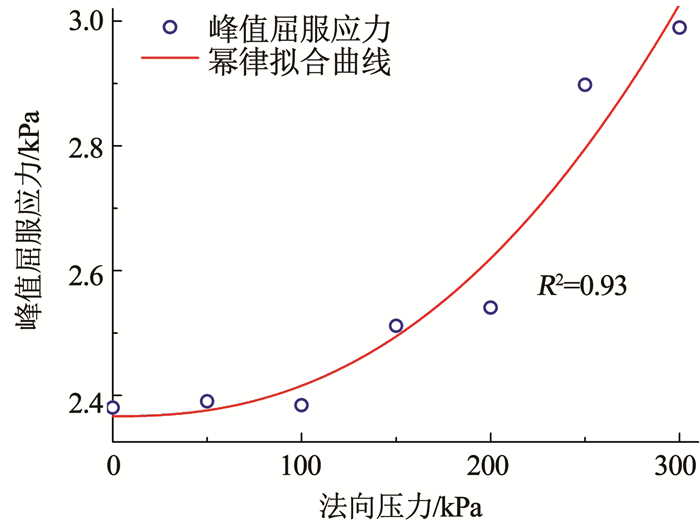
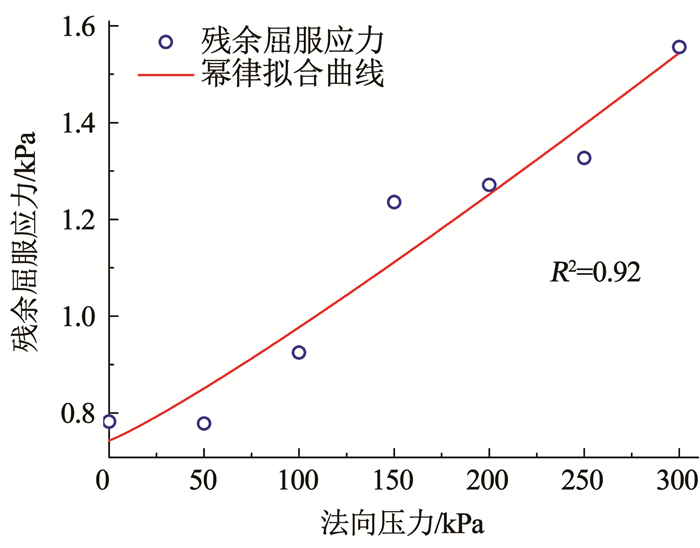
显然,泡沫改良砾砂渣土的流变参数与压力具有相关性。屈服应力随法向压力增大而增大,原因在于泡沫体积减小和土骨架收缩变形使试样压密后颗粒相对运动需克服更大的初始内摩擦力; 塑性黏度随法向压力增大而增大,原因在于孔隙内泡沫溶液随法向压力增大而黏度增大,进一步使试样剪切流动难度增大,表现为塑性黏度增大。因此,把试样视为流变参数为常数的经典非牛顿流体不能准确反映盾构改良渣土在大压力梯度环境下的流变特性。学者们针对不同改良渣土的试验结果,分别用不同的函数形式拟合流变参数的压力相关性曲线[7, 13]。因此进一步对两类剪切情况下法向压力- 屈服应力、法向压力- 塑性黏度的曲线进行函数拟合,通过最小二乘法拟合最优的函数形式,发现法向压力与屈服应力呈幂律关系(见图 14、16),法向压力与塑性黏度呈线性关系(见图 15、17),说明泡沫改良砾砂在高压状态下越难从固体转化为流体。最终可得到对应两类剪切应力流变参数的压力相关性公式:
|
图 14 法向压力- 峰值屈服应力拟合曲线 Fig. 14 Fitting curves of normal pressure and peak yield stress |

|
图 15 法向压力- 峰值塑性黏度拟合曲线 Fig. 15 Fitting curves of normal pressure and peak viscosity |
|
图 16 法向压力- 残余屈服应力拟合曲线 Fig. 16 Fitting curves of normal pressure and residual yield stress |
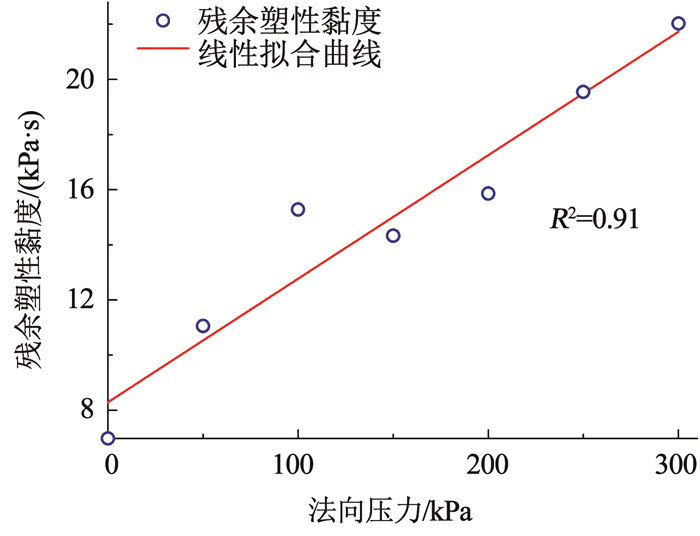
|
图 17 法向压力- 残余塑性黏度拟合曲线 Fig. 17 Fitting curves of normal pressure and residual viscosity |
峰值屈服应力τ0(p)=2.37+9.03×10-7p2.37
峰值塑性黏度μ(p)=22.01+1.98×10-2p
残余屈服应力τ0(p)=0.74+1.34×10-3p1.12
残余塑性黏度μ(p)=8.29+4.48×10-2p
4 结论与展望1) 侧限压缩试验结果揭示了泡沫改良砾砂的压缩特性,随着法向压力增加,试样压缩应变呈对数方式增加; 十字板剪切试验结果揭示了泡沫改良砾砂的剪切强度特性,剪切应力先达到峰值而后稳定至残余值,随着法向压力和十字板转速的增加,剪切试样的峰值和残余剪切应力均有增加。
2) 泡沫改良砾砂的力学行为服从可压缩宾汉姆模型,本文基于流变学提出了泡沫改良砾砂压缩系数和密度的压力相关性公式,也探讨了泡沫改良渣土的剪切应力- 应变率关系,拟合得到两类剪切变形情况下对应的流变参数及其压力相关性公式。
3) 根据峰值剪切应力- 应变率关系拟合得到的流变参数适于坍落度试样坍落、盾构满舱模式下土舱内渣土连续流动或启动掘进时盾构旋转部件附近区域渣土发生大剪切变形的情况。根据残余剪切应力- 应变率关系拟合得到的流变参数适于盾构正常掘进时旋转部件附近渣土剪切破坏后以松散状态继续变形或螺旋输送机内渣土被断续排出的情况。
4) 本文提出的反映改良渣土压缩特性和流变特性的流体理论模型及其参数有助于CFD数值模拟重现或预测盾构带压环境下改良渣土的流动变形。进一步地,综合本文提出的分析方法和CFD数值模拟能更好地探讨改良渣土流体特性、改良参数与盾构掘进参数的相关性,更具备评价优化盾构渣土改良状态的潜力。
| [1] |
王海波, 王树英, 胡钦鑫, 等. 盾构砂性渣土- 泡沫混合物渗透性影响因素研究[J]. 隧道建设, 2018, 38(5): 833. WANG Haibo, WANG Shuying, HU Qinxin, et al. Study of influencing factors of permeability of sand-foam mixture for shield tunneling[J]. Tunnel Construction, 2018, 38(5): 833. DOI:10.3973/j.issn.2096-4498.2018.05.017 |
| [2] |
刘朋飞, 王树英, 阳军生, 等. 渣土改良剂对黏土液塑限影响及机理分析[J]. 哈尔滨工业大学学报, 2018, 50(6): 91. LIU Pengfei, WANG Shuying, YANG Junsheng, et al. Effect of soil conditioner on Atterberg limits of clays and its mechanism[J]. Journal of Harbin Institute of Technology, 2018, 50(6): 91. DOI:10.11918/j.issn.0367-6234.201707025 |
| [3] |
LIU Pengfei, WANG Shuying, HU Qinxin, et al. Effect of dispersant on the tangential adhesion strength between clay and metal for EPB shield tunnelling[J]. Tunnelling & Underground Space Technology, 2020, 95: 103144. DOI:10.1016/j.tust.2019.103144 |
| [4] |
HUANG Shuo, WANG Shuying, XU Changjie, et al. Effect of grain gradation on the permeability characteristics of coarse-grained soil conditioned with foam for EPB shield tunneling[J]. KSCE Journal of Civil Engineering, 2019, 23(11): 4662. DOI:10.1007/s12205-019-0717-7 |
| [5] |
QUEBAUD S, SIBAI M, HENRY J. Use of chemical foam for improvements in drilling by earth-pressure balanced shields in granular soils[J]. Tunnelling and Underground Space Technology, 1998, 13(2): 173. DOI:10.1016/S0886-7798(98)00045-5 |
| [6] |
YE Xinyu, WANG Shuying, YANG Junsheng, et al. Soil conditioning for EPB shield tunneling in argillaceous siltstone with high content of clay minerals: case study[J]. International Journal of Geomechanics, 2017, 17(4): 05016002. DOI:10.1061/(ASCE)GM.1943-5622.0000791 |
| [7] |
孟庆琳. 盾构螺旋输送机承压输送机理研究及控制中的应用[D]. 大连: 大连理工大学, 2012 MENG Qinglin. Research and application in control of conveying mechanism of screw conveyor under pressure of EPBS[D]. Dalian: Dalian University of Technology, 2012 |
| [8] |
武力, 屈福政, 孙伟, 等. 基于离散元的土压平衡盾构密封舱压力分析[J]. 岩土工程学报, 2010, 32(1): 18. WU Li, QU Fuzheng, SUN Wei, et al. Discrete numerical model for analysis of chamber pressure of earth pressure balance shield machine[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(1): 18. |
| [9] |
QU Tongming, WANG Shuying, HU Qinxin. Coupled discrete element-finite difference method for analysing effects of cohesionless soil conditioning on tunneling behaviour of EPB shield[J]. KSCE Journal of Civil Engineering, 2019, 23(10): 4538. DOI:10.1007/s12205-019-0473-8 |
| [10] |
AZIMI A H. Analysis of slump test for sand-foam mixtures[J]. Journal of Material in Civil Engineering, 2017, 29(9): 04017109. DOI:10.1061/(ASCE)MT.1943-5533.0001971 |
| [11] |
TALEBI K, MEMARIAN H, ROSTAMI J, et al. Modeling of soil movement in the screw conveyor of the earth pressure balance machines (EPBM) using computational fluid dynamics[J]. Tunnelling & Underground Space Technology, 2015, 47: 136. DOI:10.1016/j.tust.2014.12.008 |
| [12] |
MORI L, MOONEY M, CHA M. Characterizing the influence of stress on foam conditioned sand for EPB tunneling[J]. Tunnelling & Underground Space Technology, 2018, 71: 454. DOI:10.1016/j.tust.2017.09.018 |
| [13] |
张檑. 基于离散元法的改性砂卵石土体的流变性能研究[D]. 北京: 中国地质大学(北京), 2014 ZHANG Lei. Study on rheological properties of conditioned sandy pebble soil based on DEM[D]. Beijing: China University of Geosciences(Beijing), 2014 |
| [14] |
LIU Pengfei, WANG Shuying, SHI Yufeng, et al. Tangential adhesion strength between clay and steel for various soil softnesses[J]. Journal of Material in Civil Engineering, 2019, 31(5): 04019048. DOI:10.1061/(ASCE)MT.1943-5533.0002680 |
| [15] |
NGUYEN Q D, SOGER D V. Direct yield stress measurement with the vane method[J]. Journal of Rheology, 1985, 29(3): 335. DOI:10.1122/1.549794 |
| [16] |
ASTM. Standard test method for laboratory miniature vane shear test for saturated fine-grained clayey soil: D4648[S]. West Conshohocken, PA, 2011
|
| [17] |
曹文贵, 王江营, 翟友成. 考虑残余强度影响的结构面与接触面剪切过程损伤模拟方法[J]. 土木工程学报, 2012, 45(4): 127. CAO Wengui, WANG Jiangying, ZHAI Youcheng. Study of simulation method for the shear deformation of rock structural planes and interfaces with consideration of residual strength[J]. China Civil Engineering Journal, 2012, 45(4): 127. DOI:10.15951/j.tmgcxb.2012.04.001 |
 2021, Vol. 53
2021, Vol. 53


