2. 北京交通大学 土木建筑工程学院,北京 100044;
3. 北京建筑大学 理学院,北京 102616
2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;
3. School of Science, Beijing University of Civil Engineering and Architecture, Beijing 102616, China
土体作为一种颗粒类材料,其力学特性十分复杂[1-3]。尤其砂土,其力学特性与其所处的物理状态直接相关,表现为松砂的剪缩以及密砂的剪胀特性[4-5]。此外,砂土的松密状态不仅与其相对密度有关,还取决于剪切过程中所施加的围压大小。对于具有相同相对密度的砂土,在围压较低时可能发生剪胀,在高围压下则可能发生剪缩[4, 6]。饱和松砂在剪切过程中甚至可以达到静力液化状态,这也是在实际工程中时常遇到的问题[7-8]。发展一个可以描述饱和砂土复杂力学特性的本构模型,也是学者们一直致力于研究的课题。
尽管砂土存在这种特殊的力学特性,无论初始时处于什么样的物理状态,最后都将达到体应变为零的临界状态[9]。很多学者在临界状态理论的基础上,引入状态参数,来建立砂土的本构模型[10-18]。状态参数由相对密度和围压两个因素共同确定,可以反映材料的松密状态,从而使建立的本构模型能够考虑加载过程中因状态变化而引起的力学行为。此外,一些研究[19-20]认为砂土的临界状态在试验中较难得到,以临界状态线作为状态参量的参考线,可能会导致不能准确地描述砂土的变形特性。并且他们将相变状态作为参考点,建立了基于相变状态的边界面本构模型。近年来,也有学者在临界状态理论或边界面理论的框架下,通过修正其中的一些本构关系,来建立可描述砂土复杂力学特性(剪胀性、循环加载特性等)的弹塑性本构模型[21-23]。如Wei等[22]通过对状态相关弹性模量以及塑性硬化模量进行统一描述,只需要一组弹性参数和硬化参数便可反映不同细粒含量砂土的力学特性。Liang等[23]通过将非正交塑性流动规则应用于改进的椭圆屈服函数,可直接确定塑性流动方向,并提出了一个新的硬化参数来描述剪切过程中体积的收缩和膨胀变化,将非正交塑性流动法则与提出的硬化参数结合,使该模型能够合理地描述砂土的剪胀应力- 应变关系。
砂土本构模型的建立大都以经典弹塑性理论为基础,这也是目前应用最广泛的本构模型理论,比如著名的剑桥模型。然而,这些模型所采用的本构方程大都是通过试验结果拟合得出的经验公式,缺少严格的理论基础。也有一些模型基于热力学理论,通过分析土骨架变形过程中的耗散能以及土体的热力学势,定义自由能函数以及耗散势函数,利用热力学原理推导出流动法则和屈服准则,也称为超塑性模型[16]。这类模型并没有摆脱经典弹塑性力学模型的构建思路,仍需要规定屈服准则、流动法则等概念。近年来,一些学者基于颗粒物质流体热动力学理论建立土体的本构模型,并且在饱和以及非饱和黏土中得到了成功应用[24-27]。该理论用一种简单的宏观连续方法,同时考虑了土体宏观和细观行为的区别和联系,是一种能反映土体多尺度特性的理论模型。
本文基于颗粒层次上的能量耗散机制,建立了一个针对饱和砂土的热力学本构模型。模型引入颗粒温度的概念来反映颗粒层次(细观)上的耗散。通过迁移系数和能量密度函数模型将饱和砂土的耗散机制与宏观的力学行为建立联系。这些使得模型能够更深入描述饱和砂土的能量耗散机理及其引发的宏观力学特性。并将考虑状态参数的剪胀方程与模型参数相结合,有效地描述饱和砂土在剪切过程中由于相对密度和有效围压的变化对土体强度和变形特性的影响。
1 模型理论框架 1.1 颗粒熵和颗粒温度从物质结构角度来看,岩土类材料等的颗粒物质与常见的水、空气等普通流体,或金属、晶体等普通固体有显著差别。除了具有宏观和微观两个空间层次外,岩土类材料还多出一个颗粒层次,或称细观层次。该层次上的相互作用为颗粒之间的接触力,即除了微观层次分子的热运动外,还存在颗粒层次上的无规则运动,如颗粒间的滑移、碰撞、滚动等,也称为颗粒间的涨落运动。热力学中,微观层次分子的无序运动在宏观层次上的表现形式为热力学熵S或温度T。凝聚态物理学家们通过将颗粒间的涨落运动与微观分子的无序运动进行类比,用颗粒熵Sg或颗粒温度Tg的概念来描述颗粒层次上的涨落运动[28]。与微观分子热运动不同的是,颗粒之间的相互作用一般是非弹性的,这将产生能量的耗散,并且如果没有持续性的激励,颗粒的涨落运动将以宏观能量耗散的形式发生衰减,直至涨落消失并重新达到平衡态。对于具有多尺度的岩土类材料,这种处理方法简单有效,从能量耗散的角度出发,抓住材料多尺度行为的本质特征。
由于颗粒之间的非弹性运动,使得Sg会不断地向S转移,类似于熵增加方程,颗粒熵的运动方程可表示为
| $ \rho^{\mathrm{s}} \dot{\vartheta}_{\mathrm{g}}=R_{\mathrm{g}} / T_{\mathrm{g}}-I_{\mathrm{g}} $ | (1) |
式中:ρs为固相的表征密度; ϑg=Sg/ρs为比熵; Ig为颗粒熵的衰减率,是由颗粒温度Tg引起的系统的熵增。即Tg为引起熵增的耗散力,Ig则为相应的耗散流,在偏离平衡态不远的非平衡态区,耗散流可以表示为耗散力的线性函数[29],因此,有Ig=γTg,γ为迁移系数。
根据Onsager关系[30],熵产生可以表示为耗散力和耗散流的乘积。若仅考虑颗粒层次上的黏滞产生的耗散,颗粒熵产生Rg可以表示为
| $ R_{\mathrm{g}}=\sigma_{i j}^{\mathrm{vg}} \cdot{\dot{\varepsilon}}_{i j} $ | (2) |
式中:
同样,二者也存在线性关系:
| $ \sigma_{i j}^{\mathrm{vg}}=\lambda_{i j k l}^{\mathrm{g}} \cdot \dot{\varepsilon}_{k l} $ | (3) |
式中:λgijkl为颗粒层次上的迁移系数,与颗粒温度相关,在各向同性条件下,可表示为
| $ \lambda_{i j k l}^{\mathrm{g}}=\lambda_{\mathrm{sg}} T_{\mathrm{g}} \delta_{i l} \delta_{j k}+\left(\lambda_{\mathrm{vg}}-\frac{\lambda_{\mathrm{sg}}}{3}\right) T_{\mathrm{g}} \delta_{i j} \delta_{l k} $ | (4) |
式中λvg和λsg为颗粒层次上的迁移系数。
此外,与颗粒涨落运动相关的能量密度wg可表示为颗粒密度和颗粒温度的函数[28]:
| $ w_{\mathrm{g}}=b \rho^{\mathrm{s}} T_{\mathrm{g}}^{2} / 2 $ | (5) |
式中b为材料参数。
根据热力学共轭关系可知:
| $ S_{\mathrm{g}}=\rho^{\mathrm{s}} \vartheta_{\mathrm{g}}=\frac{\partial w_{\mathrm{g}}}{\partial T_{\mathrm{g}}}=\rho^{\mathrm{s}} b T_{\mathrm{g}} $ | (6) |
因此,可得出ϑg=bTg。结合上述关系式可得到颗粒温度的运动方程:
| $ \dot{T}_{\mathrm{g}}=\frac{\lambda_{\mathrm{sg}}}{b} \frac{\dot{e}_{i j} \dot{e}_{i j}}{\rho^{\mathrm{s}}}+\frac{\lambda_{\mathrm{vg}}}{b} \frac{\dot{\varepsilon}_{\mathrm{v}} \dot{\varepsilon}_{\mathrm{v}}}{\rho^{\mathrm{s}}}-\frac{\gamma}{b} \frac{T_{\mathrm{g}}}{\rho^{\mathrm{s}}} $ | (7) |
式中:εv=εkk为体应变,eij=εij-
令c2=(ηs)2λsg/γ,c3=(ηs)2λvg/γ,c4=γ/b,则式(7)可表示为
| $ \dot{T}_{\mathrm{gg}}=c_{2} c_{4} \frac{\dot{e}_{i j} \dot{e}_{i j}}{\rho^{\mathrm{s}}}+c_{3} c_{4} \frac{\dot{\varepsilon}_{\mathrm{v}} \dot{\varepsilon}_{\mathrm{v}}}{\rho^{\mathrm{s}}}-c_{4} \frac{T_{\mathrm{gg}}}{\rho^{\mathrm{s}}} $ | (8) |
式中Tgg=ηs2Tg是为简化表达而定义的颗粒温度的表示形式。
1.2 应力的表达砂土的平衡态热力学全微分形式可以表示为
| $ \mathrm{d} w=\pi_{i j} \mathrm{~d} \varepsilon_{i j}^{\mathrm{e}}+T_{\mathrm{g}} \mathrm{d} S_{\mathrm{g}}+T \mathrm{~d} S+\sum\limits_{a=S, L}\left(\mu_{\mathrm{ca}} \mathrm{d} \rho^{a}+v_{i}^{a} \mathrm{~d} m_{i}^{a}\right) $ | (9) |
式中:w为总能量密度,mia为动量,εije为弹性应变,πij为有效Cauchy应力,μca为化学势。由此可得一些热力学关系式,如πij=∂w/∂εije。土体在受力过程中,应力在其弹性变形上做的功将转变为土体的弹性势能密度we,因此,可得πij=∂we/∂εije。
通过类比赫兹接触,将接触球比作颗粒固体,将弹簧比作胡克固体,给出的颗粒类材料的弹性势能密度函数如下[28]:
| $ w_{\mathrm{e}}=B\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{0.5}\left[\frac{2}{5}\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{2}+\frac{1}{\varsigma}\left(\varepsilon_{\mathrm{s}}^{\mathrm{e}}\right)^{2}\right] $ | (10) |
式中:εse=
Zhan等[24]针对孔隙中含有水的黏性土材料,将上式修正为
| $ w_{\mathrm{e}}=B\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}+c\right)^{\beta}\left[\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{2}+\zeta\left(\varepsilon_{\mathrm{s}}^{\mathrm{e}}\right)^{2}\right] $ | (11) |
式中ζ为材料参数,相当于式(10)中的1/ ς,因此,对于砂土,ζ=3/5。当β取为1.5时更满足岩土材料的情形。
针对饱和砂土情形,不考虑黏聚力的影响,可将式(11)表示为
| $ w_{\mathrm{e}}=B\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{1.5}\left[\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{2}+\zeta\left(\varepsilon_{\mathrm{s}}^{\mathrm{e}}\right)^{2}\right] $ | (12) |
因此,可得πij的表达式:
| $ \begin{aligned} \pi_{i j}=& \frac{\partial w_{\mathrm{e}}}{\partial \varepsilon_{i j}^{\mathrm{e}}}=B\left[3.5\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{2.5} \delta_{i j}+\right.\\ &\left.1.5 \zeta\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{0.5}\left(\varepsilon_{\mathrm{s}}^{\mathrm{e}}\right)^{2} \delta_{i j}+2 \zeta\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{1.5} e_{i j}^{\mathrm{e}}\right] \end{aligned} $ | (13) |
定义弹性体积模量Kg和弹性剪切模量Gg分别为
| $ K_{\mathrm{e}}=B\left[3.5\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{1.5}+1.5 \zeta\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{-0.5}\left(\varepsilon_{\mathrm{s}}^{\mathrm{e}}\right)^{2}\right] $ | (14) |
| $ G_{\mathrm{e}}=B \zeta\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{1.5} $ | (15) |
πij又可以表示为类似于Cauchy应力的形式:
| $ \pi_{i j}=K_{\mathrm{e}} \varepsilon_{\mathrm{v}}^{\mathrm{e}} \delta_{i j}+2 G_{\mathrm{e}} e_{i j}^{\mathrm{e}} $ | (16) |
此外,有效平均应力和剪应力可分别表示为
| $ p^{\prime}=\frac{\pi_{k k}}{3}=B\left[3.5\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{2.5}+1.5 \zeta\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{0.5}\left(\varepsilon_{\mathrm{s}}^{\mathrm{e}}\right)^{2}\right] $ | (17) |
| $ q=\sqrt{\frac{3}{2} s_{i j} s_{j i}}=\sqrt{6} \zeta B\left(\varepsilon_{\mathrm{v}}^{\mathrm{e}}\right)^{1.5} \varepsilon_{\mathrm{s}}^{\mathrm{e}} $ | (18) |
由饱和土的等向固结压缩曲线可知,孔隙比e与ln(p′/pa)近似成线性关系:
| $ \varGamma=e+\lambda \ln \left(p^{\prime} / p_{\mathrm{a}}\right) $ | (19) |
式中:λ为压缩曲线的斜率,Г为特殊孔隙比。
在等向固结条件下,对式(17)无量纲化后两边取对数可得ln(p′/pa)=ln(B/pa)+ln A,其中,A=3.5(eve)2.5,在一定压力下可视为定值。假设B可表示成B0exp(Ξ)的形式,B0为材料常数,则有
| $ \ln \left(p^{\prime} / p_{\mathrm{a}}\right)=\varXi+\ln \left(B_{0} / p_{\mathrm{a}}\right)+\ln A $ | (20) |
对比式(20)与式(19),可以近似得出B=B0 exp
土体的不可逆变形是由颗粒间的非弹性相互作用引起。颗粒温度的引入可描述颗粒间相互作用的强弱,可以将土体的耗散机制与宏观变形建立关系,从而确定土体不可逆变形的大小。颗粒间的非弹性相互作用会产生耗散,有效应力πij则为引起熵增的耗散力,与之对应的耗散流为不可逆的变形率,即塑性变形率
| $ \dot{\varepsilon}_{i j}^{\mathrm{p}}=\eta_{i j k l} {\pi}_{k l} $ | (21) |
式中:ηijkl为迁移系数,与颗粒温度相关。类似地,在各向同性条件下其形式可表示为
| $ \eta_{i j k l}=\left(T_{\mathrm{g}}\right)^{a} \frac{\eta_{\mathrm{s}}}{2 G_{\mathrm{e}}} \delta_{i l} \delta_{j k}+\left(T_{\mathrm{g}}\right)^{a}\left(\frac{\eta_{\mathrm{v}}}{3 K_{\mathrm{e}}}-\frac{\eta_{\mathrm{s}}}{6 G_{\mathrm{e}}}\right) \delta_{i j} \delta_{l k} $ | (22) |
式中:ηv和ηs为相应的迁移系数; 指数a为反映率相关的参数[24],当取0.5时,为率无关,本模型中a取为0.5。
将式(16)、(22)代入式(21),可得到塑性应变率的表达式为
| $ \dot{\varepsilon}_{i j}^{\mathrm{p}}=\eta_{\mathrm{v}}\left(T_{\mathrm{g}}\right)^{0.5} \varepsilon_{\mathrm{v}}^{\mathrm{e}} \delta_{i j}+\eta_{\mathrm{s}}\left(T_{\mathrm{g}}\right)^{0.5} \varepsilon_{\mathrm{s}}^{\mathrm{e}} $ | (23) |
令c1=ηv/ηs,则土体的弹性体应变率和弹性剪应变率可分别表示为
| $ \dot{\varepsilon}_{\mathrm{v}}^{\mathrm{e}}=\dot{\varepsilon}_{\mathrm{v}}-3 c_{1}\left(T_{\mathrm{gg}}\right)^{0.5} \varepsilon_{\mathrm{v}}^{\mathrm{e}} $ | (24) |
| $ \dot{\varepsilon}_{\mathrm{s}}^{\mathrm{e}}=\dot{\varepsilon}_{\mathrm{s}}-\left(T_{\mathrm{gg}}\right)^{0.5} \varepsilon_{\mathrm{s}}^{\mathrm{e}} $ | (25) |
根据临界状态土力学理论[9],当达到临界状态时,体应变不再发生变化,此时的孔隙比与作用于土体上的有效应力之间存在着独特的关系。大量的试验结果表明,砂土材料的临界状态线更适用于幂函数来描述,Li和Dafalias[12]将砂土的临界状态线表达为
| $ e_{\mathrm{c}}=e_{\varGamma}-\lambda_{\mathrm{c}}\left(p^{\prime} / p_{\mathrm{a}}\right)^{\xi} $ | (26) |
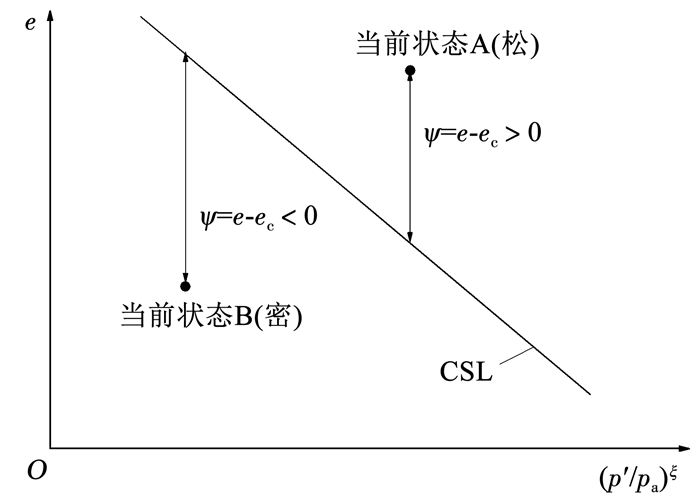
式中:λc为e-(p′/pa)ξ平面内曲线的斜率,如图 1所示; eΓ、ξ为曲线的参数; pa为大气压力。
|
图 1 临界状态和状态参数示意 Fig. 1 Schematic of critical state and state parameters |
Been等[10]引入了一种状态参数来描述砂土的松密状态,定义为ψ=e-ec,即当前孔隙比e和与e具有相同有效应力的临界状态孔隙比ec之差,如图 1所示。当ψ>0时,砂土处于松的状态,反之则处于密的状态。状态参数的定义同时包含了相对密度和压力两个因素,可以反映砂土在加载过程中的状态变化。也有研究[14-15]将状态参数定义为ψ=e/ec,二者的意义是相同的。
1.5 剪胀方程剪胀性是岩土材料的基本特性之一,剪胀方程的合理描述对建立砂土的本构模型起着决定性的作用。一般将塑性体应变增量与塑性剪应变增量之比定义为剪胀比d,d=
| $ d=d_{0}\left(e^{m \psi}-\frac{\eta}{M}\right)=\frac{d_{0}}{M}\left(M e^{m \psi}-\eta\right) $ | (27) |
式中:η=q/p′为应力比; ψ=e-ec为状态参数; M为临界状态应力比; d0、m为非负常数,可由试验确定。当m=0,d0=M时,式(27)退化为剑桥剪胀公式,d=M-η。
由式(24)和(25)可知,
| $ c_{1}=\frac{d_{0}}{3 M \varepsilon_{\mathrm{v}}^{\mathrm{e}}}\left(M e^{m \psi}-\eta\right) \varepsilon_{\mathrm{s}}^{\mathrm{e}} $ | (28) |
本文提出的本构模型中涉及了较多的热力学概念和变量,有些可能是土力学中不常用、不能由土体试验直接测量的量。但这些量都是客观存在的量,并非空泛的名字和符号。模型所涉及的参数如下:与弹性势能密度函数相关的参数,包括B0、ζ、λ; 与颗粒运动相关的迁移系数,包括ηv、ηs、λvg、λsg、b、γ; 与剪胀方程相关的参数,包括eΓ、ξ、λc、M、d0。其中,对于与颗粒运动相关的迁移系数并不需要一一标定,因为模型最终计算所需的参数为c1-c4(c1=ηv/ηs,c2=(ηs)2λsg/γ, c3=(ηs)2λvg/γ, c4=γ/b),只需要标定c1-c4的值即可。具体标定方法如下:
1) 与剪胀方程相关的参数的标定可参考文献[12]来确定,里面给出了具体的确定方法。M为临界应力比; eΓ、ξ、λc可根据临界状态线的试验数据拟合得出; m可根据在d=0时的相变状态确定; d0可根据εv-εs曲线来确定。
2) 与弹性势能密度函数相关的参数,B0和λ可通过等向固结曲线来确定(式(17)),λ为压缩曲线的斜率,ζ可通过达到临界状态时的应力比以及剪应力的大小确定。
3) 与应变演化相关的参数c1,可根据式(28)确定; c4可通过应力松弛试验进行标定,当进行应力松弛试验时,
以文献[31-32]中对Toyoura砂进行的系列试验,包括等向压缩试验,排水和不排水剪切试验,来验证本文所提出模型的有效性。模型计算时,弹性体应变的初始值可通过等向压缩及回弹试验来确定,弹性剪应变的初始值为零。模型中的状态参数直接取自文献[12],其他参数通过1.6节所述方法进行确定。状态相关参数:M=1.25,ξ=0.7,eГ=0.934,λc=0.019,m=3.5,d0=10,Gs=2.636;热力学模型相关参数:c3=90 000,c4=800,B0=1.064×108 MPa,λ=0.45,ζ=15。
图 2为对不同孔隙比Toyoura砂压缩试验的模拟结果,其中实线为模型参数c3的标定结果,虚线为验证结果。可以看出,不同密实度的砂土,其固结压缩曲线在e-ln p′平面内的斜率基本一致,模型的模拟结果可以和试验结果较好地吻合。

|
图 2 不同孔隙比Toyoura砂压缩试验的模拟 Fig. 2 Simulation of compression tests of Toyoura sand with different void ratios |
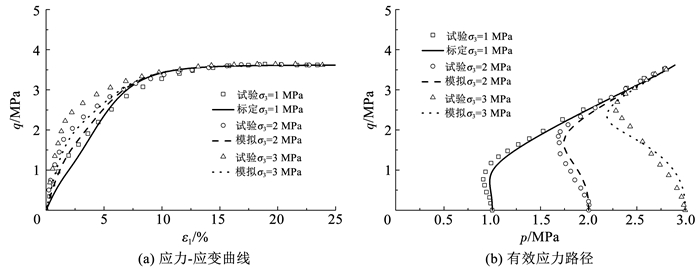
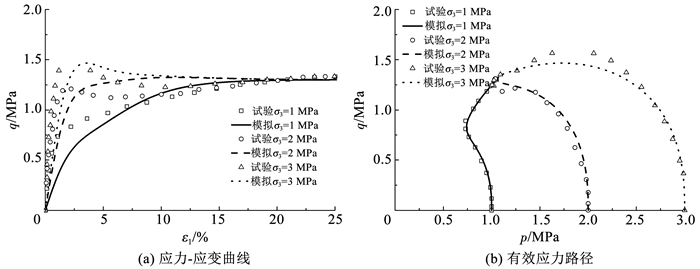
图 3~5为不同孔隙比e为0.735、0.833、0.907的试样,在不同初始围压σ3为1、2、3 MPa下的不排水剪切试验模拟结果。可以看出,当砂土孔隙比较小时(图 3),不同围压下的试样均表现为剪切硬化,并且先剪缩,后剪胀。初始围压较大时,土样相对疏松,剪缩量也较大,而随后的剪胀量相对较小。随着孔隙比的增大(图 4),试样的剪缩量也随之增大,而随后的剪胀量减小。当围压较大时,基本不发生剪胀,并且发生明显的软化现象。当孔隙比较大时(图 5),不同围压下的试样均表现出明显的软化现象,并且试样一直表现为剪缩。模型模拟结果可以很好地反映出砂土不排水的剪切特性。
|
图 3 e=0.735不排水剪切试验模拟 Fig. 3 Simulation of undrained shear tests for e=0.735 |
|
图 4 e=0.833不排水剪切试验模拟 Fig. 4 Simulation of undrained shear tests for e=0.833 |

|
图 5 e=0.907不排水剪切试验模拟 Fig. 5 Simulation of undrained shear tests for e=0.907 |
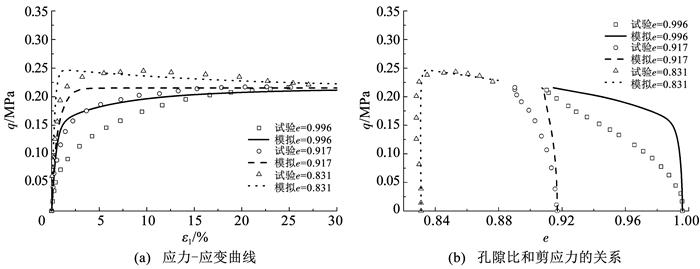
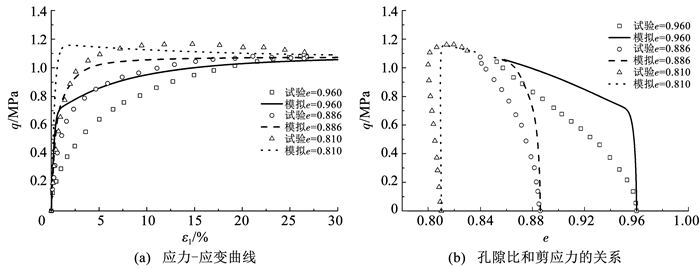
图 6、7分别为不同初始孔隙比e为0.831、0.917、0.996和e为0.810、0.886、0.960的试样,在初始围压0.1和0.5 MPa下的排水剪切试验过程中剪应力和孔隙比(体应变)的模拟结果。当孔隙比较大时,试样一直表现为剪缩,并表现出剪切硬化,当孔隙比较小时(e=0.831),试样先发生剪缩,而后剪胀,并伴随着轻微的软化现象。可以看出,总体的模拟结果与试验结果基本一致,但孔隙比较大时模拟结果与试验结果有一定的偏差。一方面由于模型参数均是以较小孔隙比的试样进行标定(图 2、3),使得在较小孔隙比下的模拟效果更好。另一方面对于排水剪切,模拟过程假设孔隙水压力为0,而实际试验过程中,对于孔隙比较大的试样排水剪切发生体缩,会有较小的正的孔隙水压力产生,在一定程度上可加速排水过程,使得试验结果孔隙比的变化率要比模拟结果的大,剪切强度随轴向应变的增加速率要比模拟结果的小,并且孔隙比越大,这种现象越明显。尽管模拟结果与试验结果存在一定的偏差,但可以反映出总体的变化趋势。
|
图 6 p′0=0.1 MPa排水剪切试验模拟 Fig. 6 Simulation of drained shear tests for p′0=0.1 MPa |
|
图 7 p′0=0.5 MPa排水剪切试验模拟 Fig. 7 Simulation of drained shear tests for p′0=0.5 MPa |
由于耗散对砂土的力学行为有很大影响,一般用熵和热力学语言来阐述最为方便和可靠,还能保证模型与基本物理原理不相冲突。本文基于颗粒层次上的能量耗散机制,结合引入状态参数的剪胀方程,提出了一个可描述饱和砂土剪胀性的热力学本构模型。模型引入颗粒熵和颗粒温度的概念,通过混合物理论构建饱和砂土的热力学恒等式,得出饱和砂土非弹性变形的本构关系。改进了原有的弹性势能函数形式,使得其更适合描述饱和砂土的力学行为,并通过迁移系数和能量函数模型将饱和砂土的耗散机制与宏观的物理力学行为建立联系。模型的形式较为简单,不涉及传统模型中的屈服准则、流动法则等概念,对于具有多尺度的砂土类材料,这种处理方法简单有效,从能量耗散的角度出发,抓住材料多尺度行为的本质特征。通过一组模型参数便可以描述饱和砂土在剪切过程中由于相对密度和有效围压的变化对强度和变形特性的影响。基于模拟计算与Toyoura砂等向压缩、三轴不排水以及排水剪切试验结果的对比,验证了模型描述饱和砂土压缩和剪切特性的能力。
本文尝试从颗粒物质热动力学角度出发,建立砂土的本构模型,尽管模型体现出了一定的优势,相对于经典的弹塑性本构模型也有其不足之处,如模型暂不能考虑与率相关的硬化特性和各向异性,以及级配效应等,这也是模型后续逐步完善的地方。
| [1] |
BAI B, REN Y, RAO D Y. The transport of solid particle suspension at different alkalinities in saturated porous media[J]. Journal of Porous Media, 2020, 23(3): 207. DOI:10.1615/JPorMedia.2020025647 |
| [2] |
刘俊伟, 王明明, 凌贤长, 等. 桩- 砂土界面循环弱化宏细观机制[J]. 哈尔滨工业大学学报, 2019, 51(2): 146. LIU Junwei, WANG Mingming, LING Xianchang, et al. Macroscopic and microscopic mechanism of cyclic degradation behavior on pile-sand interface[J]. Journal of Harbin Institute of Technology, 2019, 51(2): 146. DOI:10.11918/j.issn.03676234.201801049 |
| [3] |
YANG G C, BAI B. A thermodynamic model to simulate the thermo-mechanical behavior of fine-grained gassy soil[J]. Bulletin of Engineering Geology and the Environment, 2020, 79(5): 2325. DOI:10.1007/s10064-019-01694-w |
| [4] |
LI X S, DAFALIAS Y F, WANG Z L. State-dependent dilatancy in critical state constitutive modelling of sand[J]. Canadian Geotechnical Journal, 1999, 36(4): 599. DOI:10.1139/cgj-36-4-599 |
| [5] |
刘洋, 樊猛, 晏洲毅. 常偏应力剪切条件下砂土失稳模式的离散元模拟[J]. 岩土工程学报, 2020, 42(3): 467. LIU Yang, FAN Meng, YAN Zhouyi. DEM simulation of instability mode in sand under constant shear drained conditions[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(3): 467. DOI:10.11779/CJGE202003008 |
| [6] |
蒋明镜, 石安宁, 刘俊, 等. 结构性砂土力学特性三维离散元分析[J]. 岩土工程学报, 2019, 41(增刊2): 1. JIANG Mingjing, SHI Anning, LIU Jun, et al. Three-dimensional distinct element analysis of mechanical properties of structured sands[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S2): 1. DOI:10.11779/CJGE2019S2001 |
| [7] |
许成顺, 潘霞, 冯超群, 等. 液化循环流动土体动剪切特性试验研究[J]. 土木工程学报, 2020, 53(3): 95. XU Chengshun, PAN Xia, FENG Chaoqun, et al. Experimental research on dynamic shear characteristics of liquefaction circulating flow soil[J]. China Civil Engineering Journal, 2020, 53(3): 95. DOI:10.15951/j.tmgcxb.2020.03.011 |
| [8] |
韩智光, 程晓辉. 可液化砂土微生物处置试验[J]. 哈尔滨工业大学学报, 2016, 48(12): 103. HAN Zhiguang, CHENG Xiaohui. An experimental study of microorganism's treatment on liquefiable sands[J]. Journal of Harbin Institute of Technology, 2016, 48(12): 103. DOI:10.11918/j.issn.0367-6234.2016.12.014 |
| [9] |
ROSCOE K H, SCHOFIELD A N, WROTH C P. On the yielding of soils[J]. Géotechnique, 1958, 8(1): 22. DOI:10.1680/geot.1958.8.1.22 |
| [10] |
BEEN K, JEFFERIES M G. A state parameter for sands[J]. Géotechnique, 1985, 35(2): 99. DOI:10.1680/geot.1985.35.2.99 |
| [11] |
WAN R G, GUO R G. A simple constitutive model for granular soils: modified stress-dilatancy approach[J]. Computers and Geotechnics, 1998, 22(2): 109. DOI:10.1016/S0266-352X(98)00004-4 |
| [12] |
LI X S, DAFALIAS Y F. Dilatancy for cohesionless soils[J]. Géotechnique, 2000, 50(4): 449. DOI:10.1680/geot.2000.50.4.449 |
| [13] |
张建民. 砂土的可逆性和不可逆性剪胀规律[J]. 岩土工程学报, 2000, 22(1): 12. ZHANG Jianmin. Reversible and irreversible dilatancy of sand[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(1): 12. DOI:10.3321/j.issn:1000-4548.2000.01.002 |
| [14] |
LI X S. A sand model with state-dependent dilatancy[J]. Géotechnique, 2002, 52(3): 173. DOI:10.1680/geot.52.3.173.41008 |
| [15] |
罗刚, 张建民. 考虑物理状态变化的砂土本构模型[J]. 水利学报, 2004, 7: 26. LUO Gang, ZHANG Jianmin. Constitutive model for sand considering the variation of its physical state[J]. Journal of Hydraulic Engineering, 2004, 7: 26. DOI:10.3321/j.issn:0559-9350.2004.07.005 |
| [16] |
秦理曼, 迟世春, 林皋. 基于热力学的砂土不排水统一模型[J]. 岩石力学与工程学报, 2006, 25(7): 1316. QIN Liman, CHI Shichun, LIN Gao. A unified model for undrained triaxial tests on sand based on thermodynamics[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1316. |
| [17] |
姚仰平, 张民生, 万征, 等. 基于临界状态的砂土本构模型研究[J]. 力学学报, 2018, 50(3): 589. YAO Yangping, ZHANG Minsheng, WAN Zheng, et al. Constitutive model for sand based on the critical state[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(3): 589. DOI:10.6052/0459-1879-17-334 |
| [18] |
李舰, 刘凯, 尹振宇, 等. 非饱和砂土及黏土的水- 力耦合双屈服面模型[J]. 岩土工程学报, 2020, 42(1): 72. LI Jian, LIU Kai, YIN Zhenyu, et al. Hydro-mechanical double-yield-surface model for unsaturated sand and clay[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(1): 72. DOI:10.11779/CJGE202001008 |
| [19] |
张卫华, 赵成刚, 傅方. 饱和砂土相变状态边界面本构模型[J]. 岩土工程学报, 2015, 32(5): 724. ZHANG Weihua, ZHAO Chenggang, FU Fang. The bounding-surface constitutive model for unsaturated sands based on the phase transformation state[J]. Chinese Journal of Applied Mechanics, 2015, 32(5): 724. |
| [20] |
赵春雷, 蔡国庆, 赵成刚, 等. 饱和砂土的循环边界面本构模型[J]. 固体力学学报, 2017, 38(3): 244. ZHAO Chunlei, CAI Guoqing, ZHAO Chenggang, et al. Cyclic constitutive model of saturated sand based on the bounding surface theory[J]. Chinese Journal of Solid Mechanics, 2017, 38(3): 244. DOI:10.19636/j.cnki.cjsm42-1250/o3.2017.03.003 |
| [21] |
万征, 孟达. 复杂加载条件下的砂土本构模型[J]. 力学学报, 2018, 50(4): 929. WAN Zheng, MENG Da. A constitutive model for sand under complex loading conditions[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(4): 929. DOI:10.6052/0459-1879-18-047 |
| [22] |
WEI X, YANG J. A critical state constitutive model for clean and silty sand[J]. Acta Geotechnica, 2019, 14(2): 329. DOI:10.1007/s11440-018-0675-0 |
| [23] |
LIANG J, LU D, DU X, et al. Non-orthogonal elastoplastic constitutive model for sand with dilatancy[J]. Computers and Geotechnics, 2020, 118: 103329. DOI:10.1016/j.compgeo.2019.103329 |
| [24] |
ZHANG Z C, CHENG X H. A thermo-mechanical coupled constitutive model for clay based on extended granular solid hydrodynamics[J]. Computers and Geotechnics, 2016, 80: 373. DOI:10.1016/j.compgeo.2016.05.010 |
| [25] |
杨光昌, 白冰. 基于颗粒物质热动力学理论的非饱和土热水力耦合模型研究[J]. 岩土工程学报, 2019, 41(9): 1688. YANG Guangchang, BAI Bing. A thermo-hydro-mechanical coupled model for unsaturated soils based on thermodynamic theory of granular matter[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1688. DOI:10.11779/CJGE201909013 |
| [26] |
BAI B, YANG G C, LI T, et al. A thermodynamic constitutive model with temperature effect based on particle rearrangement for geomaterials[J]. Mechanics of Materials, 2019, 139: 103180. DOI:10.1016/j.mechmat.2019.103180 |
| [27] |
YANG G C, BAI B. Thermo-hydro-mechanical model for unsaturated clay soils based on granular solid hydrodynamics theory[J]. International Journal of Geomechanics, 2019, 19(10): 04019115. DOI:10.1061/(ASCE)GM.1943-5622.0001498 |
| [28] |
孙其诚, 厚美瑛, 金峰, 等. 颗粒物质物理与力学[M]. 北京: 科学出版社, 2011. SUN Qicheng, HOU Meiying, JIN Feng, et al. Physics and mechanics of granular matter[M]. Beijing: Science Press, 2011. |
| [29] |
DEGROOT S R, MAZUR P. Non-equilibrium thermodynamics[M]. New York: Dover Publications, 1984.
|
| [30] |
ONSAGER L. Reciprocal relations in irreversible processes[J]. Physical Review, 1931, 37(2): 405. DOI:10.1103/physrev.37.405 |
| [31] |
MESRI G, VARDHANABHUTI B. Compression of granular materials[J]. Canadian Geotechnical Journal, 2009, 46: 369. DOI:10.1139/T08-123 |
| [32] |
VERDUGO R, ISHIHARA K. The steady state of sandy soils[J]. Soils and Foundations, 1996, 36(2): 81. DOI:10.3208/sandf.36.2_81 |
 2021, Vol. 53
2021, Vol. 53


