2. 西安建筑科技大学 土木工程学院,西安 710055;
3. 深圳市建筑设计研究总院有限公司,广东 深圳 518032
2. School of Civil Engineering, Xi′an University of Architecture and Technology, Xi′an 710055, China;
3. Shenzhen General Institute of Architectural Design and Research Co., Ltd., Shenzhen 518032, Guangdong, China
随着经济发展、社会进步、城镇化水平不断提高,地铁隧道和地下管廊等城市地下空间的开发和利用已成为西安城市建设的重要内容之一。加之西安地处汾渭盆地地裂缝帶[1-2],广泛存在的地裂缝使大面积土地资源浪费,结构破坏,多数地下生命线工程被剪断或拉裂[3-4]。因此,为了提高土地利用率和地裂缝场地结构抗震性能,保证城市道路、地下管廊及地铁隧道等结构的安全性,对地裂缝场地进行抗震性能研究具有重要的工程应用价值。
目前,国内外学者对地裂缝进行了不同角度的研究[5-7]。彭建兵等[8]对西安地裂缝形成的地质背景、活动特性和成因机理等进行了研究。胡志平等[9]以位于长安立交处的“y”型地裂缝为对象,开展了1∶ 15的振动台试验,发现了“y”型地裂缝场地主次裂缝的地震响应差异。熊仲明等[10]采用振动台试验和数值模拟相结合的方式,证实了地裂缝场地对上部框架结构动力响应有较大影响。王瑞等[11]也对地震波在地裂缝处的传播规律进行了研究。但这些研究大多未涉及地裂缝土体本构关系,仅仅采用简单的静力本构或线性化模型。土体作为一种三相非均质介质,其应力- 应变关系复杂多变,在地震作用下地裂缝处土体动力本构关系更复杂。因此,为了获得较合适的地裂缝场地土体动力本构关系模型,以便准确研究普通场地和地裂缝场地不同土层分布的动力响应规律,开展地震作用下地裂缝场地土体动力本构研究尤为重要。
本文以f4地裂缝场地振动台试验为基础,通过ABAQUS有限元软件建立了3种不同本构的地裂缝场地实体模型,并将不同土体本构关系下的模拟结果与试验结果进行对比,找到了较合适的土体动力本构模型。基于此,建立了6种不同土层分布的数值模型,找出了影响地裂缝场地动力响应的上下盘效应及其放大效应的规律,给出了上下盘效应影响的范围。
1 土体本构模型应用 1.1 土体本构模型对比分析本课题组所研究的地裂缝场地均受动荷载,具有复杂多变的应力- 应变关系。在以往学者对土体动力本构模型研究总结[12-14]的基础上,选取了等效线性化模型、多屈服面模型、边界面模型、多机构概念的塑性理论及以往研究多采用的静力弹塑性摩尔- 库伦模型5种土体本构模型,这些模型的优缺点及使用条件的对比分析见表 1。
| 表 1 各种本构模型优缺点 Tab. 1 Advantages and disadvantages of various constitutive models |
对比4种动力本构模型发现:等效线性化模型应用广泛,应用经验丰富; 边界面模型能够反映土体在动力荷载作用下的复杂变形特性; 而多屈服面模型对计算机要求较高,多机构概念的塑性理论研究相对较少。因此,初步选择土体动力本构模型为等效线性化模型和边界面模型,静力本构模型为ABAQUS自有的摩尔- 库伦模型进行分析。
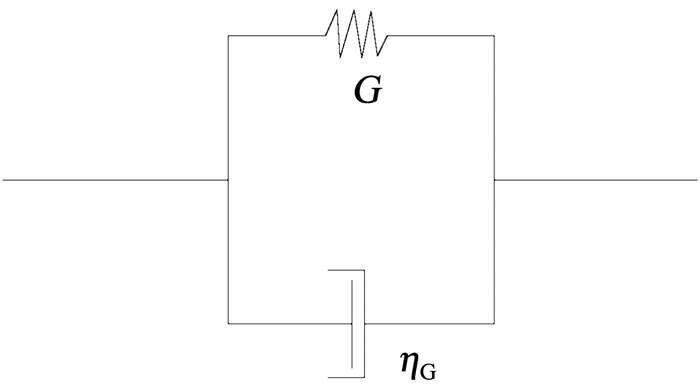
1.2 等效线性化模型开发应用等效线性化模型通过多次线性迭代的手段来考虑土体的动力非线性性质。该模型通过黏弹性Kelvin模型反映土体在动荷载下的滞回效应[12]。Kelvin模型示意如图 1所示,其中G为剪切模量,ηG为剪切黏滞系数。
|
图 1 Kelvin模型示意 Fig. 1 Kelvin model diagram |
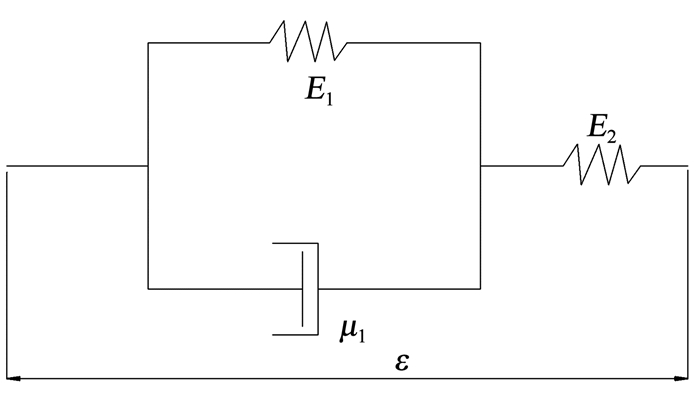
ABAQUS子程序中提供了二次开发所得HK体模型的用户子程序,模型示意如图 2所示,E为弹性模量,μ1为HK体黏滞系数,ε为应变。等效线性模型计算土层地震反应的关键在于确定等效剪切模量和等效阻尼比。
|
图 2 HK体模型示意 Fig. 2 HK model diagram |
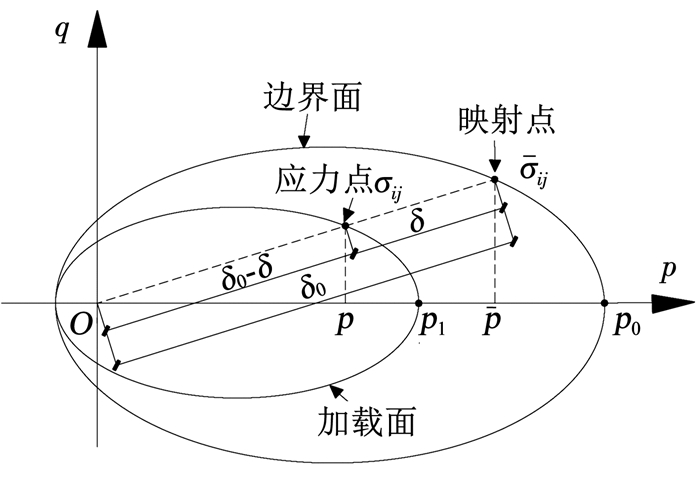
边界面模型能够较好地模拟土体在动力循环荷载作用下产生的塑性累计变形。根据以往关于边界面模型的研究[14],以零弹性区中椭圆边界面模型为例,加卸载时的映射中心为坐标原点,如图 3所示。该模型的边界面和加载面均采用辛克维兹- 潘德形式。
|
图 3 模型的映射准则 Fig. 3 Model mapping criteria |
边界面模型的增量应力- 应变关系为
| $ {\rm{d}}{\sigma _{ij}} = \left[ {D_{ijkl}^{\rm{e}} - h(L)\frac{{D_{ijab}^{\rm{e}}\frac{{\partial Q}}{{\partial {\sigma _{cd}}}}{{\left( {\frac{{\partial F}}{{\partial {\sigma _{ab}}}}} \right)}^{\rm{T}}}D_{cdkl}^{\rm{e}}}}{{{K_{\rm{p}}} + {{\left( {\frac{{\partial F}}{{\partial {\sigma _{ab}}}}} \right)}^{\rm{T}}}D_{abcd}^{\rm{e}}\frac{{\partial Q}}{{\partial {{\bar \sigma }_{cd}}}}}}} \right]{\rm{d}}{\varepsilon _{kl}} $ | (1) |
式中:F(σij, qn)=0为边界面的表示形式,Q(σ ij, qn)=0为塑性势函数,Kp为塑性模量,h(L)为亥维塞(Heavisid)函数,D为弹性模量。
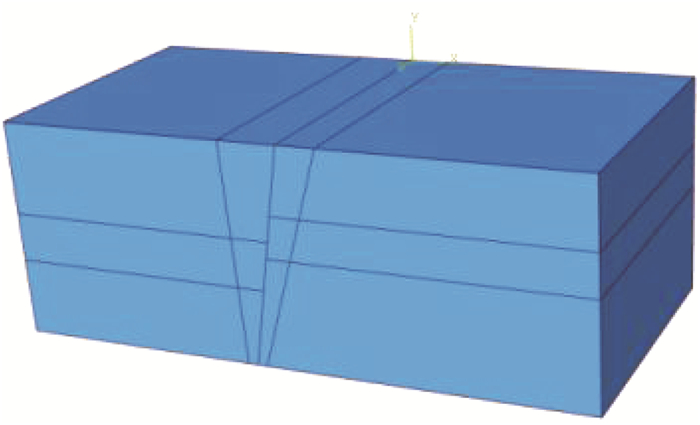
2 ABAQUS 3种本构模型建立 2.1 模型参数设置根据西安地裂缝场地勘察与工程设计规程以及宋彦辉等[15]给出的地裂缝影响带宽度和影响区域,建立整体尺寸为45 m×22.5 m×22.5 m的地裂缝场地土体模型,并在上盘地裂缝区宽度取6 m,下盘取4.5 m,且沿高度方向向下逐渐尖灭,同时地裂缝影响区土体的弹性模量、黏聚力和摩擦角均考虑15%的劣化,而密度考虑5%的增强,所建立的模型如图 4所示。
|
图 4 土体模型 Fig. 4 Soil model |
模型选用C3D8R三维实体单元进行模拟,土体模型单元在水平方向尺寸略大于高度方向,再结合王松涛等[16]关于上下方向传播剪切波的研究,选择沿高度方向单元网格尺寸约为1.5 m。同时,对地裂缝所在尖灭区域内土体的网格进行加密处理,网格划分如图 5所示。

|
图 5 网格划分模型 Fig. 5 Meshing model |
土体地裂缝处的接触面,法向作用设置为硬接触,切向接触设置为摩擦接触,摩擦系数为0.3。垂直于振动方向的横向两侧面设置黏弹性人工边界[17],模型底面为固定端,其他各面为自由端。
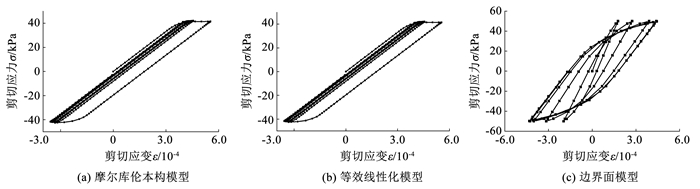
2.3 土体本构设置为了验证上述3种本构模型的滞回效应,分别建立了1 m×1 m×1 m的土体模型,并对3种本构模型施加频率为1 Hz、单幅值为50 kPa的正弦波循环荷载,模型计算得滞回曲线关系如图 6所示。
|
图 6 不同本构模型的滞回曲线 Fig. 6 Hysteretic curves of different constitutive models |
本试验在西安建筑科技大学教育部结构与抗震重点实验室完成[18],在该试验基础上提取部分数据用于分析验证。试验选取原地裂缝场地尺寸为45 m×22.5 m×22.5 m的土体,按1∶ 15的几何相似比缩尺后装入3 m×1.5 m×1.5 m的层状剪切模型土箱。试验土箱[19]由13层矩形钢框架组成,在垂直于振动方向贴30 mm厚的聚苯乙烯泡沫板作为柔性边界,在平行于振动方向贴2 mm厚橡胶卷作为滑动边界,在箱底粘贴间隔为500 mm的方木作为摩擦边界,具体如图 7所示。

|
图 7 模型土箱设计(mm) Fig. 7 Model soil box design(mm) |
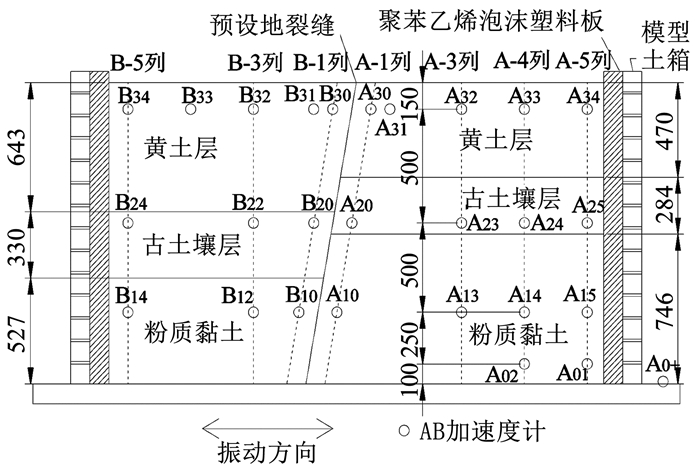
选取距地裂缝不同距离的上下盘加速度测点进行分析,如图 8所示。
|
图 8 测点布置(mm) Fig. 8 Layout of measuring points(mm) |
选取江油波、El-Centro波和基岩波3种地震波分4级(0.1g,0.2g,0.4g和0.8g)进行加载,每级加载前后用0.05g白噪声进行扫频。
4 地裂缝场地本构模型的确定 4.1 试验加速度分析图 9为土体不同位置处的加速度放大系数(即不同位置处的加速度与输入峰值加速度的比值)。可以看出,沿土体高度方向,除个别测点外,加速度放大系数均大于1,且随土体高度增大逐渐增大,尤其在黄土层处放大效应最明显,说明软弱黄土层可以加大放大效应。沿水平方向,加速度放大系数最大值出现在靠近地裂缝的测点,且相同距离下,上盘测点的加速度放大系数大于下盘测点,说明地裂缝场地存在明显的上下盘效应。同一地震波作用下,随着输入峰值加速度的增加,土体加速度放大系数减少,说明高强度地震强度下土体塑性变形增加,土体的塑性耗能和阻尼耗能增加。

|
图 9 加速度放大系数 Fig. 9 Acceleration amplification factors |
为了找出更适合于地裂缝场地土体的动力本构模型,将3种本构模型的数值模拟结果与试验结果进行对比分析。选取在0.1g、0.2g及0.4g El-Centro波和江油波作用下的试验台面加速度响应作为数值模拟输入的地震波。将试验模型测点B30、B32和A30相对应位置的数值模型测点定义为B1、B2和A1,对比对象为3种本构模型各测点数值模拟峰值加速度与试验峰值加速度的相对差值Δ,即
| $ \Delta = \left| {\frac{{{A_{\rm{m}}} - {A_{\rm{s}}}}}{{{A_{\rm{s}}}}}} \right| $ | (2) |
式中:Am为数值模拟模型峰值加速度,As为试验所得峰值加速度,计算所得结果如表 2所示。此外,为了直观表达试验值与计算值的变化关系,选取加速度放大效应最明显的试验上盘测点B30与数值模拟对应上盘测点B1,绘制加速度时程对比曲线,如图 10、11所示。
| 表 2 试验值与计算值峰值加速度相对差值Δ Tab. 2 Relative difference of peak acceleration between test values and calculated values |

|
图 10 0.2g江油波作用下B30与B1测点加速度时程对比 Fig. 10 Acceleration time history comparison of B30 and B1 under the action of 0.2g Jiangyou wave |
|
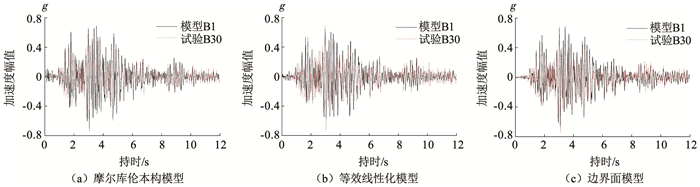
图 11 0.4g江油波作用下B30与B1测点加速度时程对比 Fig. 11 Acceleration time history comparison of B30 and B1 under the action of 0.4g Jiangyou wave |
由图 10、11可知,在江油波作用下,0.2g强度作用时,3种本构模型所得加速度时程曲线与试验加速度时程曲线较一致,但等效线性化模型拟合效果较差,边界面模型拟合效果较好; 0.4g作用时,3种本构模型所得峰值加速度与试验峰值加速度几乎同时出现,边界面模型时程曲线与试验加速度时程曲线吻合更高,但摩尔- 库伦模型和等效线性化模型出现多点加速度峰值。
由表 2可知,在不同强度的El-Centro波作用下,边界面模型算得的各测点相对差值最小,等效线性化模型次之,摩尔- 库伦模型最大; 在江油波作用下,0.1g作用时,3种本构相对差值大小顺序为:等效线性化模型 < 摩尔- 库伦模型 < 边界面模型,而0.2g、0.4g作用时,相对差值大小顺序为:边界面模型 < 摩尔- 库伦模型 < 等效线性化模型。综上可知:在低强度地震作用下,3种本构模型的数值模拟计算结果与试验结果较一致,土体处于弹性阶段,等效线性化模型拟合度更高; 高地震作用下,土体发生较大的塑性变形,考虑土体塑性变形的边界面模型拟合度最好。
4.3 峰值加速度对比分析为了进一步验证上述边界面模型的可行性,选取0.4g基岩波、江油波和El-Centro波作用下试验所得地裂缝场地地表中线上各测点的峰值加速度与数值模拟所得对应测点的峰值加速度进行对比分析,试验值与模拟计算值对比如图 12所示。可以看出,在0.4g强度3种波作用下,试验值和计算值均在离地裂缝最近测点处达到最大,且随着测点到地裂缝距离的增加逐渐减少。同时,除个别测点外,上盘测点的峰值加速度大于下盘对应测点的峰值加速度,表现出明显的上下盘效应。此外,在El-Centro波作用下,计算值与试验值在下盘远离地裂缝处相差最大,仅为3.45%;在江油波作用下,计算值与试验值在上盘靠近地裂缝处相差最大,仅为3.33%;在基岩波作用下,计算值与试验值在下盘靠近地裂缝处相差最大,仅为4.42%。综合以上分析说明边界面模型可以较准确地反应地裂缝场地土体动力响应规律。

|
图 12 峰值加速度对比 Fig. 12 Peak acceleration comparison |
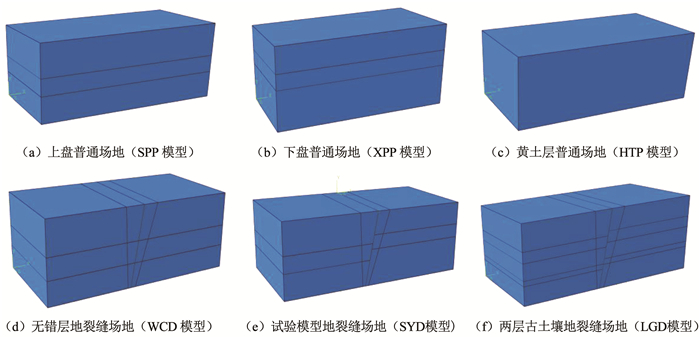
考虑到原地裂缝场地土层分布较为复杂,以试验模型的土层分布为基础,采用4.2、4.3节模拟结果较好的边界面模型为材料本构,建立不同土层分布形式的地裂缝场地模型和普通场地模型,并对6种工况名称进行了简化,各工况如图 13所示。
|
图 13 不同工况下有限元模型 Fig. 13 Finite element models under different working conditions |
本次数值模拟模型尺寸和模型单元的选择与上文所建模型相同。输入地震波仍采用试验的3种地震波,其强度分别为0.1g、0.2g和0.4g。
5.2 数值模拟结果分析为了分析不同土层分布形式对地震响应的影响,在模型结果中提取各工况下地表中线上与地裂缝不同距离处各测点的峰值加速度,绘制出测点位置与峰值加速度关系曲线,如图 14所示。

|
图 14 不同工况的地表峰值加速度 Fig. 14 Peak acceleration under different working conditions |
对比图 14中SPP、XPP和HTP模型的峰值加速度曲线可知,在El-Centro波作用下,各工况的普通场地同一测点的峰值加速度表现为HTP>SPP> XPP; 不同强度江油波作用下,除0.1g的规律性略有差异外,其他工况模型加速度表现为SPP>XPP> HTP; 不同强度基岩波作用下,各工况模型峰值加速度表现为XPP>SPP>HTP,这是因为从XPP到SPP再到HTP模型,黄土层厚度逐渐增加,粉质黏土层逐渐减少,而黄土的密度和剪切模量最小。
对比图 14中SYD与WCD模型的峰值加速度曲线可知,在El-Centro波和江油波作用下,SYD模型峰值加速度曲线与WCD模型峰值曲线在上盘处基本相同,在下盘处略有差异,为WCD模型> SYD模型; 在基岩波作用下,SYD模型与WCD模型峰值加速度曲线在上盘处基本相同,在下盘处略有差异,为SYD模型>WCD模型。这是因为SYD模型与WCD模型在上盘处土层分布相同,而在下盘处WCD模型的黄土层变厚,粉质黏土层变薄,土体刚度减小,自振周期变大。
对比图 14中SYD与LGD模型峰值加速度曲线可知,在不同强度的El-Centro波与江油波作用下,SYD模型与LGD模型变化趋势一致,均表现了明显的放大效应和上下盘效应,但峰值加速度大小存在差异,SYD模型>LGD模型; 而在不同强度的基岩波作用下SYD模型 < LGD模型。可能因为SYD模型比LGD模型上部覆盖较厚的软弱黄土层,使SYD模型自振周期较长。
对比图 14中与试验模型相应的SYD模型和普通场地的XPP与SPP模型可知,不同地震作用下,普通场地模型与地裂缝场地模型均出现交汇点。由于土体结构和地震波特性的差异,SPP和XPP模型与地裂缝场地SYD模型相比出现不同的交汇距离,地裂缝上盘影响宽度大于下盘影响宽度,取各自的包络值,上盘为11 m左右,下盘为9 m左右。
6 结论以f4地裂缝场地振动台试验为基础,通过ABAQUS有限元软件建立了采用不同本构的地裂缝场地模型,并将模拟结果与试验结果进行对比,找到了较合适的土体动力本构模型; 建立了6种不同土层分布的数值模型,分析了不同土层分布结构对场地土体动力响应的影响,得出如下结论:
1) 沿土层高度方向,加速度放大系数大于1且逐渐增加,黄土层处放大效应更明显:沿水平方向,加速度放大系数在地裂缝处最大并向两侧递减,且距地裂缝相同距离处上盘测点放大系数略大于下盘测点。随着加载强度的增加,放大系数减小。
2) 当地震强度较小时,3种本构模型各测点加速度时程与试验相应测点加速度时程基本一致,且峰值加速度相对差值较小,其中等效线性化模型拟合效果更好。随着地震强度的增大,等效线性化模型加速度时程曲线拟合程度不断降低,加速度峰值相对差值也不断增加。而边界面模型在高地震强度作用下的加速度时程曲线拟合较好,说明采用边界面模型可以有效模拟地裂缝场地土在地震荷载作用下产生的塑性累积变形。
3) 普通场地和地裂缝场地均对地震有放大效应,但不同的土层分布放大效果不同; 地裂缝场地均表现出加速度放大效应和形似“八”的上下盘效应,其上盘影响最大值为11 m,下盘为9 m。
| [1] |
LIU Nina, HUANG Qiangbing, WANG Li, et al. Dynamic characteristics research of a ground fissure site at Xi'an, China[J]. Tunnelling and Underground Space Technology, 2018, 82: 182. DOI:10.1016/j.tust.2018.08.044 |
| [2] |
慕焕东, 邓亚虹, 李荣建, 等. 西安地裂缝场地动力响应规律及影响因素分析[J]. 地震工程学报, 2019, 41(2): 418. MU Huandong, DENG Yahong, LI Rongjian, et al. Dynamic response and influence factors of ground fissure sites in Xi'an[J]. China Earthquake Engineering Journal, 2019, 41(2): 418. DOI:10.3969/j.issn.1000-0844.2019.02.418 |
| [3] |
李忠生, 高虎艳, 宋彦辉, 等. 西安地铁四号线沿线长安地裂缝研究[J]. 土木工程学报, 2013, 46(8): 98. LI Zhongsheng, GAO Huyan, SONG Yanhui, et al. Investigation and research on Chang'an ground fissure along[J]. China Civil Engineer Journal, 2013, 46(8): 98. |
| [4] |
LIU Chao, SU Lijun, XU Xingqian. Effect of ground fissures on subsidence in Xi'an Metro Line 2[J]. Applied Mechanics and Materials, 2013, 353/354/355/356: 333. DOI:10.4028/www.scientific.net/amm.353-356.333 |
| [5] |
邓亚虹, 李丽, 慕焕东, 等. 西安地区地裂缝带Q3原状黄土流变特性试验研究[J]. 岩土力学, 2015, 36(7): 1847. DENG Yahong, LI Li, MU Huandong, et al. Experimental research on rheological properties of Q3 intact loess within ground fissures belt in Xi'an region[J]. Rock and Soil Mechanics, 2015, 36(7): 1847. DOI:10.16285/j.rsm.2015.07.004 |
| [6] |
LIU Nina, FENG Xiaoyang, HUANG Qiangbing. Dynamic characteristics of a ground fissure site[J]. Earthquake Engineering & Structural Dynamics, 2019, 248: 220. |
| [7] |
LIU Hui, DENG Kazhong, LEI Shaogang, et al. Mechanism of formation of sliding ground fissure in loess hilly areas caused by underground mining[J]. International Journal of Mining Science and Technology, 2015, 25(4): 553. DOI:10.1016/j.ijmst.2015.05.006 |
| [8] |
彭建兵. 西安地裂缝灾害[M]. 北京: 科学出版社, 2012. PENG Jianbing. Ground fracture disaster in Xi'an[M]. Beijing: Science Press, 2012. |
| [9] |
胡志平, 王启耀, 罗丽娟, 等. "y"形地裂缝场地主次裂缝地震响应差异的振动台试验[J]. 土木工程学报, 2014, 47(11): 98. HU Zhiping, WANG Qiyao, LUO Lijuan, et al. Shaking table test on seismic response difference between primary and secondary ground fissures on sites with y-shape ground fissure[J]. China Civil Engineering Journal, 2014, 47(11): 98. DOI:10.15951/j.tmgcxb.2014.11.045 |
| [10] |
熊仲明, 韦俊, 陈轩, 等. 跨越地裂缝框架结构振动台试验及数值模拟研究[J]. 工程力学, 2018, 35(5): 214. XIONG Zhongming, WEI Jun, CHEN Xuan, et al. Research on shaking table test and numerical modelling of frame structure crossing ground fissure[J]. Engineering Mechanics, 2018, 35(5): 214. DOI:10.6052/j.issn.1000-4750.2017.06.0473 |
| [11] |
王瑞, 胡志平, 夏香波, 等. 西安地裂缝界面处地震波传播规律[J]. 岩土力学, 2016, 37(增刊2): 642. WANG Rui, HU Zhiping, XIA Xiangbo, et al. Propagation law of seismic wave across ground fissure interface in Xi'an[J]. Rock and Soil Mechanics, 2016, 37(S2): 642. DOI:10.16285/j.rsm.2016.S2.081 |
| [12] |
谢伦武, 熊峰, 姚梓渝, 等. 基于MATLAB和ABAQUS的土体等效线性化方法二次开发[J]. 地震工程与工程振动, 2015, 35(1): 135. XIE Lunwu, XIONG Feng, YAO Ziyu, et al. Secondary development for equivalent linear method based on MATLAB and ABAQUS[J]. Earthquake Engineering and Engineering Dynamics, 2015, 35(1): 135. DOI:10.13197/j.eeev.2015.01.135.xielw.016 |
| [13] |
李舰, 王鹏月, 海路, 等. 膨胀性非饱和土本构模型的隐式和显式积分算法的比较[J]. 岩石力学与工程学报, 2018, 37(7): 1731. LI Jian, WANG Pengyue, HAI Lu, et al. Implicit and explicit integration schemes of a constitutive model for unsaturated expansive clays[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(7): 1731. DOI:10.13722/j.cnki.jrme.2018.0055 |
| [14] |
费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2010. FEI Kang, ZHANG Jianwei. Application of ABAQUS in geotechnical engineering[M]. Beijing: China Water Resources and Hydropower Press, 2010. |
| [15] |
宋彦辉, 李忠生. 地裂缝活动对两侧土体性质的影响[J]. 土木建筑与环境工程, 2012, 34(增刊1): 200. SONG Yanhui, LI Zhongsheng. Influence of earth fissure activity to physical and mechanical properties of soils[J]. Journal of Civil Architectural & Environmental Engineering, 2012, 34(S1): 200. |
| [16] |
王松涛, 曹资. 现代抗震设计方法[M]. 北京: 中国建筑工业出版社, 1997. WANG Songtao, CAO Zi. Modern seismic design method[M]. Beijing: China Building Industry Press, 1997. |
| [17] |
谷音, 刘晶波, 杜义欣. 三维一致黏弹性人工边界及等效黏弹性边界单元[J]. 工程力学, 2007(12): 31. GU Yin, LIU Jingbo, DU Yixin. 3D consistent viscous-spring artificial boundary and viscous-spring boundary element[J]. Engineering Mechanics, 2007(12): 31. |
| [18] |
熊仲明, 张朝, 陈轩. 地震作用下地裂缝场地地震动参数试验研究[J]. 岩土力学, 2019, 40(2): 421. XIONG Zhongming, ZHANG Chao, CHEN Xuan. Model test on ground motion parameters of site with fissures under seismic loading[J]. Rock and Soil Mechanics, 2019, 40(2): 421. DOI:10.16285/j.rsm.2017.1407 |
| [19] |
曹文冉, 田伟, 李春. 双向叠层剪切箱的研制及模型土体振动台试验研究[J]. 岩土工程学报, 2017, 39(增刊2): 249. CAO Wenran, TIAN Wei, LI Chun. Development of 2-D laminar shear box and shaking table tests on model soil[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(S2): 249. |
 2021, Vol. 53
2021, Vol. 53


