2. 南方煤矿瓦斯与顶板灾害预防控制安全生产重点实验室 (湖南科技大学),湖南 湘潭 411201;
3. 煤矿安全开采技术湖南省重点实验室(湖南科技大学),湖南 湘潭 411201
2. Work Safety Key Lab on Prevention and Control of Gas and Roof Disasters for Southern Coal Mines (Hunan University of Science and Technology), Xiangtan 411201, Hunan, China;
3. Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines (Hunan University of Science and Technology), Xiangtan 411201, Hunan, China)
在矿井巷道及地下硐室开挖过程中,巷道围岩应力必然重新分布,应力状态发生改变,同时,峰值应力不断向深部转移,使得巷道围岩受到了不同程度的损伤,产生岩石强度弱化的结果[1-2]。相较于浅部巷道围岩,深部巷道围岩呈大变形、难支护等特征,如何有效控制深部大变形是深部围岩控制的热点问题[3-5]。深部巷道大变形的主要力学原因在于巷道开挖过程中,巷道围岩表面岩体三维状态应力不断卸载,应力重新分布过程中单轴再加载。岩石在不同的加卸载状态下,往往会引起岩石变形特征,强度大小以及破坏形式发生明显的变化,针对卸荷影响下岩石的力学特性问题,国内外许多研究学者从岩石围压不同卸载路径[2, 6-8]、卸载速率下变形破坏[9-11]方面取得了丰富的理论研究成果。如周家文等[12]通过细观力学分析岩石内部微裂纹,研究了岩石应力应变特征曲线及断裂损伤力学特性,得到了根据应力应变曲线计算损伤变量的方法;朱俊等[13]基于不同加载速率对大理岩特征应力进行了研究,得到了大理岩在不同加载速率下的特征应力规律;张国凯等[14]分析了特征应力对应的宏-细观表征,从多个角度共同量化了岩石损伤演化过程。岩石加载过程中原始裂隙扩展,新生裂隙萌发、断裂都会释放能量,这种以弹性波形式释放出来能量的现象称为声发射,因此,声发射与岩石力学响应存在着密切的内在联系[15-17]。苏晓波等[18]开展了单轴循环加卸载压缩试验,通过声发射手段揭示了含黏结面花岗岩的能量变化规律;程爱平等[19]对胶结充填体进行单轴压缩试验,并在加载过程进行声发射监测,得到应变率与声发射的时序关系;王平等[20]对加锚预制裂隙岩体进行单轴破断试验,并在加载过程中进行声发射监测,得到锚杆与预制裂隙岩体的相互关系。
综上,国内外研究学者基于损伤力学理论研究岩石破坏特征成果颇为丰富,但是,建立岩石宏观破坏特征与细观微裂纹分布关系仍是评价岩石稳定性的重点与难点问题。实际上,深部高应力巷道开挖强卸荷扰动下必然导致围岩的损伤劣化,巷道开挖后围岩应力重新分布,受力状态发生改变,围岩继续损伤直至破坏,对巷道围岩的稳定性产生严重威胁。
目前,对于不同损伤程度岩石单轴加载下力学特性与破坏特征的研究较少,认识还不够深入,因此,基于三轴加载- 卸载试验得到损伤岩石,对损伤岩石进行单轴再加载试验,结合声发射技术,通过试验结果与理论分析,从岩石内部细观力学出发,对岩石宏观力学特性进行阐述分析,研究不同应力条件下岩石细观力学机制对宏观力学特性的影响。以期对工程施工岩石稳定性评价提供理论依据。
1 试件的制备与试验步骤试验所用试件均取自同一区域岩石,避免试件之间的离散性,经过切割、锯磨等工艺得到直径约50 mm、高度约100 mm的圆柱试件,见图 1,试件端面不平行度小于0.05 mm,满足煤炭工业部的测定方法要求。

|
图 1 部分石灰岩样照片 Fig. 1 Photos of partial limestone samples |
首先进行15 MPa三轴压缩测试,围压与轴压加载速率均为0.02 kN/s,同时加载,待围压加载至预设值时将轴压加载速率调整为0.1 kN/s,加载至试件破坏,得到完整石灰岩抗压强度约为430.96 kN。
1.2 损伤岩石的制备Martin等[21]指出,岩石载荷加载到峰值强度40%之后,试件内部会出现新的裂纹,损伤发生。根据完整石灰岩特定围压下峰值抗压强度进行卸载试验,卸载点分别为50%、55%、60%、65%、70%峰值强度,累计5种工况,加载速率同上,轴向压力加载至预设值,稳定1 min后进行轴压和围压的卸载(下文统称此条件下的岩样为损伤岩石),如图 2所示。另外,采用RSM-sy5智能声波检测仪进行波速检测。

|
图 2 损伤石灰岩图片 Fig. 2 Images of damaged limestone |
轴压加载速率均为0.02 kN/s,采用AEwin声发射系统采集岩石破坏过程中声发射数据。
1.4 完整石灰岩单轴加载试验加载速率同损伤岩石单轴再加载速率,对比天然无损伤岩样与损伤岩样的破坏变形差异。试验过程采用RMT-150岩石力学试验系统,见图 3,满足试验要求。试验技术路线如图 4。

|
图 3 RMT-150岩石力学试验系统 Fig. 3 RMT-150 rock mechanics test system |

|
图 4 试验技术路线 Fig. 4 Roadmap of the experimental technology |
图 5给出石灰岩样损伤后单轴再加载试验应力- 应变对比曲线。纵观岩样单轴加载特征曲线,天然岩石在应力较低时,应力- 应变曲线略向上弯曲,呈上凹形,当应力增加到一定值后,曲线逐渐变为直线,随后瞬间跌落,没有明显的屈服阶段,表现出塑- 弹性体岩石性质。经历50%、55%和60%峰值强度损伤后,岩样单轴再加载过程中得到的曲线特征非常相近,在应力较低时,应力- 应变曲线向上弯曲,呈上凹形,当应力增加到一定值后,岩石变形过渡为一直线段,随后转变为向下弯曲曲线,曲线似S型,随后瞬间跌落,表现出塑- 弹- 塑性体岩石性质。经历65%峰值强度损伤后,峰前应力- 应变曲线也呈S形,不过曲线斜率较为平缓。峰值后应力从跌落式瞬间下降转化为台阶式缓慢下降,此类岩石具有较高的压缩性。经历70%峰值强度损伤后,开始有很小一段甚至可以忽略的直线部分,然后很快出现非弹性的曲线部分,并继续不断地蠕变,表现出弹- 黏性体岩石性质。岩石应力- 应变曲线差异性可以归因于随着卸荷点的增大,岩石孔隙率逐渐增加,内聚力不断减小。

|
图 5 损伤岩石单轴加载特征曲线 Fig. 5 Uniaxial loading characteristic curves of damaged rock |
上述分析表明:峰值前应力- 应变曲线依上凹形—S形—蠕变形过渡,峰值后应力跌落速度有所减缓依瞬间跌落—台阶状缓慢下降过渡。岩样表现出从脆性破坏向延性破坏转化的特征,依“塑- 弹性体岩石性质”—“塑- 弹- 塑性体岩石性质”—“弹- 黏性体岩石性质”过渡。
3 初始损伤与波速的关系分析从图 6可以看出,卸荷点小于55%峰值强度三轴加载程度,加载过程中原始裂隙压密,新产生的裂纹对波速的影响小于原始裂隙,波速出现了增大的现象:大于55%峰值强度三轴加载程度,岩石新裂隙萌发、扩展、逐渐贯通,出现明显的扩容现象,岩石体积增大,新裂隙的产生和扩展阻碍了纵波的传播,纵波在裂隙处发生反射、折射以及绕射,传播路径变长,从而传播的时间增加,波速减小。

|
图 6 卸荷点与波速关系曲线 Fig. 6 Relation between unloading point and wave velocity |
岩石波速和声发射特征参数的累积都是衡量岩石完整程度的指标。本文将对波速与声发射对岩石损伤程度评价进行优劣比较,以期更为准确地表征岩石损伤量。制作损伤岩石前后分别进行声波与声发射监测,并对两者监测结果进行比较,结果如表 1所示。
| 表 1 岩石损伤前后试验结果 Tab. 1 Experimental results before and after rock damage |
为了比较两个参数的优劣,对试验结果进行方差分析[1],方差是表示数据波动大小的评价指标,通常用S2表示,样本容量相同的情况下,方差值越大,数据波动越大,偏离中心值程度越大,越不稳定。方差计算公式为
| ${S^2} = \frac{1}{{n - 1}}\sum\limits_1^n {{{\left( {{X_i} - \bar {X}{\rm{ }}} \right)}^2}} $ | (1) |
考虑到两参数量纲不一致,无法直接进行比较,归一化处理后进行方差计算,公式变为
| ${S^2}_1 = \frac{{{S^2}}}{{X{^2}}} = \frac{1}{{n - 1}}\sum\limits_1^n {{{\left( {{\rm{ }}\frac{{{X_i} - \bar X}}{X}} \right)}^2}} $ | (2) |
声发射特征参数与波速方差表示为S1AE2和S1V2,计算结果为S1AE2=(0.041 6)<S1V2=(0.104),可以看出,声发射参数数据更为稳定,对损伤变量表征更为可靠。
4 声发射能量累计数分析能量累计数是声发射监测装置在岩石破坏过程中捕捉的能量释放量,实践与理论表明,能量累计数可以反映岩石基本的破坏情况。
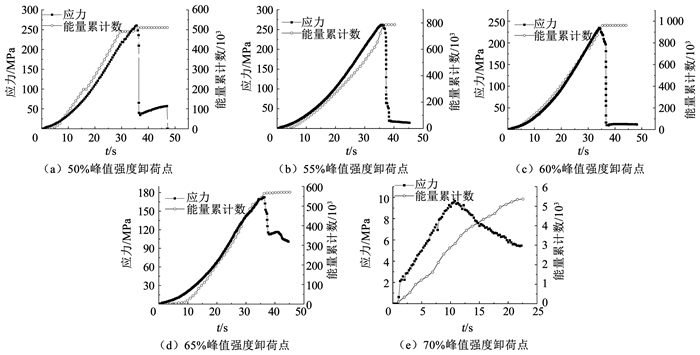
将本次试验数据绘制为应力- 时间- 能量累计数关系曲线,如图 7所示,可以看出,卸荷点处于65%峰值强度前,声发射能量累计数在加载过程中大致可以分为3个阶段,即平稳阶段、稳定增长阶段、二次平稳阶段。
|
图 7 不同卸荷点下应力、能量累计数与时间的关系 Fig. 7 Relation between stress, energy accumulation, and time at different unloading points |
1) 平稳阶段处于岩石试件初始压密阶段。声发射能量变化极其微小,在零值附近波动,说明在初始压密阶段几乎没有能量释放。
2) 稳定增长阶段贯穿于新裂隙产生、裂隙扩展阶段。随着裂隙的不断增多,声发射能量释放量呈近似线性稳定增长趋势,并在裂纹逐渐贯通至宏观裂纹时声发射能量增长速率达到最大值。在此阶段,岩石内部微裂纹萌生、扩展、贯穿为贯通裂纹,因此,内部不断释放能量,能量累计数随岩石的破坏过程呈线性关系。
3) 二次平稳阶段。岩石破坏后,能量曲线处于平稳状态,将其定义为二次稳定阶段,由此表明岩石已经失去承载能力。
此外,卸荷点处于70%峰值强度时,岩石出现了明显的宏观裂隙,单轴再加载过程可以看作天然石灰岩加载至残余强度状态,残余应力为10 MPa左右,声发射能量累计数最大值仅为5.5×103,处于比较低的状态,与低卸荷点声发射能量累计数比较,卸荷点处于70%峰值强度岩石声发射能量累计数极其微小,能量累计数曲线近似为线性增长。因此,可以将卸荷点处于70% 峰值强度岩石单轴再加载过程声发射能量累计数变化规律囊括于二次平稳阶段。
5 岩石破坏形态及机理分析 5.1 岩石加载- 卸载过程能量分布岩石的变形破坏过程是裂纹在其内部萌发、扩展、贯穿的过程,从能量守恒理论角度来讲,岩石受载变形破坏过程归因于能量的积聚、耗散和释放,单位体积的岩体单元在外力作用下产生变形,根据热力学第一定律,外力功产生的总输入能量为
| $U = {U^{\rm{d}}} + {U^{\rm{e}}}$ | (3) |
式中:U为外界载荷对岩石试件所做的功;Ud为单元耗散能,主要用于岩石微裂纹的萌生、扩展和贯穿以及内部的摩擦,导致不可恢复的残余应变;Ue为单元可释放弹性应变能,主要储存于岩石试件内部。
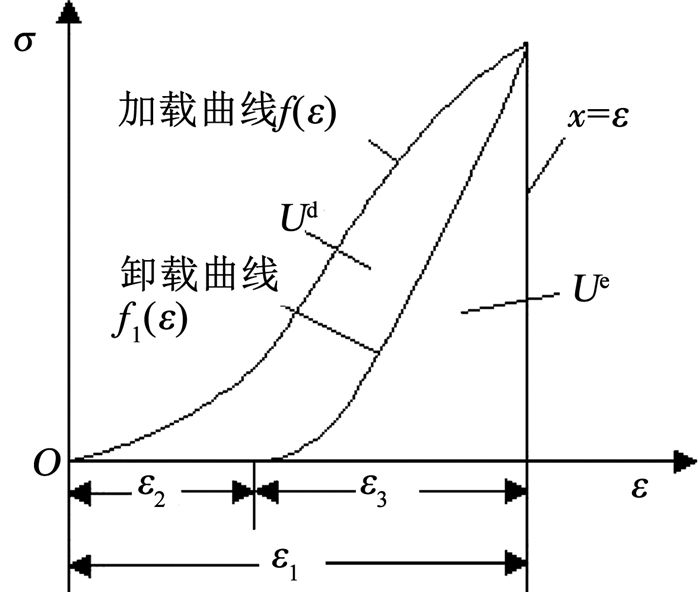
图 8为典型的峰前卸荷应力- 应变特征曲线,岩石加载- 卸载过程中经历了压密阶段、弹性阶段、弹塑性阶段、塑性阶段,在此过程中,岩石变形分为可恢复变形(弹性变形)与不可恢复变形(塑性变形),在不同阶段,岩石的吸收释放能量与破坏程度密切相关,单位体积中岩石吸收的能量U、单元耗散能Ud与弹性应变能Ue关系如图 8所示,岩石吸收的能量U为加载曲线、x=ε表示的函数曲线和x轴所围成的面积;单元耗散能Ud为卸载曲线、x=ε表示的函数曲线和x轴所围成的面积。能量耗散是岩石破坏的本质属性,因此,损伤岩石缺陷部分变形破坏过程与能量的交换密不可分,能量积聚反映岩石在为破坏储存能量,能量的耗散表示岩石承载力的衰减。
|
图 8 岩石加载卸载过程能量的分布 Fig. 8 Distribution of energy in rock loading and unloading process |
由上可知,岩石吸收的能量U为加载曲线f(ε)、x=ε表示的函数曲线和x轴所围成的面积,由于加载曲线方程不确定,利用积分的方法难以计算出结果,采用定积分可以计算出
| $U = \smallint f\left( \varepsilon \right){\rm{d}}\varepsilon = \sum\limits_{i = 0}^n {\frac{1}{2}\left( {{\sigma _{i + 1}} - {\sigma _i}} \right)({\varepsilon _{i + 1}} - {\varepsilon _i})} $ | (4) |
单元耗散能Ud为卸载曲线f1(ε)、x=ε表示的函数曲线和x轴所围成的面积,同样采用定积分的方法表示为
| ${U^{\rm{d}}} = \smallint {f_1}\left( \varepsilon \right){\rm{d}}\varepsilon = \sum\limits_{i = 0}^n {\frac{1}{2}\left( {{\sigma _{i + 1}} - {\sigma _i}} \right)({\varepsilon _{i + 1}} - {\varepsilon _i})} $ | (5) |
特别地ε2≤εi≤ε3。其中:ε为总应变,ε3为弹性应变,ε2为残余应变。
进一步,弹性应变能为
| ${U^{\rm{e}}} = U - {U^{\rm{d}}}$ | (6) |
图 9为不同卸荷点与能量的关系曲线,从能量演化角度来看,可以分为两个阶段,即能量积聚阶段与能量耗散阶段。能量积聚阶段:总能量与弹性能曲线几乎重合,基本上没有能量的耗散。该阶段试件内部损伤低,外力做功主要以弹性能的形式储存起来。能量耗散阶段:轴向应力不断增大,轴向应变增加,因此,轴向应力对试件做的功不断升高,而弹性能基本保持不变,耗散能增加较快,该阶段外力做的功主要用于形成岩石内部损伤以及宏观破坏,能量被耗散。

|
图 9 卸荷点与能量关系曲线 Fig. 9 Relation between unloading point and energy |
图 10为天然岩石和卸荷损伤石灰岩单轴压缩破坏形态照片。可以看出,破坏特征主要为:

|
图 10 损伤石灰岩破坏特征 Fig. 10 Failure characteristics of damaged limestone |
1) 破坏程度存在差异。在相同围压条件下,随着试件卸荷点的增大,破碎程度呈减小趋势。随着卸荷点的增大,岩石试件损伤程度越高,即单元耗散能越高,损伤试件内部微裂纹越发育。损伤程度较小时,岩样内部微裂纹较少,完整性较好,内部微裂隙在岩石破坏过程中起次要作用,损伤试件在加载过程中,主裂纹贯通之前,试件吸收的能量处于较高水平,使得更多细观裂纹扩展,逐步产生对岩石破坏起到主导地位的裂隙,导致试件破坏程度更大;而当损伤程度较大时,岩样内部微裂隙发育,甚至扩展贯通为裂隙。损伤程度较高试件产生明显的裂隙,在单轴再加载过程中,这些裂隙对于岩石的破坏起到主导作用,新产生的细观裂纹来不及充分地扩展、贯穿,因此,试件失去承载能力时仍处于比较完整的块度。
2) 破坏形式存在差异。天然岩石在单轴加载条件下发生共轭剪切破坏,出现明显的扩容现象,相比较而言,损伤岩石以张拉破坏为主,并伴随有扩容现象,特别地,卸荷点在60%峰值强度之前的石灰岩试件扩容现象非常明显,卸荷点在60%峰值强度之后的石灰岩试件扩容现象不是特别明显,这个现象也可以从能量角度进行解释。岩石试件处于比较低的损伤水平时,试件内部裂纹萌发数量较少,未能发育为起主导作用的裂隙,在单轴再加载过程中不断吸收能量,为裂隙的扩展、贯通储存能量,直到吸收的能量足以对岩石进行破坏,能量瞬间耗散,岩石破碎,体积出现明显增大。相反,岩石试件处于较高的损伤水平时,试件内部裂隙发育,微裂纹贯通为主导裂隙所需的能量较少,耗散能释放的梯度较为平缓,主要用于岩石内部的摩擦作用,因此,扩容现象不是特别明显。
5.3 岩石破坏机理研究表明,岩石内部存在大量微裂纹,微裂纹的扩展对宏观破坏特性影响特别明显,因此,以下基于弹塑性断裂力学对断裂扩展力学特性进行分析。
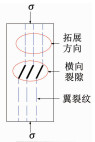
在静力载荷条件下,裂纹尖端出现应力集中,当尖端应力强度因子KⅠ>KⅠC时,在裂纹尖端位置会沿着主应力方向产生翼裂纹。
大量试验结果表明,裂纹起裂方向与最大拉应力方向垂直,因此,按Ⅰ型裂纹扩展,如图 11所示。
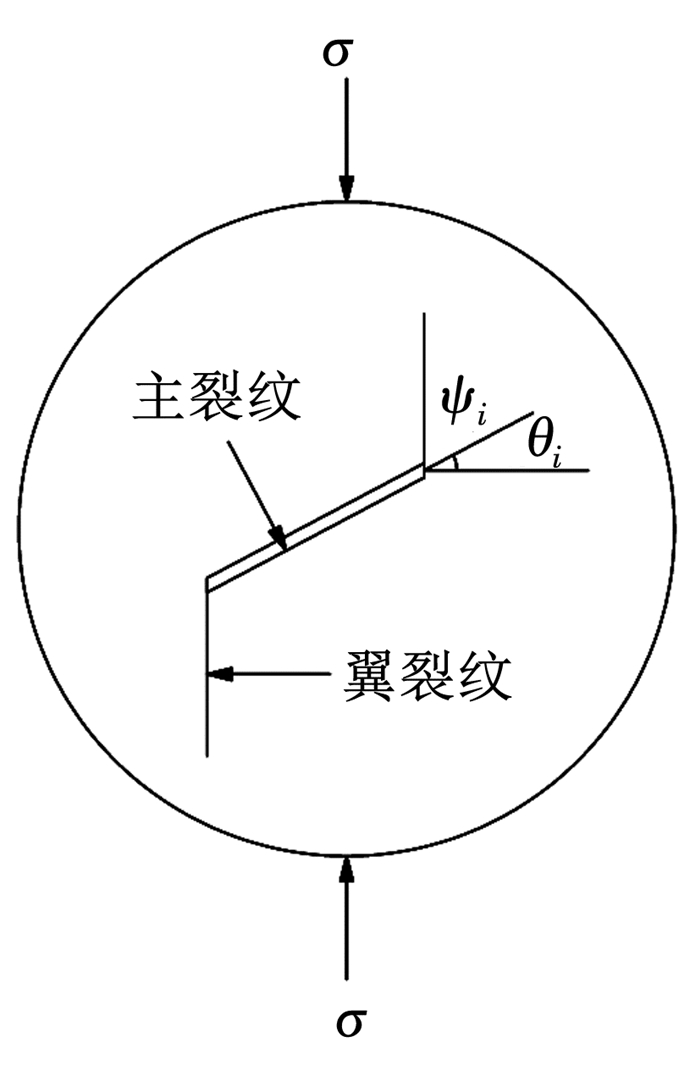
|
图 11 岩石内部微裂纹扩展模式 Fig. 11 Micro-crack propagation mode in rock |
裂纹面上所承受的正应力和剪应力分别为(这里取压应力为正)[22]:
| ${\sigma _{{\rm{ne}}}} = \sigma {\rm{si}}{{\rm{n}}^2}\psi $ | (7) |
| ${\tau _{{\rm{ne}}}} = \frac{\sigma }{2}{\rm{sin}}2\psi $ | (8) |
式中ψ为裂纹面与主应力的夹角。
由最大周向正应力理论可知,翼裂纹沿周向最大正应力方向扩展。翼型裂纹尖端瞬时应力强度因子可以表示为
| ${K_{\rm{I}}} = \frac{2}{{\sqrt 3 }}{\tau _{\rm{e}}}\;\sqrt {{\rm{ \mathsf{ π} }}a} = \frac{2}{{\sqrt 3 }}({\tau _{{\rm{ne}}}} - {\sigma _{{\rm{ne}}}}{f_{\rm{e}}})H({\tau _{\rm{e}}})\sqrt {{\rm{ \mathsf{ π} }}a}$ | (9) |
| $H({\tau _{\rm{e}}}) = \left\{ \begin{array}{l} 1, {\tau _{\rm{e}}} = {\tau _{{\rm{ne}}}} - {\sigma _{{\rm{ne}}}}{f_{\rm{e}}} > 0\\ 0, {\tau _{\rm{e}}} = {\tau _{{\rm{ne}}}} - {\sigma _{{\rm{ne}}}}{f_{\rm{e}}} \le 0 \end{array} \right.$ | (10) |
式中:fe为裂纹面摩擦因数,a为裂纹迹长。当KⅠ>KⅠC时,裂纹起裂。
岩石内部微裂纹随机分布,纵向排列裂纹与横向排列裂纹交错存在,对于单轴压缩下裂纹面扩展,在外部载荷达到裂纹断裂扩展条件时,裂纹尖端发生起裂,通常符合下式:
| ${\theta _i} + {\psi _i} \approx 90^\circ $ | (11) |
式中:θi为裂纹倾角,ψi为裂纹扩展角度。
岩石内部裂纹扩展模式如图 11所示,可以看出,单轴压缩下裂纹扩展基本符合式(11),岩石内部微裂纹相互作用概念模式如表 2,岩石内部微裂纹扩展导致翼裂纹相互影响的断裂力学作用,纵向裂纹扩展主要反映在岩石单裂隙劈裂破坏特征(如65%卸荷点岩石实际破坏模式),横向裂纹扩展导致岩石出现多裂纹劈裂扩展(如50%卸荷点岩石实际破坏模式)。裂纹尖端应力状态以及裂纹分布的差异,造成岩石实际破坏形态存在差异性。但不难看出,岩石内部微裂纹的力学特性对宏观破坏形态影响非常明显。
| 表 2 石灰岩破坏概念模式 Tab. 2 Conceptual model of limestone failure |
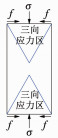
相比损伤岩石,完整岩石可假设为均质、连续、各向同性的材料。在单轴加载过程中,岩石上下边界存在摩擦力,导致岩石试件上下端部处于三向应力状态下,岩石破坏特征表现为锥形破坏,与王平等[2]研究结果一致。
综上,未损伤岩石变形破坏以X共轭剪切破坏为主,损伤岩石存在单裂隙劈裂破坏与多裂纹劈裂扩展破坏两种模式,此研究结果对工程实践具有一定的理论借鉴意义,但岩样内部微裂纹的存在形式、扩展方向还需要进一步研究。
6 讨论通过对试样定位结果与破坏特征的比较发现,岩石声发射定位系统可以较好地反应破坏特征。实际上,岩石试件为非均质体,其特征为非连续、各向异性,因此,破坏特征与理论分析存在一定的差异性。从图 12(a)可以看出定位点的分布极不均匀,从而出现了一侧破坏严重、另一侧破坏轻微的特点,如图 12(c)和12(d)。整体看来,岩石试件破坏模式主要为劈裂破坏,其原因在于主裂隙的扩展、贯通带动翼裂纹的发展,翼裂纹之间亦产生相互作用。从图 12(d)看出,岩石出现了剪切与劈裂组合的破坏形式,从而可以得出,岩石的破坏模式与细观岩石力学关系比较复杂,主裂纹与主裂纹的关系、翼裂纹与翼裂纹的关系以及主裂纹与翼裂纹的交互关系还需要进一步的研究分析。

|
图 12 定位点与岩石破坏对比 Fig. 12 Comparison of location and rock failure |
从前面分析可知,理论假设破坏概念模型与实际破坏特征存在差异,主要由于岩石内部微裂纹分布决定宏观力学特性,本文单抽离出来纵向裂纹扩展与横向裂纹扩展对岩石宏观破坏的影响,实际上,岩石内部微裂纹的存在错综复杂,裂纹扩展相互影响,为了更进一步研究岩石的宏观破坏机理,还需建立在细观力学很好的认识基础之上。
7 结论1) 损伤岩石单轴加载应力- 应变曲线表明,初始损伤岩石单轴加载抗压峰值强度随着卸荷点的增加而呈非线性规律减小。随着卸荷点的增加,石灰岩由脆性破坏向延性破坏转化,且转化过程在70%卸荷点发生突变,充分体现了岩石卸荷效应。
2) 根据应力- 时间- 能量累计数关系曲线,声发射能量累计数与岩石受压全过程对应良好,在岩石弹性变形阶段到非稳定破裂发展阶段范围,声发射能量累计数呈近似线性增长趋势,在孔隙裂隙压密阶段及峰后阶段,声发射能量累计数处于平稳发展阶段。此外,从70%峰值强度卸荷点损伤岩石来看,石灰岩峰后阶段能量累计数平稳发展阶段实际上是处于较低增长率的发展阶段。
3) 基于弹塑性断裂力学对细观微裂纹力学特性进行分析。微裂纹分布状态影响翼裂纹的扩展形式,从而决定了岩石宏观破坏模式,未损伤岩石变形破坏以X共轭剪切破坏为主,损伤岩石存在单裂隙劈裂破坏与多裂纹劈裂扩展破坏两种模式,岩石细观力学特性对宏观力学响应影响明显。
| [1] |
任恒, 朱永建, 王平, 等. 白砂岩试件初始损伤后再加载力学特性试验分析[J]. 矿业工程研究, 2019, 34(1): 23. REN Heng, ZHU Yongjian, WANG Ping, et al. Experimental analysis of mechanical properties of reloading after initial damage of white sandstone specimens[J]. Mineral Engineering Research, 2019, 34(1): 23. |
| [2] |
王平, 朱永建, 冯涛, 等. 砂岩试件加载- 卸荷- 加载损伤弱化试验分析[J]. 煤炭学报, 2016, 41(12): 2960. WANG Ping, ZHU Yongjian, FENG Tao, et al. Test and analysis of sandstone damage-weakening under loading-unloading-loading[J]. Journal of China Coal Society, 2016, 41(12): 2960. DOI:10.13225/j.cnki.jccs.2016.1118 |
| [3] |
余伟健, 吴根水, 安百富, 等. 裂隙岩体巷道大变形特征与稳定性控制[J]. 采矿与安全工程学报, 2019, 36(1): 103. YU Weijian, WU Genshui, AN Baifu, et al. Large deformation characteristics and stability control of roadway with fractured rock mass[J]. Journal of Mining & Safety Engineering, 2019, 36(1): 103. DOI:10.13545/j.cnki.jmse.2019.01.015 |
| [4] |
王卫军, 袁超, 余伟健, 等. 深部高应力巷道围岩预留变形控制技术[J]. 煤炭学报, 2016, 41(9): 2156. WANG Weijun, YUAN Chao, YU Weijian, et al. Control technology of reserved surrounding rock deformation in deep roadway under high stress[J]. Journal of China Coal Society, 2016, 41(9): 2156. DOI:10.13225/j.cnki.jccs.2016.0118 |
| [5] |
王卫军, 袁超, 余伟健, 等. 深部大变形巷道围岩稳定性控制方法研究[J]. 煤炭学报, 2016, 41(12): 2921. WANG Weijun, YUAN Chao, YU Weijian, et al. Stability control method of surrounding rock in deep roadway with large deformation[J]. Journal of China Coal Society, 2016, 41(12): 2921. DOI:10.13225/j.cnki.jccs.2016.1115 |
| [6] |
MENG Qingbin, ZHANG Mingwei, HAN Lijiun, et al. Effects for acoustic emission and energy evolution of rock specimens under the uniaxial cyclic loading and unloading compression[J]. Rock Mechanics and Rock Engineering, 2016, 49(10): 3873. DOI:10.1007/s00603-016-1077-y |
| [7] |
戴兵, 赵国彦, 杨晨, 等. 不同应力路径下岩石峰前卸荷破坏能量特征分析[J]. 采矿与安全工程学报, 2016, 33(2): 367. DAI Bing, ZHAO Guoyan, YANG Chen, et al. Energy evolution law of rocks in process of unloading failure under different paths[J]. Journal of Mining & Safety Engineering, 2016, 33(2): 367. DOI:10.13545/j.cnki.jmse.2016.02.028 |
| [8] |
QIU Shili, FENG Xiating, XIAO Jianqing, et al. An experimental study on the pre-peak unloading damage evolution of marble[J]. Rock Mechanics and Rock Engineering, 2014, 47(2): 401. DOI:10.1007/s00603-013-0394-7 |
| [9] |
ZHAO X G, WANG J, CAI M, et al. Influence of unloading rate on the strainburst characteristics of Beishan granite under true-triaxial unloading conditions[J]. Rock Mechanics and Rock Engineering, 2014, 47(2): 467. DOI:10.1007/s00603-013-0443-2 |
| [10] |
杨小彬, 韩心星, 刘恩来, 等. 单轴循环加卸载岩石非均匀变形演化特征[J]. 煤炭学报, 2018, 43(2): 449. YANG Xiaobin, HAN Xinxing, LIU Enlai, et al. Properties of non-uniform deformation evolution of rock under uniaxial cyclic loading and unloading[J]. Journal of China Coal Society, 2018, 43(2): 449. DOI:10.13225/j.cnki.jccs.2017.1119 |
| [11] |
杨小彬, 韩心星, 刘恩来, 等. 循环加卸载下花岗岩非均匀变形演化的声发射特征试验研究[J]. 岩土力学, 2018, 39(8): 2732. YANG Xiaobin, HAN Xinxing, LIU Enlai, et al. Experimental study on the acoustic emission characteristics of non-uniform deformation evolution of granite under cyclic loading and unloading test[J]. Rock and Soil Mechanics, 2018, 39(8): 2732. DOI:10.16285/j.rsm.2018.0048 |
| [12] |
周家文, 杨兴国, 符文熹, 等. 脆性岩石单轴循环加卸载试验及断裂损伤力学特性研究[J]. 岩石力学与工程学报, 2010, 29(6): 1172. ZHOU Jiawen, YANG Xingguo, FU Wenxi, et al. Experimental test and fracture damage mechanical characteristics of brittle rock under uniaxial cyclic loading and unloading conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(6): 1172. |
| [13] |
朱俊, 邓建辉, 黄弈茗, 等. 大理岩特征应力的加载速率效应研究[J]. 哈尔滨工业大学学报, 2020, 52(2): 75. ZHU Jun, DENG Jianhui, HUANG Yiming, et al. Study of loading rate effect on characteristic stresses of marble[J]. Journal of Harbin Institute of Technology, 2020, 52(2): 75. DOI:10.11918/201811171 |
| [14] |
张国凯, 李海波, 王明洋, 等. 岩石单轴压缩下损伤表征及演化规律对比研究[J]. 岩土工程学报, 2019, 41(6): 1074. ZHANG Guokai, LI Haibo, WANG Mingyang, et al. Comparative study on the damage characterization and damage evolution of rock under uniaxial compression[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(6): 1074. DOI:10.11779/CJGE201906011 |
| [15] |
邓绪彪, 刘远征, 邢矿, 等. 基于声发射时空演化的岩石全应力- 应变曲线阶段特征分析[J]. 岩石力学与工程学报, 2018, 37(增刊2): 4086. DENG Xubiao, LIU Yuanzheng, XING Kuang, et al. Analysis based on AE space-time evolution characteristics for stage division of whole stress-strain curve of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(S2): 4086. DOI:10.13722/j.cnki.jrme.2018.0594 |
| [16] |
吴贤振, 刘建伟, 刘祥鑫, 等. 岩石声发射振铃累计计数与损伤本构模型的耦合关系探究[J]. 采矿与安全工程学报, 2015, 32(1): 28. WU Xianzhen, LIU Jianwei, LIU Xiangxin, et al. Study on the coupled relationship between AE accumulative ring-down count and damage constitutive model of rock[J]. Journal of Mining & Safety Engineering, 2015, 32(1): 28. DOI:10.13545/j.cnki.jmse.2015.01.005 |
| [17] |
李庶林, 周梦婧, 高真平, 等. 增量循环加卸载下岩石峰值强度前声发射特性试验研究[J]. 岩石力学与工程学报, 2019, 38(4): 724. LI Shulin, ZHOU Mengjing, GAO Zhenping, et al. Experimental study on acoustic emission characteristics before the peak strength of rocks under incrementally cyclic loading-unloading methods[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(4): 724. DOI:10.13722/j.cnki.jrme.2018.1410 |
| [18] |
苏晓波, 纪洪广, 裴峰, 等. 单轴压缩荷载下含黏结面花岗岩能量演化研究[J]. 哈尔滨工业大学学报, 2018, 50(8): 161. SU Xiaobo, JI Hongguang, PEI Feng, et al. Study on energy evolution law of defective granite specimen under uniaxial compressive loading and unloading[J]. Journal of Harbin Institute of Technology, 2018, 50(8): 161. DOI:10.11918/j.issn.0367-6234.201710130 |
| [19] |
程爱平, 张玉山, 王平, 等. 胶结充填体应变率与声发射特征响应规律[J]. 哈尔滨工业大学学报, 2019, 51(10): 130. CHENG Aiping, ZHANG Yushan, WANG Ping, et al. Strain rate and acoustic emission characteristic response law of cemented backfill[J]. Journal of Harbin Institute of Technology, 2019, 51(10): 130. DOI:10.11918/j.issn.0367-6234.201810134 |
| [20] |
王平, 冯涛, 朱永建, 等. 加锚预制裂隙类岩体锚固机制试验研究及其数值模拟[J]. 岩土力学, 2016, 37(3): 793. WANG Ping, FENG Tao, ZHU Yongjian, et al. Experimental study and numerical simulation of anchoring mechanism of anchored rocklike material with prefabricated fracture[J]. Rock and Soil Mechanics, 2016, 37(3): 793. DOI:10.16285/j.rsm.2016.03.023 |
| [21] |
MARTIN C D, CHANDLER N A. The progressive fracture of Lac du Bonnet granite[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1995, 32(4): 41. DOI:10.1016/0148-9062(95)96972-E |
| [22] |
赵延林, 曹平, 万文, 等. 随机卸荷岩体裂纹流变断裂模型与数值模拟[J]. 中南大学学报(自然科学版), 2015, 46(12): 4647. ZHAO Yanlin, CAO Ping, WAN Wen, et al. Model and numerical simulation of rheological fracture of random unloading rock mass cracks[J]. Journal of Central South University (Science and Technology), 2015, 46(12): 4647. DOI:10.11817/j.issn.1672-7207.2015.12.035 |
 2021, Vol. 53
2021, Vol. 53