2. 重庆交通大学 土木工程学院,重庆 400074
2. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China
各种岩体工程中,岩石都会受到地应力场的影响,岩体开挖时应力场会重新分布,复杂应力状态可能会导致岩石发生变形和破坏。强度准则就是研究各种应力场作用下岩石的强度及确定岩石破坏时的塑性区范围,是岩石工程稳定性评估和结构优化设计的基础。由于Mohr-Coulomb(M-C)、Griffith和Hoek-Brown(H-B)强度准则表达式简单且强度参数物理意义明确,在岩体工程理论和数值计算分析中广泛应用。其中,M-C准则为线性准则,无法反映岩石强度随围压增加呈非线性增加的关系,因而只适用于低围压的情况[1];虽然Griffith和H-B准则更符合实际情况,但高围压下与试验数据偏差较大[2-3]。为此,一些学者[4-6]改进了M-C和H-B准则,通过减去一个含围压的非线性项使其对三轴试验数据的拟合精度更高,但增加了参数数量及其确定的难度。上述强度准则认为岩石破坏强度只与大和小主应力有关,均未考虑中间主应力的影响,与真三轴试验数据明显不符。
大量真三轴试验结果证明,中主应力对岩石强度有显著影响[7-9],一是以中、小主应力相等为初始点,岩石的强度随着中主应力的增加先增加后减小,但始终高于常规三轴试验强度;二是岩石越致密坚硬,中主应力效应越大。一些学者在大量试验和理论分析的基础上,提出了多种岩石三维强度准则,可归纳为两类: 1)依据强度理论和试验数据构建新的岩石强度准则表达式,如由Misses强度理论推导的考虑静水压力的Drucker-Prager(D-P)强度准则[10];尤明庆[11]基于试验数据提出了指数形式的岩石真三轴强度准则,但该准则认为岩石强度随着中主应力的增加始终是增大的,与真三轴试验结果明显不符。2)基于常规三轴强度准则对拉压过渡带考虑中主应力修正,如Mogi和俞茂宏分别将中主应力引入M-C准则中,构建了Mogi经验强度准则和统一强度准则[12-13],从不同的角度描述了岩石强度的多轴性;张强等[14]在指数型强度准则[2]的基础上,引入罗德过渡函数导出了岩石三维强度准则;目前主要集中于H-B准则三维化的研究,国内外学者已提出了多种三维化H-B准则,如Priest等[15-19]的研究。这些三维化的H-B强度准则有效地推进了强度理论的发展,但仍未摆脱H-B准则的初始缺点,且存在表达式过于复杂或不满足偏平面上外凸的强度特性,与真三轴试验结果差别较大;线性的M-C准则适应性更差。
大量研究结果表明,岩石强度在子午面上随着静水压力的增加而增大,但增加幅度先增大后减小并最终趋于零,经典的M-C和H-B准则无法准确描述岩石强度的这一变化过程。因此,准确的常规三轴强度准则是构建真三轴强度准的基础。本文将依据从原文献中搜集的大量常规三轴和真三轴试验数据,先构建符合子午面上岩石强度变化规律的强度准则,再通过引入中主应力参数和罗德应力参数考虑中主应力的影响,从而建立一种新的岩石非线性真三轴强度准则。
1 现有典型岩石强度准则 1.1 改进的Mohr-Coulomb准则为了描述岩石强度随围压变化的非线性,Singh等[4]在M-C准则的基础上减去了一个二次项,提出了改进的Mohr-Coulomb(MM-C)强度准则,表达式如下:
| $ \sigma_{1}-\sigma_{3}=2 c \frac{\cos \varphi}{1-\sin \varphi}+\frac{2 \sin \varphi}{1-\sin \varphi} \sigma_{3}-A \sigma_{3}^{2} $ | (1) |
| $ A=\frac{1}{\sigma_{\mathrm{crti}}} \frac{\sin \varphi_{0}}{1-\sin \varphi_{0}} $ | (2) |
式中:c和φ分别为黏聚力和内摩擦角;σcrti为临界围压,通常取为σc;c0和φ0分别为低围压下岩石的黏聚力和内摩擦角。当围压达到临界围压后(即σ3=σcrti),式(1)满足∂(σ1-σ3)/∂σ3=0,其计算结果为定值。
1.2 Hoek-Brown准则1980年,Heok和Brown[20]依据大量常规三轴试验结果,针对完整坚硬岩石提出了带有经验性质的Heok-Brown(H-B)强度准则,该准则本身就具有非线性特征,为了使其更具有普适性,随后又提出了广义H-B准则[21],表达式如下:
| $ \left(\sigma_{1}-\sigma_{3}\right)=\sigma_{\mathrm{c}}\left(m \sigma_{3} / \sigma_{\mathrm{c}}+s\right)^{a} $ | (3) |
式中:σc为单轴抗压强度;m、s和a为岩石材料参数,与岩石性质及扰动破碎程度有关。对于完整岩石,为了方便计算分析以及在进行H-B准则的三维化时,通常取s=1.0和a=0.5。
1.3 指数型强度准则依据常规三轴试验所得岩石强度随围压的变化关系,You等[2, 22]提出了指数型的强度准则,并对比了十几种准则对试验结果的预测精度,表明指数型准则最优,其数学表达式如下:
| $ \sigma_{1}-\sigma_{3}=\sigma_{\infty}-\left(\sigma_{\infty}-\sigma_{\mathrm{c}}\right) \exp \left[-\frac{\left(k_{0}+1\right) \sigma_{3}}{\sigma_{\infty}-\sigma_{\mathrm{c}}}\right] $ | (4) |
式中:σc为岩石的单轴抗压强度,σ∞为岩石的极限主应力差,k0表示σ3=0时岩石强度的影响系数。
1.4 Drucker-Prager准则1952年,Drucker和Prager[10]在Mises强度准则的基础上,考虑静水压力导出了Drucker-Prager(D-P)准则,该准则屈服面为圆锥体形状,在π平面上为一簇光滑的圆曲线,表述形式简洁,应用较为广泛。以应力不变量表述的D-P准则的表达式如下:
| $ F=\alpha I_{1}+\sqrt{J_{2}}-\kappa=0 $ | (5) |
式中:α和κ为D-P准则参数,I1和J2分别为应力张量第一不变量和偏应力张量第二不变量。
MM-C准则[4]认为三轴等围压应力条件下围压超过临界围压时岩石抗压强度不再发生变化,临界围压的确定较为模糊,通常选择岩石的单轴抗压强度作为临界围压,所得预测值与试验结果存在明显不符。H-B准则[20-21]虽然能够表征岩石强度随围压增加的非线性变化,但较高围压下的预测值明显大于试验结果。指数型准则[2, 22]虽然是目前公认预测精度较高的岩石强度准则[6],由式(4)可知,等围压应力条件下岩石的偏应力随着围压的增加始终是增大的,与试验结果也存在不符之处。以上3种准则均无法预测真三轴应力条件下的岩石强度。D-P准则[10]在等围压条件下岩石强度与围压将退化为线性关系,无法反映岩石强度随围压的非线性变化。针对上述几种典型岩石强度准则的不足,以下将基于大量试验结果提出更符合实际情况的岩石非线性真三轴强度准则。
2 幂函数型岩石强度准则的构建岩石的强度特性和破坏模型与受到的应力状态密切相关,岩石的应力状态通常用大主应力σ1、中主应力σ2和小主应力σ3来表征,主应力之间总要满足F(σ1, σ2, σ3)≤0。岩石的强度特性主要由常规三轴试验(σ1>σ2=σ3)测得,即要满足F(σ1, σ3)≤0,若等号成立F=0,岩石破坏,通常将强度准则写成如下形式:
| $ \sigma_{\mathrm{s}}=f\left(\sigma_{3}\right) $ | (6) |
基于圆柱体岩石试样的常规三轴试验结果,利用数学方法可以确定函数f的形式用于描述强度σs与围压σ3的关系。
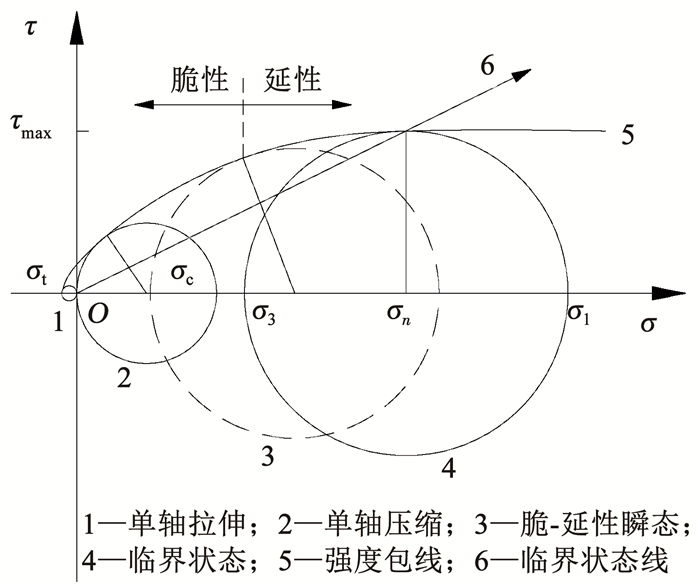
2.1 等围压条件下强度准则根据常规三轴试验结果,岩石的破坏强度包线在τ-σ坐标系中呈向下凹的非线性特征,随着围压的增加逐渐趋于平缓,围压足够大时为水平线,如图 1所示。Barton[23]将围压足够大时剪切强度不变的初始点定为岩石的临界状态,达到临界状态后对应的主应力差(σ1-σ3)达到最大值,随围压不再变化,保持为定值。根据图 1中岩石强度包线的变化规律,定义临界围压对应主应力差的最大值为Q∞,令其值为Q∞=(1+k)σc,σc为单轴抗压强度,k为岩石达到临界状态时的影响系数。为了避免确定临界围压带来的不便和参数的增多,同样采用以(1+k)σc作为临界围压σcrti,构建一种新的适用于三轴等围压条件下的岩石强度准则,表达式如下:
|
图 1 完整岩石的Mohr圆强度包线 Fig. 1 Mohr circle strength envelop of intact rock |
当0≤σ3≤(1+k)σc时,
| $ \sigma_{\mathrm{s}}-\sigma_{3}=(1+k) \sigma_{\mathrm{c}}-k \sigma_{\mathrm{c}}\left[1-\frac{\sigma_{3}}{(1+k) \sigma_{\mathrm{c}}}\right]^{m} $ | (7a) |
当σ3≥(1+k)σc时,主应力差为定值,即
| $ \sigma_{\mathrm{s}}-\sigma_{3}=(1+k) \sigma_{\mathrm{c}} $ | (7b) |
式中:σs为岩石的常规三轴压缩强度,此时其数值与σ1相等;m为围压σ3=0时的影响系数。根据式(7)可知,当σ3=(1+k)σc,则σs=2(1+k)σc,此时岩石的常规三轴压缩强度等于临界围压的两倍。对式(7a)进行求导可得m和k之间的关系为
| $ m=\left.\frac{(1+k)}{k} \cdot \frac{\mathrm{d}\left(\sigma_{\mathrm{s}}-\sigma_{3}\right)}{\mathrm{d} \sigma_{3}}\right|_{\sigma_{3}=0} $ | (8) |
对式(7a)两边取对数,可得
| $ m=\ln \left(1+\frac{1}{k}-\frac{\sigma_{\mathrm{s}}-\sigma_{3}}{k \sigma_{\mathrm{c}}}\right) / \ln \left[1-\frac{\sigma_{3}}{(1+k) \sigma_{\mathrm{c}}}\right] $ | (9) |
岩石力学性质非常复杂,三维应力状态下表现出显著的非线性强度特性,在子午面上具有明显的静水压力效应,在偏平面上表现出明显的中主应力效应[14]。定义中主应力参数β来反映应力状态如下:
| $ \beta=\frac{\sigma_{2}-\sigma_{3}}{\sigma_{1}-\sigma_{3}}, 0 \leqslant \beta \leqslant 1 $ | (10) |
弹塑性理论中,往往引入罗德应力参数μ以表示中主应力的影响,其代表应力状态的中主应力与大、小主应力的相对比值,即
| $ \mu=\frac{2 \sigma_{2}-\sigma_{1}-\sigma_{3}}{\sigma_{1}-\sigma_{3}},-1 \leqslant \mu \leqslant 1 $ | (11) |
由式(10)和(11)不难证明,μ和β之间存在如下关系:
| $ \mu=2 \beta-1 $ | (12) |
当μ=-1和β=0时,即σ1>σ2=σ3为常规三轴压缩试验;当μ=1和β=1时,即σ1=σ2>σ3为常规三轴拉伸试验。通常情况下3个主应力之间的关系为σ1>σ2>σ3,则μ介于-1和1;β介于0和1。
考虑小、中主应力对岩石强度的影响,在上述所建等围压条件下强度准则(见式(7))的基础上,引入中主应力参数β和罗德应力参数μ,构建由两个幂函数公式联合表示的岩石真三轴强度准则,即
| $ \sigma_{1}=\sigma_{\mathrm{s}}+H\left(\sigma_{2}-\sigma_{3}, \sigma_{3}\right) $ | (13) |
| $ \begin{gathered} H\left(\sigma_{2}-\sigma_{3}, \sigma_{3}\right)=Q_{\mathrm{D}} \beta^{n}\left(1-\mu^{2}\right)= \\ Q_{\mathrm{D}}\left(\frac{\sigma_{2}-\sigma_{3}}{\sigma_{\mathrm{s}}-\sigma_{3}}\right)^{n}\left[1-\left(\frac{2 \sigma_{2}-\sigma_{\mathrm{s}}-\sigma_{3}}{\sigma_{\mathrm{s}}-\sigma_{3}}\right)^{2}\right] \end{gathered} $ | (14) |
式中:QD为中主应力影响的岩石强度的最大值;n为岩石强度达到最大值时的参数;当σ2=σ3时满足H(σ2-σ3, σ3)=0,σ1=σs即为常规三轴压缩强度,由式(7)求得。
由式(14)对中主应力σ2进行求导,可得
| $ \frac{\partial H}{\partial \sigma_{2}}=\frac{Q_{\mathrm{D}} \beta^{n-1}}{\sigma_{\mathrm{s}}-\sigma_{3}}\left[n\left(1-\mu^{2}\right)-4 \mu \beta\right] $ | (15) |
令∂H/∂σ2=0,由于真三轴试验中β≠0,因而有n(1-μ2)-4μβ=0,并结合式(10)~(12)可得
| $ \beta=1-\frac{1}{n+2}, \mu=1-\frac{2}{n+2} $ | (16) |
| $ \sigma_{2}=\sigma_{3}+\left(\sigma_{\mathrm{s}}-\sigma_{3}\right)\left(1-\frac{1}{n+2}\right) $ | (17) |
小主应力σ3一定的情况下,当中主应力σ2满足式(17)时,真三轴岩石强度达到最大值。
3 强度准则的评估标准岩石强度准则参数的确定方法及其预测精度的评估标准有多种形式,根据相关文献[5]建议采用最小二乘法选择以均方根误差(RMSE, ERMS)最小为目标函数来确定强度参数;选择两种方法来评估强度准则的预测精度:回归系数R-平方值(R2)和平均相对误差(MAPE, EMAP)。MAPE简单有效,可直接反映预测误差的绝对值大小。其中,ERMS、R2和EMAP分别定义为
| $ E_{\mathrm{RMS}}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left(\sigma_{1, i}^{\mathrm{pre}}-\sigma_{1, i}^{\exp }\right)^{2}} $ | (18) |
| $ R^{2}=1-\frac{\sum\limits_{i=1}^{N}\left(\sigma_{1, i}^{\exp }-\sigma_{1, i}^{\text {pre }}\right)^{2}}{\sum\limits_{i=1}^{N}\left(\sigma_{1, i}^{\exp }-E\left[\sigma_{1}^{\exp }\right]\right)^{2}} $ | (19) |
| $ E_{\mathrm{MAP}}=\frac{\sum\limits_{i=1}^{N}\left|\frac{\sigma_{1, i}^{\mathrm{pre}}-\sigma_{1, i}^{\exp }}{\sigma_{1, i}^{\exp }}\right|}{N} \times 100 \% $ | (20) |
式中:σ1, ipre为岩石强度准则的预测强度;σ1, iexp为岩石的试验强度;E[·]为期望(或为统计平均值)的符号;N为试验数据的样本数。清晰可知,ERMS越小,R2越大,EMAP越小,强度准则越可靠,预测精度越高;最理想的强度准则为ERMS=EMAP=0,R2=1。
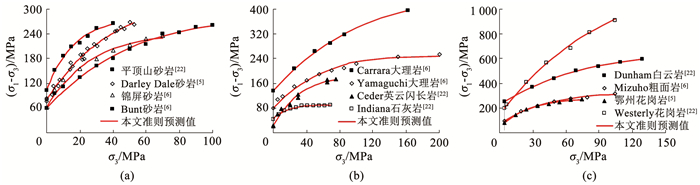
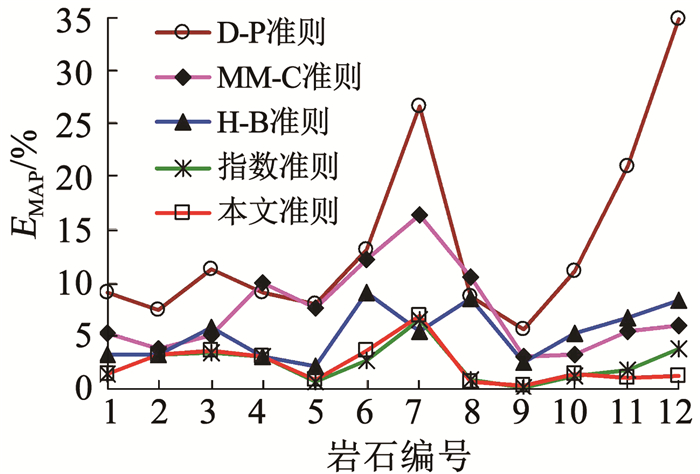
4 准强度准则验证及比较 4.1 常规三轴试验结果验证及比较根据已有文献[5-6, 22]报道,统计了12种岩石的常规三轴压缩试验结果,将这12种岩石编号为1~12号,分别对应平顶山砂岩、Darley Dale砂岩、锦屏石岩、Bunt砂岩、Carrara大理岩、Yamaguchi大理岩、Cedar石英闪长岩、Indiana石灰岩、Dunham白云岩、Mizuho粗面岩以及Westerly花岗岩。针对上述12种岩石的常规三轴压缩试验结果,利用式(7)和(18)在MATLAB软件中编写程序确定相关参数(见表 1),得到了所建等围压条件下强度准则预测值与岩石试验强度的对比情况,如图 2所示。可以看出,岩石的常规三轴试验强度随着围压的增加而增大,增加幅度逐渐减小,且围压足够大时增加幅度近似为零,具有明显的非线性特征;本文强度准则的预测值曲线与试验强度曲线有非常高的吻合程度。由表 1可知,本文强度准则对所有岩石强度预估的相关性回归系数R2均在0.98以上,且平均相对误差EMAP均在4%以下(除7号岩石为6.83%),如图 5所示。7号岩石(Ceder英云闪长岩)的EMAP略大与其试验强度的离散程度较大有关,见图 2(b)。以上分析表明本文强度准则能够很好地预测不同类型岩石在不同围压下的试验强度,具有良好的普遍适用性。
| 表 1 本文准则对岩石常规三轴强度的预测结果 Tab. 1 Prediction results of the proposed nonlinear strength criterion for conventional triaxial strengths |
|
图 2 本文强度准则对12种岩石试验强度的预测 Fig. 2 Prediction of the proposed strength criterion for 12 kinds of rocks |
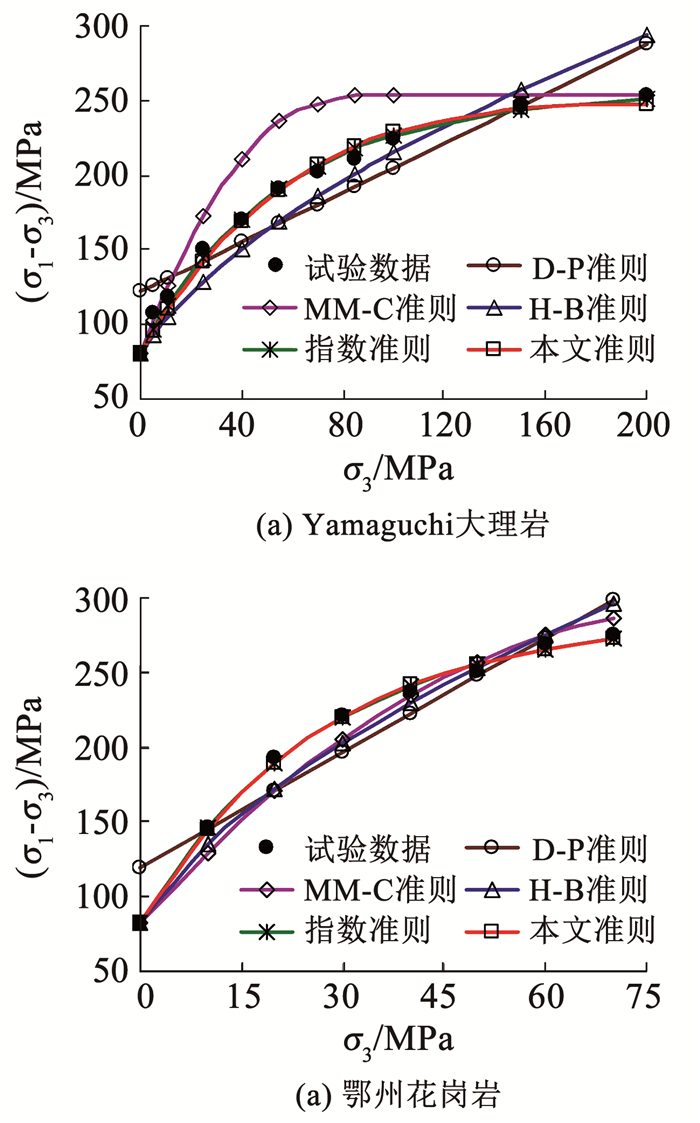
选择7号Yamaguchi大理岩和11号鄂州花岗岩为对象,充分比对本文强度准则与其他4种典型强度准则之间的差异性,对岩石常规三轴试验强度的预测情况如图 3所示。
|
图 3 不同强度准则对不同岩石强度预测的比较 Fig. 3 Comparison of prediction results of five strength criterions for different rocks |
由图 3可以看出,本文强度准则和指数准则(目前被认为预测精度较高的强度准则[6])对岩石试验强度的预测精度最高,两者预测值与试验结果几乎完全重合;H-B准则的预测值在低围压时偏小,而高围压时又有明显的偏大现象;对于MM-C准则,当围压超过临界围压(单轴抗压强度)时岩石强度随围压不再发生变化,导致其预测精度较差;当围压小于临界围压时,其预测精度与H-B准则相当;D-P准则退化为常规三轴应力状态时,岩石强度与围压之间是线性关系,故预测精度最差。
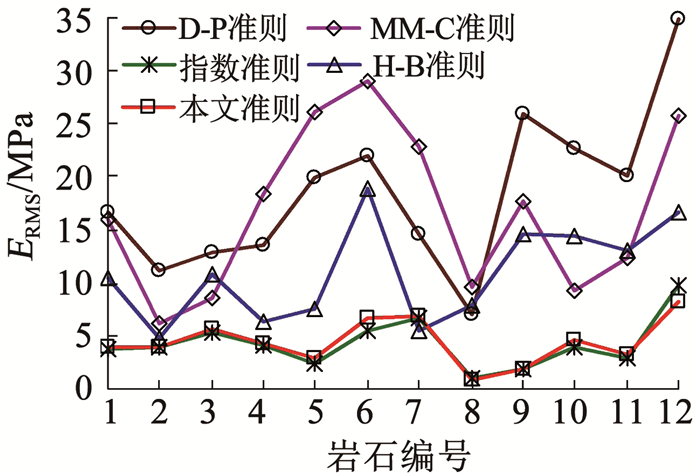
为了进一步比较分析上述5种岩石强度准则对岩石强度预测的差异性,图 4、5分别给出了12种岩石的均方根误差ERMS和平均相对误差EMAP。同样可以看出,本文强度准则与指数准则预测得到的不同类型岩石的ERMS和EMAP非常接近,远小于其他3种强度准则;本文强度准则、指数准则、H-B准则、MM-C准则和D-P准则对所有12种岩石预估所得ERMS的平均值分别为4.431、4.276、10.903、16.804和18.429 MPa,所得EMAP的平均值分别为2.32%、2.43%、5.28%、7.39%和13.74%,也可以看出,本文强度准则和指数准则对岩石强度的预测精度最优,依次是H-B准则、MM-C准则和D-P准则。由表 1、图 4、5还可以看出,当围压小于单轴抗压强度σc时,MM-C准则与H-B准则的预测精度相当;当围压大于σc时,前者的预测精度将变得很差,与其选择σc作为临界围压有直接关系。
|
图 4 不同岩石强度准则预测的均方根误差比较 Fig. 4 Comparison of root mean square error (ERMS) of different rock strength criterions |
|
图 5 不同岩石强度准则预测的平均相对误差比较 Fig. 5 Comparison of mean absolute percentage error (EMAP) of five strength criterions for different rocks |
真三轴应力条件的岩石试验强度是评估岩石强度准则的重要方面,利用相关文献[17-19]报道的8种岩石的真三轴试验数据对建立的岩石强度准则进行验证。对这8种岩石进行13~20编号,依次为Westerly花岗岩、KTB闪岩、Dunam白云岩、Mizuho粗面岩、Yuubari板岩、Solenhofen石灰岩、Shirahama砂岩和Manazuru安山岩,利用式(13)~(17)和式(18)在MATLAB软件中编写程序,确定这些岩石材料的强度参数,见表 2。
| 表 2 本文准则对岩石真三轴强度的预测结果 Tab. 2 Prediction results of the proposed nonlinear strength criterion for true triaxial strengths |
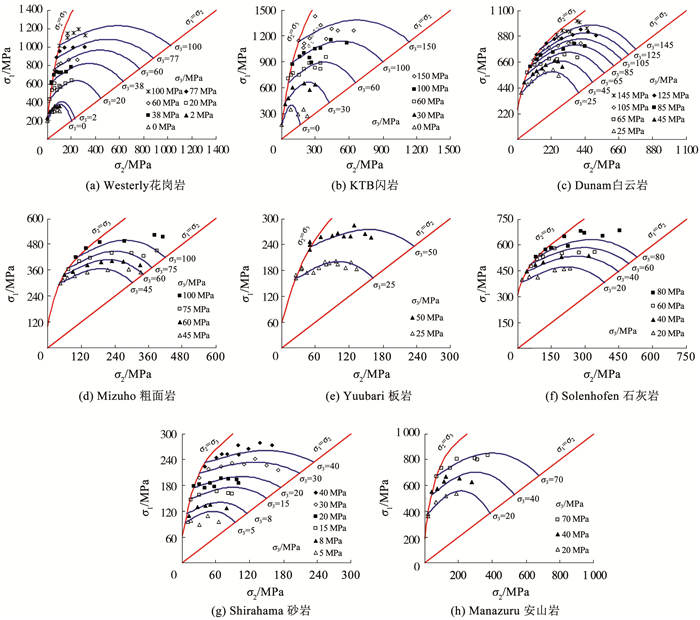
图 6给出了所建真三轴强度准则预测值与8种岩石真三轴试验数据的对比。图中对角线σ1=σ2和实线σ2=σ3中间所夹上凸形弧状实线为本文真三轴强度准则的理论计算曲线,左侧红色实线为本文等围压条件下强度准则的理论计算曲线;左右侧边界红色实线分别为常规三轴压缩和拉伸的状态线。由图 6可以看出,本文建立的真三轴强度准则与岩石试验数据有较高的吻合度,能够较好地反映中主应力效应使岩石强度明显增强的影响,也很好地反映了岩石强度从常规三轴压缩到三轴拉伸过程中,岩石强度随中主应力增加先增大后减小的变化规律;左侧σ2=σ3的压缩曲线与右侧σ1=σ2的拉伸状态线之间的差值呈现出逐渐增大的变化趋势,由σc逐渐增加到(1+k)σc;由式(7)可知围压足够大时,图 6中左右两侧压缩和拉伸状态线为平行线,较好地反映了岩石的静水压力效应,但经典的M-C准则、H-B准则和D-P准则并不符合这一规律,这也是本文强度准则的优势。由表 2可知,本文真三轴强度准则对上述8种岩石预估的相关性回归系数R2均大于0.9,其中有5种岩石超过了0.96。以上说明所建岩石真三轴强度准则能够较好地预测不同应力状态下不同类型岩石的强度。
|
图 6 本文强度准则对8种岩石真三轴试验强度的预测 Fig. 6 Prediction of the proposed strength criterion for true triaxial test results of eight kinds of rocks |
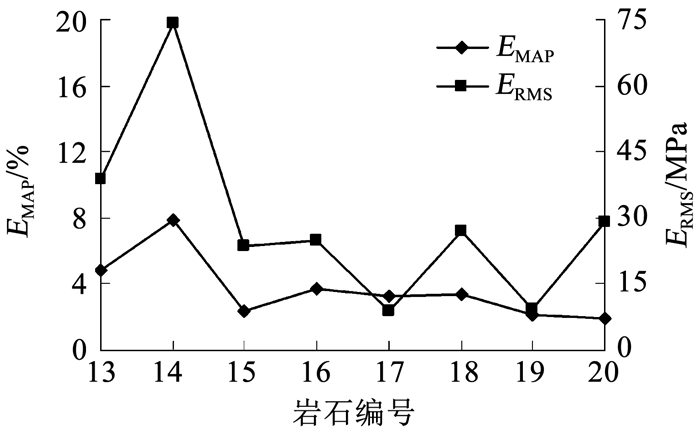
本文强度准则对8种真三轴岩石试验结果预测得到的均方根误差ERMS和平均相对误差EMAP,如图 7所示。可以看出,所建强度准则预测所得的ERMS和EMAP除14号岩石外(分别为74.23 MPa和7.79%),其余7种岩石均分别在40 MPa和5%以下;14号岩石(KTB闪岩)的ERMS和EMAP相比其他岩石较大,主要原因在于围压σ3=150 kPa时真三轴试验所得KTB闪岩大主应力随中主应力变化的离散程度非常大(见图 6(b)),导致了所建强度准则对KTB闪岩的预测精度较差。以上分析说明本文强度准则对不同类型岩石的真三轴试验强度同样有较高的预测精度,具有良好的普遍适用性。
|
图 7 本文强度准则对8种岩石真三轴试验结果预测的均方根误差和平均相对误差 Fig. 7 ERMS and EMAP values of the proposed strength criterion for different rocks under true triaxial stress states |
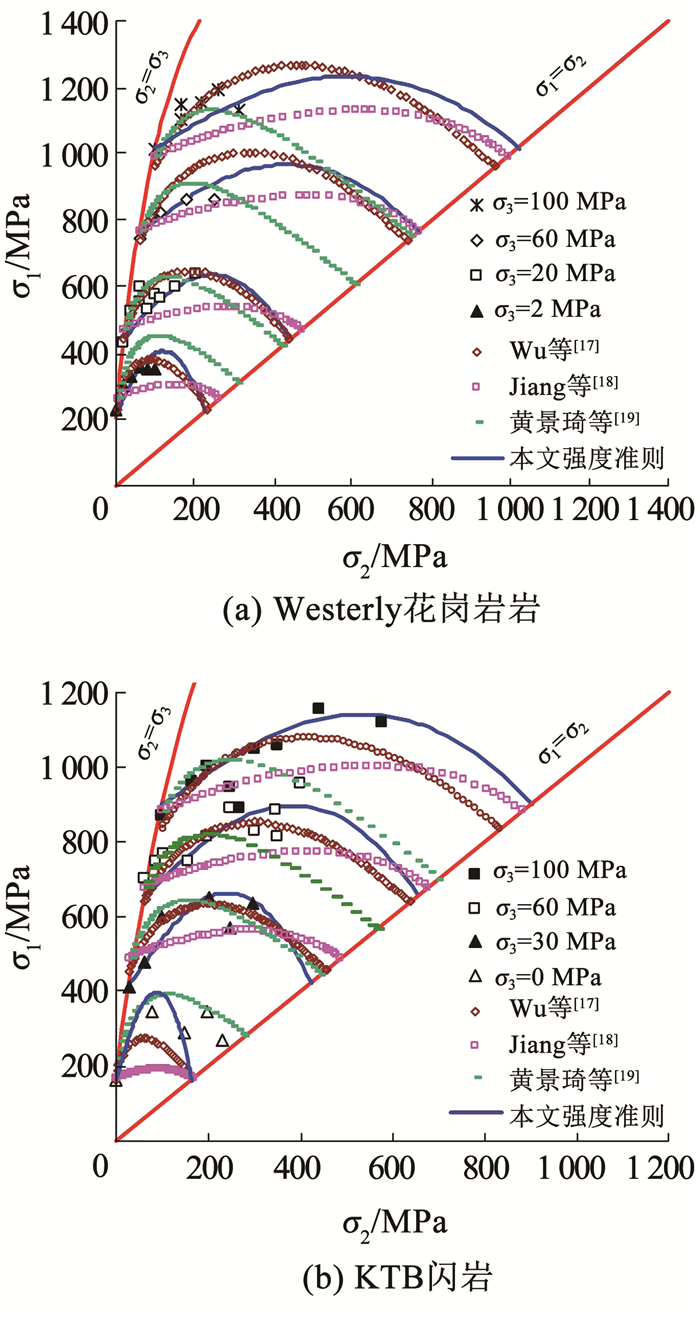
选择13号Westerly花岗岩和14号KTB闪岩为对象,对比本文强度准则与已有3种真三轴强度准则[17-19]对岩石真三轴试验强度的预测情况,分析不同强度准则之间的差异性,如图 8所示。其中,文献[17-19]均是在H-B准则基础上建立的真三轴强度准则。可以看出,4种强度准则均可描述小主应力σ3一定时中主应力σ2变化对大主应力σ1的影响规律;文献[18]所建强度准则显示σ1受σ2影响幅度很小,预测值与试验结果差距很大;文献[19]所建强度准则显示σ1在σ2较小时达到最大值后又随σ2快速减小,且多数情况下左侧压缩状态线上的σ1明显小于右侧拉伸状态线上的σ1,与实际情况不太相符;相比本文强度准则, 多数情况文献[17]所建强度准则的预测值在σ2较小时略有偏大,在σ2较大时又有所偏小,而本文所建强度准则与试验结果更为接近。综合比较,本文强度准则略优于文献[17],依次是文献[19]和文献[18]提出的强度准则。
|
图 8 不同真三轴强度准则对不同岩石强度预测的比较 Fig. 8 Comparison of prediction results of different true triaxial strength criterions for different rocks |
由平均正应力p和广义剪应力q分别与主应力之间关系可以得到p-q应力空间上强度准则子午面的变化特征;由π平面坐标轴与主应力空间坐标轴之间的关系可以得到强度准则在π平面上的空间特征,计算公式如下
| $ \left\{\begin{array}{l} p=\sigma_{\mathrm{m}}=\left(\sigma_{1}+\sigma_{2}+\sigma_{3}\right) / 3 \\ q=\sqrt{\left(\sigma_{1}-\sigma_{2}\right)^{2}+\left(\sigma_{2}-\sigma_{3}\right)^{2}+\left(\sigma_{3}-\sigma_{1}\right)^{2}} / \sqrt{2} \end{array}\right. $ | (21) |
| $ \sigma_{1}^{\prime}=\sqrt{\frac{2}{3}} \sigma_{1}, \sigma_{2}^{\prime}=\sqrt{\frac{2}{3}} \sigma_{2}, \sigma_{3}^{\prime}=\sqrt{\frac{2}{3}} \sigma_{3} $ | (22) |
式中σ′1、σ′2和σ′3分别为π平面坐标轴对应的主应力。
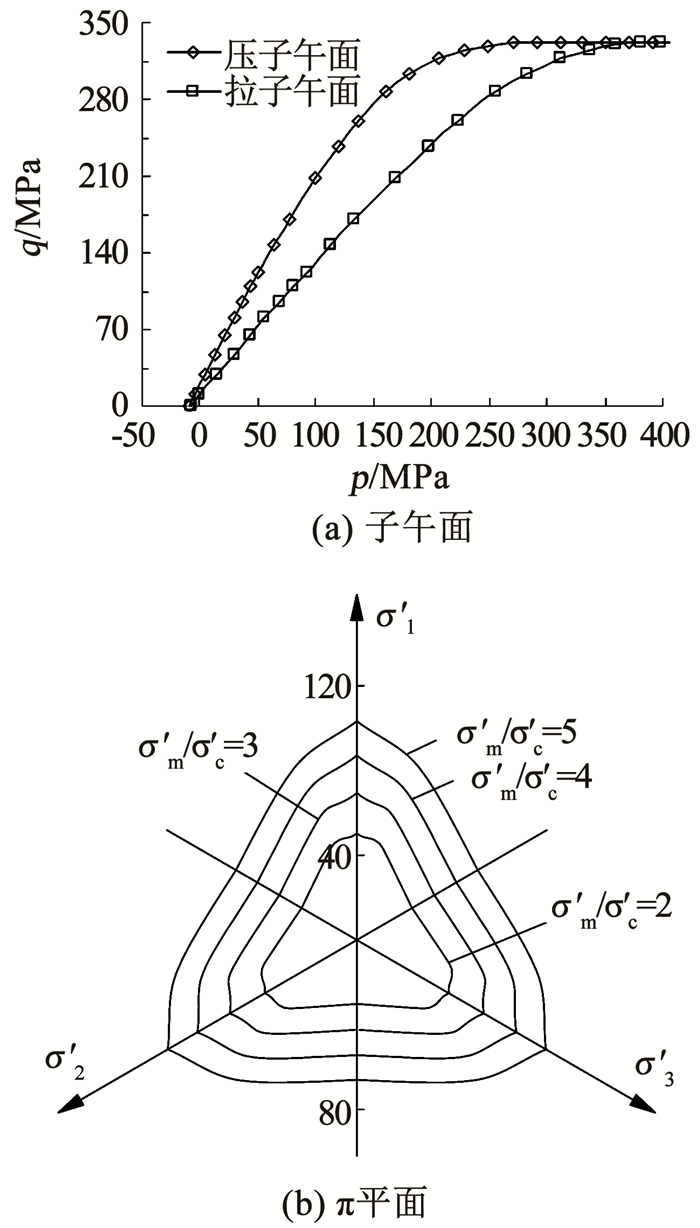
以19号Shirahama砂岩为对象,取表 2中的强度参数,所建强度准则的p-q应力空间上子午面和主应力空间偏平面上的形状特征如图 9所示。
|
图 9 本文强度准则的空间特征 Fig. 9 Space characteristics of the proposed strength criterion |
由图 9(a)可以看出,子午面上的强度曲线具有明显的非线性特征,随着静水压力的增加,拉、压子午面上的偏应力差值由零逐渐增大,再逐渐减小为零,与岩石静水压力效应一致,验证了4.2节中的分析,这也是本文强度准则优于其他强度准则的关键。由图 9(b)可以看出,本文强度准则在π平面上近似为一簇连续顶角外凸的曲线三角形,随着σ′m/σ′c的增加逐渐向外扩展,基本满足屈服面外凸的要求,拉压区间呈弧形过渡,能够反映不同应力条件下的中主应力对最大主应力的影响规律,较好地反映了中主应力效应;顶角压应力点处并不是光滑的弧形,且随着σ′m/σ′c的增加压力点处的顶角更加明显,说明平均正应力的增加会影响压应力区间上大、中和小主应力之间的分配关系。
6 结论1) 12种岩石的常规三轴试验结果对比表明,本文强度准则预测值与不同类型岩石的试验强度非常接近,所得相关性系数R2均在0.98以上,本文强度准则、指数准则、H-B准则、MM-C准则和D-P准则对12种岩石常规三轴试验强度预测所得EMAP的平均值分别为2.32%、2.43%、5.28%、7.39%和13.74%,本文强度准则略好于指数准则,后3种准则的预测精度依次降低,说明本文强度准则具有良好的普遍适用性。
2) 8种岩石的真三轴试验结果对比表明,本文强度准则与不同类型岩石的试验强度吻合程度较好,能够很好地反映大主应力随中主应力的增加呈先增大后减小的变化规律,所得R2均在0.9以上(有5种岩石的R2大于0.96),说明本文强度准则能够较好地预测不同应力状态下岩石的真三轴试验强度。
3) 本文强度准则在拉、压子午面上的偏应力差值随平均正应力由零逐渐增加再逐渐减小为零,在π平面上近似为一簇连续顶角外凸的曲线三角形,且随着平均正应力增加逐渐向外扩展,拉、压区间呈弧形过渡,很好地反映了岩石静水压力效应和中主应力对大主应力的影响规律。
| [1] |
SINGH M, SINGH B. A strength criterion based on critical state mechanics for intact rocks[J]. Rock Mechanics and Rock Engineering, 2005, 38(3): 243. DOI:10.1007/s00603-004-0042-3 |
| [2] |
YOU M. Comparison of the accuracy of some conventional trixial strength criteria for intact rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48: 852. DOI:10.1016/j.ijrmms.2011.05.006 |
| [3] |
朱合华, 张琦, 章连洋. Hoek-Brown强度准则研究进展与应用综述[J]. 岩石力学与工程学报, 2013, 32(10): 1945. ZHU Hehua, ZHANG Qi, ZHANG Lianyang. Review of research progresses and applications of Hoek-Brown strength criterion[J]. Chinese Journal of Rock Mechanics and Mining Sciences, 2013, 32(10): 1945. |
| [4] |
SINGH M, RAJ A, SINGH B. Modified Mohr-Coulomb criterion for non-linear triaxial and polyaxial strength of intact rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(4): 546. DOI:10.1016/j.ijrmms.2011.02.004 |
| [5] |
李斌. 高围压条件下岩石破坏特征及强度准则研究[D]. 武汉: 武汉科技大学, 2015 LI Bin. Study on rock failure characteristics and rock strength criteria under high confining pressure[D]. Wuhan: Wuhan University of Science and Technology, 2015 http://cdmd.cnki.com.cn/article/cdmd-10488-1015582936.htm |
| [6] |
李斌, 王大国, 刘艳章, 等. 三轴条件下改进的Hoek-Brown准则的修正[J]. 煤炭学报, 2017, 42(5): 1173. LI Bin, WANG Daguo, LIU Yanzhang, et al. Improvement of modifed Hoek-Brown criterion under conventional triaxial compression conditions[J]. Journal of China Coal Society, 2017, 42(5): 1173. |
| [7] |
AL-AJMI A M, ZIMMERMAN R W. Relation between the Mogi and the Coulomb failure criteria[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(3): 431. DOI:10.1016/j.ijrmms.2004.11.004 |
| [8] |
YAO Y, HU J, ZHOU A, et al. Unified strength criterion for soils, gravels, rocks, and concretes[J]. Acta Geotechnica, 2015, 10: 749. DOI:10.1007/s11440-015-0404-x |
| [9] |
傅鹤林, 史越, 龙燕, 等. 中主应力系数对岩石强度准则的影响[J]. 中南大学学报(自然科学版), 2018, 49(1): 158. FU Helin, SHI Yue, LONG Yan, et al. Influence of intermediate principle stress coefficient on rock strength criterion[J]. Journal of Central South University (Science and Technology), 2018, 49(1): 158. |
| [10] |
DRUNKER D C, PRAGER W. Soil mechanics and plastic analysis in limit design[J]. Quarterly of Applied Mathematics, 1952, 10: 157. DOI:10.1090/qam/48291 |
| [11] |
尤明庆. 岩石指数型强度准则在主应力空间的特征[J]. 岩石力学与工程学报, 2009, 28(8): 1541. YOU Mingqing. Characteristics of the exponential strength criterion of rock in principal stress space[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1541. DOI:10.3321/j.issn:1000-6915.2009.08.004 |
| [12] |
MOGI K. Experimental rock mechanics[M]. London: Taylor and Francis, 2007: 51.
|
| [13] |
俞茂宏. 线性和非线性的统一强度理论[J]. 岩石力学与工程学报, 2007, 26(4): 662. YU Maohong. Linear and nonlinear unified strength theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 662. DOI:10.3321/j.issn:1000-6915.2007.04.002 |
| [14] |
张强, 李诚, 郭强, 等. 指数型岩石真三轴强度准则[J]. 岩土工程学报, 2018, 40(4): 625. ZHANG Qiang, LI Cheng, GUO Qiang, et al. Exponential true triaxial strength criterial for rock[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 625. |
| [15] |
PRIEST S D. Determination of shear strength and three dimensional yield strength for the Hoek-Brown criterion[J]. Rock Mechanics and Rock Engineering, 2005, 38(6): 299. DOI:10.1007/s00603-005-0056-5 |
| [16] |
ZHANG L, ZHU H. Three-dimensional Hoek-Brown strength criterion for rocks[J]. Journal of Geothechnical and Geoenvironmental Engineering, 2007, 133(9): 1128. DOI:10.1061/(ASCE)1090-0241(2007)133:9(1128) |
| [17] |
WU S, ZHANG S, ZHANG G. Three-dimensional strength estimation of intact rocks using a modified Hoek-Brown criterion based on a new deviatoric function[J]. Journal of Rock Mechanics and Mining Sciences, 2018, 107: 181. DOI:10.1016/j.ijrmms.2018.04.050 |
| [18] |
JIANG Hua, ZHAO Jindong. A simple three-dimensional failure criterion for rocks based on the Hoeck-Brown criterion[J]. Rock Mechanics and Rock Engineering, 2015, 48(5): 1807. DOI:10.1007/s00603-014-0691-9 |
| [19] |
黄景琦, 杜修力, 马超, 等. 岩石三维强度准则的研究[J]. 工程力学, 2018, 35(3): 30. HUANG Jingqi, DU Xiuli, MA Chao, et al. Study on three-dimensional strength criterion for rocks[J]. Engineering Mechanics, 2018, 35(3): 30. |
| [20] |
HOEK E, BROWN E T. Empirical strength criterion for rock masses[J]. Journal of the Geotechnical Engineering Division, 1980, 106(9): 1013. DOI:10.1016/0022-1694(80)90029-3 |
| [21] |
HOEK E, BROWN E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics and Mining Science, 1997, 34(8): 1165. DOI:10.1016/S0148-9062(97)00305-7 |
| [22] |
YOU M. Mechanical characteristics of the exponential strength criterion under conventional triaxial stresses[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(2): 195. DOI:10.1016/j.ijrmms.2009.12.006 |
| [23] |
BARTON N. Shear strength criteria for rock, rock joints, rockfill and rock masses[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2013, 5(4): 249. DOI:10.1007/978-3-642-32814-5-1 |
 2021, Vol. 53
2021, Vol. 53


