2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
中国多年冻土分布极为广泛,其面积约为2.15×106 km2,占中国陆地总面积的22.4%[1]。多年冻土冻融过程中冰水相变导致的土体“体缩”和“体胀”现象会使地表产生变形,无论是体积收缩引起的沉降变形还是体积膨胀引起的抬升变形,均会对多年冻土区生态环境和基础设施的稳定性造成影响[2]。研究多年冻土区地表变形与影响因素间的相关关系,在丰富冻土学理论的同时可以为多年冻土区地表变形问题的深入研究提供参考。
多年冻土区地表变形有诸多监测方法,目前常用的有水准测量[3]、变形仪器测量[4-6]、GPS测量[7]等。上述方法可以获得多年冻土区单点高精度的地表变形信息,但在大时空尺度变形测量中存在很多局限性。近年来,随着遥感技术的快速发展,利用合成孔径雷达干涉技术(interferometric synthetic aperture radar,D-InSAR)对多年冻土区地表变形的监测取得了很多研究成果。有研究表明,InSAR监测结果与野外现场实测存在一定差异,但总体而言,InSAR技术为多年冻土区地表变形大时空尺度监测提供了新的方法,其监测精度可达厘米至毫米级[8-12]。
多年冻土区地表变形是诸多因素综合作用的复杂过程。国内外学者从不同的角度分析了地表变形的影响因素,并探讨了地表变形与影响因素间的关系。张建明等[5]从多年冻土区地表变形机理来源出发,指出多年冻土区路基工程地表总变形源于路堤的压密变形、活动层的冻融循环变形及冻土层的融沉变形,主要受活动层厚度、年平均地温、体积含冰量、地质构造等因素的影响,且体积含冰量越大,地表融沉变形越大。马巍等[6]结合大量的野外实测数据,对比分析得出多年冻土区地表变形演化过程与下伏多年冻土温度变化一致。董昶宏等[13]通过对比分析66个监测点野外变形数据与年平均地温、体积含冰量、气温、太阳辐射、地质条件等因素之间的关系,指出多年冻土区地表变形与年平均地温、体积含冰量、工程地质条件密切相关,且地表沉降量与体积含冰量呈正比关系。受地表变形实测数据来源限制,上述对多年冻土区地表变形影响因素及相关性的研究主要集中在单点尺度上,且主要以定性分析为主。近年来,随着遥感技术的快速发展,一些学者开展了面域范围内多年冻土区地表变形与影响因素相关性的定量分析。Zhao等[10]分析得出青藏高原多年冻土区地表变形与当地气温和降水有明显的负相关关系,相关系数分别为-0.80~-0.45和-0.95~-0.75。曾旭倩等[14]研究表明,东北多年冻土区地表变形随土壤含水量的增大而增大,且二者存在明显的正相关关系,相关系数为0.51。但总体而言,目前在面域范围内对多年冻土区地表变形与影响因素相关性的研究还很少。在全球气候持续升温和人类活动日益加剧的大背景下,多年冻土区地表变形在诸多因素的影响下将如何发展变化,是亟待探究的复杂问题。
鉴于此,首先采用InSAR技术获取了2015年6月—2019年6月间青藏工程走廊多年冻土区的地表变形信息,并利用野外实测数据对其精确度进行了验证;然后,借助GIS平台,根据经验计算模型,获取了研究区地表变形影响因素基础数据分布情况;最后,利用简单相关和偏相关分析法,探究了研究区地表变形与影响因素间的相关性,结果可为多年冻土区地表变形问题的深入研究提供科学参考。
1 研究区概况青藏工程走廊始于青海省格尔木市,止于西藏自治区拉萨市,全长约1 120 km,穿越多年冻土区约550 km,其中高温冻土约275 km,高含冰量冻土约221 km,高温高含冰量多年冻土约134 km[15]。本文以走廊内多年冻土区段(西大滩—安多)为研究区,探究多年冻土区地表变形与影响因素的相关性。如图 1所示,研究区地理坐标位于东经91°E~95°E、北纬32°N~36°N之间,海拔介于3~7 km。研究区地形地貌复杂多变,包括中高山区、高平原、盆地、低山丘陵、河谷及融区等,复杂多变的地形地貌给地表变形信息的获取带来了诸多困难。近年来持续更新的遥感影像,为获取面域范围内精确的地表变形提供了强有力的支持。

|
图 1 研究区地理位置 Fig. 1 Location of the study area |
选用欧空局(ESA)通过数据分发系统(http://scihub.copernicus.eu)提供的空间分辨率为20 m的Sentinel-1A影像数据和美国太空总署(https://nex.nasa.gov.nex/)提供的空间分辨率为30 m的高程数字模型(DEM),获取研究区地表变形信息。其中,Sentinel-1A数据的时间为2015年6月—2019年6月(其中2015年11月—2016年5月无数据),平均每月一景数据,共计43景。所有数据均为降轨数据,VV极化方式,入射角约39°的干涉宽幅工作模式下的TOPS数据。
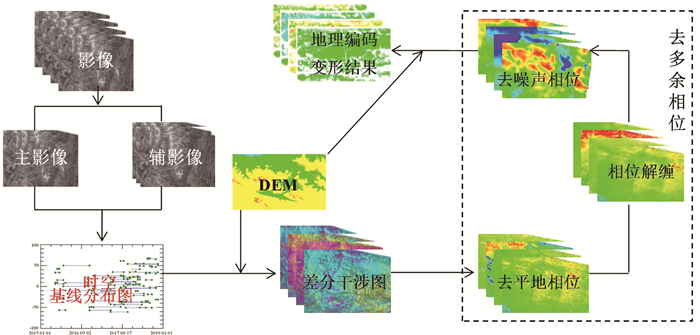
2.1.2 方法利用SBAS-InSAR技术处理收集的Sentinel-1A数据,以获取研究区地表变形。SBAS计算中,先根据时空基线阈值及多普勒频率差组合生成干涉像对,然后借助DEM数据对各像对逐一进行差分干涉运算,去除总相位中包含的地形相位和其他多余相位,获取地表变形相位(式(1)),最后利用最小二乘法或奇异分解法,根据变形相位与变形量之间的关系,获取地表时序变形[16]。图 2为SBAS技术数据处理具体流程。
| $\begin{array}{l} \Delta \varphi \left( {x, y} \right) = {\rm{ }}{\varphi _{{\rm{def}}}}\left( {x, y} \right) + {\varphi _{{\rm{DEM}}}}\left( {x, y} \right) + {\varphi _{{\rm{res}}}}\left( {x, y} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2k{\rm{ \mathsf{ π} }} \approx \frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }[d({t_{\rm{b}}}, \left( {x, y} \right)) - d({t_{\rm{a}}}, \left( {x, y} \right))] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }\frac{{{B_ \bot }\Delta H}}{{S\sin \theta }} + {\varphi _{{\rm{res}}}}\left( {x, y} \right) + 2k{\rm{ \mathsf{ π} }} \end{array}$ | (1) |
|
图 2 SBAS-InSAR数据处理流程 Fig. 2 Schematization of SBAS-InSAR method for data processing |
式中:Δφ(x, y)为差分干涉图中像元的总相位;φdef(x, y)为地表变形引起的相位;φDEM(x, y)为地表高程误差引起的相位;φres(x, y)为其他因素引起的相位,如平地相位、噪声相位等;2kπ表示相位为缠绕相位; d(ta, (x, y)) 和d(tb, (x, y))分别为ta、tb时刻影像相对于初始影像在视线向的累积变形量,初始影像变形恒为0;λ为雷达波长; B⊥为垂直基线距; ΔH为高程误差; S为视线斜距; θ为入射角。
SBAS数据处理过程中,首先根据获取数据的时空分布规律,设定其空间和时间基线阈值分别为100 m和365 d,生成干涉像对连接图。为提高监测结果的精度,逐一剔除了依据气温数据划分的冻结期(12月—次年4月)和融化期(5—11月)数据生成的连接图,仅筛选同时期干涉像对参与变形计算。其次,利用获取的DEM数据逐一对干涉图进行差分干涉处理,获取去除地形相位后的差分干涉相位图。再次,利用Goldstein滤波法去除噪声误差,提高干涉图清晰度;利用Minimum Cost Flow方法进行相位初步解缠,解缠过程中以青藏公路沿线深入多年冻结层中的桥墩为控制点,考虑到研究区变形量级相对较小,设置解缠阈值为0.2;利用空间低通三角滤波和时间高通线性滤波法去除大气延迟相位,以获取精确的地表变形相位信息。最后,利用最小二乘法计算研究区地表变形量,为保证计算结果的精确性,仅对相干系数大于0.5的高相干性像元进行了计算,并利用DEM数据对结果进行地理编码。对于没有参与变形计算的低相干点(相干系数小于0.5),利用克里金插值法进行差值计算[17],从而得到整个研究区的地表变形分布图。
2.2 地表变形结果图 3为利用SBAS-InSAR方法,结合Sentinel-1A数据获取的研究区地表年变形速率分布,正值表示地表呈现向上的抬升速率,负值表示地表呈现向下的沉降速率。可以看出,研究区地表变形空间分布差异大,年变形速率介于-33~15 mm/a,这可能与地质条件、局地冻土特征等因素有关。但就整个研究区而言,地表有缓慢下沉趋势,整个研究区地表年变形速率的平均值为-13 mm/a,这与前人基于野外实测数据的分析结果一致[5, 18]。

|
图 3 研究区地表年变形速率分布 Fig. 3 Distribution of ground surface annual deformation rate in study area |
此外,从图 3可以看出,研究区大部分地区相对稳定,地表年变形速率较小,在楚玛尔河高平原、五道梁、沱沱河、通天河及安多等区域,地表存在较大的年变形速率,且以沉降速率为主,这可能与气温升高背景下研究区内多年冻土的年平均地温升高和冰融化等因素有关。
2.3 精度验证为验证InSAR监测结果的精确性,获取了同时期野外4个监测点(见图 1)的现场实测变形数据。变形测量用沉降杆,观测采用水准仪进行人工定期观测。由图 4可以看出,4个监测点现场测量值与InSAR测量值之间的绝对误差分别为1.4~12.6、1.6~15.3、1.2~9.4、1.3~38.2 mm,平均绝对误差分别为9.8、7.2、4.3、7.9 mm。可以看出,对于监测点1、2和3,两种监测结果间的绝对误差范围均较小,而监测点4,大部分时间点的绝对误差较小,个别时间点的绝对误差较大,可达38.2 mm,这可能与局地降水等因素有关。但总体而言,InSAR监测的多年冻土区地表变形与野外现场监测数据较吻合,4个监测点的平均绝对误差均小于10 mm,结果可信度高,可用于后续地表变形与影响因素相关性的分析。

|
图 4 InSAR监测与现场监测地表变形结果对比 Fig. 4 Comparison of ground surface deformation results between InSAR measurement and in-situ observation |
研究结果显示,多年冻土区地表总变形主要由活动层的冻融循环变形、多年冻土上限处的融沉变形以及多年冻土层的蠕变变形组成[5]。其中冻融循环变形是多年冻土冻融过程中土结构受冷生作用影响产生的,与活动层的厚度关系最为密切[5]。融沉变形主要是土中冰融化后多年冻土上限下移造成的,与体积含冰量密切相关[18]。蠕变变形是多年冻土升温导致土物理力学性质改变而产生的,主要与年平均地温有关[6]。由此可见,活动层厚度、体积含冰量及年平均地温是影响多年冻土区地表变形的主要因素。鉴于此,主要探讨地表变形与这3个影响因素间的相关关系。
3.1 活动层厚度活动层厚度是指地表至多年冻土上限处的深度,其计算方法众多[19-21]。本文研究区的活动层厚度分布采用庞强强等根据野外实测数据校正得到的模型[21]计算:
| $h = \sqrt {\frac{{2{\lambda _{\rm{f}}}I}}{{L{\gamma _{{\rm{ck}}}}(W - {W_{\rm{u}}})}}} $ | (2) |
式中:h为活动层厚度,m;λf为土体导热系数,W/(m·℃);L为冰融化潜热,L=3.3×105 J/kg;γck为土体干容重,kg/m3;W为土体中总的体积含水量,%;Wu为土体中的未冻水体积分数,%。各参数具体取值见文献[21]。I为多年冻土区地表的融化指数(℃·d),计算过程如下:
| $\left\{ \begin{array}{l} I = {t_{\rm{s}}} \times {L_{\rm{s}}}\\ {L_{\rm{s}}} = 365(\beta /{\rm{ \mathsf{ π} }}), {\rm{ }}{t_{\rm{s}}} = {t_{\rm{m}}} + \alpha (\sin \beta /\beta )\\ \alpha = ({t_{\rm{w}}} - {t_{\rm{c}}})/2, {\rm{ }}\beta = {\cos ^{ - 1}}( - {t_{\rm{m}}}/\alpha )\\ {t_{\rm{m}}} = 62.434 - 0.152E - 0.768N - 0.004\;63H\\ {t_{\rm{c}}} = 56.086 - 0.042E - 1.579N - 0.004\;57H\\ {t_{\rm{w}}} = 69.443 - 0.371E - 0.035N - 0.004\;78H \end{array} \right.$ | (3) |
式中:E和N分别为十进制表示的经度(°)和纬度(°),H为地表高程(m),tm为地表的年平均温度(℃),tc为最冷月份地表的月平均温度(℃),tw为最暖月份地表的月平均温度(℃)。图 5(a)为计算得到的研究区活动层厚度分布。

|
图 5 青藏工程走廊地表变形影响因素分布 Fig. 5 Distribution of influential factors on ground surface deformation along QTEC |
年平均地温指地温年变化深度(即多年冻土年较差为零)处的地温,是反应多年冻土变化动态和划分冻土带的主要指标之一[22]。诸多学者根据年平均地温与纬度、经度、高程等因素间的相关关系,建立了青藏高原年平均地温计算模型[22-24]。基于GIS平台,利用经验模型[24]获取研究区年平均地温的分布:
| $t = 50.633 - 0.830N - 0.005H$ | (4) |
式中:t表示年平均地温(℃),N和H分别表示纬度(°)和地表高程(m)。计算结果如图 5(b)所示。
3.3 体积含冰量体积含冰量主要是指多年冻土上限附近处的体积含冰量。学者们基于野外实测数据建立了体积含冰量计算模型[25-26]。利用下述模型计算研究区的体积含冰量[26]:
| ${I_{\rm{v}}} = 0.34 \times {S_{\rm{T}}} + 0.29 \times {I_{{\rm{NDV}}}} + 0.24 \times {S_{\rm{D}}} + 0.13 \times t$ | (5) |
式中:Iv表示体积含冰量(%);ST表示土质类型,由中国科学院南京土壤研究所提供,并根据土体导热系数对土质进行赋值[21];SD表示地表坡度信息,通过美国太空总署提供的30 m精度的数字高程模型(DEM)提取得到;INDV表示地表植被覆盖归一化指数,利用Landsat数据借助ENVI平台提取;t表示年平均地温,通过式(4)计算。式中ST、SD、INDV和t均为利用GIS平台得到的归一化值(无量纲)。根据式(5)对各变量进行叠加,计算的研究区体积含冰量分布图如5(c)所示。
4 多年冻土区地表变形与影响因素相关性 4.1 相关性分析方法目前,大时空尺度范围内多变量相关性研究最常用的方法有简单相关分析和偏相关分析。简单相关分析可以确定两个变量间的线性相关性,但该结果随其他变量的变化而变化[27]。偏相关分析是在控制或消除其他变量影响的条件下,衡量两个变量间的净相关关系[27]。各相关系数具体计算如下。
4.1.1 简单相关系数计算| ${R_{xy}} = \frac{{\sum\limits_{i = 1}^n {\left[ {\left( {{x_i} - \bar x} \right)\left( {{y_i} - \bar y} \right)} \right]} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}\sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} } } }}$ | (6) |
式中:Rxy为两个变量的相关系数,x, y和
| ${r_{xy.z}} = \frac{{{r_{xy}} - {r_{xz}}{r_{yz}}}}{{\sqrt {\left( {1 - r_{xz}^2} \right)\left( {1 - r_{yz}^2} \right)} }}$ | (7) |
式(7)也称一阶偏相关系数,用于分析3个变量间的偏相关性。其中rxy.z为将变量z消除后变量x与y之间的偏相关系数,rxy、rxz、ryz分别为变量x与y、x与z及y与z间的简单相关系数。4个及以上变量间的高阶偏相关系数计算公式如下:
| ${r_{xy.{z_1}{z_2} \ldots {z_m}}} = \frac{{{r_{xy.{z_1}{z_2} \ldots {z_{m - 1}}}} - {r_{x{z_m}.{z_1}{z_2} \ldots {z_{m - 1}}}}{r_{y{z_m}.{z_1}{z_2} \ldots {z_{m - 1}}}}}}{{\sqrt {\left( {1 - r_{x{z_m}.{z_1}{z_2} \ldots {z_{m - 1}}}^2} \right)\left( {1 - r_{y{z_m}.{z_1}{z_2} \ldots {z_{m - 1}}}^2} \right)} }}$ | (i) |
显著性检验用于反映样本统计量和假设总体参数间的显著性差异[27]。检验中运用小概率原理,事先假定判断界限,即显著性水平(α=0.05)。当计算的显著性概率(P)小于α时,两个变量间存在显著相关性,反之两个变量间无显著相关性。
4.2 地表变形与影响因素相关性图 6为逐区域统计计算的各像元地表变形随影响因素的变化关系。可以看出,研究区地表年变形速率随体积含冰量增大而增大,在体积含冰量小于10%的区域,年变形速率均值为-8 mm/a,在体积含冰量大于50%的区域,年变形速率均值增至-17 mm/a。同时可以看出,地表年变形速率随年平均地温的升高增幅明显,在年平均地温低于-2 ℃的区域,地表年变形速率均值为-11 mm/a;在年平均地温介于-0.5 ~0 ℃时,地表年变形速率均值为-19 mm/a。此外,地表年变形速率随活动层厚度的增大而增大,但增幅不明显,在活动层厚度小于2 m的区域,年变形速率均值为-14 mm/a;在活动层厚度大于4 m的区域,年变形速率均值为-18 mm/a。

|
图 6 研究区地表年变形速率随影响因素变化 Fig. 6 Variation of ground surface annual deformation rate with influential factors in study area |
由图 6可以看出,多年冻土区地表年变形速率随3个影响因素的增大而增大,且随体积含冰量和年平均地温的增大幅度较活动层厚度明显,这与前人得出的年平均地温和体积含冰量是导致多年冻土区地表融沉的主要原因的结论一致[5-6]。上述分析显示了地表变形与影响因素间的变化关系,但无法体现地表变形与影响因素的相关程度。为进一步定量分析地表变形与影响因素间的相关性,逐区域逐像元统计计算地表变形与影响因素间的简单相关系数及偏相关系数。
4.2.1 地表变形与影响因素简单相关分析表 1~3为研究区地表年变形速率与影响因素在不同区域的简单相关系数(R)。由表 1可以看出,当含冰量高于30%时,多年冻土区地表变形与体积含冰量之间存在密切关系,简单相关系数大于0.8,相应的P<0.05。而在其他体积含冰量区域相关性较差,简单相关系数介于0.2~0.6,P均大于0.05。总体而言,多年冻土区地表变形与体积含冰量具有正强相关关系,平均简单相关系数为0.61。
| 表 1 地表变形与不同体积含冰量简单相关系数 Tab. 1 Simple correlation coefficient between ground surface deformation and volume ice content |
| 表 2 地表变形与不同年平均地温简单相关系数 Tab. 2 Simple correlation coefficient between ground surface deformation and mean annual ground temperature |
| 表 3 地表变形与不同活动层厚度简单相关系数 Tab. 3 Simple correlation coefficient between ground surface deformation and active layer thickness |
如表 2所示,在年平均地温高于-1 ℃的区域,地表变形与年平均地温关系密切,简单相关系数大于0.8,相应的P<0.05。在年平均地温低于-1 ℃的区域,二者间的简单相关系数介于0.2~0.6,P均大于0.05,说明相关性不显著。与体积含冰量相似,多年冻土区地表变形与年平均地温具有正强相关关系,平均简单相关系数为0.64。
由表 3可知,多年冻土区地表变形与活动层厚度呈现一定的相关性,在小于3.0 m区间范围内,二者存在弱相关关系,简单相关系数介于0.2~0.4。在3.0 m以上区间,二者简单相关系数介于0.4~0.6,有中等相关性。除4.0 m以上活动层厚度,其他区域的P均大于0.05,表明相关性不显著。总体而言,多年冻土区地表变形与活动层厚度具有正弱相关关系,平均简单相关系数为0.38。
4.2.2 地表变形与影响因素偏相关分析表 4~6为地表变形与影响因素在不同区域的偏相关系数(r)。由表 4可知,去除活动层厚度和年平均地温因素的影响后,当体积含冰量高于30%时,多年冻土区地表变形与体积含冰量依然存在极强正相关关系,偏相关系数大于0.8,相应的P<0.05。但与简单相关分析结果不同的是,在体积含冰量为10%~20%和20%~30%的区域,地表变形与体积含冰量的相关关系显著,偏相关系数介于0.6~0.8,相比简单相关系数有明显的增幅。此外,在体积含冰量低于10%的区域,虽偏相关系数相比简单相关系数有所增大,但地表变形与体积含冰量的关系仍不显著,P>0.05。总体而言,去除活动层厚度和年平均地温的影响后,多年冻土区地表变形与体积含冰量之间存在正强相关关系,平均偏相关系数为0.75。
| 表 4 地表变形与不同体积含冰量偏相关系数 Tab. 4 Partial correlation coefficient between ground surface deformation and volume ice content |
| 表 5 地表变形与不同年平均地温偏相关系数 Tab. 5 Partial correlation coefficient between ground surface deformation and mean annual ground temperature |
| 表 6 地表变形与不同活动层厚度偏相关系数 Tab. 6 Partial correlation coefficient between ground surface deformation and active layer thickness |
由表 5可以看出,去除活动层厚度和体积含冰量因素的影响后,在年平均地温高于-1 ℃区域,多年冻土区地表变形与年平均地温仍具有显著相关关系,偏相关系数大于0.8,相应的P<0.05。在年平均地温低于-2 ℃的区域,二者间的相关性仍不显著,偏相关系数介于0.2~0.4,P>0.05。与简单相关分析结果不同的是,在年平均地温介于-2~-1 ℃时,地表变形与年平均地温的相关性明显增强,二者存在正强相关关系,相比简单相关系数,偏相关系数增幅明显,约为0.62。总体而言,去除活动层厚度和体积含冰量影响后,多年冻土区地表变形与年平均地温间存在正强相关关系,平均偏相关系数为0.70。
如表 6所示,去除体积含冰量和年平均地温因素的影响后,多年冻土区地表变形与活动层厚度的相关关系变化不大,在3.0 m以上活动层厚度区间,二者有正中等相关关系,偏相关系数介于0.4~0.6。在3.0 m以下活动层厚度区间,二者相关性不显著,P>0.05。与简单相关分析结果不同的是,在活动层厚度为3.0~4.0 m时,多年冻土区地表变形与活动层厚度相关性显著,P<0.05。总体而言,去除体积含冰量和年平均地温影响后,多年冻土区地表变形与活动层厚度间存在正中等相关关系,平均偏相关系数为0.42。
综上,在体积含冰量大于30%、年平均地温高于-1 ℃的多年冻土区,地表变形与影响因素存在强相关性,偏相关系数均大于0.8,P<0.05。在体积含冰量为10%~30%、年平均地温为-2~-1 ℃、活动层厚度大于3 m的多年冻土区,地表变形与影响因素存在较强的相关性,偏相关系数介于0.4~0.8,P<0.05。而在其他区域,地表变形与影响因素间的相关关系较弱,偏相关系数介于0~0.4,P>0.05。但总体而言,多年冻土区地表变形与体积含冰量和年平均地温均存在正强相关关系,平均偏相关系数分别为0.75和0.70。而多年冻土区地表变形与活动层厚度间的相关性较差,二者存在正中等相关关系,偏相关系数为0.42。由此可以看出,多年冻土区地表变形与体积含冰量和年平均地温的相关性较强,与活动层厚度的相关性较弱,且前两者的相关性明显强于后者。
对比多年冻土区地表变形与影响因素的简单相关分析和偏相关分析结果,可以看出二者间存在较大的差异。主要表现为去除其他两个因素的影响后,地表变形与影响因素净相关系数(偏相关系数)相比综合相关系数(简单相关系数)明显增大。这也说明了由于不同变量间的复杂相关关系,简单相关分析在一定程度上增强或削弱了地表变形与影响因素间的相关性,而偏相关分析通过去除多余因素的影响,更好地揭示了多年冻土区地表变形与不同因素间的相关关系。
5 结论1) 研究区地表变形空间差异大,年变形速率介于-33~15 mm/a,但整个研究区的地表年变形速率均值为-13 mm/a,地表有缓慢下沉趋势。InSAR监测结果有较高的可信度,与野外4个监测点现场实测数据的平均绝对误差分别为9.8、7.2、4.3、7.9 mm,均小于10 mm。
2) 在体积含冰量大于30%、年平均地温高于-1 ℃的多年冻土区,地表变形与影响因素存在强相关性。在体积含冰量介于10%~30%、年平均地温介于-2~-1 ℃、活动层厚度大于3 m的多年冻土区,地表变形与影响因素存在较强的相关性。在其他区域,地表变形与影响因素间的相关性较弱。
3) 多年冻土区地表变形与体积含冰量存在正强相关关系,简单相关系数和偏相关系数均值分别为0.61和0.75。多年冻土区地表变形与年平均地温也存在正强相关关系,简单相关系数和偏相关系数均值分别为0.64和0.70。多年冻土区地表变形与活动层厚度相关性较弱,简单相关系数和偏相关系数均值为0.38和0.42。
4) 总体而言,多年冻土区地表变形与体积含冰量和年平均地温的相关性较强,与活动层厚度的相关性较弱,且前两者的相关性明显强于后者。
| [1] |
周幼吾, 郭东信, 邱国庆, 等. 中国冻土[M]. 北京: 科学出版社, 2000. ZHOU Youwu, GUO Dongxin, QIU Guoqing, et al. Geocryology in China[M]. Beijing: Science Press, 2000. |
| [2] |
张中琼, 吴青柏, 周兆叶. 多年冻土区冻融灾害风险性评价[J]. 自然灾害学报, 2012, 21(2): 142. ZHANG Zhongqiong, WU Qingbai, ZHOU Zhaoye. Risk assessment of freeze thawing disaster in permafrost zone[J]. Journal of Natural Disasters, 2012, 21(2): 142. |
| [3] |
刘永智, 吴青柏, 张建明, 等. 青藏高原多年冻土地区公路路基变形[J]. 冰川冻土, 2002, 24(1): 10. LIU Yongzhi, WU Qingbai, ZHANG Jianming, et al. Deformation of highway roadbed in permafrost regions of the Tibetan Plateau[J]. Journal of Glaciology and Geocryology, 2002, 24(1): 10. DOI:10.3969/j.issn.1000-0240.2002.01.002 |
| [4] |
刘尧军, 岳祖润, 李忠. 青藏铁路高原冻土区段路基沉降变形和地温监测[J]. 铁道标准设计, 2003(4): 26. LIU Yaojun, YUE Zurun, LI Zhong. Monitoring the deformation and temperature of embankment in permafrost regions of Qinghai-Tibet Railway[J]. Railway Standard Design, 2003(4): 26. DOI:10.3969/j.issn.1004-2954.2003.04.011 |
| [5] |
张建明, 刘端, 齐吉琳. 青藏铁路冻土路基沉降变形预测[J]. 中国铁道科学, 2007(3): 12. ZHANG Jianming, LIU Duan, QI Jilin. Estimation on the settlement and deformation of embankment along Qinghai-Tibet Railway in permafrost regions[J]. China Railway Science, 2007(3): 12. DOI:10.3321/j.issn:1001-4632.2007.03.003 |
| [6] |
马巍, 刘端, 吴青柏. 青藏铁路冻土路基变形监测与分析[J]. 岩土力学, 2008, 29(3): 571. MA Wei, LIU Duan, WU Qingbai. Monitoring and analysis of embankment deformation in permafrost regions of Qinghai-Tibet Railway[J]. Rock and Soil Mechanics, 2008, 29(3): 571. DOI:10.16285/j.rsm.2008.03.005 |
| [7] |
MA Fuxun, XI Ruijie, XU Nan. Analysis of railway subgrade frost heave deformation based on GPS[J]. Geodesy and Geodynamics, 2016, 7(2): 143. DOI:10.1016/j.geog.2016.04.001 |
| [8] |
李震, 李新武, 刘永智, 等. 差分干涉SAR冻土形变检测方法研究[J]. 冰川冻土, 2004, 26(4): 389. LI Zhen, LI Xinwu, LIU Yongzhi, et al. Detecting the displacement field of thaw settlement by means of SAR interferometry[J]. Journal of Glaciology and Geocryology, 2004, 26(4): 389. DOI:10.3969/j.issn.1000-0240.2004.04.003 |
| [9] |
RYKHUS R, LU Z. InSAR detects possible thaw settlement in the Alaskan Arctic Coastal Plain[J]. Canadian Journal of Remote Sensing, 2008, 34(2): 100. DOI:10.5589/m08-018 |
| [10] |
ZHAO Rong, LI Zhiwei, FENG Guangcai, et al. Monitoring surface deformation over permafrost with an improved SBAS-InSAR algorithm: with emphasis on climatic factors modeling[J]. Remote Sensing of Environment, 2016, 184: 276. DOI:10.1016/j.rse.2016.07.019 |
| [11] |
周华云, 赵林, 田黎明, 等. 基于Sentinel-1数据对青藏高原五道梁多年冻土区地面形变的监测与分析[J]. 冰川冻土, 2019, 41(3): 525. ZHOU Huayun, ZHAO Lin, TIAN Liming, et al. Monitoring and analysis of surface deformation in the permafrost area of Wudaoliang on the Tibetan Plateau based on Sentinel-1 data[J]. Journal of Glaciology and Geocryology, 2019, 41(3): 525. DOI:10.7522/j.issn.1000-0240.2019.0072 |
| [12] |
张正加. 高分辨率SAR数据青藏高原冻土环境与工程应用研究[D]. 北京: 中国科学院遥感与数字地球研究所, 中国科学院大学, 2017 ZHANG Zhengjia. Research on Qinghai-Tibet permafrost environment and engineering using high resolution SAR images[D]. Beijing: Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, 2017 http://cdmd.cnki.com.cn/article/cdmd-80070-1017720991.htm |
| [13] |
董昶宏, 赵相卿. 青藏铁路多年冻土区路基变形特征及影响因素分析[J]. 铁道标准设计, 2013(6): 5. DONG Changhong, ZHAO Xiangqing. Analysis on subsidence deformation features and influence factors in permafrost regions on Qinghai-Tibet Railway[J]. Highway Standard Design, 2013(6): 5. DOI:10.13238/j.issn.1004-2954.2013.06.003 |
| [14] |
曾旭婧. 基于Sentinel-1A的北黑高速路段多年岛状冻土变形研究[D]. 哈尔滨: 东北林业大学, 2017 ZENG Xujing. Monitoring island permafrost deformation over Bei′an-Heihe expressway based on Sentinel-1A data[D]. Harbin: Northeast Forestry University, 2017 http://cdmd.cnki.com.cn/article/cdmd-10225-1018800585.htm |
| [15] |
柴明堂, 张建明, 穆彦虎, 等. 青藏公路多年冻土区路基病害易发性概率模型[J]. 长安大学学报(自然科学版), 2017, 37(4): 76. CHAI Mingtang, ZHANG Jianming, MU Yanhu, et al. Probability model for subgrade hazards susceptibility of Qing-Tibet Highway in permafrost[J]. Journal of Chang′an University (Natural Science Edition), 2017, 37(4): 76. DOI:10.19721/j.cnki.1671-8879.2017.04.010 |
| [16] |
BERARDINO P, FORNARO G, LANARI R, et al. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2375. DOI:10.1109/TGRS.2002.803792 |
| [17] |
VANBEERS W C M, KLEIJNEN J P C. Kriging for interpolation in random simulation[J]. Journal of the Operational Research Society, 2003, 54(3): 255. DOI:10.1057/palgrave.jors.2601492 |
| [18] |
YU Fan, QI Jilin, YAO Xiaoliang, et al. In-situ monitoring of settlement at different layers under embankments in permafrost regions on the Qinghai-Tibet Plateau[J]. Engineering Geology, 2013, 160: 44. DOI:10.1016/j.enggeo.2013.04.002 |
| [19] |
KUDRYAVTSEV V A. Principles of permafrost forecasting during engineering and geocryological investigations (in Chinese)[M]. Lanzhou: Lanzhou University Press, 1992: 67.
|
| [20] |
NELSON F E, SHIKLOMANOV N I, MUELLER G R, et al. Estimating active-layer thickness over a large region: Kuparuk River basin, Alaska, USA[J]. Arctic and Alpine Research, 1997, 29(4): 367. DOI:10.2307/1551985 |
| [21] |
庞强强, 李述训, 吴通华, 等. 青藏高原冻土区活动层厚度分布模拟[J]. 冰川冻土, 2006(3): 390. PANG Qiangqiang, LI Shuxun, WU Tonghua, et al. Simulated distribution of active layer thickness in frozen ground regions of Tibet Plateau[J]. Journal of Glaciology and Geocryology, 2006(3): 390. DOI:10.3969/j.issn.1000-0240.2006.03.014 |
| [22] |
吴青柏, 李新, 李文君. 青藏公路沿线冻土区域分布计算机模拟与制图[J]. 冰川冻土, 2000, 22(4): 323. WU Qingbai, LI Xin, LI Wenjun. Compute simulation and mapping of the regional distribution of permafrost along the Qinghai-Xizang highway[J]. Journal of Glaciology and Geocryology, 2000, 22(4): 323. DOI:10.3969/j.issn.1000-0240.2000.04.005 |
| [23] |
鲁嘉濠, 牛富俊, 林战举, 等. 考虑局地因素坡向影响的青藏高原工程走廊冻土分布与制图研究[J]. 地理与地理信息科学, 2012, 28(3): 63. LU Jiahao, NIU Fujun, LIN Zhanju, et al. Permafrost modeling and mapping along the Qinghai-Tibet engineering corridor considering slope-aspect[J]. Journal of Glaciology and Geocryology, 2012, 28(3): 63. |
| [24] |
南卓铜, 李述训, 刘永智. 基于年平均地温的青藏高原冻土分布制图及应用[J]. 冰川冻土, 2002(2): 142. NAN Zhuotong, LI Shuxun, LIU Yongzhi. Mean annual ground temperature distribution on the Tibetan Plateau: permafrost distribution mapping and further application[J]. Journal of Glaciology and Geocryology, 2002(2): 142. DOI:10.3969/j.issn.1000-0240.2002.02.006 |
| [25] |
吴青柏, 董献付, 刘永智. GIS支持下的青藏公路沿线高含冰量冻土空间分布模型[J]. 冰川冻土, 2004, 增刊1(137). WU Qingbai, DONG Xianfu, LIU Yongzhi. Spatial distribution model of high ice content frozen soil along Qinghai-Xizang highway-A GIS aided model[J]. Journal of Glaciology and Geocryology, 2004, 增刊1(S1): 137. DOI:10.3969/j.issn.1000-0240.2004.z1.024 |
| [26] |
ZHANG Zhongqiong, WU Qingbai. Thermal hazards zonation and permafrost change over the Qinghai-Tibet Plateau[J]. Natural Hazards, 2012, 61(2): 403. DOI:10.1007/s11069-011-9923-4 |
| [27] |
赵明扬, 孙长忠, 康磊. 偏相关系数在林冠截留影响因子分析中的应用[J]. 西南林业大学学报, 2013, 33(2): 61. ZHAO Mingyang, SUN Changzhong, KANG Lei. Application of partial correlation coefficient to canopy interception impacting factor analysis[J]. Journal of Southwest Forestry University, 2013, 33(2): 61. |
 2021, Vol. 53
2021, Vol. 53


