2. 中国人民解放军军事科学院 国防科技创新研究院,北京 100071
2. National Innovation Institute of Defense Technology, Academy of Military Sciences PLA China, Beijing 100071, China
碰撞角约束(impact angle constraints, IAC)可以有效提高导弹对目标的打击效果,对防御武器也具有很好的突防效果(例如垂直打击),是当前导弹制导领域研究的重点问题之一[1]。
碰撞角约束制导律(impact angle constrained guidance law, IACG)通常由比例导引律(proportional navigation, PN)加上碰撞角偏差控制项组成,目的是使碰撞角偏差在终点时刻收敛至极小值[2]。最优控制理论是设计IACG的主要方法之一。Zarchan[3]基于施瓦茨不等式,推导了一种碰撞角约束最优制导律,称为“弹道成型制导律”(trajectory shaping guidance law, TSG)。陈克俊等[4]基于线性二次型最优控制理论,推导了一种落角约束最优制导律。然而,上述2种制导律都不能使导弹指令过载在拦截时刻收敛至0。最近,He等[5]基于最优误差动力学理论,提出了可使导弹指令过载在命中时刻收敛至0的一种碰撞角约束最优制导律(impact angle constrained optimal guidance law,IACOG),可增强导弹在末段对干扰的鲁棒性,提高了制导律的实用性。
滑模控制对系统的干扰和不确定性具有较强的鲁棒性,很多学者基于高阶滑模控制理论,提出了多种碰撞角约束滑模制导律(impact angle constrained sliding mode guidance law,IACSMG)[6-8]。近期,同时满足飞行时间约束和碰撞角约束的制导律设计逐渐成为导弹制导领域研究的热点问题[9-10]。
然而目前已有的各种IACG仍然存在一些缺陷,例如:IACOG的推导过程通常基于线性化假设,并且引入了剩余飞行时间估计[5],导致制导律性能并非理论上的全局有效;IACSMG的指令加速度形式较为复杂,且引入的测量量较多,使其实用性受到限制[6-10]。
实际上,仅使用经典纯比例导引律(PPN)就可以实现对固定目标的碰撞角约束制导。Lu等[11]首先基于PPN表达式的直接积分,提出了变比例导引系数的三维碰撞角约束PPN制导策略,可适用于变速飞行器。胡正东等[12]在此基础上进一步推导了以高度为特征变量的垂直打击三维自适应PPN。然而,上述2种方法未深入探究PPN打击固定目标的解析解, 可能导致某些应用上的不便。
本文基于PPN拦截固定目标的解析解,重新设计三维空间中的碰撞角约束制导律。PPN的指令加速度垂直于导弹速度矢量[13],在拦截固定目标时,导弹速度矢量与弹目相对速度矢量重合。根据PN的统一方法[14],可以认为此时PPN与理想比例导引律(ideal proportional navigation law,IPN)[15]是等价的。IPN在拦截非机动目标时有解析解,因而可以基于此直接得到PPN拦截固定目标的解析解。文献[16]基于以上方法,设计了基于PPN的二维碰撞角约束制导律(2D-PPNIACG)。
本文在文献[16]的基础上,首先深入分析了2D-PPNIACG对固定目标的拦截制导性能,包括最大过载、能量消耗和捕获区域。然后基于对空间几何关系的深入分析和合理近似,提出了在俯冲平面和转弯平面同时实现碰撞角约束的基于PPN的三维碰撞角约束制导律(3D-PPNIACG)。最后通过数值仿真算例,验证了所提出制导律的有效性与可靠性。
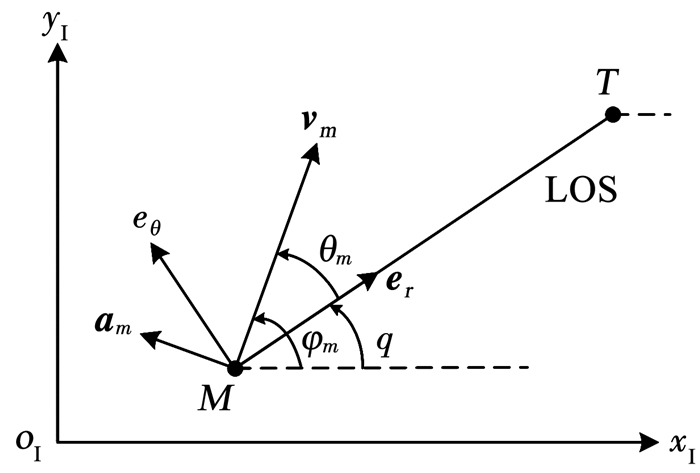
1 二维PPNIACG回顾二维拦截几何如图 1所示。oI-xIyI为参考惯性系,q为视线角;er为视线方向单位矢量,由OIXI轴逆时针旋转角度q得到;eθ为垂直于视线方向的单位矢量,由er逆时针旋转90°获得;vm为导弹(用下标m来表示)速度矢量,vm为导弹的速度大小;φm为导弹速度倾角,以逆时针方向为正;am为导弹加速度矢量,am为导弹加速度大小;θm=φm-q为导弹前置角。
|
图 1 二维拦截几何 Fig. 1 Two-dimensional engagement geometry |
在动坐标系(er, eθ)内构建的二维相对运动方程为
| $ \left\{\begin{array}{l} \ddot{r}-r \omega_{s}^{2}=a_{t r}-a_{m r} \\ \dot{r \omega}_{s}+2 \dot{r} \omega_{s}=a_{t \theta}-a_{m \theta} \end{array}\right. $ | (1) |
式中:r为弹目相对距离,q为视线角,ωs=
| $ \left\{\begin{array}{l} v_{m} \cos \theta_{m}=-\dot{r}=-v_{r} \\ v_{m} \sin \theta_{m}=-r \dot{q}=-v_{\theta} \end{array}\right. $ | (2) |
PN的统一结构为[14]
| $ \boldsymbol{a}_{\mathrm{PN}}=N \boldsymbol{L} \times \boldsymbol{\omega}_{s} $ | (3) |
式中L为参考速度矢量。对于PPN,有L=-vm。
当目标固定时,有
| $ \boldsymbol{v}_{t}=0, \boldsymbol{a}_{t}=0 $ | (4) |
因而有
| $ \boldsymbol{v}=\boldsymbol{v}_{t}-\boldsymbol{v}_{m}=-\boldsymbol{v}_{m}=\dot{r} \boldsymbol{e}_{r}+{r} \dot{q}\boldsymbol{e}_{\theta} $ | (5) |
因此也可将PPN的指令加速度写为
| $ \boldsymbol{a}_{\mathrm{PPN}}=N\left(-\boldsymbol{v}_{m}\right) \times \boldsymbol{\omega}_{s}=\dot{N} q\left(r \dot{q} \boldsymbol{e}_{r}-\dot{r} \boldsymbol{e}_{\theta}\right) $ | (6) |
将式(4)和式(6)代入式(1),相对运动方程变为
| $ \left\{\begin{array}{l} \ddot{r}-r \dot{q}^{2}=-N \dot{r} \dot{q}^{2} \\ r \ddot{q}+2 \dot{r} \dot{q}=N \dot{r} \dot{q} \end{array}\right. $ | (7) |
由式(7)的第2式可推导出:
| $ \dot{q}=\dot{q}_{0}\left(\frac{r}{r_{0}}\right)^{(N-2)} $ | (8) |
式中:
再将式(8)代入式(7)的第1式,可推导出:
| $ \dot{r}^{2}=v_{0}^{2}-r_{0}^{2} \dot{q}_{0}^{2}\left(\frac{r}{r_{0}}\right)^{2(N-1)} $ | (9) |
并且可进一步推导出[16]:
| $ \sin \theta_{m}=\sin \theta_{m 0}\left(\frac{r}{r_{0}}\right)^{(N-1)} $ | (10) |
由式(10)可知,PPN在拦截固定目标时,导弹前置角会随弹目相对距离的减小而逐渐收敛至0,即导弹速度方向将逐渐收敛于视线方向。
对PPN还可进一步推导出[16]:
| $ \theta_{m}-\theta_{m 0}=(N-1)\left(q-q_{0}\right) $ | (11) |
于是可得
| $ \begin{aligned} q=&q_{0}+\frac{\theta_{m}-\theta_{m 0}}{N-1}= \\ &q_{0}+\frac{\sin ^{-1}\left[\sin \theta_{m 0}\left(r / r_{0}\right)^{N-1}\right]-\theta_{m 0}}{N-1} \end{aligned} $ | (12) |
由于式(10)已经表明了θm将随r减小而逐渐收敛至0,即θmf=0,因此由式(12)可知
| $ \varphi_{m f}=q_{f}+\theta_{m f}=q_{f}=q_{0}-\frac{\theta_{m 0}}{N-1} $ | (13) |
由式(13)可知,对拦截固定目标的情况,PPN的拦截碰撞角φmf由初始视线角q0、导弹初始前置角θm0和比例导引系数N所共同决定。
文献[16]所提出的2D-PPNIACG为:先选择合适的常值N,再构造合适的弹目初始几何关系,使导弹沿当前状态无控飞行,当弹目相对运动状态满足式(13)时即自动转入PPN制导,然后可获得想要的拦截碰撞角φmf。并且,在使用PPN进行拦截碰撞角约束制导的过程中,可以根据实时的q(t)、θm(t)情况,计算实时所需的比例导引系数,即
| $ N(t)=1+\frac{\theta_{m}(t)}{q(t)-q_{f}} $ | (14) |
式(14)将导致比例导引系数N的时变性。对其取变分可得
| $ |\delta N|=\frac{\left|\delta \theta_{m}\right|}{\left|q-q_{f}\right|}+\frac{\left|\theta_{m}\right|}{\left(q-q_{f}\right)^{2}}|\delta q| $ | (15) |
由于在导弹飞行过程中,在控制稳定的情况下,实际前置角、视线角和理论制导弹道之间的误差是很小的,因而所引起的N的变化也是很小的。根据式(15),当接近拦截终点时刻时,q趋近于qf,此时可将N固定,以避免奇异现象的发生。
2 拦截性能分析导弹在打击目标的飞行过程中,所关心的问题主要有:最大过载、能量消耗与捕获区域。
2.1 最大过载最大过载即为导弹在拦截飞行过程中可能出现的最大指令加速度。由式(6)可得
| $ \left|\boldsymbol{a}_{\mathrm{PPN}}\right|=N v_{m}|\dot{q}|=N v_{m}\left|\dot{q}_{0}\right|\left(\frac{r}{r_{0}}\right)^{(N-2)} $ | (16) |
意味着PPN指令加速度也会随着弹目距离的减小而逐渐降低至0,则其最大过载出现在初始时刻,即
| $ \left|\boldsymbol{a}_{\mathrm{PPN}}\right|_{\max }=N v_{m}\left|\dot{q}_{0}\right| $ | (17) |
在制导律分析中,通常可将指令加速度的积分(即导弹拦截所消耗的速度增量)作为导弹的能量消耗。
由式(16)可进一步计算出整个拦截过程中PPN所需的速度增量为
| $ \begin{aligned} |\Delta v|=& \int_{t_{0}}^{t_{f}}\left|\boldsymbol{a}_{\mathrm{PPN}}(t)\right| \mathrm{d} t=\int_{t_{0}}^{t_{f}} \frac{\left|\boldsymbol{a}_{\mathrm{PPN}}(t)\right|}{\dot{r}} \frac{\mathrm{d} r}{\mathrm{~d} t} \mathrm{~d} t=\\ &-\int_{r_{0}}^{0} \frac{N v_{m}\left|\dot{q}_{0}\right|\left(r / r_{0}\right)^{(N-2)}}{\sqrt{v_{0}^{2}-r_{0}^{2} \dot{q}_{0}^{2}\left(r / r_{0}\right)^{2(N-1)}}} \mathrm{d} r=\\ & \frac{N v_{m}\left|\theta_{0}\right|}{(N-1)} \end{aligned} $ | (18) |
可近似认为此即为导弹飞行的能量消耗。
2.3 捕获区域当导弹从某个特定的相对运动状态区域内出发时,如果可确保对目标的拦截捕获,则此初始相对运动状态区域即为捕获区域。
要使导弹实现对目标的打击,需要使弹目相对距离降低至0,且此时保证导弹朝着目标飞行,即弹目接近速度小于0,即
| $ r_{f}=0, \dot{r}_{f}<0 $ | (19) |
此即为捕获的定义[14]。将式(7)的自变量从时间t变成视线角q,即
| $ \dot{x}=\frac{\mathrm{d} x}{\mathrm{~d} t}=\frac{\mathrm{d} x}{\mathrm{~d} q} \frac{\mathrm{d} q}{\mathrm{~d} t}=x^{\prime} \dot{q} \Rightarrow x^{\prime}=\frac{\dot{x}}{\dot{q}} $ | (20) |
式中:x为任意因变量,上标“′”代表对q求导。则式(7)可以改写为
| $ \left\{\begin{array}{l} v_{r}^{\prime}-v_{\theta}=-N v_{\theta}, v_{r}(0)=\dot{r}_{0} \\ v_{\theta}^{\prime}+v_{r}=N v_{r}, v_{\theta}(0)=r_{0} \dot{q}_{0} \end{array}\right. $ | (21) |
再考虑:
| $ \bar{v}_{r}=\frac{v_{r}}{v_{m}}=\frac{v_{r}}{v_{0}}, \bar{v}_{\theta}=\frac{v_{\theta}}{v_{m}}=\frac{v_{\theta}}{v_{0}} $ | (22) |
可将式(21)无量纲化,即
| $ \left\{\begin{array}{l} \bar{v}_{r}^{\prime}-\bar{v}_{\theta}=-N \bar{v}_{\theta}, \bar{v}_{r}(0)=-\sin \psi_{0} \\ \bar{v}_{\theta}^{\prime}+\bar{v}_{r}=N \bar{v}_{r}, \bar{v}_{\theta}(0)=\cos \psi_{0} \end{array}\right. $ | (23) |
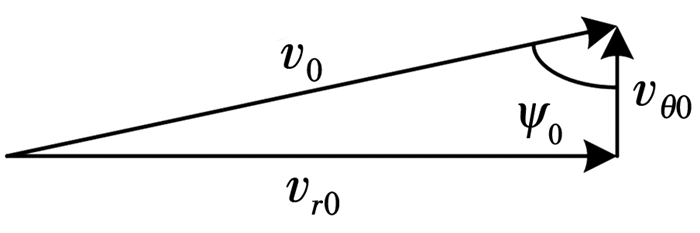
式中,ψ0=cos-1(vθ0/v0)=cos-1(vθ0/vm)为初始相对速度与初始视线的偏离程度,如图 2所示。
|
图 2 初始相对速度相对于初始视线的偏离程度 Fig. 2 Deviation of initial relative velocity with respect to initial line of sight (LOS) |
求解式(23)可得
| $ \left\{\begin{array}{l} \bar{v}_{r}(q)=-\sin \left(k q+\psi_{0}\right) \\ \bar{v}_{\theta}(q)=\cos \left(k q+\psi_{0}\right) \end{array}\right. $ | (24) |
式中,需满足k=N-1>0。由式(19)、(20)和式(22),捕获的定义可以转换为:
| $ \bar{v}_{r}\left(q_{f}\right)<0, \bar{v}_{\theta}\left(q_{f}\right)=0 $ | (25) |
式中,由vθ(qf)=0可推导出
| $ \cos \left(k q+\psi_{0}\right)=0 \Rightarrow q_{f}=\frac{1}{k}\left(\frac{\pi}{2}-\psi_{0}\right) $ | (26) |
将其代入式(24)的第1式,有
| $ \bar{v}_{r}(q)=-\sin \left(\frac{\pi}{2}\right)=-1<0 $ | (27) |
可知,只要满足N>1即k>0,则对固定目标,无论导弹从任何条件下出发,在不考虑最大过载约束的情况下,PPN都能实现对目标的拦截。
但是以上结论需排除一个特例,即θm0=-180°的情况,此时视线转率
在通常情况下,导弹经过中制导后,在末制导的初始时刻总是朝着目标飞行的,因此可以只考虑θm0∈(-90°, 90°)的情况。此时除了θm0=0的特殊情况外,视线转率均大于0,则PPN可拦上目标。而θm0=0等价于
如果考虑导弹过载限制,由式(2)的第2式和式(17),若需使其小于某最大值α,需使:
| $ N v_{m}\left|\dot{q}_{0}\right| \leqslant \alpha \Rightarrow\left|\dot{q}_{0}\right| \leqslant \frac{\alpha}{N v_{m}} \Leftrightarrow\left|\theta_{m 0}\right| \leqslant \sin ^{-1}\left(\frac{r_{0} \alpha}{N v_{m}^{2}}\right) $ | (28) |
式中,需满足N>2。式(28)即为以θm0表示的PPN对固定目标的捕获区域。可知,当导弹受到过载限制时,前置角不能过大,否则不能实现对固定目标的拦截。
3 基于PPN的拦截碰撞角约束制导策略三维制导律的经典设计方法是将三维相对运动在两个相互垂直的平面内进行解耦,分别设计二维制导律,然后再进行三维空间中的综合。
三维拦截几何如图 3所示。

|
图 3 基于经典垂直分解的三维拦截几何 Fig. 3 Three-dimensional engagement geometry based on classic orthogonal decomposition method |
图 4中,oI-xIyIzI为参考惯性系,oI-xsyszs为视线坐标系,oI-xvyvzv为导弹速度坐标系,qε为视线俯仰角、qβ为视线方位角,φ′m为俯仰前置角,ψ′m为偏航前置角,xvoIyv平面为俯冲平面,xvoIzv平面为转弯平面。
|
图 4 俯冲平面内的2D-PPNIACG Fig. 4 2D-PPNIACG in vertical plane |
导弹的控制力主要是气动升力和侧向力,其方向沿速度系的yv和zv方向。因此,可以认为导弹制导律的指令加速度为
| $ \boldsymbol{a}_{m}=a_{m y v} \boldsymbol{y}_{v}+a_{m zv} \boldsymbol{z}_{v} $ | (29) |
在小角假设下,对导弹在三维空间中的碰撞角约束制导,可将其解耦为俯冲平面内的落角约束制导和转弯平面内的碰撞角约束制导。
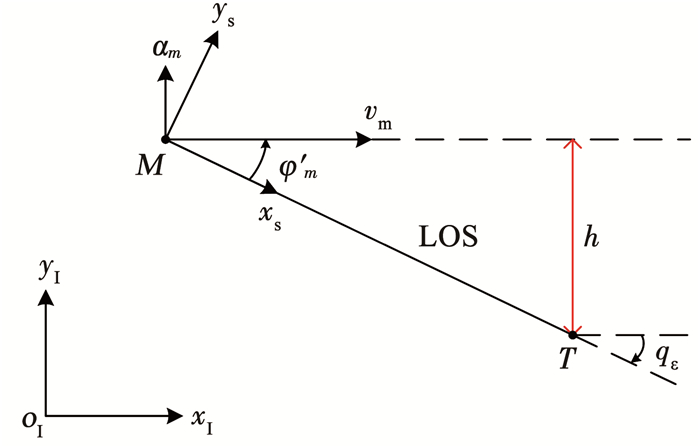
3.1 俯冲平面落角约束制导假设拦截过程中ψ′m总为较小值,可以近似认为俯冲平面xvoIyv和视线铅垂面xsoIys。此时俯冲平面内弹目空间几何的近似关系如图 4所示。
可使
| $ a_{m y v}=N_{y} v_{m} \dot{q}_{\varepsilon} $ | (30) |
并使用文献[16]中的2D-PPNIACG制导策略。
先使导弹在一定高度h下保持平飞,针对预设的比例导引系数Ny,有
| $ \tilde{q}_{\varepsilon f}(t)=q_{\varepsilon}(t)-\frac{\varphi_{m}^{\prime}(t)}{N_{y}-1} $ | (31) |
当
| $ \left|\tilde{q}_{\varepsilon f}(t)-q_{\varepsilon f}\right| \leqslant \delta_{\varepsilon} $ | (32) |
时,采用式(30)进行制导控制。式中,δε为设定的门限值。
为增强制导律的鲁棒性,可采用式(14)进行比例导引系数的实时更新,即
| $ N_{y}(t)=1+\frac{\varphi_{m}^{\prime}(t)}{q_{\varepsilon}(t)-q_{\varepsilon f}} $ | (33) |
导弹飞行过程中,为快速降低|
| $ a_{m y v}=a_{\max } \operatorname{sgn}\left[\tilde{q}_{\varepsilon f}(t)-q_{\varepsilon f}\right] $ | (34) |
如此即可实现落角约束制导,即
| $ \lim \limits_{t \rightarrow t_{f}} q_{\varepsilon}(t)=q_{\varepsilon f} $ | (35) |
式中tf为拦截终点时刻。
注意,在使用PPNIACG进行落角约束制导时,可使导弹初始时刻距离目标较远,使|qε0|较小。由图 4可知,在导弹平飞过程中,|qε|不断增大,相应φ′m也在不断增大。假设可以使导弹较远处向目标平飞,设qε0=-20°,并且限制在qε=-60°之前转入PPN。为保证制导控制系统的鲁棒性,通常取N=3~5时。此时根据式(31),可得落角可能的范围是-25°~-90°,可以满足一般落角约束控制的要求。
3.2 转弯平面碰撞角约束制导对转弯平面,可近似认为qε和φ′m均为较小值,则可认为xsoIx″平面与xIoIx′平面重合。
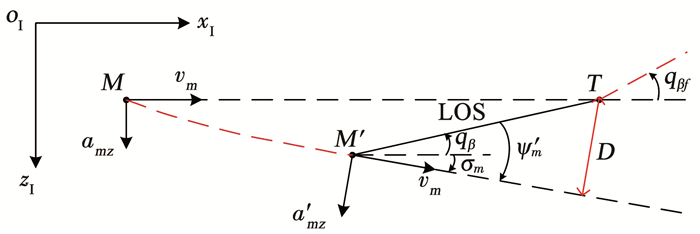
如图 5所示,不失一般性,假设初始时刻导弹向目标飞行,即
| $ q_{\beta}\left(t_{0}\right)=0, \psi_{m}^{\prime}\left(t_{0}\right)=0 $ | (36) |
|
图 5 转弯平面内的2D-PPNIACG Fig. 5 2D-PPNIACG in horizontal plane |
此时若直接使用PPN进行制导控制,则导弹将直接飞向目标,将有qβf(tf)=qβf。
因此可以首先采用最大过载或偏置比例导引(BPPN),使导弹产生一个较大的零控脱靶量D(类比于图 4中的飞行高度h),以获得产生碰撞角约束的可能性。
当导弹速度方向产生一定偏移,并因此产生一定的零控脱靶量D后,可使
| $ a_{m y z}=-N_{z} v_{m} \dot{q}_{\beta} $ | (37) |
针对预设的比例导引系数Nz,有
| $ \tilde{q}_{\beta f}(t)=q_{\beta}(t)-\frac{\psi_{m}^{\prime}(t)}{N_{z}-1} $ | (38) |
当
| $ \left|\tilde{q}_{\beta f}(t)-q_{\beta f}\right| \leqslant \delta_{\beta} $ | (39) |
时,采用式(37)进行制导控制。式中,δβ为设定的门限值。
为增强制导律的鲁棒性,可采用式(14)进行比例导引系数的实时更新,即
| $ N_{z}(t)=1+\frac{\psi_{m}^{\prime}(t)}{q_{\beta}(t)-q_{\beta f}} $ | (40) |
导弹飞行过程中,为快速降低|
| $ a_{m z v}=a_{\max } \operatorname{sgn}\left[q_{\beta f}-\tilde{q}_{\beta f}(t)\right] $ | (41) |
如此即可实现落角约束制导,即
| $ \lim \limits_{t \rightarrow t_{f}} q_{\beta}(t)=q_{\beta f} $ | (42) |
式中tf为拦截终点时刻。
4 仿真算例文献[16]通过与弹道成型制导律(TSG)[3]和一种最优碰撞角约束制导律(IACOG)[5]的仿真对比分析,已经验证了2D-PPNIACG的有效性和优越性。
本文通过数值仿真算例,验证3D-PPNIACG的有效性和可靠性。导弹与目标的初始运动状态见表 1。
| 表 1 初始弹目相对运动状态 Tab. 1 Initial status of missile with respect to target |
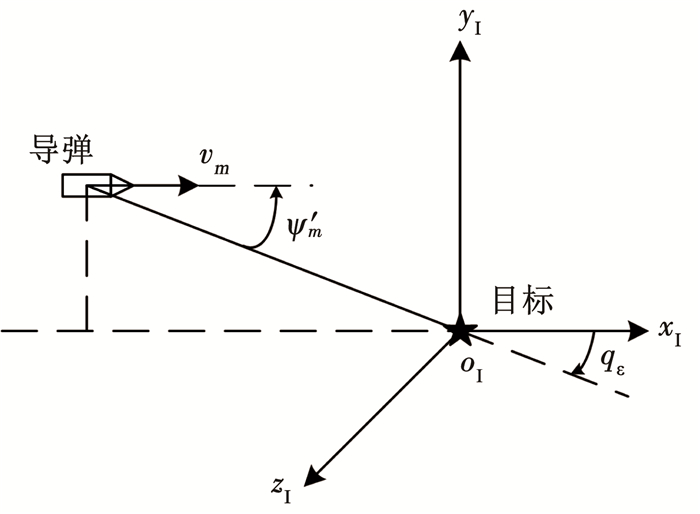
由表 1可知,初始俯仰前置角φ′m0=20°,初始偏航前置角ψ′m0=0°。初始时刻导弹朝目标平飞,如图 6所示。
|
图 6 初始时刻拦截几何 Fig. 6 Initial engagement geometry |
采用基于PPN的拦截碰撞角约束制导策略所给出的3D-PPNIACG对导弹进行制导控制。设俯冲平面内的落角约束为qεf=-90°,转弯平面内的碰撞角约束为qβf=60°。
对俯冲平面,设Ny=3,δε=5°;对转弯平面,同样设Nz=3,δβ=5°。
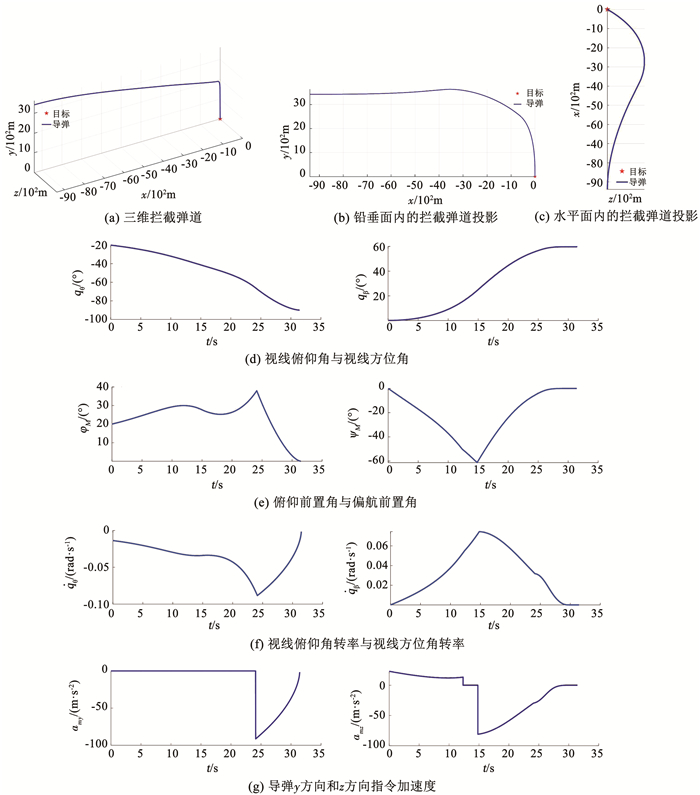
4.1 理想情况仿真结果首先不考虑导弹测量误差与执行机构响应延迟等干扰和影响因素。仿真结果如图 7所示。
|
图 7 理想情况仿真结果 Fig. 7 Simulation results under ideal condition |
由图 7(a)~图 7(c)可知,本文所设计的3D-PPNIACG可以实现俯冲平面的落角约束和转弯平面内的碰撞角约束,导弹的飞行弹道较为平滑。
由图 7(d)、图 7(e)可知,在导弹的俯冲和转弯平面内,前置角φ′m、ψ′m收敛至0,而视线角均收敛到了所设计终端约束值qεf=-90°和qβf=60°极小的领域内。由图 7(f)可知,在导弹飞行过程中,两个方向视线转率的绝对值总保持在0.1 rad/s内,并且在拦截末段视线转率逐渐降低至0附近。由图 7(g)可知,在俯冲平面内,导弹在y方向的加速度先为0,当弹目相对运动状态符合PPNIACG的拦截几何关系时,转入PPNIACG制导。此时导弹的加速度先达到某个最大值,然后逐渐降低至0。在转弯平面内,导弹先采用BPPN进行转弯;然后转为平飞;当弹目相对运动状态满足PPNIACG的拦截几何时,转入PPNIACG制导。此时导弹的加速度同样先达到某个最大值,然后逐渐降低至0。在制导过程中,导弹的最大过载都没有超过其饱和过载。
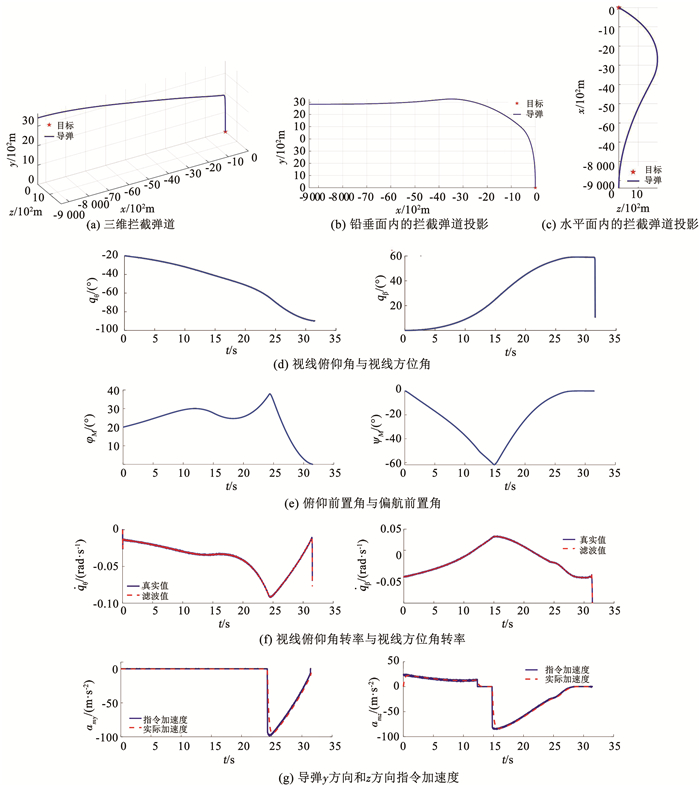
4.2 考虑现实影响因素的仿真结果在理想情况仿真条件的基础上,考虑视线转率测量误差为1×10-4 rad/s,将弹体执行机构响应延迟近似为一阶惯性环节,时间常数τ=0.2 s,设导弹y方向和z方向的饱和过载均为amax=100 m/s2,并且考虑当弹目相对距离小于50 m时,认为导弹导引头进入盲区,使制导指令切换为0,仿真结果如图 8所示。
|
图 8 现实干扰因素影响下的仿真结果 Fig. 8 Simulation results under realistic disturbances |
由图 8(a)~8(c)可知,在考虑现实影响因素的情况下,3D-PPNIACG也可以实现俯冲平面的落角约束和转弯平面内的碰撞角约束。
由图 8(d)可知,在存在测量误差、执行机构响应延迟、导引头盲区等现实干扰因素的情况下,视线俯仰角收敛到了所设计终端约束值qεf=-90°附近,视线方位角除最终时刻出现跳跃外,均位于qβf=60°附近。实际上,qβ在终端时刻的跳跃主要是由于相对距离进入导引头盲区后指令加速度切换为0导致的。
由图 8(e)可知,在导弹的俯冲和转弯平面内,前置角φ′m、ψ′m收敛至0。
由图 8(f)可知,在导弹飞行过程中,两个方向视线转率真实值和滤波值的绝对值总保持在0.1 rad/s内,并且在拦截末段视线转率逐渐降低至0附近。由于导引头盲区的影响,视线转率在终点时刻出现跳跃。
由图 8(g)可知,导弹在y方向的加速度先为0,当弹目相对运动状态符合PPNIACG的拦截几何关系时,转入PPNIACG制导。此时导弹加速度指令先达到某个最大值,然后逐渐降低至0。在转弯平面内,导弹先采用BPPN进行转弯;然后转为平飞;当弹目相对运动状态满足PPNIACG的拦截几何时,转入PPNIACG制导。此时导弹的加速度指令同样先达到某个最大值,然后逐渐降低至0。受一阶惯性环节的影响,导弹实际加速度稍微之后于指令加速度,其从0阶跃到最大值的过程趋于平缓。在实际的制导律应用过程中,导弹的姿控系统本身具有时滞性,同时可以使用滤波器对攻角指令进行平滑处理,并且对攻角指令的最大值施加限制,因而对于在转入PPN制导时,所产生的突然的加速度指令阶跃并不会对导弹的控制稳定产生较大影响。值得注意的是,可以根据式(17)对导弹可能产生的最大过载进行设计和估计,从而避免过载饱和现象的出现。在本仿真算例中,导弹的最大过载就没有超过其饱和过载。
仿真所得导弹脱靶量为0.005 6 m,俯冲平面内的落角偏差为-1.570 8°,转弯平面内的碰撞角偏差在终端跳跃前为1.047 2°。可知本文所提出的3D-PPNIACG在考虑现实干扰因素的影响下,对固定目标的碰撞角约束打击仍然具有较好的拦截制导性能。
5 结论1) 本文基于纯比例导引律(PPN)对固定目标的解析解,深入分析了基于纯比例导引的二维碰撞角约束制导律(2D-PPNIACG)的拦截制导性能,包括最大过载、能量消耗与捕获区域。
2) 进一步基于小角假设和三维拦截制导的垂直分解方法,提出了基于纯比例导引的三维碰撞角约束制导律(3D-PPNIACG),对固定目标可同时实现俯冲平面内的落角约束打击和转弯平面内的碰撞角约束打击。
3) 通过对数值仿真算例的分析可知,无论在理想情况下,还是在考虑测量误差、执行机构响应延迟、导引头盲区等现实干扰因素的情况下,3D-PPNIACG对固定目标都具有良好的拦截制导性能。
4) 本文所提出的3D-PPNIACG基于经典的PPN制导律,不需要估计剩余飞行时间等状态变量,其结构简单、易于实现、鲁棒性好,因而具有良好的应用前景。
| [1] |
HAN Tuo, HU Qinglei, XIN Ming. Analytical solution of field-of-view limited guidance with constrained impact and capturability analysis[J]. Aerospace Science and Technology, 2020, 97: 105586. DOI:10.1016/j.ast.2019.105586 |
| [2] |
KIM B S, LEE J G, HAN H S. Biased PNG law for impact with angular constraint[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 277. DOI:10.1109/7.640285 |
| [3] |
ZARCHAN P. Tactical and strategic missile guidance[M]. Reston: AIAA, 2012: 569.
|
| [4] |
陈克俊, 赵汉元. 一种适用于攻击地面固定目标的最优再人机动制导律[J]. 宇航学报, 1994, 15(1): 1. CHEN Kejun, ZHAO Hanyuan. An optimal reentry maneuver guidance law applying to attack the ground fixed target[J]. Journal of Astronautics, 1994, 15(1): 1. |
| [5] |
HE Shaoming, LEE C H. Optimality of error dynamics in missile guidance problems[J]. Journal of Guidance, Control, and Dynamics, 2018, 41(7): 1620. DOI:10.2514/1.G003343 |
| [6] |
HE Shaoming, LIN Defu, WANG Jiang. Integral global sliding mode guidance for impact angle control[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(4): 1843. DOI:10.1109/TAES.2018.2876588 |
| [7] |
YE Qing, LIU Chunsheng, SUN Jingliang. A backstepping-based guidance law for an exoatmospheric missile with impact angle constraint[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(2): 547. DOI:10.1109/TAES.2018.2852419 |
| [8] |
WANG Xianghua, TAN C P, ZHOU Donghua. Observer-based PIGC for missiles with impact angle constraint[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(5): 2226. DOI:10.1109/TAES.2018.2883878 |
| [9] |
CHEN Xiaotian, WANG Jinzhi. Sliding-mode guidance for simultaneous control of impact time and angle[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(2): 394. DOI:10.2514/1.G003893 |
| [10] |
KANG Shen, TEKIN R, HOLZAPFEL F. Generalized impact time and angle control via look-angle shaping[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(3): 695. DOI:10.2514/1.G003765 |
| [11] |
LU Ping, DOMAN D B, SCHIERMAN J D. Adaptive terminal guidance for hypervelocity impact in specified direction[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2): 269. DOI:10.2514/1.14367 |
| [12] |
胡正东, 曹渊, 蔡洪. 一种打击地面固定目标的自适应比例导引律[J]. 系统仿真学报, 2009, 21(13): 4084. HU Zhengdong, CAO Yuan, CAI Hong. Adaptive proportional guidance law for ground stationary target[J]. Journal of System Simulation, 2009, 21(13): 4084. DOI:10.16182/j.cnki.joss.2009.13.069 |
| [13] |
SHNEYDOR N A. Missile guidance and pursuit: Kinematics, dynamics, and control[M]. Cambridge: Woodhead Publishing, 1998: 109.
|
| [14] |
YANG C D, YANG C C. A unified approach to proportional navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(2): 557. DOI:10.1109/7.575895 |
| [15] |
YUAN P J, CHERN J S. Ideal proportional navigation[J]. Journal of Guidance, Control, and Dynamics, 1992, 15(5): 1161. DOI:10.2514/3.20964 |
| [16] |
黎克波, 廖选平, 梁彦刚, 等. 基于纯比例导引的拦截碰撞角约束制导策略[J]. 航空学报, 2020, 41(S2): 724277. LI Kebo, LIAO Xuanping, LIANG Yangang, et al. Guidance strategy with impact angle constraint based on pure proportional navigation[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(S2): 724277. DOI:10.7527/S1000-6893.2020.24277 |
 2021, Vol. 53
2021, Vol. 53


